Abstract
Weighted k-nearest neighbor (WKNN)-based Wi-Fi fingerprinting is popular in indoor location-based services due to its ease of implementation and low computational cost. KNN-based methods rely on distance metrics to select the nearest neighbors. However, traditional metrics often fail to capture the complexity of indoor environments and have limitations in identifying non-linear relationships. To address these issues, we propose a novel WKNN-based Wi-Fi fingerprinting method that incorporates distance metric learning. In the offline phase, our method utilizes a Siamese network with a triplet loss function to learn a meaningful distance metric from training fingerprints (FPs). This process employs a unique triplet mining strategy to handle the inherent noise in FPs. Subsequently, in the online phase, the learned metric is used to calculate the embedding distance, followed by a signal-space distance filtering step to optimally select neighbors and estimate the user’s location. The filtering step mitigates issues from an overfitted distance metric influenced by hard triplets, which could lead to incorrect neighbor selection. We evaluate the proposed method on three benchmark datasets, UJIIndoorLoc, Tampere, and UTSIndoorLoc, and compare it with four WKNN models. The results show a mean positioning error reduction of 3.55% on UJIIndoorLoc, 16.21% on Tampere, and 16.49% on UTSIndoorLoc, demonstrating enhanced positioning accuracy.
1. Introduction
Due to the limitations of Global Navigation Satellite Systems (GNSSs) in indoor environments, such as signal blockage and attenuation, alternative positioning technologies for indoor location-based services (LBSs) have gained significant attention. Wi-Fi fingerprinting has become a popular choice for indoor positioning due to the widespread Wi-Fi infrastructure, with wireless access points (WAPs) commonly installed for wireless LAN, and the prevalence of mobile devices equipped with Wi-Fi networking capabilities.
Wi-Fi fingerprinting relies on unique signal patterns, or “fingerprints”, generated by WAPs to estimate the position of a device based on received signal strength indicators (RSSIs) [1]. This method is widely applicable since most mobile devices can measure RSSIs. It consists of two phases: the offline phase, where Wi-Fi fingerprints (FPs) are collected at specific reference points (RPs) to construct a radio map, and the online phase, where the user’s current FP is matched against this map to estimate their position. Various machine learning (ML) techniques are used in this mapping process.
Machine learning and deep learning techniques have been extensively explored for Wi-Fi fingerprinting-based indoor localization. Traditional machine learning methods, such as K-nearest neighbors (KNN) [2,3,4,5], support vector machines (SVMs) [6,7,8], and random forests (RFs) [9,10,11], have been applied to fingerprinting. Recent developments in deep learning models, such as multi-layer perceptrons (MLPs) with autoencoders [12,13], convolutional neural networks (CNNs) [14], and recurrent neural networks (RNNs) [13], have demonstrated the potential to capture complex, non-linear relationships in RSSI data. However, these advanced models often require large-scale labeled datasets and intensive training.
Among the various machine learning techniques used for Wi-Fi fingerprinting, KNN and its variants remain widely used due to their simplicity, ease of implementation, and low computational cost [2,3,4,5]. Unlike deep learning models, which involve complex training and require extensive datasets, KNN-based methods can be readily deployed in environments where collecting large-scale labeled data is challenging. KNN directly uses the similarities between the current fingerprint and pre-collected reference fingerprints for positioning, making it inherently aligned with the nature of Wi-Fi fingerprinting. Weighted KNN (WKNN), which assigns higher weights to closer neighbors, further refines position estimation, increasing its accuracy [4]. Advanced WKNN methods, such as SAWKNN [15] and APD-WKNN [16], address specific challenges by dynamically adjusting k based on signal strength or introducing new distance metrics to enhance neighbor selection. To further improve the performance of Wi-Fi fingerprinting, various data-driven approaches have been proposed, including dataset preprocessing [17], the integration of trajectory or historical data [18,19], and the measurement of RSSIs over time using techniques such as pedestrian dead reckoning (PDR) [20].
Despite these advancements, the accuracy of KNN-based methods continues to depend heavily on the choice of distance metric, which is used to identify the nearest neighbors. Traditional metrics such as Euclidean and Manhattan distances [2,3,4,5,15] often fail to capture the complexity of indoor environments, leading to suboptimal accuracy. While methods like APD-WKNN introduce handcrafted metrics, they are still limited by the inability to fully capture the non-linear relationships in the Wi-Fi signal space.
To overcome these limitations, we propose a novel WKNN-based Wi-Fi fingerprinting method utilizing distance metric learning. Our method employs a Siamese network with triplet loss [21] to learn an effective distance metric for fingerprint positioning. The network uses an MLP architecture with fully connected layers, dropout, and L2 normalization of the embeddings. To enhance the learning process, we introduce a triplet mining method to select meaningful triplets. Additionally, to handle the inherent noise in fingerprints caused by fluctuations in RSSIs, we integrate the learned distance metric with signal-space distance for improved neighbor selection.
The main contributions of our work are summarized as follows:
- We have designed a distance metric learning method for Wi-Fi fingerprint positioning using a Siamese network with triplet loss and an MLP architecture, including a novel triplet mining technique.
- We propose a WKNN-based positioning method that combines the learned distance metric with signal-space distance to address noise in fingerprints due to RSSI fluctuations.
- We conducted extensive performance evaluations on the UJIIndoorLoc [22], Tampere [23], and UTSIndoorLoc [14] datasets, demonstrating the superiority of our method over existing baselines such as WKNN with inverse distance weighting (IDW) using Euclidean [3] and Manhattan distances [5], SAWKNN [15], and APD-WKNN [16].
The remainder of this paper is organized as follows. Section 2 reviews prior research on Wi-Fi-based indoor localization and distance metric learning. Section 3 introduces an overview of the proposed method. Section 4 details the architecture of the Siamese network and triplet mining strategies. Section 5 provides a description of the online phase for WKNN-based positioning using a learned distance metric, along with a filtering step using signal-space distance to handle incorrect neighbor selection. Section 6 presents an extensive performance evaluation comparing our approach against baselines. Following this, Section 7 discusses the sensitivity of the hyperparameters, the real-time applicability, and the limitations of the proposed method. Finally, Section 8 concludes the paper with a summary.
2. Related Work
2.1. Wi-Fi-Based Indoor Localization
Wi-Fi-based indoor localization has emerged as a widely used framework for enabling LBSs. This popularity stems from the existing Wi-Fi infrastructure, where WAPs deployed for wireless local area networks (WLANs) can be leveraged for localization without requiring additional hardware installation. Wi-Fi-based indoor positioning systems utilize these pre-existing networks, reducing deployment costs and simplifying implementation. Approaches to Wi-Fi-based indoor localization are generally categorized into two types: geometric mapping and fingerprinting.
Geometric mapping methods rely on measurements such as time of arrival (ToA) [24,25,26] and angle of arrival (AoA) [24,27,28,29] to estimate a device’s position. Time of arrival (ToA) represents the time at which a signal reaches the receiver and is used to calculate the distance between the device and the receiver based on this measurement. This estimated distance is then applied to estimate the device’s location through trilateration. However, due to the limited bandwidth of Wi-Fi signals (typically between 20 and 160 MHz), ToA-based distance estimation has low resolution, leading to decreased accuracy. To mitigate this, some methods [25,26] employ virtual bandwidth to improve ToA accuracy. However, these methods require precise time synchronization across all APs or rely on channel hopping, which disrupts regular data communication.
AoA-based methods utilize multiple antennas and array signal processing techniques to analyze the phase differences between antennas to calculate the angle of arrival, and this value is then used for triangulation to estimate the user’s location. As demonstrated by SpotFi [24], employing parametric algorithms such as MUSIC [30] can further enhance the precision of angle estimation. These methods are effective under ideal conditions. However, they require specialized hardware, as in some AoA-based methods [27,28]. Additionally, they are vulnerable to coherent signals, which can lead to decreased accuracy in complex indoor environments. In contrast, fingerprinting-based approaches are data-driven, predicting the user’s location in an online phase using signal patterns collected during an offline phase. These techniques do not require specialized hardware, instead leveraging pre-existing Wi-Fi signal data to perform localization.
Fingerprinting-based approaches have gained popularity due to their practicality and ease of deployment. They require only standard signal strength measurements, such as RSSIs, which are accessible on most Wi-Fi-enabled devices. This makes fingerprinting adaptable to a wide range of indoor environments without the need for expensive or specialized infrastructure.
Wi-Fi fingerprinting operates in two phases: an offline phase and an online phase. During the offline phase, RSSI measurements are collected from multiple WAPs at predefined RPs, creating a radio map that links signal patterns to known locations. In the online phase, the user’s device collects RSSI measurements from its environment, which are matched against the radio map to estimate the user’s position.
A variety of machine learning algorithms are commonly employed to enhance positioning accuracy. SVM-based positioning methods [6,7,8] utilize Wi-Fi signals or RSSI data to learn distinctive, location-specific signal patterns, constructing hyperplanes to separate and classify these locations. However, SVM-based methods can face limitations with slower training and prediction times in large or high-dimensional datasets. RF-based methods [9,10,11] use multiple decision trees to handle large-scale fingerprint datasets effectively. However, RF-based methods require significant computational resources, especially during the training phase. Recent studies have explored artificial neural networks (ANNs), where MLPs with autoencoders, CNNs, and RNNs model complex and sequential patterns in RSSI data, offering enhanced positioning accuracy and flexibility [12,13,14]. While each approach provides unique advantages, challenges such as high computational costs and parameter tuning remain, particularly in large-scale environments.
KNN and its variants remain particularly attractive for Wi-Fi fingerprinting, not only because of their simplicity and ease of implementation but also due to their low computational cost and ability to handle small datasets effectively [2,3,4,5]. KNN-based methods estimate a user’s location by identifying the k-nearest RPs based on the similarity between the query fingerprint (RSSI vector) and the fingerprints stored in the radio map [2]. In the KNN positioning algorithm, this similarity is measured by calculating the distance between the RSSI vector of the target location and the radio map, and methods based on Euclidean distance [2,3] and Manhattan distance [4,5] have been studied. The distance metrics between the target location and each stored fingerprint are calculated and ranked in ascending order, with the k closest RPs being selected. The average coordinates of these k-nearest RPs, whose RSSI values most closely match the query fingerprint, are then used as the estimated position of the target location. Weighted KNN (WKNN) enhances the positioning process by assigning weights to neighbors based on their distance, giving closer reference points greater influence on the position estimation [4]. This approach takes into account the varying impact of each reference point on the final location estimate, using a weighted average of the coordinates to improve positioning accuracy.
Advanced KNN-based variants, such as SAWKNN [15] and APD-WKNN [16], have been developed to address specific challenges. One issue with traditional WKNN methods, which use a fixed k value, is that they may experience performance degradation when the optimal k value varies depending on location. Thus, SAWKNN was proposed as a method for dynamically adjusting the k value according to the environment. APD-WKNN addresses the limitations of traditional distance metrics, which do not accurately reflect physical distance. Due to the indoor signal propagation path and RSSI attenuation, RSSI and positional information do not follow a simple linear relationship. Therefore, APD-WKNN uses an independently developed approximate position distance (APD), which balances the RSSI and signal propagation distance differences according to the spatial signal attenuation law, enabling a more accurate selection of RPs. While SAWKNN and APD-WKNN provide improvements over traditional KNN in terms of accuracy, they still rely on manually crafted distance metrics. As a result, the configured distance metric fails to accurately reflect physical distance and fingerprint similarity [31].
Various approaches have been explored to enhance the performance of WKNN-based Wi-Fi fingerprinting, including dataset preprocessing [17], the integration of user trajectory or historical data [18,19], or the measurement of RSSIs over a period using PDR techniques [20]. Hou et al. [17] employed robust principal component analysis (RPCA) with an adaptive k-selection using the Jenks natural breaks algorithm (JNBA) to improve noise filtering. However, Hou et al.’s method [17] requires multiple RSSI samples obtained through repeated scans to perform RPCA. Leng et al. [18] introduced a fusion of Euclidean and cosine distances to improve robustness to device heterogeneity, with an adaptive k-selection strategy based on trajectory data. However, this approach requires a Kalman filter, which relies on time-series data, necessitating multiple scans over time. Zhang et al. [19] enhanced accuracy by adapting the number of selected RPs based on historical trajectory information. This approach, however, relies on Wi-Fi fingerprint data from the user’s historical trajectory. Poulose et al. [20] used a sensor fusion framework combining IMU-based PDR with Wi-Fi RSSI data, requiring user movement for accurate position estimation.
Additionally, Narasimman et al. [32] focused on data adaptation by normalizing labels across different buildings and using only the strongest AP signals. This study was primarily concerned with data adaptation rather than accuracy improvement, placing it outside the primary scope of our work.
Our proposed method specifically targets WKNN-based instant positioning, where positioning is achieved using only the RSSI values from APs at a given location through a single Wi-Fi scan for high usability. This approach is designed with two primary conditions in mind: (1) positioning should be achievable with a single scan, without requiring multiple scans over time, which excludes the use of time-series data; (2) instant positioning should not rely on user movement to obtain location estimates, as our goal is to provide a system with high usability and rapid response times. However, the methods in [17,18,19,20] cannot meet these requirements, as they require either multiple Wi-Fi scans or user movement, making them unsuitable for instant positioning applications.
In contrast to APD-WKNN, which estimates physical distance based on a signal propagation model, our approach leverages distance metric learning to directly learn the physical distance relationships between reference points. This allows the model to better capture the underlying spatial structure of the environment, resulting in improved positioning accuracy.
2.2. Distance Metric Learning
Distance metric learning is a machine learning technique that aims to learn a distance function tailored to a specific task or dataset. Unlike traditional distance metrics, such as Euclidean or Manhattan distances, which measure distances in a fixed manner, distance metric learning adapts the metric based on the underlying data distribution. The goal is to learn a distance function that places similar data points closer together and dissimilar points farther apart in the feature space. This approach has proven effective in applications such as face recognition [21], image retrieval, and text classification, where relationships between data points are complex and non-linear.
In our work, we apply distance metric learning to Wi-Fi fingerprinting-based indoor localization. We employ a Siamese network with triplet loss [21] to learn a specialized distance metric for fingerprint data. This network takes pairs of RSSI fingerprints from different RPs as input and learns an embedding space where the fingerprints from the same or nearby locations are positioned closer together, while those from different locations are placed farther apart. The learned distance metric improves neighbor selection in the KNN algorithm, ensuring that only the most relevant RPs are considered for position estimation. To address the inherent noise in RSS measurements, we combine the learned distance metric with signal-space distance. This hybrid approach enhances the robustness of neighbor selection, improving the adaptability and accuracy of our method, particularly in complex indoor environments with fluctuating signals and multipath effects.
3. Overview of the Proposed Method
Figure 1 illustrates our Wi-Fi fingerprinting method, which consists of two main components: distance metric learning and WKNN-based positioning. Distance metric learning aims to create a better representation of Wi-Fi fingerprints, while WKNN-based positioning leverages these learned metrics to enhance location estimation.
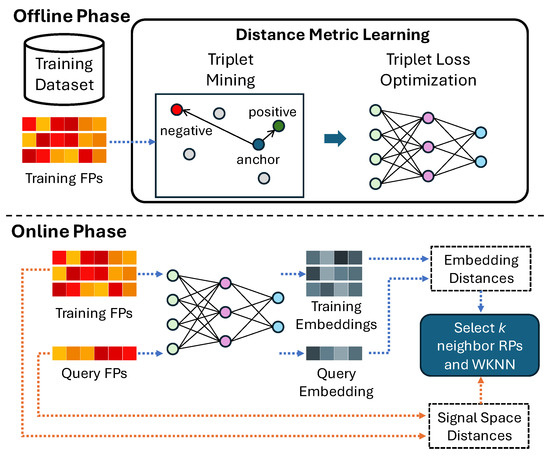
Figure 1.
Overview of our proposed method.
In the offline phase, a Siamese network with a triplet loss function is employed to learn a meaningful distance metric from the training FPs. Triplet mining is used during training to select informative triplets—sets of anchor, positive, and negative samples—ensuring that the model learns the effective separation between similar and dissimilar fingerprints. The model is optimized by minimizing the triplet loss to improve its ability to distinguish between nearby and distant locations in the embedding space.
In the online phase, the learned distance metrics are utilized for WKNN-based positioning. However, relying solely on these metrics can lead to incorrect neighbor selection due to noisy fingerprint data. To address this, we introduce an additional filtering step using signal-space distance, which considers only the observed WAPs in each fingerprint. This step ensures that the most relevant neighbors are selected, enhancing the accuracy of the position estimation. With these refined neighbors, the WKNN algorithm is performed to determine the device’s location.
In the following sections, we provide a detailed explanation of each component, highlighting how they contribute to improving positioning accuracy.
4. Distance Metric Learning for Wi-Fi Fingerprint
This section details the distance metric learning process used in our Wi-Fi fingerprinting method. In traditional Wi-Fi fingerprinting, simple distance metrics such as Euclidean distance often fail to capture the complex relationships between fingerprints due to RSSI fluctuations and environmental noise. Our method addresses these limitations by employing a Siamese network architecture and a triplet mining strategy to learn a robust and adaptable distance metric.
4.1. Network Architecture
Figure 2 illustrates our Siamese network, which is structured as an MLP with fully connected (FC) layers and dropout layers to prevent overfitting. The MLP uses ReLU activation functions to capture the non-linear patterns inherent in Wi-Fi fingerprint data. Dropout is applied between the layers to reduce overfitting and improve generalization.
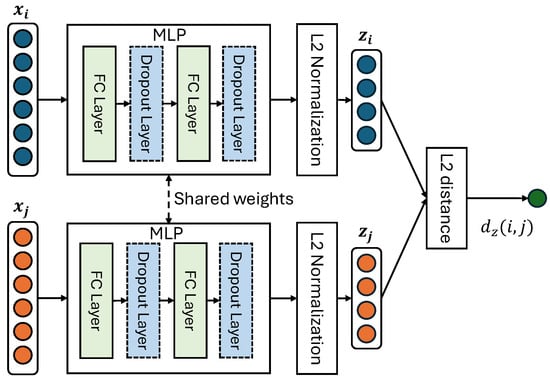
Figure 2.
The Siamese network for distance metric learning. The network learns an embedding space where similar fingerprints are positioned closer together.
Our training dataset consists of various FPs collected from different environments. Before they are fed into the network, the RSSI values are min-max normalized based on the observed Wi-Fi RSSI range in the dataset. Any missing values in the FPs are replaced with the minimum RSSI value to maintain uniform input dimensions.
Let represent the min-max-normalized vector of the fingerprint for the i-th RP, where is the RSSI of the k-th WAP at the i-th RP. The normalized input vector is then fed into the MLP to produce an embedding . L2 normalization is applied to the embeddings to ensure that all vectors lie on the unit hypersphere, which stabilizes the learning process by fixing the scale of the embeddings. The distance between two fingerprints is computed as the Euclidean distance between their embeddings:
4.2. Triplet Mining and Triplet Loss
Training the network involves defining triplets consisting of an anchor, a positive, and a negative based on their positional distances (see Figure 3a). An RP is classified as a positive if its position distance from the anchor is less than a threshold ; otherwise, it is classified as a negative. In multi-building, multi-floor environments, additional constraints are applied: the positive must be from the same building and floor as the anchor.
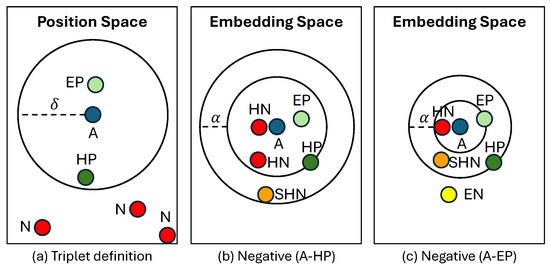
Figure 3.
Triplets in the position space and embedding space (A: anchor; N: negative; EP: easy positive; HP: hard positive; EN: easy negative; SHN: semi-hard negative; HN: hard negative).
The triplet loss function, which guides the training process, is defined as follows:
where is the set of triplets, and is a margin parameter. This loss function encourages the embedding distance between the anchor and the positive () to be smaller than the distance between the anchor and the negative () by at least . Intuitively, this creates an embedding space where fingerprints from nearby locations are positioned closer together, while those from distant locations are separated. This separation improves the accuracy of positioning in the online phase.
To construct the set in (2), we use a two-step triplet mining strategy designed to handle the inherent noise in Wi-Fi RSSI data:
- Online Triplet Mining: We divide the RPs in the training dataset into batches and dynamically mine triplets within each batch during training. This strategy ensures that meaningful triplets are dynamically selected as the model learns.
- Easy Positive and Semi-Hard Negative Mining: For each anchor, we select the closest positive in the embedding space, reducing the variance caused by noisy positives. Then, for each anchor–positive pair, we choose semi-hard negatives that satisfy . This approach avoids overly hard triplets, which can lead to overfitting and suboptimal model performance. Figure 3b,c illustrate the effects of selecting easy positives to stabilize the training process by reducing the number of challenging hard negatives.
Algorithm 1 provides a detailed methodology for selecting triplets during training. The algorithm takes each RP index within the batch B as input. Initially, the triplet set T is defined as an empty set. For each anchor a within the batch B, the following steps are performed: To reduce variance caused by noisy positives, the easy positive that is closest to the anchor a is selected such that the distance is minimized. Next, to avoid overly hard triplets, a semi-hard negative sample n is selected that satisfies (where is a margin parameter). The chosen positive sample p, negative sample n, and anchor a are then used to form a triplet , which is added to the triplet set T. The algorithm repeats this process for each anchor a in the batch B and outputs the set of triplets T.
| Algorithm 1 Triplet mining algorithm. |
| Input: Batch Output: Triplet set for each anchor a in do end for |
In summary, our distance metric learning process employs a Siamese network with a carefully designed triplet mining strategy to handle the complexity and variability of Wi-Fi fingerprints. This process creates an embedding space that reflects the true spatial relationships among RPs. The next section will describe how the learned distance metric is integrated into the WKNN-based positioning method to improve location estimation accuracy.
5. Proposed WKNN-Based Positioning Method
In this section, we present our WKNN-based positioning method, which uses inverse distance weighting (IDW) to enhance the accuracy of location estimation. The IDW approach assigns higher weights to closer neighbors, thereby reducing the impact of distant, less relevant RPs. However, selecting improper neighbors remains a challenge due to the noise in Wi-Fi fingerprints. To address this, we introduce a filtering process using a signal-space distance metric.
For a query FP, denoted by , let represent the k selected neighbors, the embedding distance between the FP at the i-th RP and the query FP, the position label of the i-th RP, and the estimated position. The position estimate is given by
In Equation (3), is the estimated position of the query FP, and represents the position of the i-th RP. The term acts as the weight, giving higher influence to RPs with smaller embedding distances. This weighting mechanism helps to enhance the accuracy of the position estimation by prioritizing the most relevant neighbors.
To address the inclusion of improper neighbors when selecting RPs with the k smallest for , we further filter the neighbors using the signal-space distance. The signal-space distance metric accounts for unobserved WAPs in the fingerprints, making it more robust to incomplete or noisy data. It is defined as the Euclidean distance on the sub-vector where the query FP has observed RSSI values:
where is the RSSI from the k-th WAP for the query FP.
The neighbor selection process is as follows. We introduce integer parameters M and k to control the selection process. First, we select M RPs that have the M smallest among all RPs in the training dataset. Then, from these M RPs, we select the k RPs with the smallest . These selected RPs form , and the position is then computed using (3).
6. Performance Evaluation
In this section, we evaluate the performance of our proposed WKNN-based positioning method using three publicly available datasets. The evaluation aims to compare the accuracy and robustness of our method against several baseline algorithms, including Euclidean WKNN (Euc-WKNN) [3], Manhattan WKNN (Man-WKNN) [5], SAWKNN [15], and APD-WKNN [16], across varying indoor environments. We examine several performance metrics to provide a thorough analysis of positioning accuracy.
6.1. Experimental Setup
To evaluate the effectiveness of our method in practical scenarios, we use three public datasets: UJIIndoorLoc [22], Tampere [23], and UTSIndoorLoc [14]. Table 1 presents the key characteristics of these datasets. Each dataset offers a comprehensive evaluation environment that encompasses spatial variations as well as diversity in users and devices. In our experiments, each dataset is preprocessed to normalize the RSSI values and handle missing entries by substituting them with a minimum RSSI value.

Table 1.
Key characteristics of the three datasets.
We compare our method with Euc-WKNN [3], Man-WKNN [5], SAWKNN [15], and APD-WKNN [16], as they represent a range of commonly used techniques in Wi-Fi fingerprinting. Euc-WKNN and Man-WKNN use in (3) as the Euclidean and Manhattan distances for FPs, respectively. SAWKNN and APD-WKNN incorporate adaptive weighting strategies to enhance accuracy. This selection provides a diverse set of benchmarks for assessing the efficacy of our method.
We conducted a grid search to optimize the hyperparameters, exploring various combinations to identify the best configuration for our model. The grid settings for hyperparameters are listed in Table 2. The search covered multiple learning rates, batch sizes, dropout rates, hidden layer dimensions, and distance thresholds. The optimal hyperparameters, as determined by the grid search, are presented in Table 3.

Table 2.
Grid settings for hyperparameter optimization.

Table 3.
Hyperparameters for our method.
For a fair comparison, we conducted a grid search to optimize the hyperparameters of the baseline models. The grid search ranges for each method are as follows: Euc-WKNN: k from 1 to 20; Man-WKNN: k from 1 to 20; SAWKNN: from 0.05 to 0.75 in increments of 0.05; and APD-WKNN: k from 3 to 8 and C from 3 to 20. The final parameters used to obtain the experimental results are presented in Table 4.

Table 4.
The hyperparameters for the baseline methods.
6.2. Experimental Results
Positioning error statistics are compared in Table 5. Our proposed WKNN-based method consistently achieves lower mean errors compared to all baseline methods across the three datasets. The most significant improvement is observed in the UJI dataset, where our method reduces the mean error by up to 34.77% compared to Man-WKNN. On the Tampere dataset, the mean error reduction is 23.51% compared to Euc-WKNN. These results demonstrate the robustness of our method in diverse indoor environments.

Table 5.
Comparison of positioning error statistics.
Figure 4, Figure 5 and Figure 6 illustrate the cumulative distribution function (CDF) of positioning errors for each method across the three datasets.
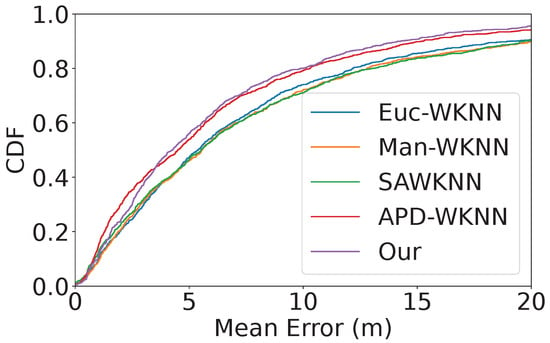
Figure 4.
Cumulative distribution function of positioning errors with UJIIndoorLoc.
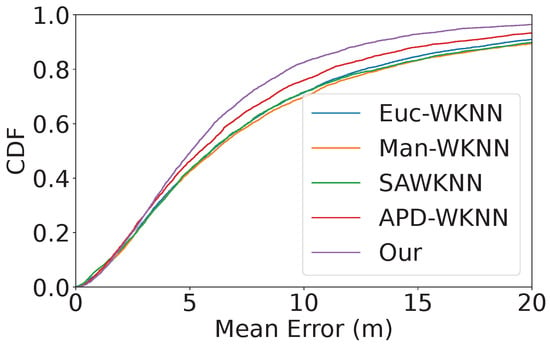
Figure 5.
Cumulative distribution function of positioning errors with Tampere.
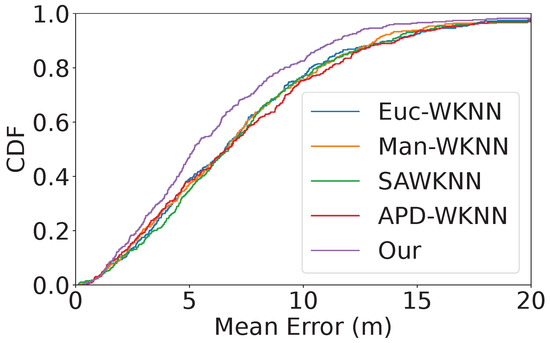
Figure 6.
Cumulative distribution function of positioning errors with UTSIndoorLoc.
For the UJIIndoorLoc dataset, our method achieves the lowest mean error of 6.53 m, outperforming APD-WKNN at 6.77 m. In contrast, SAWKNN, Man-WKNN, and Euc-WKNN exhibit higher mean errors, with Euc-WKNN reaching 8.68 m. The median error for our method is 4.26 m, indicating consistent performance across the majority of predictions. This is an improvement over APD-WKNN, which has a median error of 4.50 m. At the 90th percentile, our method demonstrates better robustness to outliers with an error of 14.26 m, compared to APD-WKNN’s 15.21 m and SAWKNN’s 19.69 m.
For the Tampere dataset, our method achieves a mean error of 6.67 m, significantly improving upon APD-WKNN at 7.96 m and Euclidean WKNN at 8.71 m. The median error is also the lowest among the methods, with our approach recording 5.05 m, compared to SAWKNN’s 5.93 m and APD-WKNN’s 5.47 m. At the 90th percentile, our method shows superior resilience against large errors, with an error of 13.10 m, outperforming APD-WKNN at 16.57 m and Euclidean WKNN at 19.02 m.
For the UTSIndoorLoc dataset, our method again achieves the best performance, with a mean error of 6.28 m, compared to Euc-WKNN at 7.38 m and SAWKNN at 7.51 m. The median error for our method is 5.20 m, providing more consistent predictions than APD-WKNN at 6.61 m and SAWKNN at 6.72 m. In terms of the 90th percentile error, our method achieves 11.35 m, outperforming APD-WKNN at 14.09 m and Euc-WKNN at 13.82 m, indicating excellent robustness in minimizing extreme errors.
Across all three datasets, our proposed method consistently achieves the lowest mean, median, and 90th percentile error, demonstrating superior performance over the baseline methods. The improvements are particularly evident in the 90th percentile error, highlighting the robustness of our approach to outliers and large errors.
7. Discussion
7.1. Analysis of Impact and Sensitivity of Hyperparameters
To assess the impact and sensitivity of our model to variations in hyperparameter values, we analyzed grid search results from the UJIIndoorLoc dataset. Starting from the optimal hyperparameter configuration shown in Table 3, we varied each parameter while keeping the others fixed.
7.1.1. Hidden Layer Dimensions
As shown in Table 6, hidden layer dimensions have a substantial impact on mean positioning error, with different configurations producing a wide range of errors. For instance, the optimal configuration of [512, 512] yielded the lowest mean error at 6.55, while configurations such as [512, 128] and [256, 256, 64] resulted in higher errors of 6.75 and 6.92, respectively. However, no consistent trend emerges across different configurations, as performance does not reliably improve or worsen with increased or decreased layer size. These findings highlight the importance of carefully selecting hidden layer dimensions to achieve optimal model performance.

Table 6.
Mean positioning error for different hidden layer configurations (Top 10 configuration).
7.1.2. Dropout Rate
As presented in Table 7, higher dropout rates lead to a clear decrease in positioning accuracy. While a dropout rate of 0.1 achieves the lowest mean error at 6.55, increasing the dropout rate to 0.5 raises the error to 6.86, and further increases to 0.7 or above result in errors exceeding 7.5. This suggests that high dropout rates adversely impact model performance, likely due to excessive information loss in the training process, emphasizing the need for a balanced approach in dropout rate selection.

Table 7.
Mean positioning error for different dropout rates.
7.1.3. Distance Threshold
The distance threshold parameter, which determines the maximum distance within which reference points are considered positive samples, impacts the model’s training by influencing the selection of samples with similar embeddings. As shown in Table 8, our results reveal no clear tendency in performance improvement or degradation as the distance threshold is varied. For example, while the optimal threshold of 15.0 yields the lowest mean error (6.55), adjusting the threshold to 10.0 slightly increases the mean error to 6.62, and further adjustments yield varying results without a distinct pattern. This lack of a consistent trend suggests that, although the distance threshold plays an essential role in positive selection, its specific value does not linearly correlate with performance changes.

Table 8.
Mean positioning error for different distance thresholds.
7.1.4. Margin
The margin parameter in the triplet loss is varied to examine its effect on embedding separation. Table 9 shows that the best performance occurs at a margin of 0.1, producing a mean error of 6.55 m. Larger margins result in greater positioning errors, which suggests that a smaller margin facilitates more effective separation without pushing embeddings too far apart.

Table 9.
Mean positioning error for different margin values.
7.1.5. Learning Rate
Table 10 shows the effect of varying the learning rate. The optimal rate of 0.0001 results in the lowest error of 6.55 m. Higher rates lead to increased errors, with the largest error of 7.02 m at a rate of 0.01. This trend suggests that lower learning rates help the model converge effectively.

Table 10.
Mean positioning error for different learning rates.
7.1.6. Batch Size
The batch size plays an essential role in both the efficiency of triplet mining and memory utilization. Our analysis, with the results shown in Table 11, shows that larger batch sizes yield better performance, with a batch size of 512 achieving the lowest mean error of 6.55. As the batch size increases, more triplets are mined, which can improve the model’s ability to learn an effective distance metric. However, larger batch sizes also require more memory, posing practical limitations. Balancing batch size with memory capacity is thus crucial to optimizing performance while ensuring efficient resource usage.

Table 11.
Mean positioning error for different batch sizes.
7.1.7. M and k Values
The analysis of M and k values, as shown in Table 12 and Table 13, highlights their impact on positioning accuracy through neighbor selection. The configuration and achieves the lowest error, 6.54 m, indicating an effective balance in selecting relevant neighbors. Increasing k initially reduces the error by incorporating additional useful neighbors in the positioning estimate, enhancing accuracy. However, beyond this optimal k value, further increases lead to rising errors. This trend suggests that larger k values introduce less relevant, more distant neighbors that likely add noise to the position estimation process, underscoring the importance of carefully tuning k to optimize neighbor selection for accurate positioning.

Table 12.
Mean positioning error for different M and k values (.

Table 13.
Mean positioning error for different M and k values (.
7.1.8. Summary
In summary, our analysis demonstrates varied sensitivity across hyperparameters, with certain parameters, such as the dropout rate and batch size, showing a clear impact on positioning error. Specifically, low dropout rates and larger batch sizes resulted in improved performance, indicating that these parameters are particularly influential in model stability and effective triplet mining. Parameters such as hidden layer dimensions and the distance threshold exhibited less consistent patterns, suggesting that their influence is more context-dependent and may require individual testing for specific datasets. Overall, careful selection and optimization of hyperparameters are crucial for maximizing the model’s effectiveness.
7.2. Real-Time Applicability
Despite the potential increase in computational cost with the introduction of deep learning techniques, our method is designed to maintain real-time applicability. Specifically, computationally costly deep learning model training is used only in the offline phase for distance metric learning. In this phase, a Siamese network with triplet loss is applied to learn a custom distance metric based on Wi-Fi fingerprint data. Although this training process is computationally intensive, it is conducted in the offline phase and therefore does not affect the efficiency of the real-time positioning phase.
In the online phase for real-time positioning, the proposed method’s main operations of embedding using the trained model and selecting neighbors have low computational costs. As a result, the computational costs of this stage are comparable to those of conventional WKNN-based methods, ensuring real-time applicability.
To further validate the real-time feasibility of our method, additional measurements were conducted to assess computation time in the online positioning phase. Table 14 shows the computation time for positioning with each baseline method and the proposed method. The experimental results indicate that our approach has no significant difference in computational costs compared to other WKNN methods, confirming its practicality for real-time applications.

Table 14.
Comparison of positioning time.
7.3. Limitations
7.3.1. High Computational Cost in Offline Training Phase
The triplet mining process requires calculating pairwise distances among all embeddings within each batch to generate triplets, which incurs a significant computational cost due to the quadratic scaling of comparisons as batch size increases. Additionally, the number of generated triplets far exceeds the number of RPs, resulting in a high computational load during the offline phase. Consequently, our method requires more memory and processing time for training, leading to a longer training duration compared to conventional methods that rely solely on RPs for learning. While this process is conducted offline and thus does not affect real-time location estimation, the high computational cost during the training phase remains a potential limitation. Reducing this computational burden without sacrificing performance is an ongoing challenge.
7.3.2. Fixed Hyperparameters and Limited Model Architecture
In the current method, hyperparameters such as M and k are fixed during online phases. However, studies [15,18] suggest that employing adaptive k-selection strategies can improve the neighbor selection. Future research could explore adaptive mechanisms for M and k to further enhance the accuracy of the model by optimizing the neighbor selection.
Additionally, we primarily evaluated the proposed method using an MLP model, demonstrating that MLPs can effectively support distance metric learning for Wi-Fi fingerprinting. However, there is potential for further improvement by exploring a wider range of model architectures. For example, incorporating advanced models such as CNNs or Graph Neural Networks (GNNs) could better capture the complex relationships within Wi-Fi fingerprint data, potentially enhancing performance.
8. Conclusions
In this paper, we present a novel WKNN-based Wi-Fi fingerprinting method for indoor positioning that leverages deep distance metric learning through a Siamese triplet network. Our approach introduces a distance metric learning technique specifically designed for Wi-Fi fingerprints, utilizing a triplet loss function and an effective triplet mining strategy to select meaningful triplets for training. This allows the model to learn an optimized distance metric, improving the similarity-based selection of neighbors. Furthermore, we propose a WKNN-based positioning method that integrates the learned distance metric with signal-space distance, enhancing neighbor selection and improving the overall positioning accuracy. This combination ensures the robust handling of signal fluctuations and environmental interference, which are common challenges in indoor environments. The effectiveness of the proposed method is validated through extensive evaluations on three public datasets—UJIIndoorLoc, Tampere, and UTSIndoorLoc. Our method consistently outperforms existing WKNN-based methods, including Euclidean WKNN, Manhattan WKNN, SAWKNN, and APD-WKNN, demonstrating significant improvements in both accuracy and robustness across all datasets. In future work, we aim to enhance model positioning accuracy by exploring adaptive M and k and advanced model architectures.
Author Contributions
Conceptualization, J.-H.P. and D.K.; methodology, J.-H.P.; software, D.K.; validation, J.-H.P., D.K. and Y.-J.S.; formal analysis, D.K.; investigation, J.-H.P.; resources, J.-H.P.; data curation, D.K.; writing—original draft preparation, J.-H.P.; writing—review and editing, J.-H.P. and D.K.; visualization, J.-H.P.; supervision, Y.-J.S.; project administration, Y.-J.S.; funding acquisition, Y.-J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly supported by Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean Government (MSIT) (No. RS-2019-II191906); the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No.20214810100010); Artificial Intelligence Graduate School Program (POSTECH) and Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2022R1A6A1A03052954).
Data Availability Statement
The data supporting the results presented in this paper are currently not publicly available but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| KNN | K-nearest neighbor |
| WKNN | weighted k-nearest neighbor |
| GNSS | Global Navigation Satellite Systems |
| LBS | indoor location-based service |
| WAP | wireless access point |
| RP | reference point |
| ML | machine learning |
| SVM | support vector machine |
| RF | random forest |
| MLP | multi-layer perceptron |
| ANN | artificial neural network |
| CNN | convolutional neural network |
| RNN | recurrent neural network |
| WLAN | wireless local area network |
| ToA | time of arrival |
| AoA | angle of arrival |
| APD | approximate position distance |
| FP | fingerprint |
| FC | fully connected |
| IDW | inverse distance weighting |
| CDF | cumulative distribution function |
| PDR | pedestrian dead reckoning |
| RPCA | robust principal component analysis |
| JNBA | Jenks natural breaks algorithm |
| GNN | graph neural network |
References
- Jagannath, A.; Jagannath, J.; Kumar, P.S.P.V. A comprehensive survey on radio frequency (RF) fingerprinting: Traditional approaches, deep learning, and open challenges. Comput. Netw. 2022, 219, 109455. [Google Scholar] [CrossRef]
- Bahl, P.; Padmanabhan, V. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM, Tel Aviv, Israel, 26–30 March 2000; pp. 775–784. [Google Scholar] [CrossRef]
- Brunato, M.; Battiti, R. Statistical learning theory for location fingerprinting in wireless LANs. Comput. Netw. 2005, 47, 825–845. [Google Scholar] [CrossRef]
- Niu, J.; Wang, B.; Shu, L.; Duong, T.Q.; Chen, Y. ZIL: An energy-efficient indoor localization system Using zigBee radio to detect wifi fingerprints. IEEE J. Sel. Areas Commun. 2015, 33, 1431–1442. [Google Scholar] [CrossRef]
- Binghao, L. Indoor positioning techniques based on wireless LAN. In Proceedings of the 1st IEEE International Conference on Wireless Broadband & Ultra Wideband Communications, Sydney, NSW, Australia, 13–16 March 2006. [Google Scholar]
- Wu, Z.; Fu, K.; Jedari, E.; Shuvra, S.R.; Rashidzadeh, R.; Saif, M. A fast and resource efficient method for indoor positioning using received signal strength. IEEE Trans. Veh. Technol. 2016, 65, 9747–9758. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, J.; Wang, W.; Hu, J. Indoor 2.5D positioning of WiFi based on SVM. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–7. [Google Scholar]
- Rezgui, Y.; Pei, L.; Chen, X.; Wen, F.; Han, C. An efficient normalized rank based SVM for room level indoor WiFi localization with diverse devices. Mob. Inf. Syst. 2017, 2017, 6268797. [Google Scholar] [CrossRef]
- Guo, X.; Ansari, N.; Li, L.; Li, H. Indoor localization by fusing a group of fingerprints based on random forests. IEEE Internet Things J. 2018, 5, 4686–4698. [Google Scholar] [CrossRef]
- Gomes, R.; Ahsan, M.; Denton, A. Random forest classifier in SDN framework for user-based indoor localization. In Proceedings of the 2018 IEEE International Conference on Electro/Information Technology (EIT), Rochester, MI, USA, 3–5 May 2018; pp. 537–542. [Google Scholar]
- Maung, N.A.M.; Lwi, B.Y.; Thida, S. An enhanced RSS fingerprinting-based wireless indoor positioning using random forest classifier. In Proceedings of the 2020 International Conference on Advanced Information Technologies (ICAIT), Yangon, Myanmar, 4–5 November 2020; pp. 59–63. [Google Scholar]
- Kim, K.S.; Lee, S.; Huang, K. A scalable deep neural network architecture for multi-building and multi-floor indoor localization based on Wi-Fi fingerprinting. Big Data Anal. 2018, 3, 4. [Google Scholar] [CrossRef]
- Wang, R.; Li, Z.; Luo, H.; Zhao, F.; Shao, W.; Wang, Q. A robust Wi-Fi fingerprint positioning algorithm using stacked denoising autoencoder and multi-Layer perceptron. Remote Sens. 2019, 11, 1293. [Google Scholar] [CrossRef]
- Song, X.; Fan, X.; Xiang, C.; Ye, Q.; Liu, L.; Wang, Z.; He, X.; Yang, N.; Fang, G. A novel convolutional neural network based indoor localization framework with WiFi fingerprinting. IEEE Access 2019, 7, 110698–110709. [Google Scholar] [CrossRef]
- Hu, J.; Liu, D.; Yan, Z.; Liu, H. Experimental analysis on weight K -nearest neighbor indoor fingerprint positioning. IEEE Internet Things J. 2019, 6, 891–897. [Google Scholar] [CrossRef]
- Wang, B.; Gan, X.; Liu, X.; Yu, B.; Jia, R.; Huang, L.; Jia, H. A novel weighted KNN algorithm based on RSS similarity and position distance for Wi-Fi fingerprint positioning. IEEE Access 2020, 8, 30591–30602. [Google Scholar] [CrossRef]
- Hou, C.; Xie, Y.; Zhang, Z. FCLoc: A novel indoor Wi-Fi fingerprints localization approach to enhance robustness and positioning accuracy. IEEE Sens. J. 2022, 23, 7153–7167. [Google Scholar] [CrossRef]
- Leng, Y.; Huang, F.; Tan, W. A WiFi Fingerprint Positioning Method Based on SLWKNN. IEEE Sens. J. 2024. [CrossRef]
- Zhang, H.; Wang, Z.; Xia, W.; Ni, Y.; Zhao, H. Weighted adaptive KNN algorithm with historical information fusion for fingerprint positioning. IEEE Wirel. Commun. Lett. 2022, 11, 1002–1006. [Google Scholar] [CrossRef]
- Poulose, A.; Kim, J.; Han, D.S. A sensor fusion framework for indoor localization using smartphone sensors and Wi-Fi RSSI measurements. Appl. Sci. 2019, 9, 4379. [Google Scholar] [CrossRef]
- Schroff, F.; Kalenictbhenko, D.; Philbin, J. FaceNet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar] [CrossRef]
- Torres-Sospedra, J.; Montoliu, R.; Martínez-Usó, A.; Avariento, J.P.; Arnau, T.J.; Benedito-Bordonau, M.; Huerta, J. UJIIndoorLoc: A new multi-building and multi-floor database for WLAN fingerprint-based indoor localization problems. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Republic of Korea, 27–30 October 2014; pp. 261–270. [Google Scholar] [CrossRef]
- Lohan, E.S.; Torres-Sospedra, J.; Leppäkoski, H.; Richter, P.; Peng, Z.; Huerta, J. Wi-Fi Crowdsourced Fingerprinting Dataset for Indoor Positioning. Data 2017, 2, 32. [Google Scholar] [CrossRef]
- Kotaru, M.; Joshi, K.; Bharadia, D.; Katti, S. SpotFi: Decimeter Level Localization Using WiFi. SIGCOMM Comput. Commun. Rev. 2015, 45, 269–282. [Google Scholar] [CrossRef]
- Vasisht, D.; Kumar, S.; Katabi, D. Decimeter-level localization with a single WiFi access point. In Proceedings of the 13th Usenix Conference on Networked Systems Design and Implementation, Santa Clara, CA, USA, 16–18 March 2016; NSDI’16. pp. 165–178. [Google Scholar]
- Xiong, J.; Sundaresan, K.; Jamieson, K. Tonetrack: Leveraging frequency-agile radios for time-based indoor wireless localization. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 537–549. [Google Scholar]
- Xiong, J.; Jamieson, K. ArrayTrack: A fine-grained indoor location system. In Proceedings of the 10th USENIX Conference on Networked Systems Design and Implementation, Lombard, IL, USA, 2–5 April 2013; NSDI’13. pp. 71–84. [Google Scholar]
- Gjengset, J.; Xiong, J.; McPhillips, G.; Jamieson, K. Phaser: Enabling Phased Array Signal Processing on Commodity Wi-Fi Access Points. GetMobile Mob. Comput. Commun. 2015, 19, 6–9. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, D.; Song, R.; Yin, P.; Chen, Y. Multiple wifi access points co-localization through joint aoa estimation. IEEE Trans. Mob. Comput. 2023, 23, 1488–1502. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Hu, J.; Hu, C. A WiFi Indoor Location Tracking Algorithm Based on Improved Weighted K Nearest Neighbors and Kalman Filter. IEEE Access 2023, 11, 32907–32918. [Google Scholar] [CrossRef]
- Narasimman, S.C.; Alphones, A. Dumbloc: Dumb indoor localization framework using wifi fingerprinting. IEEE Sens. J. 2024, 24, 14623–14630. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).