Performance Analysis of Reconnaissance Coverage for HUAV Swarms under Communication Interference Based on Different Architectures
Abstract
1. Introduction
- We consider a communication model for HUAV swarms in an environment with unknown communication interference. We aim to accurately reflect the real-time communication status of the HUAV swarm, thereby laying a foundation for subsequent algorithm design and simulation validation.
- A coverage-oriented artificial potential field (COAPF) algorithm is devised to address the limitations of traditional APF-based methods in defining targets and obstacles as well as attractive and repulsive force functions under the environmental condition of unknown communication interference. This algorithm serves to provide guidance for the HUAV swarm in efficiently accomplishing reconnaissance and coverage tasks.
- Based on the COAPF algorithm, a multidimensional verification and analysis process is conducted to investigate the performance differences of HUAV swarms executing reconnaissance and coverage tasks under centralized, distributed, and centralized–distributed architectures. This study provides insights and support for subsequent deployments of HUAV swarms to efficiently execute reconnaissance and coverage tasks in unknown communication interference environments.
2. System Model
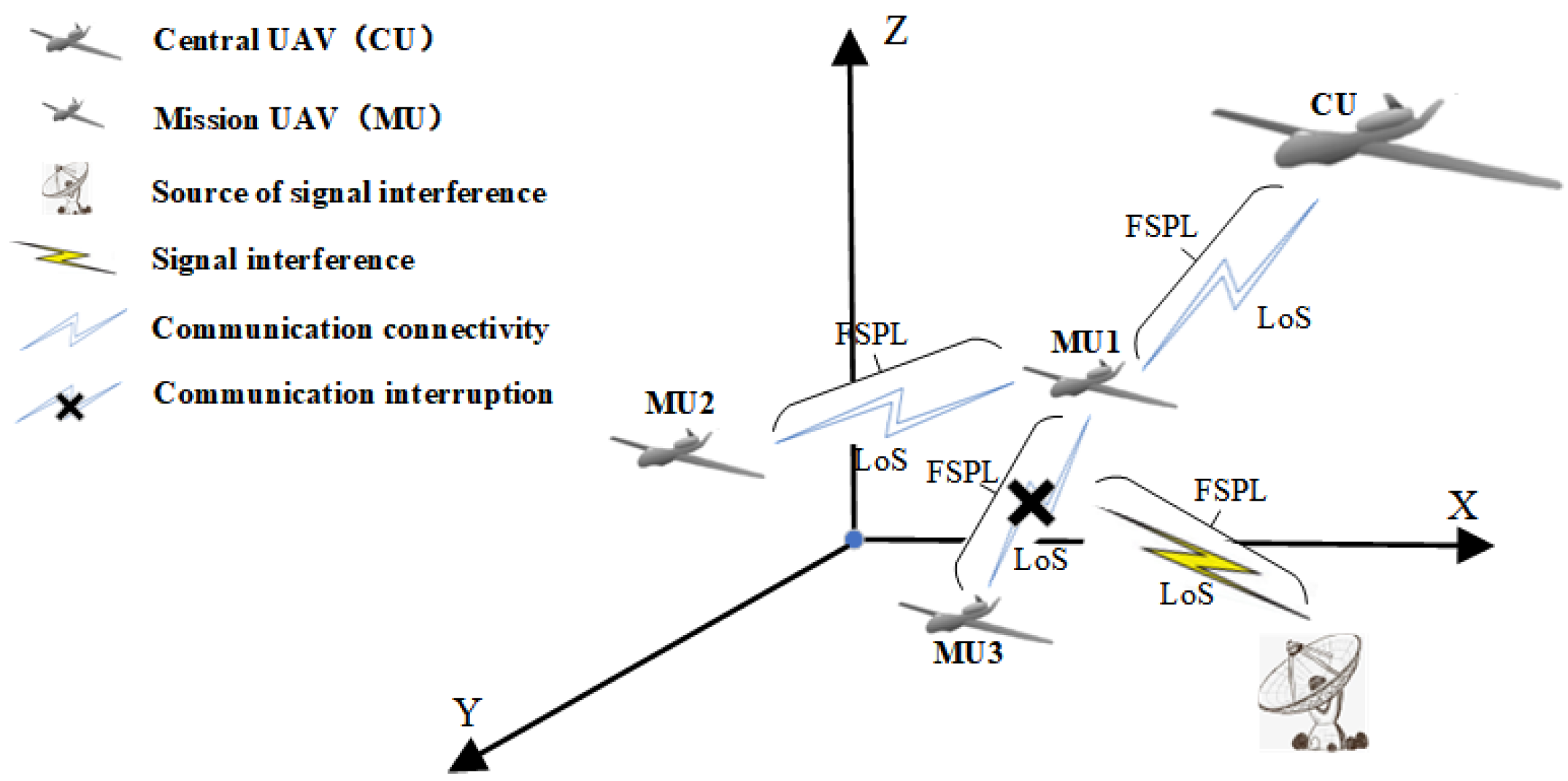
2.1. Environment Model
2.2. HUAV Swarm Model
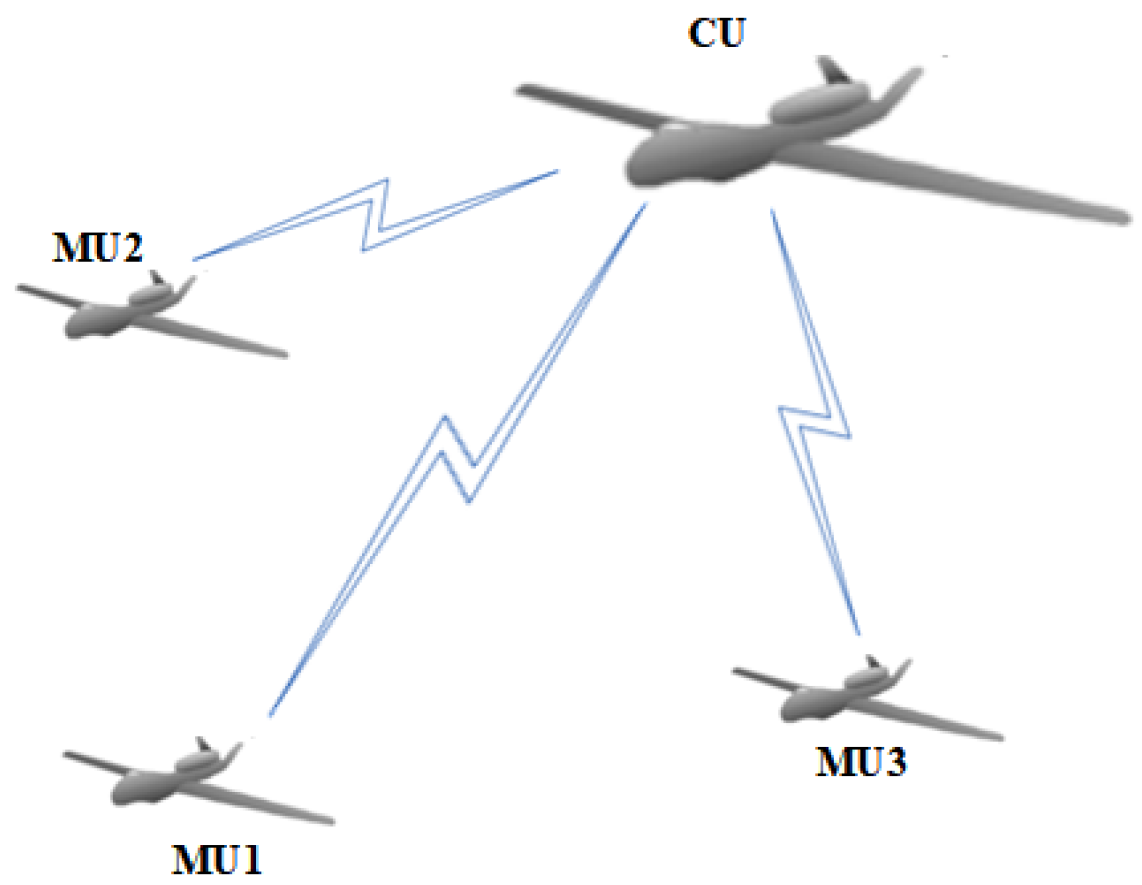
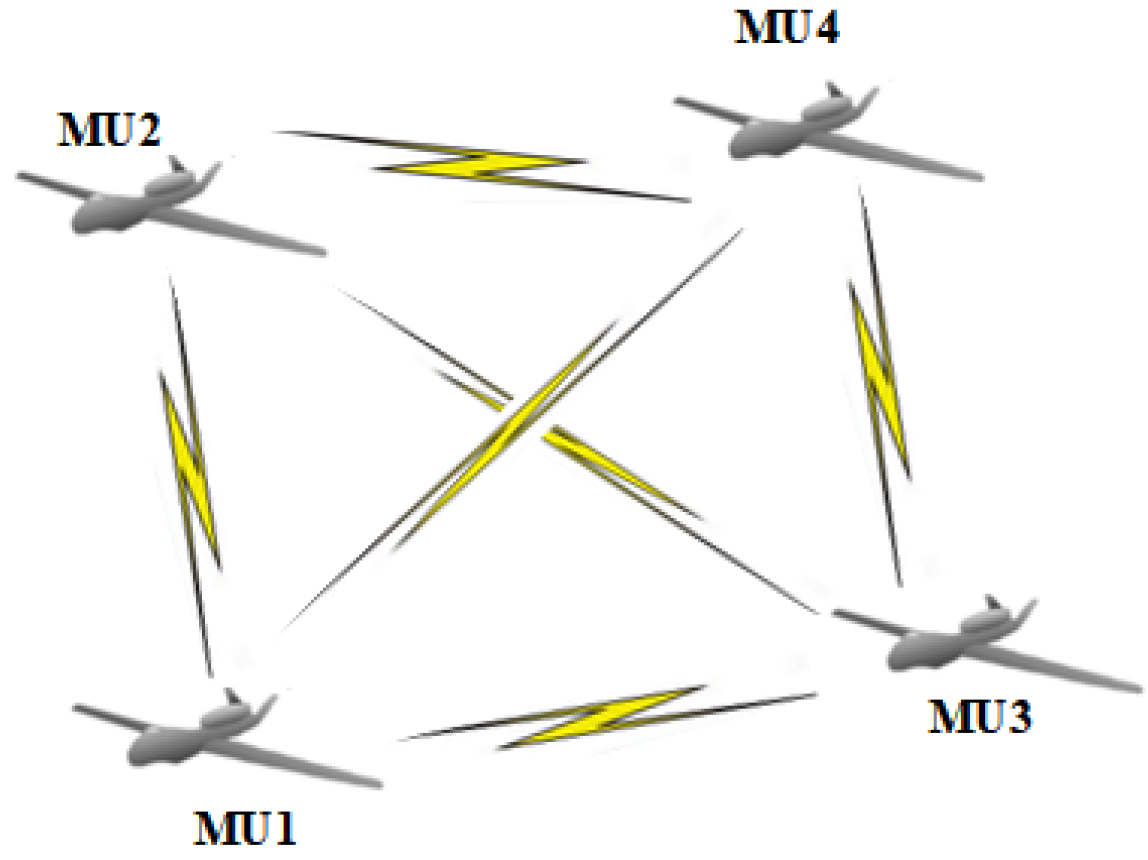
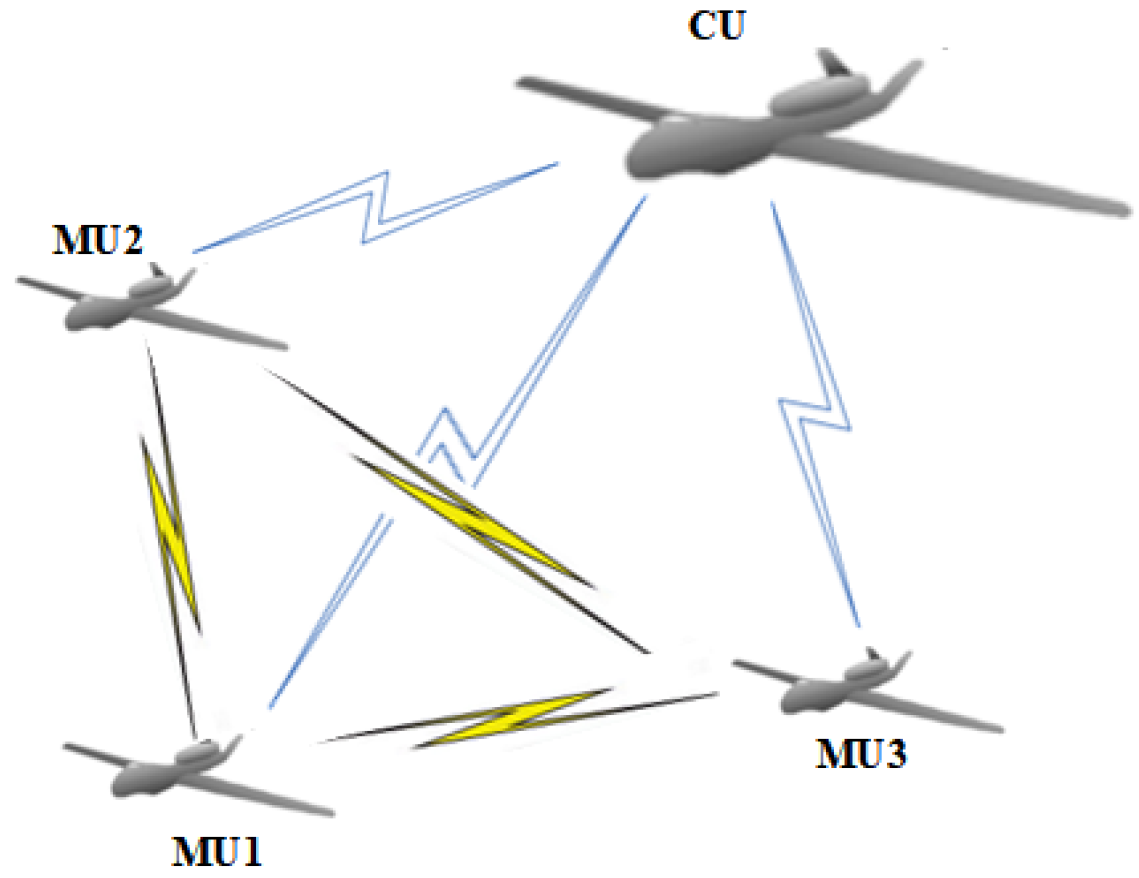
2.3. HUAV Swarm Architectures
2.3.1. Centralized Architecture
2.3.2. Distributed Architecture
2.3.3. Centralized–Distributed Architecture
2.4. Mathematical Model
2.4.1. Constraints
- (1)
- Complete Coverage Constraint
- (2)
- Communication Constraint
2.4.2. Objective Function
3. HUAV Swarm Reconnaissance and Coverage Based on COAPF Algorithm
3.1. Design of COAPF Algorithm
3.2. COAPF Algorithm for Different Architectures
3.2.1. COAPF Algorithm Oriented towards Centralized Architecture
3.2.2. COAPF Algorithm Oriented towards Distributed Architecture
3.2.3. COAPF Algorithm Oriented towards Centralized–Distributed Architecture
| Algorithm 1: COAPF Algorithm Based on Centralized Architecture |
 |
| Algorithm 2: COAPF Algorithm Based on Distributed Architecture |
 |
| Algorithm 3: COAPF Algorithm Based on the Distributed–Collective Architecture |
 |
3.2.4. Resolving Decision Conflicts
| Algorithm 4: Decision Conflict Resolution Algorithm |
 |
4. Simulations and Results Analysis
4.1. Simulation Design
4.2. Comparative Simulations
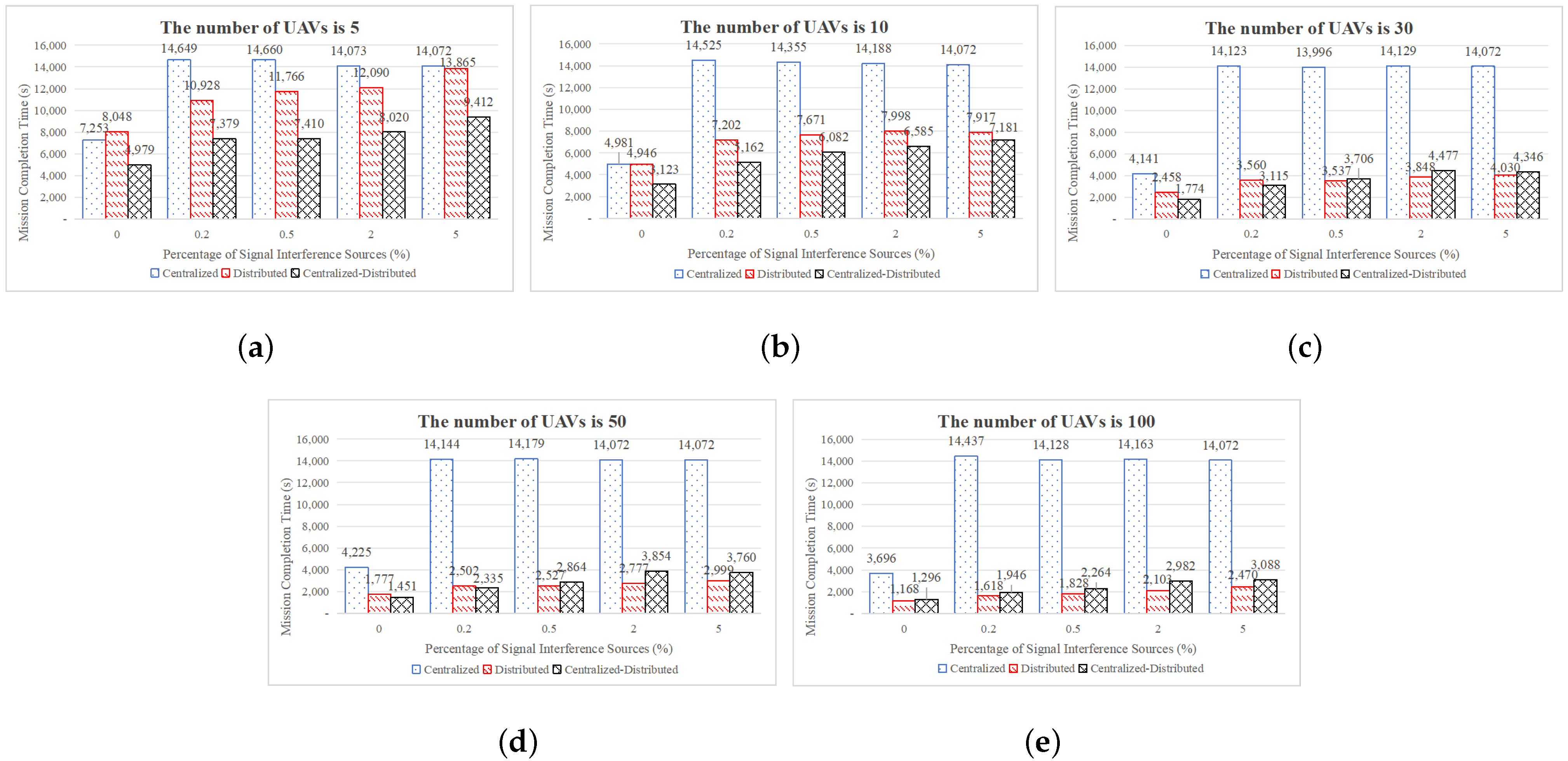
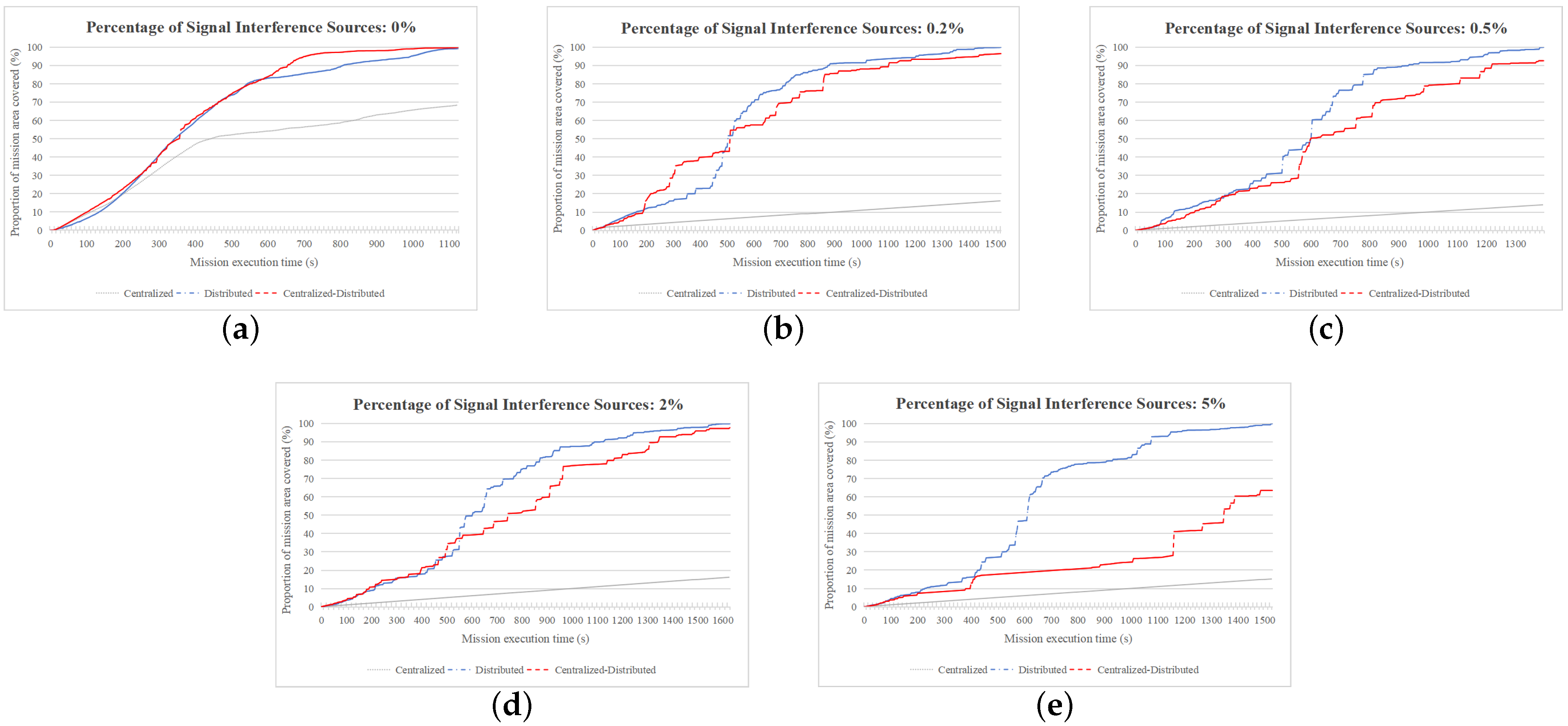
4.2.1. Comparison of Total Area Coverage Time
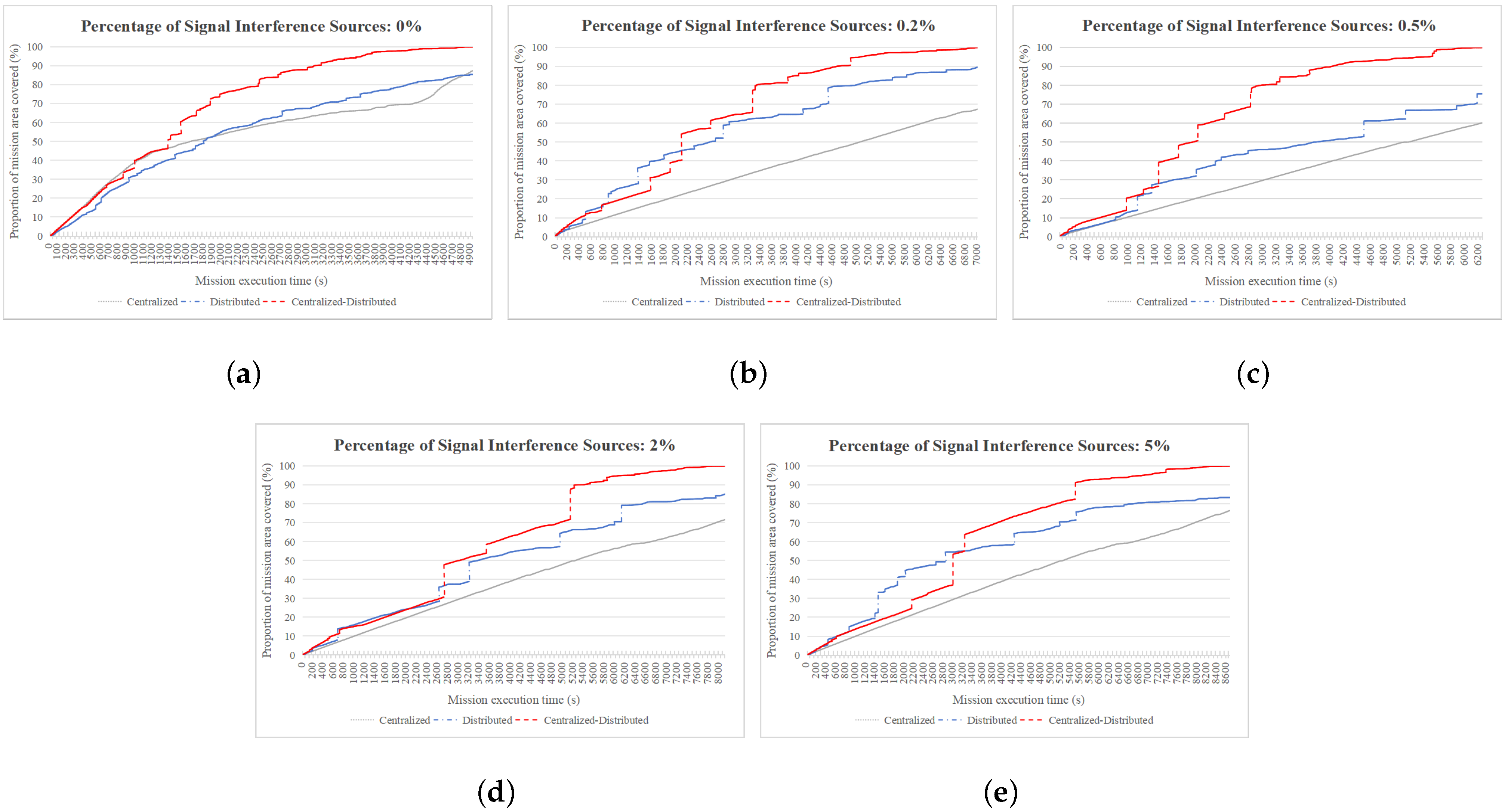
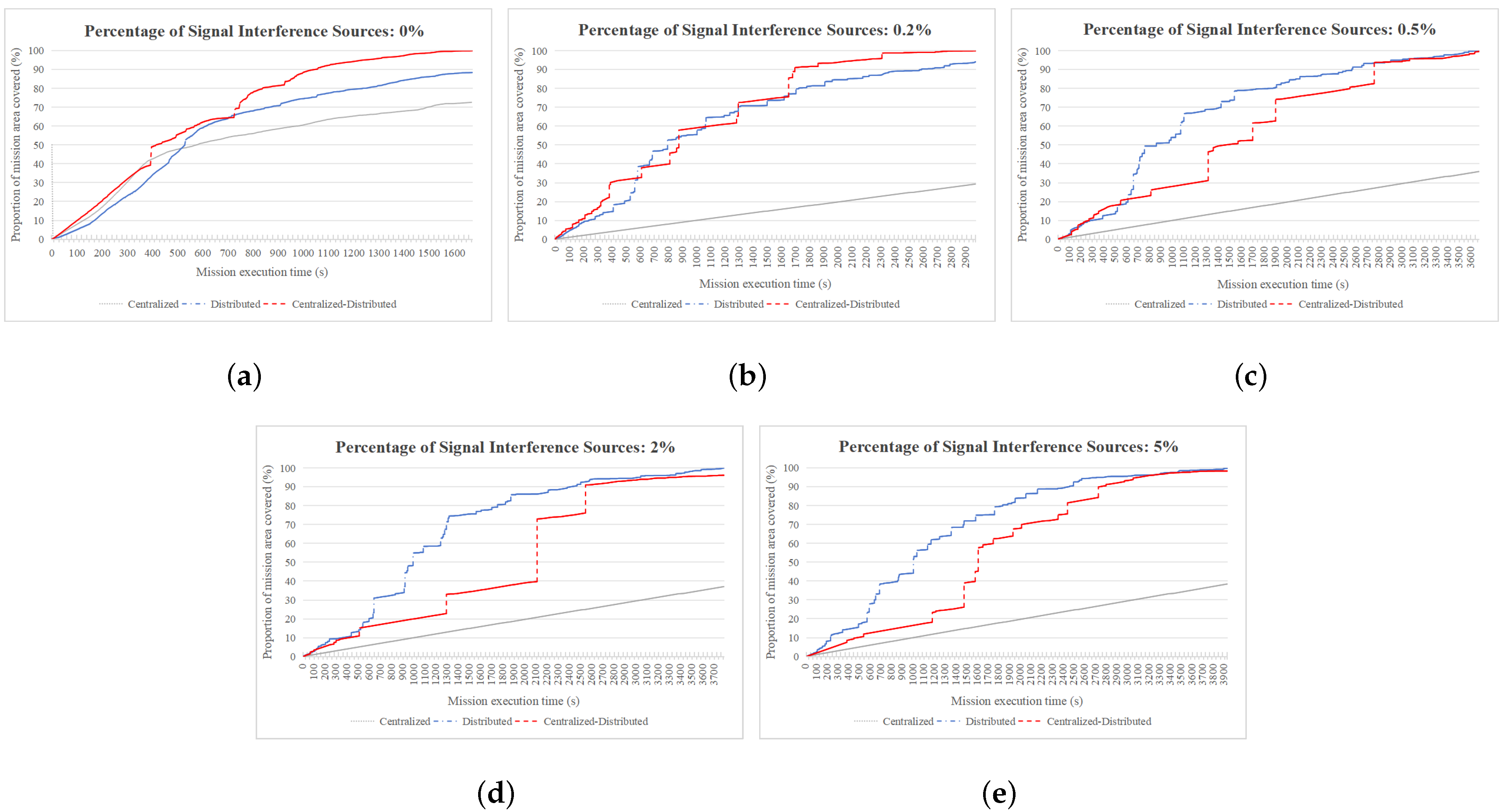
4.2.2. Comparison of Regional Coverage Speeds
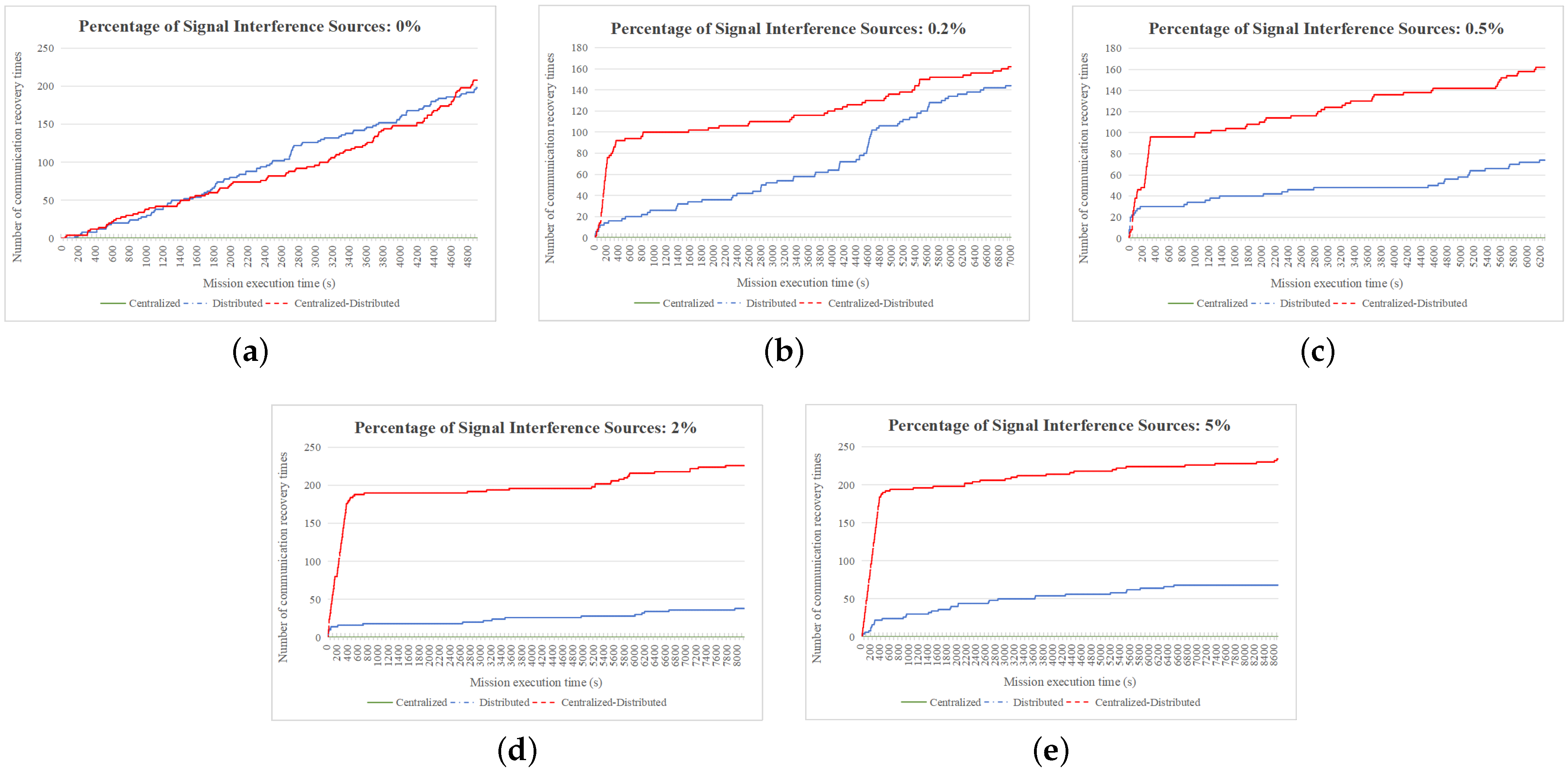
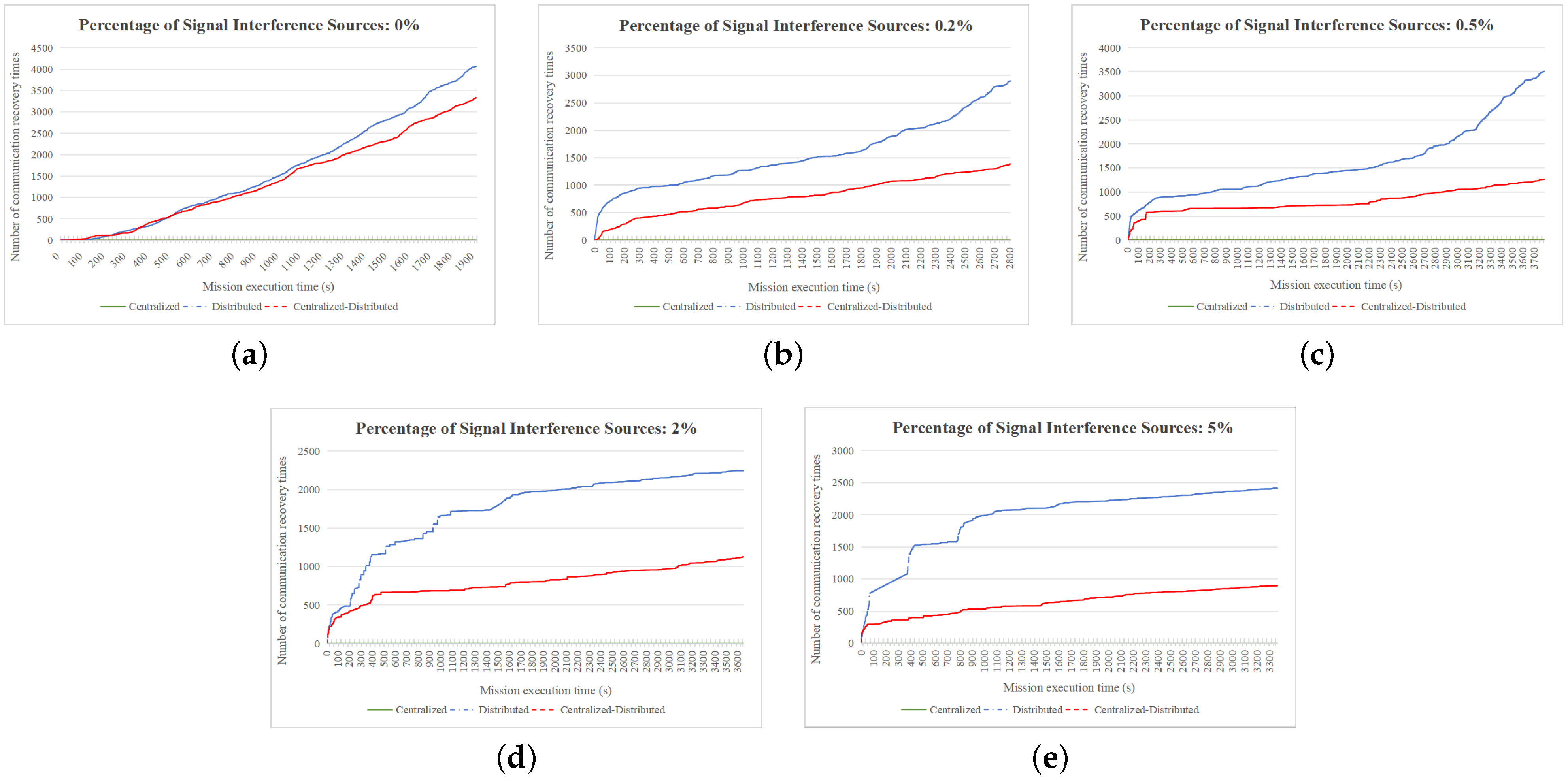
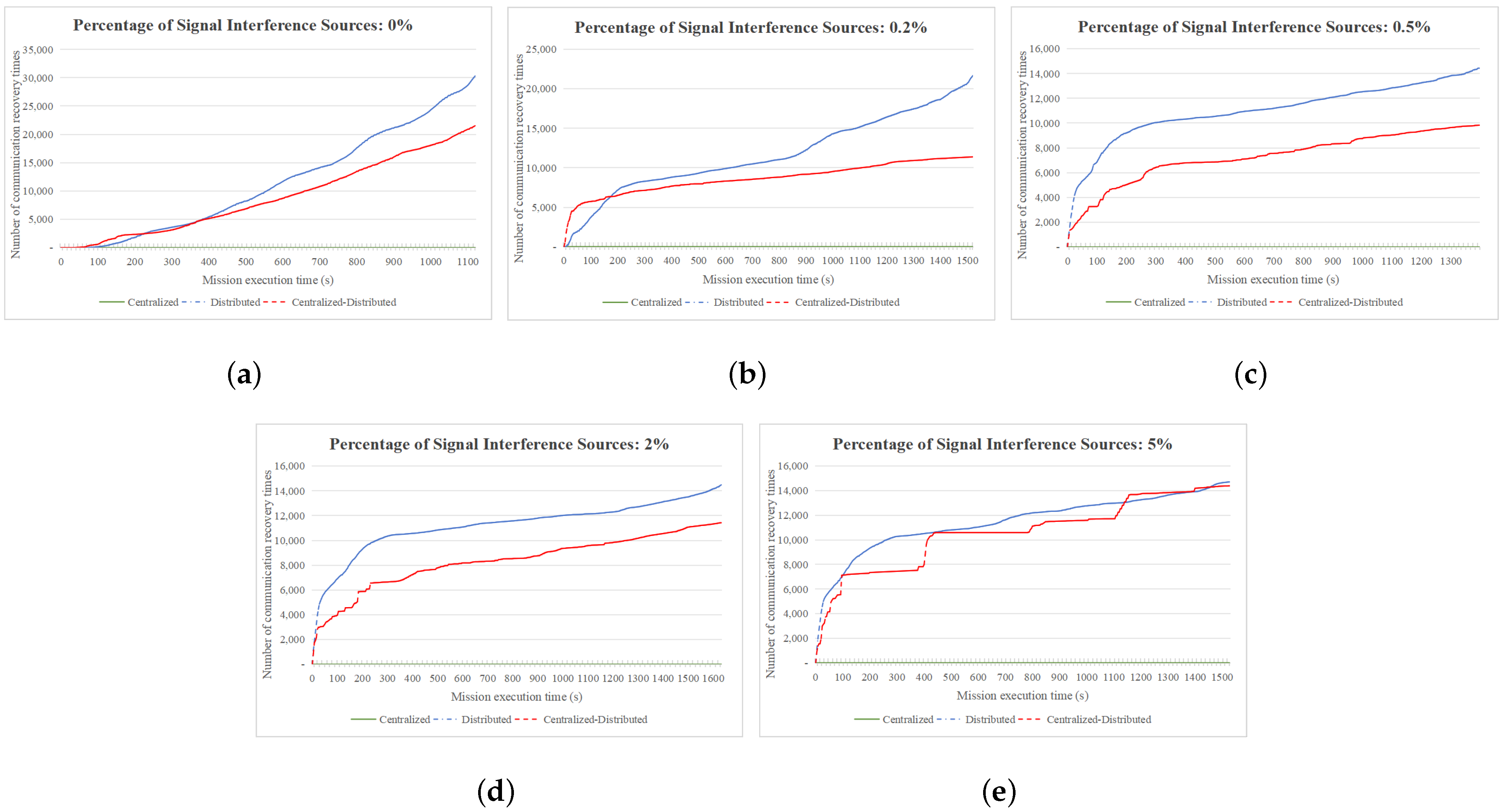
4.2.3. Comparison of Communication Recovery Times
4.2.4. Analysis of Significance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| HUAV | Heterogeneous Unmanned Aerial Vehicle |
| APF | Artificial Potential Field |
| COAPF | Coverage-Oriented Artificial Potential Field |
| SI | Signal Interference |
| CU | Central UAV |
| MU | Mission UAV |
| LoS | Line-of-Sight |
| SNR | Signal-to-Noise Ratio |
References
- Sajid, M.; Mittal, H.; Pare, S.; Prasad, M. Routing and scheduling optimization for UAV assisted delivery system: A hybrid approach. Appl. Soft Comput. 2022, 126, 109225. [Google Scholar] [CrossRef]
- Peng, C.; Qiu, S. A decomposition-based constrained multi-objective evolutionary algorithm with a local infeasibility utilization mechanism for UAV path planning. Appl. Soft Comput. 2022, 118, 108495. [Google Scholar] [CrossRef]
- Stolfi, D.H.; Brust, M.R.; Danoy, G.; Bouvry, P. A competitive Predator–Prey approach to enhance surveillance by UAV swarms. Appl. Soft Comput. 2021, 111, 107701. [Google Scholar] [CrossRef]
- Mazaherifar, A.; Mostafavi, S. UAV placement and trajectory design optimization: A survey. Wirel. Pers. Commun. 2022, 124, 2191–2210. [Google Scholar] [CrossRef]
- Saraswat, D.; Bhattacharya, P.; Singh, A.; Verma, A.; Tanwar, S.; Kumar, N. Secure 5G-assisted UAV access scheme in IoBT for region demarcation and surveillance operations. IEEE Commun. Stand. Mag. 2022, 6, 58–66. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, J. Distributed cooperative complete coverage path planning in an unknown environment based on a heuristic method. Unmanned Syst. 2024, 12, 149–160. [Google Scholar] [CrossRef]
- Yin, D.; Yang, X.; Yu, H.; Chen, S.; Wang, C. An air-to-ground relay communication planning method for UAVs swarm applications. IEEE Trans. Intell. Veh. 2023, 8, 2983–2997. [Google Scholar] [CrossRef]
- Shi, Y.; Yi, C.; Chen, B.; Yang, C.; Zhu, K.; Cai, J. Joint online optimization of data sampling rate and preprocessing mode for edge–cloud collaboration-enabled industrial IoT. IEEE Internet Things J. 2022, 9, 16402–16417. [Google Scholar] [CrossRef]
- Alsuhli, G.; Fahim, A.; Gadallah, Y. A survey on the role of UAVs in the communication process: A technological perspective. Comput. Commun. 2022, 194, 86–123. [Google Scholar] [CrossRef]
- Shi, Y.; Yi, C.; Wang, R.; Wu, Q.; Chen, B.; Cai, J. Service migration or task rerouting: A two-timescale online resource optimization for MEC. IEEE Trans. Wirel. Commun. 2023. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H. Radio Resource Management for Cellular-Connected UAV: A Learning Approach. IEEE Trans. Commun. 2023, 71, 2784–2800. [Google Scholar] [CrossRef]
- Chopra, S.; Egerstedt, M. Spatio-temporal multi-robot routing. Automatica 2015, 60, 173–181. [Google Scholar] [CrossRef]
- Morgan, D.; Subramanian, G.P.; Chung, S.J.; Hadaegh, F.Y. Swarm assignment and trajectory optimization using variable-swarm, distributed auction assignment and sequential convex programming. Int. J. Robot. Res. 2016, 35, 1261–1285. [Google Scholar] [CrossRef]
- Oh, H.; Shin, H.S.; Kim, S.; Chen, W.H. Communication-aware trajectory planning for unmanned aerial vehicles in urban environments. J. Guid. Control Dyn. 2018, 41, 2271–2282. [Google Scholar] [CrossRef]
- Fei, B.; Bao, W.; Zhu, X.; Liu, D.; Men, T.; Xiao, Z. Autonomous Cooperative Search Model for Multi-UAV With Limited Communication Network. IEEE Internet Things J. 2022, 9, 19346–19361. [Google Scholar] [CrossRef]
- Ozkan, O. Optimization of the distance-constrained multi-based multi-UAV routing problem with simulated annealing and local search-based matheuristic to detect forest fires: The case of Turkey. Appl. Soft Comput. 2021, 113, 108015. [Google Scholar] [CrossRef]
- Yang, L.; Meng, F.; Zhang, J.; Hasna, M.O.; Di Renzo, M. On the performance of RIS-assisted dual-hop UAV communication systems. IEEE Trans. Veh. Technol. 2020, 69, 10385–10390. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y. Machine learning empowered trajectory and passive beamforming design in UAV-RIS wireless networks. IEEE J. Sel. Areas Commun. 2020, 39, 2042–2055. [Google Scholar] [CrossRef]
- Li, M.; Cheng, N.; Gao, J.; Wang, Y.; Zhao, L.; Shen, X. Energy-efficient UAV-assisted mobile edge computing: Resource allocation and trajectory optimization. IEEE Trans. Veh. Technol. 2020, 69, 3424–3438. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV communications via joint trajectory and power control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, C.; Yeoh, P.L.; Wang, K.; Elkashlan, M.; Vucetic, B.; Li, Y. Secure communications for UAV-enabled mobile edge computing systems. IEEE Trans. Commun. 2019, 68, 376–388. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, Q.; Yan, S.; Shu, F.; Li, J. UAV-enabled secure communications: Joint trajectory and transmit power optimization. IEEE Trans. Veh. Technol. 2019, 68, 4069–4073. [Google Scholar] [CrossRef]
- Yuan, Z.; Du, C.; Chen, J.; Ling, F. Central-distributed control model of UAV group and its application in perception module. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 677–681. [Google Scholar]
- Qi, W.; Yang, W.; Xing, L.; Yao, F. Modeling and Solving for Multi-Satellite Cooperative Task Allocation Problem Based on Genetic Programming Method. Mathematics 2022, 10, 3608. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, Y.; Wen, L.; Han, B. An intelligent cooperative mission planning scheme of UAV swarm in uncertain dynamic environment. Aerosp. Sci. Technol. 2020, 100, 105826. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Giacomossi, L.; Souza, F.; Cortes, R.G.; Cortez, H.M.M.; Ferreira, C.; Marcondes, C.A.; Loubach, D.S.; Sbruzzi, E.F.; Verri, F.A.; Marques, J.C.; et al. Autonomous and collective intelligence for UAV swarm in target search scenario. In Proceedings of the 2021 Latin American Robotics Symposium (LARS), 2021 Brazilian Symposium on Robotics (SBR), and 2021 Workshop on Robotics in Education (WRE), Natal, Brazil, 11–15 October 2021; pp. 72–77. [Google Scholar]
- Yin, H. Artificial Potential Field Based Real-time Obstacle-free Motion Planning for Unmanned Aerial Vehicle. Ph.D. Thesis, Syracuse University, Syracuse, NY, USA, 2020. [Google Scholar]
- Han, G.L. Automatic parking path planning based on ant colony optimization and the grid method. J. Sens. 2021, 2021, 8592558. [Google Scholar] [CrossRef]
| Literature | Environment Information | Online/Offline Planning | UAV Swarm Architecture | Static/Dynamic Communication Distance Constraints |
|---|---|---|---|---|
| [1,2,6,14,19] | known | offline | centralized | - |
| [11] | known | offline | centralized | static |
| [24] | known | offline | centralized-distributed | - |
| [3,18,25,26,27,28] | unknown | online | distributed | - |
| [7,12,13,15] | unknown | online | distributed | static |
| This study | unknown | online | centralized, distributed, centralized-distributed | dynamic |
| Parameter | Value | |
|---|---|---|
| Mission UAV Reconnaissance Range Diameter (m) | ||
| Central UAV Reconnaissance Range Diameter (m) | ||
| Grid Side Length (m) | 200 | |
| Mission Area Length (km) | 10 | |
| Mission Area Width (km) | 10 | |
| Number of Grids in the Mission Area | 2500 | |
| Mission UAV Speed (m/s) | 50 | |
| Central UAV Speed (m/s) | 50 | |
| Central UAV Signal Transmission Power (db) | −8 | |
| Mission UAV Signal Transmission Power (db) | −16 | |
| Carrier Frequency of the Channel between UAVs (MHz) | 2000 | |
| Signal-to-Noise Ratio Threshold (db) | −7 | |
| Basic Path Loss for Line-of-Sight | 0.11 | |
| Communication in Suburban Areas (db) | ||
| Interfering Source Signal Transmission Power (db) | 10 | |
| Communication Background Noise (db) | −113 | |
| Gravitational Field Constant | 1 | |
| Repulsive Field Constant | 1 |
| Percentage of Signal Interference Sources (%) | Number of Signal Sources Intensity (db) | Average Interference Intensity (db) | Maximum Communication Distance of CU under Average Signal Interference Intensity (m) | Maximum Communication Distance of MU under Average Signal Interference Intensity (m) |
|---|---|---|---|---|
| 0 | 0 | −113 | 6628 | 2639 |
| 0.2 | 5 | −96.07 | 944 | 376 |
| 0.5 | 10 | −90.17 | 478 | 190 |
| 2 | 50 | −83.35 | 218 | 87 |
| 5 | 125 | −76.58 | 100 | 40 |
| Scale of HUAVs | Proportion of Signal Interference Sources | C-D | C-CD | D-C | D-CD | CD-C | CD-D |
|---|---|---|---|---|---|---|---|
| 5 | 0 | + | - | - | - | + | + |
| 5 | 0.2 | - | - | + | - | + | + |
| 5 | 0.5 | = | - | + | - | + | + |
| 5 | 2 | - | - | + | - | + | + |
| 5 | 5 | - | = | + | - | + | + |
| B-W | −2 | −4 | 3 | −5 | 5 | 5 | |
| 10 | 0 | - | - | + | - | + | + |
| 10 | 0.2 | - | = | + | - | + | + |
| 10 | 0.5 | - | - | + | - | + | + |
| 10 | 2 | - | - | + | - | + | + |
| 10 | 5 | - | - | + | - | + | + |
| B-W | −5 | −4 | 5 | −5 | 5 | 5 | |
| 30 | 0 | - | - | = | - | + | + |
| 30 | 0.2 | - | - | + | - | + | + |
| 30 | 0.5 | - | - | + | = | + | - |
| 30 | 2 | - | - | + | + | + | - |
| 30 | 5 | - | - | + | + | + | - |
| B-W | −5 | −5 | 4 | 0 | 5 | −1 | |
| 50 | 0 | - | - | + | - | + | + |
| 50 | 0.2 | - | - | + | - | + | + |
| 50 | 0.5 | - | - | + | + | + | = |
| 50 | 2 | - | - | + | + | + | - |
| 50 | 5 | - | - | + | + | + | - |
| B-W | −5 | −5 | 5 | 1 | 5 | 0 | |
| 100 | 0 | - | - | + | = | = | = |
| 100 | 0.2 | - | - | + | + | + | - |
| 100 | 0.5 | - | - | + | + | + | - |
| 100 | 2 | - | - | + | + | + | - |
| 100 | 5 | - | - | + | + | + | - |
| B-W | −5 | −5 | 5 | 4 | 4 | −4 | |
| B | 1 | 0 | 23 | 9 | 24 | 14 | |
| S | 1 | 2 | 1 | 2 | 1 | 2 | |
| W | 23 | 23 | 1 | 14 | 0 | 9 | |
| sum(B-W) | −22 | −22 | 21 | −5 | 24 | 5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Chen, B.; Zhao, Y.; Hu, F.; Liu, C.; Li, Y. Performance Analysis of Reconnaissance Coverage for HUAV Swarms under Communication Interference Based on Different Architectures. Electronics 2024, 13, 4067. https://doi.org/10.3390/electronics13204067
Fan Y, Chen B, Zhao Y, Hu F, Liu C, Li Y. Performance Analysis of Reconnaissance Coverage for HUAV Swarms under Communication Interference Based on Different Architectures. Electronics. 2024; 13(20):4067. https://doi.org/10.3390/electronics13204067
Chicago/Turabian StyleFan, Yongjian, Bing Chen, Yunlong Zhao, Feng Hu, Chunyan Liu, and Yang Li. 2024. "Performance Analysis of Reconnaissance Coverage for HUAV Swarms under Communication Interference Based on Different Architectures" Electronics 13, no. 20: 4067. https://doi.org/10.3390/electronics13204067
APA StyleFan, Y., Chen, B., Zhao, Y., Hu, F., Liu, C., & Li, Y. (2024). Performance Analysis of Reconnaissance Coverage for HUAV Swarms under Communication Interference Based on Different Architectures. Electronics, 13(20), 4067. https://doi.org/10.3390/electronics13204067







