Abstract
Active front-end (AFE) rectifiers have become widely employed in power systems to achieve unity power factor and harmonic mitigations. The typical modeling approaches applied for AFE rectifiers in the literature mostly relied on two baselines: the detailed model and the time-average model. The former approach deals with the switching element model (SEM), which leads to significant harmonics in currents with distorted waveforms. The latter approach uses the average-value model (AVM) to overcome the currents’ harmonics as well as provide fast responses. However, even the AVM baseline has shown problems during the starting stage (lack of control signals) and over the dead-time periods, which causes serious issues in the implementation process. This paper presents an improved dynamic AVM for AFE rectifiers by precisely considering the issues mentioned above, along with the practical starting procedure and desirable initialization. The studied AFE rectifier is developed using the voltage-oriented control (VOC) technique based on the different modeling methodologies, including SEM, Conventional AVM, and the proposed AVM. The performance of all models is analyzed and compared using simulation results with MATLAB/Simulink R2023a Function blocks for all the algorithm parts and SimScape elements for the electrical circuit model. The simulation results illustrate that the performance of the proposed AVM approach can closely resemble the behavior of the SEM baseline with low harmonic distortion. To evaluate the performance of the proposed model, several case studies are investigated to verify the AFE rectifier operation, regarding mostly the total harmonic distortion (THD) wherein the THD percentages are improved to 4.78 and 2.5 from 5.14 and 2.78 for low- and high-power loads, respectively.
1. Introduction
The power systems have undergone a huge transformation due to the development of power converters and renewable energy resources [1]. Power quality challenges, the widespread employing of high-order filters, and the overall decrease in the impact of the power grid due to distributed generation are the main changes that have caused this transition [2]. To address these challenges, many approaches have been investigated to guarantee the proper control and operation of power systems equipped with power converters. Among these solutions, smart transformers, also called power electronic transformers, have been widely applied to interface medium- and low-voltage systems through fully controllable power electronic devices [3]. Similarly, power electronic transformations have played a key role in the onboard systems for transportation applications, aircraft, and shipboard [4,5]. Active rectifiers, as a first stage in those applications, have become the most attractive approaches towards smart power systems.
Active front-end (AFE) rectifiers have been widely used in medium-to-high-power adjustable speed drives, high-voltage DC systems, electric vehicles, and traction battery chargers to achieve regenerative operation and meet energy efficiency and harmonic requirements. In many applications where improved harmonic distortion is demanded, conventional front-end devices have been replaced by AFE rectifiers [6]. In addition, the AFE rectifiers can improve the reactive power balance by operating at a near unity power factor or by compensating the inductive/capacitive impact of other loads in the vicinity. Moreover, the fast transient feature of the new generation of AFE rectifiers enables superior ride-through capability during system disturbances.
Several marine vessels have utilized DC power systems for their simple controllability, high efficiency, and high reliability based on AFE rectifiers and synchronous generators [7]. AFE rectifiers have been employed in high-power electric vehicle (EV) charging stations, and those vehicles are promising future transportation systems. AFE rectifiers reduce the distortions produced via the operation of the EV charging infrastructures by minimizing harmonic disturbances and operating close to the unity power factor (PF) [8,9]. In [10], an AFE rectifier with a PF correction (PFC) capability is proposed for power quality improvement in telecom applications using a sensorless voltage control strategy to tackle harmonic issues and boost overall performance. Modular multilevel converter-based AFE rectifier topology is studied in [11] under unbalanced power grid conditions to improve the steady-state performance of the system that feeds the variable-speed motor drive. Variable-speed motor drives are a massive part of the grid-connected loads in distribution networks that use either conventional diode bridge rectifiers along with inverters or AFE rectifiers to adjust the operating frequency [12]. Recently, modular power converters with AFE rectifiers have been extensively utilized by motor drives to improve their harmonic characteristics and raise the overall power quality. In [13], a modular AFE rectifier with a common DC link is extended for multidrive configuration to mitigate harmonic distortions based on the electronic phase shifting technique. To elevate the modular AFE rectifier behavior, it is useful to separate the rectifier module from the drive unit and consider it as the main interface circuit between the AC power grid and the motor drive system’s DC link and deploy a robust and feasible control strategy.
The typical control techniques developed for the AFE rectifiers are voltage-oriented control (VOC) [14], virtual flux-based strategies [15], and direct power control (DPC) [16]. Several other control approaches have been proposed for the AFE converters, including predictive hybrid pulse–width modulation (PWM) [17], predictive duty cycle control [18], multicarrier-based PWM [19], synchronous space vector modulation [20], proportional–integral (PI) controller with anti-windup scheme [21], and digital control with multiloop tuning approaches [22]. Dynamic transient simulation of AFE rectifiers is a powerful item widely developed by many researchers to evaluate the effect of switched loads on power grids. Although several transient simulation tools with extensive elements can be used to develop a detailed switching model of the AFE converter, such detailed schemes contain heavy computational burdens and may cause long simulation times for large distribution networks with a large number of interfaced loads. Dynamic modeling, particularly the average-value model (AVM), is a powerful method that averages or mitigates the high-order harmonics of the AFE rectifier while maintaining the capability to precisely estimate the system’s dynamic behavior [23]. Dynamic AVM approach, as a precise alternative to the switching PWM models, has been widely developed for the line-commutated AFE rectifiers, wherein slower (non-switched) dynamic functions are acquainted via related AC and DC sides variables based on their average-value equations instead of the individual discrete switching functions [24,25,26,27,28,29]. Consequently, the AVM approaches are efficient and fast for system-level simulation studies. An AVM-based line-commutated AC-DC converter is investigated in [30] when the AC power grid is in unbalanced conditions. The studied AVM methodology relies on the system parameters to achieve fast simulations for the converter. The AVM approaches can be divided into analytical and parametric schemes, wherein the parametric AVM includes high accuracy and is very promising for electromagnetic transient simulation studies.
For AVM of AFE rectifiers that operate based on conventional PWM strategies, the models are typically performed by rotating reference frame operators [31,32,33]. In [34], the double Fourier series of PWM was studied to figure out the dead-time effect by inserting a correction value. These results extended to clarify the dead-time impact on the conventional PWM signals [35]. However, all these approaches can only be performed in a switching function baseline and cannot be employed in a time-average model. In [36], an improved dynamic model of an AFE converter is studied using the calculation of the duty cycle impact and considering the distortion by modeling the voltage drop on the semiconductor switching devices as an error of the duty cycle. However, those methods ignore the effect of duty cycle distortion over the zero crossing points of the current when they are being altered to null. Moreover, this voltage drop on the switching devices does not directly distort the DC link current and, consequently, should not be considered a duty cycle distortion. Another technique presented in [37] for modeling a motor drive is adding the effect of the dead time to the modulation space vectors; however, this approach did not consider the impact of voltage drops on switching devices. The overall dead-time definition procedure, as well as its impact on output current and voltage distortions, are comprehensively explained in [38]. The definition in [38] is the well-known two-level distortion model based on the duration of the switch’s conduction mode within one period. The study [39] extended the conventional definition of the two-level dead-time distortion approximation and improved it to a three-level distortion model by dividing the duty cycle of phase output voltage into three separate levels based on the maximum peak ripple of phase currents along with the switching frequency amount. However, it still suffers from the zero-crossing harmonics in currents.
This article provides improved AVM (IAVM) for the AFE rectifiers based on the VOC approach to enhance the performance of the time-average simulation using several dynamic case studies, including startup and load variations. To validate the accuracy of the studied time-average approach, the result of the proposed IAVM simulation was compared with the standard AVM (SAVM) and the switching element model (SEM) simulations based on the same control strategy. While some SAVM-based AFE rectifiers have been developed to overcome the aforementioned issues related to the converters, some challenges have remained unsolved, such as starting stage without command signals from the controllers, the impact of inrush currents, the effect of dead-time distortion, and fully considering the voltage drop on switching devices. To address these issues, an improved AVM distortion model is proposed with the following contributions:
- Practical SEM, SAVM, and IAVM simulation models are built for the AFE rectifiers;
- The AFE rectifiers are initialized in proper ways to implement the startup procedure in the absence of command control signals;
- The inrush current is limited during the startup period using a pre-charge circuit;
- A robust closed-loop control strategy is proposed to keep the unity power factor;
- The dead-time impact on the rectifier is improved by the proposed advanced AVM;
- The effect of switching devices’ voltage drop is accurately considered in the models;
- The operations of the models are compared to validate the accuracy of the proposed IAVM performance.
Section 2 describes different topologies for the three-phase AFE rectifiers. Section 3 discusses the proposed time average model for the AFE topology as well as its VOC implementation. Section 4 illustrates the simulation results of the case studies. Section 5 concludes this research work and provides some outlooks on AFE rectifiers.
2. AFE Rectifier Models
As explained in Section 1, three-phase rectifiers are widely utilized in power system applications as front-end converters because of their reliability and simplicity. Therefore, this section explores the mathematical model of the AFE rectifiers with both switched models based on PWM switching strategies and a dynamic time-average model.
2.1. Switched (PWM) Model
Figure 1 depicts the physical topology of the three-phase AFE rectifier, i.e., the SEM model, based on the VOC scheme. The control strategy can be simulated by software-based function modules and then implemented by hardware tools in digital processors with related requirements, including analog-to-digital (A/D) and digital-to-analog (D/A) converters. The dynamic performance of the AFE rectifier topology is practically measured by a dynamic signal analyzer to verify the responses of the rectifier. As shown in Figure 1b, an AFE rectifier, regardless of the switching or average-value model, utilizes a cascaded control approach with outer and inner closed loops. The VOC scheme, as one of the common cascade control methods, uses the outer control loop to regulate the rectifier DC link voltage value via a classic PI controller. The output of the DC link voltage controller provides the reference of the d-axis component of the current vector, which is required to maintain the AFE rectifier output DC voltage at a desired value. To achieve unity PF, another control loop is required to keep the q-axis current at zero. Accordingly, these DC signals, as d- and q-axis current references, are delivered to the inner voltage control loops to regulate the rectifier’s voltage vectors in the d–q axis.
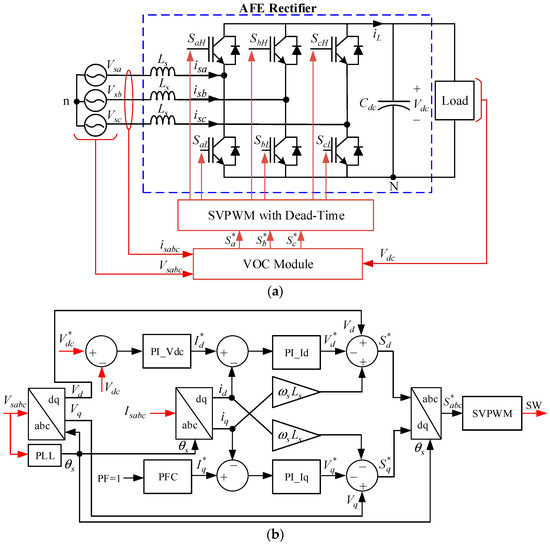
Figure 1.
AFE rectifier topology. (a) SEM configuration. (b) VOC scheme.
In the SEM approach, the active semiconductor switches of the AFE rectifier are considered to be in on/off states to connect or disconnect the DC link voltage to the output load based on the controlled time discontinuous signals. The AC side dynamic requirements of the AFE rectifier with the SEM approach can be developed by Kirchhoff’s voltage law (KVL) equations [40] as follows:
where , , and are the AC side phase voltages, and , , and represent the line currents. , , and denote the switching states of the upper switching devices, i.e., , , and based on Figure 1a, which are equal to 1 when the switch is closed and 0 when the switch is open. The lower switches of the rectifier legs, i.e., , , and are switched complementarily with a specific amount of dead-time applied to gating signals of the upper and lower switches in the same leg. The DC link voltage and capacitor are denoted by and , respectively, and is the rectifier output current.
To employ the VOC scheme, Equations (1) and (3) are transformed into the d–q reference frame as follows:
where and represent the phase voltages in the d–q frame, and are the line currents in the d–q frame, and are the switching states in the d–q frame, and is the power grid angular frequency synchronized to the utility by a software phase-locked loop (PLL).
To acquire the desired DC link voltage , the switching states and should be determined properly, then passed on three-phase values and transformed into the space vector PWM (SVPWM) module. To achieve this goal, according to Figure 1b, the power grid voltages in the d–q axis are added to the output signals of the current controllers and , along with decoupling terms to provide reference switching states, and , as follows:
It should be noted that the VOC scheme requires three AC current sensors, two AC voltage sensors, and one DC voltage sensor. In addition, a PLL is demanded to attain the power grid voltage angle, which is used in the Parke transformation.
2.2. Dynamic Average-Value Model
The standard dynamic average-value model, i.e., SAVM, of the AFE rectifier includes controlled current sources to replace the switching elements and modulation indexes ranging from 0 to 1 instead of switching states. The dynamic model of the AFE rectifier under the synchronous reference frame can be obtained by replacing the time-discontinuous switch states and with time-continuous functions named modulation indexes and in Equations (4)–(6) as follows:
where these time-continuous modulation indexes are, namely, the duty cycles of the phases’ switching devices and can be expressed as follows:
wherein is the one switching period.
Figure 2 shows the overall block diagram of the SAVM for the AFE rectifiers, along with their controller structure. The dynamics explained in Equations (9)–(11) are developed on the right-hand side of Figure 2b with the SAVM of the AFE rectifier block diagram. The DC link voltage regulation and the d–q axis currents’ controls are implemented by the VOC block diagrams illustrated on the left-hand side of Figure 2b. The difference between the desired DC link voltage and the actual , as an error command, is fed into a PI regulator to control the DC link voltage using the proportional gain () and integral gain (). To maintain the DC link voltage at a desired level as well as receive power from the AC grid at unity PF, the output of the DC voltage PI regulator is multiplied by the grid voltages in the d–q axis to accordingly produce the current references in the d–q terms and , which are in perfect match with the grid phase currents. To accurately consider the load impact on the dynamic model, the load current is multiplied by a load coefficient , which is determined by the type and magnitude of the output load, and then applied to the q-axis current control loop as a feedforward term. The current control loops employ the proportional (P) regulator with a gain to generate the modulation indexes in the d–q axis and as the switching duty cycles as expressed below:
where is the approximated value of the grid side filter inductor , multiplied by the grid angular frequency and current terms to compensate the cross-coupling terms of and in the AFE rectifier dynamic model on the right-hand of Figure 2b. To perfectly decouple the current control loops as well as simplify the overall controller implementation, the value can be considered the same as the practical amount [41].
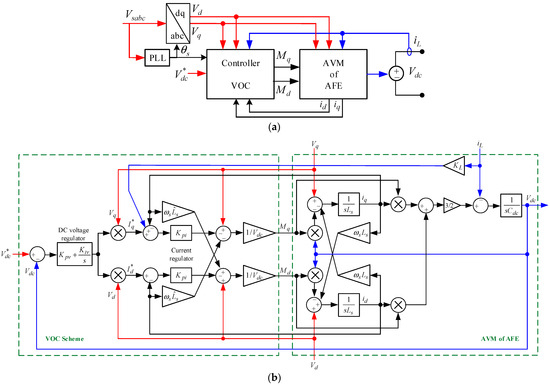
Figure 2.
Dynamic SAVM for the AFE rectifier with VOC. (a) Overall rectifier configuration. (b) Block diagram of the dynamic structure.
3. Proposed Improved AVM
As discussed earlier, the AVM-based AFE rectifiers provide fast simulation running time with less memory usage. However, using linear equations for modeling and integrating them with an ideal switching process leads to impractical voltage and current waveforms with zero distortions. Another drawback of the SAVM approach in comparison with the SEM baseline is the lack of the startup procedure simulation ability because it cannot offer the switching signals in the off status before enabling the controller module. To address those issues, an improved AVM, the IAVM, is proposed for AFE rectifiers to mitigate the dead-time impacts on total harmonic distortion (THD) of currents and precisely start the simulation with an auxiliary circuit model. Figure 3 illustrates the complete structure of the proposed IAVM, including an enhanced distortion model to reduce the dead-time harmonics and auxiliary circuit for the startup process. In this approach, the AFE rectifier is modeled as a controlled current source , which is calculated as
where is the vector of the proposed enhanced phases’ duty cycles. Accordingly, the can be obtained as
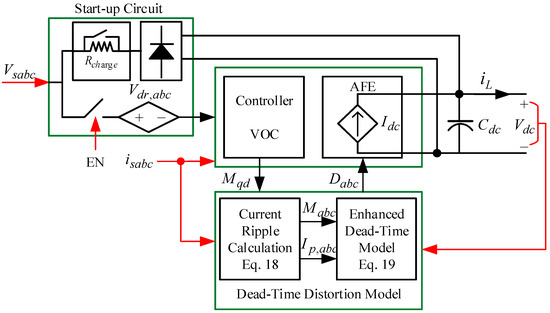
Figure 3.
The overall scheme of the proposed IAVM for AFE rectifiers.
Each block of the proposed IAVM approach along with will be clarified in the following subsections.
3.1. Enhanced Dead-Time Distortion Model
Dead-time of switching devices causes zero crossing distortion on phase currents’ waveforms of the three-phase AFE rectifiers due to its impact on the deviation of the duty cycle of phase voltages (namely ) from the command duty cycles produced by controller output ( in Equation (12)). This deviation is a result of phase currents’ signs that compel rectifier leg output voltages to be equal to either DC link voltage or zero during dead-time () narrow intervals, correspondingly leading to different from the command duty cycle as follows:
The duty cycle definition in Equation (17), as a conventional two-level distortion model, causes higher harmonics on phases’ currents, which leads to a high THD. To enhance the definition of the dead-time distortion, one effective solution is dividing the into more than two general levels to tackle the current zero crossing distortions. This target can be achieved by considering a ripple current to allocate relevant duty cycles instead of zero. To estimate the ripple current () for each rectifier phase leg, the difference between peak-to-peak ripples () is demanded to be precisely calculated based on the AFE rectifier parameters and variables as follows [42,43]:
here, the modulation index is considered in the range of 0 to because of utilizing the SVPWM scheme instead of sinusoidal PWM. From , the ripple current for each phase current can be approximated as .
According to the ripple current, an improved duty cycle based on an enhanced dead-time distortion model, which is approximated in five levels, is defined to reduce the THD of IAVM as follows [43]:
where is the total time delay over the for each switching period based on the IGBTs turn-on time () and turn-off time (), which can be calculated as
To avoid the gradient transition between turning duty cycle levels ON and OFF, introduced in Equation (15) by active switching devices, an additional three levels are presented in this study using to mitigate the dead-time distortion on currents. Since the dead-time intervals are too short in practice, these half-point values are feasible approximations. The studied five-level dead-time distortion model is illustrated in Figure 4 and integrates the ripple current calculator with the enhanced duty cycle model. A limiter is also added to the model to maintain the outputs of duty cycles in a range between 0 and 1 [43].
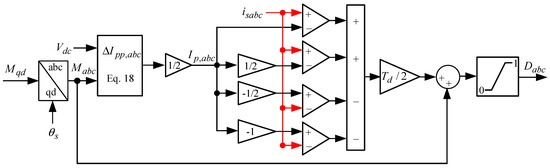
Figure 4.
Block diagram of the enhanced dead-time distortion model.
3.2. Improved Startup Procedure
The practical startup circuit model, as the main part of this IAVM approach, is implemented to enhance the proposed IAVM performance by precisely taking into account the voltage drops of the switching devices (e.g., IGBTs and the freewheeling diodes) and employing a standard three-phase diode rectifier with an enable switch.
According to Figure 3, the total voltage drop () of each phase leg of the AFE rectifier on the IGBTs () and diodes () is implemented as a controlled voltage source. To accurately calculate the as a function of voltages duty cycles and phase currents polarities, the forward voltages of the IGBT switches () and diodes () are required, along with their internal resistances and , respectively. Consequently, the total voltage drop of each phase can be calculated as [43,44]
where
As the last part of the IAVM approach, the three-phase standard diode rectifier is added, along with the enable switch (shown by the EN switch in Figure 3), to simulate the AFE rectifier before connecting to the VOC controller. The reason behind this is that during the AVM-based rectifier startup for real hardware test of AFE, there are no control signals to enable the IGBT switches ON and OFF. In other words, IAVM will short-circuit the three phases during startup. To avoid this issue, an enabled switch will disconnect the IAVM circuit before the VOC controller is initiated. As a result, the proposed IAVM baseline operation is similar to the SEM before the controller is connected and is verified by the simulation results in the following section.
4. Results
To verify the performance of the proposed methodologies, a grid-connected AFE rectifier system with a PFC module, whose nominal circuit parameters as well as controller gains are listed in Table 1, is considered for implementation. Simulation studies are conducted in MATLAB/Simulink R2023a environment to demonstrate the validity of the detailed switching model, along with the electrical circuit utilized in all mentioned approaches, including SEM, SAVM, and IAVM. The proposed IAVM baseline and SAVM are implemented by MATLAB S-Functions for all the blocks and the SimScape Tools for all electrical circuits employed in the SEM baseline. The tested AFE rectifier topology is shown in Figure 5, wherein a pre-charging relay is used for soft-starting the system.

Table 1.
Main parameters of the studied AFE rectifier.
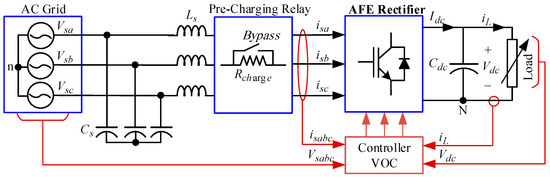
Figure 5.
AFE rectifier with control methodology for test verification.
Several case studies are implemented to compare the operation of the proposed IAVM with the other two algorithms in the conditions of startup and transient behaviors discussed in the following subsections.
4.1. Case 1: Startup Performance
In this study, the transient behavior of the IAVM is tested during the startup conditions under the zero load (open circuit output) to validate the starting procedure performance in comparison with the SAVM and SEM approaches. Figure 6 shows the simulation results under startup transient to start and bring the AFE rectifier DC link voltage from 0 to the desired value of 600 V with zero active power and, consequently, zero phase currents. The operation procedure of this case study includes four stages. During the first stage (from starting to 0.2 s, as shown in Figure 6a), the so-called pre-charging stage, the DC link capacitor is slowly charged from 0 to a safe limit of around 80% of the peak value of input line to line grid voltage (around 440 V) through three pre-charge resistors for each phase. All IGBT devices are OFF during this stage, and pre-charging resistors in series with the boost inductors are connected to the output capacitor via an auxiliary three-phase diode rectifier to limit the current. During the second stage, from 0.2 s to 0.3 s, the bypass relay 1 short-circuits the pre-charging resistors; then, the capacitor is normally charged to using the inductors and the auxiliary diode rectifier. It should be noted that during these two stages, the VOC controller is not connected to the AFE rectifier; thus, control signals are not yet applied to the rectifier. When the voltage reaches over 85% of the desired DC link voltage (600 V), the VOC controller is switched ON and starts the third stage. In the third stage, the auxiliary diode rectifier is disconnected, and the controller is connected to the AFE rectifier by considering the total voltage drop in the IAVM algorithm. During this stage, the controlled d–q axis currents are restricted to 50 A for soft starting, and then at the fourth stage (at 0.35 s), the current upper limit is set to 80 A, allowing a nominal current to flow. According to Figure 6a, by considering this four-stage procedure, the DC link voltage can safely reach its desired value without producing a huge inrush current. The simulation waveforms of for all three baselines closely match each other except for some differences among them during the third stage when the first current limiter is disabled. The simulation results of three-phase grid currents in Figure 6b illustrate the operational differences between the proposed IAVM and the other two approaches as current ripples during no-load conditions. It is observed that the IAVM-based AFE rectifier has lower ripples than the SAVM baseline and significantly lower than the SEM baseline. This is because of the development of enhanced duty cycles for the IAVM to reduce the zero crossing current ripples, as shown in Figure 6c in the upper waveform for the d-axis current.
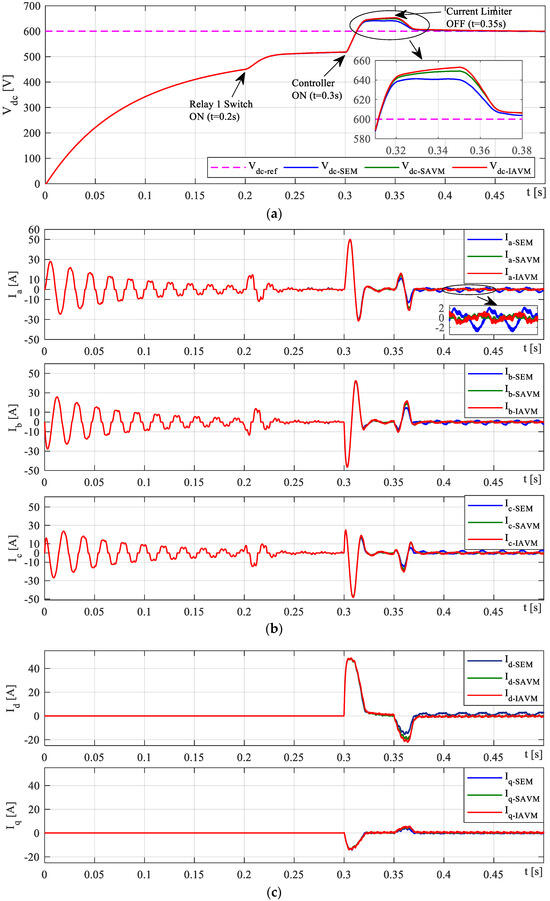
Figure 6.
AFE rectifier no-load startup waveforms for the SEM, SAVM, and IAVM based on the proposed startup procedure. (a) Rectifier DC link voltage; (b) AC-side currents; (c) D-q currents.
To better reveal the studied startup performance differences, some simulations are carried out without startup stages, as shown in Figure 7. From Figure 7a, the phase current peak value is very high when there is no pre-charge relay; however, using the pre-charge relay limits the starting current at a lower level than the nominal current. In addition, without the pre-charging procedure, the controlled d–q-axis currents contain excessive overshoot and undershoot, which is more than 40 A for q-axis current undershoot.
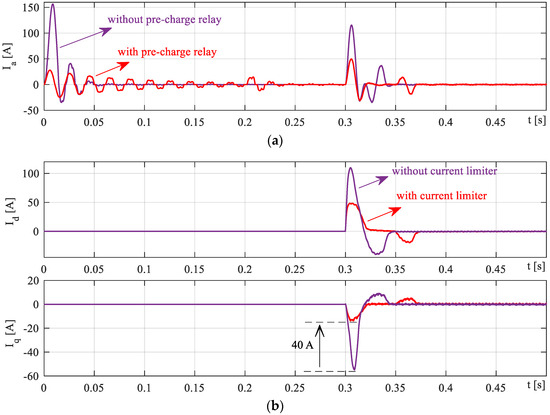
Figure 7.
No-load startup procedure waveforms for the IAVM baseline: (a) AC-side A-phase currents; (b) D-q currents.
4.2. Case 2: Load Responses
The AFE rectifier steady-state current waveforms for the three mentioned baselines are illustrated in Figure 8 for operating power of 3.6 kW and 7.2 kW. Despite Case 1, where the two AVM baselines have similar current waveforms, this case provides different current results, especially at lower power levels because of the longer range of the ripple current . From Figure 8a, for output power 3.6 kW, the current waveform for the SEM approach depicts significant ripples due to switching elements at the high switching frequency. For the SAVM approach, some ripples are still shown because of the conventional two-level duty cycle; however, the IAVM baseline shows better current waveforms where such significant ripples no longer exist. These variances are precisely shown in Figure 8c by their d-axis currents. Similar behaviors are also illustrated by the current waveforms at the output power of 7.2 kW, although the ripple distortions in this study are not as significant as in the previous study with the power level of 3.6 kW.
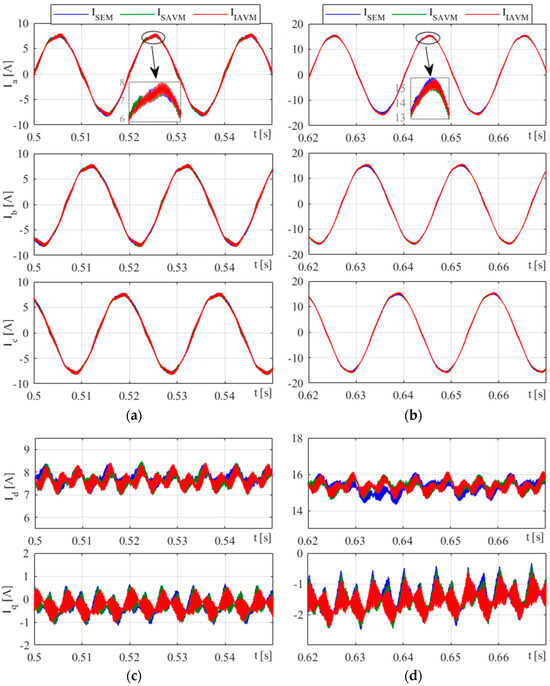
Figure 8.
Load responses of AFE rectifier for the SEM, SAVM, and IAVM baselines: (a) AC-side currents for 3.6 kW load; (b) AC-side currents for 7.2 kW load; (c) D–q currents during 3.6 kW load; (d) D–q currents during 7.2 kW load.
Table 2 summarizes the harmonic distortion results of this case study for both output power levels with THD %, reporting that the IAVM current waveforms include the lowest harmonic distortion for both power rates. It is depicted that at a high-power rate, the harmonic distortion is decreased dramatically for all the models, and THD evaluation is almost the same for the SEM and IAVM baselines. Therefore, the best performance of the proposed IAVM approach can be obtained for applications with low and medium power demands.

Table 2.
Harmonic comparisons for the AFE rectifier models during the steady-state operation.
4.3. Case 3: Transient Performance
This study deals with performance comparisons between the physical SEM and time average model IAVM AFE rectifier during load changes and step transient conditions. Figure 9 shows the rectifier responses for the mentioned baselines during step changes in output resistive loads to ensure the proposed model’s smooth operation. For a fixed DC link voltage reference of 600 V, Figure 9a depicts that both baselines track the desired voltage, although the SEM contains more fluctuations than the IAVM. However, the main difference is illustrated by the controlled d–q axis currents, especially with d-axis current ripples, as shown in Figure 9d. Those significant fluctuations in the d-axis current for the SEM baseline cause more harmonic distortions as well as high switching losses.
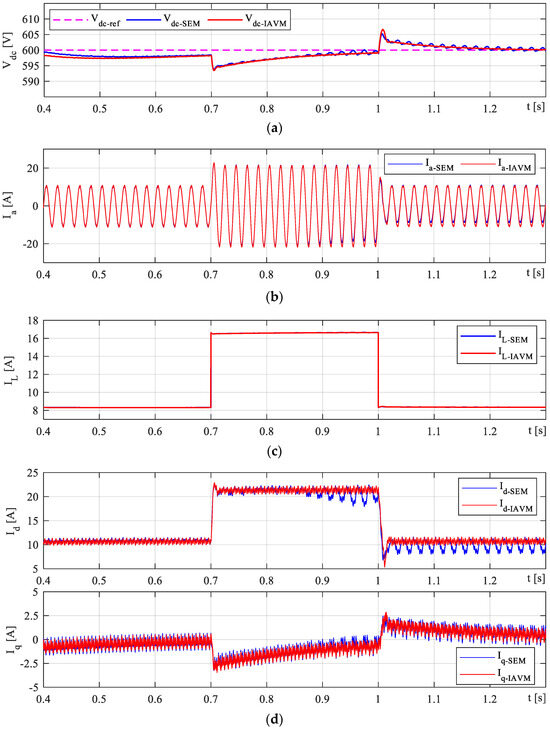
Figure 9.
AFE rectifier transient waveforms for the SEM and IAVM based on the VOC technique: (a) Rectifier DC link voltage; (b) AC-side A-phase current; (c) Load current; (d) D-q currents.
Finally, to verify the unity PF, A-phase voltage and current are simulated for different load amounts using the IAVM baseline, as shown in Figure 10. It is clear that both voltage and current waveforms are in perfect angle match, which leads to proper PFC over low and high output powers.
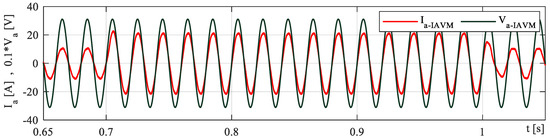
Figure 10.
PF studies for the AFE rectifier during transient operation for the proposed IAVM.
5. Conclusions
This article presents a useful methodology to implement dynamic AVM of AFE rectifiers under VOC-based controllers. Unlike the SEM baselines, the use of AVM approaches can significantly decrease the computational burden (which is about 200 times faster than a SEM baseline) while maintaining the transient performance of these topologies. An enhanced AVM baseline is proposed by precisely considering the dead-time distortions and total voltage drops on switching devices during various operating circumstances. Based on the comparative studies, it has been illustrated that such an improved model includes fewer harmonic distortions and lower current ripples. A good part of the proposed model is the practical startup circuit, which leads to the smoothest operation of the AFE rectifier. In addition, it is shown that the IAVM has low THD because of employing the enhanced five-level duty cycle scheme by developing the conventional two-level dead-time distortion model with maximum peak ripple of phase currents. It is evaluated that the proposed IAVM can be an accurate alternative for the actual SEM-based AFE rectifier, which can be used in industries to develop software. Furthermore, the proposed system can be utilized for modern plug-in electric vehicle battery chargers because of its quick response and lower current distortions.
Funding
This research received no external funding.
Data Availability Statement
Derived data supporting the findings of this study are available from the author on request.
Acknowledgments
The author would like to thank Hamed Hashemi-Dezaki with the Optics11 company for his careful help during the simulations and also express his appreciation to Petr Kadanik from the AMP X company for clarifications on the project challenges.
Conflicts of Interest
The author has been involved as a senior software developer in Company ZF Engineering Pilsen s.r.o.
References
- Buticchi, G.; Lam, C.-S.; Xinbo, R.; Liserre, M.; Barater, D.; Benbouzid, M.; Gomis-Bellmunt, O.; Pamos-Paja, C.A.; Kumar, C.; Zhu, R. The role of renewable energy system in reshaping the electrical grid scenario. IEEE Open J. Ind. Electron. 2021, 2, 451–468. [Google Scholar] [CrossRef]
- Ebadpour, M. A Multiport Isolated DC-DC Converter for Plug-in Electric Vehicles Based on Combination of Photovoltaic Systems and Power Grid. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 1–3 February 2021. [Google Scholar]
- Esenboğa, B.; Demirdelen, T. Soft-Switching Smart Transformer Design and Application for Photovoltaic Integrated Smart City Power Distribution. Sustainability 2023, 15, 32. [Google Scholar] [CrossRef]
- Ebadpour, M.; Sharifian, M.B.B. Cascade H-Bridge Multilevel Inverter with Low Output Harmonics for Electric/Hybrid Electric Vehicle Applications. Int. Rev. Electr. Eng. 2012, 7, 3248–3256. [Google Scholar]
- Planès, T.; Delbecq, S.; Pommier-Budinger, V.; Bénard, E. Modeling and Design Optimization of an Electric Environmental Control System for Commercial Passenger Aircraft. Aerospace 2023, 10, 260. [Google Scholar] [CrossRef]
- Alduraibi, A.; Yaghoobi, J.; Solatialkaran, D.; Zare, F. A Modular Power Converter with Active Front-End System to Mitigate Harmonics in Distribution Networks. IEEE Trans. Emerg. Sel. Topics Power Electron. 2021, 9, 1725–1735. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Sul, S.-K. Stability Analysis of Active Front End and Permanent Magnet Synchronous Generator with Back EMF-Based Sensorless Control for DC Marine Vessels. IEEE Trans. Power Electron. 2023, 38, 5411–5421. [Google Scholar] [CrossRef]
- Zhaksylyk, A.; Rasool, H.; Abramushkina, E.; Chakraborty, S.; Geury, T.; El Baghdadi, M.; Hegazy, O. Review of Active Front-End Rectifiers in EV DC Charging Applications. Batteries 2023, 9, 150. [Google Scholar] [CrossRef]
- Bagheri, N.; Alipour, H.; Mohammadian, L.; Beiza, J.; Ebadpour, M. A Multiport Isolated Resonant LLC Converter for Grid-Tied Renewable Energy Powered Bidirectional EV Charger. Int. J. Ind. Electron. Control Optim. 2023, 6, 37–48. [Google Scholar]
- Prakash, P.P.; Kalpana, R.; Singh, B.; Bhuvaneswari, G. Design and Implementation of Sensorless Voltage Control of Front-End Rectifier for Power Quality Improvement in Telecom System. IEEE Trans. Ind. Appl. 2018, 54, 2438–2448. [Google Scholar] [CrossRef]
- Gong, Z.; Wu, X.; Dai, P.; Zhu, R. Modulated Model Predictive Control for MMC-Based Active Front-End Rectifiers under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2018, 66, 2398–2409. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, L.; Yi, P.; Cui, Y.; Murthy, P.S.; Bazzi, A.M. Conducted Emissions Suppression of Active Front End (AFE) Drive Based on Random Switching Frequency PWM. IEEE Trans. Ind. Appl. 2020, 56, 6598–6607. [Google Scholar] [CrossRef]
- Zare, F.; Davari, P.; Blaabjerg, F. A Modular Active Front-End Rectifier with Electronic Phase Shifting for Harmonic Mitigation in Motor Drive Applications. IEEE Trans. Ind. Appl. 2017, 53, 5440–5450. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in ac adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G. Virtual-flux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Cano, J.M.; Jatskevich, J.; Norniella, J.G.; Davoudi, A.; Wang, X.; Martinez, J.A.; Mehrizi-Sani, A.; Saeedifard, M.; Aliprantis, D.C. Dynamic Average-Value Modeling of Direct Power-Controlled Active Front-End Rectifiers. IEEE Trans. Power Deliv. 2014, 29, 2458–2466. [Google Scholar] [CrossRef]
- Gendrin, M.; Gauthier, J.-Y.; Lin-Shi, X. A Predictive Hybrid Pulse-Width-Modulation Technique for Active-Front-End Rectifiers. IEEE Trans. Power Electron. 2017, 32, 5487–5496. [Google Scholar] [CrossRef]
- Song, Z.; Tian, Y.; Chen, W.; Zou, Z.; Chen, Z. Predictive Duty Cycle Control of Three-Phase Active-Front-End Rectifiers. IEEE Trans. Power Electron. 2016, 31, 698–710. [Google Scholar] [CrossRef]
- Hou, C.-C. A Multicarrier PWM for Parallel Three-Phase Active Front-End Converters. IEEE Trans. Power Electron. 2013, 28, 2753–2759. [Google Scholar] [CrossRef]
- Wiechmann, E.P.; Burgos, R.P.; Holtz, J. Active Front-End Converter for Medium-Voltage Current-Source Drives Using Sequential-Sampling Synchronous Space-Vector Modulation. IEEE Trans. Ind. Electron. 2003, 50, 1275–1289. [Google Scholar] [CrossRef]
- Divakar; Dwivedi, P.; Bose, S.; Pandey, S. Comparative Analysis of PI Control with Anti-Windup Schemes for Front-end Rectifier. In Proceedings of the IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020. [Google Scholar]
- Cittanti, D.; Gregorio, M.; Bossotto, E.; Mandrile, F.; Bojoi, R. Full Digital Control and Multi-Loop Tuning of a Three-Level T-Type Rectifier for Electric Vehicle Ultra-Fast Battery Chargers. Electronics 2021, 10, 1453. [Google Scholar] [CrossRef]
- Chiniforoosh, S.; Jatskevich, J.; Yazdani, A.; Sood, V.; Dinavahi, V.; Martinez, J.; Ramirez, A. Definitions and applications of dynamic average models for the analysis of power systems. IEEE Trans. Power Deliv. 2010, 25, 2655–2669. [Google Scholar] [CrossRef]
- Cross, A.; Baghramian, A.; Forsyth, A. Approximate, average, dynamic models of uncontrolled rectifiers for aircraft applications. IET Power Electron. 2009, 2, 398–409. [Google Scholar] [CrossRef]
- Aliprantis, D.C.; Sudhoff, S.D.; Kuhn, B.T. A brushless exciter model incorporating multiple rectifier modes and preisach’s hysteresis theory. IEEE Trans. Energy Convers. 2006, 21, 136–147. [Google Scholar] [CrossRef]
- Daryabak, M.; Filizadeh, S.; Bagheri Vandaei, A. Dynamic phasor modeling of LCC-HVDC systems: Unbalanced operation and commutation failure. Can. J. Elect. Comput. Eng. 2019, 42, 121–131. [Google Scholar] [CrossRef]
- Sudhoff, S.D.; Corzine, K.A.; Hegner, H.J.; Delisle, D.E. Transient and dynamic average-value modeling of synchronous machine fed load-commutated converters. IEEE Trans. Energy Convers. 1996, 11, 508–514. [Google Scholar] [CrossRef]
- Jatskevich, J.; Pekarek, S.D.; Davoudi, A. Fast procedure for constructing an accurate dynamic average-value model of synchronous machine-rectifier system. IEEE Trans. Energy Convers. 2006, 21, 435–441. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Amiri, N.; Wang, L.; Jatskevich, J. Parametric average-value modeling of thyristor-controlled rectifiers with internal faults and asymmetrical operation. IEEE Trans. Power Del. 2019, 34, 773–776. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Amiri, N.; Jatskevich, J. Average-Value Modeling of Line-Commutated AC–DC Converters with Unbalanced AC Network. IEEE Trans. Energy Convers. 2021, 36, 3533–3544. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. A unified dynamic model and control for the voltage-source converter under unbalanced grid conditions. IEEE Trans. Power Deliv. 2006, 21, 1620–1629. [Google Scholar] [CrossRef]
- Ebadpour, M.; Radmand, F. Hyper-plane sliding mode control of non-minimum phase grid-connected zeta converter. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 1–3 February 2021. [Google Scholar]
- Nikkhajoei, H.; Iravani, R. Dynamic model and control of ac-dc-ac voltage-source converter system for distributed resources. IEEE Trans. Power Deliv. 2007, 22, 1169–1178. [Google Scholar] [CrossRef]
- Lau, W.H.; Zhou, B.; Chung, H.S.H. Compact analytical solutions for determining the spectral characteristics of multicarrier-based multi-level PWM. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1577–1585. [Google Scholar] [CrossRef]
- Chierchie, F.; Stefanazzi, L.; Paolini, E.E.; Oliva, A.R. Frequency analysis of PWM inverters with dead-time for arbitrary modulating signals. IEEE Trans. Power Electron. 2014, 29, 2850–2860. [Google Scholar] [CrossRef]
- Ahmed, S.; Boroyevich, D.; Wang, F.; Burgos, R. Development of a new voltage source inverter (VSI) average model including low-frequency harmonics. In Proceedings of the 25th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010. [Google Scholar]
- Guha, A.; Narayanan, G. Average modeling of a voltage source inverter with dead-time in a synchronous reference frame. In Proceedings of the 2013 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Bangalore, India, 10–13 November 2013. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics. In Converters, Application Design, 3rd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Shen, Z.; Jiang, D. Dead-time effect compensation method based on current ripple prediction for voltage-source inverters. IEEE Trans. Power Electron. 2019, 34, 971–983. [Google Scholar] [CrossRef]
- Banerji, A.; Patil, A.; Patil, S.; Pakhare, A.; Ugale, R.T. Design, analysis and fast tuning of active front end rectifier controller with comparative performance evaluation. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022. [Google Scholar]
- Hou, C.-C.; Cheng, P.-T. Experimental verification of the active front-end converters dynamic model and control designs. IEEE Trans. Power Electron. 2011, 26, 1112–1118. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Evaluation of current ripple amplitude in three-phase PWM voltage source inverters. In Proceedings of the International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia, 5–7 June 2013. [Google Scholar]
- Rahman, A.N.; Chiu, H.J.; Lian, K.L. Enhanced Time Average Model of Three Phase Voltage Source Converter Taking Dead-Time Distortion Effect into Account. IEEE Access 2021, 9, 23648–23659. [Google Scholar] [CrossRef]
- Ebadpour, M.; Jamshidi, M.; Talla, J.; Hashemi-Dezaki, H.; Peroutka, Z. Digital Twin Model of Electric Drives Empowered by EKF. Sensors 2023, 23, 2006. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).