Implementation of an FPGA-Based 3D Shape Measurement System Using High-Level Synthesis
Abstract
1. Introduction
2. Principles of Phase Measurement Methods
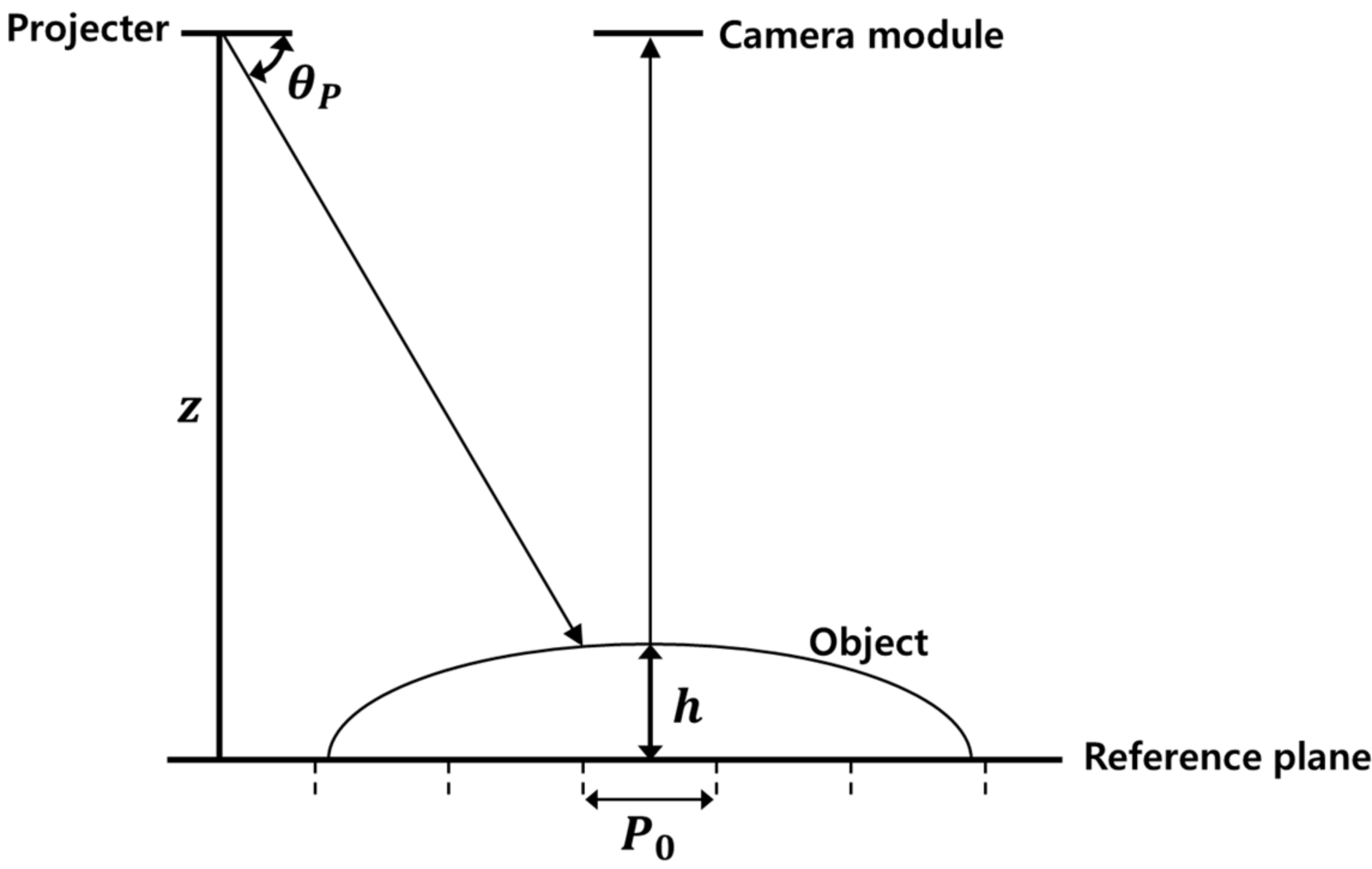
2.1. Phase Measuring Profilometry (PMP)
2.2. Dual-Wavelength TPU Method
3. The 3D Shape Measurement Algorithm Accelerator
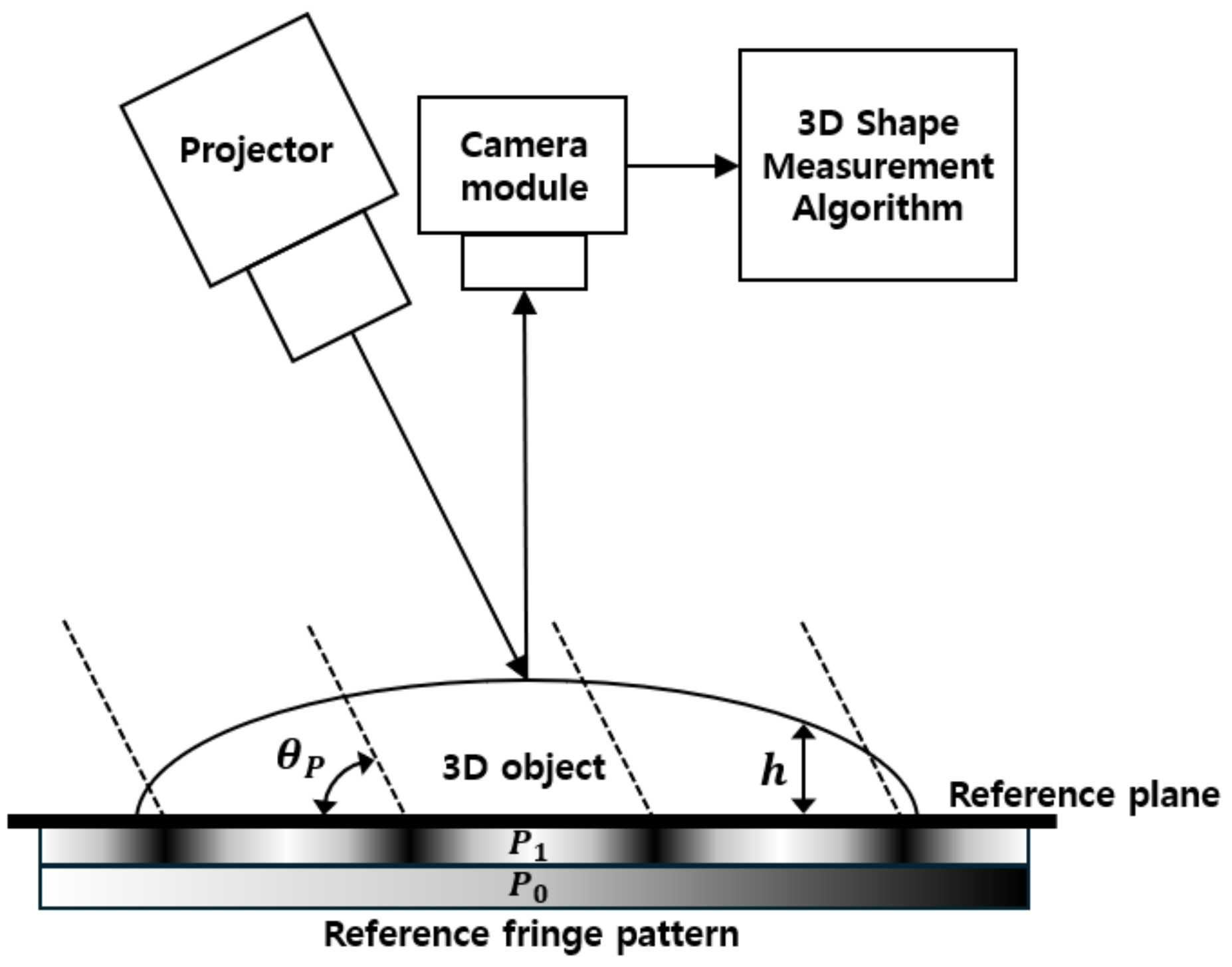
3.1. The 3D Shape Measurement Algorithm
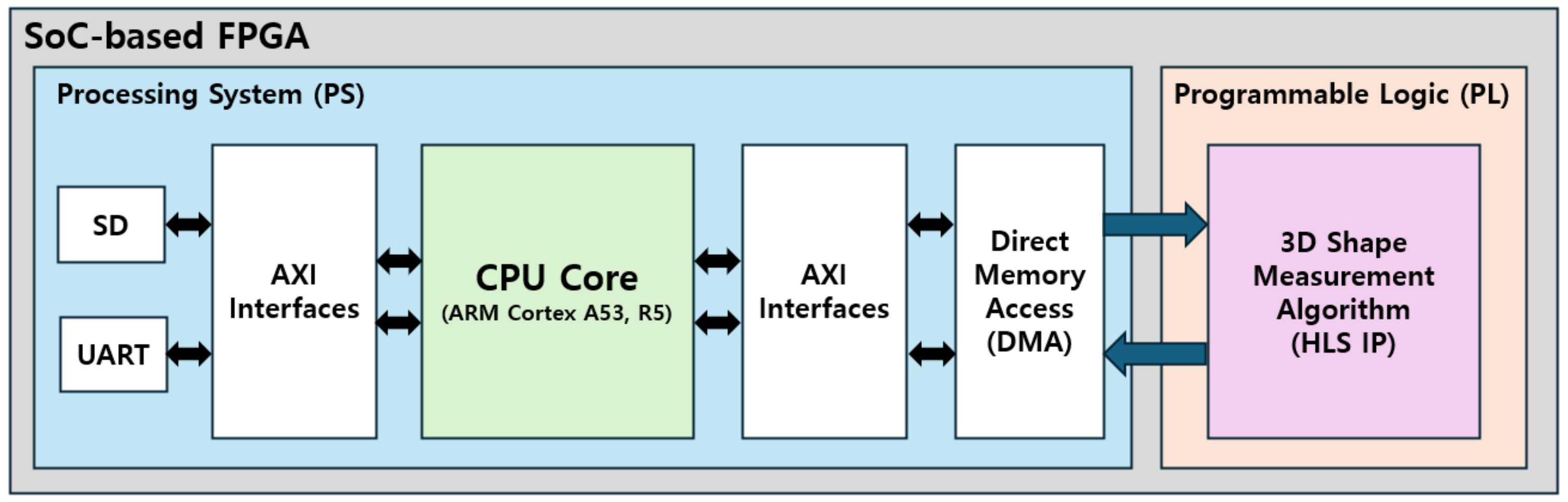
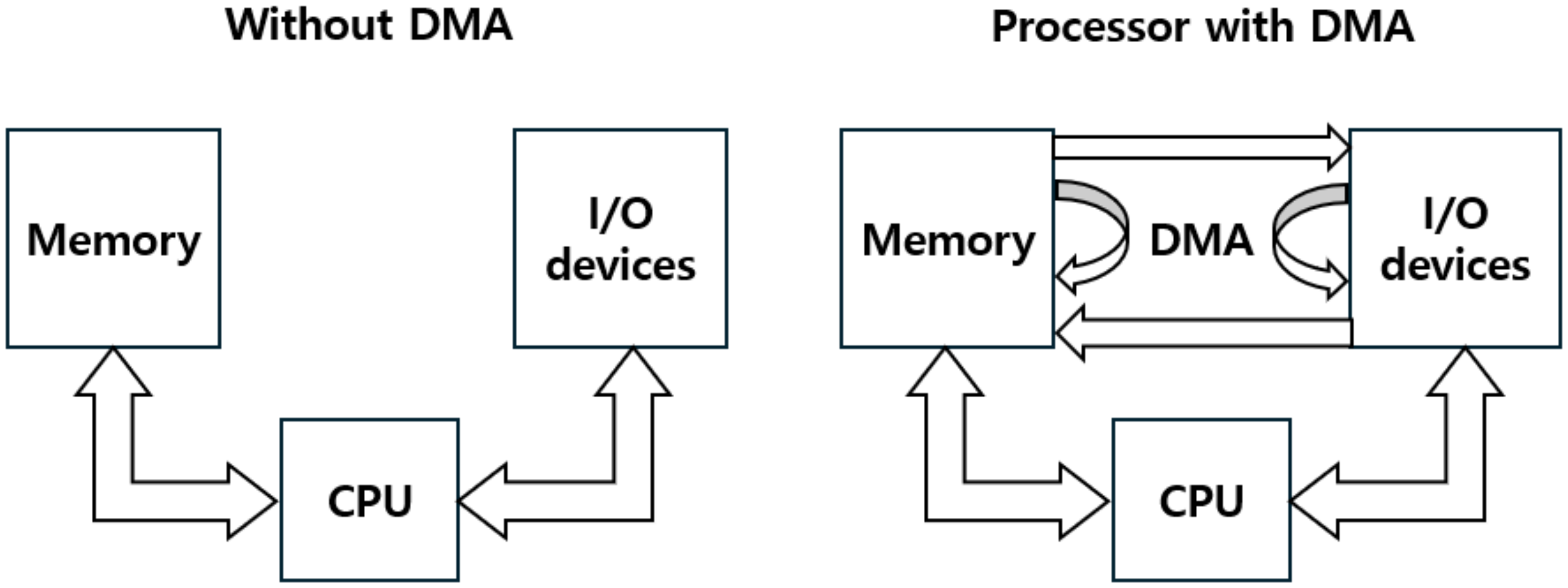
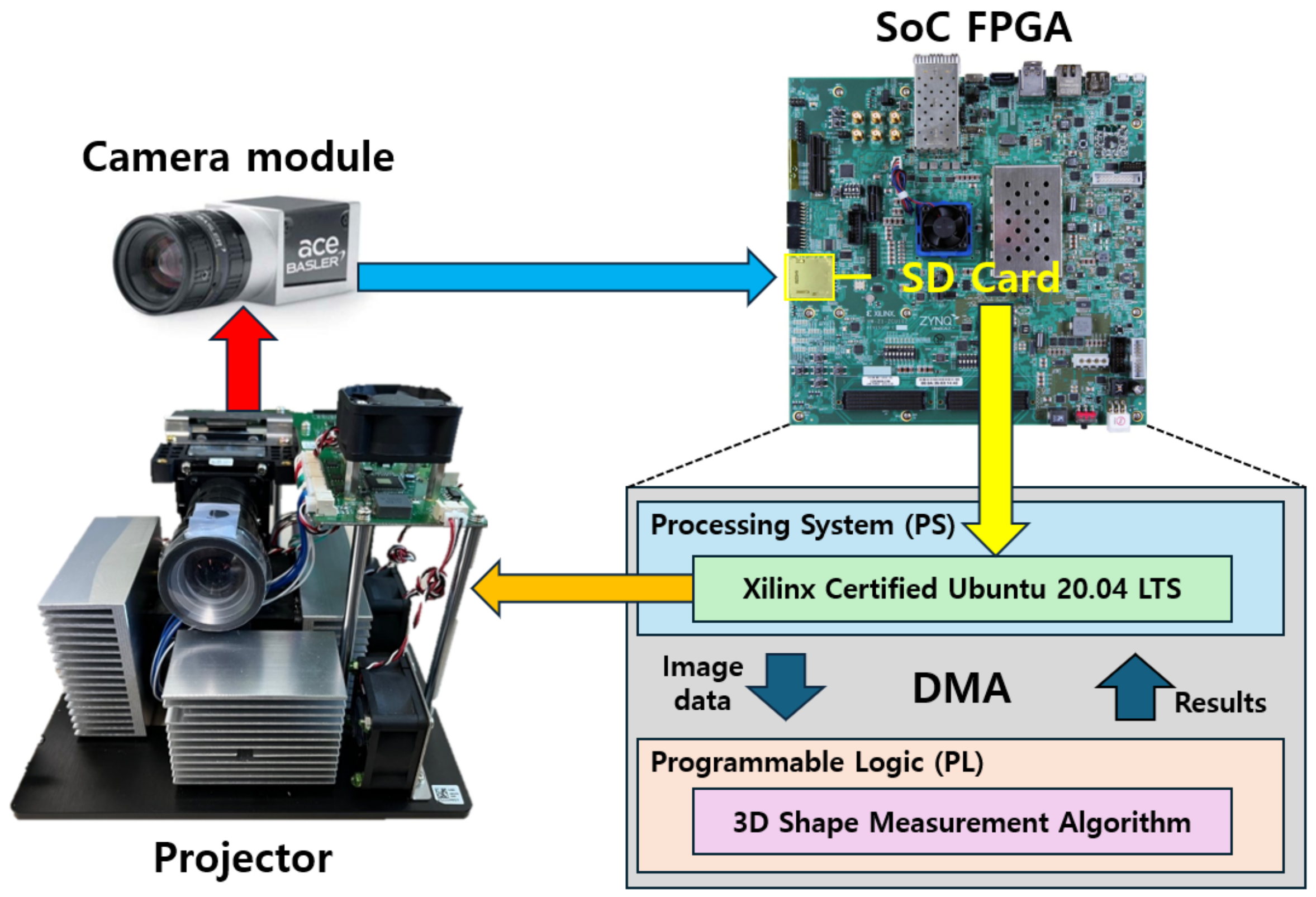
3.2. Structure of the SoC-Type FPGA-Based Algorithm Accelerator
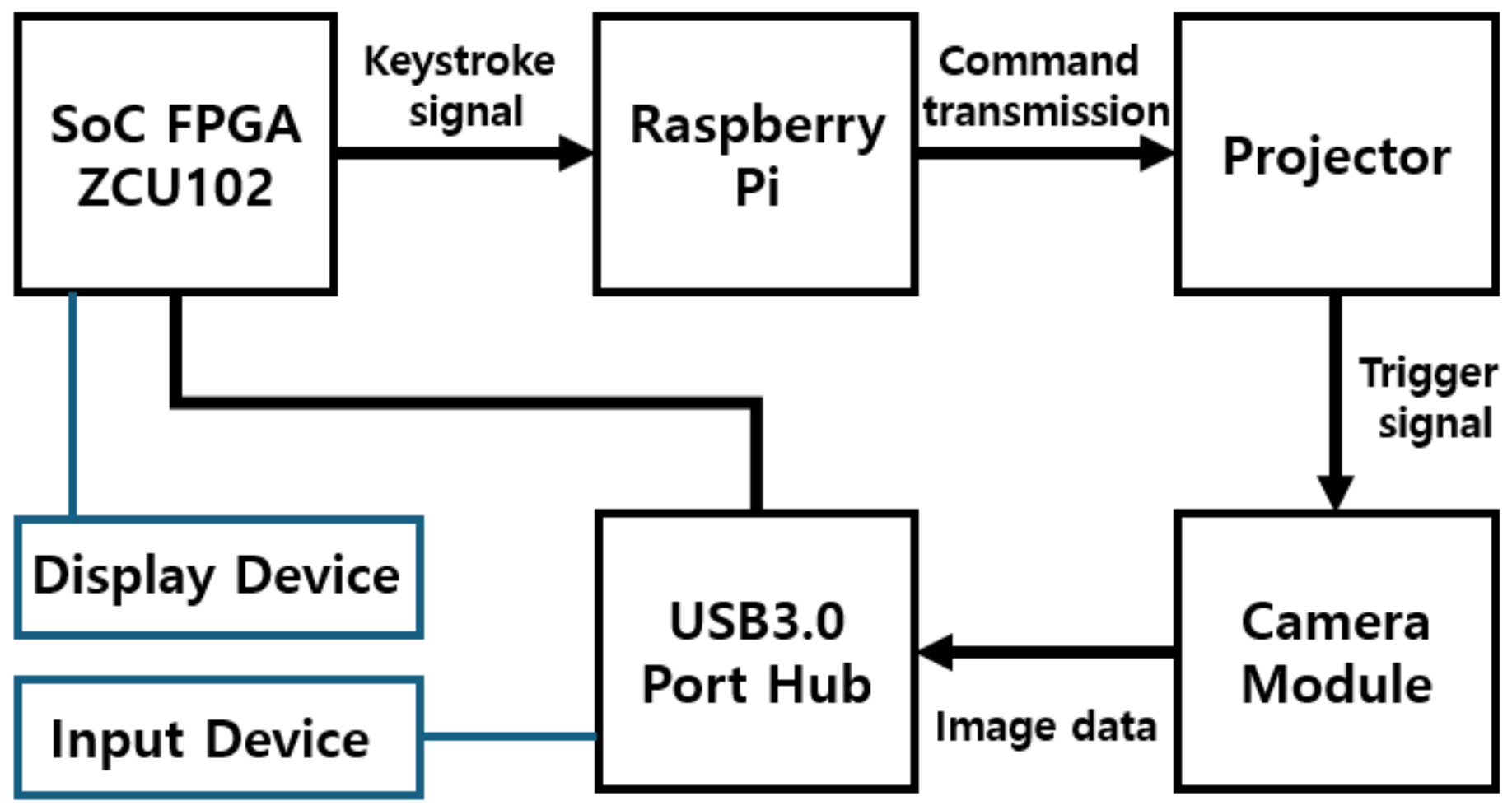
4. SoC-Type FPGA-Based 3D Shape Measurement System
4.1. Design of the SoC-Type FPGA-Based 3D Shape Measurement System
4.2. Structure of the SoC-Type FPGA-Based 3D Shape Measurement System
5. Experiments
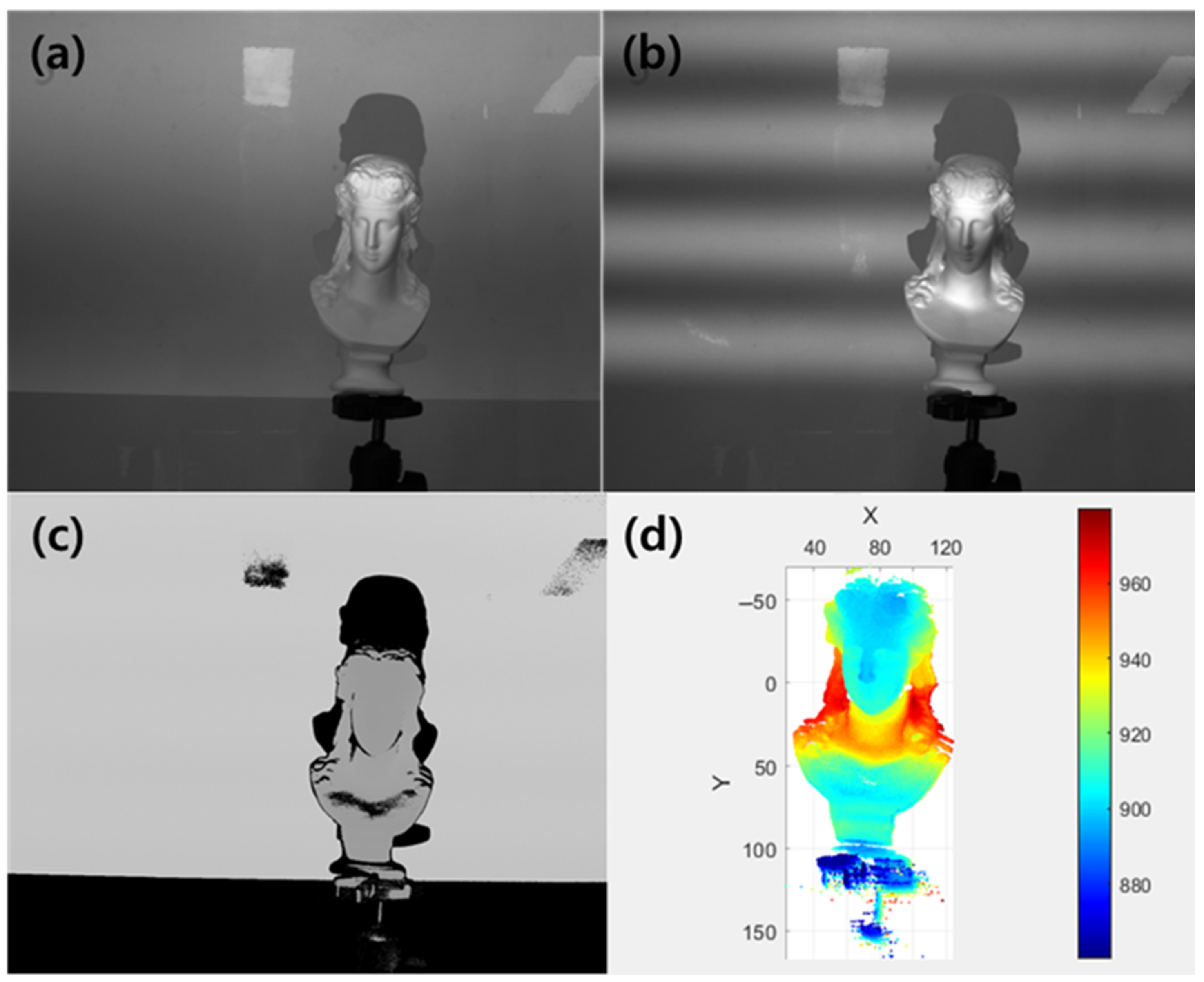
5.1. Experimental Environment and Methods
5.2. Experimental Results and Performance Evaluation
6. Conclusions
6.1. Summary of Major Findings
6.2. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, G.-S.; Park, Y.-C. A Study on the Compensation of Thermal Errors for Phase Measuring Profilometry. JKAIS 2019, 20, 598–603. [Google Scholar]
- Kim, C.-H.; Ha, M.-H.; Yun, S.-C.; Park, T.-H. AI-based Restoration Reflection Region Method for 3D Automatic Optical Inspection. ICROS 2023, 29, 936–944. [Google Scholar] [CrossRef]
- Buytaert, J.A.N.; Aernouts, J.E.F.; Dirckx, J.J.J. Indentation measurements on the eardrum with automated projection moiré profilometry. Opt. Lasers Eng. 2009, 47, 301–309. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Hsu, F.-H.; Chen, K.-H.; Chen, J.-H.; Hsu, K.Y. Heterodyne moiré surface profilometry. Opt. Express 2014, 22, 2845–2852. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Su, X.; Li, W.; Xiang, L. Application of modulation measurement profilometry to objects with surface holes. Appl. Opt. 1999, 38, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Cao, Y.; Chen, C.; Wan, Y.; Fu, G.; Wang, Y. Computer-generated Moiré profilometry. Opt. Express 2017, 25, 26815–26824. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Cao, Y.; Li, H.; An, H.; Wu, H. Spatial computer-generated Moiré profilometry. Sens. Actuators A Phys. 2024, 367, 115054. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, Y.; Wu, H.; Xu, C.; Ruan, G.; Wu, F.; Li, C. Dynamic phase-differencing profilometry with number-theoretical phase unwrapping and interleaved projection. Opt. Express 2024, 32, 527192. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-Transform method of fringe pattern analysis for computed-based topography and interferometry. J. Opt. Soc. Am. A 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef]
- Koo, J.-M.; Cho, T.-H. 3-D Measurement of LED Packages Using Phase Measurement Profilometry. J. Semicond. Disp. Technol. 2011, 10, 17–22. [Google Scholar]
- Kim, H.J.; Kim, J.S.; Joo, H. 3-Dimensional Shape Measurement System for BGA Balls Using PMP Method. J. Inst. Control Robot. Syst. 2016, 22, 59–65. [Google Scholar] [CrossRef]
- Koo, J.-M.; Cho, T.-H. A 3D measurement system based on a double frequency method using Fourier transform profilometry. J. Korea Inst. Inf. Commun. Eng. 2015, 19, 1485–1492. [Google Scholar]
- Chen, K.; Xi, J.; Yu, Y. Quality-guided spatial phase unwrapping algorithm for fast three-dimensional measurement. Opt. Commun. 2013, 294, 139–147. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Xu, C.; Cao, Y.; Wu, H.; Li, H.; Zhang, H.; An, H. Curtain-type phase unwrapping algorithm. Opt. Eng. 2022, 61, 044103. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, W.; Zhang, Q. High-speed three-dimensional shape measurement based on shifting Gray-code light. Opt. Express 2019, 27, 22631–22644. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Chen, W.; Tan, Y. Phase-unwrapping algorithm for the measurement of three-dimensional object shapes. Appl. Opt. 1994, 33, 4497–4500. [Google Scholar] [CrossRef]
- Zheng, D.; Da, F. Phase coding method for absolute phase retrieval with a large number of codewords. Opt. Express 2012, 20, 24139–24150. [Google Scholar] [CrossRef]
- An, H.; Cao, Y.; Li, H.; Zhang, H. Temporal Phase Unwrapping Based on Unequal Phase-Shifting Code. IEEE Trans. Image Process. 2023, 32, 1432–1441. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Cao, Y.; Wu, H.; Wei, Z. Absolute phase retrieval based on fringe amplitude encoding without any additional auxiliary pattern. Opt. Express 2023, 31, 41952–41966. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Royer, D.; Yau, S.-T. GPU-assisted high-resolution, real-time 3-D shape measurement. Opt. Express 2006, 14, 9120–9129. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, D.; Wang, Z.; Kieu, H.; Le, M. Real-time, high-accuracy 3D imaging and shape measurement. Appl. Opt. 2015, 54, A9–A17. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.-H.; Lee, H.; Ok, S.-H. Acceleration of FPGA-based 3D Shape Measurement Algorithm. In Proceedings of the Summer Annual Conference of IEIE, Jeju, Republic of Korea, 26–28 June 2024. [Google Scholar]
- Agrawal, R.; de Castro, L.; Yang, G.; Juvekar, C.; Yazicigil, R.; Chandrakasan, A.; Vaikuntanathan, V.; Joshi, A. FAB: An FPGA-based Accelerator for Bootstrappable Fully Homomorphic Encryption. In Proceedings of the 2023 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Montreal, QC, Canada, 25 February–1 March 2023. [Google Scholar]
- Zhai, J.; Li, B.; Lv, S.; Zhou, Q. FPGA-Based Vehicle Detection and Tracking Accelerator. Sensors 2023, 23, 2208. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Liu, K.; Liu, W.; Sun, X.; Ding, C.; Li, S. An Overlay Accelerator of DeepLab CNN for Spacecraft Image Segmentation on FPGA. Remote Sens. 2024, 16, 89. [Google Scholar] [CrossRef]
- George, A.D.; Wilson, C.M. Onboard processing with hybrid and reconfigurable computing on small satellites. Proc. IEEE 2018, 106, 458–470. [Google Scholar] [CrossRef]
- Wang, Z.; Du, H.; Bi, H. Out-of-plane shape determination in generalized fringe projection profilometry. Opt. Express 2006, 14, 12122–12133. [Google Scholar] [CrossRef]
- Yen, H.; Tsai, D.; Yang, J. Full-Field 3-D Measurement of Solder Pastes Using LCD-Based Phase Shifting Techniques. IEEE Trans. Electron. Packag. Manuf. 2006, 29, 50–57. [Google Scholar] [CrossRef]
- Lee, H.-K. Development of a Novel 3D Sensor System by Fusing PMP and Stereo Vision. Ph.D. Dissertation, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, Korea, 2010. [Google Scholar]




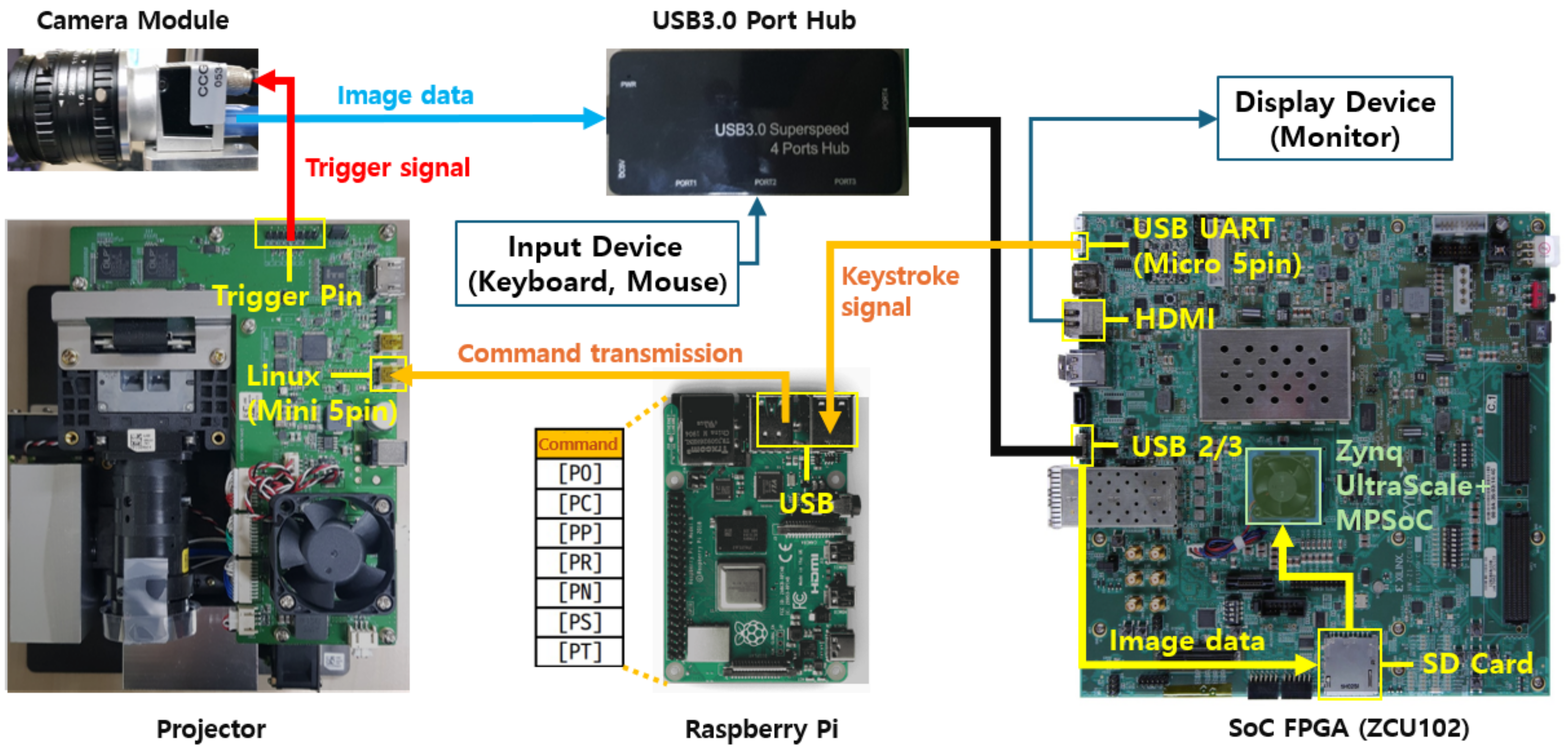



| Key Input | Command | Action |
|---|---|---|
| 1 | [PO] | Play Once |
| 2 | [PC] | Play Continuously |
| 3 | [PP] | Play Pause |
| 4 | [PR] | Play Resume |
| 5 | [PN] | Play Step |
| 6 | [PS] | Play Stop |
| 7 | [PT] | Play Restart |
| System | CPU Model | Clock Speed |
|---|---|---|
| PC | Intel Core i9-10900K | 3.70 GHz |
| SoC-type FPGA (ZCU102) | Quad-core Arm Cortex-A53 | 1.5 GHz |
| System | Software | Version |
|---|---|---|
| PC | Windows 10 | 64 bit |
| Microsoft Visual Studio | 2017 | |
| SoC-type FPGA | Xilinx Certified Ubuntu | 20.04 LTS |
| Vitis HLS | 2020.1 | |
| Vivado | 2020.1 | |
| Xilinx Vitis | 2020.1 |
| LUTs | FF | BRAM (18 K) | DSP |
|---|---|---|---|
| 85,100 | 83,585 | 198 | 637 |
| System | Time(ms) | |||
|---|---|---|---|---|
| (a) | (b) | (c) | (d) | |
| PC | 2622 | 1187 | 719 | 203 |
| SoC-type FPGA | 227 | 88.7 | 52.6 | 13.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-H.; Lee, H.; Ok, S.-H. Implementation of an FPGA-Based 3D Shape Measurement System Using High-Level Synthesis. Electronics 2024, 13, 3282. https://doi.org/10.3390/electronics13163282
Kim T-H, Lee H, Ok S-H. Implementation of an FPGA-Based 3D Shape Measurement System Using High-Level Synthesis. Electronics. 2024; 13(16):3282. https://doi.org/10.3390/electronics13163282
Chicago/Turabian StyleKim, Tae-Hyeon, Hyunki Lee, and Seung-Ho Ok. 2024. "Implementation of an FPGA-Based 3D Shape Measurement System Using High-Level Synthesis" Electronics 13, no. 16: 3282. https://doi.org/10.3390/electronics13163282
APA StyleKim, T.-H., Lee, H., & Ok, S.-H. (2024). Implementation of an FPGA-Based 3D Shape Measurement System Using High-Level Synthesis. Electronics, 13(16), 3282. https://doi.org/10.3390/electronics13163282








