Global Low-Complexity Fault-Tolerant Control for Pure-Feedback Systems with Sensor Faults
Abstract
1. Introduction
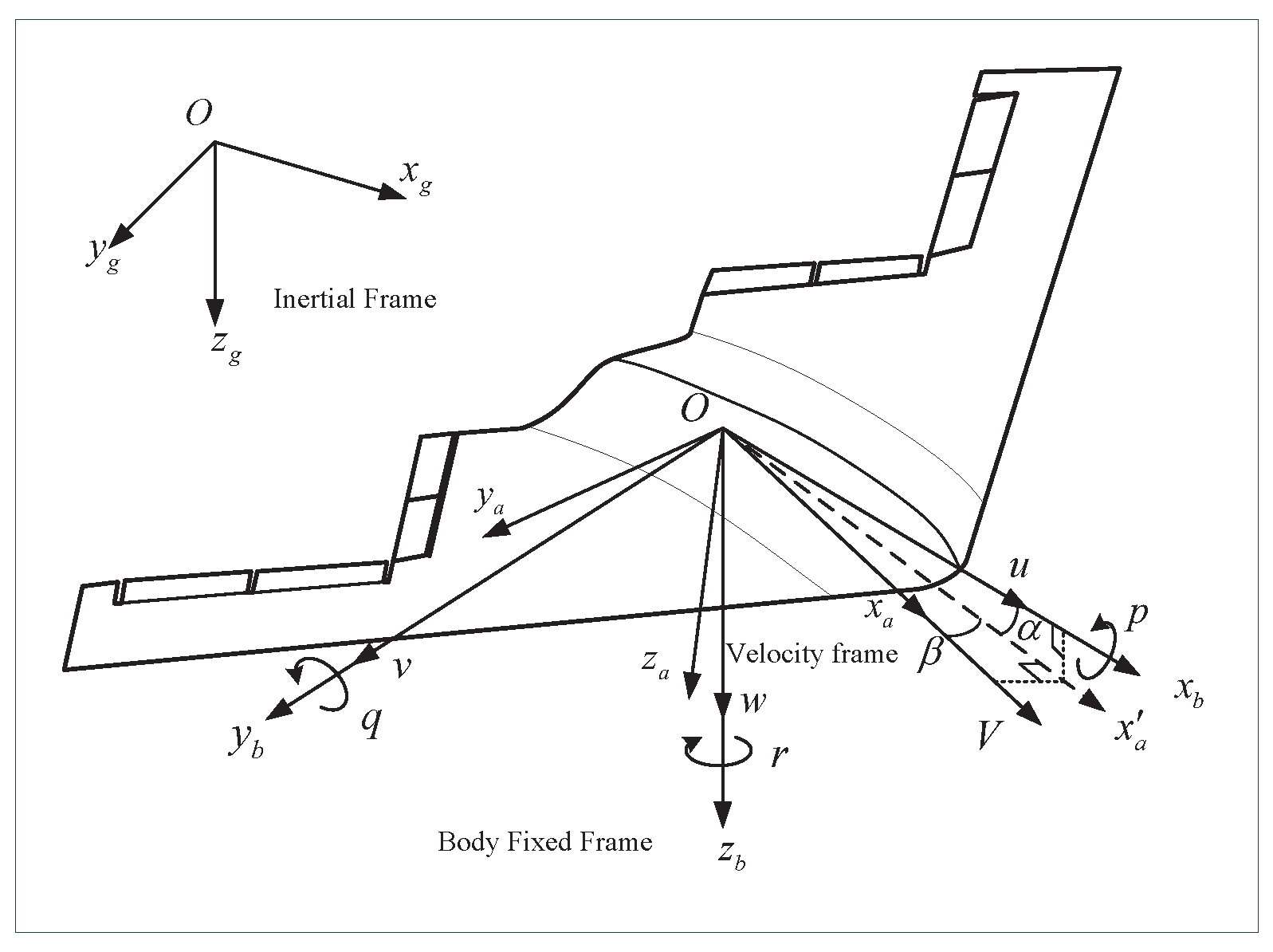
2. Problem Formulation and Preliminaries
3. Controller Design
4. Stability Analysis
5. Further Extension
5.1. Controller Design
5.2. Stability Analysis
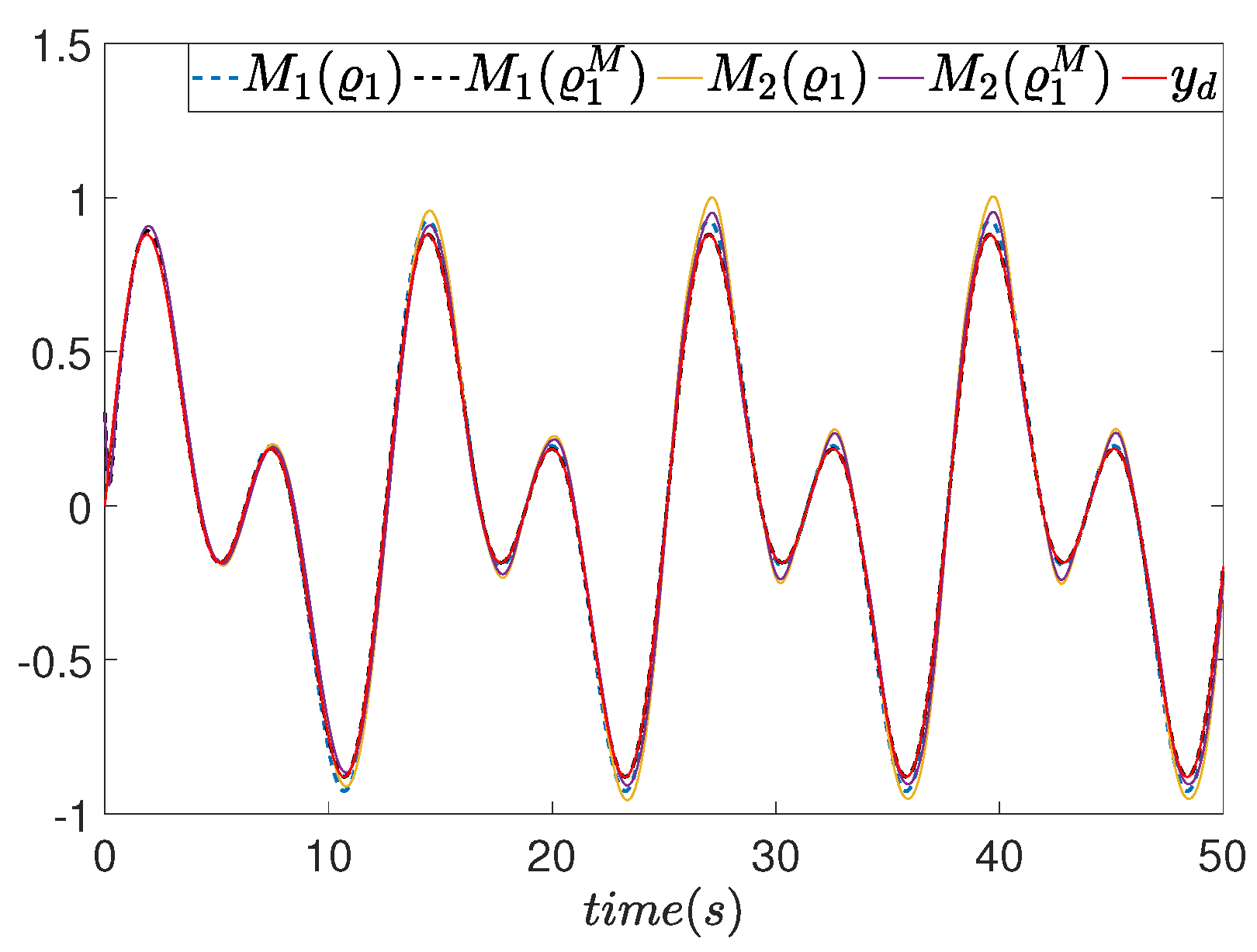
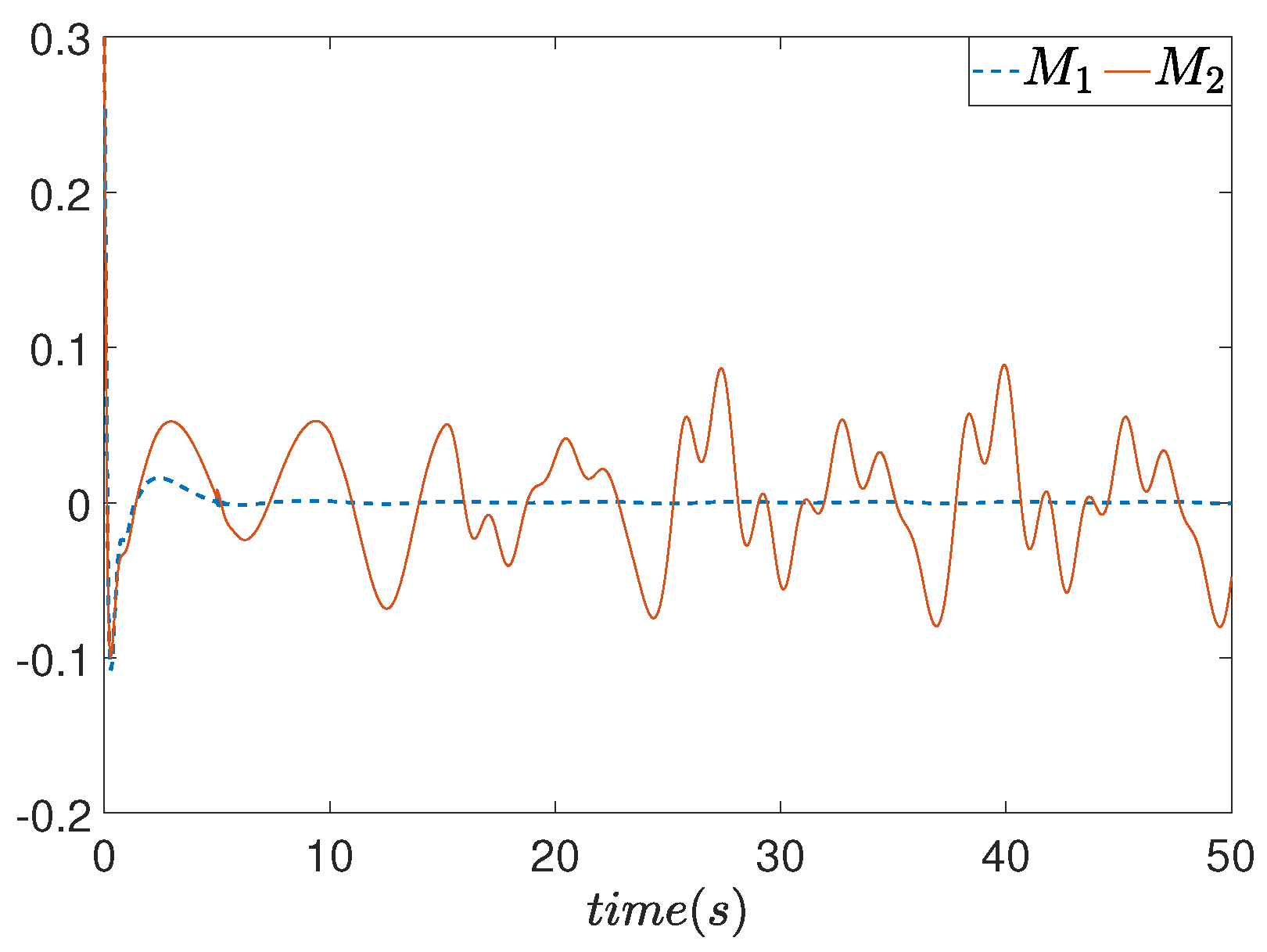
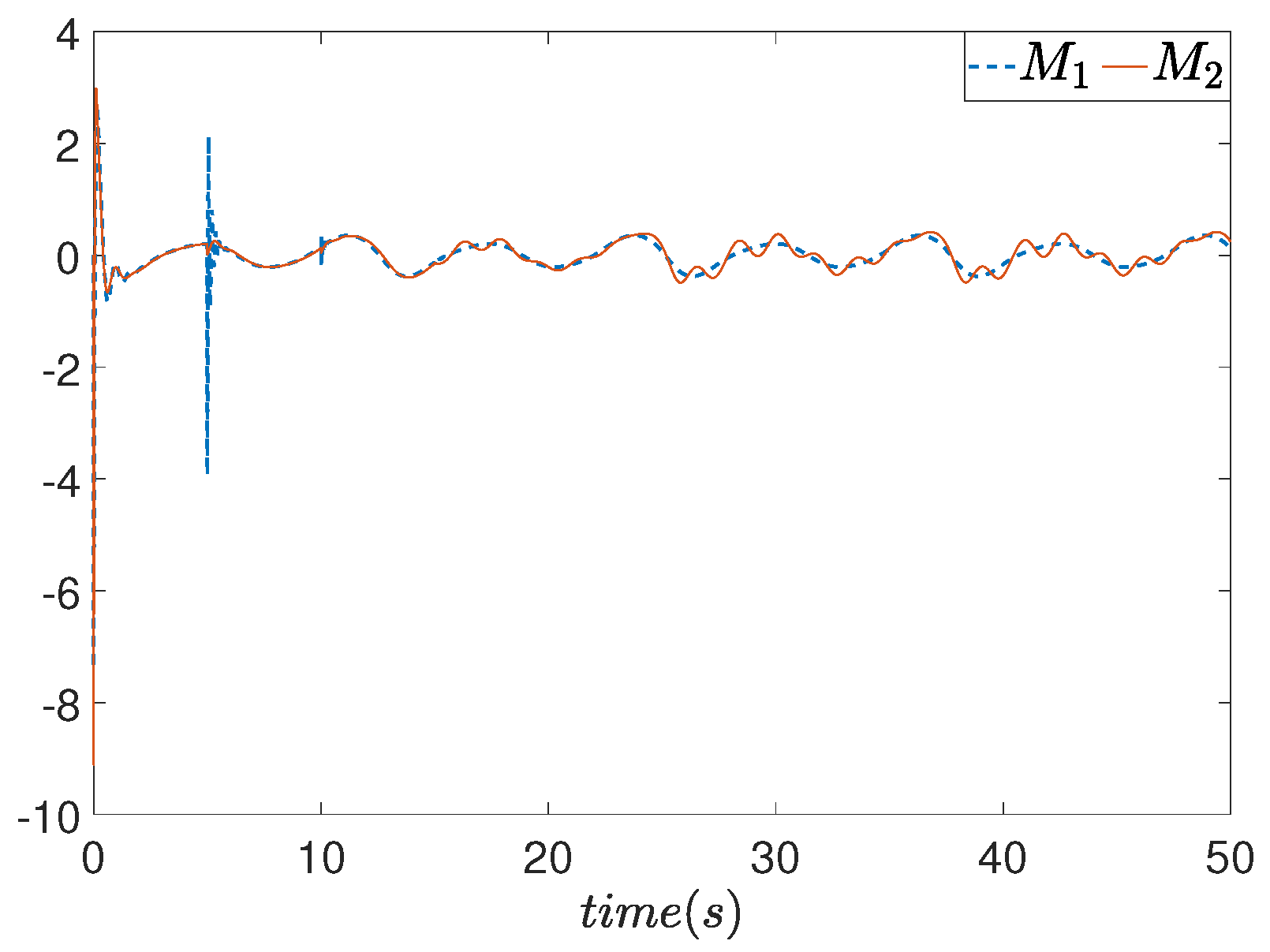
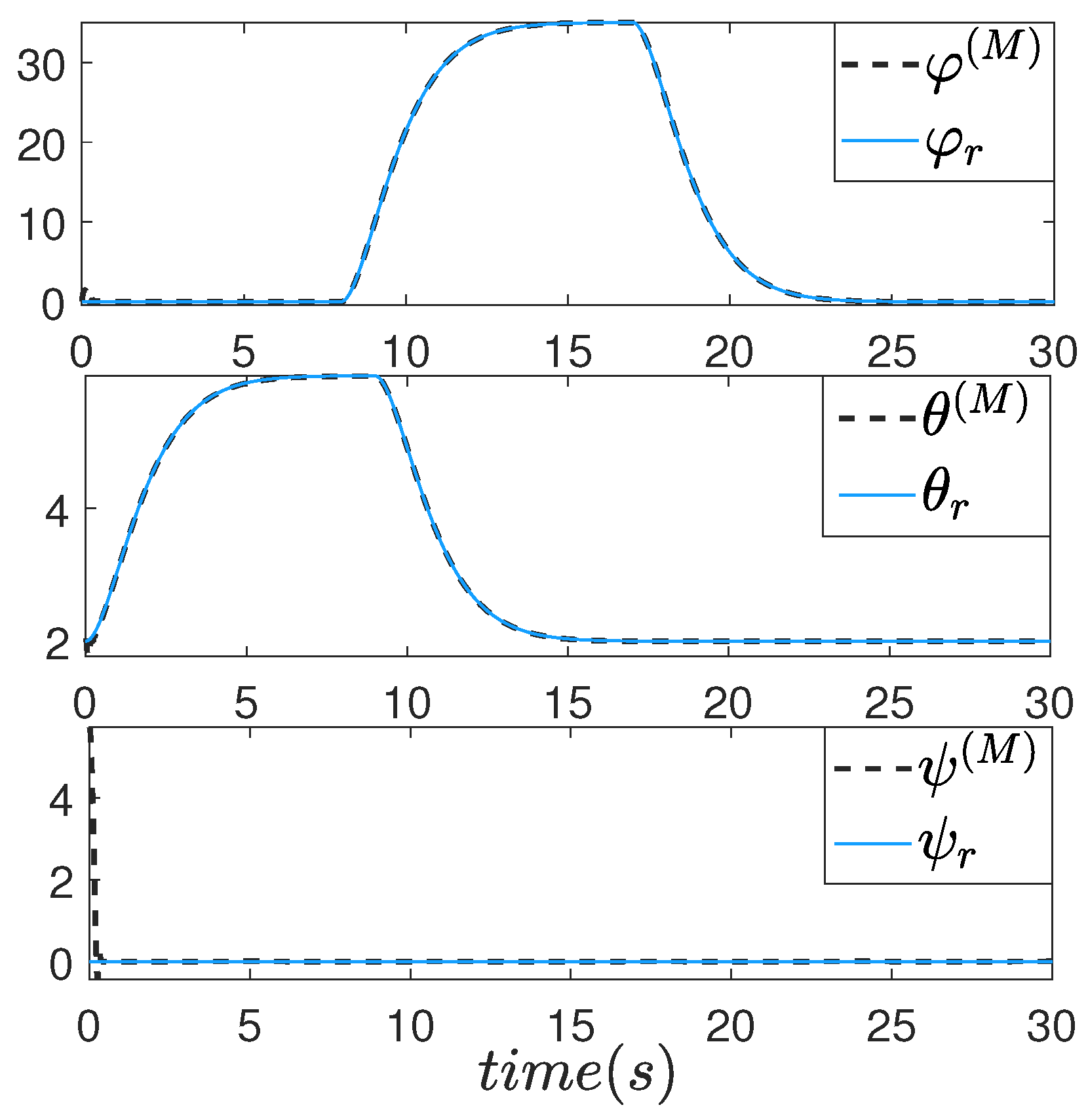
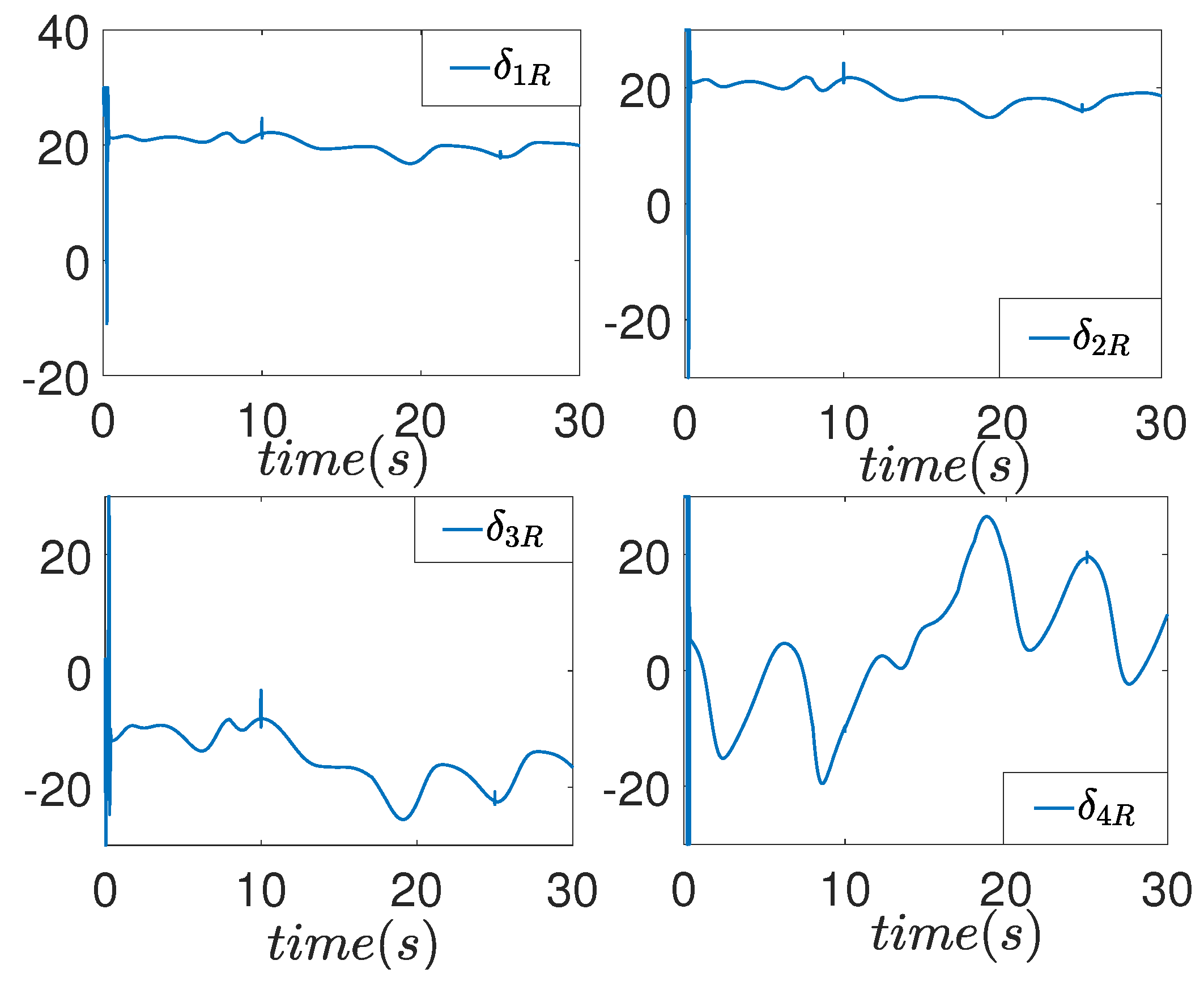
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Huang, H.; Park, J.; Huang, J.; Wang, X.; Lv, M. Adaptive fuzzy control for unknown nonlinear multiagent systems with switching directed communication topologies. IEEE Trans. Fuzzy Syst. 2023, 31, 2487–2494. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, J.; Wen, C.; Su, X. Distributed control of nonlinear systems with unknown time-varying control coefficients: A novel Nussbaum function approach. IEEE Trans. Autom. Control 2023, 68, 4191–4203. [Google Scholar] [CrossRef]
- Meng, W.; Yang, Q.; Jagannathan, S.; Sun, Y. Distributed control of high-order nonlinear input constrained multiagent systems using a backstepping-free method. IEEE Trans. Cybern. 2019, 49, 3923–3933. [Google Scholar] [CrossRef] [PubMed]
- Boulkroune, A.; Haddad, M.; Li, H. Adaptive fuzzy control design for nonlinear systems with actuation and state constraints: An approach with no feasibility condition. ISA Trans. 2023, 142, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, Q.; Hu, C. Adaptive fuzzy command filtered backstepping control for uncertain pure-feedback systems. ISA Trans. 2022, 129, 204–213. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.; Fan, P.; Fu, Z.; Wang, N.; Wang, Y. Adaptive fuzzy fixed time control for pure-feedback stochastic nonlinear systems with full state constraints. J. Frankl. Inst. 2022, 359, 4642–4660. [Google Scholar] [CrossRef]
- Shi, W. Adaptive fuzzy output-feedback control for nonaffine MIMO nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. 2021, 29, 1107–1120. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Z.; Song, S.; Wang, T. Barrier-lyapunov-based adaptive fuzzy finite-time tracking of pure-feedback nonlinear systems with constraints. IEEE Trans. Fuzzy Syst. 2022, 30, 1139–1148. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, T.; Xia, X.; Yi, Y. Finite-time adaptive neural command filtered control for pure-feedback time-varying constrained nonlinear systems with actuator faults. Neurocomputing 2022, 490, 193–205. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Z.; Tao, F.; Song, S.; Wang, T. A simplified adaptive tracking control for nonlinear pure-feedback systems with input delay and full-state constraints. Int. J. Adapt. Control. Signal Process. 2021, 35, 2521–2536. [Google Scholar] [CrossRef]
- Wang, S. Asymptotic tracking control for nonaffine systems with disturbances. IEEE Trans. Circuits Syst.-Express Briefs 2022, 69, 479–483. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, G.; Su, H.; Wang, X. Robust global coordination of networked systems with input saturation and external disturbances. IEEE Trans. Syst. Man-Cybern.-Syst. 2021, 51, 7788–7800. [Google Scholar] [CrossRef]
- Cheng, H.; Song, Y. Neuroadaptive tracking control for uncertain pure-feedback systems under dynamic constraints. Int. J. Robust Nonlinear Control 2023, 33, 6087–6102. [Google Scholar] [CrossRef]
- Niu, B.; Wang, X.; Wang, X.; Li, T. Adaptive barrier-lyapunov-functions based control scheme of nonlinear pure-feedback systems with full state constraints and asymptotic tracking performance. J. Syst. Sci. Complex. 2024, 37, 965–984. [Google Scholar] [CrossRef]
- Zhu, J.; Li, S. Adaptive output dynamic feedback control for nonaffine pure-feedback time delay system with unknown backlash-like. J. Frankl.-Inst.-Eng. Appl. Math. 2024, 361. [Google Scholar] [CrossRef]
- Zheng, A.; Huang, Y.; Na, J.; Shi, Q. Adaptive neural identification and non-singular control of pure-feedback nonlinear systems. ISA Trans. 2024, 144, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Jia, J. Non-overshooting control of nonlinear pure-feedback systems. Syst. Control. Lett. 2024, 185, 105743. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, X.; Xue, J.; Li, H.; Chen, Y. Adaptive neural control for a class of pure-feedback nonlinear systems via dynamic surface technique. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1969–1975. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Dong, X.; Xie, W.; Chen, Y.; Li, H. Adaptive fuzzy control for pure-feedback nonlinear systems with nonaffine functions being semibounded and indifferentiable. IEEE Trans. Fuzzy Syst. 2018, 26, 395–408. [Google Scholar] [CrossRef]
- Zuo, R.; Dong, X.; Chen, Y.; Liu, Z.; Shi, C. Adaptive neural control for a class of non-affine pure-feedback nonlinear systems. Int. J. Control 2019, 92, 1354–1366. [Google Scholar] [CrossRef]
- Zhai, D.; An, L.; Li, X.; Zhang, Q. Adaptive fault-tolerant control for nonlinear systems with multiple sensor faults and unknown control directions. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4436–4446. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhai, D.; Dong, J.; Zhang, Q. Adaptive fault-tolerant control with prescribed performance for switched nonlinear pure-feedback systems. J. Frankl. Inst.-Eng. Appl. Math. 2018, 355, 273–290. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Z.; Wang, C. Adaptive neural network state constrained fault-tolerant control for a class of pure-feedback systems with actuator faults. Neurocomputing 2022, 490, 431–440. [Google Scholar] [CrossRef]
- You, G.; Shen, Z.; Xu, B.; Zhang, C.; Zhao, S.; Hou, X.; Liu, Z. Adaptive fuzzy finite-time fault-tolerant control design for nonlinear pure-feedback systems with sensor faults. Int. J. Adapt. Control Signal Process. 2023, 37, 2000–2020. [Google Scholar] [CrossRef]
- Cao, L.; Li, H.; Dong, G.; Lu, R. Event-triggered control for multiagent systems with sensor faults and input saturation. IEEE Trans. Syst. Man Cybern.-Syst. 2021, 51, 3855–3866. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, D.; Li, T.; Zhang, Q. Fuzzy-approximation adaptive fault-tolerant control for nonlinear pure-feedback systems with unknown control directions and sensor failures. Fuzzy Sets Syst. 2019, 356, 28–43. [Google Scholar] [CrossRef]
- Huang, X.; Wen, C.; Song, Y. Adaptive neural control for uncertain constrained pure feedback systems with severe sensor faults: A complexity reduced approach. Automatica 2023, 147, 110701. [Google Scholar] [CrossRef]
- Bali, A.; Chouhan, S.S.; Kumar, G.; Kumar, R.; Singh, U.P. Adaptive fault-tolerant control for pure-feedback stochastic nonlinear systems with sensor and actuator faults. Circuits Syst. Signal Process. 2023, 42, 5838–5867. [Google Scholar] [CrossRef]
- Jiang, Y.; Niu, B.; Zong, G.; Zhao, X.; Zhao, P. Distributed adaptive secure consensus tracking control for asynchronous switching nonlinear MASs under sensor attacks and actuator faults. IEEE Trans. Autom. Sci. Eng. 2023; early access. [Google Scholar] [CrossRef]
- Li, D.; Han, H.; Qiao, J.F. Fuzzy-Approximation Adaptive Fault Tolerant Control for Nonlinear Constraint Systems With Actuator and Sensor Faults. IEEE Trans. Fuzzy Syst. 2024, 32, 2614–2624. [Google Scholar] [CrossRef]
- Zhou, S.; Song, Y. Prescribed performance neuroadaptive fault-tolerant compensation for MIMO nonlinear systems under extreme actuator failures. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5427–5436. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, W.; Chen, Y.; Lv, M.; Zhang, B.; Xue, J. Distributed synchronization control for multiple tailless flying-wing UAVs with predefined tracking accuracy and input nonlinearities. Int. J. Robust Nonlinear Control 2023, 33, 3491–3516. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Liu, Z.; Yao, L.; Xue, J.; Li, Q.; Chen, Y.; Jian, J. Global Low-Complexity Fault-Tolerant Control for Pure-Feedback Systems with Sensor Faults. Electronics 2024, 13, 3166. https://doi.org/10.3390/electronics13163166
Han C, Liu Z, Yao L, Xue J, Li Q, Chen Y, Jian J. Global Low-Complexity Fault-Tolerant Control for Pure-Feedback Systems with Sensor Faults. Electronics. 2024; 13(16):3166. https://doi.org/10.3390/electronics13163166
Chicago/Turabian StyleHan, Chongchong, Zongcheng Liu, Liangfu Yao, Jianping Xue, Qiuni Li, Yong Chen, and Jialong Jian. 2024. "Global Low-Complexity Fault-Tolerant Control for Pure-Feedback Systems with Sensor Faults" Electronics 13, no. 16: 3166. https://doi.org/10.3390/electronics13163166
APA StyleHan, C., Liu, Z., Yao, L., Xue, J., Li, Q., Chen, Y., & Jian, J. (2024). Global Low-Complexity Fault-Tolerant Control for Pure-Feedback Systems with Sensor Faults. Electronics, 13(16), 3166. https://doi.org/10.3390/electronics13163166






