A Metamaterial Bandpass Filter with End-Fire Coaxial Coupling

Abstract

A miniaturized metamaterial (MTM) bandpass filter (BPF) based on end-fire coaxial coupling is proposed. End-fire coaxial coupling is achieved by using the coaxial cavity to connect with the SubMiniature version A connector. The subwavelength characteristics of the MTM lead to the miniaturization advantages of the filter in transverse dimensions. Moreover, the longitudinal length of the coaxial cavity can be sharply reduced by introducing matched blocks. As a result, the proposed filter has miniaturization merit both in transverse and longitudinal dimensions. The full-wave simulation results further reveal that the MTM BPF exhibits the advantages of low loss, low reflection, and low group delay. Additionally, the fractional bandwidth is approximately 13% when |S₁₁| is less than −15 dB. The MTM BPF might have potential applications to array antennas for easily being expanded to two dimensional arrays.

1. Introduction

Bandpass filters (BPFs) are the crucial components of transceiver systems, modern communication systems, and radars, among other technologies [1,2]. As one of the primary challenges, miniaturization means smaller sizes and lighter weights and thus attracts much attention. There are many approaches to constructing compact BPFs, such as substrate integrated waveguides (SIWs), gap waveguides, and metamaterials (MTMs) [3,4,5,6,7]. For example, filters based on SIWs or MTMs with dielectric substrates have the advantage of easy integration, but this limits their application to high-power fields. Filters based on gap waveguides of the all-metal type have enlarged transverse sizes due to the electromagnetic band gap structures, though they have a higher power capacity.

Recently, one kind of all-metal type MTM, which is formed by complementary electric split ring resonators (CeSRRs) vertically or horizontally loaded with hollow waveguides, has shown the potential to address the above issues. This is because MTMs have demonstrated their miniaturization merit and high power capacity as the novel slow-wave structures in vacuum electronic devices (VEDs) [8,9,10,11,12]. The miniaturization merit and high power capacity are derived from the subwavelength property and all-metal type of the MTM, respectively. Here, the subwavelength property and the other property of the MTM (i.e., frequency selectiveness) can provide the foundation for designing miniaturized BPFs.

Furthermore, in order to construct MTM filters, coupling technologies are essential. At present, there are two kinds of coupling techniques for MTMs: waveguide coupling and coaxial coupling. Waveguide coupling is especially large in low-frequency bands because the transverse size of the waveguide is positively correlated to the wavelength [13,14,15]. As a comparison, coaxial coupling can match the MTMs well, and it has been used to develop the miniature couplers in MTM VEDs [16,17,18,19,20,21]. Moreover, with respect to end-fire coaxial coupling, the broadside one is difficult to form a two-dimensional array with. Typically, end-fire coaxial coupling has achieved a good match between SubMiniature version A (SMA) connectors and CeSRRs vertically loaded with circular waveguides [22,23].

In this paper, based on an all-metal MTM consisting of CeSRRs horizontally loaded with a hollow square waveguide, we propose end-fire coaxial coupling to construct a miniaturized BPF filter.

2. Filter Design

The overall view and side view of the proposed MTM BPF model are shown in Figure 1a,b, respectively. As one can see, the filter consists of an MTM, two coaxial cavities, and two end-fire SMA connectors. The MTM and the coaxial cavities are all-metal structures with copper as the material, and the inside is filled with air. The SMA with a 0.6 mm inner conductor radius and 2.1 mm outer conductor radius is filled with Teflon. The period number of the MTM is nt. As shown in Figure 2a, the MTM unit cell is formed by a hollow square waveguide horizontally loaded with CeSRRs [9,14]. By using the eigenmode solver in CST [24], we obtained the dispersion characteristics of the MTM. In the simulation, the periodic conditions were set in the z direction, in which a phase advance $\mathsf{\phi }$ was set between the two ends of the MTM unit cell. By scanning $\mathsf{\phi }$ from 0 to $2\pi$, we could obtain the corresponding frequencies. As a result, the dispersion curves are plotted in Figure 2b. Here, the MTM BPF operates at the passband of the MTM’s fundamental mode (mode 1) from 2.82 GHz to 3.38 GHz rather than the first higher mode (mode 2) from 3.92 GHz to 4.58 GHz. As a comparison, the hollow square waveguide with a 14.5 mm transverse length has a cut-off frequency of ~10.3 GHz. Hence, the MTM can operate below the cut-off frequency of the hollow waveguide, which ensures miniaturization of the MTM. Furthermore, the dispersion curves for different k and d values are shown in Figure 2c,d, respectively. Here, k is the scale factor which can simultaneously enlarge or reduce the parameters of the MTM. The results indicate that to enhance the filter’s operating frequency, we could adjust it by decreasing k for coarse tuning or increasing d for fine tuning.

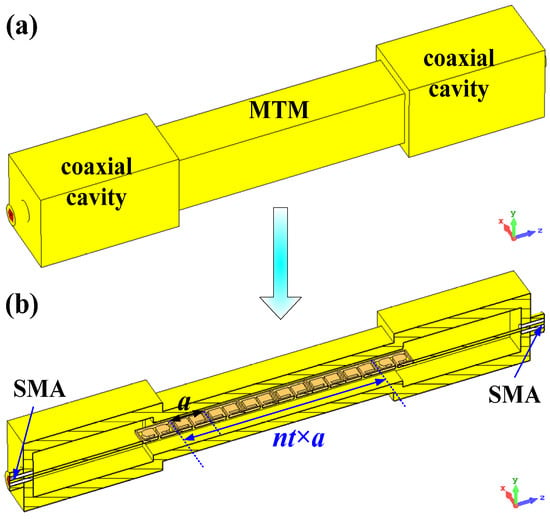
Figure 1. The MTM BPF. (a) Overall view. (b) Side view.

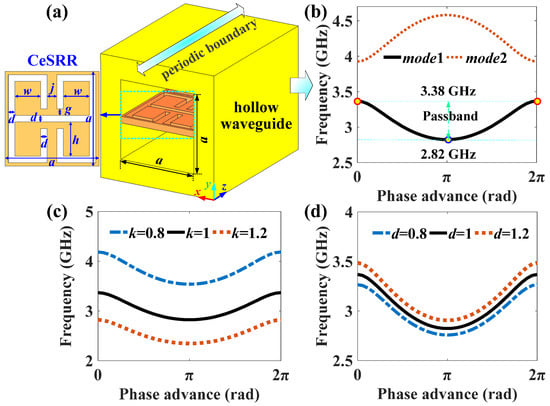
Figure 2. (a) Model of the MTM and (b) dispersion curve of the MTM (a = 14.5, d = 1, g = 1, j = 1.5, w = 4, h = 5.25, thickness = 1.2; unit = mm), with dispersion curves for different (c) k and (d) d values.

As shown in Figure 3a, the coaxial cavity consists of an inner conductor, a big square waveguide, and a dielectric filled with air. The inner conductor can be regarded as the extension of the SMA inner conductor and finally be fixed at the centre of the CeSRRs, as shown in Figure 3b. The big square waveguide with a length of zg and a transverse size of ae plays the role of the outer conductor of the coaxial cavity, as shown in Figure 3c,d. Here, the SMA, coaxial cavity, and blend edge of the CeSRRs form the end-fire coaxial coupling structure, providing a good match at the operating frequency of the MTM.

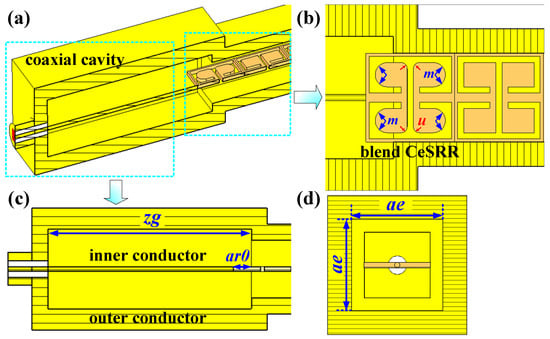
Figure 3. The model of coaxial cavity. (a) Overall view. (b) Top view. (c) Forward view. (d) Side view.

In order to achieve the transformation from the TEM mode in the SMA to the TM-dominated mode in the MTM, the longitudinal length of the coaxial cavity zg was approximately λ/2, where λ is the TEM wavelength of the coaxial cavity. Also, the length of the CeSRRs inserted into the coaxial cavity ar0 is necessary to ensure the electromagnetic wave easily enters into the MTM. By using the time domain solver in CST Microwave Studio [24], we analyzed the impact of the primary parameters on the filter performance. In the simulation, waveguide ports were set at the two ends of the filter (i.e., the end faces of the SMA connectors) to offer electromagnetic wave excitation along the z direction, and the other directions were set as electric boundaries. Figure 4a,b shows |S₁₁| for different zg and ar0 values, respectively. As one can see, the MTM BPF maintained a good match when zg and ar0 were approximately 51 mm and 4.5 mm, respectively. Meanwhile, the transverse size of the coaxial cavity should be greater than 20 mm to achieve low reflection, as shown in Figure 4c. Furthermore, as one can see in Figure 4d, the proper blend edge u of the two CeSRRs at the two ends of the MTM were beneficial for impedance matching. The |S₁₁| for different blend edge values m is shown in Figure 4e. The results indicate that m slightly influenced the reflection. As shown in Figure 4f, the electric field concentrated at the CeSRR center rather than around the CeSRR corners. This means that the change in m could hardly affect the electric field distribution and thus had a weak influence on the electromagnetic wave transmission characteristics.

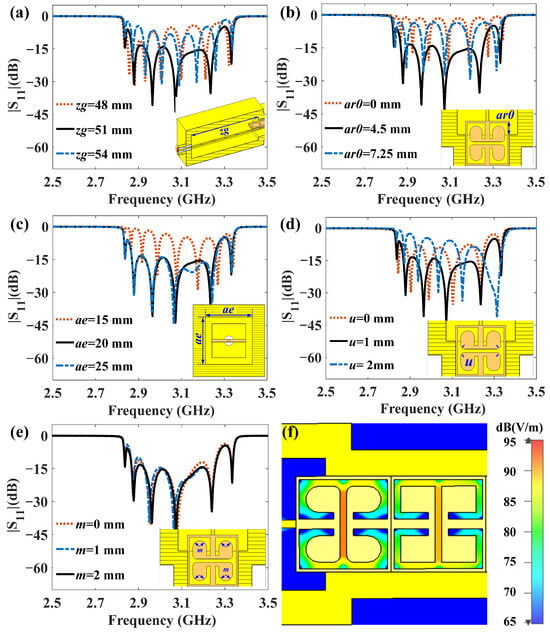
Figure 4. |S₁₁| for different (a) zg, (b) ar0, (c) ae, (d) u, (e) and m values. (f) Electric field distribution at 3 GHz.

3. Results of the MTM BPF

We obtained the optimized parameters listed in Table 1 based on the above analysis by using a full-wave simulation in CST Microwave Studio. Here, we discuss the performance of the MTM BPF for different MTM period numbers.

Table 1. Optimized parameters for the MTM BPF.

Parameter	Value (mm)	Parameter	Value (mm)
Zg	51	ar0	4.5
Ae	20	u	1
M	2

Figure 5 and Figure 6 show the |S₁₁| and |S₂₁| values for different MTM period numbers, respectively. The results show that |S₁₁| was approximately −15 dB and |S₂₁| was greater than −0.7 dB within the operating frequency band from 2.95 GHz to 3.20 GHz. The results demonstrate the good match of end-fire coaxial coupling connecting the SMA to the MTM. Furthermore, as the period number increased, the reflection remained nearly unchanged, the intersection loss slightly increased, and the out-of-band suppression was significantly enhanced. Typically, the out-of-band suppression at 2.8 GHz was 15.4 dB and 31.6 dB when the value of nt was two and six, respectively. Also, the out-of-band suppression at 3.4 GHz was enhanced by 10 dB when nt increased from 2 to 6.

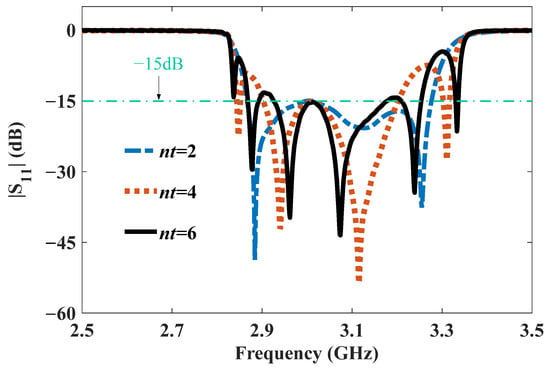
Figure 5. |S₁₁| of the MTM BPF.

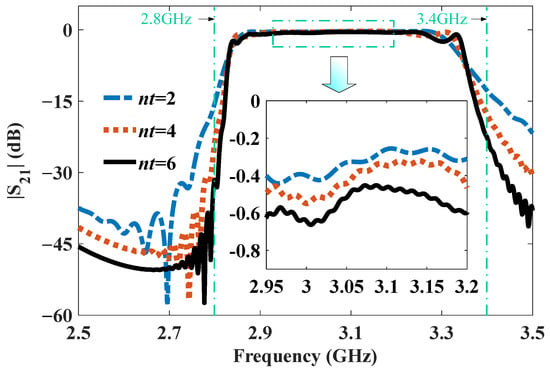
Figure 6. |S₂₁| of the MTM BPF.

Figure 7 shows the group delay for different MTM period numbers. As one can see, the group delay increased slightly with an increasing period number. Typically, the group delay curve is relatively flat and only has a roughly 2 ns fluctuation from 2.95 GHz to 3.20 GHz, even if nt = 6. The results indicate that the MTM BPF had a rather low group delay.

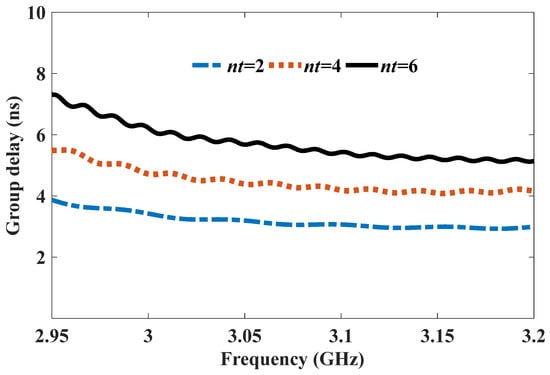
Figure 7. Group delay of the MTM BPF.

Furthermore, the electric field distribution in the MTM BPF for different period numbers at 3 GHz is shown in Figure 8. It can be seen that the electromagnetic wave at 3 GHz could be transformed from the TM-dominated mode in the MTM to the TEM mode in the coaxial cavity. The results show that the electromagnetic wave at 3 GHz could easily transport the MTM via end-fire coaxial coupling, which indicates a good match.

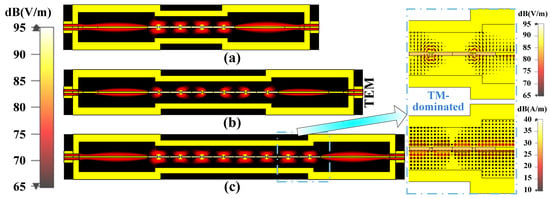
Figure 8. Electric field distribution at 3 GHz for (a) nt = 2, (b) nt = 4, and (c) nt = 6. Inset: the electric and magnetic field distribution between the MTM and the coaxial cavity.

As a comparison, the electric field distributions in the MTM BPF at 2.8 GHz and 3.4 GHz are shown in Figure 9 and Figure 10, respectively. It is clear that the electromagnetic waves at 2.8 GHz and 3.4 GHz underwent rapid attenuation after entering into the MTM. This is because the two frequencies were beyond the cut-off frequency of the MTM, as shown in Figure 2b. Additionally, as the period number increased, the electrometric waves at 2.8 GHz and 3.4 GHz would experience greater attenuation, which resulted in higher out-of-band suppression, as presented in Figure 6.

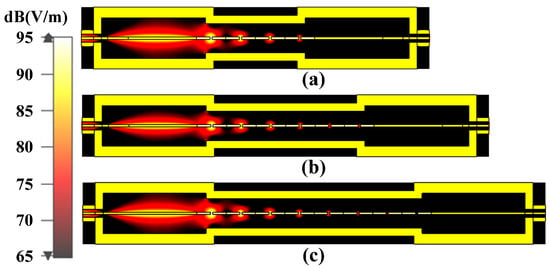
Figure 9. Electric field distribution at 2.8 GHz for (a) nt = 2, (b) nt = 4, and (c) nt = 6.

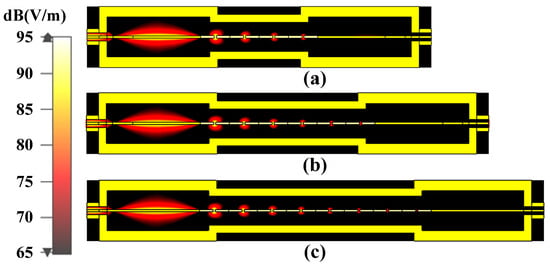
Figure 10. Electric field distribution at 3.4 GHz for (a) nt = 2, (b) nt = 4, and (c) nt = 6.

4. Discussion

Compared with the standard rectangular waveguide WR-284 with transverse dimensions of 72.14 mm × 34.04 mm operating from 2.6 GHz to 3.95 GHz, both the 20 mm × 20 mm coaxial cavity and the 14.5 mm × 14.5 mm MTM exhibited a significant reduction in transverse sizes. However, miniaturization was not achieved in the longitudinal dimension, owing to the fact that each coaxial cavity had a longitudinal length of approximately λ/2. As a result, we further discuss the performance of the MTM BPF when the longitudinal length of the coaxial cavity was much less than λ.

The MTM BPF with compact coaxial cavities is shown in Figure 11a. The transverse size of the coaxial cavity decreased to a in the y direction and maintained ae in the x direction, as shown in Figure 11b,c, respectively. Importantly, the longitudinal length zg decreased to roughly λ/10, as shown in Figure 11d. In order to compensate for the mismatch caused by the shortening of the coaxial cavity, we introduced matched blocks into the CeSRRs. The final optimized parameters of the coaxial cavity are listed in the caption of Figure 11. The corresponding |S₁₁| and |S₂₁|values are shown in Figure 12 and Figure 13, respectively. The results indicate that the fractional bandwidth was approximately 13% when |S₁₁| was less than −15 dB. Typically, |S₁₁| is close to −22 dB and |S₂₁| is roughly −0.3 dB at 3 GHz for nt = 2. As shown in Figure 14, the fluctuation in the group delay curve is less than 2 ns from 2.95 GHz to 3.25 GHz. The above results clearly indicate that the MTM BPF could realize miniaturization for both the transverse and longitudinal sizes.

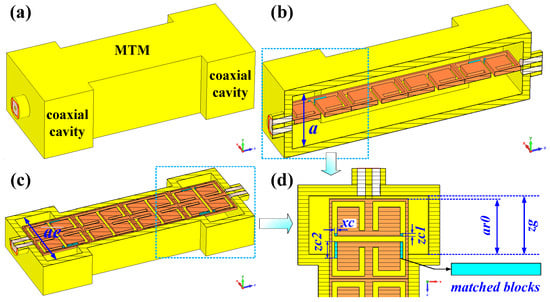
Figure 11. The MTM BPF with compact coaxial cavities (a = 14.5, ae = 22, ar0 = 10, zg = 10.5, xc = 0.5, zc1 = 0.5, zc2 = 3, thickness = 1.2; unit = mm). (a) Overall view, (b) side view in yoz plane, (c) side view in xoz plane, and (d) a zoomed-in view of the coaxial cavity.

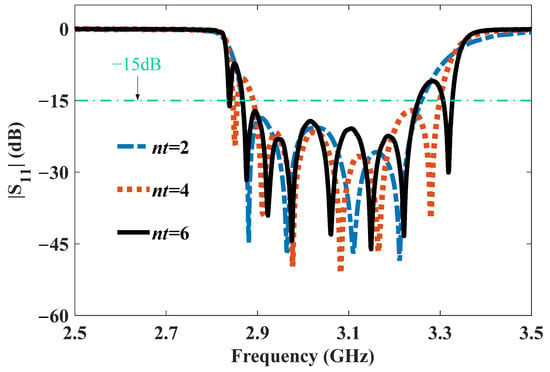
Figure 12. |S₁₁|of the MTM BPF with compact coaxial cavities for different nt values.

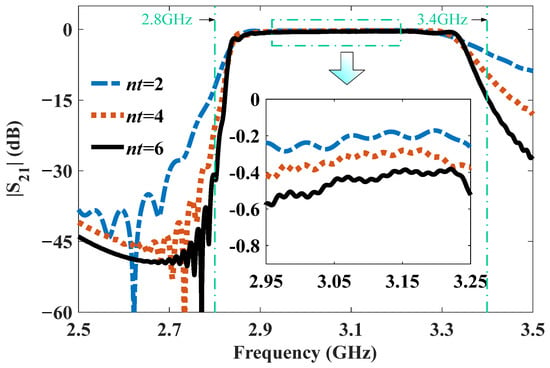
Figure 13. |S₂₁| of the MTM BPF with compact coaxial cavities for different nt values.

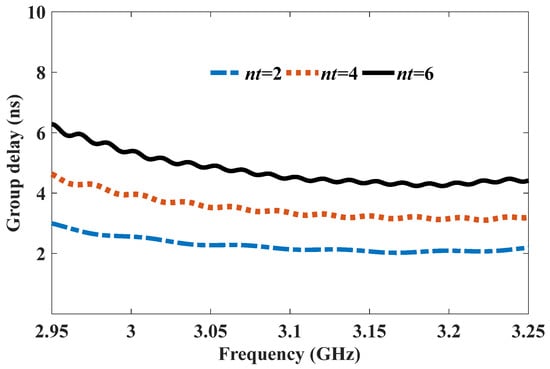
Figure 14. Group delay of the MTM BPF with compact coaxial cavities for different nt values.

A comparison between previous works and this work is listed in Table 2. With respect to the broadside ones, the MTM BPF with end-fire coaxial coupling was easily extended in the two-dimensional plane and thus could be used to develop filtering array antennas. Also, it exhibited miniaturization merit, especially in transverse sizes, over the current end-fire coaxial coupling structures for MTMs. Furthermore, when compared with the end-fire coaxial cavity resonator filters, the proposed filter exhibited slightly enhanced performance, such as wider bandwidth, lower reflection, or low loss at the same level in various dimensions. Importantly, we could adapt the coaxial cavity size of end-fire coupling to meet the demands of different applications. For example, end-fire coaxial coupling with a compact coaxial cavity is suitable for array antennas. As a comparison, end-fire coaxial coupling with a large coaxial cavity would be applied to MTM VEDs, in which the collector and the output structure can share the large coaxial cavity, thereby reducing the overall size of devices.

Table 2. Comparison between previous works and this work.

Reference	Freq. (GHz)	FB *	|S11| (dB) **	|S21| (dB) **	Coupling Type	Size (${\mathit{\lambda }}^3$) ***
[17]	4.5	4.4%	~−3	~−20	broadside	0.34 × 0.15 × 1.94
[19]	2.9	5%	~−15	~−0.8	broadside	0.2 × 0.2 × 1.25
[22]	2.43	1%	~−15	~−1	end-fire	0.81 × 0.81 × 3.2
[23]	6.6	10%	~−22	~−0.54	end-fire	0.84 × 0.84 × 3.7
[25]	3	3%	~−13.5	~−0.7	end-fire	0.17 × 0.17 × 0.58
[26]	2.8	9%	~20	~0.5	end-fire	0.24 × 0.14 × 0.73
[27]	2.28	1%	~−20	~0.9	end-fire	0.39 × 0.3 × 1.6
This work #	3	13%	~−22	~−0.3	end-fire	0.22 × 0.15 × 0.59

* FB represents the fractional bandwidth. ** The data represent the value at the central frequency estimated from figures or obtained from tables. *** Here, $\lambda$ represents the free space wavelength corresponding to the central frequency, and the sizes do not include the thickness of the metal shell. ^# The data result from the MTM BPF with compact coaxial cavities.

5. Conclusions

In this paper, we presented end-fire coaxial coupling for an MTM and then developed a novel MTM BPF with miniaturization characteristics. The bandpass characteristics were derived from the MTM. Hence, the filter’s operating frequency could be designed by enlarging or reducing the MTM for coarse tuning and adjusting the gap in the CeSRR for fine-tuning. Importantly, as the MTM period number increased, the low group delay slightly changed, and the out-of-band suppression was significantly enhanced. Furthermore, end-fire configuration can provide superior space utilization compared with the broadside type. Next, we will carry out transmission experiments.