Abstract
In this paper, we propose using a chaotic system composed of nanolasers (NLs) as a physical entropy source. Combined with post-processing technologies, this system can produce high-quality physical random number sequences. We investigated the parameter range for achieving time-delay signature (TDS) concealment in the chaotic system. This study demonstrates that NLs exhibit noticeable TDS only under optical feedback. As mutual injection strength between the master NLs (MNLs) increases, the TDS of the MNLs is gradually suppressed until they are completely concealed. Compared to MNLs, the slave NL (SNL) exhibits better TDS suppression performance. Additionally, we investigated the chaotic and highly unpredictable regions of the SNL, demonstrating that high-quality chaotic signals can be produced over a wide range of parameters. Using TDS hidden and highly unpredictable chaotic signals as the source of random entropy, the effects of different post-processing techniques on random number extraction were compared. The results indicate that effective post-processing can enhance the unpredictability of the random sequence. This study successfully utilized NLs for random number generation, showcasing the potential and application prospects of NLs in the field of random numbers.
1. Introduction
Random numbers play a crucial role in fields such as cryptography [1], data simulation [2], and secure communications [3,4,5,6,7,8,9]. They can be categorized into two types: true random numbers [10,11] and pseudo random numbers [12,13]. True random numbers, also known as physical random numbers, are generated through physical phenomena. Their generation process is unpredictable and relies entirely on the randomness of nature. Therefore, true random numbers possess characteristics of being unpredictable, being non-repetitive, and having high entropy, making them superior in applications requiring high security. However, their generation rate is relatively slow, which may not meet the demands of certain high-frequency applications. Additionally, changes in the physical environment could affect the reliability of random number generators (RNGs). Pseudo random numbers are generated by deterministic algorithms. Their sequence exhibits statistical properties resembling randomness, and they are widely used in computer science and statistics. Common pseudo random number generation algorithms include linear congruential generators, the Mersenne Twister algorithm, and the Blum Blum Shub generator. Pseudo random number generation is fast and suitable for real-time applications. However, pseudo RNGs have finite periods, which can lead to repetition. Additionally, their deterministic algorithms are vulnerable to being cracked, making them unsuitable for secure applications. In practical applications, there is a significant demand for RNGs that are fast, convenient, have high randomness, and have high security. This poses a major challenge for RNG development.
In recent years, chaos has been widely applied in high-speed physical random number generation [14,15,16,17]. Chaos systems have characteristics such as high sensitivity to initial conditions, unpredictability, and ergodicity. These features make them a potential tool for generating high-quality random numbers. Semiconductor lasers (SLs) are the most practical and important type of lasers, and typically have stable output. However, when subjected to external perturbations they exhibit rich nonlinear dynamic characteristics, including steady state, periodicity, period doubling, and chaos. As research on chaotic lasers progresses, many methods have been proposed by researchers for generating random numbers using chaotic lasers. Uchida et al. utilized the chaotic characteristics of SLs to achieve high-speed random number generation through optical feedback mechanisms [18]. They detailed the implementation principle of this method, the generation rate, and experimental results regarding the quality of the generated random numbers. This research has attracted attention from research groups worldwide, sparking a surge of interest in generating high-speed random numbers using chaotic lasers. Reidler et al. achieved ultrafast random number generation by optimizing the feedback mechanism and sampling techniques of the SL [19]. They also conducted detailed studies on the relationship between the random number generation rate and SL parameters. Li et al. investigated a SL with distributed feedback from a fiber Bragg grating for random bit generation, achieving output rates ranging from 0.3 to 100 Gbit/s [20]. Xiang et al. constructed a ring network composed of three SLs and used it for random number generation. By linearly combining the outputs of three SLs, seven channels of chaotic entropy sources can be obtained. With minimal post-processing techniques introduced, seven-channel random bit outputs can be achieved [21].
The currently confirmed techniques for generating chaotic light include optical feedback [22,23], optical injection [24,25], and optoelectronic feedback [26]. Compared to optical injection and optoelectronic feedback, optical feedback structure has the advantages of being simple in design, being low cost, and having rich dynamics. However, chaotic signals outputted by SLs under optical feedback exhibit notable time-delay signature (TDS). By analyzing TDS, it may be possible to infer the operational state of chaotic SLs or the generation patterns of random numbers, thereby compromising randomness. Therefore, researchers have proposed various schemes to suppress TDS. Shore et al. studied the TDS of chaotic signals in three cascaded vertical-cavity surface-emitting lasers, analyzing the parameter range of frequency detuning for achieving TDS hiding in this system [27]. Wu et al. proposed a mutually coupled SL system where modulating the coupling strength and frequency detuning simultaneously generates two chaotic signals with hidden TDS [28]. Nguimdo et al. investigated the possibility of hiding TDS in semiconductor ring lasers (SRLs), achieving promising results [29]. Our research group investigated the TDS and bandwidth of a chaotic system composed of three cascaded SRLs. The study showed that the cascaded coupling scheme can enhance the dynamical characteristics of the lasers [30].
In recent years, novel semiconductor nanolasers (NLs) have become a focal point of research in the field of optoelectronics. Their unique structures and characteristics have shown extensive potential across multiple application domains. NLs provide new possibilities for various application scenarios due to their small size, high performance, and high-density integration. These attributes make NLs crucial components in many modern optoelectronic and nanotechnology applications. Currently, there are numerous reports on the fabrication of various NL structures, as well as the analysis of their nonlinear dynamics and characteristics. When analyzing the nonlinear dynamics of conventional SLs, spontaneous emission is often ignored. Considering the microstructure of NLs, Erwin et al. introduced the Purcell factor and the spontaneous emission coupling factor to describe the dynamics of NLs influenced by spontaneous emission [31]. Satter et al. conducted studies on the nonlinear dynamic behaviors of NLs under optical feedback, phase-conjugate feedback, and optical injection, evaluating the impact of relevant parameters on NLs’ dynamic behavior [32,33,34,35]. Han et al. constructed a mutually coupled NL system and analyzed its dynamic characteristics. They pointed out that the system can maintain steady-state output at higher mutual injection intensities. Additionally, they conducted an analysis of the dynamic behavior under the combined effects of optical feedback and optical injection [36,37,38]. Xiang et al. investigated the dynamic characteristics of NLs with double chaotic optical injection, which can output signals with TDS hidden over a wide range of parameters [39]. Our research group investigated the dynamic behavior of mutually coupled NL systems with open-loop, semi-open-loop, and closed-loop structures [40]. Furthermore, we conducted a detailed study on the TDS hiding capability of the closed-loop mutually coupled NL system, specifically analyzing the impact of parameter mismatches on chaos synchronization [41]. Our research group has also proposed RNGs based on NL systems in terms of applications [42,43]. This includes studying the nonlinear dynamic characteristics of chaotic entropy sources and generating random sequences that have passed randomness verification. The studies explored the dynamic characteristics of different systems, laying the foundation for chaos-based applications. However, there is still a significant amount of exploration space remaining in the study of NLs.
This article proposes a scheme for generating random numbers utilizing a chaotic system composed of three NLs as a random entropy source. The rest of the article’s structure is as follows. Section 2 presents the theoretical model of the chaotic system and two different post-processing schemes. In Section 3, we first investigated the parameter ranges for achieving TDS concealment in the master NLs (MNLs) and slave NL (SNL). Moreover, we utilized the 0–1 chaos test and permutation entropy (PE) to study the chaotic regions and highly unpredictable regions of the SNL output. Next, we fixed the parameters to ensure the output of chaotic signals with TDS concealment and high complexity and studied the impact of different post-processing methods on random number extraction. In Section 4, the research results are summarized. The chaotic system effectively achieves concealed TDS and demonstrates high unpredictability. Combining post-processing techniques enables the generation of random numbers passing NIST tests. Moreover, effective post-processing can enhance the randomness of the random sequence.
2. Theoretical Model
Figure 1 shows the structure of the chaotic entropy source based on NLs. Two MNLs achieve chaotic output through optical feedback and mutual injection, and their outputs are simultaneously injected into the SNL.
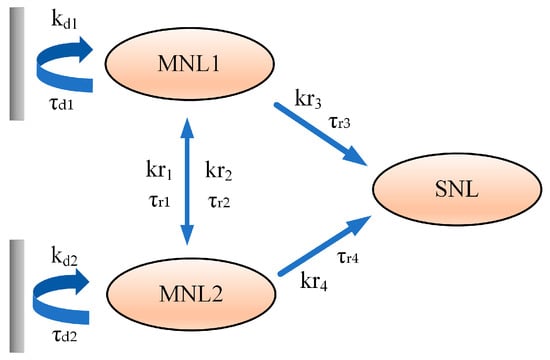
Figure 1.
Structure of the chaotic entropy source based on NLs.
The dynamical behaviors of MNLs and SNL can be derived from the NL rate equations based on the optical feedback and optical injection structures, as follows [33,35]:
Here, the subscripts represent MNL1, MNL2, and SNL, respectively. , , and represent the photon density, carrier density, and phase, respectively. represents the frequency detuning between the MNLs, and represents the frequency detuning between the MNLs and the SNL.
In Equations (1) and (2), the penultimate term represents the optical feedback component. represent the feedback rate, and denote feedback delay of the two feedback paths. can be expressed as follows [33]:
In Equations (1) and (2), the last term represents the mutual injection between MNLs, while the last two terms in Equations (4) and (5) denote the injection of the two MNLs into the SNL, respectively. can be written as follows [35]:
The introduction of the autocorrelation function (ACF) quantifies the TDS. The time-varying photon density ACF can be expressed as described in [44,45,46], where represents the time series, and is the time shift, as follows:
Table 1 lists the parameter settings used for simulation [33,35], while the remaining parameters will be provided in the following sections.

Table 1.
The parameter values set for NLs in the numerical simulation.
RNGs based on chaotic lasers mainly consists of three parts: a chaotic laser entropy source, acquisition devices, and post-processing. Extracting random numbers from the chaotic laser entropy source requires necessary acquisition devices. Typically, photodetectors (PDs) are used to convert chaotic light signals into electrical signals. Subsequently, these electrical signals are quantized using a 1-bit or multi-bit analog-to-digital converter (ADC) to generate random binary numbers. The raw signals generated by the chaotic entropy source may contain some biases and correlations, necessitating post-processing techniques to improve the quality and randomness of the generated random numbers. We proposed two different post-processing schemes, as shown in Figure 2, and explored the influence of different post-processing approaches on extracting random sequences. In Scheme 1, the random sequence is obtained by directly extracting the least significant bits (LSBs) from the binary sequence quantized by an 8-bit ADC. Scheme 2 introduces exclusive-OR (XOR) operation, combining the unshifted sequence with the shifted sequence using XOR to form a new sequence. The final random sequence is obtained by retaining the LSBs.
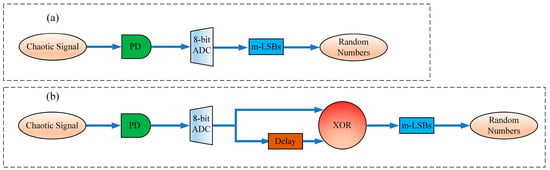
Figure 2.
Block diagram of RNG based on chaotic signals, Scheme 1 (a) and Scheme 2 (b); PD: photodetector; ADC: analog-to-digital convertor; m-LSBs: m least significant bits; XOR: exclusive-OR.
3. Results and Discussion
The rate equations of the chaotic entropy source are numerically solved using the Fourth-Order Runge–Kutta algorithm. Due to the presence of TDS, there may be certain periodicity or correlation in the random number sequence, thus affecting the randomness of the random numbers. Hiding the TDS of the chaotic entropy source can improve the quality and security of the generated random number sequences, making it more suitable for various applications with high requirements for randomness. Therefore, achieving TDS hiding in the chaotic system is the focus of this study. Next, we will explore the TDS of the MNLs and the SNL separately.
To analyze the concealment performance of TDS, we use the ACF for analysis. The smaller the ACF value, the better the TDS concealment performance. When it is less than 0.2, it is generally considered successful in suppressing TDS. Based on previous research, it was found that NLs only under optical feedback cannot entirely conceal the TDS. Therefore, we explore the influence of increasing mutual injection strength on TDS concealment of MNLs under fixed feedback parameters. Under the fixed feedback parameter we compared the time series and ACF of the output from MNLs when the mutual injection strengths were and . Figure 3a depicts that, when the mutual injection strength is , corresponding to the case where MNLs are only under optical feedback, there is a clear TDS. Figure 3b illustrates that, when the injection strength increases to , the oscillation range of the chaotic signal expands, and the TDS is significantly suppressed but still noticeable. This indicates that larger injection strength may help hide the TDS of MNLs.
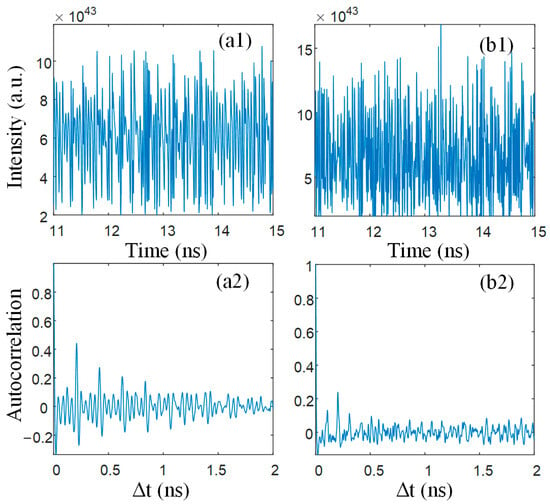
Figure 3.
The MNL outputs in time domains (a1,b1) and ACF (a2,b2) under different mutual injection strengths. (a) and (b) .
Next, we analyzed in detail the variation trend of the ACF peak values of the MNLs and the SNL as the mutual injection intensity increases. We fixed the feedback parameter at and set the injection intensity from the MNLs to the SNL at . From Figure 4, it can be observed that, when the mutual injection strength is , the MNLs exhibit significant TDS. By increasing the mutual injection strength, the ACF peak values of the MNLs gradually decrease until they are less than 0.2. However, the ACF peak values of the SNL were much lower than those of the MNLs. When the mutual injection strength between the MNLs exceeds , the ACF peak value of the SNL is already less than 0.2. In summary, although the TDS of the MNLs is gradually suppressed as the mutual injection intensity increases, the SNL achieves TDS concealment over a wide range of mutual injection intensities. Therefore, compared to the MNLs, the SNL can better conceal the TDS.
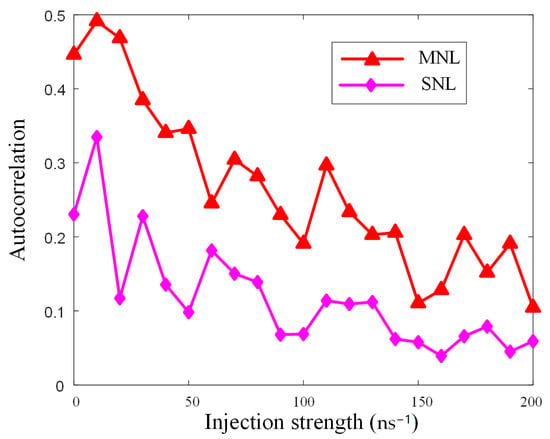
Figure 4.
The trend of the ACF peak values of the MNLs and the SNL, with varying mutual injection strength between the MNLs.
To further analyze the TDS concealment performance of the SNL, we studied the trend of the peak values of the ACF of the SNL with varying injection strengths from the MNLs. This includes scenarios where the MNL output signals exhibit significant TDS and where TDS is completely suppressed. From Figure 4, it is evident that there is a noticeable TDS when the mutual injection strength between the MNLs is , while, when the mutual injection strength is , the TDS is completely suppressed. From Figure 5, it can be observed that, when the MNLs exhibit significant TDS, the value of the ACF drops below 0.2 when the injection strength from the MNLs to the SNL exceeds . When the TDS of the MNLs is significantly suppressed, the ACF remains below 0.2 across the entire range of injection strengths. This indicates that the TDS of the SNL can be effectively suppressed, with a more pronounced effect when the TDS of the MNLs is completely suppressed and injected into the SNL.
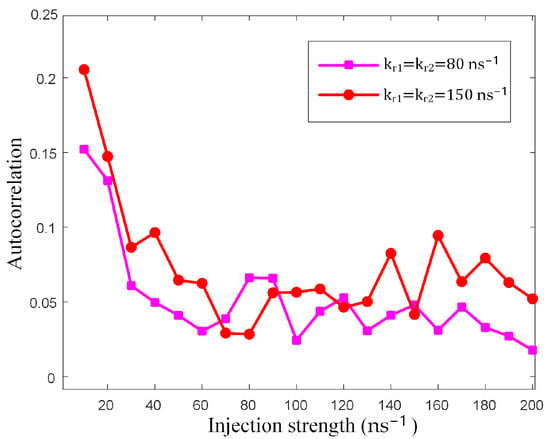
Figure 5.
The trend of the peak values of the ACF of the SNL with varying injection strengths from the MNLs.
The advantage of physical random numbers lies in their genuine unpredictability, and the unpredictability of random numbers lies in the inherent characteristics of their generation method. Therefore, the complexity of the output signal from a chaotic entropy source determines the randomness of the random sequence. The 0–1 chaos test is a numerical method used to determine chaotic behavior [47]. The 0–1 chaos test analyzes time series data by calculating a statistic called the 0–1 measure. If the value of the 0–1 measure is close to 1, it indicates that the system exhibits chaotic behavior; if the value is close to 0, it suggests that the system is quasi-periodic or stable. PE [48] is a tool used for time series analysis that measures the complexity of a time series to determine the dynamical characteristics of a system. Because it is robust to noise and computationally efficient, PE is particularly well-suited for handling data from nonlinear and chaotic systems. Low PE indicates that the time series has high predictability, suggesting that the system may be quasi-periodic or deterministic. High PE indicates that the time series has high complexity, suggesting that the system may be random or chaotic. Figure 6a depicts the chaotic region of the SNL output, showing that the SNL operates in a chaotic state across almost the entire parameter range. This is because the MNLs operate in a chaotic state solely under the influence of optical feedback. The chaotic signals are further enhanced through mutual injection between the MNLs and additional injection into the SNL. Figure 6b shows the complexity region of the chaotic signals of the SNL output, which is consistent with the chaotic region. Highly unpredictable chaotic signals can be output across nearly the entire parameter range. This lays the foundation for extracting high-quality random numbers in subsequent steps.
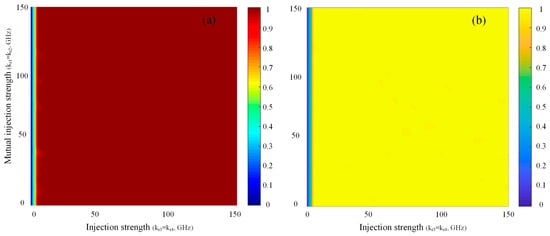
Figure 6.
The two-dimensional map of the 0–1 chaos test (a) and PE (b) of the SNL.
TDS and unpredictability are important factors affecting the quality of random numbers. Similarly, the bandwidth and statistical properties of the chaotic laser entropy source also have significant effects on random number extraction. The bandwidth of the chaotic entropy source determines the generation rate of random numbers, while the statistical properties determine the statistical characteristics of the random sequence. While ensuring complete hiding of the TDS, adjusting relevant parameters to maximize bandwidth and ensure the chaotic entropy source possesses favorable statistical properties. The specific parameter settings are as follows: . Figure 7 shows the time series, ACF curve, power spectrum, and amplitude distribution of the chaotic entropy source under the aforementioned parameter settings. The chaotic system outputs chaotic signals with large amplitude fluctuations and completely suppression of the TDS. The effective bandwidth is approximately 100 GHz, and the statistical properties closely resemble an ideal Gaussian distribution.
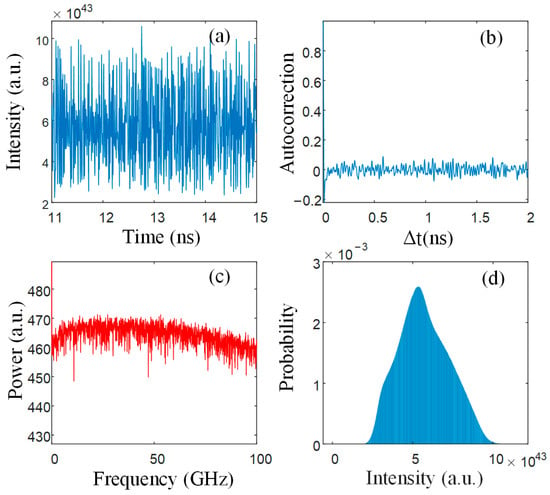
Figure 7.
Time series (a), ACF (b), power spectrum (c), and amplitude distribution (d) of the chaotic signals.
The characteristics of the chaotic entropy source and the post-processing technologies together determine the quality of the random number sequence. Next, we compared the performance of obtaining random numbers under two different post-processing schemes. In the first scheme, we converted the optical signals into electrical signals using a PD. Subsequently, we employed an 8-bit ADC to quantize the signals into a binary sequence and extracted the LSBs to obtain the final random sequence. In the second scheme, after sampling and quantizing the signals into an 8-bit binary sequence, we first shift the binary sequence and then performed XOR processing on the binary sequences before and after the shift. Finally, we extract the LSBs to obtain the random number sequence.
Quantizing chaotic signals using an 8-bit ADC is a process of converting continuous chaotic signals into discrete digital signals. An 8-bit ADC has digitization levels, which means that the entire input range of the analog signal is divided into 256 discrete voltage intervals. Each quantization level corresponds to a unique 8-bit binary number, ranging from 00000000 (0) to 11111111 (255). However, this quantization process can be affected by issues such as uneven binary distribution and weak randomness. To address these issues, it is common practice to extract the LSBs. The uniformity of the amplitude distribution determines the balance of random bits 0 and 1. Figure 8 shows the results of extracting the LSBs in Scheme 1. When retaining eight LSBs, the amplitude distribution remains consistent with the original chaotic entropy source. When the highest significant bit is discarded, the amplitude distribution still exhibits non-uniformity. However, as the number of discarded LSBs increases, the uniformity of the random sequence improves. Similarly, in Scheme 2, when retaining eight and seven LSBs after the XOR operation, the amplitude distribution is also non-uniform (Figure 9). Similarly, by discarding the LSBs, the random sequence also becomes increasingly balanced. Below, we validate the randomness of the obtained random sequence.
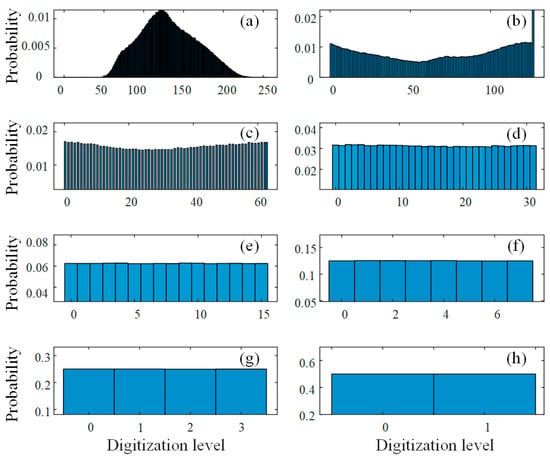
Figure 8.
The amplitude distribution when retaining m-LSBs in Scheme 1: (a) m = 8; (b) m = 7; (c) m = 6; (d) m = 5; (e) m = 4; (f) m = 3; (g) m = 2; (h) m = 1.
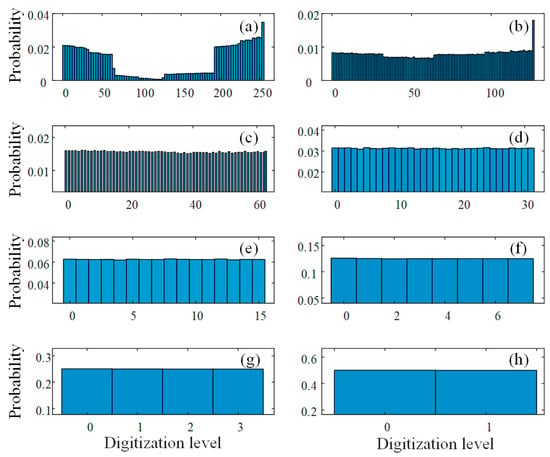
Figure 9.
The amplitude distribution when retaining m-LSBs in Scheme 2: (a) m = 8; (b) m = 7; (c) m = 6; (d) m = 5; (e) m = 4; (f) m = 3; (g) m = 2; (h) m = 1.
The NIST randomness tests are standard tests used to assess and validate the quality of RNGs. They comprise a total of 15 tests, including various classical statistical methods such as frequency tests, sequence tests, block tests, independence tests, and so on. We select 1000 sets of 1 Mbit random number samples for testing, with the significance level set at 0.01. Passing the NIST test requires that the uniformity p-value of each subtest item is larger than 0.0001 and the sample pass proportion falls within the range of 0.99 ± 0.0094392.
The original output of the chaotic laser may not be a perfectly uniformly distributed random sequence, but rather exhibit some bias. Therefore, post-processing techniques are typically applied to transform and adjust the generated random numbers. Effective post-processing can enhance the uniformity of the random sequence, increase randomness, and thereby allow for more LSBs to be retained in generating random numbers. In Figure 10, we compared the number of NIST subtest items passed when retaining eight to one LSBs under two different post-processing schemes. In Scheme 1, retaining one to four LSBs allowed passing all tests in the NIST test suite. However, in Scheme 2, retaining one to five LSBs allowed passing all tests in the NIST test suite, which means an additional LSB can be retained. From this, it can be inferred that both post-processing schemes can generate physical random numbers based on this chaotic system. However, the second scheme can more effectively increase the random number generation rate. Table 2 lists the detailed results of preserving the most LSBs that can be subjected to NIST testing in different schemes.
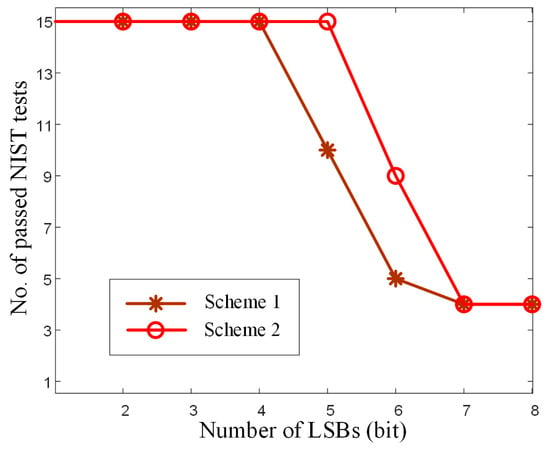
Figure 10.
The number of NIST subtests passed when retaining eight to one LSBs in Scheme 1 and Scheme 2.

Table 2.
The NIST test results for Scheme 1 and Scheme 2.
4. Conclusions
This paper proposes a scheme to generate random numbers using a chaotic system composed of three NLs as the random entropy source. Two MNLs achieve chaotic output through optical feedback and mutual injection, and their outputs are simultaneously injected into the SNL. We investigated the TDS concealment performance of both the MNLs and the SNL separately. Under only simple optical feedback, the MNLs exhibit a significant TDS. With the increase in mutual injection strength, the TDS of the MNLs are gradually suppressed. Compared to the MNLs, the TDS concealment performance of the SNL is better, achieving almost complete TDS concealment across the entire parameter range. Additionally, we explored the chaotic regions and complexity of the chaotic signals output by the SNL. The results show that SNL can output highly complex chaotic signals over a wide range of parameters. Next, we proposed two post-processing schemes for extracting random numbers. The research indicates that both post-processing schemes can generate random numbers that pass NIST tests. However, in Scheme 2, one more LSB can be retained, compared to Scheme 1, when subjected to NIST testing. Therefore, effective post-processing can enhance the performance of RNGs. This study confirms the feasibility of NLs as random entropy sources in random number generation, providing new solutions for applications in information security, cryptography, and random simulation. Moving forward, we will intensify our research on the security of RNGsbased on NLs to ensure their safety and reliability.
Author Contributions
Methodology, J.Z., G.L. and P.M.; validation, R.L. and P.M.; investigation, G.L., J.Z. and P.M.; writing—original draft preparation, G.L. and R.L.; writing—review and editing, J.Z. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Project: The Talent Project of Chengdu Technological University (2023RC013).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum Cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, F.; Liu, B. Random Number Generators for Large-Scale Parallel Monte Carlo Simulations on FPGA. J. Comput. Phys. 2018, 360, 93–103. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, C.; Chen, H. A Novel Color Image Encryption Algorithm Based on Hyperchaotic System and Permutation-Diffusion Architecture. Int. J. Bifurc. Chaos 2019, 29, 1950115. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, F.; Yu, F. A Robust Synchronization-Based Chaotic Secure Communication Scheme With Double-Layered and Multiple Hybrid Networks. IEEE Syst. J. 2020, 14, 2508–2519. [Google Scholar] [CrossRef]
- Yu, F.; Li, L.; Tang, Q.; Cai, S.; Song, Y.; Xu, Q. A Survey on True Random Number Generators Based on Chaos. Discret. Dyn. Nat. Soc. 2019, 2019, e2545123. [Google Scholar] [CrossRef]
- Peng, F.; Zhu, X.; Long, M. An ROI Privacy Protection Scheme for H.264 Video Based on FMO and Chaos. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1688–1699. [Google Scholar] [CrossRef]
- Datcu, O.; Macovei, C.; Hobincu, R. Chaos Based Cryptographic Pseudo-Random Number Generator Template with Dynamic State Change. Appl. Sci. 2020, 10, 451. [Google Scholar] [CrossRef]
- Gu, K.; Jia, W.; Wang, G.; Wen, S. Efficient and Secure Attribute-Based Signature for Monotone Predicates. Acta Inform. 2017, 54, 521–541. [Google Scholar] [CrossRef]
- Zhao, Q.; Yin, H. Gbits/s Physical-Layer Stream Ciphers Based on Chaotic Light. Optik 2013, 124, 2161–2164. [Google Scholar] [CrossRef]
- Abutaleb, M.M. A Novel True Random Number Generator Based on QCA Nanocomputing. Nano Commun. Netw. 2018, 17, 14–20. [Google Scholar] [CrossRef]
- Hasan, R.S.; Tawfeeq, S.K.; Mohammed, N.Q.; Khaleel, A.I. A True Random Number Generator Based on the Photon Arrival Time Registered in a Coincidence Window between Two Single-Photon Counting Modules. Chin. J. Phys. 2018, 56, 385–391. [Google Scholar] [CrossRef]
- Yu, F.; Wan, Q.; Jin, J.; Li, L.; He, B.; Liu, L.; Qian, S.; Huang, Y.; Cai, S.; Song, Y.; et al. Design and FPGA Implementation of a Pseudorandom Number Generator Based on a Four-Wing Memristive Hyperchaotic System and Bernoulli Map. IEEE Access 2019, 7, 181884–181898. [Google Scholar] [CrossRef]
- Rezk, A.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Reconfigurable Chaotic Pseudo Random Number Generator Based on FPGA. AEU-Int. J. Electron. Commun. 2019, 98, 174–180. [Google Scholar] [CrossRef]
- Li, N.; Kim, B.; Chizhevsky, V.N.; Locquet, A.; Bloch, M.; Citrin, D.S.; Pan, W. Two Approaches for Ultrafast Random Bit Generation Based on the Chaotic Dynamics of a Semiconductor Laser. Opt. Express OE 2014, 22, 6634–6646. [Google Scholar] [CrossRef] [PubMed]
- Bucci, M.; Germani, L.; Luzzi, R.; Trifiletti, A.; Varanonuovo, M. A High-Speed Oscillator-Based Truly Random Number Source for Cryptographic Applications on a Smart Card IC. IEEE Trans. Comput. 2003, 52, 403–409. [Google Scholar] [CrossRef]
- Cao, L.; Min, L.; Zang, H. A Chaos-Based Pseudorandom Number Generator and Performance Analysis. In Proceedings of the 2009 International Conference on Computational Intelligence and Security, Beijing, China, 11–14 December 2009; Volume 1, pp. 494–498. [Google Scholar]
- Kanter, I.; Aviad, Y.; Reidler, I.; Cohen, E.; Rosenbluh, M. An Optical Ultrafast Random Bit Generator. Nat. Photon 2010, 4, 58–61. [Google Scholar] [CrossRef]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast Physical Random Bit Generation with Chaotic Semiconductor Lasers. Nat. Photon 2008, 2, 728–732. [Google Scholar] [CrossRef]
- Reidler, I.; Aviad, Y.; Rosenbluh, M.; Kanter, I. Ultrahigh-Speed Random Number Generation Based on a Chaotic Semiconductor Laser. Phys. Rev. Lett. 2009, 103, 024102. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Z.; Li, S.-S.; Zhuang, J.-P.; Chan, S.-C. Random Bit Generation at Tunable Rates Using a Chaotic Semiconductor Laser under Distributed Feedback. Opt. Lett. OL 2015, 40, 3970–3973. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, B.; Wang, Y.; Han, Y.; Wen, A.; Hao, Y. 2.24-Tb/s Physical Random Bit Generation with Minimal Post-Processing Based on Chaotic Semiconductor Lasers Network. J. Light. Technol. JLT 2019, 37, 3987–3993. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, Y.; Ji, H. Sensing by Dynamics of Lasers with External Optical Feedback: A Review. Photonics 2022, 9, 450. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Y.; He, H. Enhancing the Bandwidth of the Optical Chaotic Signal Generated by a Semiconductor Laser with Optical Feedback. IEEE Photonics Technol. Lett. 2008, 20, 1633–1635. [Google Scholar] [CrossRef]
- Komarov, A.; Komarov, K.; Niang, A.; Sanchez, F. Nature of Soliton Interaction in Fiber Lasers with Continuous External Optical Injection. Phys. Rev. A 2014, 89, 013833. [Google Scholar] [CrossRef]
- Yarunova, E.A.; Krents, A.A.; Molevich, N.E.; Anchikov, D.A. Suppression of Spatiotemporal Instabilities in Broad-Area Lasers with Pump Modulation by External Optical Injection. Bull. Lebedev Phys. Inst. 2021, 48, 55–58. [Google Scholar] [CrossRef]
- Tang, S.; Liu, J.M. Chaotic Pulsing and Quasi-Periodic Route to Chaos in a Semiconductor Laser with Delayed Opto-Electronic Feedback. IEEE J. Quantum Electron. 2001, 37, 329–336. [Google Scholar] [CrossRef]
- Priyadarshi, S.; Hong, Y.; Pierce, I.; Shore, K.K. Experimental Investigations of Time-Delay Signature Concealment in Chaotic External Cavity VCSELs Subject to Variable Optical Polarization Angle of Feedback. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1700707. [Google Scholar] [CrossRef]
- Wu, J.-G.; Wu, Z.-M.; Tang, X.; Lin, X.-D.; Deng, T.; Xia, G.-Q.; Feng, G.-Y. Simultaneous Generation of Two Sets of Time Delay Signature Eliminated Chaotic Signals by Using Mutually Coupled Semiconductor Lasers. IEEE Photon. Technol. Lett. 2011, 23, 759–761. [Google Scholar]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van Der Sande, G. Loss of Time-Delay Signature in Chaotic Semiconductor Ring Lasers. Opt. Lett. 2012, 37, 2541. [Google Scholar] [CrossRef]
- Mu, P.; He, P.; Li, N. Simultaneous Chaos Time-Delay Signature Cancellation and Bandwidth Enhancement in Cascade-Coupled Semiconductor Ring Lasers. IEEE Access 2019, 7, 11041–11048. [Google Scholar] [CrossRef]
- Lau, E.K.; Lakhani, A.; Tucker, R.S.; Wu, M.C. Enhanced Modulation Bandwidth of Nanocavity Light Emitting Devices. Opt. Express OE 2009, 17, 7790–7799. [Google Scholar] [CrossRef]
- Sattar, Z.A.; Shore, K.A. Dynamics of Nanolasers Subject to Optical Injection and Optical Feedback. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXIV, San Francisco, CA, USA, 13–18 February 2016; SPIE: New York, NY, USA, 2016; Volume 9742, pp. 38–47. [Google Scholar]
- Abdul Sattar, Z.; Shore, K.A. External Optical Feedback Effects in Semiconductor Nanolasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 500–505. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Shore, K.A. Phase Conjugate Feedback Effects in Nano-Lasers. IEEE J. Quantum Electron. 2016, 52, 1–8. [Google Scholar] [CrossRef]
- Abdul Sattar, Z.; Ali Kamel, N.; Shore, K.A. Optical Injection Effects in Nanolasers. IEEE J. Quantum Electron. 2016, 52, 1–8. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Analysis of High-Frequency Oscillations in Mutually-Coupled Nano-Lasers. Opt. Express OE 2018, 26, 10013–10022. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Shore, K.A. Dynamical Characteristics of Nano-Lasers Subject to Optical Injection and Phase Conjugate Feedback. IET Optoelectron. 2018, 12, 25–29. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Modulated Mutually Coupled Nano-Lasers. IEEE J. Quantum Electron. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Qu, Y.; Xiang, S.; Wang, Y.; Lin, L.; Wen, A.J.; Hao, Y. Concealment of Time Delay Signature of Chaotic Semiconductor Nanolasers With Double Chaotic Optical Injections. IEEE J. Quantum Electron. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, G.; Liu, X.; Hu, G.; Wang, K.; Mu, P. Dynamics and Concealment of Time-Delay Signature in Mutually Coupled Nano-Laser Chaotic Systems. Photonics 2023, 10, 1196. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, P.; Guo, G.; Liu, X.; He, P. Bidirectional Chaotic Synchronization Communication of Closed-Loop Mutually Coupled Nano-Lasers. Electronics 2024, 13, 239. [Google Scholar] [CrossRef]
- Liu, G.; Mu, P.; Wang, K.; Guo, G.; Liu, X.; He, P. Random Numbers Generated Based on Dual-Channel Chaotic Light. Electronics 2024, 13, 1603. [Google Scholar] [CrossRef]
- Liu, G.P.; Mu, P.H.; Guo, G.; Liu, X.T.; Hu, G.S. High-Quality Random Bit Generation Based on a Cascade-Coupled Nano-Laser System. Laser Phys. Lett. 2024, 21, 035206. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, N.; Lv, Y.; Wang, C.; Li, G.; Lin, S.; Qiu, K. Security-Enhanced Chaos Communication with Time-Delay Signature Suppression and Phase Encryption. Opt. Lett., OL 2016, 41, 3690–3693. [Google Scholar] [CrossRef]
- Xiang, S.; Wen, A.; Pan, W.; Lin, L.; Zhang, H.; Zhang, H.; Guo, X.; Li, J. Suppression of Chaos Time Delay Signature in a Ring Network Consisting of Three Semiconductor Lasers Coupled with Heterogeneous Delays. J. Light. Technol. 2016, 34, 4221–4227. [Google Scholar] [CrossRef]
- Zhao, A.; Jiang, N.; Liu, S.; Xue, C.; Qiu, K. Wideband Time Delay Signature-Suppressed Chaos Generation Using Self-Phase-Modulated Feedback Semiconductor Laser Cascaded with Dispersive Component. J. Light. Technol. 2019, 37, 5132–5139. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the Implementation of the 0–1 Test for Chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).