Cost-Efficient Approximation for Magnitude of a Complex Signal

Abstract

In this paper, a signal model and a mathematical analysis of an efficient approach are derived to acquire the approximate magnitude of a complex signal by inducing a pre-biased or a pre-scaled factor in the design criteria. According to the deductive results, the pre-biased or pre-scaled factor can be 2∼3 dB, which is determined through its application. The numerical evaluations show that the mean square error (MSE) of the proposed efficient approach for the random signal is around −33 dB. Based on the design templates for the considered approaches, the occupied areas of the proposed type-1 and -2 approaches are merely 0.13 and 0.09 times the area of the direct-method, respectively. As a result, the proposed efficient approach is certainly a cost-efficient method for obtaining the approximate magnitude of a complex signal.

1. Introduction

For digital baseband signal processing, magnitude calculation for a complex signal is vital to achieve magnitude detection, automatic gain control (AGC), channel estimation, etc. Magnitude calculation is achieved in the works [1,2,3,4,5] using a magnitude detector. The studies [6,7,8,9,10,11] showed that magnitude calculation is carried out to achieve amplitude detection in AGC. Additionally, magnitude calculation is employed to achieve channel estimation in digital baseband receivers [12].

In general, magnitude calculation can be achieved by three approaches, such as the direct method used in [3,6,7,8,9], $\alpha$Max + $\beta$Min used in [1,2] and the COordinate Rotation DIgital Computer (CORDIC) used in [4,5]. It is worth noting that a cost-efficient approach is presented to replace the direct-method, $\alpha$Max + $\beta$Min and CORDIC, and to be used in AGC design [10,11] as well as channel estimations [12]. Importantly, the cost-efficient approach with a pre-biased (or a pre-scaled) factor was first applied to the channel estimation of a baseband receiver [12]. However, neither a signal model nor a mathematical analysis of the cost-efficient approach were provided in [10,11,12].

In this paper, both a signal model and a mathematical analysis of the presented approach with a pre-biased (or a pre-scaled) factor are derived to provide evidence that it is reasonable and inexpensive to carry out the calculation of a complex magnitude. In addition, a numerical simulation and the hardware complexity show that the presented approach is indeed a cost-efficient method for determining the approximate magnitude of a complex signal.

This paper is organized as follows: The conventional approaches to magnitude calculation are reviewed in Section 2. The signal model and the mathematical analysis of the cost-efficient approximation are described in Section 3. The numerical evaluation is shown in Section 4. Case studies and performance comparisons are described in Section 5 and Section 6, respectively. Finally, the conclusions are given in Section 7.

2. Review of Conventional Approaches

In view of a complex signal x, the direct method for calculating the complex signal magnitude r [13] is expressed as

$$r=\sqrt{a^2+b^2}$$

(1)

where a and b are the real and imaginary parts of the complex signal x, respectively. Obviously, Equation (1) is an inefficient approach since it is composed of two operations of multiplication, one operation of addition and one operation of calculating the square-root.

On the other hand, it is well known that $\alpha$Max + $\beta$Min [3,14,15] and CORDIC [4,16] can be applied to calculate the complex signal magnitude. The $\alpha$Max + $\beta$Min approach is easily achieved by binary-shift and addition operations [17] and, therefore, its approximate magnitude ${\widehat{r}}_1$ is given as

$${\widehat{r}}_1\approx \alpha ·\mathrm{Max}+\beta ·\mathrm{Min}$$

(2)

where $\alpha$ and $\beta$ would be 1 and $\frac{1}{2}$, 1 and $\frac{1}{4}$, 1 and $\frac{3}{8}$, $\frac{15}{16}$ and $\frac{15}{32}$ [15], etc. Additionally, Max = $max\left(\right|a|,|b\left|\right)$ and $\mathrm{Min}=min\left(\right|a|,|b\left|\right)$, where $|·|$ is an absolute-value operation for a real number. In summary, the precision of the $\alpha$Max + $\beta$Min approach is determined by the selection of $\alpha$ and $\beta$.

The CORDIC algorithm is a variety of computations using iterative operation. The vectoring mode with circular rotation of the CORDIC algorithm [16] can be used to calculate the complex signal magnitude and is given as

$$\begin{array}{ccc}\hfill a_{i+1}& =& a_i-d_i·b_i·2^{-i}\hfill \\ \hfill b_{i+1}& =& b_i+d_i·a_i·2^{-i}\hfill \\ \hfill c_{i+1}& =& c_i-d_i·e_i\hfill \end{array}$$

(3)

where i denotes the iteration number. $d_i=-sign\left(b_i\right)$ and $e_i=ta{n}^{-1}\left(2^{-i}\right)$, where $sign(·)$ is defined to be −1 or 1 depending on whether the argument is negative or positive, respectively. For $a_0=a$, $b_0=b$ and $c_0=0$, after N iterations, the CORDIC outputs are given as

$$a_N\approx K·\sqrt{a^2+b^2},b_N\approx 0\mathrm{and}{c}_N\approx ta{n}^{-1}(b/a)$$

(4)

where K is equivalent to $\prod \sqrt{1+2^{-2i}}$ and converges to 1.6467. It is clear that the complex signal magnitude ${\widehat{r}}_2$ of the CORDIC approach can be obtained as follows:

$${\widehat{r}}_2\approx \frac{1}{K}·a_N$$

(5)

In order to minimize the hardware complexity in Equation (5), $\frac{1}{K}$ can be approximated to 0.60725, which is easily achieved with the shift-and-add operation as $\frac{1}{2}·(1+2^{-2})·(1-2^{-5})·(1+2^{-8})·(1-2^{-10})$ [18]. It is important that the precision of the CORDIC algorithm is proportional to the number of iterations. In other words, its outcome requires extra latencies resulting from more iterative numbers.

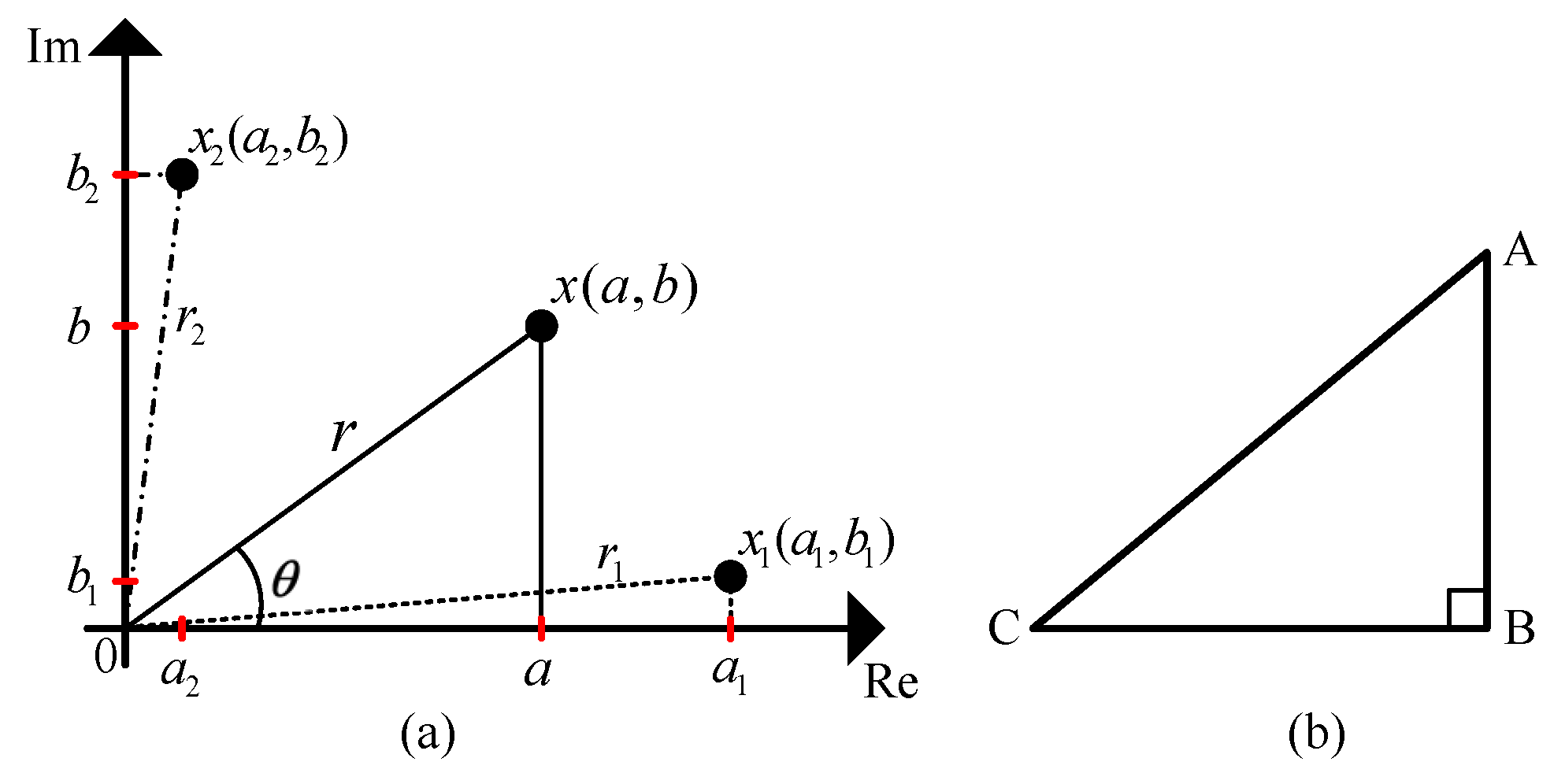
3. Signal Model of Cost-Efficient Approximation

For a complex signal $x=a+jb$, its Cartesian coordinate representation is illustrated in Figure 1a, where a and b are the real and imaginary parts of the complex signal x, respectively. The real and imaginary parts of the complex signal can be used to express the x- and y-axes in a Cartesian coordinate system, individually. In addition, r is a distance from the coordinate point x to the origin and also represents the magnitude of the complex signal x, as described in Equation (1). Apparently, the connection between x, a and the origin takes the shape of a triangle $▵xa0$.

Based on the Triangle inequality [19], the inequality of the triangle $▵ABC$, as shown in Figure 1b, is given as

$$\overline{AC}\le \overline{AB}+\overline{BC}$$

(6)

Similarly, the triangle $▵xa0$, as depicted in Figure 1a, has the same characteristic as that described in

$$r\le \left|a\right|+\left|b\right|$$

(7)

where $|·|$ represents an absolute value of a real number. Equation (7) indicates that the complex signal x would be located at any quadrant. Without loss of generality, the magnitude of a complex signal x can be reformulated as

$${\widehat{r}}_3\approx \lambda ·\left(\right|a|+\left|b\right|)$$

(8)

where $\lambda$ is defined as a scaling factor. Regarding $\lambda$ value, there are two important characteristics, described as follows:

• $\lambda \approx 1.0$ iff either $\left|a\right|\approx 0$ or $\left|b\right|\approx 0$. The complex signal x can be located at or near x- or y-axis, as shown in Figure 1a, such as $x_1$ or $x_2$, respectively.
• $\lambda \approx 0.707$ iff $\left|a\right|\approx \left|b\right|$. The complex signal x can be situated at $\theta \approx \pm {45}^{\circ }$ or $\pm {135}^{\circ }$ as illustrated in Figure 1a, such as x located at $\theta =45$.

Accordingly, the value of $\lambda$ has the following relationship:

$${\lambda }_{min}\le \lambda \le {\lambda }_{max}$$

(9)

where ${\lambda }_{max}=1.0$ and ${\lambda }_{min}=0.707$. In the worst case in (9), the signal power of (8) is lower than that of (1) with 3 dB. In addition, in the best case in (9), the signal power of (8) is identical to that of (1). In other words, from a signal power point of view, the difference between (1) and (8) is within 3 dB and can be pre-biased or pre-scaled in the design criteria for various applications. Therefore, under this condition for the proposed efficient approach, Equation (8) can be reformulated as

$${\widehat{r}}_3\approx \left(\right|a|+\left|b\right|)+\mathcal{S}$$

(10)

where $\mathcal{S}$ denotes the pre-biased factor. In summary, Equation (10) can be employed to approximate the complex signal magnitude with a pre-biased factor.

4. Numerical Evaluation

In order to evaluate the performances of various magnitude estimations, we use two types of signals, which are the signal around the unit circle and the random signal, to examine the related performance indexes, including the maximum absolute error and the mean square error (MSE). The evaluated errors of various estimations are compared with the direct method as described in (1). All numerical evaluations are modeled by MATLAB with floating-point format, and the results are illustrated in

Table 1. Numerical evaluation for various approaches.

		#CORDIC	$\mathit{\alpha }$Max + $\mathit{\beta }$Min		This Work *Equation (8)
			$\mathit{\alpha }=\mathbf{1}$, $\mathit{\beta }=\frac{\mathbf{3}}{\mathbf{8}}$	$\mathit{\alpha }=\frac{\mathbf{15}}{\mathbf{16}}$, $\mathit{\beta }=\frac{\mathbf{15}}{\mathbf{32}}$
Unit Circle	Max. |error|%	0.23	6.80	6.25	20.57
	MSE × 10−3	0.00	2.27	1.20	9.90
Random Signal	Max. |error|%	0.19	6.49	4.80	15.70
	MSE × 10−3	0.00	0.13	0.07	0.55

#: iterations of CORDIC operation; *: The pre-scaled factor of 2 dB.

.

• Unit Circle: The signal located on a unit circle is definitely a complex format, which means that the magnitude of the complex signal is equivalent to one. It is easy to examine the related performance indexes. Magnitude evaluation on the unit circle for various methods is shown in Figure 2. For the CORDIC approach constructed by using five iterations, the MSE is almost the same as that of the direct method. Regarding the $\alpha$Max + $\beta$Min approach, both the maximum absolute error and the MSE of $\alpha =\frac{15}{16}$ and $\beta =\frac{15}{32}$ are lower than those of $\alpha =1$ and $\beta =\frac{3}{8}$. The MSEs of $\alpha =\frac{15}{16}$ and $\beta =\frac{15}{32}$, as well as $\alpha =1$ and $\beta =\frac{3}{8}$, are about −29 and −26 dB, respectively. In view of the proposed efficient approach, the MSE is around −20 dB with a pre-scaled factor of 2 dB.
• Random Signal: Assuming a complex signal sample $x_n=a_n+j{b}_n$, where n is the sample index, both $a_n$ and $b_n$ are Gaussian random variables with zero-mean. For the numerical evaluation, the $wgn(·)$ function [20] of MATLAB is employed to generate the random signal samples, and the number of evaluated complex signal samples $x_n$ is larger than 5 × ${10}^6$. Additionally, the maximum signal power of the random signal samples is normalized to 1. Similarly, the MSE of CORDIC is identical to that of the direct method. The MSEs of $\alpha =\frac{15}{16}$ and $\beta =\frac{15}{32}$, as well as $\alpha =1$ and $\beta =\frac{3}{8}$, are around −42 and −39 dB, respectively. For the proposed efficient approach, the MSE is approximately −33 dB with a pre-scaled factor of 2 dB.
  In summary, although the accuracy of the proposed efficient approach is not the best compared with the other approaches, the MSE for the random signal can reach around −33 dB, which is acceptable for this application [12]. According to the result shown in (9), the deviation between the direct method and the efficient approach is definitely less than or equivalent to 3 dB. Consequently, the pre-biased or pre-scaled factor of the proposed efficient approach can be 2∼3 dB, which is determined by the application.

5. Case Study

5.1. Amplitude Detector of Digital AGC (DAGC) for Wi-Fi Systems

In order to provide a high signal-to-noise (SNR) signal for further digital baseband signal processing such as coarse/fine symbol boundary detection, coarse/fine carrier frequency offset (CFO) estimation, coarse/fine sampling clock offset (SCO) estimation and channel estimation, it is crucial to employ DAGC and voltage gain amplification (VGA), driving the received signal close to the full-scale level of an analog-to-digital converter (ADC).

Without loss of generality, an IEEE 802.11n 2 × 2 Wi-Fi system, as shown in Figure 3a, is adopted as a test vehicle to evaluate DAGC using the cost-efficient approximation of complex signal amplitude. In addition, the DAGC architecture is illustrated in Figure 3b. Based on the test evaluation, it easily extends to more antenna combinations. A physical layer convergence procedure (PLCP) header with a mixed-format (MF) high-throughput (HT) packet structure is illustrated in Figure 4, where the PLCP is composed of non-HT (legacy) training fields and HT training fields. In the legacy short training field (L-STF), the coarse tuning of DAGC has to be carried out before coarse symbol boundary detection and coarse CFO estimation. In the following legacy long training field (L-LTF), HT-STF, HT-LTF and HT data, the fine tuning of DAGC will be continued to maintain the received signal level.

A MATLAB program is developed to model the front end of a 2 × 2 multiple-input–multiplie-output (MIMO) system for evaluating DAGC operation and reliability. The channel model is produced by the MATLAB function wlanTGnChannel [20], and the related parameters are described as follows:

• Delay profile model and root-mean-square (RMS) delay spread: The delay profile of model-B with RMS delay spread of 15 ns.
• Maximum delay: 80 ns.
• Number of clusters: 2.
• Number of taps: 9.
• Number of antennas: 1 × 1 for single-input–single-output (SISO) channel in legacy training field, and 2 × 2 for MIMO channel in HT training field.
• Distance between transmitter and receiver: 15 m.

The other parameters of wlanTGnChannel are set to default. According to Figure 3b and Equation (8), the amplitude detector ${\widehat{r}}_n$ of DAGC can be obtained as follows:

$${\widehat{r}}_n=\lambda \left(\right|y_{n,R}|+|y_{n,I}\left|\right)$$

(11)

where $y_{n,R}$ and $y_{n,I}$ are the real and imaginary parts of the received signal $y_n$. The integral and down are fulfilled using the moving-sum average, where the lengths of the moving sum for STF and LTF are 16- and 32-sample, respectively. The ideal reference amplitudes $V_{ref}$ for STF and LTF are equivalent to 0.1086 and 0.1075, individually. For the proposed approach, as derived in Equation (11), the reference amplitudes for STF and LTF are equal to $V_{ref,S}$ = 0.1185 and $V_{ref,L}$ = 0.1340. Consider the derivation of Equation (11); both ${\lambda }_S$ and ${\lambda }_L$ for SFT and LTF are 0.92 and 0.8, respectively. It is important that the signal power of the ADC output has to be unified and maintained close to the full-scale level of ADC by the DAGC tracking loop. Consequently, both ${\lambda }_S$ and ${\lambda }_L$ for SFT and LTF can be set to 1.0 since the DAGC loop can be continually tracked to satisfy the amplitude references such as $V_{ref,S}$ and $V_{ref,L}$.

Without loss of exactness, L-SIG and HT-SIG are ignored in numerical evaluation. The simulation results for the signal-to-noise ratio (SNR) = 16 dB are shown in Figure 5, Figure 6 and Figure 7, where both vertical dashed lines express the signal transition from L-LTF to HG-STF. Regardless of legacy and HT training fields, the gain ratio for SISO between the ideal, as described in Equation (1), and the proposed approach, as derived in Equation (11), is than 0.1 dB, which means that the signal power deviation, as shown in Figure 5b, can be ignored since the deviation is much less than the ADC tolerance of 1 bit. Similarly, the gain ratio and the signal power deviations, as illustrated in Figure 6b and Figure 7b for Rx-1 and Rx-2, are 0.12 and 0.3 dB, and 0.27 and 0.32 dB, respectively. The signal power deviations for SISO, Rx-1 and Rx-2 are 0.1, 0.27 and 0.32 dB, respectively. It can be concluded that the proposed approach, as described in Equation (11), has the same performance compared with Equation (1) since the signal power deviation is much less than that of the ADC tolerance of 1 bit.

5.2. Golay-Correlator Window-Based Cancellation (GC-WNC) Equalization Technique

The approximate magnitude calculation for a complex signal, as derived in (10), was applied to GC-WNC equalization [12] for orthogonal frequency-division multiplexing (OFDM) and a single-carrier (SC) mode baseband inner receiver.

The GC-WNC equalization technique is a cooperative scheme in the time and frequency domains to combat the multipath effect in non-line-of-sight (NLOS) and LOS channels for OFDM/SC mode baseband inner receiver over 60 GHz environment for IEEE 802.15.3c [21] and 802.11ad [22]. The technique is composed of GC, WNC and frequency-domain equalization (FDE), where GC and WNC are achieved in the time domain and FDE is fulfilled on each subchannel in the frequency domain.

The GC is employed to estimate the channel impulse response (CIR) of the multipath fading channel in the time domain. However, the estimated CIR has some small-peak samples (see Figure 2 in [12]) that lead to an imperfect estimation of the channel frequency response (CFR) (see Figure 3 in [12]) by transferring the estimated CIR from the time domain to the frequency domain. As a result, the system performance is severely degraded since all of the FDE coefficients are obtained from the defective CFR. In order to minimize the estimation error between the ideal and the estimated CFR, the WNC is employed to remove the small-peak samples of the estimated CIR and further enhance the system performance. The small-peak samples of the estimated CIR can be replaced by zero iff the magnitude of the small-peak samples is less than a threshold value $W_{th}$. For the low-hardware-complexity issue, Equation (10) can be used to obtain the approximate magnitude of the small-peak samples, and the pre-biased factor can be merged into the threshold value $W_{th}$.

The design criterion of the WNC approach is based on the system SNR degradation induced by an estimation error of less than 0.25 dB. Therefore, the signal power of each removed small-peak sample has to be at least 12 dB less than that of AWGN, which means that the removed small-peak samples of 12 dB lower than AWGN can be viewed as a part of AWGN. It is obvious that the removed small-peak samples are too tiny to affect the CFR estimation. For the normal calculation, the threshold value $W_{th}$ for 64 QAM with an SNR of 26 dB has to be less than or equivalent to −38 dB, i.e., $W_{th}\le 0.0126$. Based on the numerical evaluation, as described in the previous section, and the system simulation, we choose a 3 dB deviation as the pre-biased factor described in Equation (10) [12]. Furthermore, the 3 dB pre-biased factor can be merged into the threshold value of $W_{th}$. To effortlessly conduct a comparison between the approximate magnitude of the estimated CIR and the threshold value, the threshold value is considered to be a power of two. As a consequence, $W_{th}=2^{-6}$$(=0.015625$) is used for compensating the induced error.

6. Comparison and Discussion

Considering the occupied area and the power consumption in VLSI implementation for various approaches, the related hardware architectures, as illustrated in Figure 8, are obtained by a 40 nm CMOS general process (GP) with a supply voltage of 0.9 V and an operating clock of 500 MHz, namely, a timing constraint of 2 ns. All of the hardware cells are from DesignWare library [23]. In order to conduct a fair comparison, both the input and output for the related hardware architectures are 20 bits, which means that the real and imaginary parts are 10 bits, individually. The performance evaluations, such as the occupied area and power, for various hardware architectures are extracted from the synthesis reports using Synopsys Design Complier, and further illustrated in

Table 2. Comparisons of area and power consumption for various approaches, where $\alpha =\frac{15}{16}$ and $\beta =\frac{15}{32}$ for $\alpha$Max + $\beta$Min approaches.

	Direct Method	#CORDIC	$\mathit{\alpha }$Max + $\mathit{\beta }$Min	Proposed Type-1	Proposed Type-2
Area ($\mathsf{\mu }$m2)	713.74	767.72	218.18	90.27	60.78
Power ($\mathsf{\mu }$W)	473.2	673.8	131.2	34.8	29.9
$\eta$	1	1.08	0.31	0.13	0.09
Max |error|%	0.23	8.82	4.50	15.91	15.91
MSE × 10−3	0.00	0.00	0.05	0.54	0.54

#: 5 stages of CORDIC operation.

. In addition, both Max |error|% and MSE are the evaluation results from the MATLAB simulation, where the test patterns are the same as those of the previous random signal and quantized as finite wordlength patterns. The related descriptions for the hardware architectures and the performance evaluations are listed below.

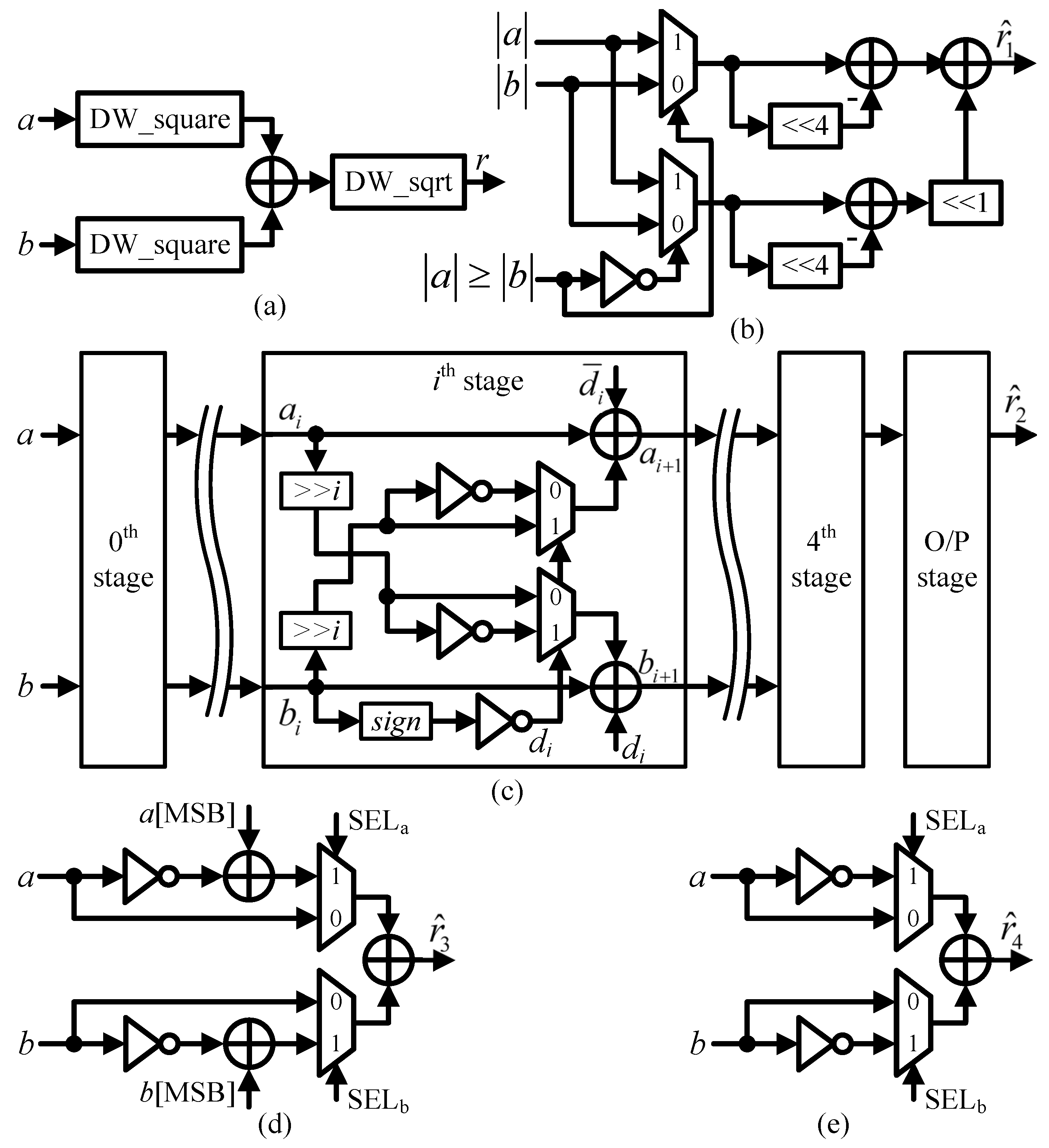
• Direct method: The hardware architecture of (1) is depicted in Figure 8a, where DW_square and DW_sqrt are DesignWare IPs [23] and perform square and the square-root calculations for a real number, respectively. Both the maximum absolute error and MSE are the smallest of all the approaches. However, both the area and power are the second largest compared with the other approaches.
• $\alpha$Max + $\beta$Min approach: The hardware architecture of (2) is illustrated in Figure 8b, where $\alpha$ and $\beta$ are equivalent to $\frac{15}{16}$ and $\frac{15}{32}$, respectively. It is worth noting that the related hardware architectures for $\left|a\right|$, $\left|b\right|$ and $\left|a\right|\ge \left|b\right|$ are not shown in Figure 8b. The MSE is around −43 dB.
• CORDIC algorithm: Due to the timing constraint of 2 ns, the CORDIC computation can not be achieved using an iterative operation. Therefore, the hardware architecture of (4) is shown in Figure 8c, including the five stages of the CORDIC process element (PE) and an output stage. In order to make a fair comparison, only $a_{i+1}$ and $b_{i+1}$, as described in (4), are obtained in the design template since $c_{i+1}$ is irrelative to find ${\widehat{r}}_2$. The hardware architecture of the CORDIC PE is sketched in the ith stage, as illustrated in the middle of Figure 8c. To reduce the hardware complexity and preserve the 10-bit resolution at the square-root output, $\frac{1}{K}$ is revised as 0.607421875, which is fulfilled by $\frac{1}{2}·\left[(1+2^{-2})-2^{-5}·(1+2^{-3})\right]$ at the output stage. Consequently, the MSE is identical to that of the direct method. Although CORDIC has merely five PEs, both its area and power are the largest compared with the other approaches.
• Proposed type-1 approach: The hardware architecture of the proposed efficient approach, as described in (10), is illustrated in Figure 8d. The absolute-value operation of a negative number is implemented by a 2’s complement operation, which is composed of an operation of a 1’s complement and the operation of a plus-one. The plus-one operation is fulfilled by the addition of the most significant bit (MSB) of the negative number, such as $a\left[\mathrm{MSB}\right]$ and $b\left[\mathrm{MSB}\right]$ in Figure 8d, since $a\left[\mathrm{MSB}\right]$ and $b\left[\mathrm{MSB}\right]$ are the sign bits. Both selections ${\mathrm{SEL}}_a$ and ${\mathrm{SEL}}_b$ of the multiplexers (MUXs) are also equivalent to $a\left[\mathrm{MSB}\right]$ and $b\left[\mathrm{MSB}\right]$, respectively, and are used to select the input positive number or the absolute value of the input negative number. Finally, the MSE is around −33 dB.
• Proposed type-2 approach: In order to further save on hardware costs in the proposed type-1 approach, the absolute-value operation is simplified as a 1’s complement operation for the negative number. Obviously, without a plus-one operation, the absolute value is viewed as precision loss that can be merged into the quantized error. It is worth noting that the quantized error due to the 1’s complement is acceptable since it is below −54 dB. Therefore, the MSE is the same as that of the type-1 approach. The hardware architecture of the proposed type-2 approach is illustrated in Figure 8e. Similarly, both selections ${\mathrm{SEL}}_a$ and ${\mathrm{SEL}}_b$ of MUXs are the same as those of the proposed type-1 approach.

According to the results shown in Table 2, the related comparisons, including area, power and performance, are summarized as follows:

• Although the performance indexes of the proposed efficient approach are not the best, the MSE for the proposed type-1 and -2 approaches can reach around −32.7 dB. Additionally, the quantized error induced by the 1’s complement of the type-2 approach is −54.2 dB, which is lower than the MSE of 21.5 dB. From an MSE point of view, the quantized error caused by the 1’s complement operation can be ignored. Consequently, the type-2 approach is an appropriate method in the considered applications [12] since the performance indexes of the type-2 approach are the same as those of the type-1 approach.
• The area of the direct method is used as the base area to reveal the hardware cost reduction efficiency $\eta$. It is clear that the areas of the CORDIC, $\alpha$Max + $\beta$Min, and type-1 and the type-2 approaches are around 1.08, 0.31, 0.13, and 0.09 times the area of the direct method, respectively.
• In fact, the CORDIC approach comprises a variety of computations. Using CORDIC to perform a single operation has no benefits, since the area of CORDIC is the largest compared with the other approaches.

7. Conclusions

In this paper, an efficient approach is presented to acquire the approximate magnitude of a complex signal. A signal model and a mathematical analysis are derived to determine the approximate magnitude of the complex signal with a pre-biased or pre-scaled factor in the design criteria. Based on the deductive results, the pre-biased or pre-scaled factor can be 2∼3 dB, which is determined by the application. Furthermore, the numerical evaluations show that the MSE of the proposed efficient approach for the random signal can reach around −33 dB. In order to save on hardware costs, the absolute value of a negative number for the proposed type-2 approach is simplified as a 1’s complement operation, where precision loss can be viewed as quantized noise and further ignored. The physical implementation results indicate that the areas of the proposed type-1 and -2 approaches are 90.27 and 60.78 mm² with a 40 nm CMOS general process, respectively. The power consumptions of the proposed type-1 and -2 approaches are 34.5 and 29.9 $\mathsf{\mu }$W with a supply voltage of 0.9 V and an operating clock of 500 MHz. Therefore, the occupied areas of the proposed type-1 and -2 approaches are only 0.13 and 0.09 times the area of the direct-method, respectively. The presented type-1 and -2 approaches with acceptable MSEs are indeed cost-efficient methods compared with the other considered approaches.