Steganography in QR Codes—Information Hiding with Suboptimal Segmentation

Abstract

This paper describes a new steganographic method for QR codes. Unlike most information-hiding techniques in this field, it does not rely on the error correction property. Instead, it uses the segmentation feature of QR codes. Encoding of data in a QR code is achieved by creating segments of specific modes, chosen according to data type in order to save space. However, the segmentation does not have to be optimal. A secret message may be embedded into a QR code by selecting an alternative segment type. The presented method generates valid QR codes that may be decoded with standard readers. The solution has been tested using several QR decoders, and it has been confirmed that only the regular message was returned. Additionally, the error correction quality of produced codes is not diminished. The described algorithm is suitable for either digital or printed media, and in both cases, QR codes retain secret data.

1. Introduction

QR codes are a very pervasive technology. Nowadays, they may be encountered in numerous places, both physically and online. From their countless applications, the most common are product labeling, personal contact information, transport ticketing, mobile payments, e-commerce, marketing, links to social networks, advertisement, and many more. In general, the purpose of QR codes is to store short information, which may be decoded with a special application, for example, on a mobile phone or using an online service.

The ubiquity of QR codes makes them good covers for information hiding. The branch of science destined for covert communication is called steganography [1,2]. A secret message is embedded into inconspicuous media, like texts, digital images, or videos. In this way, the secret is transmitted without raising the suspicion of external observers. The carrier should be a common file that occurs naturally in its place and whose presence is expected. Additionally, the structure of the cover needs to be able to store additional data. It turns out that QR codes are totally suitable for this application.

The purpose of this article is to propose a new steganographic method for QR codes. The main emphasis is placed on the robustness and low computational complexity of the presented technique. The robustness of QR codes is achieved with an error correction feature. This mechanism is able to rectify some number of discrepancies that may be introduced when the code is dirty or in dim light. However, in the presented solution, error correction is not used directly to embed secret data. Instead, overt and covert messages are placed in the same area, which gives them similar levels of robustness. The secret information is encoded using a selection of specific segmentation, which introduces linear (low) complexity to the data decoder.

This section outlines the literature review. Section 2 presents some background information about QR codes and the steganographic method itself. In Section 3, we depict outcomes of our research with some examples. Additional findings and implications are described in Section 4. Finally, Section 5 summarizes the paper.

Literature Review

There are not many papers concerning data hiding in QR codes, but we can still list several. An interesting approach is presented in [3]. The author describes a method of creating a QR code that contains two various messages. They can be recovered when the code is viewed in a straight and mirrored position. It is realized by selecting appropriate modules that decode different data thanks to the error correction property.

Incidentally, error correction is the most frequently used property for steganographic purposes. For example, Ref. [4] introduces a secret sharing system in which each share is a valid QR code. To hide a secret, shares are modified a little, just enough to conceal parts of the secret message and not to exceed error correction capacity. Later, the shares are xored to retrieve a secret QR code containing the final message. A similar approach may be found in [5]. Another secret sharing scheme based on QR codes is presented in [6]. Its authors claimed to overcome security weakness from [4] by inventing two algorithms for share division. Additionally, they achieved more flexible access structures and higher efficiency. Considering other steganographic techniques in QR codes, Ref. [7] describes a method of concealing an encrypted secret in error correction codewords, whose capacity depends on the QR code version and the chosen level of error correction. In [8], the authors use Reed–Solomon codes and list decoding for steganographic purposes. The interesting feature of this scheme is that the extracting procedure returns multiple possible messages. On the other hand, in [9], information hiding is implemented with Hamming codes. This method is based on parity checks, and the message is hidden by flipping bits when needed. Steganography in QR codes may also be realized with wet paper codes [10]. It is a technique in which the embedding area is divided into wet regions (unchangeable) and dry regions (changeable). The secret may only be placed in dry areas, which are selected with a secret key. An approach called exploiting modification direction is described in [11]. The authors of this paper improved the mentioned technique by taking into account the overflow and underflow problems in the embedding process. A slightly different algorithm has been presented in [12], where padding bytes of Reed–Solomon codes have been used for information hiding. In this way, error correction capacity of the cover QR code is not sacrificed, so the method retains strong robustness. A turtle shell matrix is utilized for data embedding, which is suitable for low-resource environments.

Another approach has been presented in [13]. Each module of a QR code is segmented into a subcell structure. The capacity depends on the print density and the camera parameters. This method of information hiding maintains backward compatibility with conventional QR readers. Such an idea has also been used in [14]. Each module of a QR code is treated as a second storage level. The hiding algorithm replaces black modules with specific textured patterns. Standard QR readers perceive these subcells as normal black modules. There are also many more steganographic methods incorporating QR codes in various steps of embedding [15,16,17,18,19]. These algorithms, however, use barcodes as a stage in the secret hiding process, but they are not as direct steganographic carriers.

A distinct approach is to use segments to conceal a secret message [20]. Segmentation of a QR code’s contents may be performed to save space by applying various encodings. Preliminary research on this topic used empty segments, each of which encoded two bits of the secret message. The advantage of this system is its robustness, but it has also the disadvantage of repetitiveness as zero-length segments are similar.

As can be seen, most of the studies focus on error correction features for data hiding. Although useful, it almost always degrades the codes and makes them more vulnerable. For this reason, there is a demand for methods based on different principles that put the main emphasis on robustness. This paper has been written to close this gap and to propose a new steganographic algorithm for QR codes. The main requirements for this method are achieving high robustness and low computational complexity.

2. Materials and Methods

2.1. Background: QR Codes

QR codes are two-dimensional barcodes designed to store short messages. They come in a number of sizes (versions), starting from $21\times 21$ up to $177\times 177$. The appearance of QR codes is very characteristic, as they consist of contrasting squares—usually white and black—called modules. Several instances are presented in Figure 1.

To make them easier to read by machine, QR codes have reserved areas destined for specific purposes. They are highlighted in Figure 2. Three concentric squares located in corners, called finding patterns, are used for pinpointing the code. Smaller squares with a single dark module in its center are called alignment patterns. They start occurring in codes of version 2, and in higher versions, we may encounter multiple copies of this marker (which can be observed in Figure 1). The timing pattern is a line of alternating bright and dark modules. It is aligned to the inner side of finding patterns, always in harmony with the alignment pattern. Modules around finding patterns encode format information required for the decoding process and, from version 7 upwards, additional version information. Finally, the whole QR code needs to be surrounded by a quiet zone—a frame of four white modules. All these elements constitute functional areas, remaining parts are used for storing the data.

The data in a QR code can be encoded with a few modes: numeric, alphanumeric, byte, and kanji (Japanese characters). What is more, a single code may contain multiple segments of data in various modes. The purpose of this feature is storage efficiency—although the data may be represented in a number of ways, some of them take less space. Selecting optimal segmentation is useful to obtain smaller codes. For example, “ABC123456” stored in a single byte segment takes 92 bits. The same input divided into two segments (alphanumeric ABC and numeric 123456) occupies $30+38=68$ bits, so we are able to save 24 bits.

The most important characteristic of QR codes is their error correction. This mechanism allows rectifying some discrepancies that may occur during reading in suboptimal lighting or when the code is dirty or partially obscured. QR code specification defines four possible levels of error correction: low, medium, quartile, and high, able to correct from 7% to 30% of damaged data. The capacity of a QR code depends on the version and error correction in the following manner: the higher the version and the lower the error correction, the more data may be stored in a code.

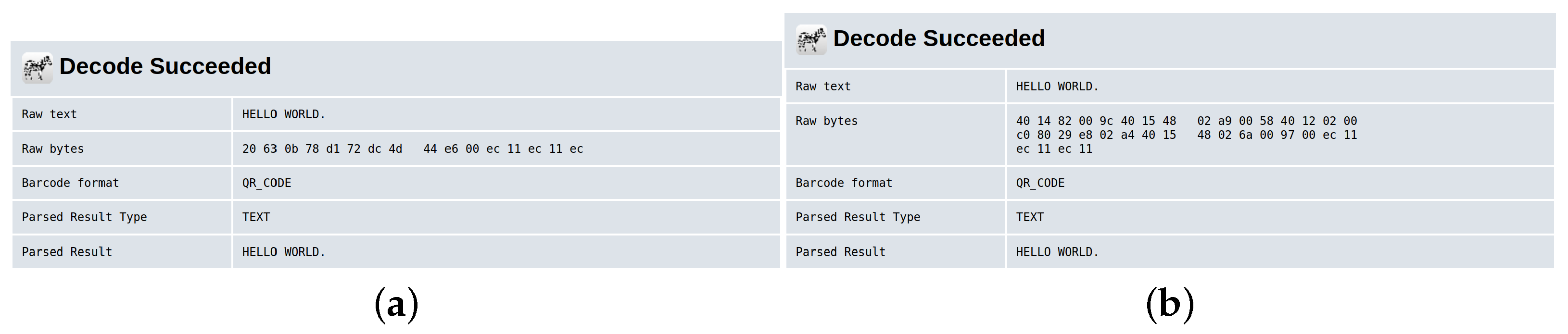
2.2. Steganographic Method of Suboptimal Segmentation

The main purpose of the presented solution is information hiding and its key feature is robustness. The proposed method operates on numeric and alphanumeric segments. The message to be hidden is in binary format. The embedding algorithm is incorporated in QR code creation when segments are generated. At the beginning, we must ensure that the number of numeric and alphanumeric segments is greater than or equal to the secret message length. If necessary, the number of segments may be increased by fragmentation. For example, a long segment may be replaced with two smaller segments of the same type.

The embedding algorithm checks segment types and compares them to the covert message consecutive bits. When the secret bit is 0, the optimal segmentation is left as is. When the secret bit is 1, the segment type is changed to byte. In this way, suboptimal encoding is selected for all segments that relate to ones.

Example 1.

Let us assume that we want to conceal a binary secret “100001011001” in a QR code. Our regular message is “HELLO WORLD.” (12 characters) and may be encoded in an optimal way as a single alphanumeric segment. However, we choose to present these data as 12 separate segments, whose types correspond to secret bits. In this way, we obtain HELLO  WORLD. (orange denotes byte segment and violet denotes alphanumeric segment), i.e.:

Segment Content	Segment Type	Encoded Bit
H	byte	1
E	alphanumeric	0
L	alphanumeric	0
L	alphanumeric	0
O	alphanumeric	0
(space)	byte	1
W	alphanumeric	0
O	byte	1
R	byte	1
L	alphanumeric	0
D	alphanumeric	0
.	byte	1

The embedding procedure has been depicted in Algorithm 1. First, we need to check if the capacity is sufficient for the secret message. Then, if needed, numeric and alphanumeric segments are divided until their number is equal to the secret message length. Finally, segment types are changed when secret bits are equal to 1. Algorithm 1 presumes that the secret message exploits all available capacity. It is also possible that the message is shorter—in such cases, the user needs to randomly select segments used for embedding and save their indices (serving as a key) so as to use them during decoding. This is, however, a very rare situation; usually, the number of segments is significantly lower than the number of secret bits.

Algorithm 1: Embedding algorithm

The extraction algorithm works in an opposite way. At first, segments are decoded from a QR code. For each of them, we analyze whether it is encoded in an optimal way. If not, 1 is added to the secret message bitstream; otherwise, we append 0 to it. At the end, the secret is returned (and optionally converted to another format if needed).

Example 2.

We decoded segments from a QR code and obtained HELLO  WORLD. (color encoding is identical as in Example 1). Then, types of these segments are analyzed. In this case we only have alphanumeric and suboptimal byte segments. Therefore, each alphanumeric segment encodes 0, and remaining byte segments denote 1. The recovered message is 100001011001, which is consistent with the previous example.

The extraction method is presented in Algorithm 2. Bits of the secret message are selected according to the segment type. Each byte segment is checked if it can be represented as numeric/alphanumeric data to exclude segments that do not contain any secret bits. Again, we present the most common case in which the secret data is longer than the overt data. Otherwise, a key is required to choose proper segments. Returned secret is a binary string, which may be cast to other formats if needed.

Algorithm 2: Extracting algorithm

3. Results

The results of the proposed algorithm are presented in this section. Figure 3 depicts output codes from previous examples. As a reminder, the secret message hidden in stego QR codes is 100001011001, and the regular message is “HELLO WORLD.”. For comparison, in the figure there are also pure QR codes (without any secrets). We may observe that the embedding process caused larger sizes of stego codes.

Another bundle of results is presented in Figure 4. This time, the secret message is 10100111001, and the regular contents of the QR codes are “KATARZYNA KOPTYRA AND MAREK R. OGIELA. STEGANOGRAPHY IN QR CODES—INFORMATION HIDING WITH SUBOPTIMAL SEGMENTATION”. All these codes have error correction levels set to L and contain the same regular message and also the same secret. In this case, stego codes are only four modules larger per side than pure (without hidden data) codes.

The interesting fact is that despite all the codes storing the same data, their appearance is different. This may be explained by division. The length of the mentioned overt message is 114 characters, and its optimal segmentation is into a single alphanumeric segment. On the other hand, the length of the secret message is 11 bits. Therefore, the embedding process may be conducted in multiple ways, each of which gives a different code.

Figure 5 presents another set of QR codes that store the same messages as previously. The difference is that now the error correction level has been chosen to Q. The codes vary because of the same reason as in Figure 4, namely, when various divisions are possible, various codes would be generated. Examples of randomly chosen divisions are shown in Figure 6. They correspond to codes presented previously in Figure 5. As can be seen, different appearances of codes are related to specific segmentation.

All codes presented in this paper are compliant with the QR standard [21]. It is possible to decode them with regular decoding software to retrieve an overt message. The solution was tested locally with the zxing “Zebra Crossing” library (written in Java and published under open-source Apache license, available on https://github.com/zxing/zxing, accessed on 25 March 2024). The original implementation returns only the overt message. With the modified extracting algorithm, we were also able to retrieve the secret message, as presented in Figure 7 (the output was cast to an integer value, so it is displayed as 1337 instead of 10100111001). Additionally, stego codes were tested on several websites that offer online QR decoding. We obtained the expected results, i.e., the overt message was displayed. The full link list is available in Appendix A. There is one online service that shows raw bytes of QR code data: https://zxing.org/ (accessed on 25 March 2024). On this website, we may observe that parsed results are identical despite different byte outputs, which are presented in Figure 8. Different amounts of bytes are connected with introduced segmentation. As we remember from Example 1, stego code contains 12 various segments instead of a single alphanumeric segment in a pure carrier. These additional segments are not visible, but each of them has a header that increases the total length of the payload. The codes were also correctly decoded on the Android application Barcode Scanner, which only revealed the regular message.

4. Discussion

The presented steganographic method uses suboptimal segmentation for data hiding. This approach is uncommon in QR code steganography, as the majority of techniques are based on the error correction property. Almost every algorithm that relies on such a feature (except [12]) degrades the number of errors possible to correct. On the other hand, the proposed approach retains high robustness at the same level as pure codes. This is because regular and secret messages share the same embedding space within code content, hence no discrepancies are introduced. However, the capacity is affected due to the fact that during embedding some segments are divided and others are encoded on more bytes than originally. As a reminder, in QR codes, segments consist of headers and data, so each additional header limits the embedding space size. The maximum length of the secret message in bits is equal to the sum of lengths of numeric and alphanumeric segments. Intuitively, it means that the capacity grows with longer regular messages. It should also be noted that additional payload bytes render resulting stego codes a little bigger than pure codes.

Despite the different concepts, the presented stego system shows some similarities to other methods. When not all the capacity is exhausted, multiple variants of a correct QR code may be generated. All these codes would store the same regular messages and identical secrets. This is caused by multiple possible divisions of a long segment into smaller segments. An example of such behavior is depicted in Figure 4 and Figure 5, in which each code contains identical data, but their appearances vary. Known algorithms from the state of the art that use error correction as embedding space achieve it differently. They may introduce errors in a multitude of ways. Another similarity (which is also an advantage of the presented technique) is compliance with the QR standard. All covers generated during this research are correct codes that may be read with a regular decoder. Regular decoders reveal only the overt data, which were tested with numerous programs, including an Android application, desktop software, and online services.

As the primary asset of the presented technique is its robustness, the codes were tested for typical situations that may hinder decoding. We simulated some practical challenges that QR codes might face, including different lighting conditions (contrast reduction), smudging the code (cloud noise), different camera settings (Gaussian blur), or damaging the code (cropping). The resulting codes are presented in Figure 9. All these tests were conducted with three decoders: zxing (online, zxing.org, accessed on 13 Jun 2024), zbarimg (local instance), and modified zxing (local). The tests were also repeated for pure code with the same regular message “HELLO WORLD.”, error correction level, and version to confirm that additional hidden data do not impair decoding efficiency. The results for both codes were very similar, as presented in

Table 1. Results of decoding modified codes. Tool1 (T1) is online zxing, tool2 (T2) is zbarimg, and tool3 (T3) is local zxing. Underlined terms mean successful decoding.

		Stego Code						Pure Code
Contrast	T1	−30	−45	−60	−75	−90	−115	−30	−45	−60	−75	−90	−115
	T2	−30	−45	−60	−75	−90	−115	−30	−45	−60	−75	−90	−115
	T3	−30	−45	−60	−75	−90	−115	−30	−45	−60	−75	−90	−115
Noise	T1	50%	100%	150%	200%	250%	300%	50%	100%	150%	200%	250%	300%
	T2	50%	100%	150%	200%	250%	300%	50%	100%	150%	200%	250%	300%
	T3	50%	100%	150%	200%	250%	300%	50%	100%	150%	200%	250%	300%
Blur	T1	1	2	3	4	5		1	2	3	4	5
	T2	1	2	3	4	5		1	2	3	4	5
	T3	1	2	3	4	5		1	2	3	4	5
Cropping *	T1	1%	5%	10%	20%	30%		1%	5%	10%	20%	30%
	T2	1%	5%	10%	20%	30%		1%	5%	10%	20%	30%
	T3	1%	5%	10%	20%	30%		1%	5%	10%	20%	30%

* Obviously, no decoder is able to retrieve data from 30% cropped code, as selected error correction level is Q, which may restore up to 25% of data.

.

The main observation is that the decoding process is software-dependent. Some applications act better than others for both pure and stego code. For example, zbarimg deals well with each type of distortion. The zxing operation, on the other hand, is different for online and local versions. It is unclear which version is available online and why the results vary. The second conclusion is that whenever the overt message was possible to recover, the secret message was also retrieved. This is a consequence of sharing the same embedding space. Such a feature provides high protection for hidden data, because to destroy them, an adversary needs to wreck the regular information as well. Also, pure and stego codes do not manifest much difference when we consider robustness. In some cases, pure codes were easier to decode, while in others, they were more difficult. It may be due to the arrangement of modules and masks, which vary in appearance when distorted. The tests proved the robustness and usefulness of the proposed method. Successful attacks distort codes so much that retrieving the regular data is impossible, which makes them rather impractical.

The main limitation of the presented method is connected with capacity. There are two aspects we need to consider. Firstly, QR codes themselves manifest scanty capacity compared to other types of carriers, such as images or videos. The highest version (40) with the lowest error correction (L) is able to store 7089 numbers or 4296 alphanumeric characters or 2953 binary data or 23,648 bits when data types are mixed. Secondly, the capacity of this method is content-dependent, i.e., the maximum number of bits is equal to the length of the regular message, specifically to the sum of lengths of numeric and alphanumeric segments. The capacity may be increased by combining with other algorithms, for example, the method of empty segments [20]. In such cases, more data may be hidden by adding to the QR code some empty segments that encode further parts of the secret or a second message. This increases the capacity when content length is too small to fit the whole payload. The upper bound of how much the capacity may be expanded is imposed by the QR standard, that is the version and error correction level.

5. Conclusions

To sum up the most important facts about the proposed steganographic system: it conceals secret data in QR codes using suboptimal segmentation. All created codes are compliant with QR standards. The main stress is placed on robustness; thus, the system achieves resistance to attacks. Additionally, our method is characterized by simplicity and low (linear) computational complexity. The drawback is that the method has limited capacity, which is expected considering the type of carrier.

Future research directions in the field of steganography in QR codes are open, especially when we consider their growing usage from year to year [22]. QR codes are omnipresent in various environments, including those of low resources and the Internet of Things [23,24]. In such conditions, low-complexity steganographic algorithms may be invented. Another idea is related to multi-secret steganography, in which more than one secret is placed in a single container [25]. QR codes offer various embedding spaces which makes them promising objects of mentioned research. Although the majority of papers from the state-of-the-art concern error correction property, many more approaches are possible. Suboptimal segmentation is just one example that encourages the encouragement of inventing new methods in this fascinating area.