Chaotic Orthogonal Composite Sequence for 5G NR Time Service Signal Capture Algorithm

Abstract

Establishing a national comprehensive PNT (Positioning, Navigation, and Timing) system has become a consensus among major countries worldwide. As a crucial component in completing the entire PNT system, the 5G NR (new radio) time service signal plays a vital role. This paper proposes a 5G NR time service signal that uses a spread spectrum system, shares the 5G signal frequency band, but does not occupy the bandwidth of the 5G communication signal. This timing service signal has relatively low power, making it appear “submerged” within the power of the 5G communication signal. The spread spectrum code for this timing signal employs the chaotic orthogonal composite sequence proposed in this paper. Compared to traditional spread spectrum sequences, this sequence offers better security than m-sequences, improved autocorrelation than Walsh sequences, and an effective suppression of the short-period characteristics exhibited when the Skew Tent-Map chaotic sequence takes special values. This paper simulates the capture of the 5G NR time service signal in an environment with a signal-to-noise ratio of 10 dB using an FFT-based parallel code phase search algorithm, successfully capturing the 5G NR time service signal and verifying the feasibility of the proposed chaotic orthogonal composite sequence as a spread spectrum code.

1. Introduction

To date, major countries around the world have proposed the establishment of a national comprehensive Positioning, Navigation and Timing (PNT) system. This refers to a national information infrastructure that, under unified organization and coordination at the national level, serves the purposes of national defense, the economy and society. It undertakes tasks such as the establishment and maintenance of national spatiotemporal benchmarks, the dissemination and acquisition of spatiotemporal information, and PNT services and applications [1,2]. Based on the existing need for more ubiquitous, integrated and intelligent systems, and also considering the actual needs and application scenarios of various users, the primary goal of the comprehensive PNT system is to provide adaptive and resilient PNT application services. A resilient comprehensive PNT application service system and network should be the main future development direction. “Resilience” here means that PNT services are not affected by environmental factors and have high availability, continuity and reliability [3,4]. The national comprehensive PNT system is an integral spatiotemporal information network that combines satellite navigation systems as the core with low-orbit satellites, ground-based 5G communications, pseudolites, autonomous sensors, and other PNT means [5,6]. It merges the capabilities of unified spatiotemporal benchmarks, network interconnection and resilient collaborative operation [7,8]. Among them, ground-based 5G communication technology is expected to become an important component of the comprehensive PNT system [9,10,11], playing a crucial role in completing the entire comprehensive PNT system and building a global intelligent society based on spatiotemporal information [12].

In recent years, the rapid development of 5G communication technology, relative to 4G communication, has achieved a communication rate of up to 10 Gbps, latency reduced to 1 ms, and the ability to connect millions of terminals per square kilometer. 5G communication technology will greatly promote the development of fields such as artificial intelligence, cloud computing, big data, autonomous driving, and the Internet of Everything, making a significant contribution to the national economy. When broadcasting timing signals using 5G communication technology, timing information can reach the nanosecond level, as opposed to the microsecond level of 4G [13,14,15].

With the deployment of 5G macro base stations and micro base stations, 5G can provide signal coverage both indoors and outdoors, allowing users to receive signals without environmental restrictions. This also makes the further exploration of 5G-based timing modes possible. Fan et al. [16] proposed a new carrier phase positioning technology suitable for new 5G wireless cellular networks, developing a clock offset estimation method based on carrier phase to achieve picosecond-level clock synchronization between base stations, which gradually converges to the Cramer-Rao lower bound (CRLB). He et al. [17] proposed a precise time protocol (M-PTP) to address the high cost of hop-by-hop deployment of IEEE 1588 PTP, achieving an precision of 11.61 ns at 5 hops according to the experimental results. Li et al. [18] analyzed the synchronization problem of longitudinal differential protection time in distribution networks based on 5G networks and proposed a time synchronization algorithm built on the NTP protocol. Chandramouli, D et al. [19] asserted that 5G-Advanced networks would become a fully feasible technological alternative or a supplement to global navigation satellite systems (GNSS) for providing time synchronization with UTC or any well-defined time reference. Hamdan, MQ et al. [20] proposed the application of related space satellites based on RTK positioning algorithms as a binary formation system to improve the timing error (TE) between user equipment (UE) and base stations, thereby enhancing the performance of 5G timing synchronization. Mahmood, A et al. [21] proposed a wireless time synchronization scheme containing a 5G air interface, discussed related timing errors, and finally identified and resolved random errors unique to dense multipath fading environments. Nande, SS et al. [22] developed synchronizing three qubits to oscillate at the same frequency by applying an external field with a wavelength of 813.32 nm during 5G timing, significantly improving the stability of the timing system under various noise intensities. Patel, D et al. [23] believed that in the 5G timing system, the radio link between base stations and user equipment (UE) would be affected by propagation delays, and they considered round-trip time (RTT) to be the only suitable method for achieving the most stringent time error budget requirements. Omri, A et al. [24,25] provided a detailed introduction to the physical layer of 5G NR, studied the performance of the 5G NR time synchronization process with imperfect channel state information (CSI), described the time synchronization process required for 5G NR, and evaluated the corresponding coverage probability and ergodic capacity under different scenarios of imperfect frequency offset correction and imperfect CSI. They ultimately concluded that the main challenge of the 5G NR system is time frequency synchronization under various newly defined frequency conditions. Wang et al. [26] proposed achieving time synchronization in the 5G NR uplink by using block interleaved frequency division multiple reference signals (RS), effectively solving the aliasing effect caused by pseudo-paths in multipath channels when the channel transitions from the frequency domain to the time domain.

In summary, the above researches are all based on the 3GPP TS 38.331 standard protocol and study the part of the system information block (SIB9) in the existing 5G air interface system information that contains timing information. Most of them focus on reducing the impact of related noise on the 5G signal transmission path and do not involve the signal itself. The timing information in this 5G timing method is already specified in the 5G signal according to the 3GPP TS 38.331 standard protocol, and it requires occupying a certain amount of 5G communication signal bandwidth. The 5G NR time service signal proposed in this paper is hidden in the 5G signal and transmitted through 5G base stations. This not only solves the disadvantage of traditional satellite timing signals being easily blocked but can also be applied to indoor scenarios where satellite signals cannot be received, providing time synchronization services for downstream devices [27,28,29]. Moreover, the 5G NR time service signal in this paper adopts a spread spectrum signal system, transmitting a weak power signal that appears to be “submerged” in the power of the 5G communication signal, sharing the 5G communication frequency band without occupying the 5G communication signal bandwidth.

Capture technology, as a key part of spread spectrum signal reception technology, ensures that the receiver can correctly identify and decode the transmitted signal, which is crucial for maintaining the integrity and reliability of the communication link. The chaotic orthogonal combination spread spectrum sequence constructed in this paper has improved security over m-sequences [30], better autocorrelation than Walsh sequences [31], and the ability to effectively suppress the short-period characteristics that appear when the Tent-Map chaotic sequence [32,33] takes special values. Using a parallel code phase search algorithm based on FFT, compared to traditional correlation capture algorithms, our approach greatly reduces the number of searches and capture time, improving the signal reception efficiency. The final simulation results show that this combination spread spectrum sequence can be effectively applied to the parallel FFT capture algorithm, significantly optimizing the number of searches and capture duration while successfully capturing the 5G NR time service signal.

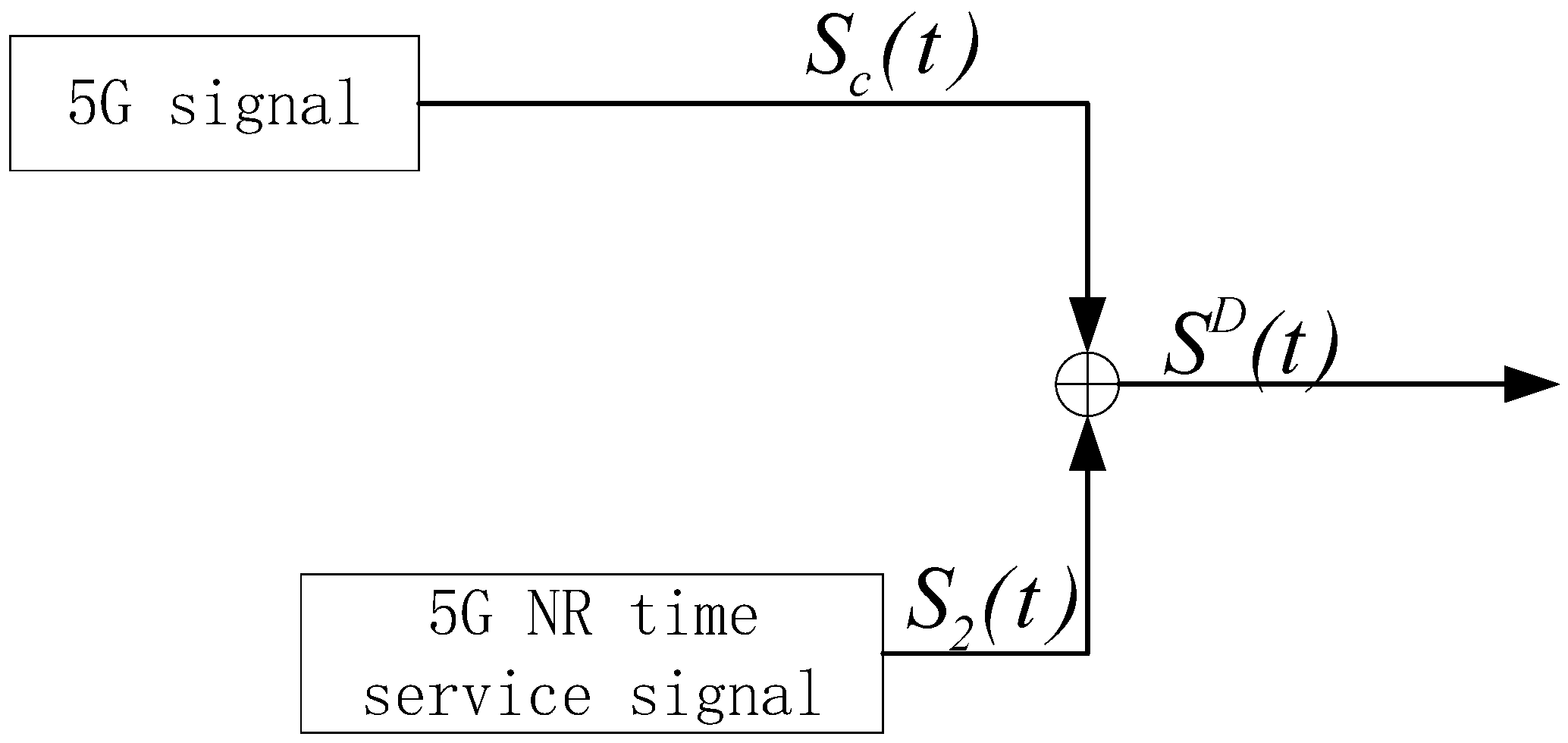
The 5G NR Time Service Signal plays a crucial role in modern communication systems and numerous other fields. It provides a precise time synchronization reference, which is particularly crucial for determining the location of positioning devices, especially in Time Difference of Arrival (TDOA) positioning technologies. In 5G networks, precise timing helps optimize the utilization of network resources, enhance data transmission efficiency, and reduce potential data conflicts. For critical infrastructure such as power grids and traffic control systems, precise timing is fundamental to ensuring stable system operation. In the realm of smart manufacturing and industrial automation, precise timing enables the synchronization of robots, sensors, and other automated devices, thereby improving production efficiency and reliability. Industries like finance and network security also benefit from precise timing, as it aids in preventing fraudulent activities, ensuring transaction orderliness, and integrity. In emergency situations such as natural disasters or security incidents, precise timing plays a crucial role in enabling rapid responses and effective resource coordination. The 5G NR Time Service Signal is one of the key technologies unlocking the full potential of 5G networks, significantly enhancing communication network performance and providing robust support for digital transformation across various sectors, thereby driving technological advancement and innovation throughout society.

2. 5G NR Time Service Signal Model

2.1. Generation of 5G NR Time Service Signal

The system principle diagram for the generation of the 5G NR time service signal is shown in Figure 1.

The 5G NR time service intermediate frequency time signal $S_1(t)$ can be expressed as:

$$S_1(t)=d(t)pn(t)$$

(1)

The signal $S_1(t)$ represents the 5G NR time service intermediate frequency signal generated by the spreading modulation of the data signal with a pseudo-random spread spectrum code. Here, $d(t)$ represents the data code, $pn(t)$ represents the pseudo-random spread spectrum code generated by the pseudo-code NCO. After generating this intermediate frequency signal, it needs to be modulated to the corresponding 5G frequency band so that the signal can be transmitted in a manner that appears submerged within the 5G frequency band.

The 5G NR time service signal $S_2(t)$ can be expressed as:

$$S_2(t)=S_1(t)c(t)$$

(2)

$$c(t)=\mathit{cos}(\omega t+\phi )$$

(3)

where $S_2(t)$ represents the 5G NR time service intermediate frequency signal modulated to the corresponding 5G frequency band, $S_1(t)$ represents the 5G NR time service signal, $c(t)$ represents the cosine carrier signal with frequency $\omega$ and initial phase $\phi$.

2.2. Generation of 5G Signal

The system principle diagram for the generation of the 5G baseband signal is shown below:

Figure 2 illustrates a simplified process for generating a 5G signal in practice. The serial data bit stream undergoes QPSK modulation (for simplicity, we assume that all subcarriers use QPSK modulation in this diagram, although in actual 5G signals, each subcarrier can use different modulation schemes). The modulated signal then undergoes serial-to-parallel conversion to allow for parallel processing (this can significantly reduce the time required to generate the 5G signal in practice, while it demands higher hardware capabilities). Each $X_k(t)$ signal is modulated by the corresponding $e^{jk{\omega }_{0}t}$ (where $k=1,2\cdots N$). The modulated signals are then summed, with their real parts modulated by a high-frequency cosine signal of frequency ${\omega }_c$ and their imaginary parts modulated by a high-frequency sine signal of frequency ${\omega }_c$. Finally, the modulated signals are summed to obtain the desired 5G signal $S_c(t)$.

This can be expressed by the following formula:

$$S_{c1}(t)=\mathit{Re}\left\{{\displaystyle \sum _{k=1}^{k=N}{X}_k{e}^{j{\omega }_{k}t}}\right\}\mathit{cos}({\omega }_{c}t)$$

(4)

$$S_{c2}(t)=\mathit{Im}\left\{{\displaystyle \sum _{k=1}^{k=N}{X}_k{e}^{j{\omega }_{k}t}}\right\}\mathit{sin}({\omega }_{c}t)$$

(5)

$$S_c(t)=S_{c1}(t)+S_{c2}(t)$$

(6)

where $N$ represents the number of subcarriers, $X_k$ represents the complex data signal of the k-th subcarrier, ${\omega }_k$ represents the subcarrier frequency, $\mathit{Re}\left\{ \right\}$ denotes the real part, $\mathit{Im}\left\{ \right\}$ denotes the imaginary part, ${\omega }_c$ represents the high-frequency carrier

2.3. Integration of 5G NR Time Service Signal with 5G Signal

In summary, the signal power of our 5G NR time service signal is much lower in practice than that of the 5G signal. It appears to be “submerged” within the 5G signal, does not occupy the 5G signal frequency band and does not interfere with the original 5G signal, as shown in the Figure 3 and Figure 4 below:

The system principle diagram for the integration of the 5G NR time service signal with the 5G signal is shown in the Figure 5 below:

The proposed 5G NR time service signal can be initially expressed by the following formula:

$$S^D(t)=S_2(t)+S_c(t)+{\vartheta }^D$$

(7)

$$S_2(t)=A^D{D}^{D}P{N}^D(t-\tau )\mathit{cos}\left[{\omega }^{D}t+{\phi }_0^D\right]$$

(8)

$${\omega }^D=2\pi \left(f_{RF}+f_d^D\right)$$

(9)

Combining the above equations, the final 5G NR time service signal that can be received by the terminal is expressed as:

$$\begin{array}{ll}{S}^D(t)& =A^D{D}^{D}P{N}^D\left(t-\tau \right)\mathit{cos}\left[{\omega }^{D}t+{\phi }_0^D\right]+\mathit{Re}\left\{{\displaystyle \sum _{k=1}^{k=N}{X}_k{e}^{j{\omega }_{k}t}}\right\}\mathit{cos}({\omega }_{c}t)\\ & +\mathit{Im}\left\{{\displaystyle \sum _{k=1}^{k=N}{X}_k{e}^{j{\omega }_{k}t}}\right\}\mathit{sin}({\omega }_{c}t)+{\vartheta }^D\end{array}$$

(10)

In the equation, $A^D$ represents the amplitude of the 5G spread spectrum downlink signal received by the terminal, $D^D$ represents the modulation data of the 5G spread spectrum downlink signal received by the terminal, $P{N}^D$ represents the spread spectrum code of the 5G spread spectrum downlink signal received by the terminal, $f_{RF}$ represents the center frequency of the 5G RF signal, $f_d^D$ represents the Doppler frequency between the terminal and the base station, ${\phi }_0^d$ represents the initial phase of the terminal carrier, ${\vartheta }^D$ represents the noise introduced after the 5G spread spectrum downlink signal is received by the terminal and passes through the channel. The resulting 5G NR time service signal can be transmitted by the base station to the terminal receiving equipment. Once the terminal equipment receives the signal, it can complete terminal time calibration.

3. 5G NR Time Service Signal Acquisition Algorithm

3.1. Chaotic Orthogonal Combination Sequence

This paper proposes a chaotic orthogonal combination sequence, which is a combination of Walsh sequences and Skew Tent-Map chaotic sequences, and thus can improve the deficiencies of traditional spread spectrum codes.

Walsh sequences are a class of orthogonal sequences widely used in communication fields such as error correction coding and secure coding. They can be derived from Hadamard matrices. A Hadamard matrix $H$ is an orthogonal square matrix composed of the elements “$+1$” and “$-1$”, where any two rows or columns are orthogonal to each other. This property can be mathematically expressed as:

$$H{H}^T=NI$$

(11)

where $H^T$ represents the transpose of $H$, $N$ is the order of $H$, and $I$ is the identity matrix. When we discuss Hadamard matrices of order $N=2^n$ (where $n$ is a positive integer), the Hadamard matrix $H_n$ can be generated by the following recursive relation:

$$H_n=\left[\begin{array}{cc}{H}_{n-1}& H_{n-1}\\ H_{n-1}& -H_{n-1}\end{array}\right],H_0=1$$

(12)

By considering each row of the Hadamard matrix as a binary sequence, an $N=2^n$ order matrix $H_n$ yields a total of $N$ sequences, each of length $N$. Any two sequences in this orthogonal set are mutually orthogonal, forming the Walsh sequences.

Chaos is a deterministic, random-like process that occurs in nonlinear dynamic systems. This process is neither periodic nor convergent and exhibits a high sensitivity to initial conditions, presenting pseudo-random characteristics. Due to its sensitive dependence on initial conditions, it can provide a large number of uncorrelated, pseudo-random yet deterministic signals that are easy to generate and regenerate, making it suitable for use as pseudo-random codes.

The Tent-Map is a classic chaotic mapping model. The Skew Tent-map used in this paper is a special form of the Tent map. It is a one-parameter, piecewise-linear, weakly-unimodal, map of the interval [0, 1]. Its iterative equation is simple, and the sequence generator is easy to implement. It can be applied to any scenario requiring the transmission of encrypted data through a common channel, offering good security and is suitable for use as a spreading code in spread spectrum systems [34,35].

Its mapping equation is:

$$x_{k+1}=\left\{\begin{array}{cc}\frac{x_k}{a},& 0<x_k<a\\ \frac{1-x_k}{1-a},& a\le x_k\le 1\end{array}\right.$$

(13)

The range of the parameter $a$ in the equation is $0<a<1$. The below figure (Figure 6) shows the chaotic mapping effect of the Skew Tent-Map.

By multiplying corresponding bits of the same set of Walsh sequences and chaotic sequences generated by Skew Tent-Map with the same order, we can obtain the chaotic orthogonal combination sequence.

If we denote the chaotic mapping sequence as $x_1(t)$, the Walsh sequence as $x_2(t)$, and the chaotic orthogonal combination sequence as $x(t)$, then the expression for the chaotic orthogonal combination sequence will be:

$$x(t)=x_1(t)x_2(t)$$

(14)

We verify the cross-correlation of the chaotic orthogonal combination sequence $x(t)$ by selecting sequences of the same order from different groups (denoted as group $i$ and group $j$) and integrate over one period.

$${\displaystyle \underset{T}{\int }{x}_i(t)x_j(t)dt=}{\displaystyle \underset{T}{\int }{x}_1^2(t)x_{2i}(t)x_{2j}(t)dt=}{\displaystyle \underset{T}{\int }{x}_{2i}(t)x_{2j}(t)dt=}0$$

(15)

As per the above equation, it is evident that the chaotic orthogonal combination sequence still retains the property of mutual orthogonality between any two sequences within the same family of Walsh sequences.

3.2. Performance Optimization Analysis of Chaotic Orthogonal Combination Sequence

When comparing the chaotic orthogonal combination sequence with m-sequences, Walsh sequences, Skew Tent-Map chaotic sequences, etc., it is found that the chaotic orthogonal combination sequence has significant advantages in terms of security, correlation and applicability.

In terms of security, m-sequences are less secure than Walsh sequences under the same number of chips. This is because Walsh sequences are generated from Hadamard matrices. For a register with N bits, m-sequences have $2^N-1$ chips because the Nth bit of the register must be 1, resulting in $2^N-1$ possible constructions. On the other hand, for Walsh sequences, when the number of chips is the same, the order of the Hadamard matrix is $2^N$, and any row or column can generate a Walsh sequence, resulting in $2^N$ possible constructions. Therefore, the security of Walsh sequences surpasses that of m-sequences. The security of the chaotic orthogonal combination sequence, being a combination of Walsh sequences and Skew Tent-Map chaotic sequences, also surpasses that of m-sequences.

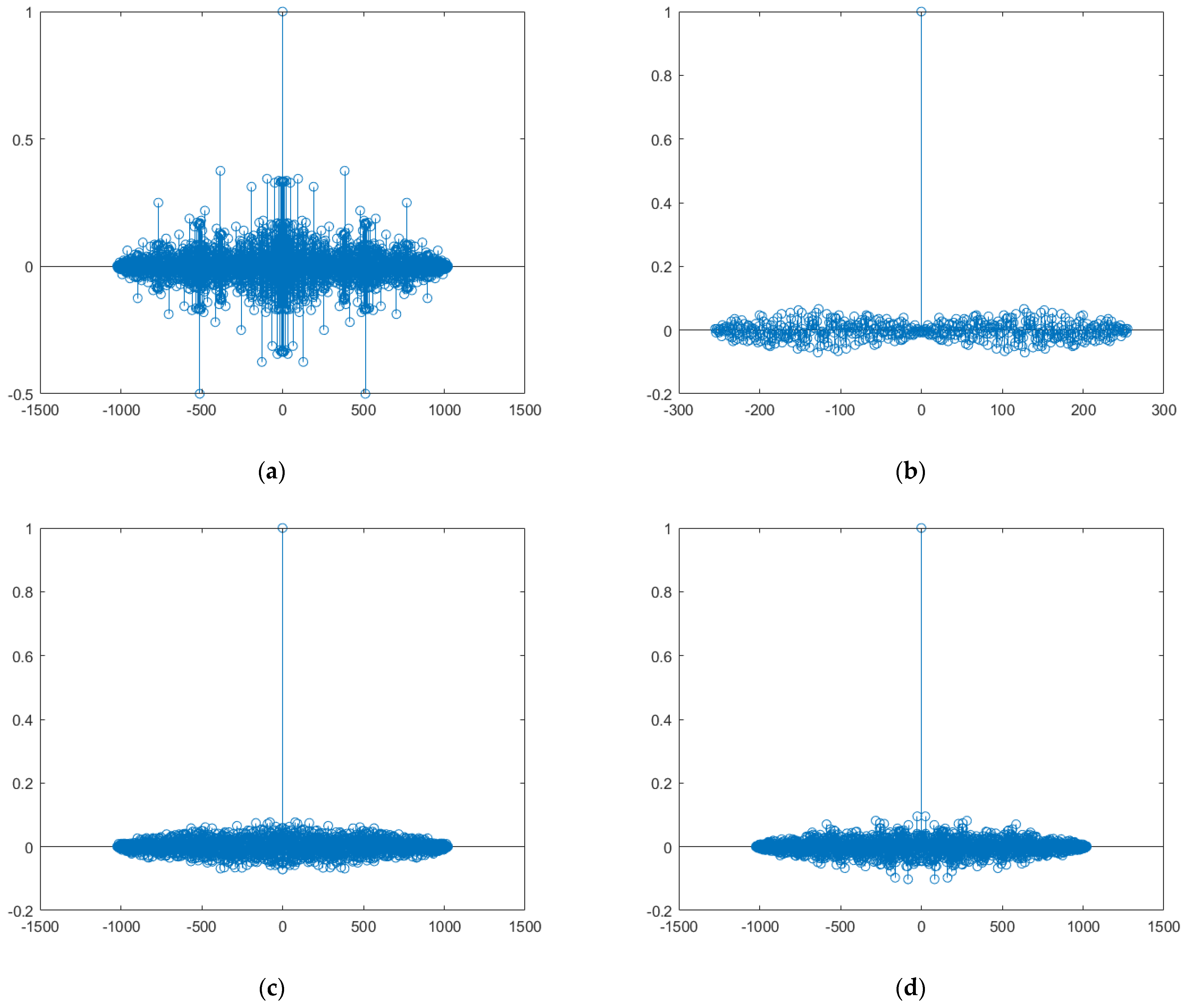
In terms of correlation, the auto-correlation of Walsh sequences is not as prominent as that of m-sequences and Skew Tent-Map chaotic sequences. As shown in Figure 7a–c, respectively, the main peak-to-side peak ratio of Walsh sequences is 2.05, while that for m-sequences it is 13.1, and that for Skew Tent-Map chaotic sequences it is 12.5. As shown in Figure 7d, the main peak-to-side peak ratio of the chaotic orthogonal combination sequence is 11.5, significantly higher than that of Walsh sequences but slightly lower than the main peak-to-side peak ratios of Skew Tent-Map chaotic sequences and m-sequences. This clearly improves the auto-correlation of Walsh sequences.

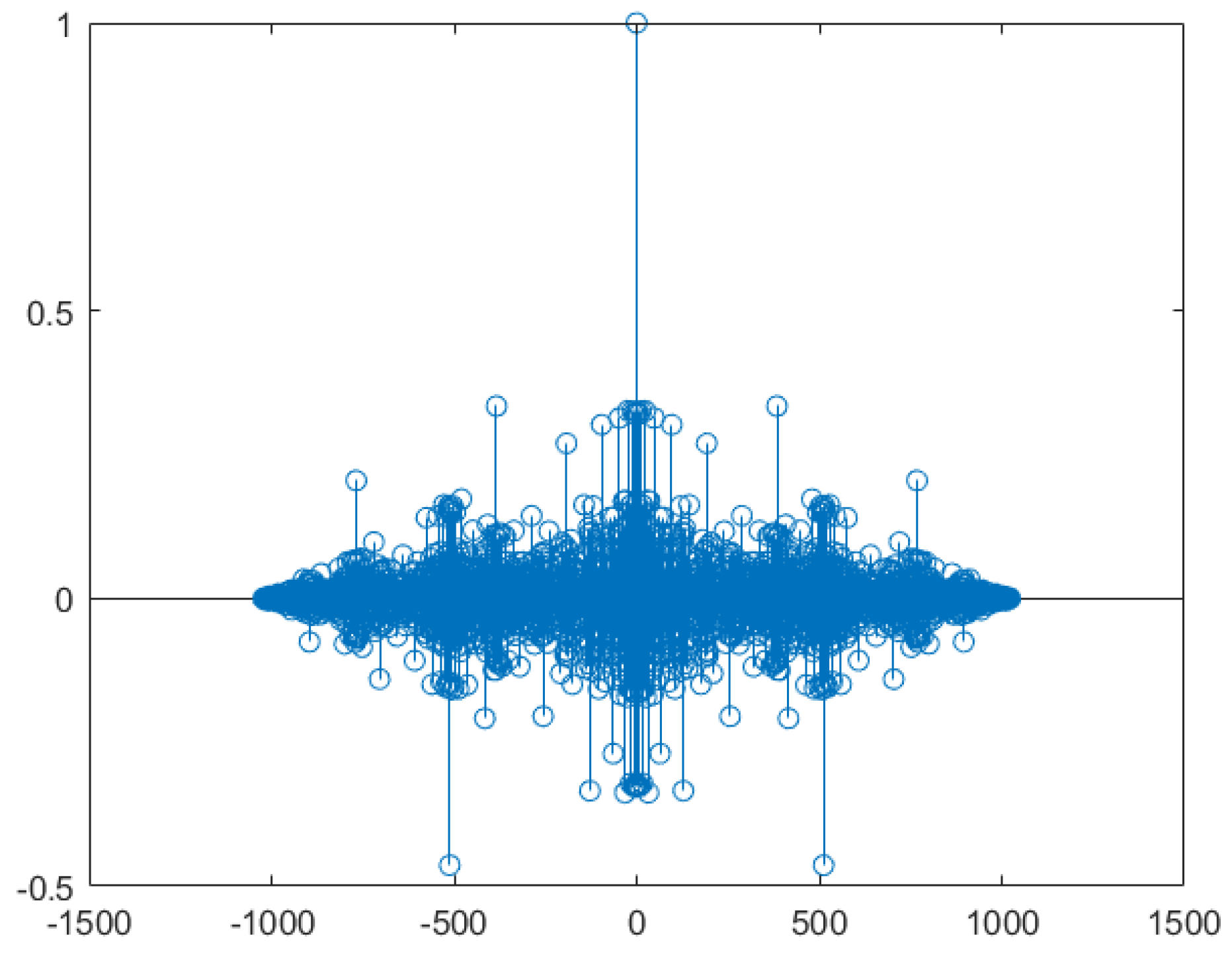
In terms of applicability, Skew Tent-Map chaotic sequences have a fatal flaw: the parameter $a$ cannot be set to 0.5. Otherwise, these sequence exhibit short-period characteristics, leading to poor auto-correlation, as shown in Figure 8.

However, when combining Skew Tent-Map chaotic sequences with Walsh sequences to form the chaotic orthogonal combination sequence, even when $a$ is set to 0.5, although the short-period characteristics of Skew Tent-Map chaotic sequence are retained, the auto-correlation of the chaotic orthogonal combination sequence is still good. As shown in Figure 9, its main peak-to-side peak ratio is 2.17, still slightly better than that of Walsh sequences.

3.3. Signal Acquisition Algorithm

The linear acquisition algorithm is a basic signal search and capture method that utilizes digital correlators to scan the signal in the time domain for both the Doppler frequency shift and the code phase [36]. The advantage of linear search is that it requires only a few digital correlators, simplifying the capture process and reducing hardware complexity. However, it sequentially searches all chips in the frequency band centered around the frequency band center, and if the desired signal is not found, the frequency value of the band center is changed, and the search is repeated for all chips. Because searches a single search unit at a time rather than a group of search units, this results in slower search speeds.

This paper adopts a parallel code phase search algorithm [37,38] that utilizes fast Fourier transform to achieve parallel search for frequency and code phase. It effectively replaces the correlation operation of digital correlators with the digital signal processing technique of Fourier transform, reducing the computational requirements for signal acquisition and speeding up the signal search process. The specific flowchart of the parallel code phase search algorithm is shown in the Figure 10 below.

According to the flowchart in Figure 10, the specific process of the parallel code phase search algorithm based on FFT is as follows:

• Multiply the input 5G NR time service intermediate frequency signal by the in-phase and quadrature signals from the local carrier generator, and filter the baseband complex signal $S(t)$ using a low-pass filter.
• Perform FFT on the baseband complex signal $S(t)$.
• Perform FFT on the pseudo-code signal generated by the local pseudo-code generator and take its conjugate.
• Multiply the results from steps 2 and 3, then perform IFFT on the product.
• Take the modulus of the result from step 4 and apply threshold decision. If strong peaks appear, signal acquisition is achieved. The peak corresponds to the pseudo-code phase, and the frequency value of the local carrier at that time is the carrier frequency of the signal. If no strong peaks appear, reset the frequency of the local carrier generator to the value of the next frequency well and repeat steps 1 to 4.

The specific algorithm for the parallel code phase search and capture based on FFT is as follows:

For a finite sequence $X(n)$ of length N, the Fourier transform can be represented as:

$$X(k)={\displaystyle \sum _{n=0}^{N-1}x(n)e^{-j2\pi kn/N}}$$

(16)

The cross-correlation of two finite sequences of length N can be represented as:

$$z(n)={\displaystyle \sum _{m=0}^{N-1}x(m)y(n+m)}$$

(17)

The convolution of two finite sequences $x(n)$ and $y(n)$ of length N can be represented as:

$$z(n)=x(n)\ast y(n)={\displaystyle \sum _{m=0}^{N-1}x(m)y(n-m)}$$

(18)

The symbol $\ast$ represents the convolution operation. From the above equations, it can be seen that the cross-correlation and convolution differ only in the sign of $y(n+m)$ and $y(n-m)$. The Fourier transform of the convolution of sequences $x$ and $y$ can be represented as:

$$\begin{array}{ll}Z(k)& =\mathcal{F}\left[x(n)\ast y(n)\right]\\ & =\mathcal{F}\left[{\displaystyle \sum _{m=0}^{N-1}x(m)}\ast y(n-m)\right]\\ & ={\displaystyle \sum _{n=0}^{N-1}{\displaystyle \sum _{m=0}^{N-1}x(m)y(n-m)e^{-j2\pi kn/N}}}\\ & ={\displaystyle \sum _{m=0}^{N-1}x(m)e^{-j2\pi km/N}}{\displaystyle \sum _{n=0}^{N-1}y(n-m)e^{-j2\pi k(n-m)/N}}\\ & =\mathcal{F}\left[x(n)\right]\mathcal{F}\left[y(n)\right]\\ & =X(k)Y(k)\end{array}$$

(19)

Here, $\mathcal{F}$ represents the Fourier transform.

From the above equation, it can be observed that the Fourier transform of the time-domain convolution of sequences $x$ and $y$ is equivalent to the product of the individual Fourier transforms of sequences $x$ and $y$ (in the frequency domain).

The Fourier transform of the “correlation” operation between sequences $x$ and $y$ is:

$$\begin{array}{ll}Z(k)& =\mathcal{F}\left[{\displaystyle \sum _{m=0}^{N-1}x(m)}\ast y(n+m)\right]\\ & ={\displaystyle \sum _{n=0}^{N-1}{\displaystyle \sum _{m=0}^{N-1}x(m)y(n+m)e^{-j2\pi kn/N}}}\\ & ={\displaystyle \sum _{m=0}^{N-1}x(m)e^{-j2\pi km/N}}{\displaystyle \sum _{n=0}^{N-1}y(n+m)e^{-j2\pi k(n+m)/N}}\\ & =X^{\ast }(k)Y(k)\end{array}$$

(20)

In the equation above, $X^{\ast }(k)$ refers to the complex conjugate of $X(k)$. Therefore, by taking the complex conjugate of the Fourier transform of sequence x and multiplying it with the Fourier transform of sequence y in the frequency domain, and then performing the inverse Fourier transform, the result of the “correlation” operation between the two sequences can be obtained. This helps to identify the peak value of the “correlation” result, completing the signal acquisition process.

Compared to traditional linear search and capture algorithms, the parallel code phase search algorithm based on FFT reduces the number of searches, thereby shortening the capture time.

The number of searches required for the linear search and capture algorithm is:

$$N_{cell}=\frac{\left(2f_{unc}\right)\left(2t_{unc}\right)}{f_{step}{t}_{step}}=\frac{f_{\Delta }}{f_{step}}2M$$

(21)

where $N_{cell}$ represents the number of search units within the linear search range, $f_{unc}$ and $t_{unc}$ are the uncertainties in signal frequency and code phase, where $2f_{unc}$ is equivalent to the frequency search range $f_{\Delta }$, and $2t_{unc}$ is equivalent to the code length M. $f_{step}$ and $t_{step}$ are the search steps for frequency and code phase, where $f_{step}$ is set to 1 kHz for frequency search in this paper, and $t_{step}$ is typically half a chip.

The capture time required for the linear search and capture algorithm is:

$$T_{tot}=N_{cell}{T}_{dwell}$$

(22)

where $T_{tot}$ denotes the time required for the linear search and capture algorithm to search the entire uncertain interval once, and $T_{dwell}$ is the dwell time, i.e., the time taken to search for a signal in each unit.

If the receiver determines that a signal has been detected during the sequential search process, it can stop the search. Assuming that the signal exists and its parameter values are randomly distributed within the two-dimensional search range, the average number of search units the receiver has searched before declaring signal acquisition is half of the total number of search units. Therefore, the estimated formula for the average acquisition time $T_{acq}$ is [39]:

$$T_{acq}=\frac{1}{2}{T}_{tot}$$

(23)

The parallel code phase search algorithm based on FFT completes $2M$ linear code phase searches in a single Fourier transform operation.

The number of searches required for the parallel code phase search algorithm based on FFT is:

$$N_{cellF}=\frac{f_{\Delta }}{f_{step}}$$

(24)

where $N_{cellF}$ represents the number of searches required for the parallel code phase search algorithm based on FFT.

The capture time required for the parallel code phase search algorithm based on FFT is:

$$T_{totF}=N_{cellF}{T}_{dwell}$$

(25)

where $T_{totF}$ represents the time required for the parallel code phase search algorithm based on FFT to search the entire uncertain interval once.

The estimated formula for the average acquisition time $T_{acq}$ for the parallel code phase search algorithm based on FFT is:

$$T_{acqF}=\frac{1}{2}{T}_{totF}$$

(26)

where $T_{acqF}$ represents the average acquisition time for the parallel code phase search algorithm based on FFT.

From the above formulas, it can be concluded that compared to the traditional linear search and capture algorithm, under the same conditions, the parallel code phase search algorithm based on FFT reduces both the capture time and the number of searches by a factor of $2M$.

4. Experimental Results and Analysis

The experiment utilizes a novel direct sequence spreading method that combines Walsh sequences and Skew Tent-Map chaotic sequences to form the chaotic orthogonal combination sequence. A 1023-bit chaotic orthogonal combination sequence was applied, with a carrier frequency of 3500 MHz, a 5 MHz intermediate frequency signal for 5G NR time service signal, a pseudo-code rate of 1.023 MHz, and a sampling frequency of 20 MHz. The simulation was conducted in an environment with a signal-to-noise ratio of 10 dB to capture the 5G NR time service signal.

In the actual simulation, the frequency search range was set to ±10 kHz centered around 5 MHz, with a frequency search step of 1 kHz. The simulation results are shown in Figure 11 and Figure 12.

Based on Figure 12, even with the addition of Gaussian white noise interference, the peak remains prominent with a main-to-side peak ratio of 13.6. The captured code phase is 8799, and the captured frequency is 5 MHz, matching the preset frequency of the 5G NR time service intermediate frequency signal, which indicates successful acquisition. Furthermore, the use of the parallel code phase search algorithm based on FFT significantly reduces the capture time, requiring only 21 searches to complete the acquisition. In contrast, using the traditional linear search method would require 21,463 searches. With a spreading code period of approximately 1 ms, the search time is reduced from 21.463 s to 0.021 s, demonstrating a significant improvement in search time compared to traditional linear search methods.

Figure 13 illustrates the acquisition probability under different SNR conditions during the acquisition process. It can be seen that the 5G NR time service signal can be successfully captured with a suitable SNR when the acquisition threshold is 3.5. When the SNR is above −15 dB, the acquisition probability reaches 100%. However, as the SNR falls below −15 dB, the acquisition probability decreases significantly with the reduction in dB value. When the SNR reaches −30 dB, the acquisition probability is nearly 0. It is obvious from Figure 13 that the lower SNR, the lower acquisition probability.

5. Conclusions

With the further improvement of the integrated PNT system and the accelerated deployment of 5G macro and small cell base stations, the limitation of user signal reception will be greatly reduced due to the wide signal coverage capabilities. Therefore, the further exploration of timing modes based on 5G is crucial. This paper proposes a 5G NR time service signal that utilizes spread spectrum modulation, transmitting a low-power signal shared in the 5G communication frequency band. Its signal power is much lower than that of the 5G signal, appearing to be “submerged” under the 5G signal and without occupying the bandwidth of the 5G communication signal. Compared to traditional spreading sequences, the proposed chaotic orthogonal combination sequence offers improved security over m-sequences, better auto-correlation than Walsh sequences, and an effective suppression of the short-period characteristics that may arise when Skew Tent-Map chaotic sequences take specific values.

In the simulation, the capture of the 5G NR time service signal was conducted in a 10 dB signal-to-noise ratio environment using the chaotic orthogonal combination sequence as the spreading code and the parallel code phase search algorithm based on FFT. This approach significantly reduced the capture time compared to traditional linear search methods, successfully acquiring the 5G NR time service signal. As a limitation of this study, it focused on the simulation of capturing the 5G NR time service signal and did not cover tracking and other aspects. Future research will continue to explore other parts of the 5G NR time service signal receiver to enhance its reception performance and further improve the timing performance of the 5G NR time service signal.