Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System
Abstract
:1. Introduction
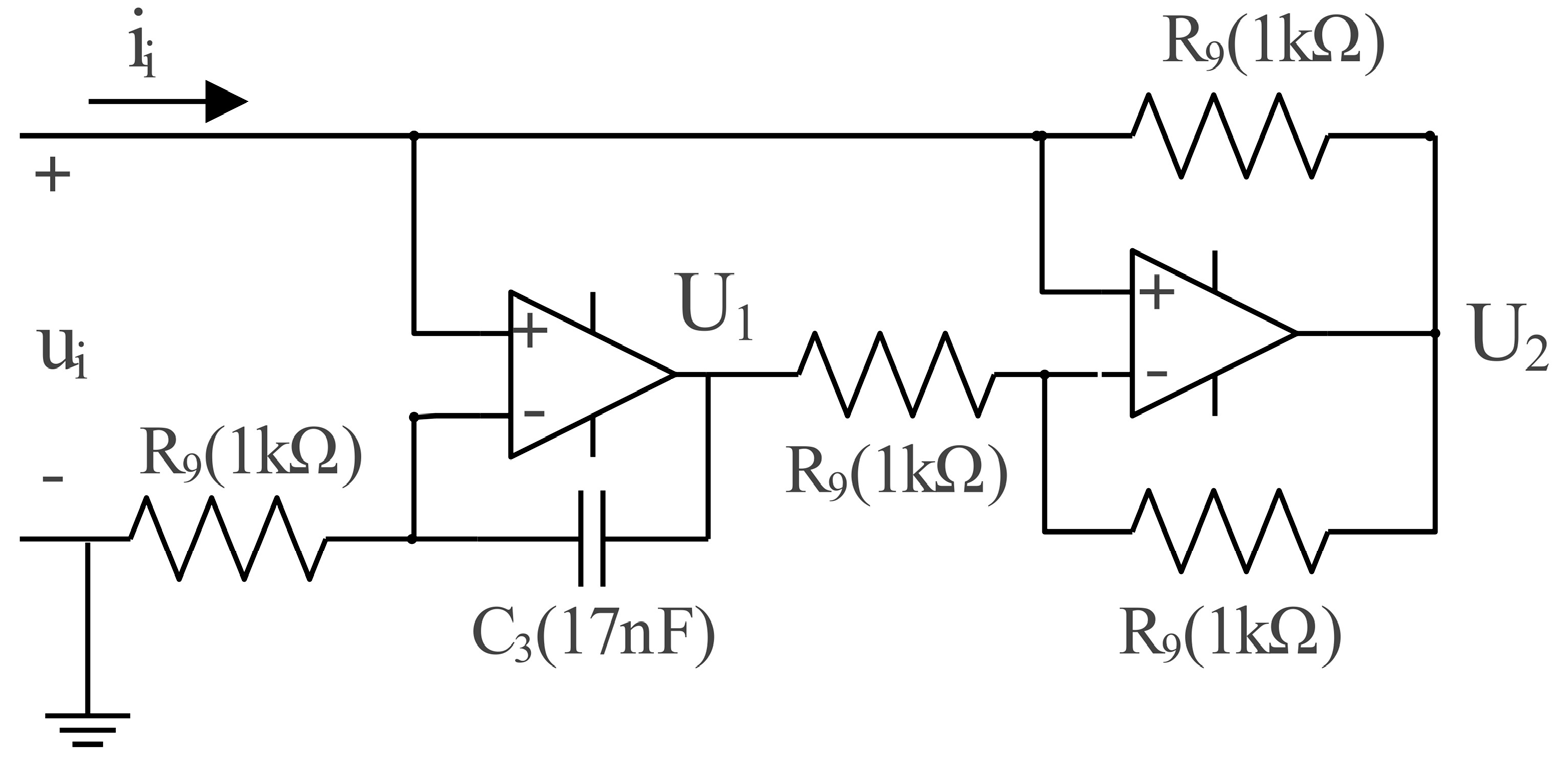
- We adopt the strategy of using active inductors instead of traditional passive inductors. Since the volume of the op amp and resistors are much smaller than that of the inductor coils, this design enables the miniaturization and integration of circuits. Meanwhile, the accuracy of the inductor is greatly improved because the inductance value can be controlled precisely by adjusting the resistance value.
- We present the theory of substituting non-autonomous systems for classical autonomous systems. According to the state equation of the circuit and the chaotic conditions of a system, the excitation current source we added can reduce the requirements for the accuracy of components and improve the robustness of the circuit.
- We connect the extension resistor in parallel with Chua’s diode to optimize the circuit structure, increasing the range of the adjustable parameter.
- The resistor connected in parallel with Chua’s diode is termed the extension resistor due to its functional role.
- The maximum error tolerance of component is defined as . is the standard value of component and is the maximum allowable deviation of component .
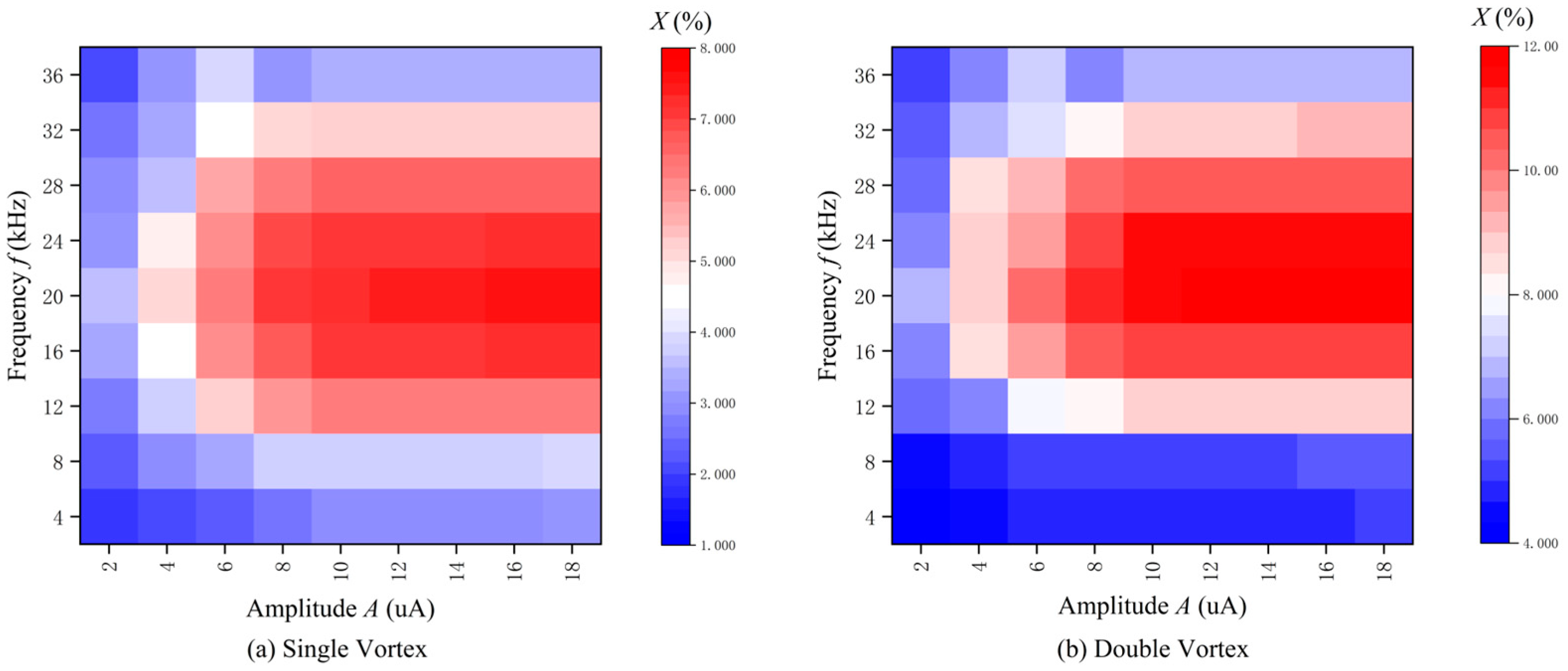
- The average maximum error tolerance X of components is defined as .
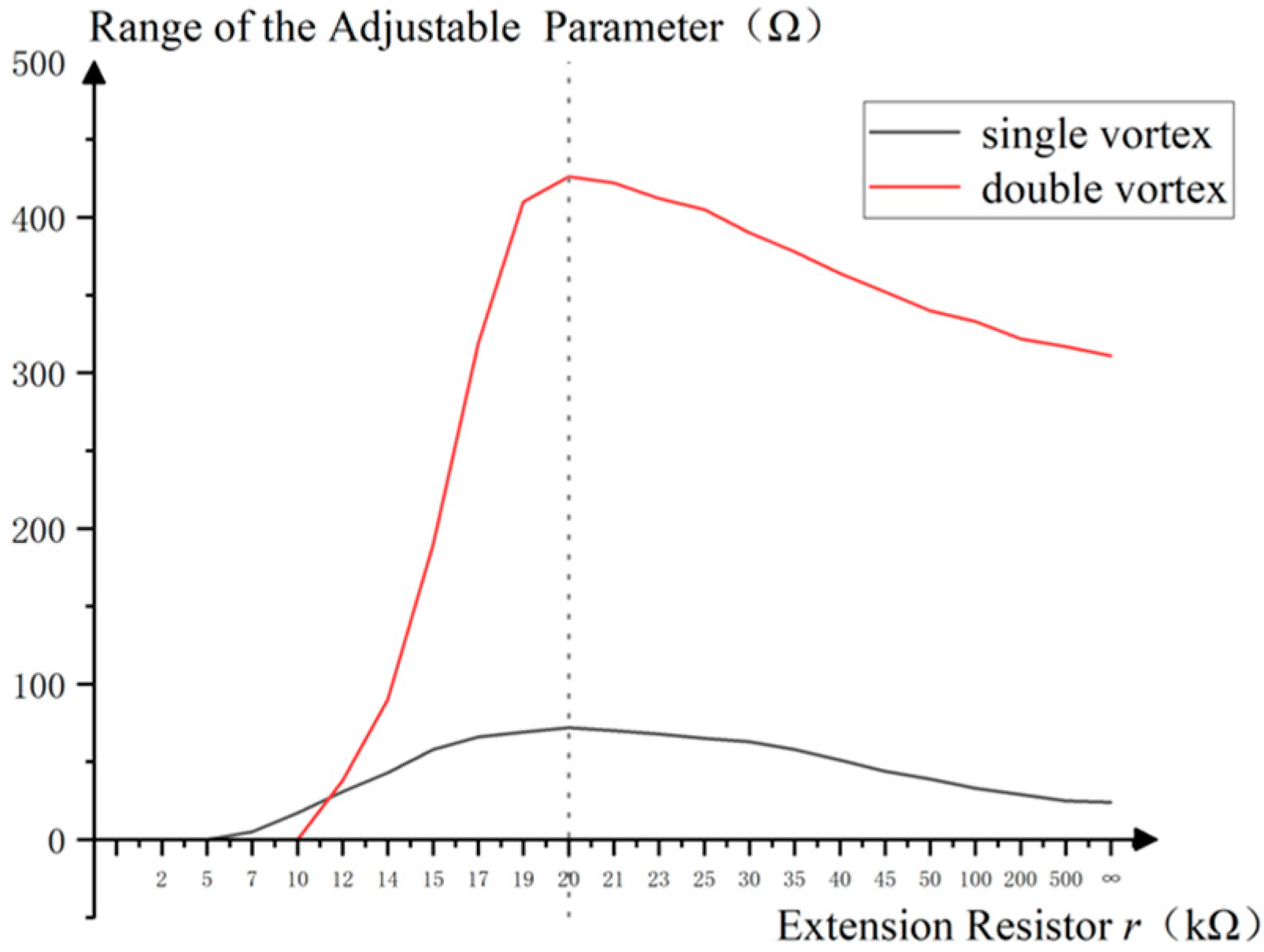
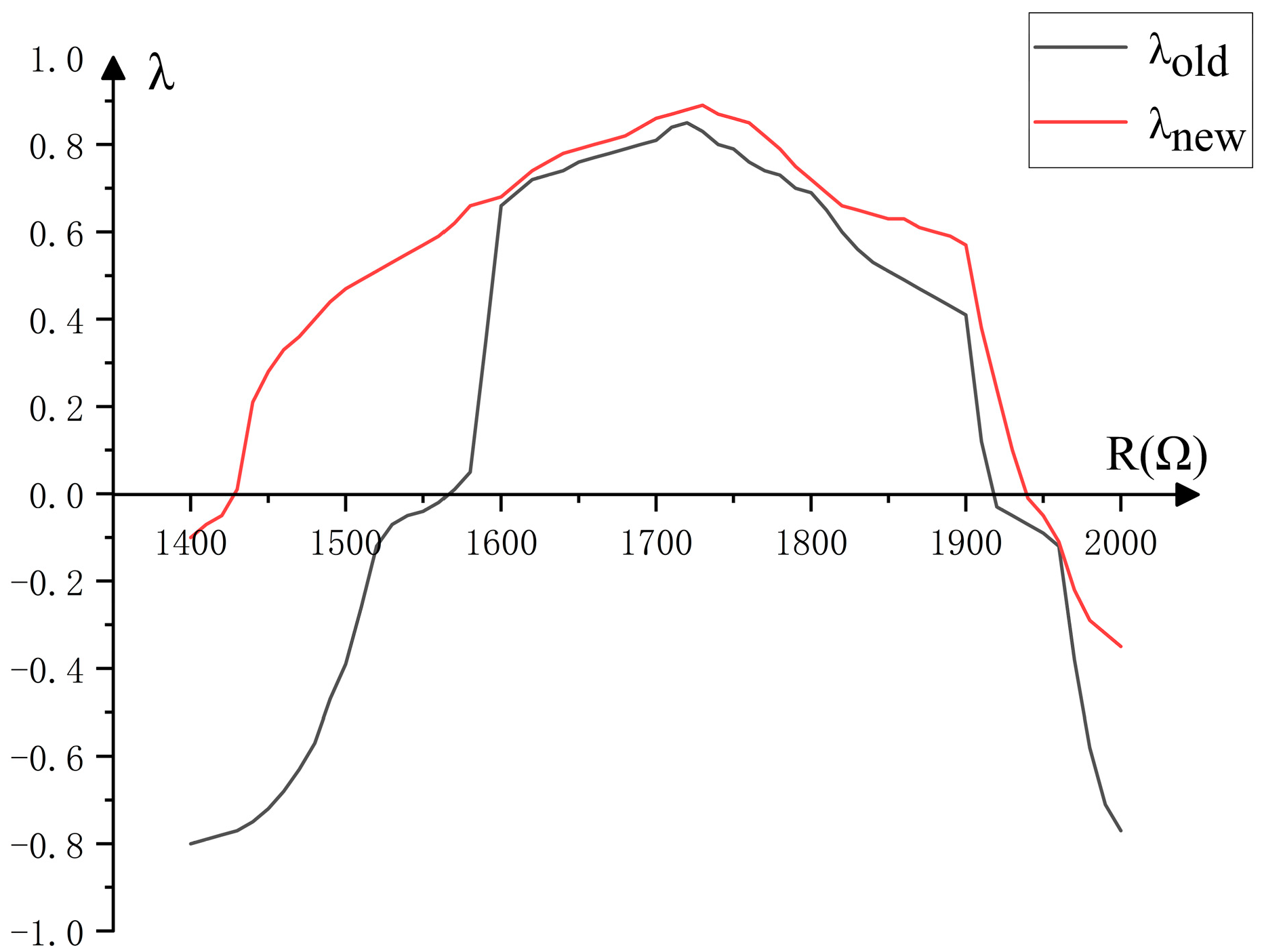
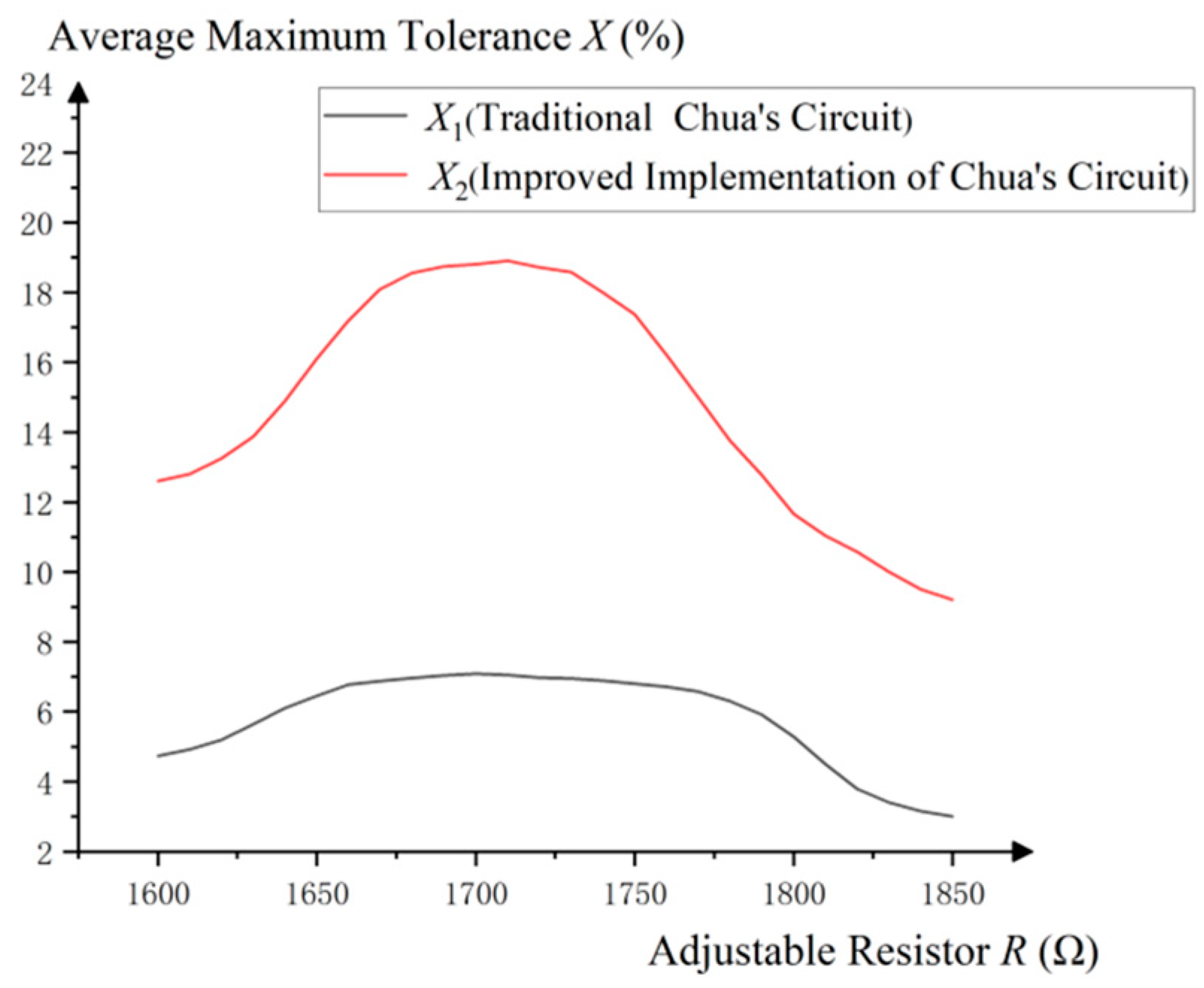
- In the context of the “range of the adjustable parameter”, the parameter refers specifically to the adjustable resistor R connecting capacitors and , and the range refers specifically to the resistance that can create chaos in a circuit.
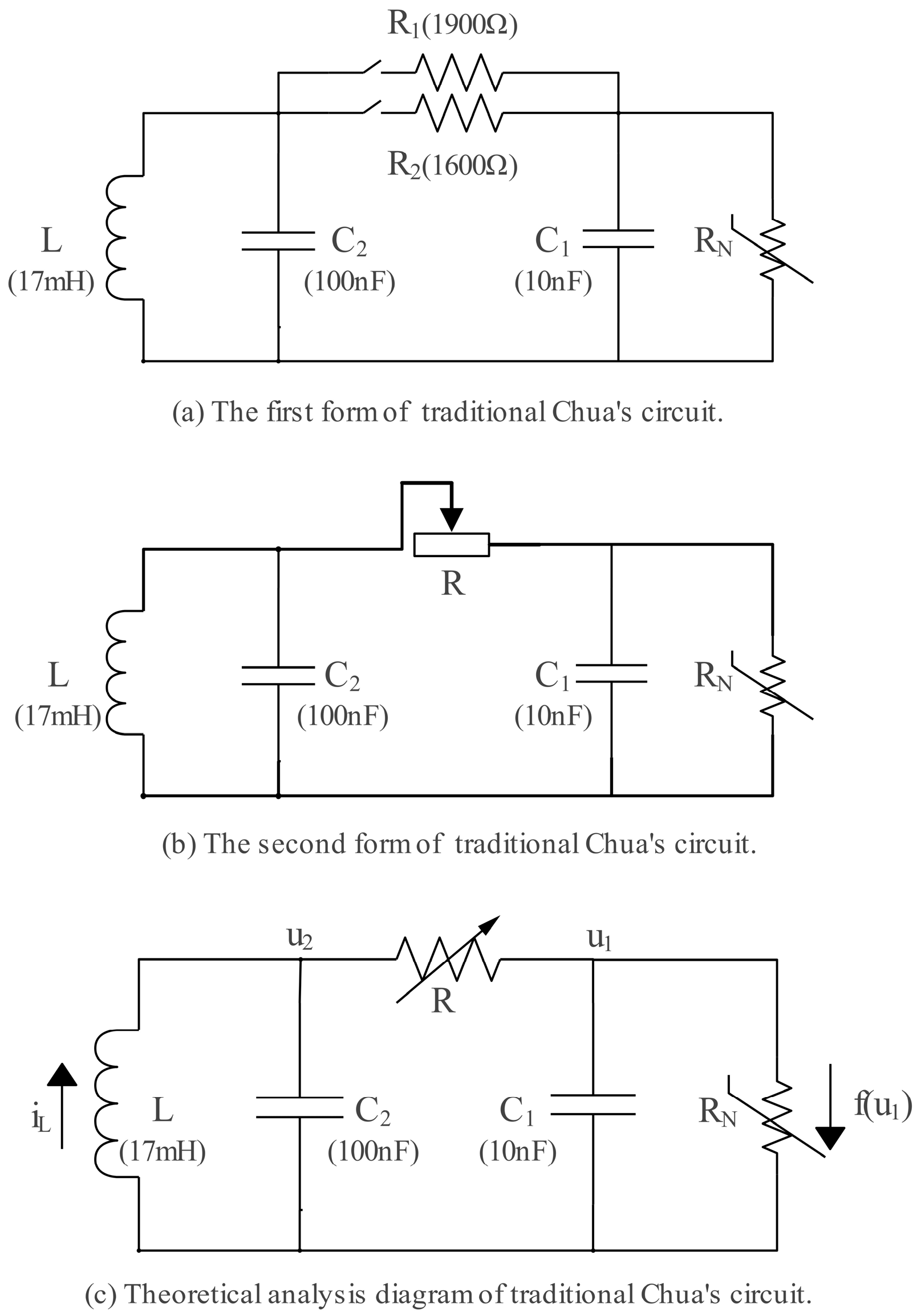
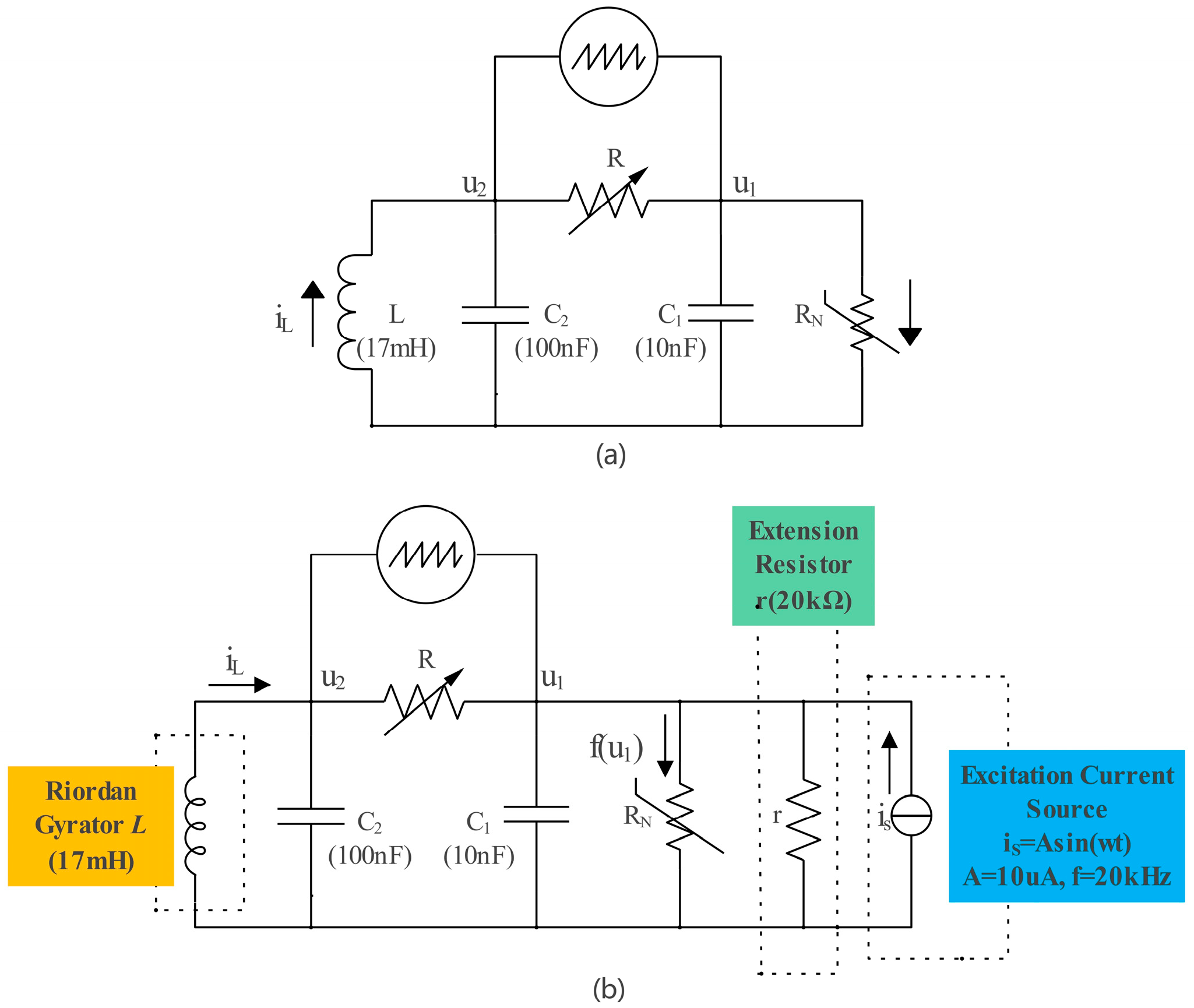
2. Traditional Chua’s Circuit
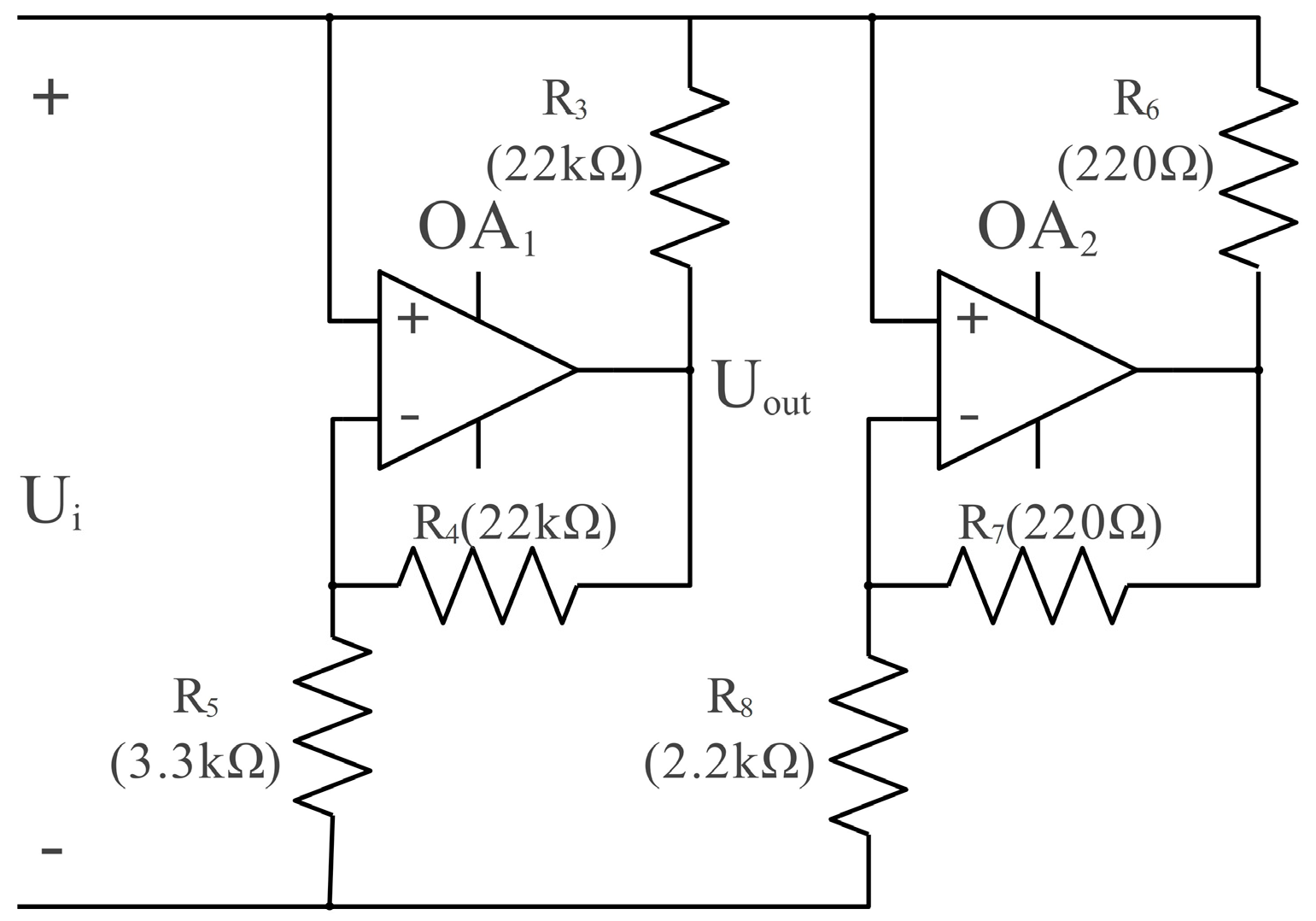
3. Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System
3.1. Extension Resistor r
3.2. Excitation Current Source
4. Theoretical Comparison
4.1. Change from Passive Inductor to Active Inductor
4.2. Improvement from an Autonomous System to a Non-Autonomous System and the Addition of an Extension Resistor
4.2.1. Robustness
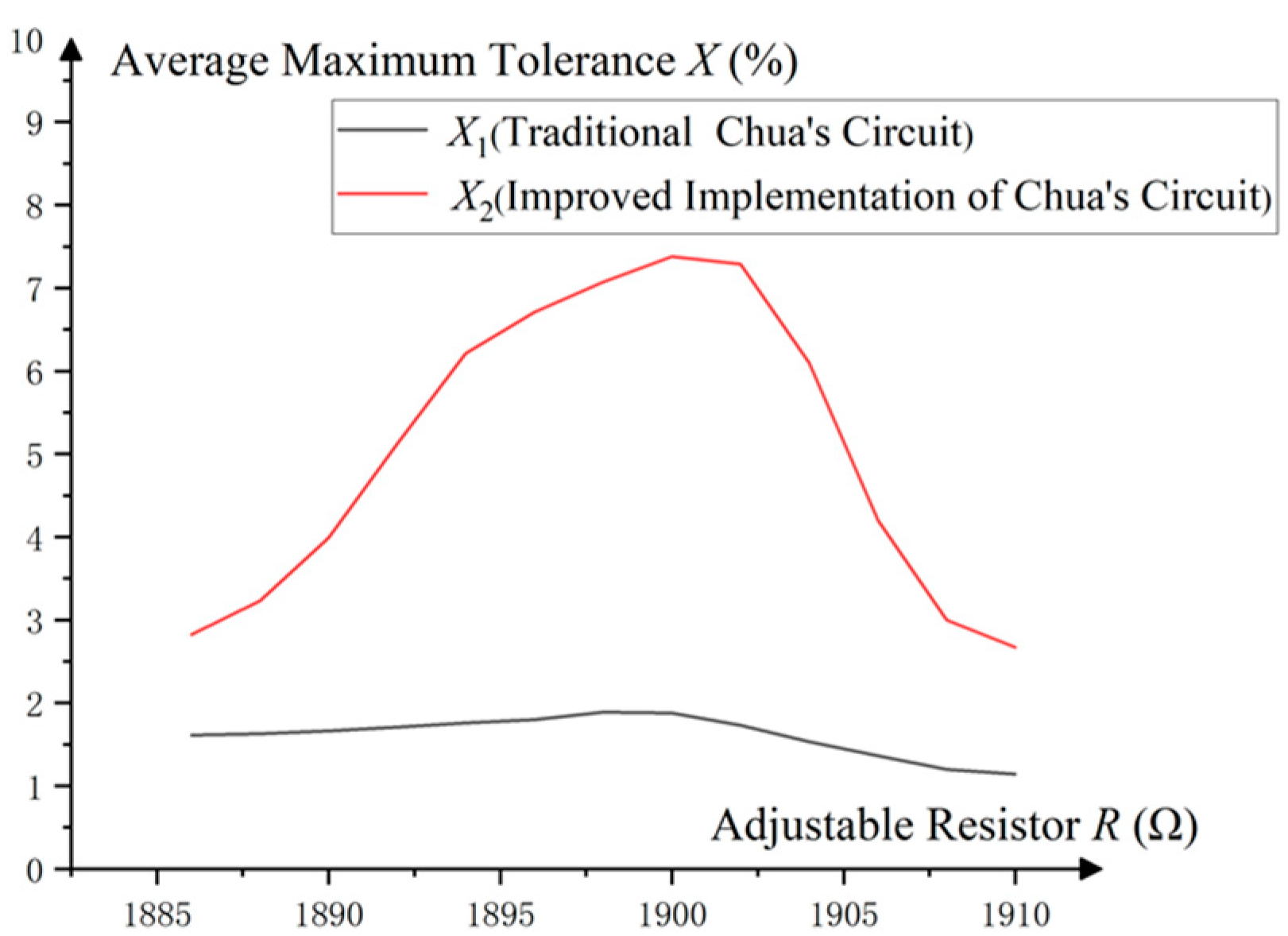
4.2.2. Range of Adjustable Parameters
5. Experimental Comparison
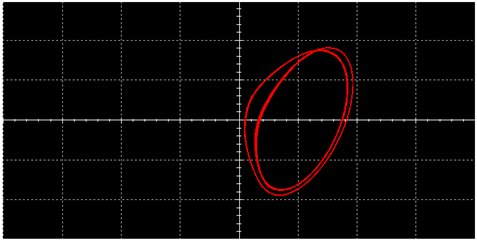
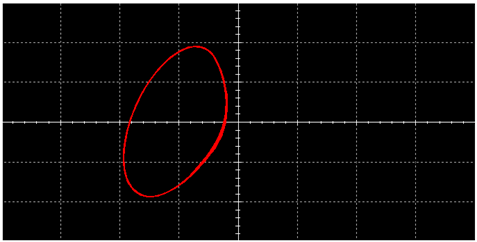
5.1. Robustness When Generating a Single Vortex
5.1.1. Test Case 1 ()
5.1.2. Test Case 2 ()
5.1.3. Test Case 3 ()
5.1.4. Brief Summary
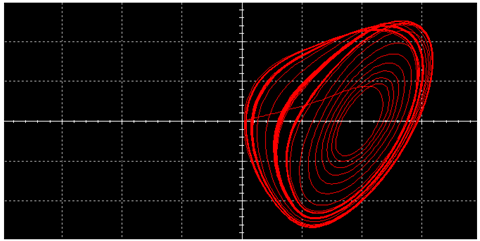
5.2. Robustness When Generating a Double Vortex
5.2.1. Test Case 1 ()
5.2.2. Test Case 2 ()
5.2.3. Test Case 3 ()
5.2.4. Brief Summary
5.3. Range of Adjustable Parameters
5.4. Summary of the Experimental Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, L.O. Chua’s circuit 10 years later. Int. J. Circuit Theory Appl. 1994, 22, 279–305. [Google Scholar] [CrossRef]
- Altman, E. Normal form analysis of Chua’s circuit with applications for trajectory recognition. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1993, 40, 675–682. [Google Scholar] [CrossRef]
- Luo, Y.; Lin, J.; Liu, J.; Wei, D.; Cao, L.; Zhou, R.; Cao, Y.; Ding, X. A robust image encryption algorithm based on Chua’s circuit and compressive sensing. Signal Process. 2019, 161, 227–247. [Google Scholar] [CrossRef]
- Arpacı, B.; Kurt, E.; Çelik, K. A new algorithm for the colored image encryption via the modified Chua’s circuit. Eng. Sci. Technol. Int. J. 2019, 23, 595–604. [Google Scholar] [CrossRef]
- Tôrres, L.A.B.; Aguirre, L.A. Inductorless Chua’s circuit. Electron. Lett. 2000, 36, 1915–1916. [Google Scholar] [CrossRef]
- Demirkol, A.S.; Demirkol, A.S.; Ascoli, A.; Ascoli, A.; Weiher, M.; Weiher, M.; Tetzlaff, R.; Tetzlaff, R. Exact Inductorless Realization of Chua Circuit Using Two Active Elements. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 1620–1624. [Google Scholar] [CrossRef]
- Duan, X.; Gao, T. A single-supply Chua’s circuit based on an active active inductor. J. Terahertz Sci. Electron. Inf. Technol. 2021, 19, 1120–1125 + 1133. [Google Scholar] [CrossRef]
- Romero, F.J.; Medina-Garcia, A.; Escudero, M.; Morales, D.P.; Rodriguez, N. Design and implementation of a floating meminductor emulator upon Riordan gyrator. AEU Int. J. Electron. Commun. 2021, 133, 153671. [Google Scholar] [CrossRef]
- Ananda, Y.R.; Satyanarayan, G.S.; Trivedi, G. A Flux Controlled MOS-Based Optimized High Frequency Meminductor Emulator. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 774–784. [Google Scholar] [CrossRef]
- Choubey, C.K.; Paul, S.K. Implementation of chaotic oscillator by designing a simple Chua’s diode using a single VDTA. AEU Int. J. Electron. Commun. 2020, 124, 153360. [Google Scholar] [CrossRef]
- Wang, N.; Xu, D.; Iu, H.H.-C.; Wang, A.; Chen, M.; Xu, Q. Dual Chua’s Circuit. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 71, 1222–1231. [Google Scholar] [CrossRef]
- Elwakil, A.; Kennedy, M. Improved implementation of Chua’s chaotic oscillator using current feedback op amp. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 76–79. [Google Scholar] [CrossRef]
- Bao, B.; Hu, F.; Chen, M.; Xu, Q.; Yu, Y. Self-Excited and Hidden Attractors Found Simultaneously in a Modified Chua’s Circuit. Int. J. Bifurc. Chaos 2015, 25, 1550075. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics. Hardw. Implement. Image Encryption Appl. 2021, 81, 71–83. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Wu, J. An Innovative Design of Chaotic Signal Generation Circuit Based on Chua’s Circuit. Chin. J. Mech. Eng. 2023, 21, 18–21. [Google Scholar] [CrossRef]
- Aghababa, M.P. Adaptive switching control of uncertain fractional systems: Application to Chua’s circuit. Int. J. Adapt. Control. Signal Process. 2018, 32, 1206–1221. [Google Scholar] [CrossRef]
- Jamal, R.K.; Abdulaali, R.S. A Comprehensive Study and Analysis of the Chaotic Chua Circuit. Iraqi J. Sci. 2022, 63, 556–570. [Google Scholar] [CrossRef]
- Chang, Y.-C. A robust tracking control for chaotic Chua’s circuits via fuzzy approach. Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 889–895. [Google Scholar] [CrossRef]
- Göhler, S.M.; Eifler, T.; Howard, T.J. Robustness Metrics: Consolidating the Multiple Approaches to Quantify Robustness. J. Mech. Des. 2016, 138, 111407. [Google Scholar] [CrossRef]
- McPhail, C.; Maier, H.R.; Kwakkel, J.H.; Giuliani, M.; Castelletti, A.; Westra, S. Robustness Metrics: How Are They Calculated, When Should They Be Used and Why Do They Give Different Results? Earth’s Futur. 2018, 6, 169–191. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Z.; Peng, M. Novel bursting patterns and the bifurcation mechanism in a piecewise smooth Chua’s circuit with two scales. Nonlinear Dyn. 2022, 108, 1755–1771. [Google Scholar] [CrossRef]
- Galajda, P.; Guzan, M.; Petržela, J. Implementation of a custom Chua’s diode for chaos generating applications. In Proceedings of the 2016 26th International Conference Radioelektronika (RADIOELEKTRONIKA), Kosice, Slovakia, 19–20 April 2016; pp. 66–70. [Google Scholar]
- Kiliç, R. A Comparative Study on Realization of Chua’s Circuit: Hybrid Realizations of Chua’s Circuit Combining the Circuit Topologies Proposed for Chua’s Diode and Inductor Elements. Int. J. Bifurc. Chaos 2003, 13, 1475–1493. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Li, S. Feixianxing Dianlu—Jichu Fenxi yu Sheji; High Education Press: Beijing, China, 2011; ISBN 978-7-04-031586-8. [Google Scholar]
- Gomes, I.; Korneta, W.; Stavrinides, S.G.; Picos, R.; Chua, L.O. Experimental observation of chaotic hysteresis in Chua’s circuit driven by slow voltage forcing. Chaos Solitons Fractals 2023, 166, 112927. [Google Scholar] [CrossRef]
- Chua, L.O. Global Unfolding of Chua’s Circuit. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 1993, E76-A, 704–734. [Google Scholar]
- Chua, L.O. Chua circuit. Scholarpedia 2007, 2, 1488. [Google Scholar] [CrossRef]
- Pisarchik, A.; Jaimes-Reátegui, R.; Rodríguez-Flores, C.; García-López, J.; Huerta-Cuellar, G.; Martín-Pasquín, F. Secure chaotic communication based on extreme multistability. J. Frankl. Inst. 2021, 358, 2561–2575. [Google Scholar] [CrossRef]
- Yasser, I.; Mohamed, M.A.; Samra, A.S.; Khalifa, F. A Chaotic-Based Encryption/Decryption Framework for Secure Multimedia Communications. Entropy 2020, 22, 1253. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, K.; Wen, C.; Soh, Y.C. A new chaotic secure communication system. IEEE Trans. Commun. 2003, 51, 1306–1312. [Google Scholar] [CrossRef]
- Esqueda, I.S. Modeling of Total Ionizing Dose Effects in Advanced Complementary Metal-Oxide-Semiconductor Technologies. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2011. [Google Scholar]
- Dingwell, J.B. Lyapunov Exponents; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; ISBN 978-0-471-74036-0. [Google Scholar]
- Abarbanel, H.D.I.; Brown, R.; Kennel, M.B. Local Lyapunov exponents computed from observed data. J. Nonlinear Sci. 1992, 2, 343–365. [Google Scholar] [CrossRef]
- Geist, K.; Parlitz, U.; Lauterborn, W. Comparison of Different Methods for Computing Lyapunov Exponents. Prog. Theor. Phys. 1990, 83, 875–893. [Google Scholar] [CrossRef]

| Single Vortex | Double Vortex | |
|---|---|---|
| Sine Wave | 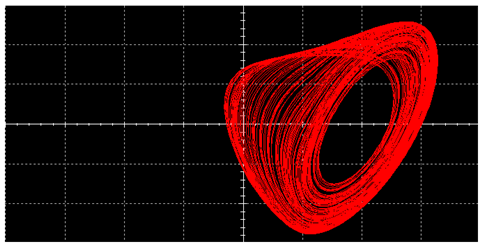 | 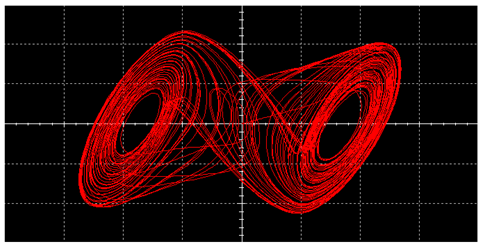 |
| Square Wave | 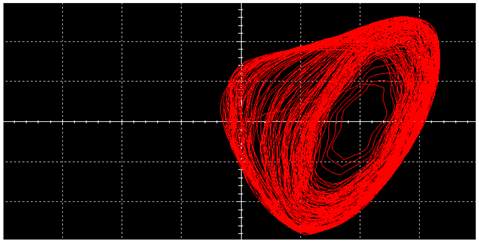 | 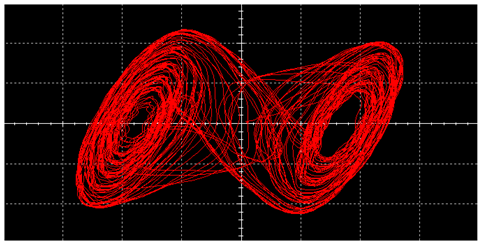 |
| Triangular Wave | 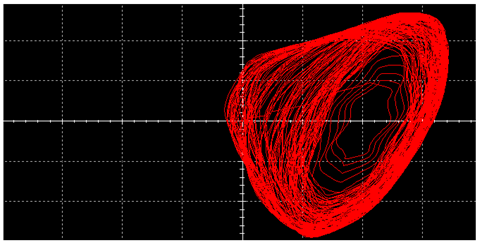 | 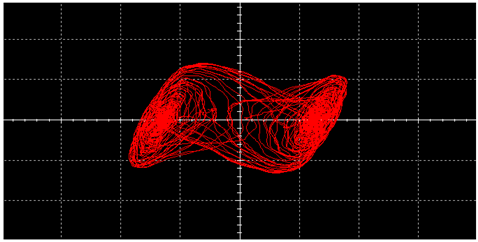 |
| No Error | 0.41 | 0.57 |
| −0.73 | 0.10 | |
| −0.85 | 0.04 | |
| −0.42 | 0.35 |
| No error | 0.66 | 0.68 |
| 0.03 | 0.38 | |
| −0.23 | 0.10 | |
| 0.18 | 0.49 |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 1.22% | 3.91% |
| 0.76% | 1.80% | |
| 3.00% | 6.25% | |
| Average (X) | 1.66% | 3.99% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 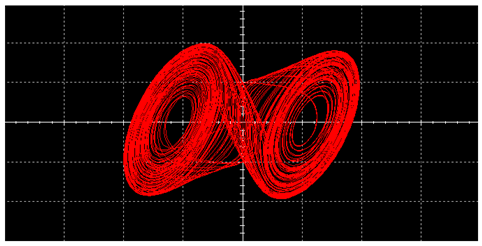 | 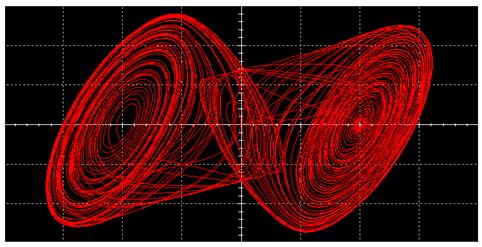 | |
 |  | ||
 | 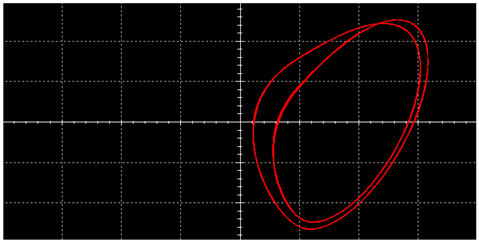 | ||
 |  | ||
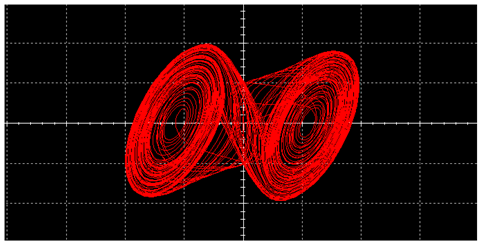 | 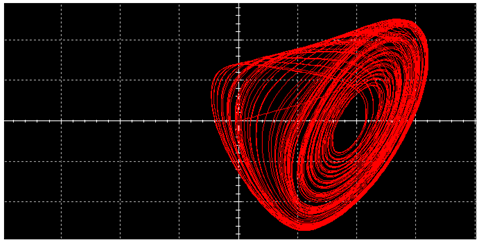 | ||
 | 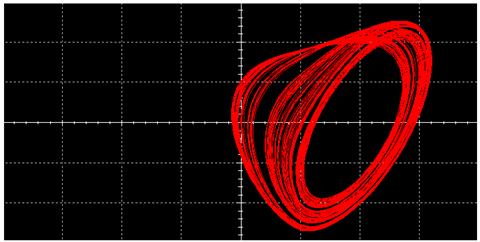 | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 1.76% | 6.97% |
| 1.12% | 5.27% | |
| 2.75% | 9.90% | |
| Average (X) | 1.88% | 7.38% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 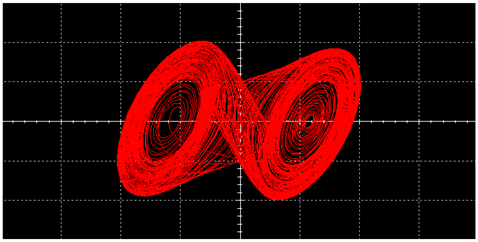 | 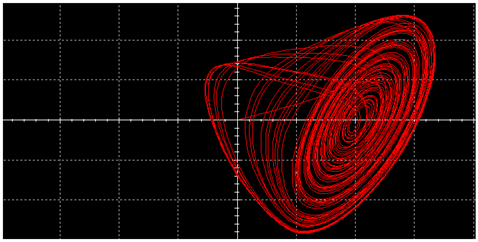 | |
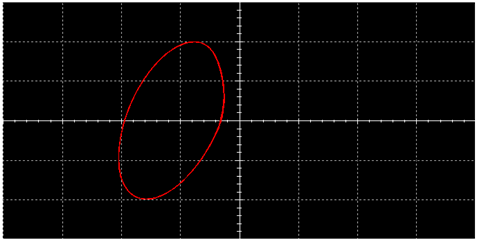 | 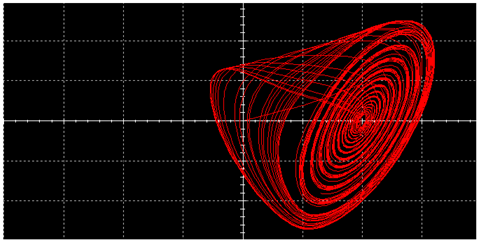 | ||
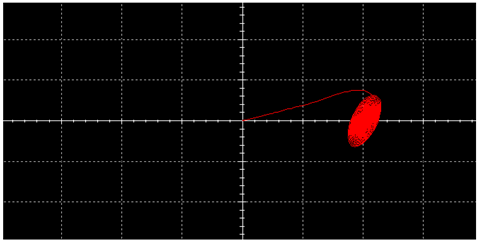 | 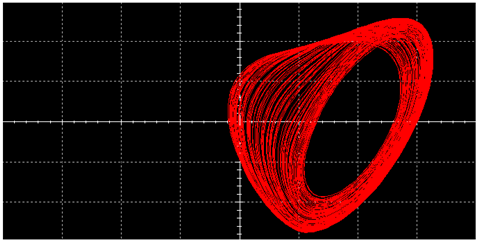 | ||
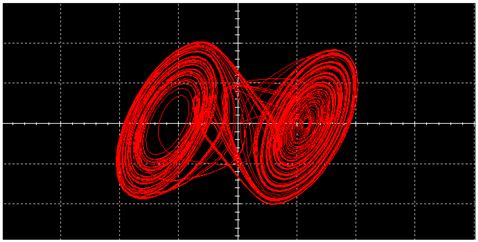 | 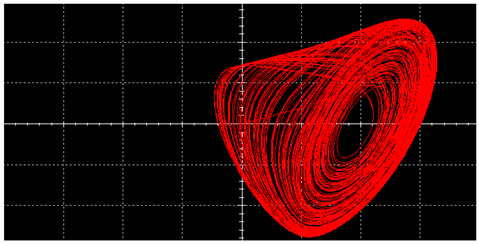 | ||
 | 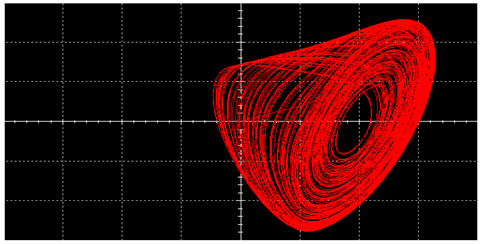 | ||
 | 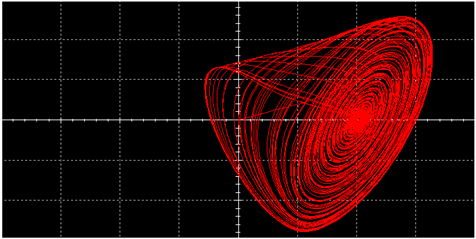 | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 0.72% | 2.12% |
| 0.28% | 0.63% | |
| 2.41% | 5.25% | |
| Average (X) | 1.14% | 2.67% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 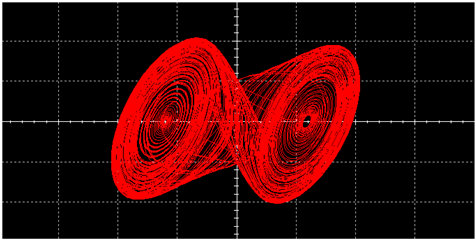 |  | |
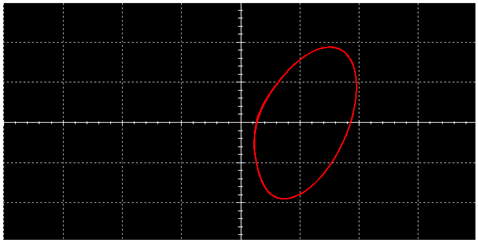 | 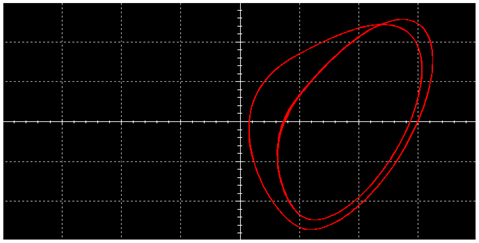 | ||
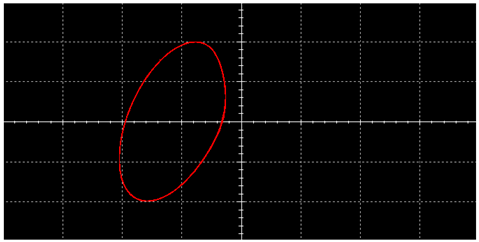 | 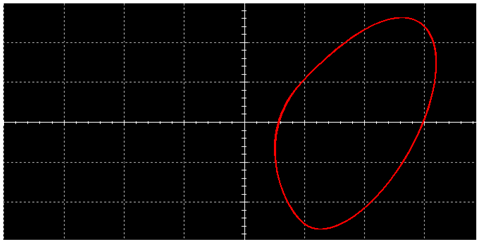 | ||
 | 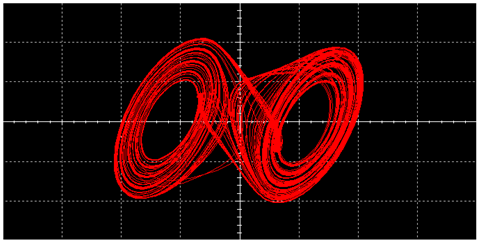 | ||
 | 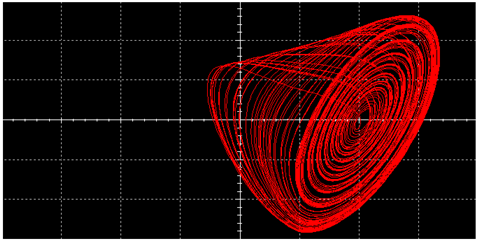 | ||
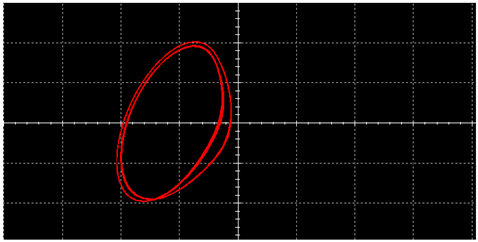 | 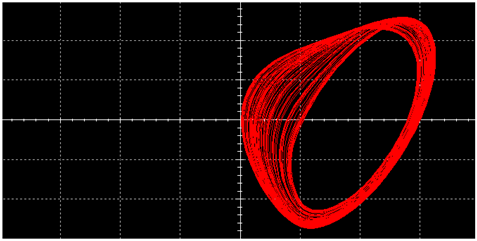 | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 5.88% | 10.82% |
| 2.60% | 5.69% | |
| 5.72% | 21.31% | |
| Average (X) | 4.73% | 12.61% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 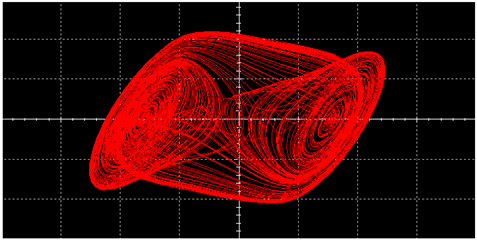 | 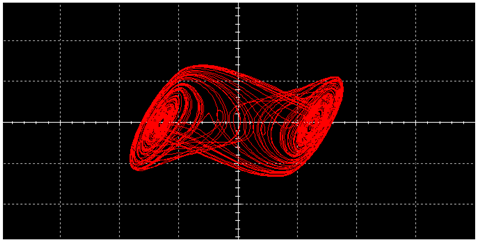 | |
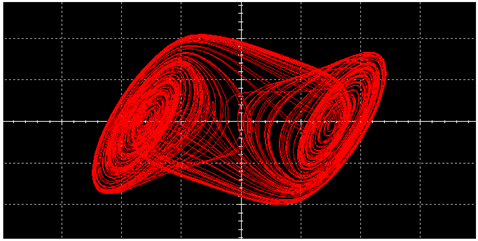 | 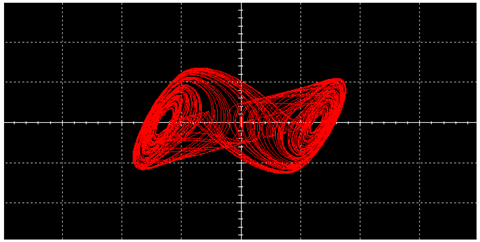 | ||
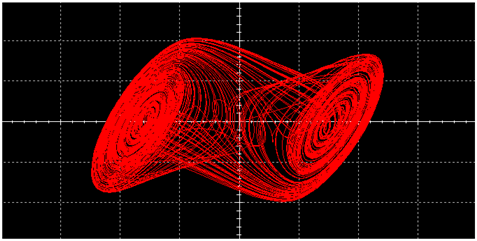 |  | ||
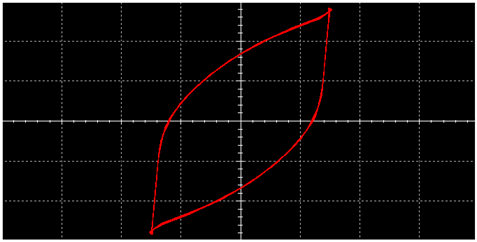 | 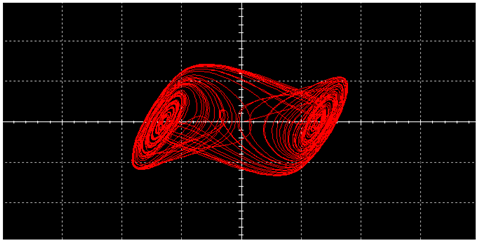 | ||
 | 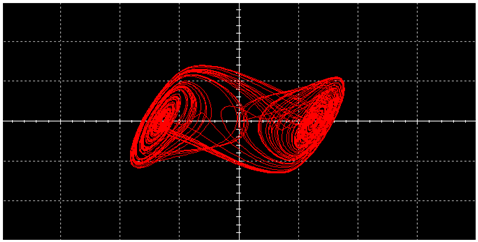 | ||
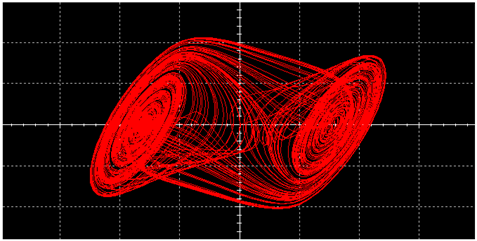 | 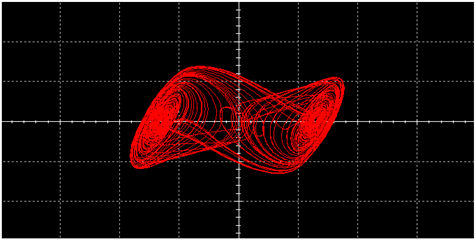 | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 7.72% | 17.49% |
| 6.24% | 12.03% | |
| 7.31% | 26.90% | |
| Average (X) | 7.09% | 18.81% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 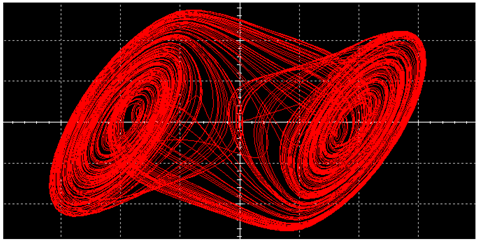 | 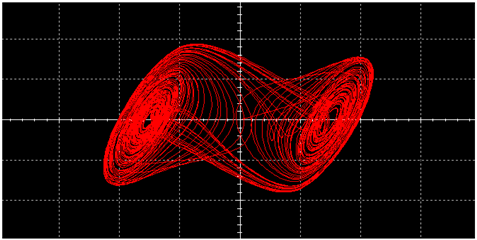 | |
 | 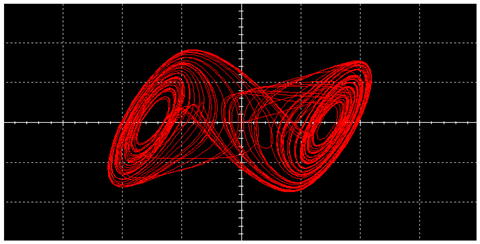 | ||
 | 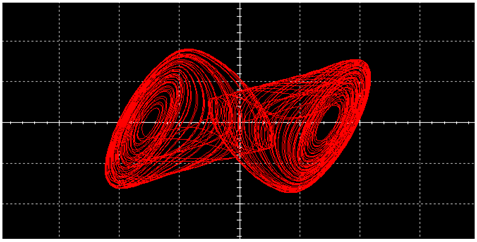 | ||
 | 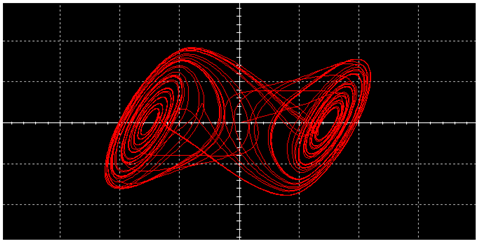 | ||
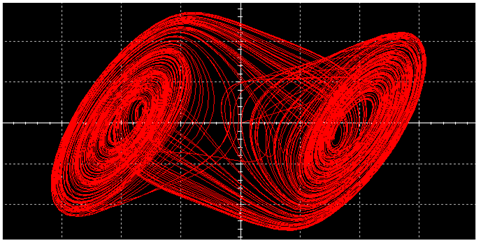 | 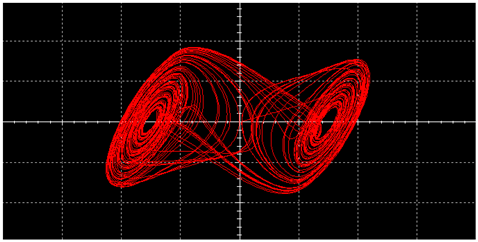 | ||
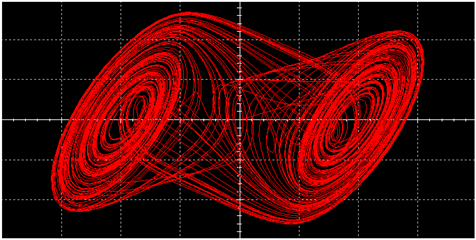 |  | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| L | 5.37% | 11.04% |
| 3.58% | 8.55% | |
| 6.92% | 15.38% | |
| Average (X) | 5.29% | 11.66% |
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | ||
|---|---|---|---|
| L | 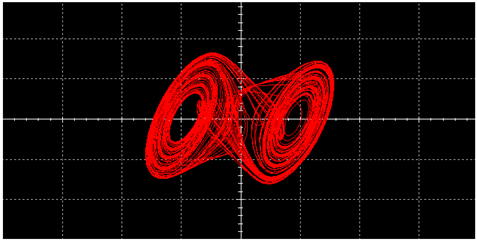 |  | |
 | 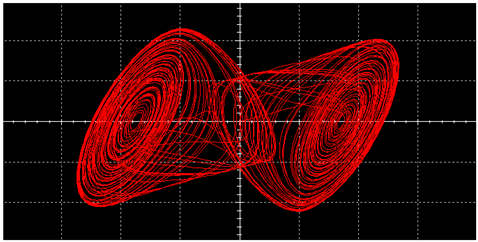 | ||
 | 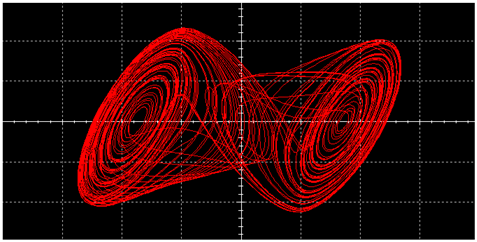 | ||
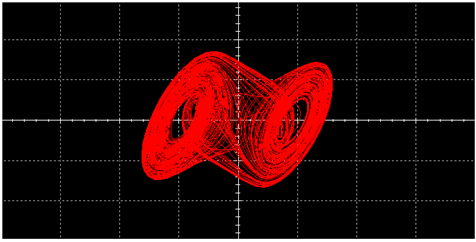 | 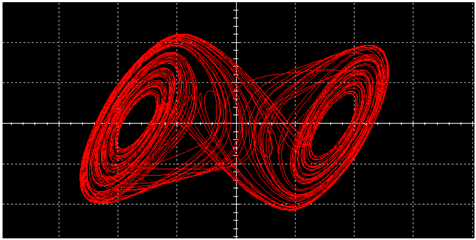 | ||
 |  | ||
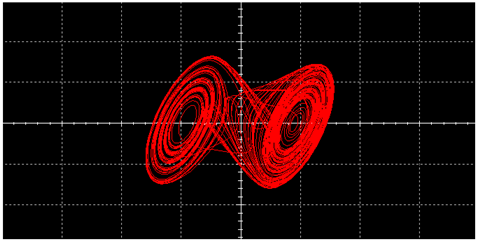 |  | ||
| Traditional Chua’s Circuit | Improved Implementation of Chua’s Circuit | |
|---|---|---|
| Point 1 | 1989 Ω | 2103 Ω |
| Periodic Motion | 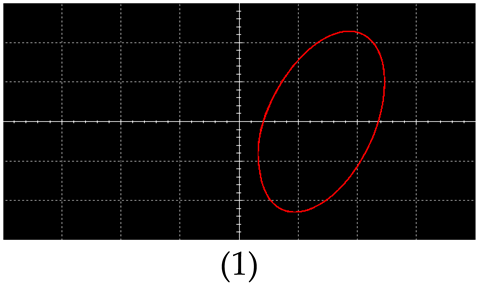 | 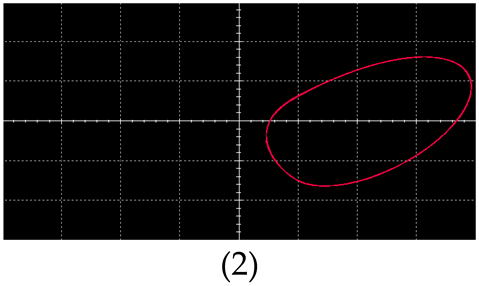 |
| Multiply Periodic Motion | 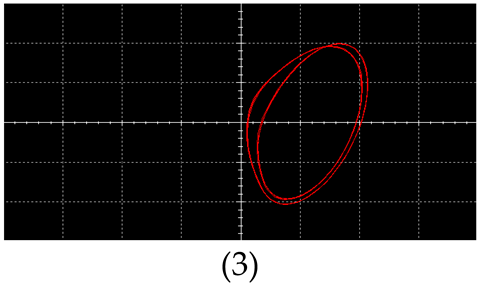 | 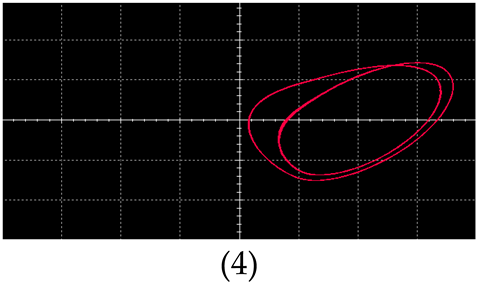 |
| Point 2 | 1910 Ω | 1939 Ω |
| Single Vortex | 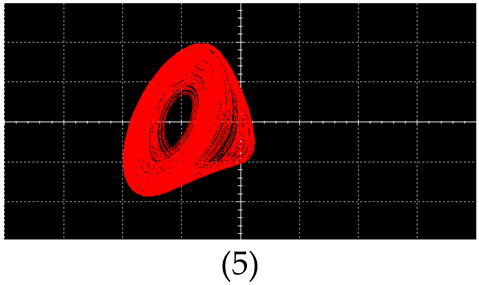 |  |
| Point 3 | 1886 Ω | 1868 Ω |
| Double Vortex |  | 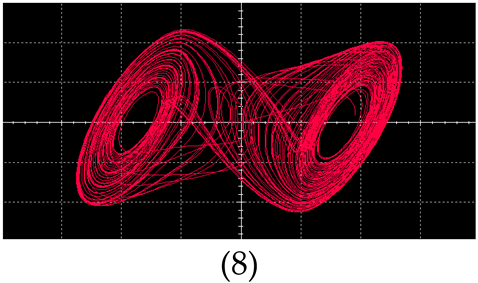 |
| Point 4 | 1575 Ω | 1442 Ω |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Time Base (ms) | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Gradation of Channel A (V/Div) | 1 | 1 | 1 | 1 | 1 | 1 | 0.5 | 0.5 |
| Gradation of Channel B (V/Div) | 5 | 2 | 5 | 2 | 5 | 2 | 2 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wen, Y.; Ning, Y.; Zhang, Z.; Li, H.; Xia, Y. Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System. Electronics 2024, 13, 2637. https://doi.org/10.3390/electronics13132637
Zhang Z, Wen Y, Ning Y, Zhang Z, Li H, Xia Y. Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System. Electronics. 2024; 13(13):2637. https://doi.org/10.3390/electronics13132637
Chicago/Turabian StyleZhang, Ziqi, Yiming Wen, Yafei Ning, Zirui Zhang, Hu Li, and Yuhan Xia. 2024. "Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System" Electronics 13, no. 13: 2637. https://doi.org/10.3390/electronics13132637
APA StyleZhang, Z., Wen, Y., Ning, Y., Zhang, Z., Li, H., & Xia, Y. (2024). Improved Implementation of Chua’s Circuit on an Active Inductor and Non-Autonomous System. Electronics, 13(13), 2637. https://doi.org/10.3390/electronics13132637







