Evolving Dispatching Rules in Improved BWO Heuristic Algorithm for Job-Shop Scheduling
Abstract
:1. Introduction
2. Rule-Based Heuristic Scheduling Framework and IBWO-DDR-AdaBoost Optimization Algorithm
2.1. JSP Problem Description
- All machines can be used at zero time, that is, all workpieces can start processing immediately after arriving at the machine;
- All workpieces have no priority and can be processed at zero time;
- Each process is processed on the designated machine, and the processing can only begin after the processing of the previous process is completed;
- Each machine can only process one work piece at the same time;
- Each workpiece can only be processed once on one machine;
- The processing sequence and processing time of each workpiece are known, and do not change with the change in the processing sequence;
- Once any process begins processing, it is not allowed to be interrupted until the end of the process.
2.2. Rule-Based Heuristic Scheduling Framework
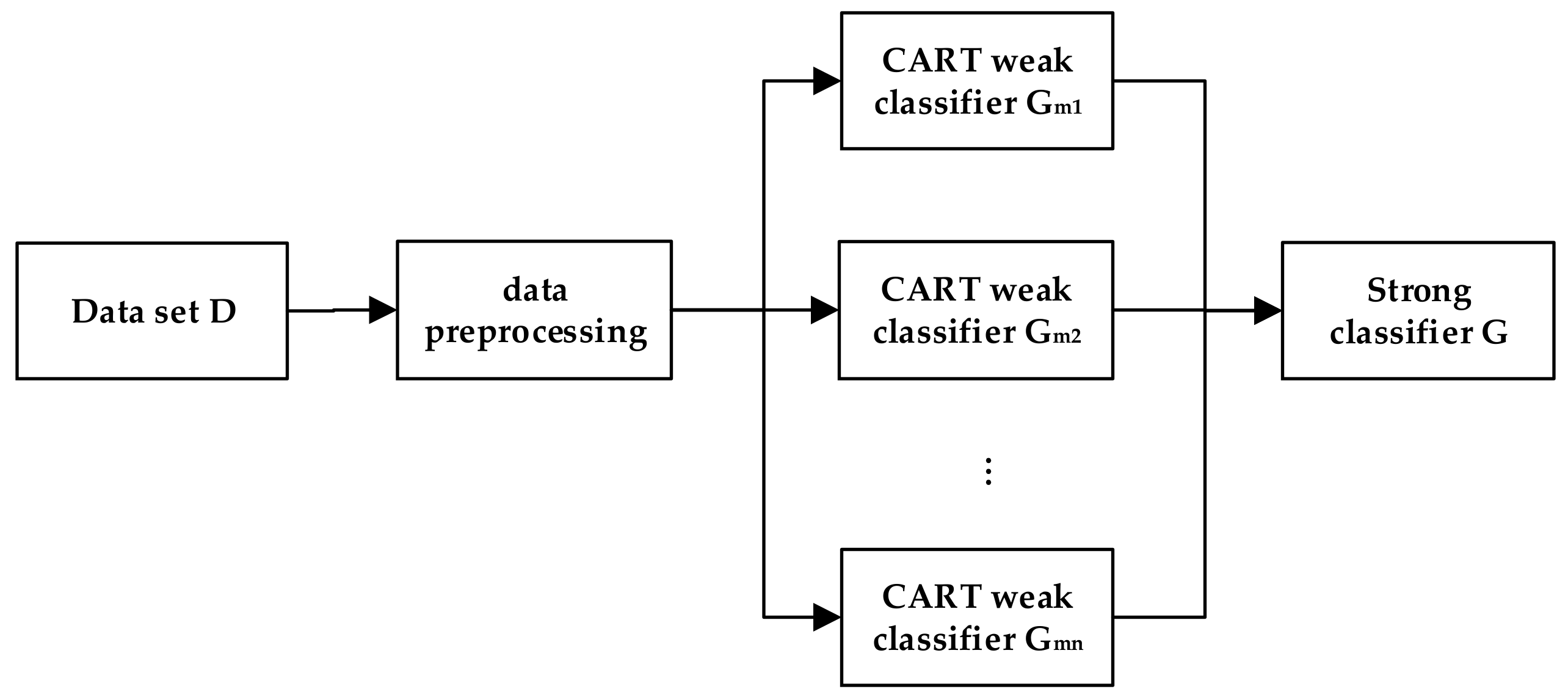
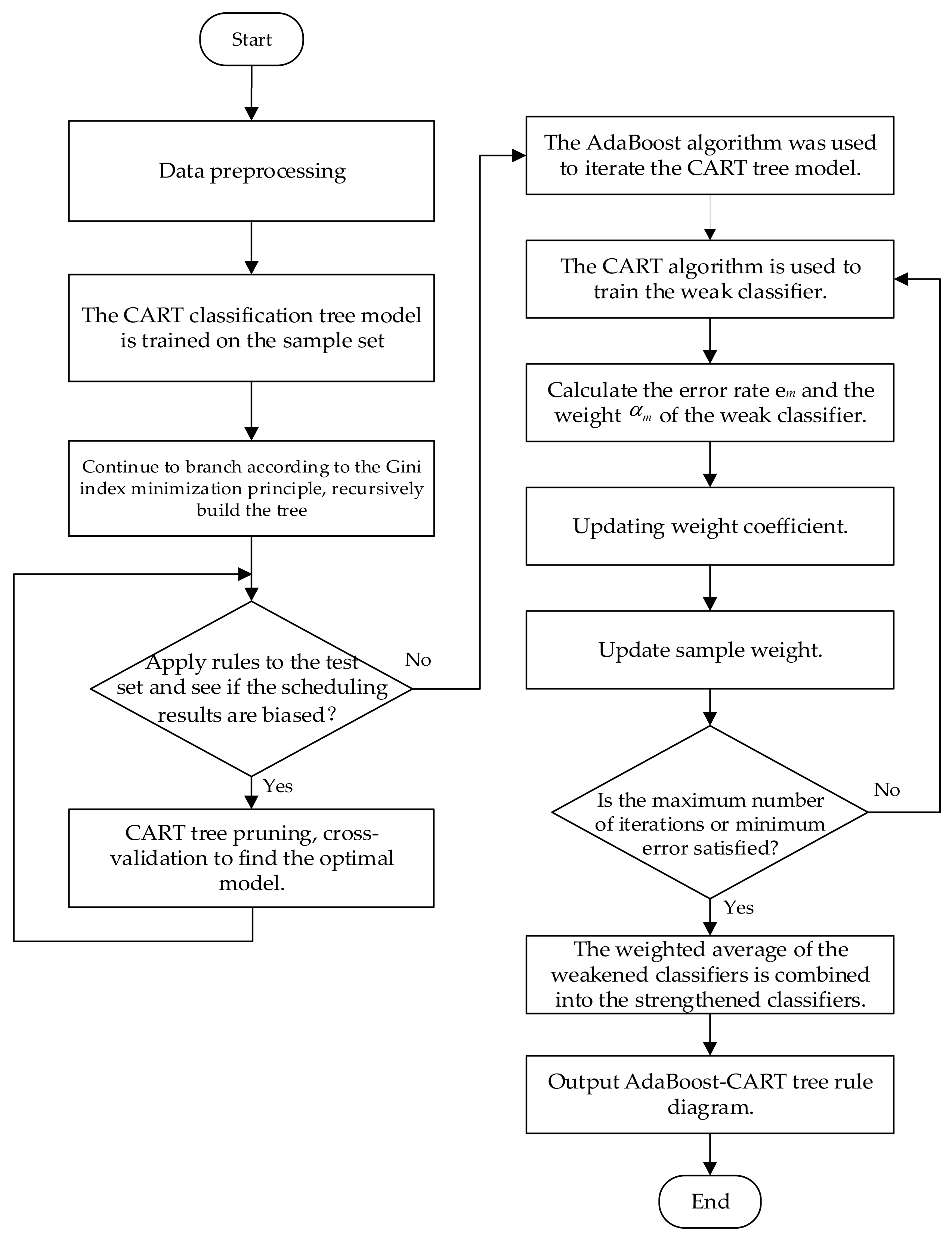
2.3. Dispatching Knowledge Mining Based on AdaBoost-CART Integrated Learning Mining Algorithm
- Perform data preprocessing on the scheduling dataset to determine the attributes, attribute values, and category values and divide the training set as well as the test set;
- Train the CART classification tree model on the sample set. The attribute with the smallest Gini index is taken as the root node of the branch;
- On top of the root node, continue branching according to the principle of Gini index minimization, recursively build the tree, and end the tree splitting when the training set contains only one category;
- Apply the obtained tree rules to the test set, and observe whether there is a deviation in the scheduling results; if there is overfitting needed to prune the CART tree, use cross-validation to find the optimal model, determine and save the model parameters, and then repeat c until the scheduling output of each test subset is basically the same as the output of the test set; proceed to step e;
- Iteratively optimize the CART classification tree model using the AdaBoost algorithm, i.e., use the CART classification tree model as a weak classifier for the AdaBoost integrated classification model;
- Train the weak classifier using the CART algorithm;
- Calculate the classification error rate and weighting coefficients of the weak classifier;
- Update the weight coefficients;
- Update the sample weights;
- Determine whether the maximum number of iterations is reached or the minimum error is satisfied, i.e., the classification error rate of the weak classifier is less than the threshold, if yes, then the weak classifier will be combined into the final strong classifier by weighted average and output the AdaBoost-CART tree rule diagram, otherwise, return to step f.
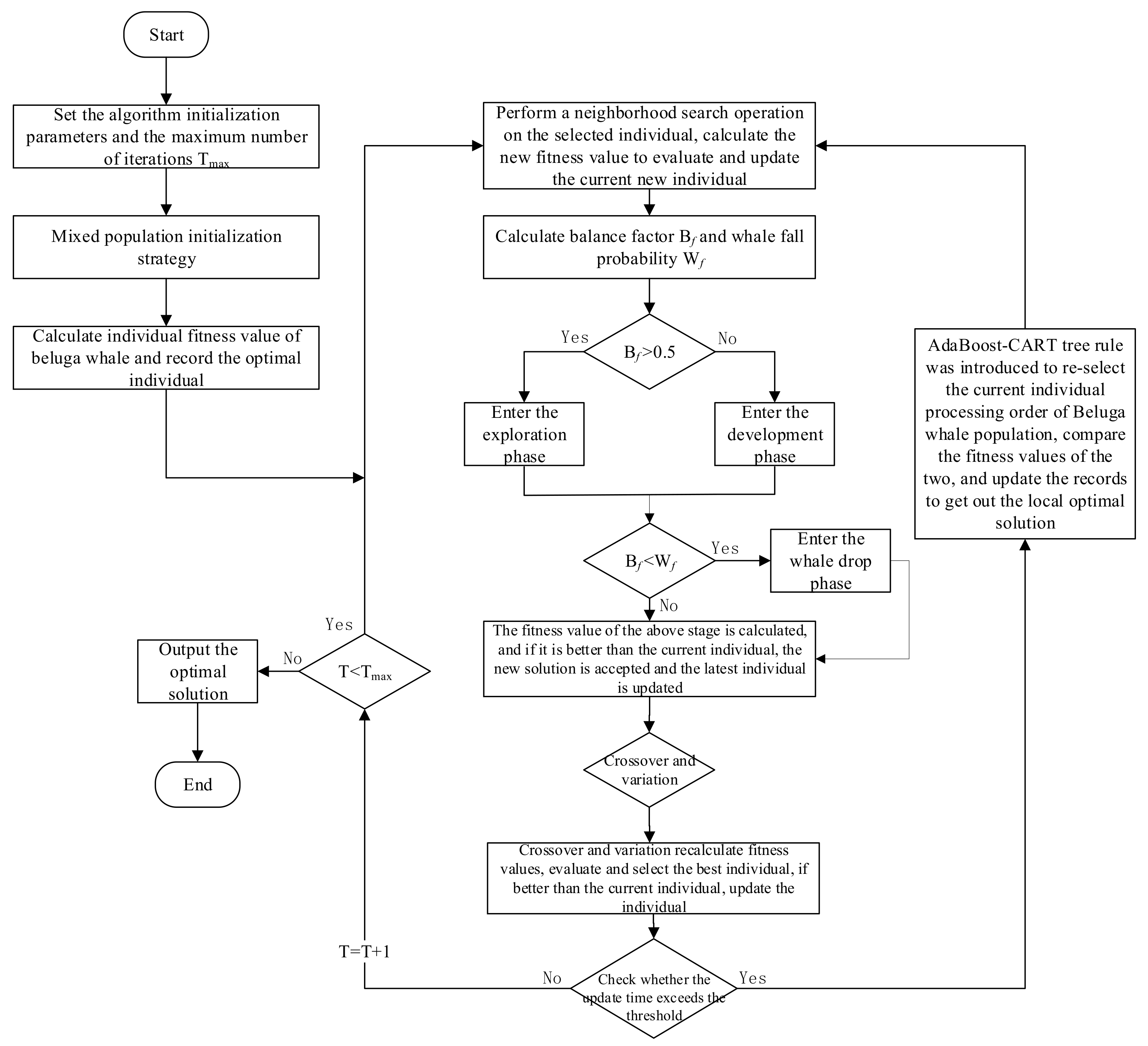
2.4. IBWO Scheduling Optimization Algorithm Based on AdaBoost-CART
2.4.1. Improvement of Standard Beluga Whale Optimization Algorithm
- Introducing the greedy idea of domain search strategy
- b.
- Crossover and mutation operations of genetic operators
2.4.2. IBWO-DDR-AdaBoost Optimization Algorithm
- Set initialization parameters and iteration termination conditions;
- Use a hybrid initialization population , , dominated by the rules of the AdaBoost-CART integrated classification model for initialization, calculate individual fitness values of beluga whales, and record the optimal individuals;
- Perform a greedy thought-based domain search strategy on the better (optimal and suboptimal) individuals, evaluate the new solution produced by them, and accept the new solution if it is better than the current individual;
- Convert the scheduling scheme into a position vector;
- Calculate the parameter values of the balance factor and the whale fall probability in the BWO algorithm, update the location of individual beluga whales at each stage of the algorithm, and generate a vector of random numbers corresponding to the process code.
- Convert the position vector into a scheduling scheme, and calculate the individual fitness value of each stage. If it is better than the current individual, update the individual;
- Perform the crossover and mutation operations of the genetic operators on the selected individuals and evaluate the new solution generated by them and accept the new solution if it is better than the current individual;
- Determine whether the update time exceeds the threshold, if so, call the excavated AdaBoost-CART tree rule, re-select the processing order of the current beluga whale population, and compare the fitness values of the two; if the fitness value is better, update and jump out of the local optimal solution. If the threshold is not exceeded, the next iteration is performed;
- Determine whether the iteration termination condition is met. If yes, go to Step j; otherwise, go back to step c;
- The algorithm ends and outputs the optimal scheduling result.
- (1)
- Encoding mechanism
- (2)
- Transformation mechanism of position vector
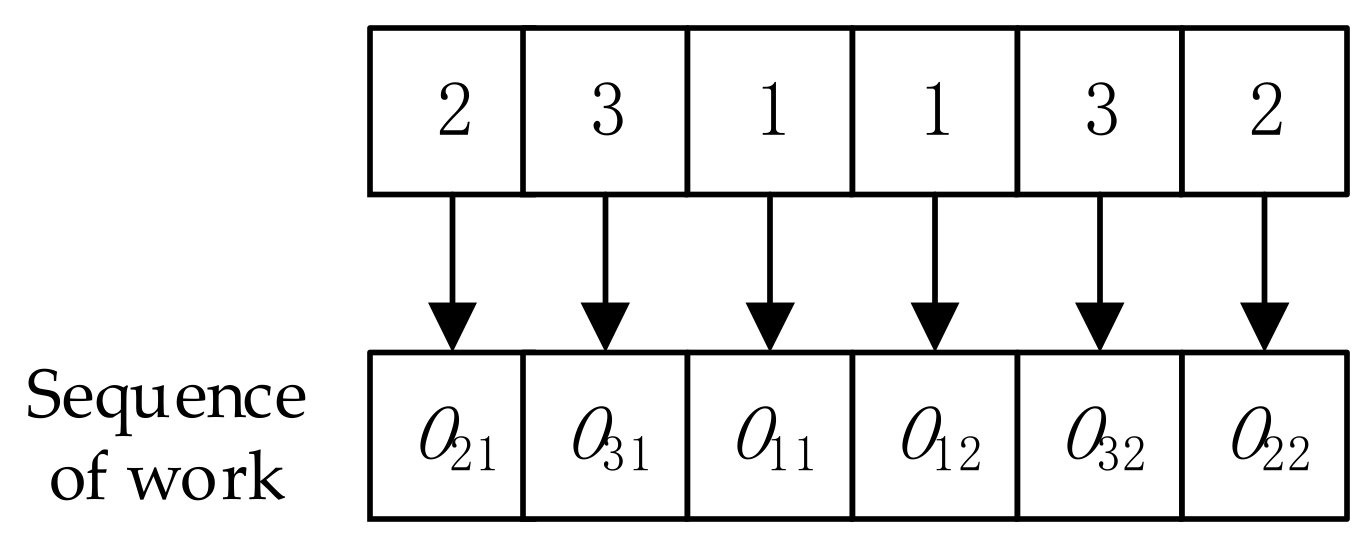
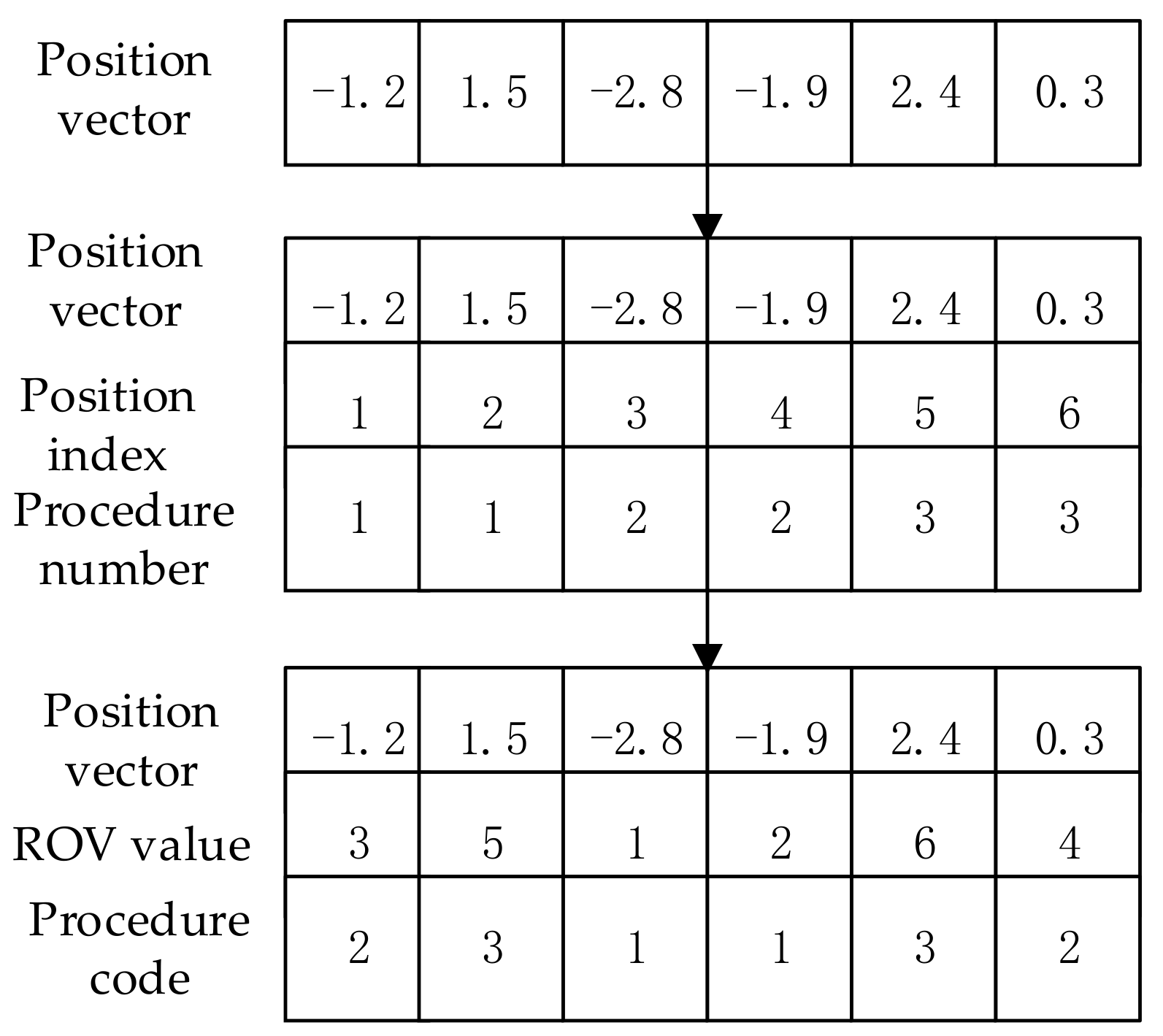
- In the conversion from discrete space to discrete space, we take any value from , being the total number of processing processes, and generate the value corresponding to each process, and then we use the ROV rule to assign the ROV value to each process, i.e., the random numbers are labelled according to the order from the smallest to the largest; for example, the smallest value of the random number in the figure −2.8 corresponds to an ROV value of 1, and the largest value of the random number is 2.4, which corresponds to an ROV value of 6. Next, the ROV values are assigned to the corresponding process codes in the order of process numbers. The random numbers corresponding to the adjusted ROV values are the updated position vectors (i.e., traverse the process numbers from left to right and select the random values corresponding to the positions from the process codes), which achieves the conversion of the scheduling scheme into position vectors, as shown in Figure 6.

- (3)
- Mixed initial population strategy
- (4)
- Fitness function
- (5)
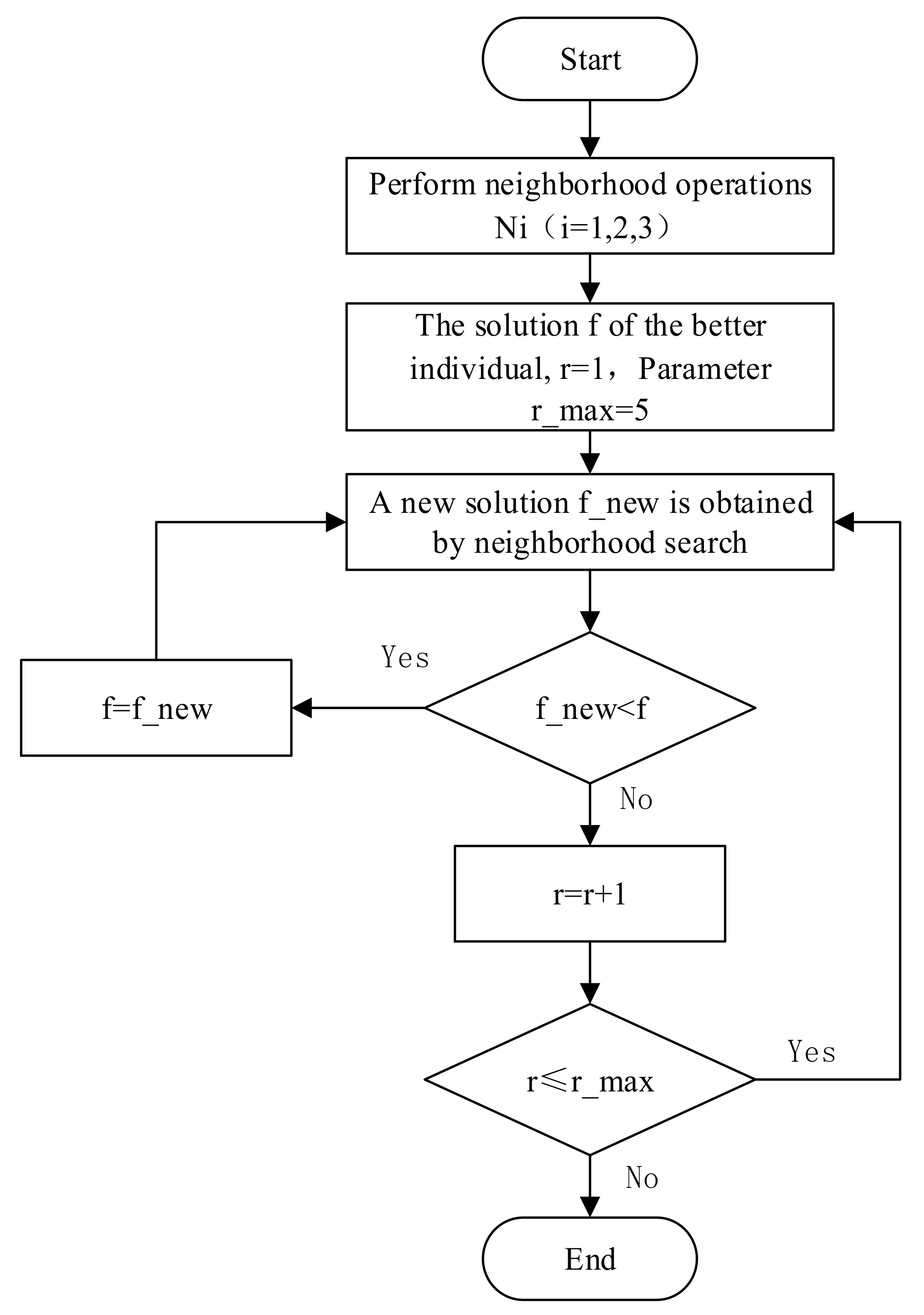
- Neighborhood search strategy based on greedy thought
- Neighborhood operation N1:
- b.
- Neighborhood operation N2:
- c.
- Neighborhood operation N3:
- (6)
- Genetic operator operation
- Crossover operation
- b.
- Mutation operation
- (7)
- Dispatching rule optimization strategy
3. Results and Discussion
3.1. Simulation Environment Construction
3.2. Representation of Dispatching Rules
3.2.1. Selection of Scheduling Sample Set
3.2.2. Select Performance Indicators and Data Representation
- PT: the processing time on the machine for a particular process for a particular workpiece;
- RPT: the sum of the times of all subsequent unprocessed processes when a particular workpiece is scheduled;
- ROPN: the number of subsequent unprocessed processes when a process is scheduled for a particular workpiece.
- Job_pt_longer (two processes of two tasks on the same machine whose processing time is longer);
- Job_rpt_longer (two processes of two tasks on the same machine who have longer remaining processing time);
- Job_ropn_more (who has more remaining operations of two tasks on the same machine).
3.2.3. Construct Sample Data Set
3.2.4. Rule Scheduling AdaBoost-CART Tree Rule
3.3. Case Study
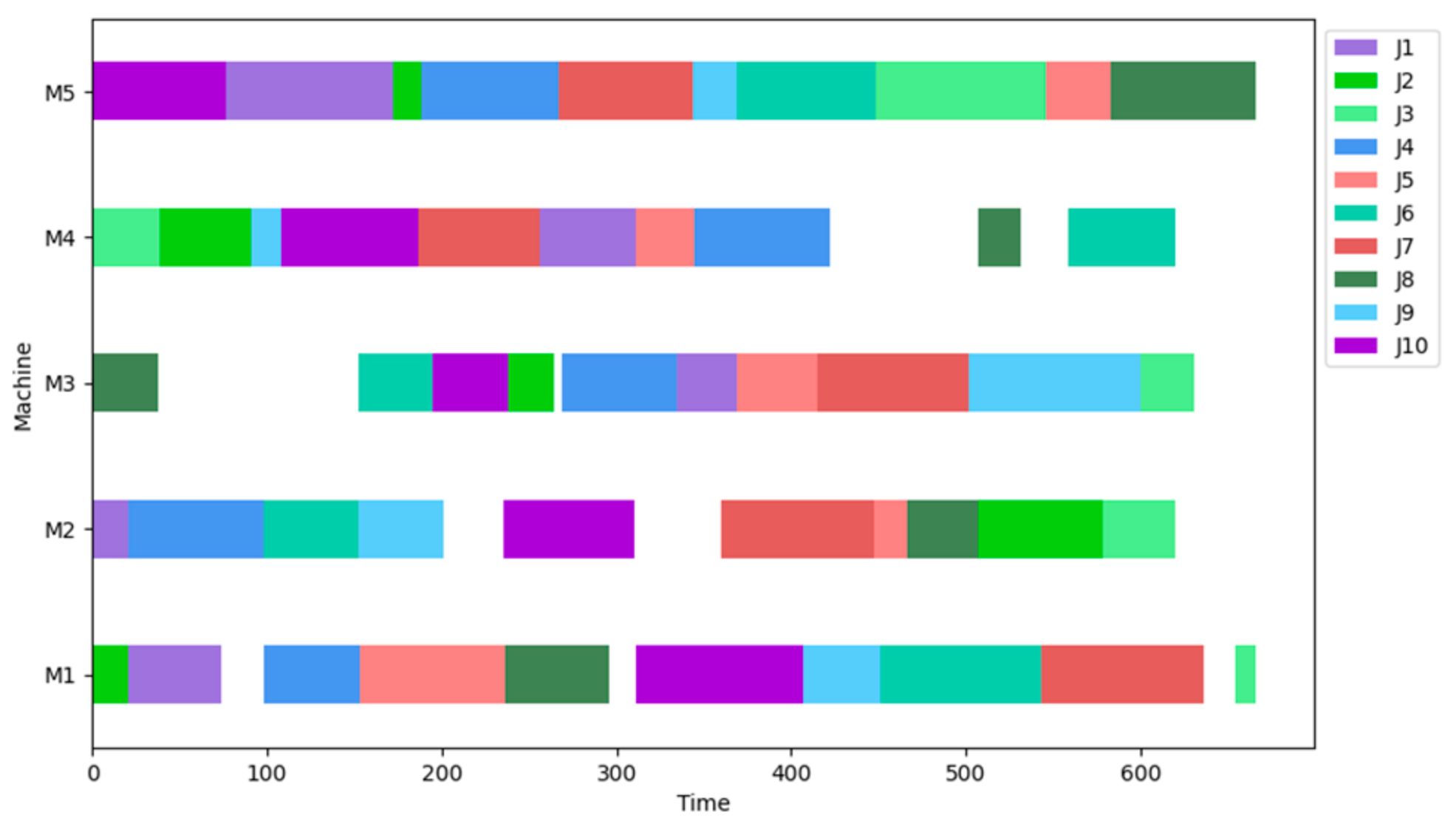
3.3.1. Simulation Analysis of LA11 Typical Example
3.3.2. Simulation Analysis of JSP Examples under Different Scales
3.3.3. Comparative Analysis of Solution Results under 40 Benchmark Test Cases
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Applegate, D.; Cook, W. A computational study of the job-shop scheduling problem. ORSA J. Comput. 1991, 3, 149–156. [Google Scholar] [CrossRef]
- Liu, T.K.; Tsai, J.T.; Chou, J.H. Improved genetic algorithm for the job-shop scheduling problem. Int. J. Adv. Manuf. Technol. 2006, 27, 1021–1029. [Google Scholar] [CrossRef]
- Kui, C.; Li, B. Research on FJSP of improved particle swarm optimization algorithm considering transportation time. J. Syst. Simul. 2021, 33, 845–853. [Google Scholar]
- Zhang, S.; Li, X.; Zhang, B.; Wang, S. Multi-objective optimization in flexible assembly job shop scheduling using a distributed ant colony system. Eur. J. Oper. Res. 2020, 283, 441–460. [Google Scholar] [CrossRef]
- Fontes DB, M.M.; Homayouni, S.M.; Gonçalves, J.F. A hybrid particle swarm optimization and simulated annealing algorithm for the job shop scheduling problem with transport resources. Eur. J. Oper. Res. 2023, 306, 1140–1157. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2022. [Google Scholar]
- Zhang, Y.; Liu, Y. Analysis and Application of Data Mining Algorithm Based on Decision Tree. J. Liaoning Petrochem. Univ. 2007, 27, 78–80. [Google Scholar]
- Salama, S.; Kaihara, T.; Fujii, N.; Kokuryo, D. Dispatching rules selection mechanism using support vector machine for genetic programming in job shop scheduling. IFAC-PapersOnLine 2023, 56, 7814–7819. [Google Scholar] [CrossRef]
- Blackstone, J.H.; Phillips, D.T.; Hogg, G.L. A state-of-the-art survey of dispatching rules for manufacturing job shop operations. Int. J. Prod. Res. 1982, 20, 27–45. [Google Scholar] [CrossRef]
- Li, X.N.; Sigurdur, O. Discovering dispatching rules using data mining. J. Sched. 2005, 8, 515–527. [Google Scholar] [CrossRef]
- Shahzad, A.; Mebarki, N. Learning dispatching rules for scheduling: A synergistic view comprising decision trees, tabu search and simulation. Computers 2016, 5, 3. [Google Scholar] [CrossRef]
- Wang, K.J.; Chen, J.C.; Lin, Y.S. A hybrid knowledge discovery model using decision tree and neural network for selecting dispatching rules of a semiconductor final testing factory. Prod. Plan. Control 2005, 16, 665–680. [Google Scholar] [CrossRef]
- Jun, S.; Lee, S. Learning dispatching rules for single machine scheduling with dynamic arrivals based on decision trees and feature construction. Int. J. Prod. Res. 2021, 59, 2838–2856. [Google Scholar] [CrossRef]
- Habib Zahmani, M.; Atmani, B. Multiple dispatching rules allocation in real time using data mining, genetic algorithms, and simulation. J. Sched. 2021, 24, 175–196. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Göçken, M.; Özbakir, L. Genetic programming based data mining approach to dispatching rule selection in a simulated job shop. Simulation 2010, 86, 715–728. [Google Scholar] [CrossRef]
- Balasundaram, R.; Baskar, N.; Sankar, R.S. A new approach to generate dispatching rules for two machine flow shop scheduling using data mining. Procedia Eng. 2012, 38, 238–245. [Google Scholar] [CrossRef]
- Wang, C.L.; Li, C.; Feng, Y.P.; Rong, G. Dispatching rule extraction method for job shop scheduling problem. J. Zhejiang Univ. Eng. Sci. 2015, 49, 421–429. [Google Scholar]
- Tian, L.; Junjia, W. Multi-target job-shop scheduling based on dispatching rules and immune algorithm. Inf. Control 2016, 45, 278–286. [Google Scholar]
- Huang, J.P.; Gao, L.; Li, X.Y.; Zhang, C.J. A novel priority dispatch rule generation method based on graph neural network and reinforcement learning for distributed job-shop scheduling. J. Manuf. Syst. 2023, 69, 119–134. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Xiong, H.; Shi, S.; Ren, D.; Hu, J. A survey of job shop scheduling problem: The types and models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Ying, C.; Qi-Guang, M.; Jia-Chen, L.; Lin, G. Advance and prospects of AdaBoost algorithm. Acta Autom. Sin. 2013, 39, 745–758. [Google Scholar]
- Yuan, Y.; Xu, H.; Yang, J. A hybrid harmony search algorithm for the flexible job shop scheduling problem. Appl. Soft Comput. 2013, 13, 3259–3272. [Google Scholar] [CrossRef]
- Poli, R. Exact schema theory for genetic programming and variable-length genetic algorithms with one-point crossover. Genet. Program. Evolvable Mach. 2001, 2, 123–163. [Google Scholar] [CrossRef]
- Thede, S.M. An introduction to genetic algorithms. J. Comput. Sci. Coll. 2004, 20, 115–123. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. Data Classif. Algorithms Appl. 2014, 37, 37–64. [Google Scholar]
- Xiong, H.; Fan, H.; Jiang, G.; Li, G. A simulation-based study of dispatching rules in a dynamic job shop scheduling problem with batch release and extended technical precedence constraints. Eur. J. Oper. Res. 2017, 257, 13–24. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y. Data-driven Job Shop production scheduling knowledge mining and optimization. Comput. Eng. Appl. 2018, 54, 264–270. [Google Scholar]
- Bergstra, J.; Komer, B.; Eliasmith, C.; Yamins, D.; Cox, D.D. Hyperopt: A python library for model selection and hyperparameter optimization. Comput. Sci. Discov. 2015, 8, 014008. [Google Scholar] [CrossRef]
- De Ville, B. Decision trees. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 448–455. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Wang, L. Job-Shop Scheduling and Its Genetic Algorithm; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]






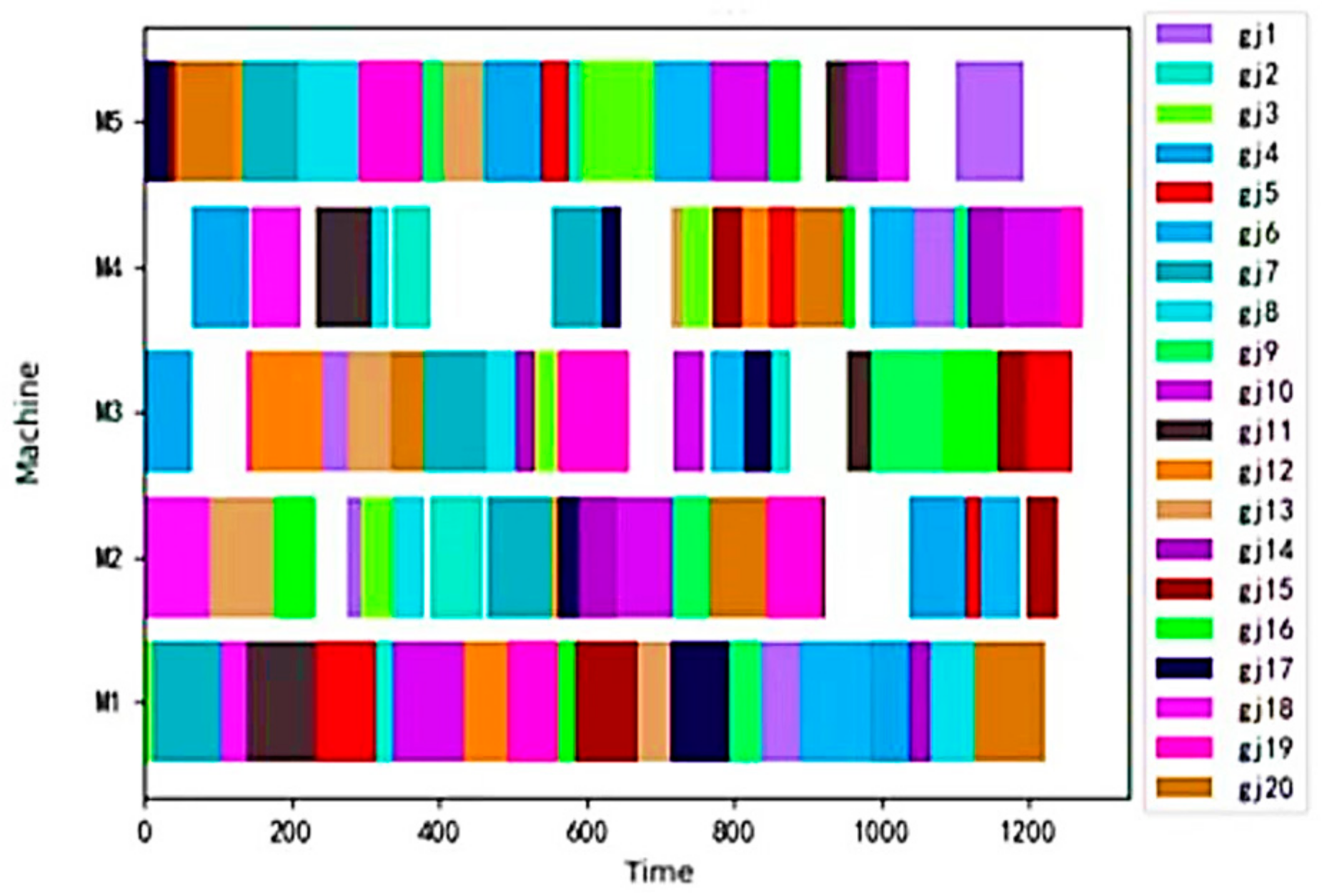
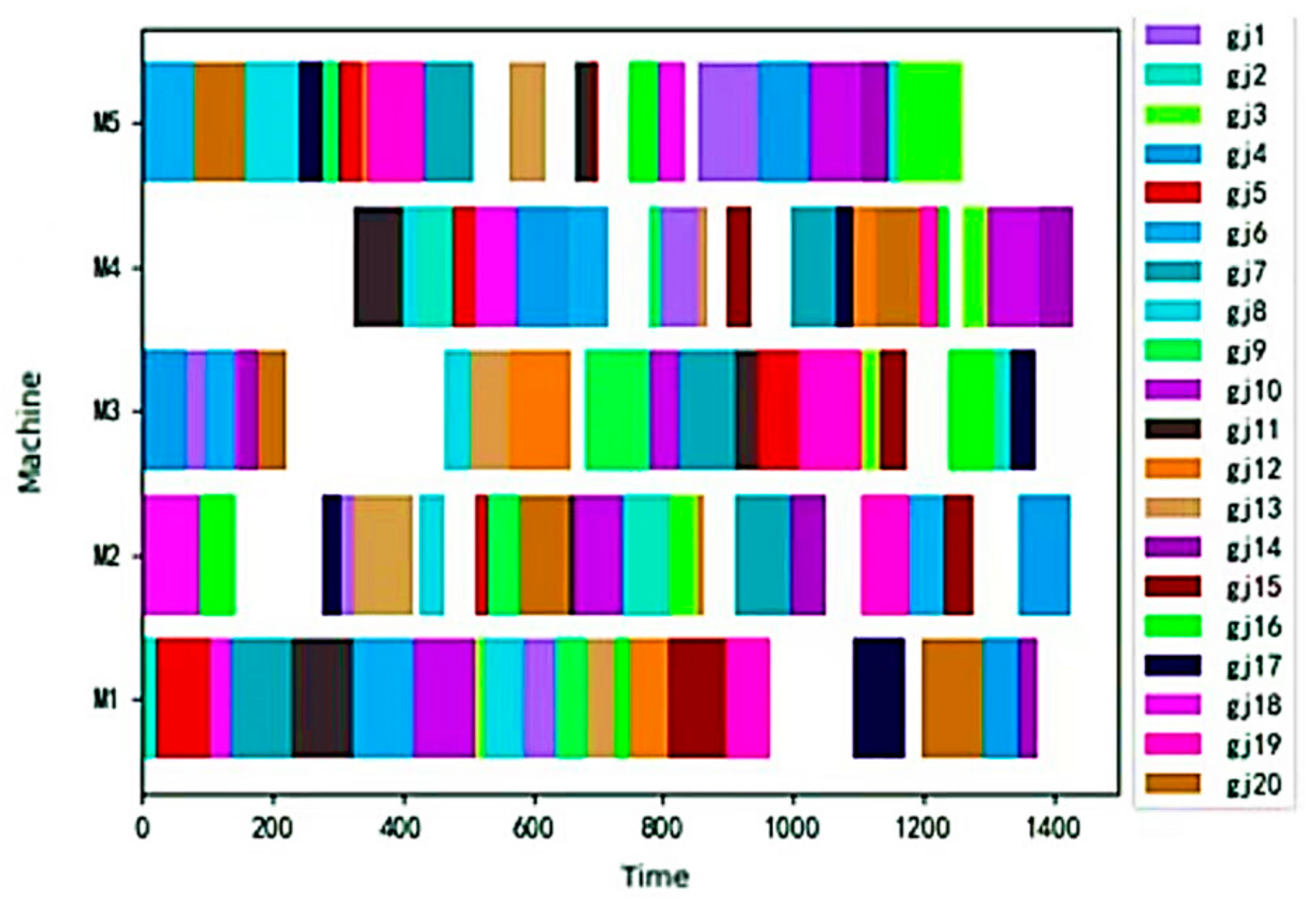






| LA01 (10 × 5) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Work Pieces | Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | |||||
| Machine | Work Time | Machine | Work Time | Machine | Work Time | Machine | Work Time | Machine | Work Time | |
| 1 | 2 | 21 | 1 | 53 | 5 | 95 | 4 | 55 | 3 | 34 |
| 2 | 1 | 21 | 4 | 52 | 5 | 16 | 3 | 26 | 2 | 71 |
| 3 | 4 | 39 | 5 | 98 | 2 | 42 | 3 | 31 | 1 | 12 |
| 4 | 2 | 77 | 1 | 55 | 5 | 79 | 3 | 66 | 4 | 77 |
| 5 | 1 | 83 | 4 | 34 | 3 | 64 | 2 | 19 | 5 | 37 |
| 6 | 3 | 54 | 3 | 43 | 5 | 79 | 1 | 92 | 4 | 62 |
| 7 | 4 | 69 | 5 | 77 | 2 | 87 | 3 | 87 | 1 | 93 |
| 8 | 3 | 38 | 1 | 60 | 2 | 41 | 4 | 24 | 5 | 83 |
| 9 | 4 | 17 | 2 | 49 | 5 | 25 | 1 | 44 | 3 | 98 |
| 10 | 5 | 77 | 4 | 79 | 3 | 43 | 2 | 75 | 1 | 96 |
| Rule Name | Rule Description |
|---|---|
| FIFO (First in First out) | Preferentially process the workpiece that enters the processing equipment first. |
| LILO (Last in First out) | Give priority to the workpiece entering the processing equipment after processing. |
| SPT (Shortest Processing Time) | Priority is given to the workpiece with the shortest processing time. |
| LPT (Longest Processing Time) | Priority is given to the workpiece with the longest processing time. |
| EDD (Earliest Due Date) | Priority is given to the workpiece with the earliest delivery date. |
| MST (Minimum Slack Time) | The workpiece with minimum relaxation time is processed preferentially. |
| LWR (Longest Work Remaining) | Priority is given to the workpiece with the longest total remaining processing time. |
| SWR (Shortest Work Remaining) | Priority is given to the workpiece with the shortest total remaining processing time. |
| MOR (Most Operations Remaining) | The workpiece with the most total remaining operands is processed first. |
| LOR (Least Operations Remaining) | Preferentially process the workpiece with the fewest total remaining operands. |
| Attributes | Attribute Values | Category Values |
|---|---|---|
| PT | L (Low value) | 0 (Priority execution) |
| RPT | H (High value) | 1 (Priority execution) |
| ROPN | L (Low value) | 0 (Priority execution) |
| PT | RPT | ROPN | Sorting Result | |
|---|---|---|---|---|
| O11 | 21 | 237 | 4 | 1 |
| O41 | 77 | 277 | 4 | 0 |
| Job_Pt_Longer | Job_Rpt_Longer | Job_Ropn_More | Sorting Result | ||
|---|---|---|---|---|---|
| O11 | O41 | 0 | 0 | 0 | 1 |
| Job_Pt_Longer | Job_Rpt_Longer | Job_Ropn_More | Sorting Result | ||
| O21 | O51 | 0 | 1 | 0 | 1 |
| O21 | O41 | 0 | 0 | 0 | 1 |
| O61 | O41 | 0 | 0 | 0 | 0 |
| O31 | O71 | 0 | 0 | 0 | 1 |
| O71 | O91 | 1 | 1 | 0 | 0 |
| O72 | O93 | 1 | 1 | 1 | 1 |
| O14 | O52 | 1 | 0 | 0 | 1 |
| O103 | O24 | 0 | 1 | 1 | 1 |
| O11 | O41 | 0 | 0 | 0 | 1 |
| O43 | O23 | 1 | 1 | 0 | 0 |
| O32 | O63 | 1 | 1 | 1 | 0 |
| O54 | O83 | 0 | 0 | 0 | 1 |
| O32 | O55 | 1 | 1 | 1 | 1 |
| O71 | O102 | 0 | 0 | 1 | 0 |
| O63 | O72 | 1 | 0 | 0 | 0 |
| O64 | O94 | 1 | 1 | 0 | 1 |
| O51 | O82 | 1 | 1 | 1 | 1 |
| O51 | O41 | 0 | 1 | 0 | 0 |
| O31 | O91 | 0 | 0 | 0 | 1 |
| O21 | O61 | 1 | 0 | 0 | 1 |
| O72 | O32 | 1 | 1 | 0 | 1 |
| Parameters | Meaning | Parameter Values |
|---|---|---|
| max_depth | The maximum depth of the decision tree | 3 |
| min_samples_split | Minimum number of samples required for internal node repartition | 2 |
| min_samples_leaf | Minimum sample number of leaf nodes | 2 |
| max_leaf_nodes | Maximum number of leaf nodes | 4 |
| Parameters | Meaning | Parameter Values |
|---|---|---|
| n_estimator | Number of weak classifiers | 100 |
| learning_rate | Learning rate | 1.0 |
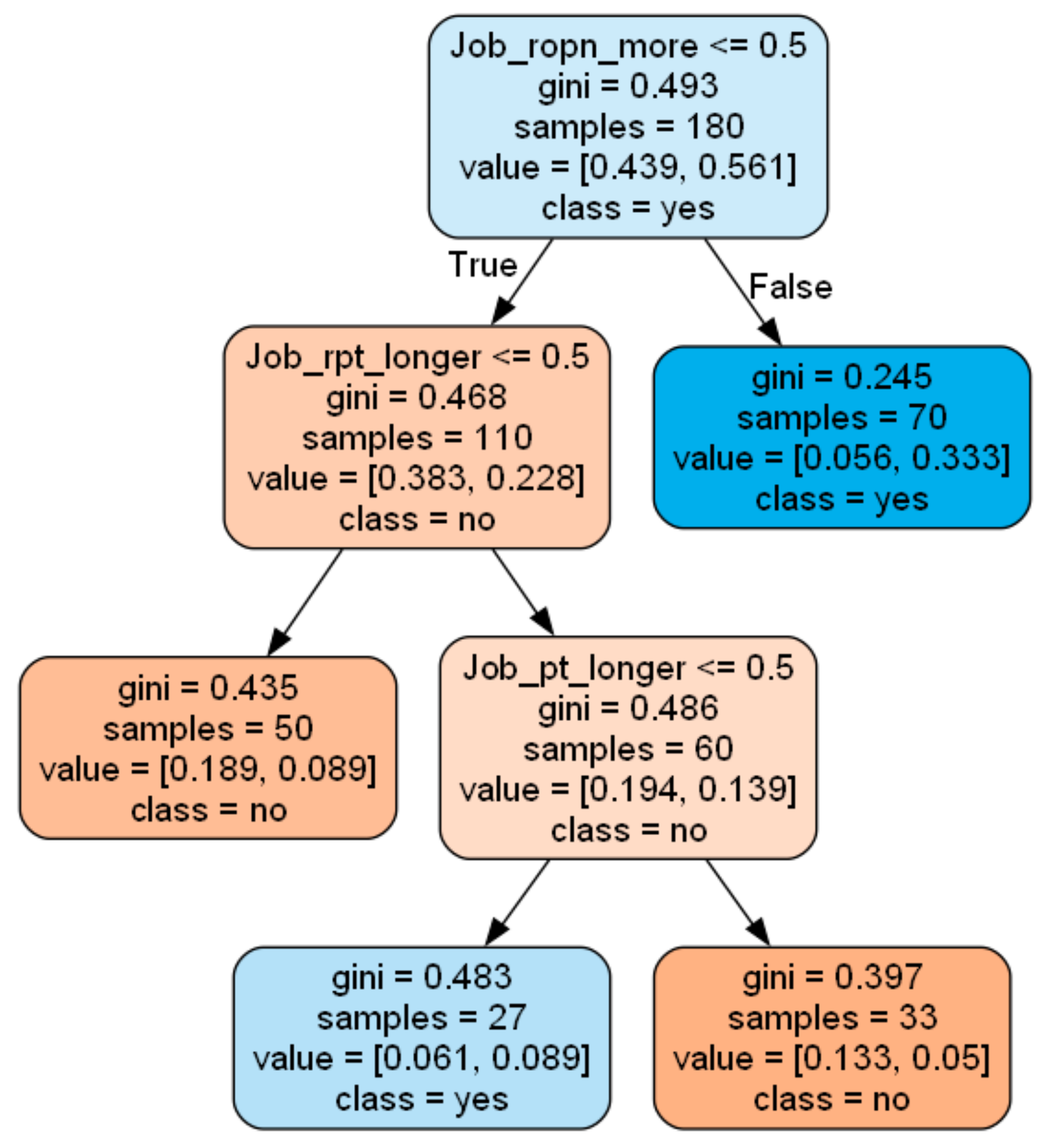
| Tree Rules | Meaning Description | |
|---|---|---|
| Rule 1 | If Job_ropn_more = True Then Job_= yes | If the number of remaining processes of the first process is greater than that of the second process , then the first process is processed first; |
| Rule 2 | If Job_ropn_more = False and Job_rpt_longer = False Then Job_= no | If the number of remaining processes of the first process is less than that of the second process and its remaining processing time is also less than , then the second process is processed preferentially; |
| Rule 3 | If Job_ropn_more = False and Job_rpt_longer = True and Job_pt_longer = True Then Job_= no | If the number of remaining processes of the first process is less than that of the second process and its remaining processing time is more, and the processing time of the first process is more than , then the second process is processed preferentially; |
| Rule 4 | If Job_ropn_more = False and Job_rpt_longer = True and Job_pt_longer = False Then Job_= yes | If the number of remaining processes of the first process is less thanthat of the second process and its remaining processing time is more than that of the second process , and the processing time of the first process is less than that of the first process , then the first process is processed first. |
| LA11 (20 × 5) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Work Pieces | Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | |||||
| Machine | Work Time | Machine | Work Time | Machine | Work Time | Machine | Work Time | Machine | Work Time | |
| 1 | 3 | 34 | 2 | 21 | 1 | 53 | 4 | 55 | 5 | 95 |
| 2 | 1 | 21 | 4 | 52 | 2 | 71 | 5 | 16 | 3 | 26 |
| 3 | 1 | 12 | 2 | 42 | 3 | 31 | 5 | 98 | 4 | 39 |
| 4 | 3 | 66 | 4 | 77 | 5 | 79 | 1 | 55 | 2 | 77 |
| 5 | 1 | 83 | 5 | 37 | 4 | 34 | 2 | 19 | 3 | 64 |
| 6 | 5 | 79 | 3 | 43 | 1 | 92 | 4 | 62 | 2 | 54 |
| 7 | 1 | 93 | 5 | 77 | 3 | 87 | 2 | 87 | 4 | 69 |
| 8 | 5 | 83 | 4 | 24 | 2 | 41 | 3 | 38 | 1 | 60 |
| 9 | 5 | 25 | 2 | 49 | 1 | 44 | 3 | 98 | 4 | 17 |
| 10 | 1 | 96 | 2 | 75 | 3 | 43 | 5 | 77 | 4 | 79 |
| 11 | 1 | 95 | 4 | 76 | 2 | 7 | 5 | 28 | 3 | 35 |
| 12 | 5 | 10 | 3 | 95 | 1 | 61 | 2 | 9 | 4 | 35 |
| 13 | 2 | 91 | 3 | 59 | 5 | 59 | 1 | 46 | 4 | 16 |
| 14 | 3 | 27 | 2 | 52 | 5 | 43 | 1 | 28 | 4 | 50 |
| 15 | 5 | 9 | 1 | 87 | 4 | 41 | 3 | 39 | 2 | 45 |
| 16 | 2 | 54 | 1 | 20 | 5 | 43 | 4 | 14 | 3 | 71 |
| 17 | 5 | 33 | 2 | 28 | 4 | 26 | 1 | 78 | 3 | 37 |
| 18 | 2 | 89 | 1 | 33 | 3 | 8 | 4 | 66 | 5 | 42 |
| 19 | 5 | 84 | 1 | 69 | 3 | 94 | 2 | 74 | 4 | 27 |
| 20 | 5 | 81 | 3 | 45 | 2 | 78 | 4 | 69 | 1 | 96 |
| Instance | LA17 | LA22 | LA26 | LA33 | LA36 | |
|---|---|---|---|---|---|---|
| n × m | 10 × 10 | 15 × 10 | 20 × 10 | 30 × 10 | 15 × 15 | |
| IBWO-AdaBoost | Avg | 791.7 | 936.3 | 1266.8 | 1755.1 | 1321.1 |
| Best | 784.0 | 929.0 | 1239.0 | 1733.0 | 1296.0 | |
| Std | 9.2 | 8.3 | 37.0 | 20.1 | 19.3 | |
| IBWO-DT | Avg | 813.8 | 982.8 | 1309.6 | 1787.8 | 1369.7 |
| Best | 810.0 | 944.0 | 1289.0 | 1755.0 | 1357.0 | |
| Std | 4.7 | 35.3 | 28.1 | 31.7 | 14.7 | |
| IBWO-RF | Avg | 809.0 | 990.9 | 1285.4 | 1788.0 | 1343.7 |
| Best | 793.0 | 969.0 | 1268.0 | 1779.0 | 1321.0 | |
| Std | 16.1 | 20.5 | 21.3 | 11.8 | 27.4 | |
| IBWO | Avg | 885.1 | 1180.2 | 1379.3 | 1944.1 | 1471.2 |
| Best | 854.0 | 1168.0 | 1364.0 | 1938.0 | 1456.0 | |
| Std | 22.4 | 18.0 | 14.4 | 8.0 | 16.9 | |
| BWO | Avg | 1004.3 | 1327.0 | 1703.2 | 2141.2 | 1678.4 |
| Best | 983.0 | 1320.0 | 1693.0 | 2120.0 | 1649.0 | |
| Std | 22.7 | 6.2 | 12.7 | 26.7 | 28.4 |
| Instance | LA01 | LA02 | LA03 | LA04 | LA05 | LA06 | LA07 | LA08 | |
|---|---|---|---|---|---|---|---|---|---|
| n × m | 10 × 5 | 10 × 5 | 10 × 5 | 10 × 5 | 10 × 5 | 15 × 5 | 15 × 5 | 15 × 5 | |
| IBWO-AdaBoost | Avg | 667.1 | 666.2 | 608.7 | 597.9 | 593.0 | 926.0 | 905.9 | 867.2 |
| Best | 666.0 | 655.0 | 597.0 | 591.0 | 593.0 | 926.0 | 890.0 | 863.0 | |
| Std | 2.2 | 11.7 | 14.0 | 6.8 | 0.0 | 0.0 | 14.3 | 5.4 | |
| dev | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | |
| IBWO-DT | Avg | 672.0 | 681.2 | 620.1 | 607.6 | 593.0 | 926.0 | 909.6 | 871.4 |
| Best | 666.0 | 655.0 | 599.0 | 593.0 | 593.0 | 926.0 | 893.0 | 863.0 | |
| Std | 6.0 | 13.6 | 13.6 | 11.9 | 0.0 | 0.0 | 12.4 | 5.5 | |
| dev | 0.0 | 0.0 | 0.3 | 0.5 | 0.0 | 0.0 | 0.3 | 0.0 | |
| IBWO-RF | Avg | 673.4 | 685.9 | 617.4 | 604.6 | 593.0 | 926.0 | 912.5 | 874.8 |
| Best | 666.0 | 655.0 | 598.0 | 593.0 | 593.0 | 926.0 | 890.0 | 863.0 | |
| Std | 8.9 | 26.5 | 14.6 | 10.8 | 0.0 | 0.0 | 12.9 | 13.4 | |
| dev | 0.0 | 0.0 | 0.2 | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | |
| IBWO | Avg | 730.0 | 718.6 | 638.5 | 649.7 | 593.0 | 926.0 | 948.6 | 932.7 |
| Best | 730.0 | 678.0 | 626.0 | 612.0 | 593.0 | 926.0 | 920.0 | 925.0 | |
| Std | 0.0 | 26.5 | 9.0 | 22.7 | 0.0 | 0.0 | 15.8 | 7.3 | |
| dev | 9.6 | 3.5 | 4.9 | 3.7 | 0.0 | 0.0 | 3.4 | 7.2 | |
| BWO | Avg | 766.0 | 806.4 | 733.3 | 727.9 | 681.0 | 1118.0 | 1111.1 | 1054.4 |
| Best | 766.0 | 748.0 | 702.0 | 729.0 | 681.0 | 1118.0 | 1058.0 | 1017.0 | |
| Std | 0.0 | 35.4 | 22.7 | 35.0 | 0.0 | 0.0 | 24.6 | 30.2 | |
| dev | 15.0 | 14.2 | 17.6 | 23.6 | 14.8 | 20.7 | 18.9 | 17.8 |
| Instance | LA09 | LA10 | LA11 | LA12 | LA13 | LA14 | LA15 | LA16 | |
|---|---|---|---|---|---|---|---|---|---|
| n × m | 15 × 5 | 15 × 5 | 20 × 5 | 20 × 5 | 20 × 5 | 20 × 5 | 20 × 5 | 10 × 10 | |
| IBWO-AdaBoost | Avg | 951.0 | 958.0 | 1227.3 | 1041.2 | 1157.1 | 1292.0 | 1222.8 | 959.3 |
| Best | 951.0 | 958.0 | 1222.0 | 1039.0 | 1150.0 | 1292.0 | 1212.0 | 945.0 | |
| Std | 0.0 | 0.0 | 9.9 | 5.6 | 11.2 | 0.0 | 9.2 | 16.1 | |
| dev | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 | |
| IBWO-DT | Avg | 951.0 | 958.0 | 1225.8 | 1049.4 | 1156.3 | 1292.0 | 1234.6 | 972.8 |
| Best | 951.0 | 958.0 | 1222.0 | 1039.0 | 1150.0 | 1292.0 | 1216.0 | 954.0 | |
| Std | 0.0 | 0.0 | 5.8 | 17.5 | 10.7 | 0.0 | 13.0 | 20.1 | |
| dev | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.8 | 1.0 | |
| IBWO-RF | Avg | 951.0 | 958.0 | 1226.4 | 1044.1 | 1169.1 | 1292.0 | 1228.4 | 959.7 |
| Best | 951.0 | 958.0 | 1222.0 | 1039.0 | 1150.0 | 1292.0 | 1212.0 | 947.0 | |
| Std | 0.0 | 0.0 | 8.9 | 10.1 | 19.0 | 0.0 | 10.1 | 11.2 | |
| dev | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 0.2 | |
| IBWO | Avg | 961.0 | 958.0 | 1273.0 | 1061.0 | 1259.0 | 1316.0 | 1295.2 | 1016.3 |
| Best | 961.0 | 958.0 | 1273.0 | 1061.0 | 1259.0 | 1316.0 | 1281.0 | 994.0 | |
| Std | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9.9 | 19.5 | |
| dev | 1.1 | 0.0 | 4.2 | 2.1 | 10.4 | 1.9 | 6.1 | 5.2 | |
| BWO | Avg | 1228.0 | 1031.0 | 1428.0 | 1228.0 | 1386.0 | 1432.0 | 1485.2 | 1216.9 |
| Best | 1228.0 | 1031.0 | 1428.0 | 1228.0 | 1386.0 | 1432.0 | 1432.0 | 1183.0 | |
| Std | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 25.6 | 26.5 | |
| dev | 29.1 | 7.6 | 16.9 | 18.2 | 20.5 | 10.8 | 18.6 | 25.2 |
| Instance | LA17 | LA18 | LA19 | LA20 | LA21 | LA22 | LA23 | LA24 | |
|---|---|---|---|---|---|---|---|---|---|
| n × m | 10 × 10 | 10 × 10 | 10 × 10 | 10 × 10 | 15 × 10 | 15 × 10 | 15 × 10 | 15 × 10 | |
| IBWO-AdaBoost | Avg | 791.7 | 873.6 | 857.6 | 928.8 | 1095.1 | 936.3 | 1071.3 | 978.6 |
| Best | 784.0 | 852.0 | 843.0 | 907.0 | 1056.0 | 929.0 | 1038.0 | 940.0 | |
| Std | 9.2 | 15.3 | 12.9 | 23.5 | 31.7 | 8.3 | 17.3 | 22.7 | |
| dev | 0.0 | 0.5 | 0.1 | 0.6 | 1.0 | 0.2 | 0.6 | 0.5 | |
| IBWO-DT | Avg | 813.8 | 870.9 | 853.8 | 928.8 | 1102.8 | 982.8 | 1077.6 | 968.4 |
| Best | 810.0 | 852.0 | 843.0 | 910.0 | 1082.0 | 944.0 | 1061.0 | 938.0 | |
| Std | 4.7 | 13.2 | 10.8 | 13.7 | 24.1 | 15.3 | 13.5 | 15.2 | |
| dev | 3.3 | 0.5 | 0.1 | 0.9 | 3.4 | 1.8 | 2.8 | 0.3 | |
| IBWO-RF | Avg | 809.0 | 881.3 | 857.1 | 937.0 | 1093.3 | 990.9 | 1055.6 | 986.2 |
| Best | 793.0 | 855.0 | 844.0 | 905.0 | 1063.0 | 969.0 | 1034.0 | 949.0 | |
| Std | 16.1 | 15.4 | 11.1 | 27.7 | 33.0 | 19.5 | 15.4 | 20.9 | |
| dev | 1.2 | 0.8 | 0.2 | 0.3 | 1.6 | 4.5 | 0.2 | 1.5 | |
| IBWO | Avg | 885.1 | 949.7 | 978.3 | 1135.8 | 1219.1 | 1180.2 | 1191.5 | 1126.0 |
| Best | 854.0 | 932.0 | 927.0 | 1100.0 | 1196.0 | 1168.0 | 1155.0 | 1094.0 | |
| Std | 22.4 | 15.9 | 36.9 | 27.6 | 12.7 | 18.0 | 14.7 | 22.7 | |
| dev | 8.9 | 9.9 | 10.1 | 22.0 | 14.3 | 26.0 | 11.9 | 17.0 | |
| BWO | Avg | 1004.3 | 1136.0 | 1021.2 | 1295.1 | 1369.9 | 1327.0 | 1353.1 | 1339.0 |
| Best | 983.0 | 1114.0 | 1115.0 | 1263.0 | 1346.0 | 1320.0 | 1324.0 | 1318.0 | |
| Std | 22.7 | 15.0 | 34.3 | 20.0 | 10.6 | 6.2 | 14.5 | 16.8 | |
| dev | 25.4 | 31.4 | 32.4 | 40.0 | 28.7 | 42.4 | 28.3 | 41.0 |
| Instance | LA25 | LA26 | LA27 | LA28 | LA29 | LA30 | LA31 | LA32 | |
|---|---|---|---|---|---|---|---|---|---|
| n × m | 15 × 10 | 20 × 10 | 20 × 10 | 20 × 10 | 20 × 10 | 20 × 10 | 30 × 10 | 30 × 10 | |
| IBWO-AdaBoost | Avg | 998.8 | 1266.8 | 1271.6 | 1258.8 | 1198.0 | 1386.9 | 1848.0 | 1919.6 |
| Best | 985.0 | 1239.0 | 1242.0 | 1235.0 | 1163.0 | 1373.0 | 1813.0 | 1883.0 | |
| Std | 13.5 | 37.0 | 29.8 | 17.0 | 30.9 | 12.0 | 25.9 | 35.4 | |
| dev | 0.8 | 1.7 | 0.6 | 1.6 | 1.0 | 1.3 | 1.6 | 1.8 | |
| IBWO-DT | Avg | 1024.3 | 1309.6 | 1288.4 | 1299.8 | 1219.18 | 1411.4 | 1878.2 | 1940.3 |
| Best | 993.0 | 1289.0 | 1258.0 | 1261.0 | 1169.0 | 1388.0 | 1846.0 | 1887.0 | |
| Std | 26.9 | 28.1 | 19.8 | 40.8 | 47.4 | 25.9 | 32.7 | 30.9 | |
| dev | 1.6 | 5.8 | 1.9 | 3.7 | 1.5 | 2.4 | 3.5 | 2.0 | |
| IBWO-RF | Avg | 1016.4 | 1285.4 | 1278.5 | 1268.9 | 1213.64 | 1406.8 | 1865.1 | 1912.6 |
| Best | 989.0 | 1268.0 | 1241.0 | 1240.0 | 1163.0 | 1381.0 | 1830.0 | 1870.0 | |
| Std | 27.8 | 21.3 | 34.2 | 27.3 | 44.8 | 30.9 | 31.0 | 41.3 | |
| dev | 1.2 | 4.1 | 0.5 | 2.0 | 1.0 | 1.9 | 2.6 | 1.1 | |
| IBWO | Avg | 1092.0 | 1379.3 | 1446.7 | 1342.4 | 1325.45 | 1471.4 | 1899.6 | 2133.0 |
| Best | 1025.0 | 1364.0 | 1428.0 | 1320.0 | 1284.0 | 1449.0 | 1878.0 | 2082.0 | |
| Std | 44.0 | 14.4 | 19.0 | 18.9 | 24.8 | 13.2 | 22.5 | 26.6 | |
| dev | 4.9 | 12.0 | 15.6 | 8.6 | 5.6 | 6.9 | 5.3 | 12.5 | |
| BWO | Avg | 1309.3 | 1703.2 | 1603.8 | 1590.9 | 1442.73 | 1662.7 | 2176.7 | 2318.3 |
| Best | 1297.0 | 1693.0 | 1593.0 | 1549.0 | 1380.0 | 1629.0 | 2140.0 | 2290.0 | |
| Std | 10.7 | 12.7 | 16.3 | 23.6 | 34.6 | 22.6 | 32.4 | 24.8 | |
| dev | 32.8 | 39.0 | 29.0 | 27.4 | 13.5 | 20.2 | 20.0 | 23.8 |
| Instance | LA33 | LA34 | LA35 | LA36 | LA37 | LA38 | LA39 | LA40 | |
|---|---|---|---|---|---|---|---|---|---|
| n × m | 30 × 10 | 30 × 10 | 30 × 10 | 15 × 15 | 15 × 15 | 15 × 15 | 15 × 15 | 15 × 15 | |
| IBWO-AdaBoost | Avg | 1755.1 | 1778.5 | 1952.9 | 1321.1 | 1440.2 | 1252.9 | 1267.5 | 1251.6 |
| Best | 1733.0 | 1751.0 | 1908.0 | 1296.0 | 1417.0 | 1223.0 | 1247.0 | 1238.0 | |
| Std | 20.1 | 20.9 | 31.8 | 19.3 | 18.0 | 19.2 | 18.0 | 15.0 | |
| dev | 0.8 | 1.7 | 1.1 | 2.2 | 1.4 | 2.3 | 1.1 | 1.3 | |
| IBWO-DT | Avg | 1787.8 | 1805.2 | 1996.5 | 1369.7 | 1482.7 | 1277.4 | 1269.8 | 1284.1 |
| Best | 1755.0 | 1781.0 | 1926.0 | 1357.0 | 1455.0 | 1257.0 | 1267.0 | 1255.0 | |
| Std | 31.7 | 23.4 | 49.3 | 14.7 | 17.1 | 15.8 | 27.5 | 19.5 | |
| dev | 2.09 | 3.49 | 2.01 | 7.02 | 4.15 | 5.10 | 2.76 | 2.70 | |
| IBWO-RF | Avg | 1788.0 | 1792.5 | 1951.2 | 1343.7 | 1465.0 | 1274.9 | 1273.1 | 1275.1 |
| Best | 1779.0 | 1751.0 | 1904.0 | 1321.0 | 1433.0 | 1245.0 | 1258.0 | 1248.0 | |
| Std | 11.8 | 25.6 | 29.7 | 27.4 | 14.1 | 23.0 | 13.3 | 28.1 | |
| dev | 3.5 | 1.7 | 0.9 | 4.2 | 2.6 | 4.1 | 2.0 | 2.1 | |
| IBWO | Avg | 1944.1 | 1965.7 | 2056.7 | 1471.2 | 1541.6 | 1476.9 | 1431.2 | 1390.0 |
| Best | 1938.0 | 1934.0 | 2028.0 | 1456.0 | 1520.0 | 1440.0 | 1380.0 | 1362.0 | |
| Std | 8.0 | 21.3 | 35.1 | 16.9 | 19.1 | 26.6 | 32.1 | 24.6 | |
| dev | 12.7 | 12.4 | 7.4 | 14.8 | 8.8 | 20.4 | 11.9 | 11.5 | |
| BWO | Avg | 2141.2 | 2154.8 | 2295.3 | 1678.4 | 1808.7 | 1657.0 | 1664.4 | 1597.1 |
| Best | 2120.0 | 2100.0 | 2252.0 | 1649.0 | 1786.0 | 1641.0 | 1626.0 | 1556.0 | |
| Std | 26.7 | 30.7 | 31.9 | 28.4 | 17.0 | 13.0 | 26.4 | 32.7 | |
| dev | 23.3 | 22.0 | 19.3 | 30.1 | 27.9 | 37.2 | 31.9 | 27.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Jin, X.; Wang, Y. Evolving Dispatching Rules in Improved BWO Heuristic Algorithm for Job-Shop Scheduling. Electronics 2024, 13, 2635. https://doi.org/10.3390/electronics13132635
Zhang Z, Jin X, Wang Y. Evolving Dispatching Rules in Improved BWO Heuristic Algorithm for Job-Shop Scheduling. Electronics. 2024; 13(13):2635. https://doi.org/10.3390/electronics13132635
Chicago/Turabian StyleZhang, Zhen, Xin Jin, and Yue Wang. 2024. "Evolving Dispatching Rules in Improved BWO Heuristic Algorithm for Job-Shop Scheduling" Electronics 13, no. 13: 2635. https://doi.org/10.3390/electronics13132635
APA StyleZhang, Z., Jin, X., & Wang, Y. (2024). Evolving Dispatching Rules in Improved BWO Heuristic Algorithm for Job-Shop Scheduling. Electronics, 13(13), 2635. https://doi.org/10.3390/electronics13132635







