A Compact, Low-Power, and Low-Jitter Fractional-N Phase-Locked Loop with a Single-Ended Ring Voltage-Controlled Oscillator in a 12 nm CMOS FinFET
Abstract
:1. Introduction
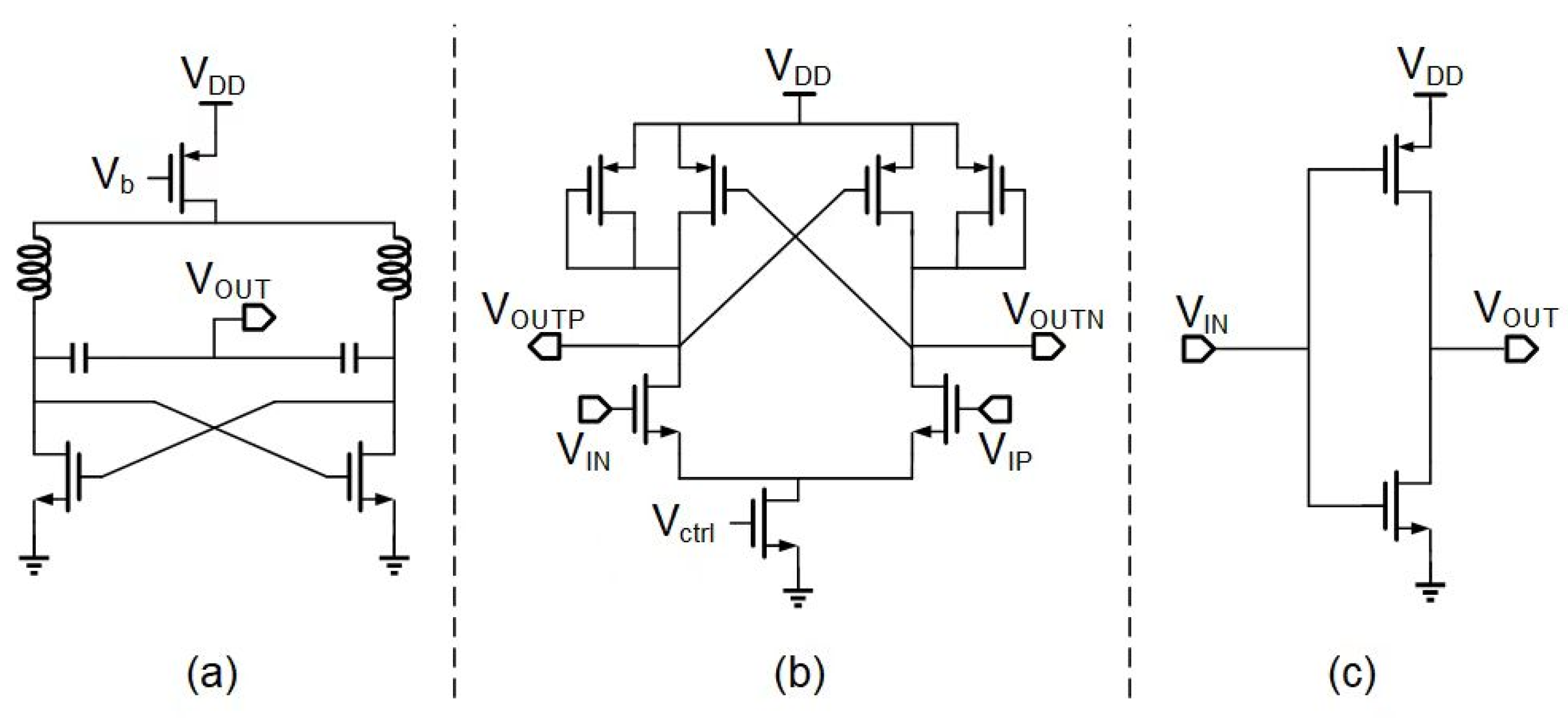
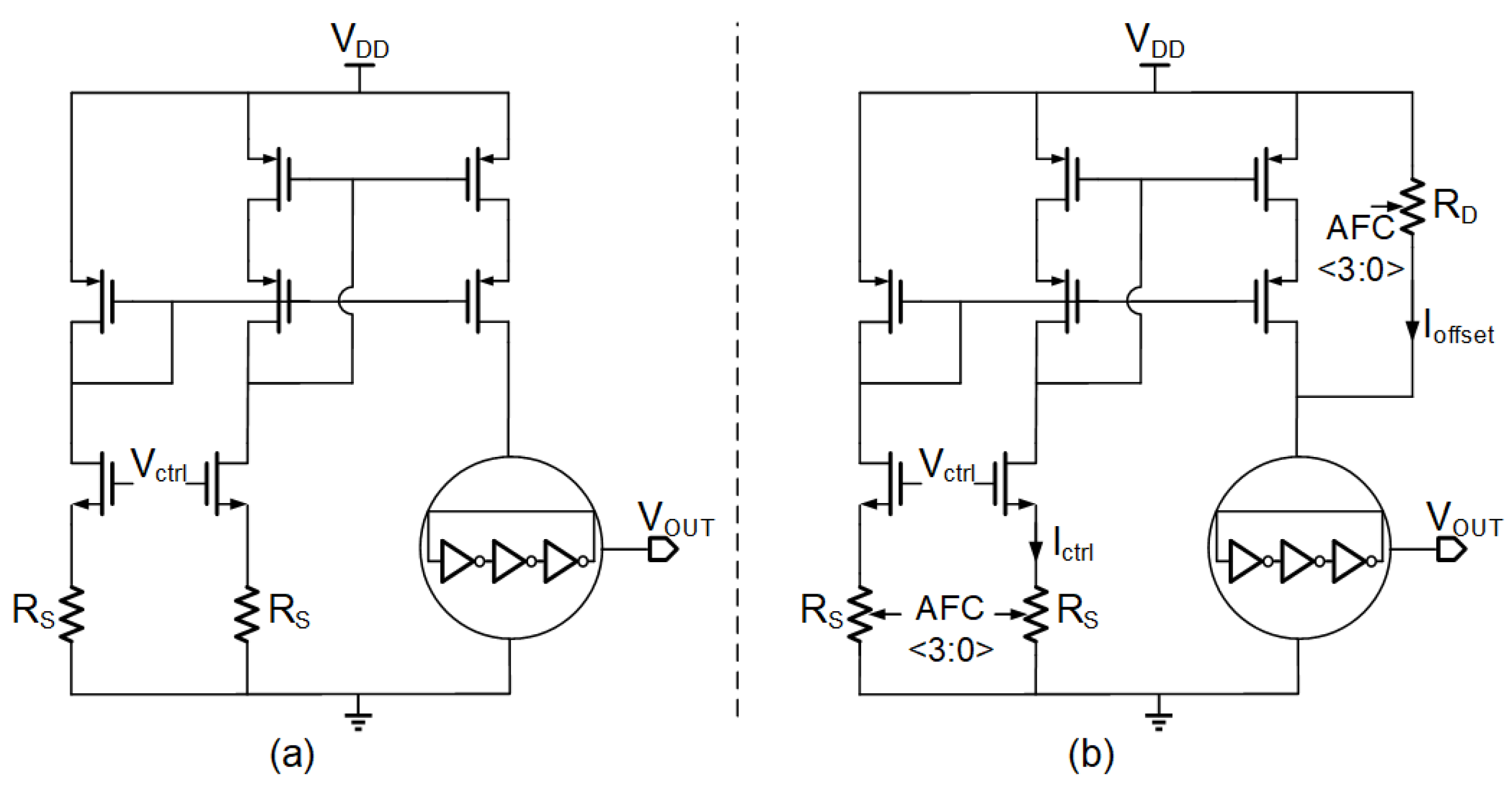
2. The Design Scheme of the Proposed Ring-VCO
3. The Structure of the Proposed PLL
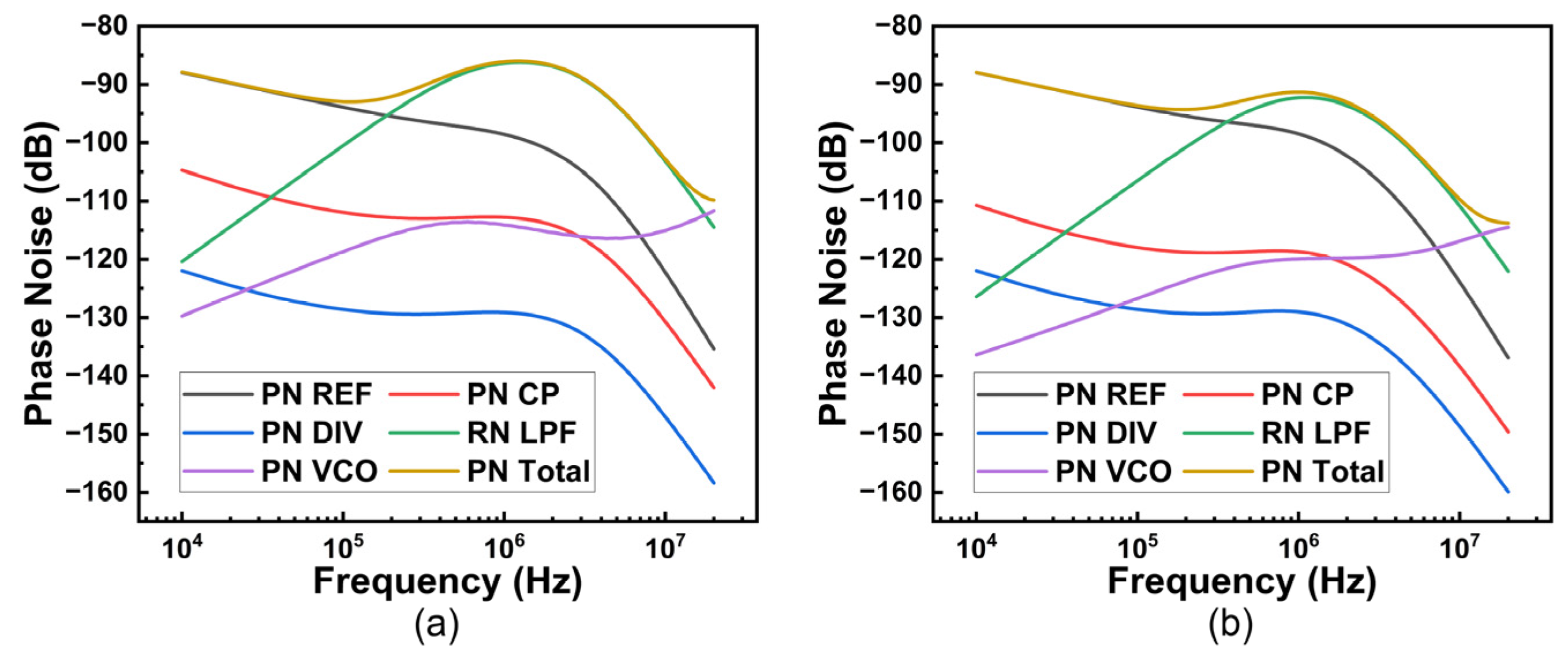
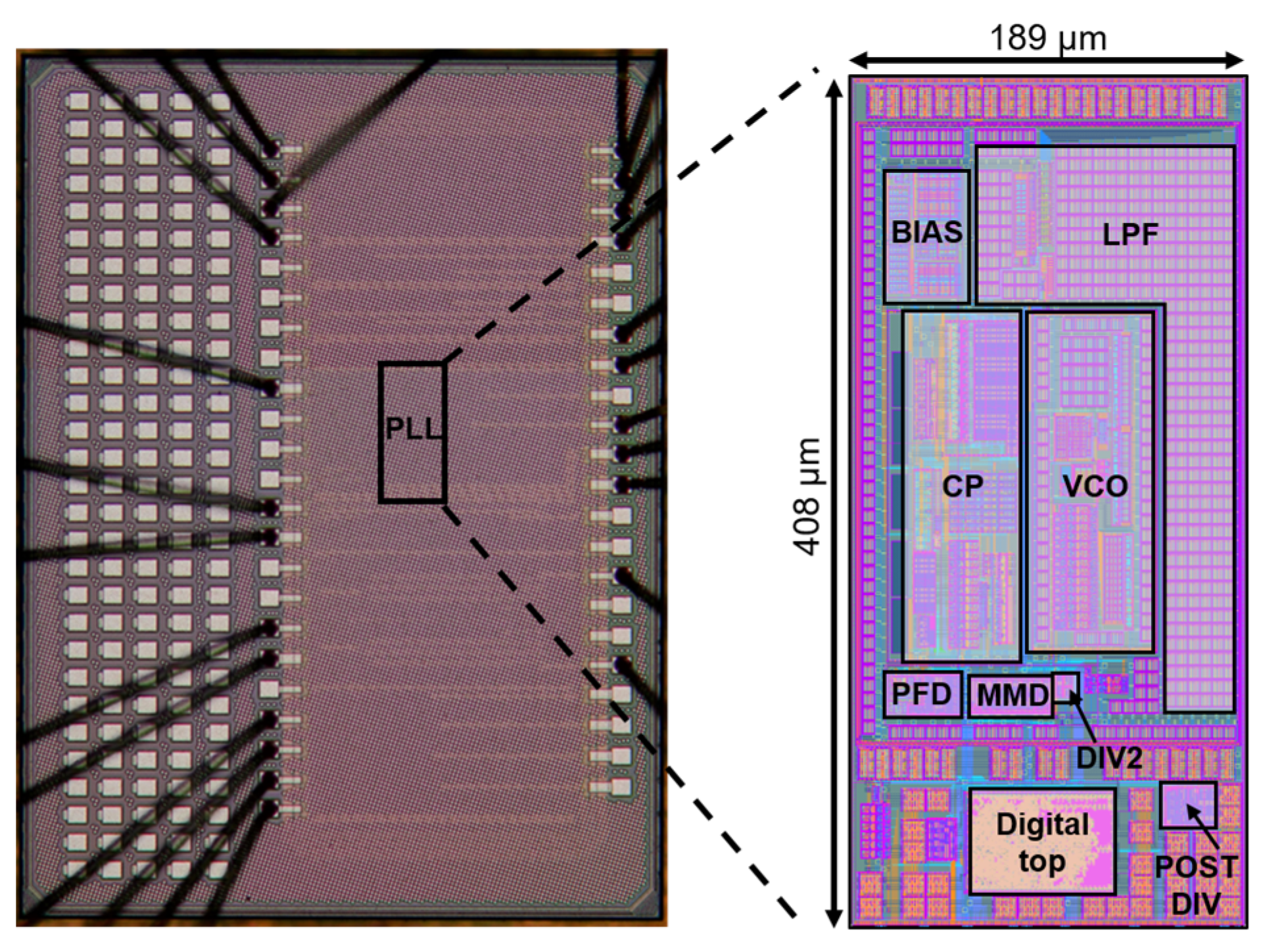
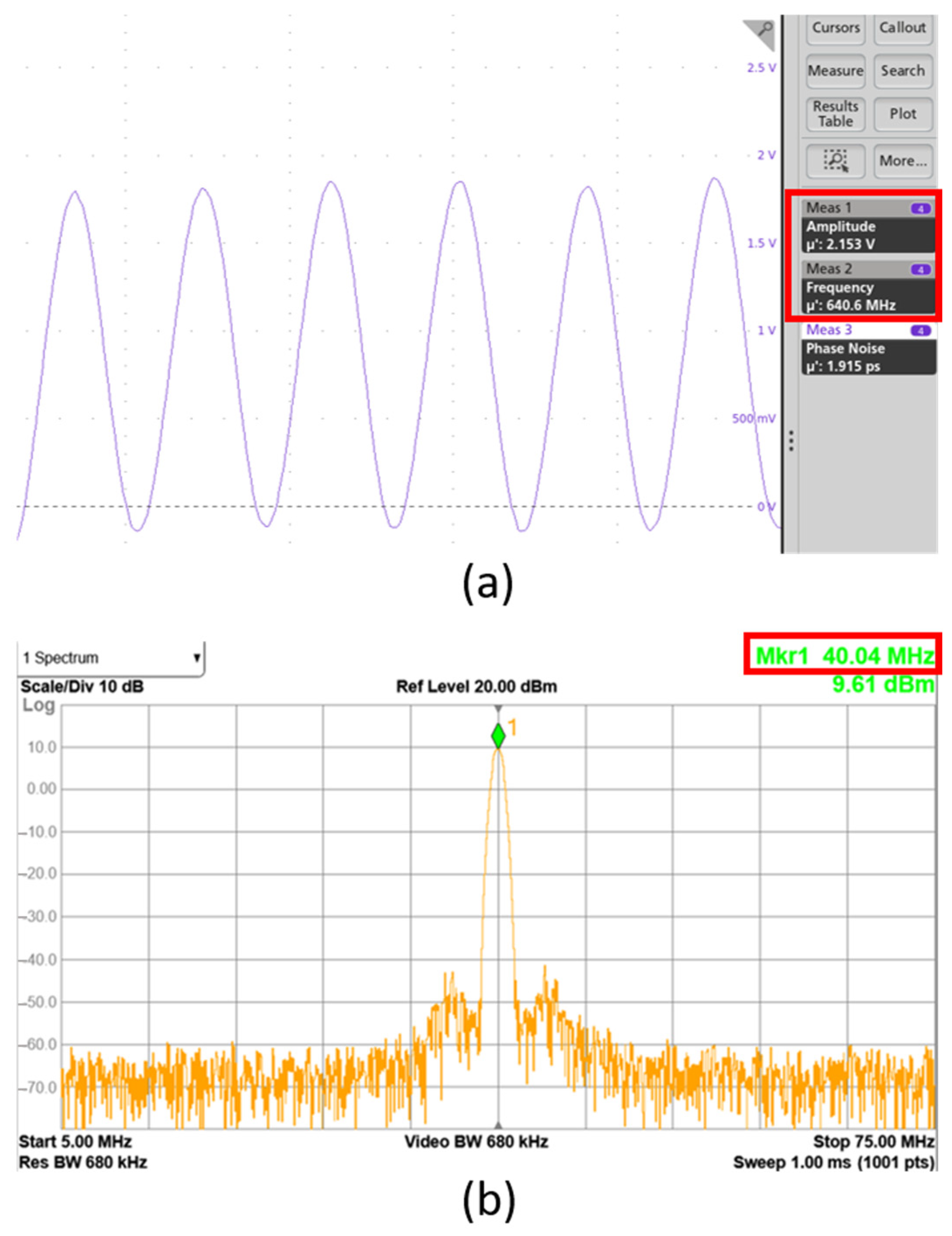
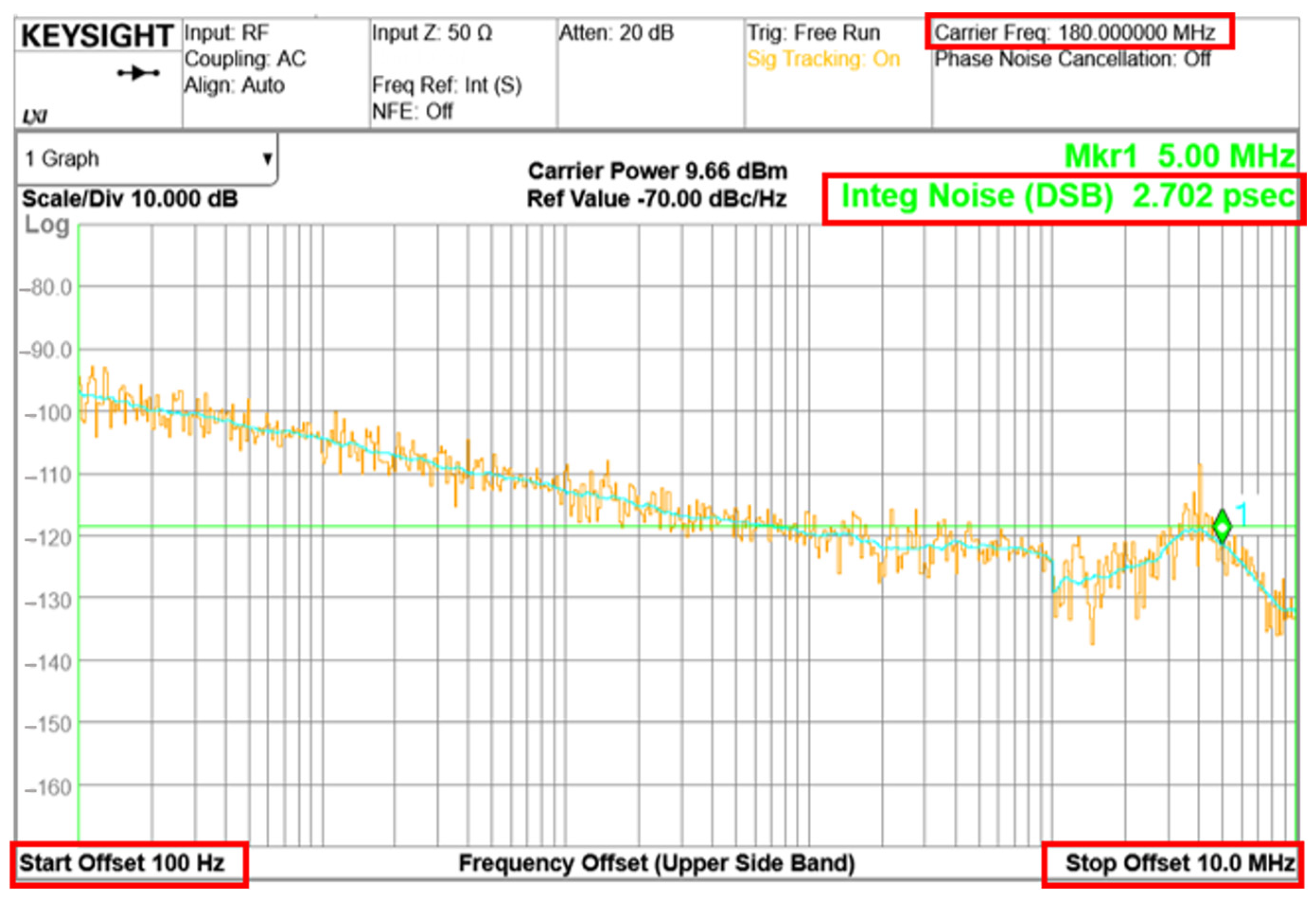
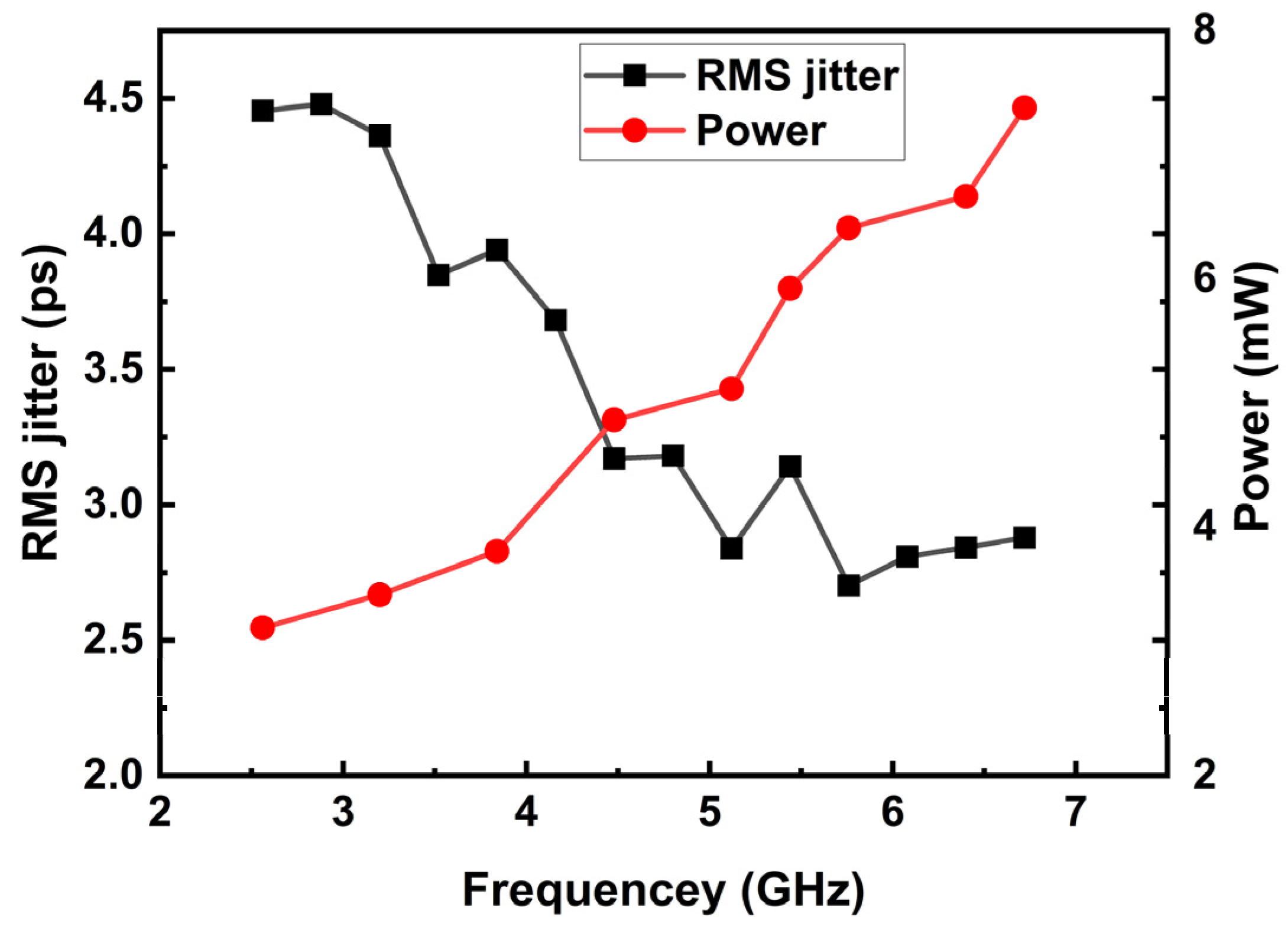
4. Test Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Herzel, F.; Razavi, B. A study of oscillator jitter due to supply and substrate noise. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1999, 46, 56–62. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative performance evaluation of orthogonal-signal-generators-based single-phase PLL algorithms—A survey. IEEE Trans. Power Electron. 2015, 31, 3932–3944. [Google Scholar] [CrossRef]
- Fahim, A.M.; Elmasry, M.I. A fast lock digital phase-locked-loop architecture for wireless applications. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2003, 50, 63–72. [Google Scholar] [CrossRef]
- Liu, A.; Huang, Z.; Li, M.; Wan, Y.; Li, W.; Han, T.X.; Liu, C.; Du, R.; Tan, D.K.P.; Lu, J. A survey on fundamental limits of integrated sensing and communication. IEEE Commun. Surv. Tutor. 2022, 24, 994–1034. [Google Scholar] [CrossRef]
- Chillara, V.K.; Liu, Y.-H.; Wang, B.; Ba, A.; Vidojkovic, M.; Philips, K.; de Groot, H.; Staszewski, R.B. 9.8 An 860 μW 2.1-to-2.7 GHz all-digital PLL-based frequency modulator with a DTC-assisted snapshot TDC for WPAN (Bluetooth Smart and ZigBee) applications. In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 172–173. [Google Scholar]
- Staszewski, R.B.; Wallberg, J.L.; Rezeq, S.; Hung, C.-M.; Eliezer, O.E.; Vemulapalli, S.K.; Fernando, C.; Maggio, K.; Staszewski, R.; Barton, N. All-digital PLL and transmitter for mobile phones. IEEE J. Solid-State Circuits 2005, 40, 2469–2482. [Google Scholar] [CrossRef]
- Thamsirianunt, M.; Kwasniewski, T.A. CMOS VCO’s for PLL frequency synthesis in GHz digital mobile radio communications. IEEE J. Solid-State Circuits 1997, 32, 1511–1524. [Google Scholar] [CrossRef]
- Elkholy, A.; Saxena, S.; Nandwana, R.K.; Elshazly, A.; Hanumolu, P.K. A 2.0–5.5 GHz wide bandwidth ring-based digital fractional-N PLL with extended range multi-modulus divider. IEEE J. Solid-State Circuits 2016, 51, 1771–1784. [Google Scholar] [CrossRef]
- Venerus, C.; Galton, I. A TDC-free mostly-digital FDC-PLL frequency synthesizer with a 2.8–3.5 GHz DCO. IEEE J. Solid-State Circuits 2014, 50, 450–463. [Google Scholar] [CrossRef]
- Kwon, K.; Abdelatty, O.A.; Wentzloff, D.D. PLL fractional spur’s impact on FSK spectrum and a synthesizable ADPLL for a Bluetooth transmitter. IEEE J. Solid-State Circuits 2023, 58, 1271–1284. [Google Scholar] [CrossRef]
- Deng, W.; Yang, D.; Ueno, T.; Siriburanon, T.; Kondo, S.; Okada, K.; Matsuzawa, A. A fully synthesizable all-digital PLL with interpolative phase coupled oscillator, current-output DAC, and fine-resolution digital varactor using gated edge injection technique. IEEE J. Solid-State Circuits 2014, 50, 68–80. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.; Qiu, J.; Huang, H.; Sun, Z.; Xu, D.; Zhang, H.; Wang, Y.; Pang, J.; Li, Z. A fully-synthesizable fractional-N injection-locked PLL for digital clocking with triangle/sawtooth spread-spectrum modulation capability in 5-nm CMOS. IEEE Solid-State Circuits Lett. 2020, 3, 34–37. [Google Scholar] [CrossRef]
- Musa, A.; Deng, W.; Siriburanon, T.; Miyahara, M.; Okada, K.; Matsuzawa, A. A compact, low-power and low-jitter dual-loop injection locked PLL using all-digital PVT calibration. IEEE J. Solid-State Circuits 2013, 49, 50–60. [Google Scholar] [CrossRef]
- Wu, W.; Yao, C.-W.; Guo, C.; Chiang, P.-Y.; Chen, L.; Lau, P.-K.; Bai, Z.; Son, S.W.; Cho, T.B. A 14-nm ultra-low jitter fractional-N PLL using a DTC range reduction technique and a reconfigurable dual-core VCO. IEEE J. Solid-State Circuits 2021, 56, 3756–3767. [Google Scholar] [CrossRef]
- Basaligheh, A.; Saffari, P.; Filanovsky, I.M.; Moez, K. A 65–81 GHz CMOS dual-mode VCO using high quality factor transformer-based inductors. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4533–4543. [Google Scholar] [CrossRef]
- Kashani, M.H.; Molavi, R.; Mirabbasi, S. A 2.3-mW 26.3-GHz G(m)-boosted differential colpitts VCO with 20% tuning range in 65-nm CMOS. IEEE Trans. Microw. Theory Tech. 2019, 67, 1556–1565. [Google Scholar] [CrossRef]
- Jo, Y.; Kim, J.; Shin, Y.; Hwang, C.; Park, H.; Choi, J. A 135fs rms-jitter 0.6-to-7.7 GHz LO generator using a single LC-VCO-based subsampling PLL and a ring-oscillator-based sub-integer-N frequency multiplier. In Proceedings of the 2023 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19 February 2023; pp. 1–3. [Google Scholar]
- Ye, S.; Jansson, L.; Galton, I. A multiple-crystal interface PLL with VCO realignment to reduce phase noise. IEEE J. Solid-State Circuits 2002, 37, 1795–1803. [Google Scholar]
- Park, P.; Park, D.; Cho, S. A 2.4 GHz fractional-N frequency synthesizer with high-OSR ΔΣ modulator and nested PLL. IEEE J. Solid-State Circuits 2012, 47, 2433–2443. [Google Scholar] [CrossRef]
- Lee, Y.; Seong, T.; Yoo, S.; Choi, J. A low-jitter and low-reference-spur ring-VCO-based switched-loop filter PLL using a fast phase-error correction technique. IEEE J. Solid-State Circuits 2017, 53, 1192–1202. [Google Scholar] [CrossRef]
- Huang, Z.; Jiang, B.; Li, L.; Luong, H.C. 2.3 A 4.2 µs-settling-time 3rd-order 2.1 GHz phase-noise-rejection PLL using a cascaded time-amplified clock-skew sub-sampling DLL. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 40–41. [Google Scholar]
- Choi, S.; Yoo, S.; Choi, J. 10.7 A 185fsrms-integrated-jitter and −245dB FOM PVT-robust ring-VCO-based injection-locked clock multiplier with a continuous frequency-tracking loop using a replica-delay cell and a dual-edge phase detector. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 194–195. [Google Scholar]
- Yang, S.; Yin, J.; Mak, P.-I.; Martins, R.P. A 0.0056-mm2 −249-dB-FoM all-digital MDLL using a block-sharing offset-free frequency-tracking loop and dual multiplexed-ring VCOs. IEEE J. Solid-State Circuits 2018, 54, 88–98. [Google Scholar] [CrossRef]
- Saxena, S.; Srikanth, M.; Jawale, S.; Sakthivel, R. Efficient VCO using FinFET. Indian J. Sci. Technol. 2015, 8, 262–270. [Google Scholar] [CrossRef]
- Kim, S.; Ham, B.; Cho, M.; Oh, S.; Lee, J.; Cho, T.B. A 14 nm FinFET Sub-Picosecond Jitter Fractional-N Ring PLL for 5G Wireless Communication. In Proceedings of the 2018 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Philadelphia, PA, USA, 10–12 June 2018; pp. 40–43. [Google Scholar]
- Zou, W.; Ren, D.; Zou, X. A wideband low-jitter PLL with an optimized Ring-VCO. IEICE Electron. Express 2020, 17, 20190703. [Google Scholar] [CrossRef]
- Kundu, S.; Kim, B.; Kim, C.H. 19.2 A 0.2-to-1.45 GHz subsampling fractional-N all-digital MDLL with zero-offset aperture PD-based spur cancellation and in-situ timing mismatch detection. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 326–327. [Google Scholar]
- Wang, B.; Yang, H.; Jia, Y. A 1-to-3 GHz 5-to-512 multiplier adaptive fast-locking self-biased PLL in 28 nm CMOS. Electronics 2022, 11, 1954. [Google Scholar] [CrossRef]
- Wang, J.S.; Chou, P.Y. Clock Period-Jitter Measurement with Low-Noise Runtime Calibration for Chips in FinFET CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 3157–3164. [Google Scholar] [CrossRef]



| 25 °C, 1.8 V, TPTN | MIN | MAX | |
|---|---|---|---|
| Default frequency range (GHz) | 4.5–7.9 | 3.6–7.2 | 5.4–8.2 |
| Maximum frequency range (GHz) | 9.5–12.5 | 8.2–11.7 | 9.9–12.3 |
| Minimum frequency range (GHz) | 0.7–4.4 | 0.4–3.8 | 1.5–4.9 |
| Kvco variation | 18.1% | 12.9% | 23.8% |
| Phase noise @ 1 MHz(dBc/Hz) | −81.45 | −83.12 | −78.77 |
| power consumption(mW) | 1.08 | 0.826 | 1.38 |
| This | [25] RFIC’18 | [26] IEICE’20 | [27] ISSCC’16 | [28] Electronics’22 | [29] TCAS-Ι’24 | ||
|---|---|---|---|---|---|---|---|
| Integ.-N | Frac.-N | ||||||
| Technology (nm) | 12 | 14 | 180 | 65 | 28 | 14 | |
| Synth. Type | Frac.-N | Frac.-N | Integ.-N | Frac.-N | Integ.-N | Integ.-N | |
| VCO Type | Single-ended ring | Ring | Ring | Ring | Ring | Ring | |
| Freq. (GHz) | 6.72 | 7 | 1.92 | 1.4 | 3 | 2.13 | |
| Area (mm2) | 0.078 | 0.1 | N/A | 0.054 | 0.028 | 0.019 | |
| Power (mW) | 6.4@5.76 GHz | 3.4@3.19 GHz | 36.3 | 17.4 | 8 | 4.6 | 1.19 |
| RMS Jitter (ps) | 2.702 | 5.068 | 0.982 | 2.61 | 2.8 | N/A | 5.67 |
| FoM * (dB) | −223.3 | −220.6 | −224.6 | −219.3 | −222 | N/A | −224.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xun, B.; Shi, Y.; Xu, X.; Li, M.; Zhu, H.; Sun, Q. A Compact, Low-Power, and Low-Jitter Fractional-N Phase-Locked Loop with a Single-Ended Ring Voltage-Controlled Oscillator in a 12 nm CMOS FinFET. Electronics 2024, 13, 2617. https://doi.org/10.3390/electronics13132617
Li Y, Xun B, Shi Y, Xu X, Li M, Zhu H, Sun Q. A Compact, Low-Power, and Low-Jitter Fractional-N Phase-Locked Loop with a Single-Ended Ring Voltage-Controlled Oscillator in a 12 nm CMOS FinFET. Electronics. 2024; 13(13):2617. https://doi.org/10.3390/electronics13132617
Chicago/Turabian StyleLi, Yunpeng, Benpeng Xun, Yiqun Shi, Xin Xu, Meng Li, Hao Zhu, and Qingqing Sun. 2024. "A Compact, Low-Power, and Low-Jitter Fractional-N Phase-Locked Loop with a Single-Ended Ring Voltage-Controlled Oscillator in a 12 nm CMOS FinFET" Electronics 13, no. 13: 2617. https://doi.org/10.3390/electronics13132617
APA StyleLi, Y., Xun, B., Shi, Y., Xu, X., Li, M., Zhu, H., & Sun, Q. (2024). A Compact, Low-Power, and Low-Jitter Fractional-N Phase-Locked Loop with a Single-Ended Ring Voltage-Controlled Oscillator in a 12 nm CMOS FinFET. Electronics, 13(13), 2617. https://doi.org/10.3390/electronics13132617





