Deep Residual-in-Residual Model-Based PET Image Super-Resolution with Motion Blur
Abstract
1. Introduction
- The actual degradation due to physiological motion in a deep learning-based SR task for medical images is considered for the first time by us.
- A degradation model focusing on noise and simplified blur for the more complex SR recovery problem is designed by us. The directional motion blur present in the image is simulated to a certain degree using a motion blur PSF. Additionally, instead of a fixed K value of inverse signal-to-noise ratio (SNR) in the Wiener filtering, which lacks flexibility, K is implemented with variable parameters.
- In the reconstruction part, to address issues such as a loss of information during computation and potential degradation during the feature extraction process, a new network based on the deep residual-in-residual network, known as DRRN, has been designed by us. This innovative approach aims to overcome problems traditionally associated with classic convolutional or fully connected layers.
- Both full-reference and no-reference indicators were utilized in the evaluation metrics as a means to obtain richer, comprehensive, and reliable evaluation results. It is evident from our results that the proposed method demonstrates excellent qualitative and quantitative performance on three datasets, achieving significant advantages over other comparative methods.
2. Methods
2.1. Degradation
2.1.1. Classical Degradation Model
2.1.2. Proposed Degradation Model
- A.
- Wiener Filter
- B.
- Motion Blur PSF
- C.
- Validation of Degradation Model
2.2. Proposed Architecture
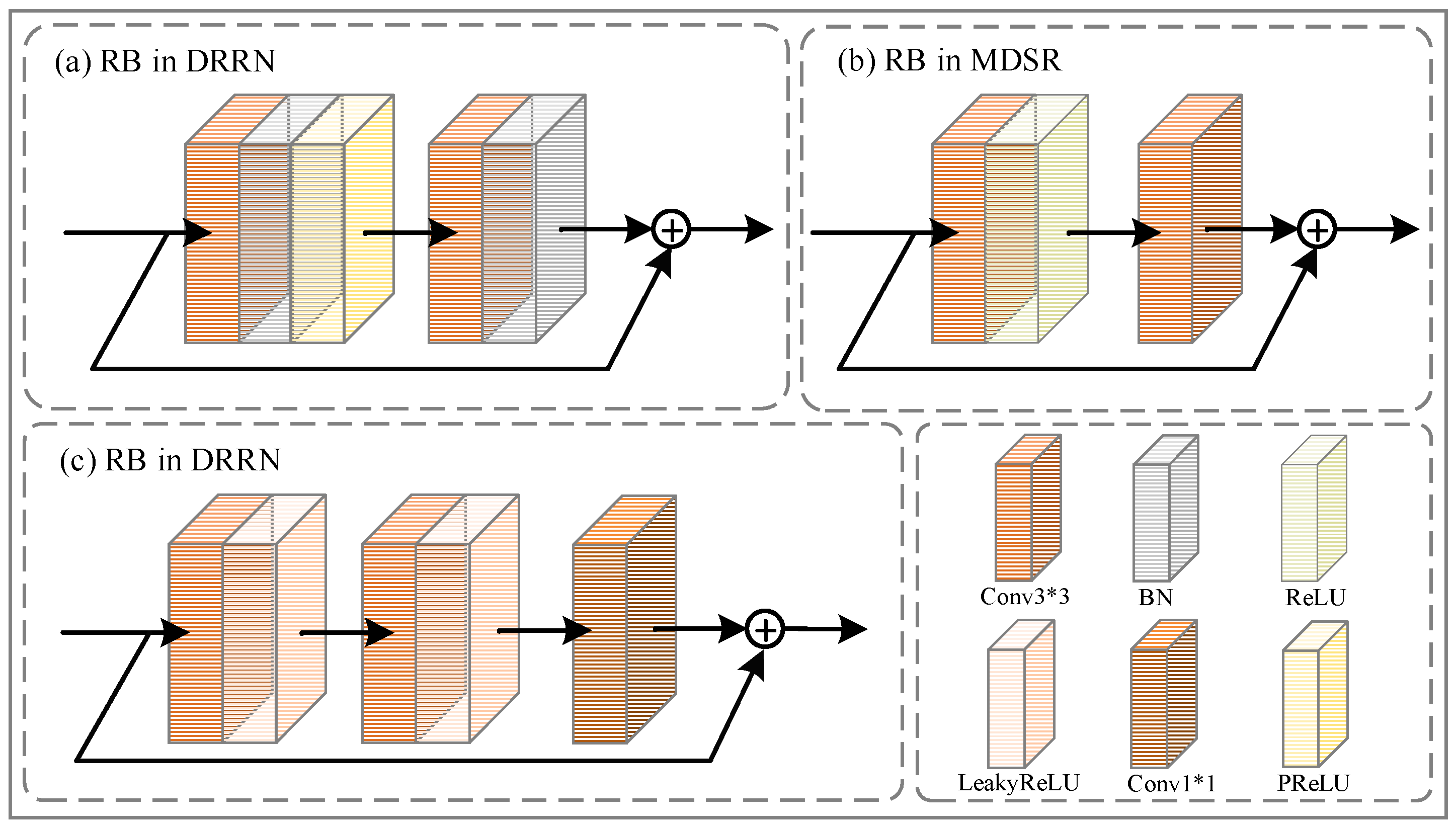
2.2.1. Deep Residual-in-Residual Block
2.2.2. Residual Block
2.3. Evaluation Metrics
2.3.1. Full-Reference Evaluation
2.3.2. No-Reference Evaluation
3. Experiments
3.1. Dataset
3.2. Implementation Details
3.3. Results
Comparison with Reference Methods
- A.
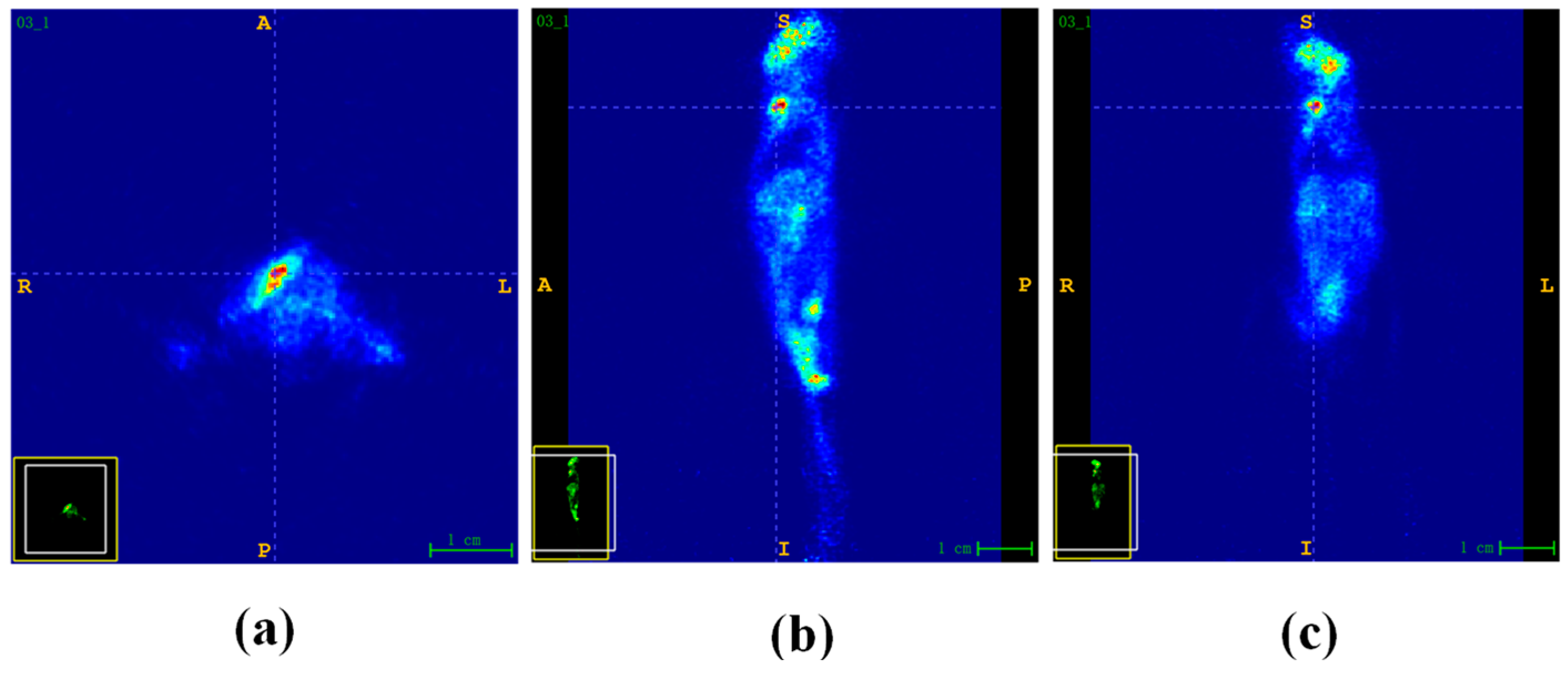
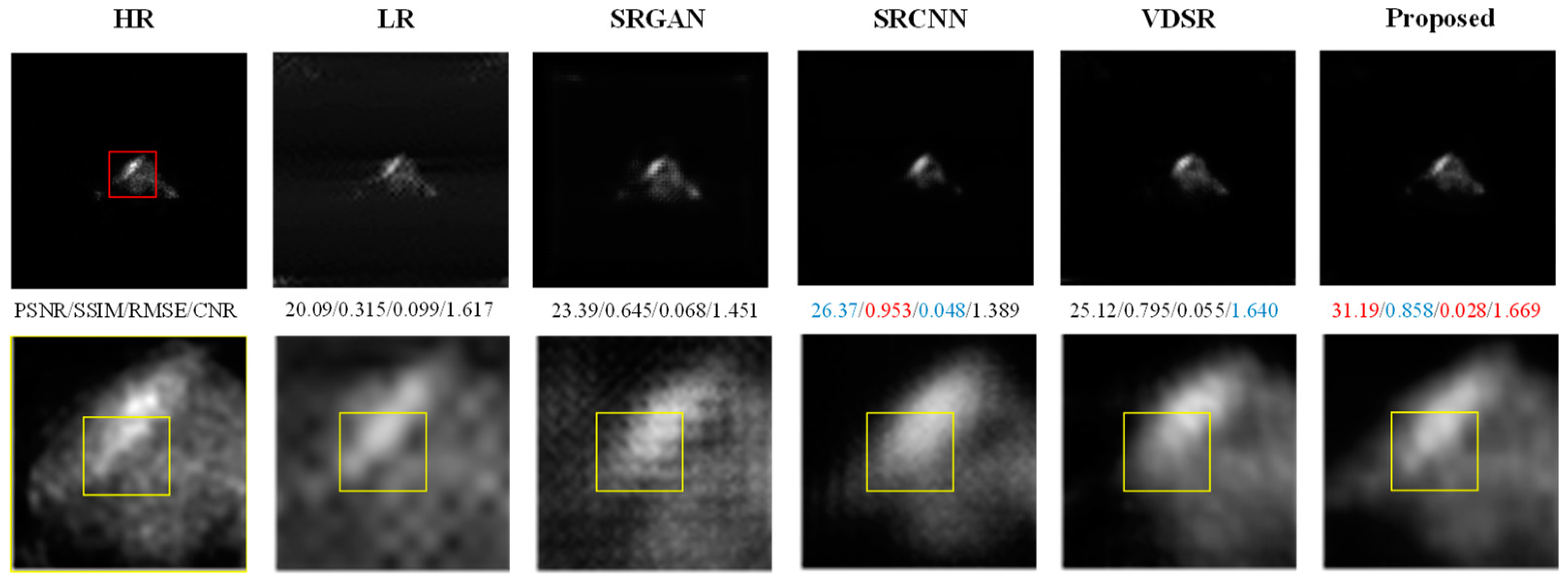
- Results on the SAPET Dataset
- B.
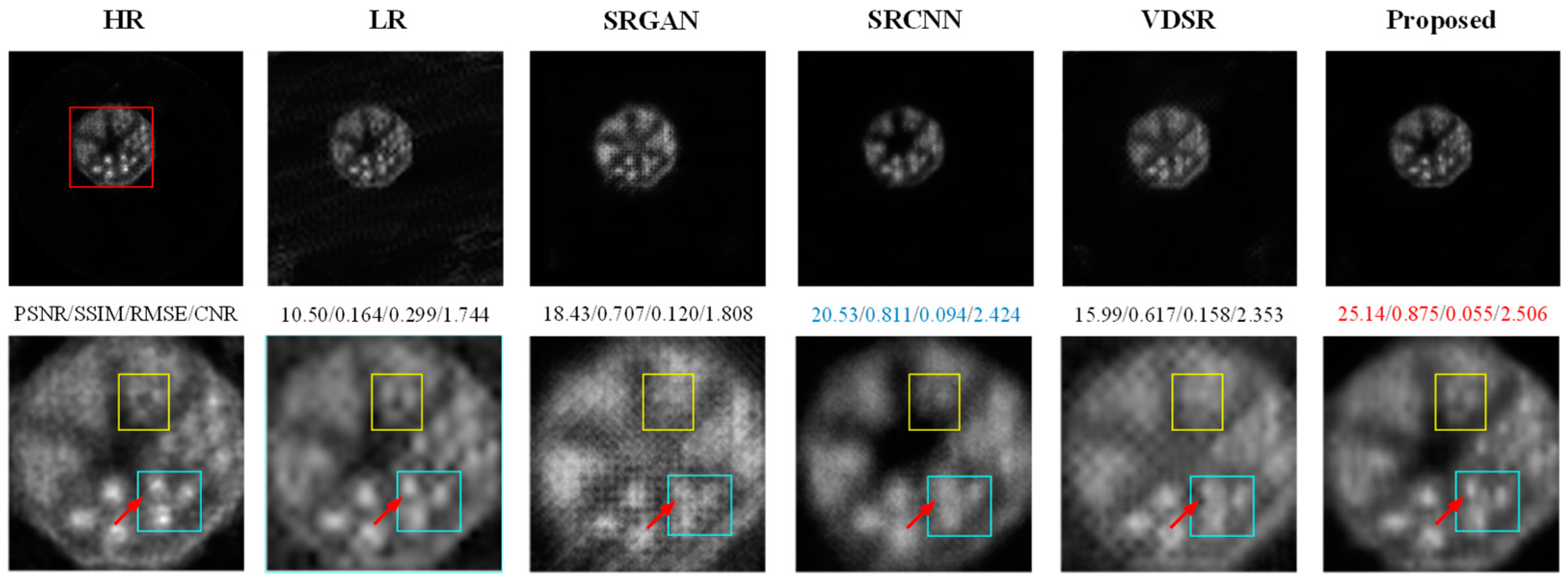
- Results on the Phantom Dataset
- C.
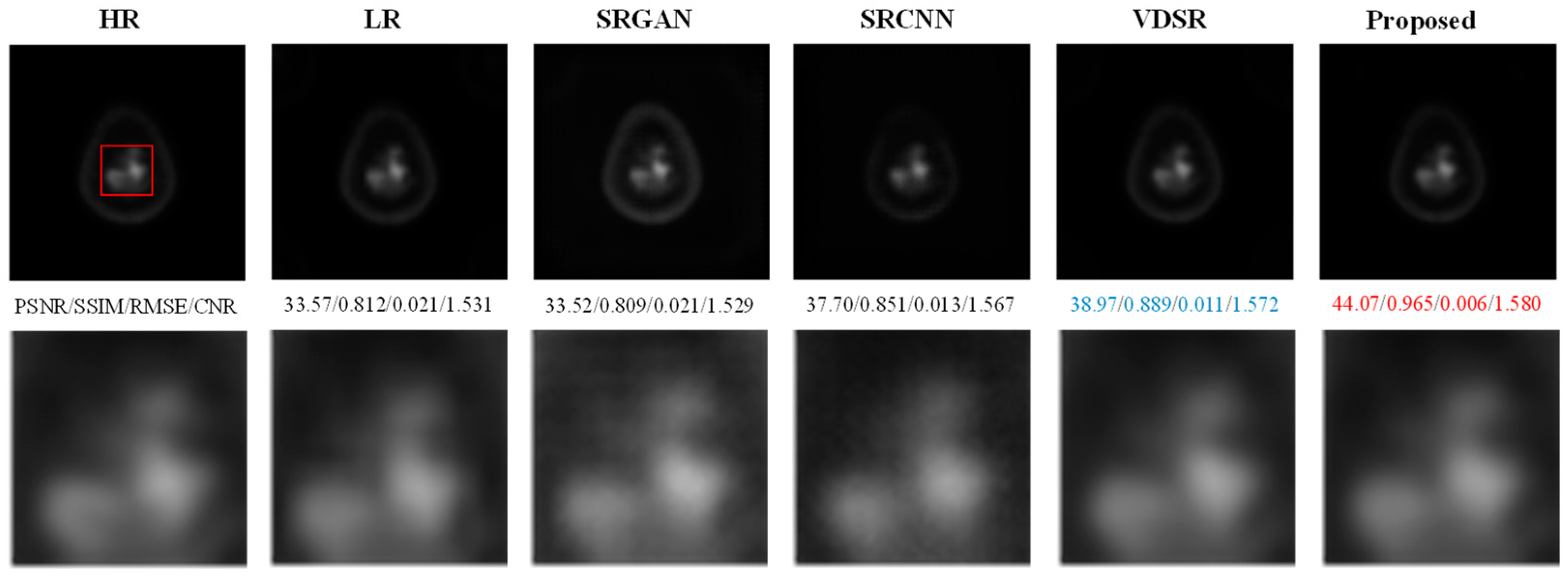
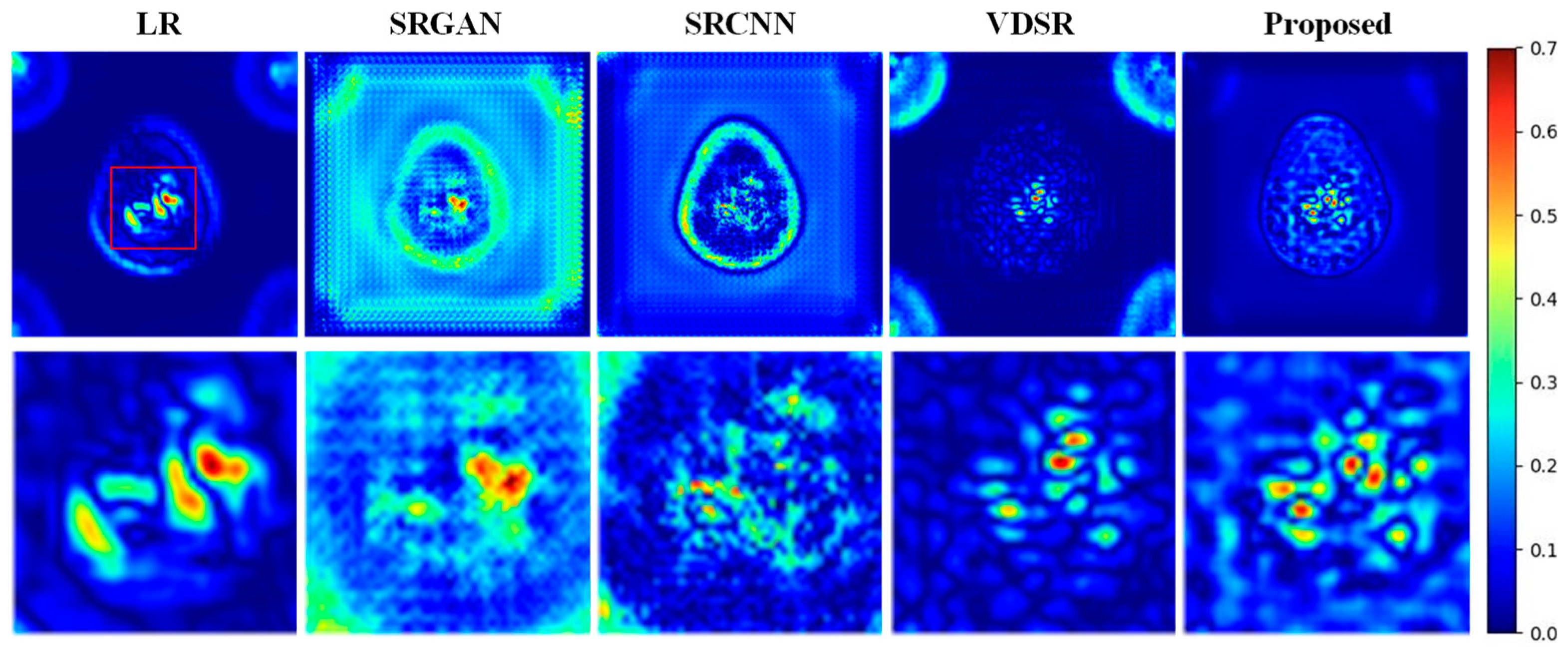
- Results on the AD Dataset
3.4. Ablation and Super Parameter Experiments
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ametamey, S.M.; Honer, M.; Schubiger, P.A. Molecular Imaging with PET. Chem. Rev. 2008, 108, 1501–1516. [Google Scholar] [CrossRef] [PubMed]
- Wollring, M.M.; Werner, J.-M.; Ceccon, G.; Lohmann, P.; Filss, C.P.; Fink, G.R.; Langen, K.-J.; Galldiks, N. Clinical Applications and Prospects of PET Imaging in Patients with IDH-Mutant Gliomas. J. Neurooncol. 2023, 162, 481–488. [Google Scholar] [CrossRef] [PubMed]
- Subramanyam Rallabandi, V.P.; Seetharaman, K. Deep Learning-Based Classification of Healthy Aging Controls, Mild Cognitive Impairment and Alzheimer’s Disease Using Fusion of MRI-PET Imaging. Biomed. Signal Process. Control 2023, 80, 104312. [Google Scholar] [CrossRef]
- Romeo, V.; Moy, L.; Pinker, K. AI-Enhanced PET and MR Imaging for Patients with Breast Cancer. PET Clin. 2023, 18, 567–575. [Google Scholar] [CrossRef] [PubMed]
- Aitken, M.; Chan, M.V.; Urzua Fresno, C.; Farrell, A.; Islam, N.; McInnes, M.D.F.; Iwanochko, M.; Balter, M.; Moayedi, Y.; Thavendiranathan, P.; et al. Diagnostic Accuracy of Cardiac MRI versus FDG PET for Cardiac Sarcoidosis: A Systematic Review and Meta-Analysis. Radiology 2022, 304, 566–579. [Google Scholar] [CrossRef] [PubMed]
- Cherry, S.R. Of Mice and Men (and Positrons)—Advances in PET Imaging Technology. J. Nucl. Med. 2006, 47, 1735–1745. [Google Scholar] [PubMed]
- Feng, L. 4D Golden-Angle Radial MRI at Subsecond Temporal Resolution. NMR Biomed. 2023, 36, e4844. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.; Rojas, C.A. Imaging Modalities (MRI, CT, PET/CT), Indications, Differential Diagnosis and Imaging Characteristics of Cystic Mediastinal Masses: A Review. Mediastinum 2023, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Yu, H.; De Man, B. An Outlook on X-ray CT Research and Development. Med. Phys. 2008, 35, 1051–1064. [Google Scholar] [CrossRef]
- Braams, J.W.; Pruim, J.; Freling, N.J.M.; Nikkeis, P.G.J.; Roodenburg, J.L.N.; Boering, G.; Vaalburg, W.; Vermey, A.; Braams, J.W. Detection of Lymph Node Metastases of Squamous-Cell Cancer of the Head and Neck with FDG-PET and MRI. J. Nucl. Med. 1995, 36, 211–216. [Google Scholar]
- Kitajima, K.; Murakami, K.; Yamasaki, E.; Kaji, Y.; Sugimura, K. Accuracy of Integrated FDG-PET/Contrast-Enhanced CT in Detecting Pelvic and Paraaortic Lymph Node Metastasis in Patients with Uterine Cancer. Eur. Radiol. 2009, 19, 1529–1536. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Tian, X.; Wang, Y.; Song, Y.; Zhang, Y.; Zhao, J.; Chen, J.-C. DAEGAN: Generative Adversarial Network Based on Dual-Domain Attention-Enhanced Encoder-Decoder for Low-Dose PET Imaging. Biomed. Signal Process. Control 2023, 86, 105197. [Google Scholar] [CrossRef]
- Cao, K.; Xia, Y.; Yao, J.; Han, X.; Lambert, L.; Zhang, T.; Tang, W.; Jin, G.; Jiang, H.; Fang, X.; et al. Large-Scale Pancreatic Cancer Detection via Non-Contrast CT and Deep Learning. Nat. Med. 2023, 29, 3033–3043. [Google Scholar] [CrossRef] [PubMed]
- Umirzakova, S.; Ahmad, S.; Khan, L.U.; Whangbo, T. Medical Image Super-Resolution for Smart Healthcare Applications: A Comprehensive Survey. Inf. Fusion 2024, 103, 102075. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, W.; Liao, Q. Interpolation-Based Image Super-Resolution Using Multisurface Fitting. IEEE Trans. Image Process. 2012, 21, 3312–3318. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, T.; Li, X.M. An Integrated Interpolation-Based Super Resolution Reconstruction Algorithm for Video Surveillance. J. Commun. 2012, 7, 464–472. [Google Scholar] [CrossRef]
- Tanaka, M.; Okutomi, M. Theoretical Analysis on Reconstruction-Based Super-Resolution for an Arbitrary PSF. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: New York, NY, USA; pp. 947–954. [Google Scholar]
- Fan, C.; Wu, C.; Li, G.; Ma, J. Projections onto Convex Sets Super-Resolution Reconstruction Based on Point Spread Function Estimation of Low-Resolution Remote Sensing Images. Sensors 2017, 17, 362. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Jiang, Y.; Liu, X.; Xu, H.; Han, Z.; Rong, H.; Yang, H.; Yan, M.; Yu, H. Machine Learning Based Single-Frame Super-Resolution Processing for Lensless Blood Cell Counting. Sensors 2016, 16, 1836. [Google Scholar] [CrossRef] [PubMed]
- Jia, K.; Wang, X.; Tang, X. Image Transformation Based on Learning Dictionaries across Image Spaces. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 367–380. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. pp. 391–407. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 294–310. [Google Scholar]
- Qiu, D.; Zhang, S.; Liu, Y.; Zhu, J.; Zheng, L. Super-Resolution Reconstruction of Knee Magnetic Resonance Imaging Based on Deep Learning. Comput. Methods Programs Biomed. 2020, 187, 105059. [Google Scholar] [CrossRef]
- Song, T.-A.; Chowdhury, S.R.; Yang, F.; Dutta, J. Super-Resolution PET Imaging Using Convolutional Neural Networks. IEEE Trans. Comput. Imaging 2020, 6, 518–528. [Google Scholar] [CrossRef]
- Qiu, D.; Cheng, Y.; Wang, X. Improved Generative Adversarial Network for Retinal Image Super-Resolution. Comput. Methods Programs Biomed. 2022, 225, 106995. [Google Scholar] [CrossRef]
- Zhu, D.; He, H.; Wang, D. Feedback Attention Network for Cardiac Magnetic Resonance Imaging Super-Resolution. Comput. Methods Programs Biomed. 2023, 231, 107313. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Tian, X.; Chen, S.; Wang, Y.; Zhao, J.; Chen, J. PET Imaging Super-Resolution Using Attention-Enhanced Global Residual Dense Network. In Proceedings of the 2023 IEEE 3rd International Conference on Computer Systems (ICCS), Qingdao, China, 22–24 September 2023; pp. 91–98. [Google Scholar]
- Qiu, D.; Zheng, L.; Zhu, J.; Huang, D. Multiple Improved Residual Networks for Medical Image Super-Resolution. Future Gener. Comput. Syst. 2021, 116, 200–208. [Google Scholar] [CrossRef]
- Zhu, D.; Sun, D.; Wang, D. Dual Attention Mechanism Network for Lung Cancer Images Super-Resolution. Comput. Methods Programs Biomed. 2022, 226, 107101. [Google Scholar] [CrossRef]
- Song, T.-A.; Chowdhury, S.R.; Yang, F.; Dutta, J. PET Image Super-Resolution Using Generative Adversarial Networks. Neural Netw. 2020, 125, 83–91. [Google Scholar] [CrossRef]
- Park, S.-J.; Ionascu, D.; Killoran, J.; Mamede, M.; Gerbaudo, V.H.; Chin, L.; Berbeco, R. Evaluation of the Combined Effects of Target Size, Respiratory Motion and Background Activity on 3D and 4D PET/CT Images. Phys. Med. Biol. 2008, 53, 3661–3679. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Hel-Or, Y. A fast super-resolution reconstruction algorithm for pure translational motion and common space-invariant blur. In Proceedings of the 21st IEEE Convention of the Electrical and Electronic Engineers in Israel, Tel-Aviv, Israel, 11–12 April 2000; Proceedings (Cat. No.00EX377). pp. 402–405. [Google Scholar] [CrossRef]
- Elad, M.; Feuer, A. Restoration of a Single Superresolution Image from Several Blurred, Noisy, and Undersampled Measured Images. IEEE Trans. Image Process. 1997, 6, 1646–1658. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 17 October 2021; pp. 1905–1914. [Google Scholar]
- Rim, J.; Lee, H.; Won, J.; Cho, S. Real-World Blur Dataset for Learning and Benchmarking Deblurring Algorithms. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXV 16. pp. 184–201. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Behjati, P.; Rodriguez, P.; Mehri, A.; Hupont, I.; Tena, C.F.; Gonzalez, J. OverNet: Lightweight Multi-Scale Super-Resolution with Overscaling Network. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 2693–2702. [Google Scholar]
- Alzheimer’s Disease Neuroimaging Initiative (ADNI). Available online: https://adni.loni.usc.edu/data-samples/access-data/ (accessed on 11 January 2023).
- itk-SNAP. Available online: http://www.itksnap.org/pmwiki/pmwiki.php (accessed on 11 January 2023).





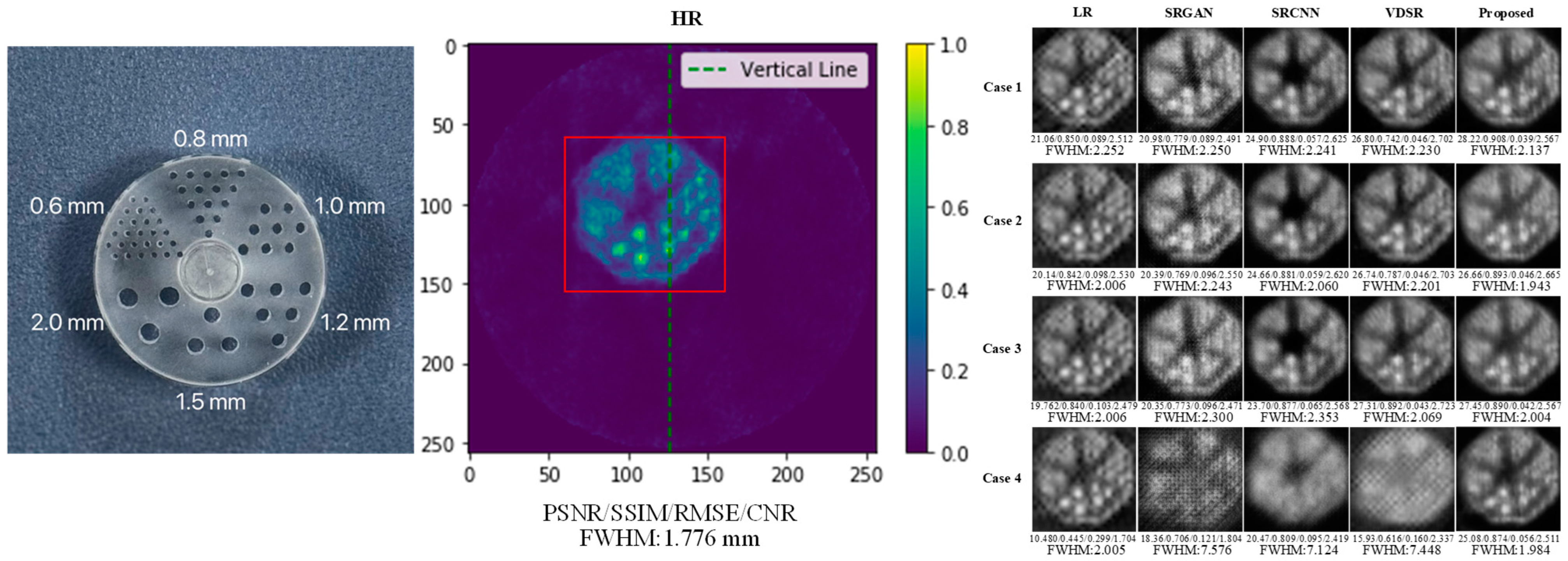

| Method | SAPET Case 1 PSNR/SSIM/RMSE/CNR | SAPET Case 2 PSNR/SSIM/RMSE/CNR | SAPET Case 3 PSNR/SSIM/RMSE/CNR | SAPET Case 4 PSNR/SSIM/RMSE/CNR |
|---|---|---|---|---|
| LR | 24.57/0.776/0.061/2.164 | 23.30/0.745/0.071/2.035 | 23.31/0.755/0.071/2.120 | 18.55/0.733/0.120/1.921 |
| SRGAN | 24.60/0.733/0.063/1.939 | 23.99/0.751/0.067/1.866 | 23.56/0.693/0.071/1.864 | 22.46/0.677/0.080/1.747 |
| SRCNN | 28.70/0.899/0.039/1.939 | 28.61/0.886/0.040/1.897 | 27.85/0.887/0.043/1.917 | 25.37/0.872/0.058/1.951 |
| VDSR | 29.53/0.821/0.036/1.954 | 30.94/0.888/0.030/2.081 | 30.94/0.888/0.030/2.081 | 23.19/0.765/0.071/1.967 |
| Proposed | 34.36/0.913/0.020/2.085 | 33.03/0.898/0.024/2.024 | 31.61/0.899/0.028/2.035 | 30.18/0.879/0.033/2.039 |
| Case 1/Case 2/Case 3/Case 4 | PSNR↑ | SSIM↑ | RMSE↓ | CNR↑ |
|---|---|---|---|---|
| Proposed VS. SRGAN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 |
| Proposed VS. SRCNN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 |
| Proposed VS. VDSR | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/=0.940/ =0.924/<0.001 |
| Method | Phantom Case 1 PSNR/SSIM/RMSE/CNR | Phantom Case 2 PSNR/SSIM/RMSE/CNR | Phantom Case 3 PSNR/SSIM/RMSE/CNR | Phantom Case 4 PSNR/SSIM/RMSE/CNR |
|---|---|---|---|---|
| LR | 18.31/0.389/0.123/1.532 | 16.78/0.335/0.147/1.567 | 16.69/0.345/0.148/1.546 | 9.947/0.160/0.318/1.078 |
| SRGAN | 20.10/0.623/0.101/1.484 | 19.70/0.613/0.106/1.472 | 19.78/0.619/0.105/1.433 | 18.03/0.569/0.128/1.147 |
| SRCNN | 22.88/0.681/0.073/1.605 | 21.41/0.653/0.087/1.618 | 20.84/0.643/0.092/1.584 | 18.16/0.523/0.125/1.468 |
| VDSR | 24.93/0.702/0.058/1.620 | 23.51/0.666/0.068/1.658 | 24.00/0.657/0.064/1.610 | 11.44/0.432/0.273/1.421 |
| Proposed | 25.52/0.725/0.053/1.556 | 23.79/0.674/0.065/1.660 | 23.43/0.660/0.069/1.612 | 22.77/0.644/0.074/1.551 |
| Case 1/Case 2/Case 3/Case 4 | PSNR↑ | SSIM↑ | RMSE↓ | CNR↑ |
|---|---|---|---|---|
| Proposed VS. SRGAN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 |
| Proposed VS. SRCNN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | =0.072<0.001/ <0.001/<0.001 |
| Proposed VS. VDSR | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | =0.020/<0.001/ <0.001/<0.001 |
| Method | Phantom Case 1 FWHM↓ | Phantom Case 2 FWHM↓ | Phantom Case 3 FWHM↓ | Phantom Case 4 FWHM↓ |
|---|---|---|---|---|
| LR | 2.252 | 2.006 | 2.006 | 2.005 |
| SRGAN | 2.250 | 2.243 | 2.300 | 7.576 |
| SRCNN | 2.241 | 2.060 | 2.353 | 7.124 |
| VDSR | 2.230 | 2.201 | 2.069 | 7.448 |
| Proposed | 2.137 | 1.943 | 2.004 | 1.984 |
| Method | ADNI Case 1 PSNR/SSIM/RMSE/CNR | ADNI Case 2 PSNR/SSIM/RMSE/CNR | ADNI Case 3 PSNR/SSIM/RMSE/CNR | ADNI Case 4 PSNR/SSIM/RMSE/CNR |
|---|---|---|---|---|
| LR | 32.39/0.819/0.024/1.457 | 32.55/0.824/0.023/1.460 | 32.97/0.832/0.022/1.469 | 33.71/0.842/0.021/1.491 |
| SRGAN | 34.33/0.861/0.019/1.481 | 33.74/0.822/0.021/1.457 | 33.78/0.820/0.020/1.460 | 33.72/0.818/0.021/1.457 |
| SRCNN | 37.62/0.853/0.013/1.500 | 37.58/0.850/0.013/1.497 | 37.56/0.850/0.013/1.497 | 37.49/0.848/0.013/1.495 |
| VDSR | 42.45/0.938/0.008/1.507 | 40.34/0.910/0.010/1.505 | 39.14/0.892/0.011/1.503 | 38.62/0.882/0.012/1.503 |
| Proposed | 44.13/0.966/0.006/1.513 | 43.13/0.957/0.007/1.513 | 43.26/0.959/0.007/1.512 | 42.81/0.968/0.007/1.507 |
| Case 1/Case 2/Case 3/Case 4 | PSNR↑ | SSIM↑ | RMSE↓ | CNR↑ |
|---|---|---|---|---|
| Proposed VS. SRGAN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 |
| Proposed VS. SRCNN | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 |
| Proposed VS. VDSR | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 | <0.001/<0.001/ <0.001/<0.001 | <0.001/<0.001/<0.001/<0.001 |
| Design | PSNR↑ | SSIM↑ | RMSE↓ |
|---|---|---|---|
| RB with ReLU | 29.49 | 0.878 | 0.036 |
| RB with PReLU | 27.02 | 0.950 | 0.048 |
| RB with LeakyReLU | 30.18 | 0.879 | 0.033 |
| Design | PSNR↑ | SSIM↑ | RMSE↓ |
|---|---|---|---|
| 0 | 27.19 | 0.872 | 0.047 |
| 1 | 29.07 | 0.880 | 0.038 |
| 2 | 30.18 | 0.879 | 0.033 |
| 3 | 28.80 | 0.879 | 0.039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Chen, S.; Wang, Y.; Han, D.; Lin, Y.; Zhao, J.; Chen, J.-C. Deep Residual-in-Residual Model-Based PET Image Super-Resolution with Motion Blur. Electronics 2024, 13, 2582. https://doi.org/10.3390/electronics13132582
Tian X, Chen S, Wang Y, Han D, Lin Y, Zhao J, Chen J-C. Deep Residual-in-Residual Model-Based PET Image Super-Resolution with Motion Blur. Electronics. 2024; 13(13):2582. https://doi.org/10.3390/electronics13132582
Chicago/Turabian StyleTian, Xin, Shijie Chen, Yuling Wang, Dongqi Han, Yuan Lin, Jie Zhao, and Jyh-Cheng Chen. 2024. "Deep Residual-in-Residual Model-Based PET Image Super-Resolution with Motion Blur" Electronics 13, no. 13: 2582. https://doi.org/10.3390/electronics13132582
APA StyleTian, X., Chen, S., Wang, Y., Han, D., Lin, Y., Zhao, J., & Chen, J.-C. (2024). Deep Residual-in-Residual Model-Based PET Image Super-Resolution with Motion Blur. Electronics, 13(13), 2582. https://doi.org/10.3390/electronics13132582







