Symmetrical Multilevel High Voltage-Gain Boost Converter Control Strategy for Photovoltaic Systems Applications
Abstract
1. Introduction
2. Behavior Model of the PV System
2.1. PV Cell Series Resistance Modeling
2.2. Proposed PV Cell Model
2.3. Proposed Model of the PV Module
3. DC-DC Converters for PV Applications
3.1. DC-DC Converters’ Topologies
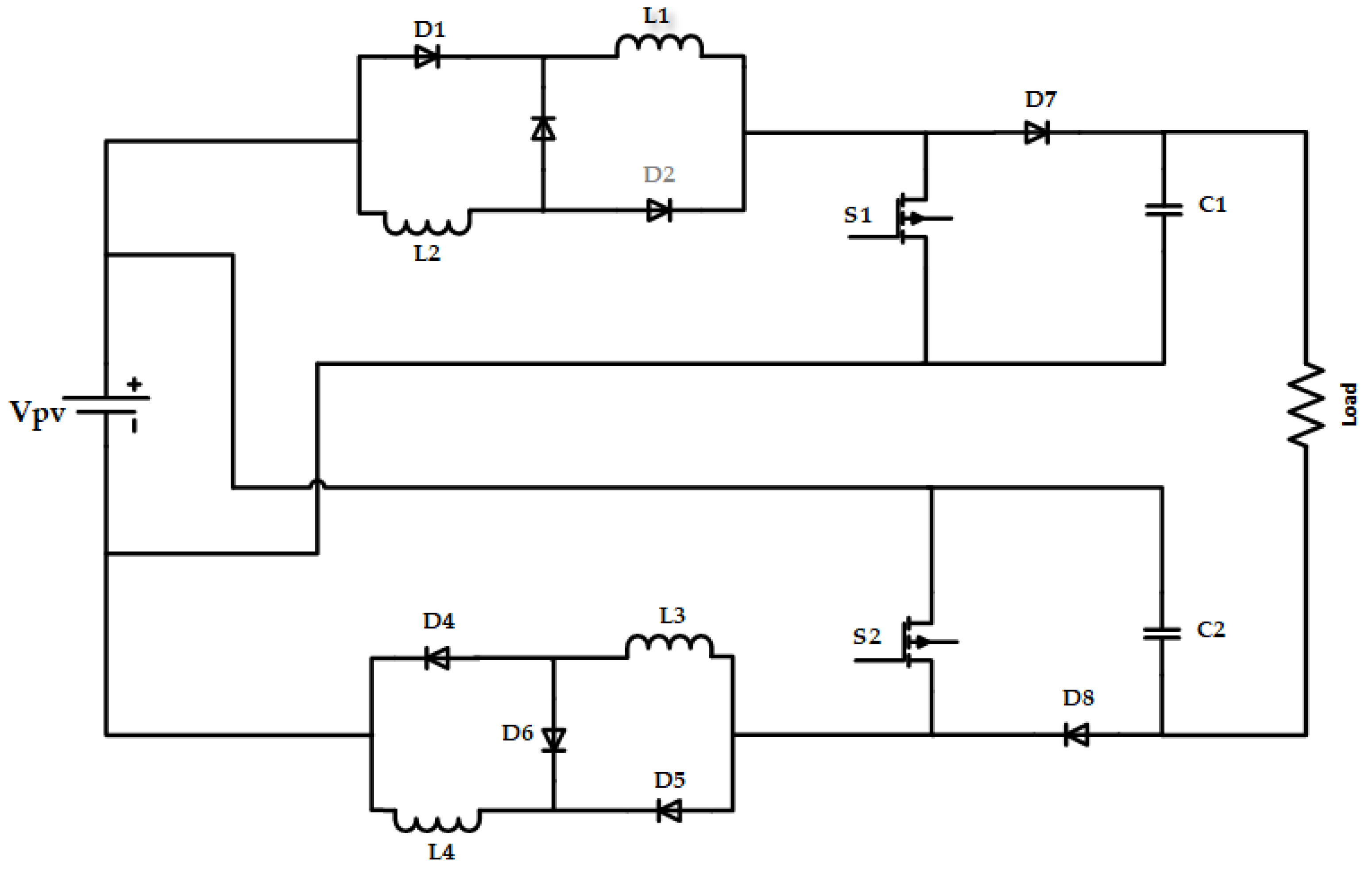
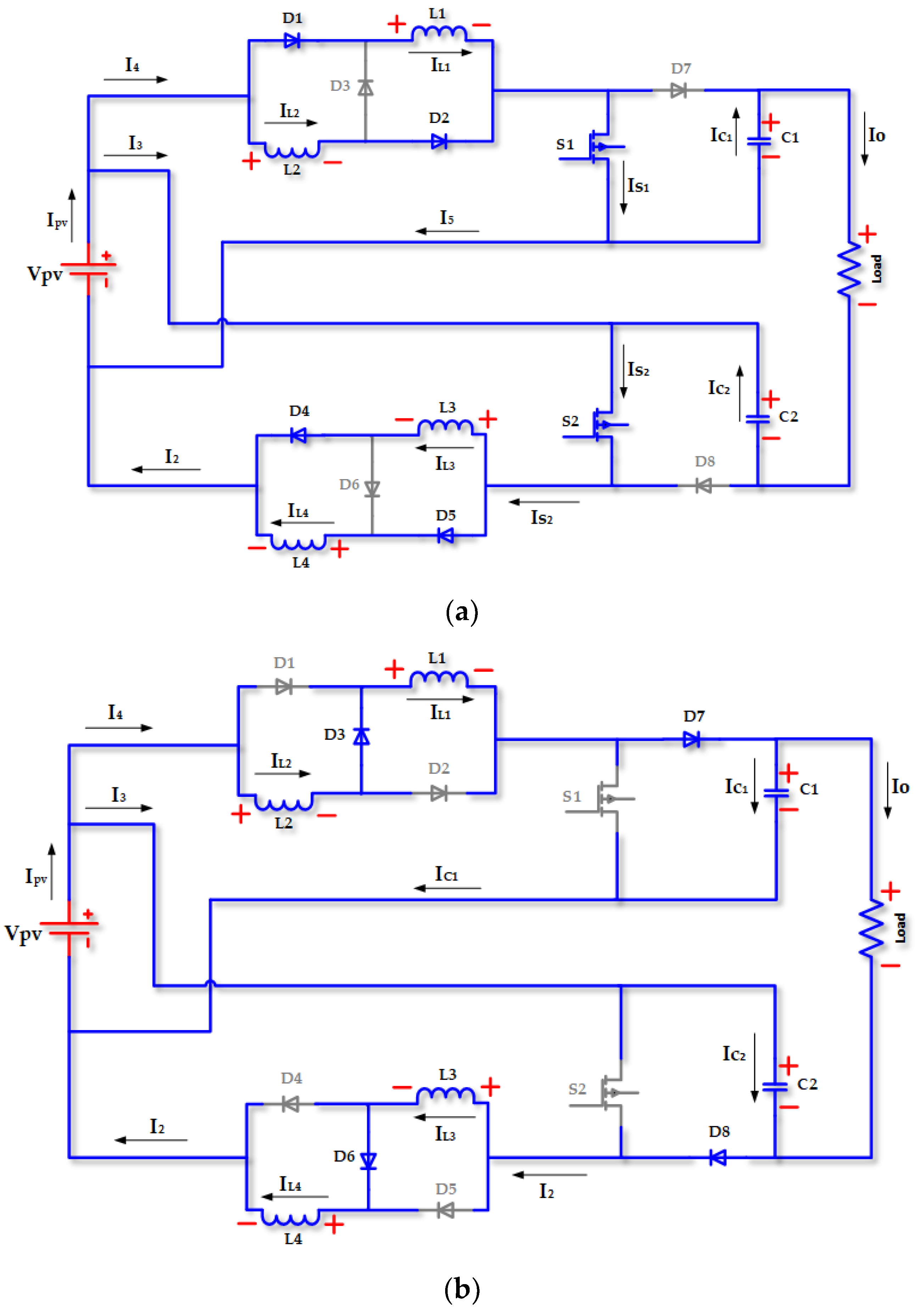
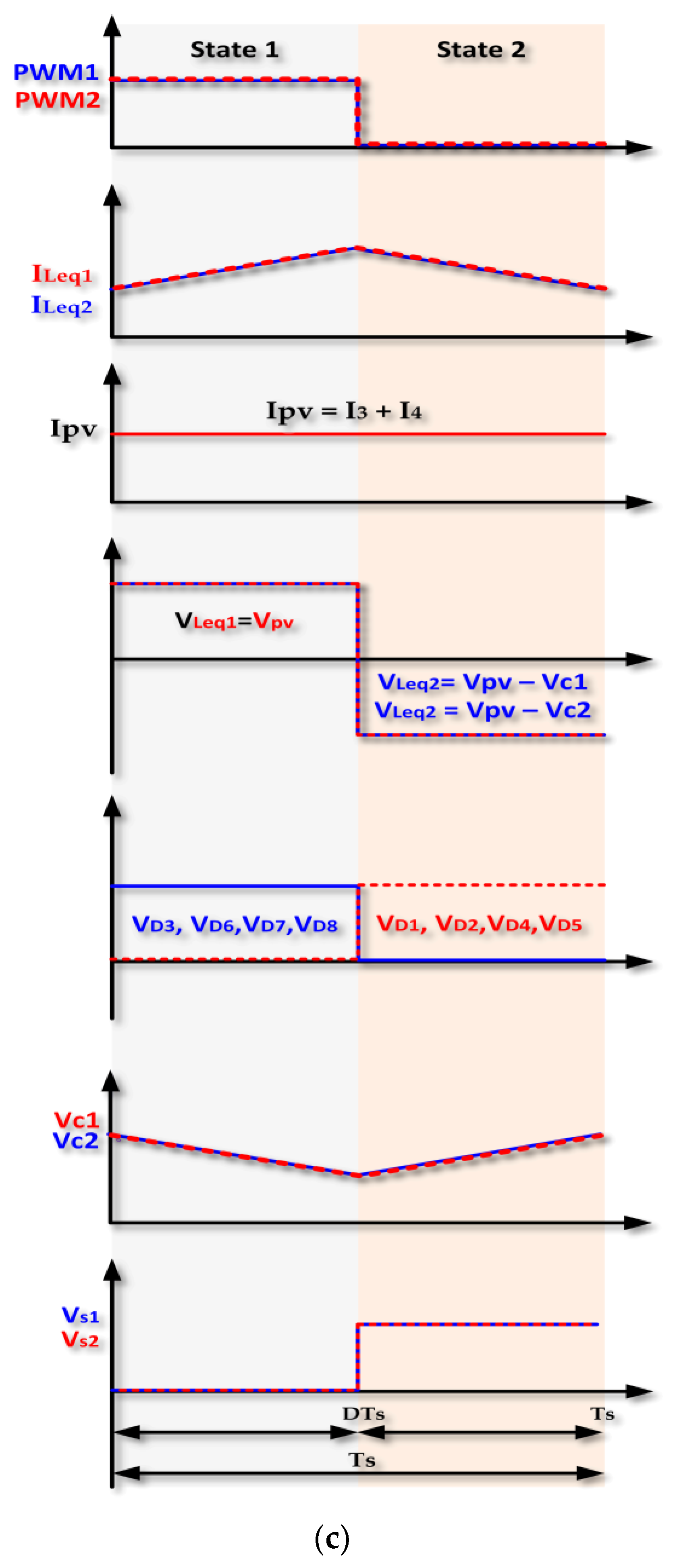
3.2. Considered DC-DC Converter Topology and Operating Analysis Based on Continuous Conduction Modes
- (a)
- State 1 (0 < t < DTs)
- (b)
- State 2 (D × Ts < t < Ts):
3.3. Passive Components-Based Inductors and Capacitances Sizing
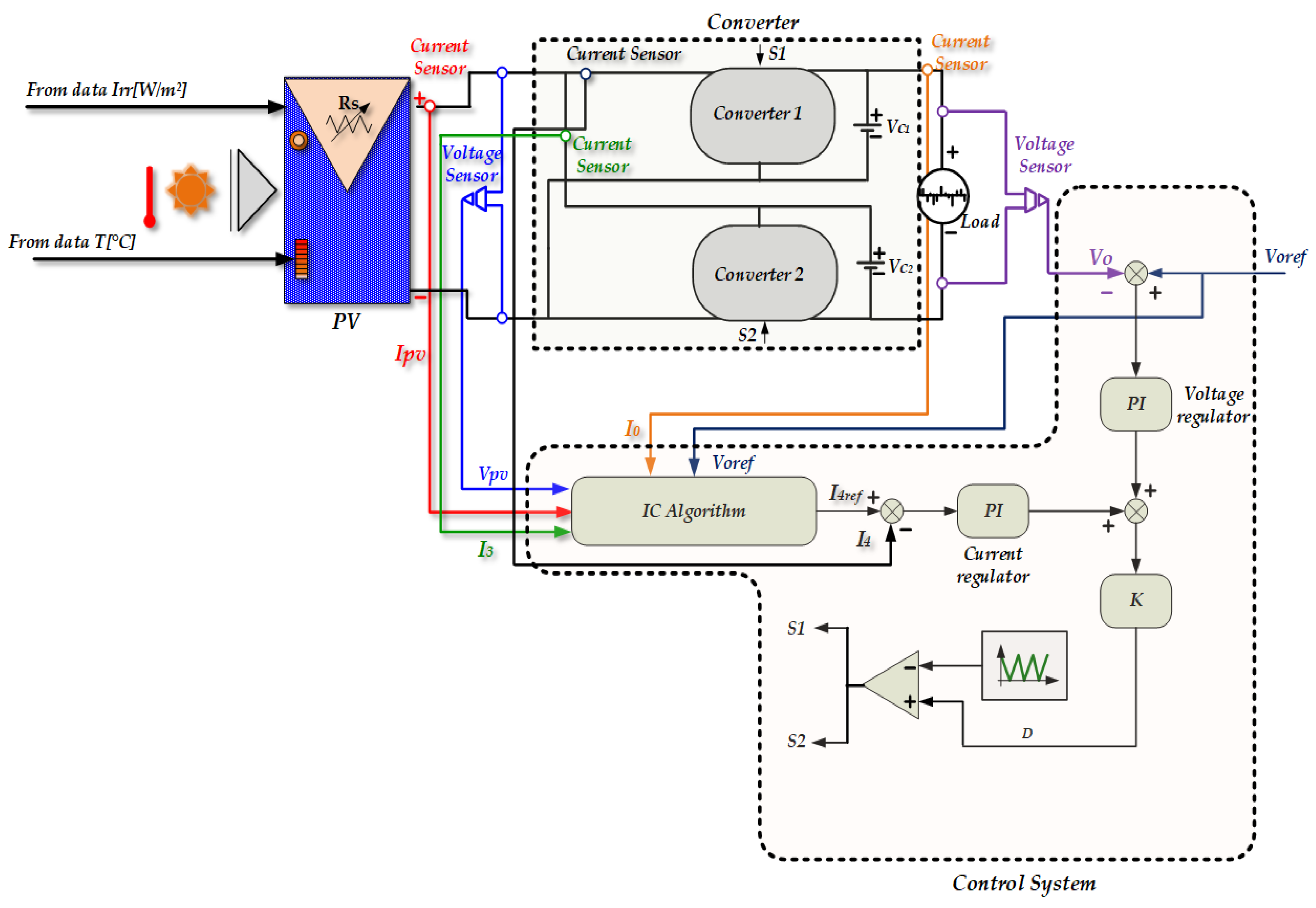
4. PV System Control Strategy
4.1. PV System MPPT Control in the Presence of Irradiance and Temperature Variations
4.2. DC-Bus Voltage and Current Control Strategies
5. Simulation Results
5.1. Simulation Conditions
5.2. Simulation Results Based on DC-Bus Voltage Reference Sudden Change
5.3. Simulation Results Based on the Load’s Current Sudden Change
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternative current |
| C | Equivalent capacity chosen |
| CC | Direct current |
| CO2 | Carbon dioxide |
| IC algorithm | Conductance increment algorithm |
| PV | Photovoltaic |
| MPPT | Maximum power point tracking |
References
- Meshael, H.; Elkhateb, A.; Best, R. Topologies and Design Characteristics of Isolated High Step-Up DC–DC Converters for Photovoltaic Systems. Electronics 2023, 12, 3913. [Google Scholar] [CrossRef]
- Siirola, J.J. Speculations on global energy demand and supply going forward. Curr. Opin. Chem. Eng. 2014, 5, 96–100. [Google Scholar] [CrossRef]
- Watari, T.; McLellan, B.C.; Giurco, D.; Dominish, E.; Yamasue, E.; Nansai, K. Total material requirement for the global energy transition to 2050: A focus on transport and electricity. Resour. Conserv. Recycl. 2019, 148, 91–103. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Kober, T.; Schiffer, H.-W.; Densing, M.; Panos, E. Global energy perspectives to 2060—WEC’s World Energy Scenarios 2019. Energy Strategy Rev. 2020, 31, 100523. [Google Scholar] [CrossRef]
- Baqar, A.; Camara, M.B.; Dakyo, B. Energy Management in the Multi-Source Systems. Energies 2022, 15, 2713. [Google Scholar] [CrossRef]
- Kadri, S.M.; Bagre, A.O.; Camara, M.B.; Dakyo, B.; Coulibaly, Y. Electrical Power distribution status in West Africa: Assessment and Perspective Overview. In Proceedings of the ICRERA 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 511–515. [Google Scholar] [CrossRef]
- Breyer, C.; Bogdanov, D.; Aghahosseini, A.; Gulagi, A.; Child, M.; Oyewo, A.S.; Farfan, J.; Sadovskaia, K.; Vainikka, P. Solar photovoltaics demand for the global energy transition in the power sector. Prog. Photovolt. Res. Appl. 2017, 26, 505–523. [Google Scholar] [CrossRef]
- Toure, M.L.; Camara, M.B.; Payman, A.; Dakyo, B. African Renewable Energy Potentialities Review for Local Weak Grids Reinforcement Study. In Proceedings of the 2023 11th International Conference on Smart Grid (icSmartGrid), Paris, France, 4–7 June 2023; ISBN 979-8-3503-1066-5. [Google Scholar] [CrossRef]
- Monteiro, J.; Pires, V.F.; Foito, D.; Cordeiro, A.; Silva, J.F.; Pinto, S. A Buck-Boost Converter with Extended Duty-Cycle Range in the Buck Voltage Region for Renewable Energy Sources. Electronics 2023, 12, 584. [Google Scholar] [CrossRef]
- Shahir, F.M.; Babaei, E. Application of high voltage gain DC-DC converter in photovoltaic system with energy storage. In Proceedings of the 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017. [Google Scholar] [CrossRef]
- De Oliveira, F.J.; Ribeiro, E.K.d.B.; Luiz, A.-S.A.; Cupertino, A.F. Operation of a high gain bidirectional DC-DC converter for photovoltaic on-grid systems. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017. [Google Scholar] [CrossRef]
- Uthirasamy, R.; Chinnaiyan, V.K.; Vishnukumar, S.; Karthick, A.; Mohanavel, V.; Subramaniam, U.; Muhibbullah, M. Design of Boosted Multilevel DC-DC Converter for Solar Photovoltaic System. Int. J. Photoenergy 2022, 2022, 1648474. [Google Scholar] [CrossRef]
- Barreto, L.H.S.C.; Praca, P.P.; Henn, G.A.L.; Camara, R.A.; Ranoyca, N.A.L.S.; Oliveira, D.S. High voltage gain boost converter battery charger applied to PV systems. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.R.; Prabhala, V.A.K.; Ferdowsi, M. A Family of High-Voltage-Gain DC–DC Converters Based on a Generalized Structure. IEEE Trans. Power Electron. 2018, 33, 8399–8411. [Google Scholar] [CrossRef]
- Allehyani, A. Analysis of a symmetrical multilevel DC-DC boost converter with ripple reduction structure for solar PV systems. Alex. Eng. J. 2022, 61, 7055–7065. [Google Scholar] [CrossRef]
- Mansour, A.S.; Amer, A.-H.H.; El-Kholy, E.E.; Zaky, M. High gain DC/DC converter with continuous input current for renewable energy applications. Sci. Rep. 2022, 12, 12138. [Google Scholar] [CrossRef] [PubMed]
- Bal, S.; Anurag, A.; Babu, B.C. Comparative analysis of mathematical modeling of Photo-Voltaic (PV) array. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, India, 7–9 December 2012; pp. 269–274. [Google Scholar] [CrossRef]
- Babu, B.C.; Gurjar, S. A Novel Simplified Two-Diode Model of Photovoltaic (PV) Module. IEEE J. Photovolt. 2014, 4, 1156–1161. [Google Scholar] [CrossRef]
- Lee, J.P.; Min, B.D.; Kim, T.J.; Yoo, D.W.; Yoo, J.Y. Design and Control of Novel Topology for Photo-Voltaic DC/DC Converter with High Efficiency under Wide Load Ranges. J. Power Electron. 2009, 9, 300–307. [Google Scholar]
- Chaibi, Y.; Allouhi, A.; Salhi, M. A simple iterative method to determine the electrical parameters of photovoltaic cell. J. Clean. Prod. 2020, 269, 122363. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 1244–1254. [Google Scholar] [CrossRef]
- Nassar-eddine, I.; Obbadi, A.; Errami, Y.; El fajri, A.; Agunaou, M. Parameter estimation of photovoltaic modules using iterative method and the Lambert W function: A comparative study. Energy Convers. Manag. 2016, 119, 37–48. [Google Scholar] [CrossRef]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J. Parameter Estimation Method to Improve the Accuracy of Photovoltaic Electrical Model. IEEE J. Photovolt. 2016, 6, 278–285. [Google Scholar] [CrossRef]
- Humada, A.M.; Darweesh, S.Y.; Mohammed, K.G.; Kamil, M.; Mohammed, S.F.; Kasim, N.K.; Tahseen, T.A.; Awad, O.I.; Mekhilef, S. Modeling of PV system and parameter extraction based on experimental data: Review and investigation. Sol. Energy 2020, 199, 742–760. [Google Scholar] [CrossRef]
- Bai, J.; Liu, S.; Hao, Y.; Zhang, Z.; Jiang, M.; Zhang, Y. Development of a new compound method to extract the five parameters of PV modules. Energy Convers. Manag. 2014, 79, 294–303. [Google Scholar] [CrossRef]
- Lo Brano, V.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Boutana, N.; Mellit, A.; Haddad, S.; Rabhi, A.; Pavan, A.M. An explicit I-V model for photovoltaic module technologies. Energy Convers. Manag. 2017, 138, 400–412. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Jemli, M.; Chebbi, S. Identification of unknown parameters of solar cell models: A comprehensive overview of available approaches. Renew. Sustain. Energy Rev. 2018, 90, 453–474. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A New Stochastic Slime Mould Optimization Algorithm for the Estimation of Solar Photovoltaic Cell Parameters. Optik 2020, 223. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Abido, M. Parameter estimation for five- and seven-parameter photovoltaic electrical models using evolutionary algorithms. Appl. Soft Comput. 2013, 13, 4608–4621. [Google Scholar] [CrossRef]
- Lawan, M.M.G.; Raharijaona, J.; Camara, M.B.; Dakyo, B. Power control for decentralized energy production system based on the renewable energies—Using battery to compensate the wind/load/PV power fluctuations. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017. [Google Scholar] [CrossRef]
- Baqar, A.; Camara, M.B.; Dakyo, B. Supercapacitors Fast Ageing Control in Residential Microgrid Based Photovoltaic/Fuel Cell/Electric Vehicle Charging Station. Energies 2023, 16, 5084. [Google Scholar] [CrossRef]
- Maria, M.; Yassine, M. Machine Learning Based Approaches for Modeling the Output Power of Photovoltaic Array in Real Outdoor Conditions. Electronics 2020, 9, 315. [Google Scholar] [CrossRef]
- Aoun, N.; Bailek, N. Evaluation of mathematical methods to characterize the electrical parameters of photovoltaic modules. Energy Convers. Manag. 2019, 193, 25–38. [Google Scholar] [CrossRef]
- Chowdhury, S.; Chowdhury, S.P.; Taylor, G.A.; Song, Y.H. Mathematical modelling and performance evaluation of a stand-alone polycrystalline PV plant with MPPT facility. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Soliman, M.A.; Al-Durra, A.; Hasanien, H.M. Electrical Parameters Identification of Three-Diode Photovoltaic Model Based on Equilibrium Optimizer Algorithm. IEEE Access 2021, 9, 41891–41901. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Identification of electrical parameters for three-diode photovoltaic model using analytical and sunflower optimization algorithm. Appl. Energy 2019, 250, 109–117. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Aljendy, R.; Al-Sumaiti, A.S.; Shoyama, M.; Ali, Z.M. Tree Growth Based Optimization Algorithm for Parameter Extraction of Different Models of Photovoltaic Cells and Modules. IEEE Access 2020, 8, 119668–119687. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Dou, B.; Zhang, G.; Wu, W. Theoretical and experimental evaluation on the electrical properties of multi-junction solar cells in a reflective concentration photovoltaic system. Energy Rep. 2022, 8, 820–831. [Google Scholar] [CrossRef]
- Available online: https://fr.enfsolar.com/pv/panel-datasheet/crystalline/34981 (accessed on 22 March 2024).
- Jalilzadeh, T.; Rostami, N.; Babaei, E.; Maalandish, M. Ultra-step-up dc–dc converter with low-voltage stress on devices. IET Power Electron. 2019, 12, 345–357. [Google Scholar] [CrossRef]
- Mahajan, S.B.; Sanjeevikumar, P.; Wheeler, P.; Blaabjerg, F.; Rivera, M.; Kulkarni, R. X-Y converter family: A new breed of buck boost converter for high step-up renewable energy applications. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–8. [Google Scholar]
- Okochi, S.; Koizumi, H. A High Step-Up Single Switch DC-DC Converter with Switched-Inductors and Switched-Capacitors. In Proceedings of the 2019 IEEE 4th International Future Energy Electronics Conference (IFEEC), Singapore, 25–28 November 2019; pp. 1–6. [Google Scholar]
- Ranjana, M.S.B.; SreeramulaReddy, N.; Kumar, R.K.P. A novel non-isolated switched inductor floating output DC-DC multilevel boost converter for fuelcell applications. In Proceedings of the 2014 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2014; pp. 1–5. [Google Scholar]
- Fardoun, A.A.; Ismail, E.H. Ultra Step-Up DC–DC Converter with Reduced Switch Stress. IEEE Trans. Ind. Appl. 2010, 46, 2025–2034. [Google Scholar] [CrossRef]
- Wu, B.; Li, S.; Liu, Y.; Smedley, K.M. A New Hybrid Boosting Converter for Renewable Energy Applications. IEEE Trans. Power Electron. 2016, 31, 1203–1215. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, D.; Wang, T.; Xu, Z. Hybrid Switched-Inductor Converters for High Step-Up Conversion. IEEE Trans. Ind. Electron. 2015, 62, 1480–1490. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Almakhles, D.J.; Padmanaban, S.; Blaabjerg, F.; Subramaniam, U.; Ionel, D.M. Analysis and Investigation of Hybrid DC–DC Non-Isolated and Non-Inverting Nx Interleaved Multilevel Boost Converter (Nx-IMBC) for High Voltage Step-Up Applications: Hardware Implementation. IEEE Access 2020, 8, 87309–87328. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Ramirez, J.M.; Peng, F.Z.; Valderrabano, A. A DC-DC multilevel boost converter. IET Power Electron. 2010, 3, 129–137. [Google Scholar] [CrossRef]
- Maalandish, M.; Hosseini, S.H.; Ghasemzadeh, S.; Babaei, E.; Alishah, R.S.; Jalilzadeh, T. Six-phase interleaved boost dc/dc converter with high-voltage gain and reduced voltage stress. IET Power Electron. 2017, 10, 1904–1914. [Google Scholar] [CrossRef]
- Saravanan, S.; Babu, N.R. Design and Development of Single Switch High Step-Up DC–DC Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 855–863. [Google Scholar] [CrossRef]
- Mahamadou, A.T.; Mamadou, B.C.; Brayima, D.; Cristian, N. Wind Power Integration in Hybrid Power System with Active Energy Management. Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 245–263. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy Management in the Decentralized Generation Systems Based on Renewable Energy-Ultracapacitors and Battery to Compensate the Wind/Load Power Fluctuations. IEEE Trans. Ind. Appl. 2015, 51, 1817–1827. [Google Scholar] [CrossRef]
- Oukkacha, I.; Camara, M.B.; Dakyo, B. Energy Management in Electric Vehicle based on Frequency sharing approach, using Fuel cells, Lithium batteries and Supercapacitors. In Proceedings of the IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 986–992, ISBN 978-1-5386-5981-6. [Google Scholar]
- Fapi, C.B.N.; Toure, M.L.; Camara, M.B.; Dakyo, B. MPPT based Fractional Short-Circuit Current—Model Predictive Control for PV System in Real Weather Conditions for Heat-Pump Applications. In Proceedings of the IEEE international conference on intelligent systems and computer vision, ISCV 2024, Fez, Morocco, 18–20 May 2022; IEEE: Piscataway, NJ, USA, 2022. ISBN 978-1-6654-9558-5. [Google Scholar]
- Available online: https://power.larc.nasa.gov/beta/data-access-viewer/ (accessed on 22 March 2024).
- Camara, M.B.; Gualous, H.; Gustin, F.; Berthon, A. Design and New Control of DC/DC Converters to Share Energy Between Supercapacitors and Batteries in Hybrid Vehicles. IEEE Trans. Vehicular Technol. 2008, 57, 2721–2735. [Google Scholar] [CrossRef]
- Tankari, M.A.; Camara, M.B.; Dakyo, B.; Nichita, C. Attenuation of power fluctuations in wind diesel hybrid system—Using ultracapacitors and batteries. In Proceedings of the IEEE 2010 XIX International Conference on Electrical Machines (ICEM), Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]



























| Irr [W/m2] | 2 × 105 | 3 × 105 | 5 × 105 | 7 × 105 | 10 × 105 |
|---|---|---|---|---|---|
| T [°C] | Rs [mΩ] | ||||
| 25.77 | 9.48 | 12.64 | 15.21 | 16.70 | 19.59 |
| 30.038 | 9.47 | 12.65 | 15.21 | 16.70 | 19.57 |
| 35.108 | 9.57 | 12.68 | 15.26 | 16.74 | 19.60 |
| 40.01 | 9.68 | 12.72 | 15.34 | 16.77 | 19.60 |
| 45.038 | 9.85 | 12.82 | 15.37 | 16.82 | 19.62 |
| 50.025 | 10.05 | 12.92 | 15.45 | 16.86 | 19.66 |
| 54.927 | 10.26 | 13.03 | 15.55 | 16.90 | 19.68 |
| 60.165 | 10.50 | 13.17 | 15.67 | 16.99 | 19.73 |
| 65.025 | 10.79 | 13.33 | 15.79 | 17.06 | 19.79 |
| 70.011 | 11.13 | 13.52 | 15.88 | 17.14 | 19.85 |
| 74.998 | 11.48 | 13.75 | 16.01 | 17.24 | 19.89 |
| 80.026 | 11.84 | 13.99 | 16.25 | 17.34 | 19.99 |
| 85.054 | 12.28 | 14.25 | 16.40 | 17.46 | 20.01 |
| Parameters | Symbol | Values |
|---|---|---|
| Rated Current | Imp | 9 A |
| Number of parallel strings in a PV module | Np,module | 1 |
| Number of cells in series in a PV module | Ns,module | 72 |
| Rated Voltage | Vmp | 38 V |
| Open-Circuit Voltage | Voc | 46.5 V |
| Topology | Components | Voltage Gain | I/O Voltage Frequency and Power Rating | Applications | |||
|---|---|---|---|---|---|---|---|
| Passive | Active | ||||||
| Inductors | Capacitors | Switches | Diodes | ||||
| [44] | 3 | 7 | 1 | 7 | 25 V/438 V 40 kHz/450 W | - | |
| [45] | 3 | 2 | 1 | 6 | 10 V 50 kHz/100 W | •Photovoltaic Multilevel Inverter System. •High Voltage Automotive Applications •Industrial Drives | |
| [46] | 2 | 4 | 1 | 5 | 5 V/36.1 V 20 kHz | ||
| [47] | 2 | 5 | 1 | 8 | 24 V/480 V 50 kHz/450 W | •Fuel Cell Applications | |
| [48] | 2 | 4 | 1 | 5 | 10 V/120 V 100 kHz/50 W | - | |
| [49] | 1 | 4 | 1 | 4 | 35 V/380 V 40 kHz/200 W | •Renewable energy •PV systems | |
| [50] | 4 | 1 | 2 | 7 | 20 V-40 V/200 V 50 kHz/200 W | •PV connected to the grid •Fuel Cell Applications | |
| [51] | 1 | 5 | 1 | 5 | 50 V/300 V 100 kHz | •PV systems •Fuel Cell Applications | |
| [52] | 2 | 7 | 2 | 10 | 12 V/120 V 50 kHz/100 W | •PV systems •Electric vehicles | |
| [53] | 6 | 8 | 6 | 14 | 24 V/213 V 25 kHz/453 W | •PV systems | |
| [54] | 2 | 4 | 1 | 4 | 30 V/300 V 24 kHz/250 W | •PV systems | |
| Proposed [18] | 4 | 2 | 2 | 8 | 270 V/1000 V 10 kHz/204 kW | •PV systems | |
| Parameters | Symbol | Values |
|---|---|---|
| Number of parallel strings in a PV string | Np,chain | 80 |
| Number of modules in series in a PV string | Ns,chain | 7 |
| PV module series resistance | Rs | Equation (1) |
| PV string voltage | Vpv | 270 V |
| DC-bus voltage reference | Voref | 1350 V |
| Inductor of coils | L1 = L2 = L3 = L4 | 2.97 mH |
| Weighting coefficient for duty cycle | K | 1/2 |
| Converter control frequency | f | 10 kHz |
| DC-bus capacitors | C1 = C2 | 933 μF |
| Proportional coefficient of DC-bus voltage controller | kpv | 8.29 |
| Integral coefficient of DC-bus voltage controller | kiv | 36,837 |
| DC-bus voltage reference low-pass filter time constant | τv | 0.225 ms |
| Proportional coefficient of the I4 current controller | kpi | 52.78 |
| Integral coefficient of the I4 current controller | kii | 234,501.8 |
| I4,ref current’s reference low-pass filter time constant | τi | 0.225 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Touré, M.L.; Camara, M.B.; Dakyo, B. Symmetrical Multilevel High Voltage-Gain Boost Converter Control Strategy for Photovoltaic Systems Applications. Electronics 2024, 13, 2565. https://doi.org/10.3390/electronics13132565
Touré ML, Camara MB, Dakyo B. Symmetrical Multilevel High Voltage-Gain Boost Converter Control Strategy for Photovoltaic Systems Applications. Electronics. 2024; 13(13):2565. https://doi.org/10.3390/electronics13132565
Chicago/Turabian StyleTouré, Mohamed Lamine, Mamadou Baïlo Camara, and Brayima Dakyo. 2024. "Symmetrical Multilevel High Voltage-Gain Boost Converter Control Strategy for Photovoltaic Systems Applications" Electronics 13, no. 13: 2565. https://doi.org/10.3390/electronics13132565
APA StyleTouré, M. L., Camara, M. B., & Dakyo, B. (2024). Symmetrical Multilevel High Voltage-Gain Boost Converter Control Strategy for Photovoltaic Systems Applications. Electronics, 13(13), 2565. https://doi.org/10.3390/electronics13132565









