Rail Surface Defect Detection Based on Dual-Path Feature Fusion
Abstract
:1. Introduction
- This study proposes a steel rail surface defect detection model based on dual-path feature fusion (DPF). The model is designed with two distinct paths to separately extract low-level and high-level features. By utilizing an attention mechanism and feature fusion, these features are integrated, preserving richer information and enhancing the accuracy and robustness of detection.
- The Dy-Bottleneck module is proposed in this paper, which incorporates a dual-path structure combining two parallel and interactive dynamic convolutions. This module dynamically adjusts based on the characteristics of the input data, allowing it to adapt to diverse datasets and complex scenarios.
- A symmetric feature attention fusion module is introduced in this study. This module combines the lightweight Convolutional Block Attention Module (CBAM) with the symmetric design of the feature pyramid network (FPN). Specifically, CBAM attention and FPN structures are employed in both the feature extraction and feature fusion stages. This symmetric design makes the module more compact and consistent, enhancing the model’s understanding and recognition ability of images for better performance.
2. Related Work
2.1. Dynamic Convolution
2.2. Convolutional Block Attention Module
2.3. Feature Pyramid
3. Methods
3.1. Overall Structure
3.2. Dy-Bottleneck Module
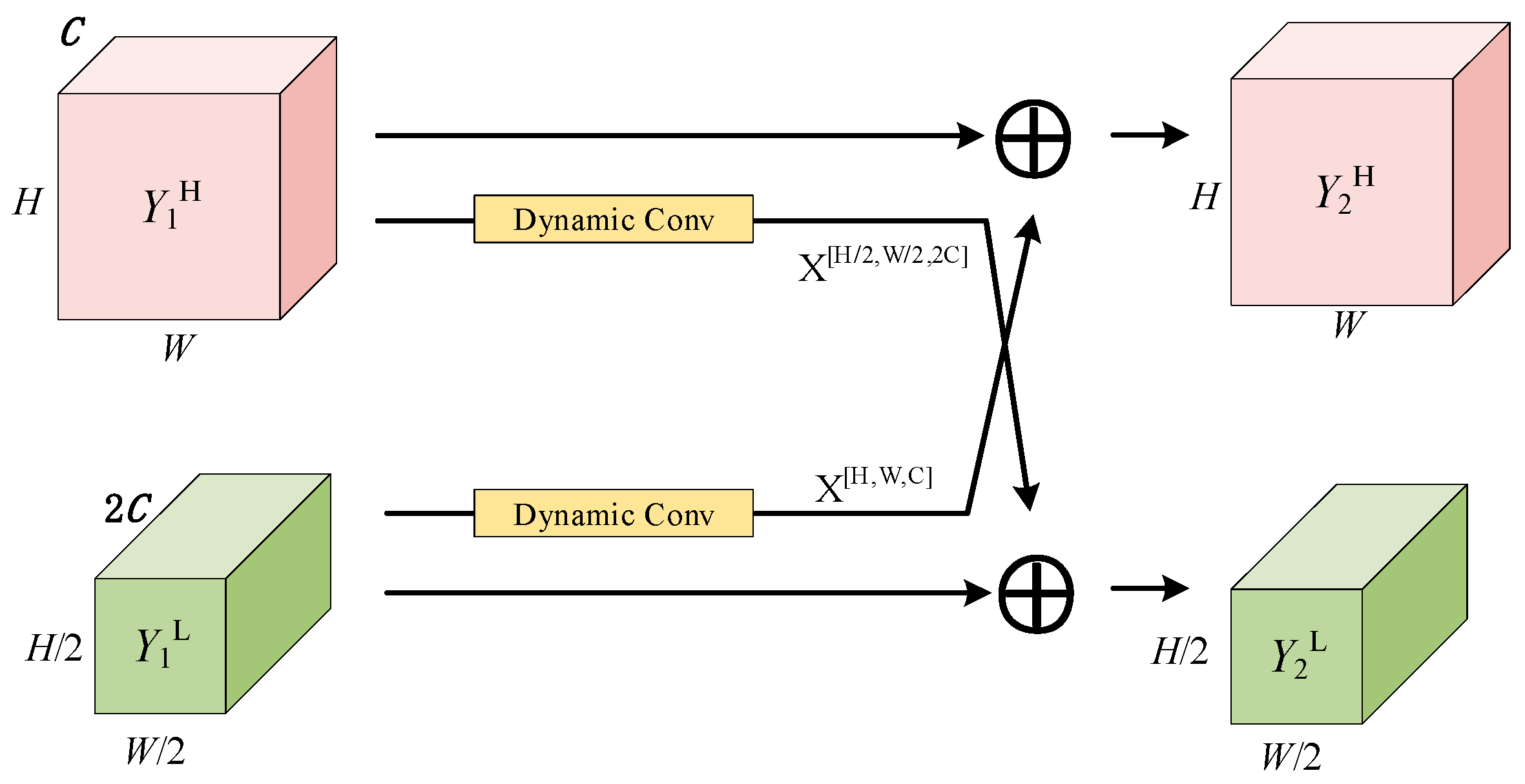
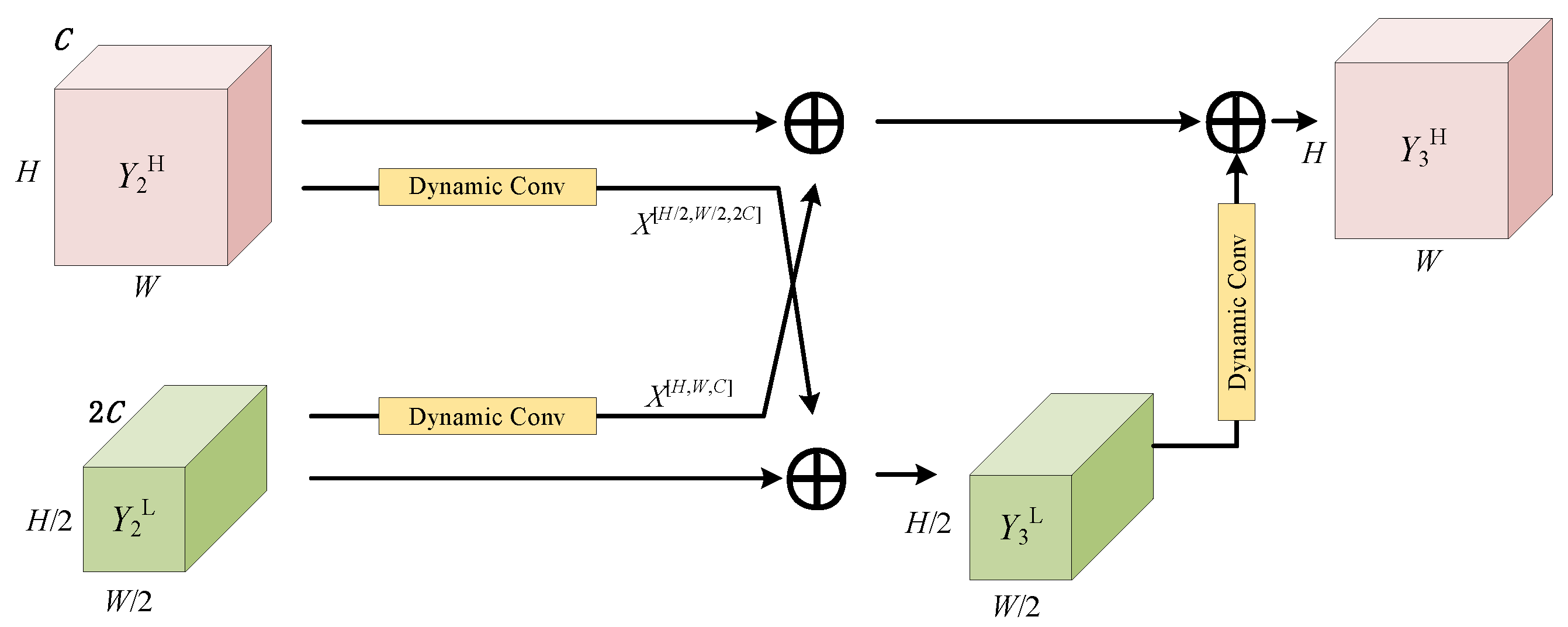
3.3. Symmetric Feature Attention Fusion Module
3.4. Detection Head
3.5. Loss Function
- (1)
- Classification Loss
- (2)
- Confidence Loss
- (3)
- Location Loss
4. Experimental Results
4.1. Datasets
4.2. Evaluation Indicators or Evaluation Metrics
4.3. Experimental Parameter Settings
4.4. Experimental Results
- (1)
- Ablation Experiment
- (2)
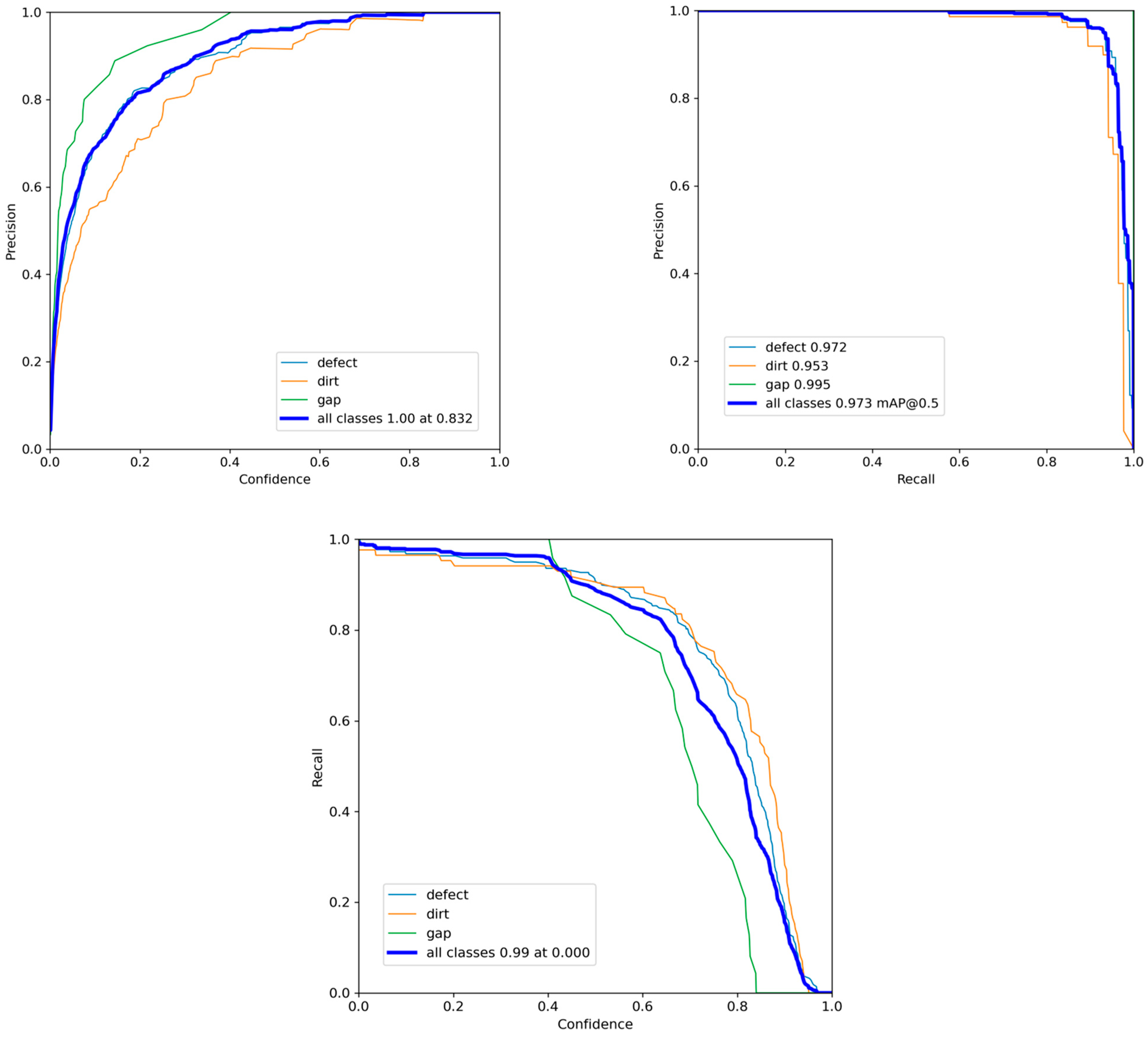
- Visualization Result Analysis
- (3)
- Comparative Experiments with Mainstream Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, R.T.; Barkan, C.P.L. Railroad accident rates for use in transportation risk analysis. Transp. Res. Rec. 2004, 1863, 88–98. [Google Scholar] [CrossRef]
- Shang, L.; Yang, Q.; Wang, J.; Li, S.; Lei, W. Detection of rail surface defects based on CNN image recognition and classification. In Proceedings of the 2018 20th International Conference on Advanced Communication Technology (ICACT), Chuncheon, Republic of Korea, 11–14 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 45–51. [Google Scholar]
- Gasparini, R.; D’Eusanio, A.; Borghi, G.; Pini, S.; Scaglione, G.; Calderara, S.; Fedeli, E.; Cucchiara, R. Anomaly detection, localization and classification for railway inspection. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3419–3426. [Google Scholar]
- Soleimanmeigouni, I.; Ahmadi, A.; Nissen, A.; Xiao, X. Prediction of railway track geometry defects: A case study. Struct. Infrastruct. Eng. 2020, 16, 987–1001. [Google Scholar] [CrossRef]
- Feng, J.H.; Yuan, H.; Hu, Y.Q.; Lin, J.; Liu, S.W.; Luo, X. Research on deep learning method for rail surface defect detection. IET Electr. Syst. Transp. 2020, 10, 436–442. [Google Scholar] [CrossRef]
- Yu, H.; Li, Q.; Tan, Y.; Gan, J.; Wang, J.; Geng, Y.A.; Jia, L. A coarse-to-fine model for rail surface defect detection. IEEE Trans. Instrum. Meas. 2018, 68, 656–666. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Q.; He, Q.; Yu, T.; Zhang, M.; Wang, P. CUFuse: Camera and ultrasound data fusion for rail defect detection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21971–21983. [Google Scholar] [CrossRef]
- Zhou, W.; Hong, J. FHENet: Lightweight feature hierarchical exploration network for real-time rail surface defect inspection in RGB-D images. IEEE Trans. Instrum. Meas. 2023, 72, 5005008. [Google Scholar] [CrossRef]
- Papaelias, M.P.; Roberts, C.; Davis, C.L. A review on non-destructive evaluation of rails: State-of-the-art and future development. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2008, 222, 367–384. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Chen, J.; Wang, S.; Wang, L. Rail Surface Defect Detection Through Bimodal RSDINet and Three-Branched Evidential Fusion. IEEE Trans. Instrum. Meas. 2023, 72, 2508714. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, Z.; Xie, F.; Yang, P.; Shi, J.; Chen, L. Automatic fastener classification and defect detection in vision-based railway inspection systems. IEEE Trans. Instrum. Meas. 2013, 63, 877–888. [Google Scholar] [CrossRef]
- Alemi, A.; Corman, F.; Lodewijks, G. Condition monitoring approaches for the detection of railway wheel defects. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 961–981. [Google Scholar] [CrossRef]
- Wei, X.; Yang, Z.; Liu, Y.; Wei, D.; Jia, L.; Li, Y. Railway track fastener defect detection based on image processing and deep learning techniques: A comparative study. Eng. Appl. Artif. Intell. 2019, 80, 66–81. [Google Scholar] [CrossRef]
- Ge, H.; Huat, D.C.K.; Koh, C.G.; Dai, G.; Yu, Y. Guided wave–based rail flaw detection technologies: State-of-the-art review. Struct. Health Monit. 2022, 21, 1287–1308. [Google Scholar] [CrossRef]
- Soukup, D.; Huber-Mörk, R. Convolutional neural networks for steel surface defect detection from photometric stereo images. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 8–10 December 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 668–677. [Google Scholar]
- Li, Y.; Trinh, H.; Haas, N.; Otto, C.; Pankanti, S. Rail component detection, optimization, and assessment for automatic rail track inspection. IEEE Trans. Intell. Transp. Syst. 2013, 15, 760–770. [Google Scholar]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective kernel networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar]
- Zhang, Q.; Yang, Y.B. Rest: An efficient transformer for visual recognition. Adv. Neural Inf. Process. Syst. 2021, 34, 15475–15485. [Google Scholar]
- Gullers, P.; Dreik, P.; O Nielsen, J.C.; Ekberg, A.; Andersson, L. Track condition analyser: Identification of rail rolling surface defects, likely to generate fatigue damage in wheels, using instrumented wheelset measurements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2011, 225, 1–13. [Google Scholar] [CrossRef]
- Dong, H.; Song, K.; He, Y.; Xu, J.; Yan, Y.; Meng, Q. PGA-Net: Pyramid feature fusion and global context attention network for automated surface defect detection. IEEE Trans. Ind. Inform. 2019, 16, 7448–7458. [Google Scholar] [CrossRef]
- Yunjie, Z.; Xiaorong, G.; Lin, L.; Yongdong, P.; Chunrong, Q. Simulation of laser ultrasonics for detection of surface-connected rail defects. J. Nondestruct. Eval. 2017, 36, 70. [Google Scholar] [CrossRef]
- Vincent, O.R.; Babalola, Y.E.; Sodiya, A.S.; Adeniran, O.J. A Cognitive Rail Track Breakage Detection System Using Artificial Neural Network. Appl. Comput. Syst. 2021, 26, 80–86. [Google Scholar] [CrossRef]
- Cheng, X.; Yu, J. RetinaNet with difference channel attention and adaptively spatial feature fusion for steel surface defect detection. IEEE Trans. Instrum. Meas. 2020, 70, 2503911. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wu, W.C.; Yin, C.C. Generation and directional decomposition of guided waves for finite-range defect detection in rail tracks. J. Mech. 2023, 39, 540–553. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate attention for efficient mobile network design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 13713–13722. [Google Scholar]
- Gibert, X.; Patel, V.M.; Chellappa, R. Deep multitask learning for railway track inspection. IEEE Trans. Intell. Transp. Syst. 2016, 18, 153–164. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, R.Y.; Li, L.; Xie, X. Simam: A simple, parameter-free attention module for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR 2021, Virtual, 18–24 July 2021; pp. 11863–11874. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 11534–11542. [Google Scholar]
- Song, X.; Wang, Y.; Li, C.; Song, L. WDC-YOLO: An improved YOLO model for small objects oriented printed circuit board defect detection. J. Electron. Imaging 2024, 33, 013051. [Google Scholar] [CrossRef]
- Dong, J.Y.; Lv, W.T.; Bao, X.M. Research progress of the PCB surface defect detection method based on machine vision. J. Zhejiang Sci-Tech Univ. 2021, 45, 379–389. [Google Scholar]
- Akram, M.W.; Li, G.; Jin, Y.; Chen, X.; Zhu, C.; Ahmad, A. Automatic detection of photovoltaic module defects in infrared images with isolated and develop-model transfer deep learning. Sol. Energy 2020, 198, 175–186. [Google Scholar] [CrossRef]
- Silva, L.H.D.S.; Azevedo, G.O.D.A.; Fernandes, B.J.; Bezerra, B.L.; Lima, E.B.; Oliveira, S.C. Automatic optical inspection for defective PCB detection using transfer learning. In Proceedings of the 2019 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Guayaquil, Ecuador, 11–15 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR 2019, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 7464–7475. [Google Scholar]
- Tan, M.; Pang, R.; Le, Q.V. Efficientdet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10781–10790. [Google Scholar]










| Main Modules | Input (Dual-Path) Size Dimensions | Output (Dual-Path) Size Dimensions | Quantity |
|---|---|---|---|
| Max pooling | 640 × 640 × 3 | 320 × 320 × 64 | 1 |
| Conv 2D | 320 × 320 × 64 | 160 × 160 × 128 | 1 |
| Dy-Bottleneck (F) | 160 × 160 × 128 | 160 × 160 × 128 and 80 × 80 × 128 | 1 |
| Dy-Bottleneck (M) 1st | 160 × 160 × 128 and 80 × 80 × 128 | 160 × 160 × 128 and 80 × 80 × 128 | 2 |
| Dy-Bottleneck (M) 2nd | 160 × 160 × 128 and 80 × 80 × 128 | 80 × 80 × 256 and 40 × 40 × 256 | 4 |
| Dy-Bottleneck (M) 3rd | 80 × 80 × 256 and 40 × 40 × 256 | 40 × 40 × 512 and 20 × 20 × 512 | 4 |
| Dy-Bottleneck (M) 4th | 40 × 40 × 512 and 20 × 20 × 512 | 40 × 40 × 512 and 20 × 20 × 512 | 2 |
| Dy-Bottleneck (L) | 40 × 40 × 512 and 20 × 20 × 512 | 20 × 20 × 1024 | 1 |
| No | Dual-Path Backbone | Dynamic Convolution | Symmetric Attention | CBAM | P (%) | R (%) | mAP@0.5 (%) |
|---|---|---|---|---|---|---|---|
| 1 | × | × | × | × | 68.4 | 70.2 | 71.5 |
| 2 | × | × | √ | × | 73.2 | 65.1 | 71.4 |
| 3 | × | × | √ | √ | 87.4 | 68.0 | 72.5 |
| 4 | √ | × | √ | √ | 91.5 | 93.6 | 97.2 |
| 5 | √ | √ | × | √ | 93.8 | 95.8 | 97.3 |
| 6 | √ | √ | √ | × | 94.1 | 94.1 | 97.3 |
| 7 | √ | √ | √ | √ | 97.5 | 93.8 | 98.3 |
| Model | P (%) | R (%) | mAP0.5 (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Defect | Dirt | Gap | Defect | Dirt | Gap | Defect | Dirt | Gap | |
| SSD [37] | 68.4 | 63.3 | 87.4 | 70.2 | 67.1 | 58.0 | 71.5 | 69.9 | 72.8 |
| Faster R-CNN [38] | 85.7 | 87.1 | 89.7 | 80.8 | 78.7 | 79.1 | 86.2 | 86.5 | 87.2 |
| YOLOv3-tiny [39] | 90.1 | 90.6 | 91.3 | 82.9 | 83.2 | 83.0 | 88.8 | 90.1 | 89.7 |
| YOLOv4 [40] | 92.3 | 91.6 | 93.2 | 87.89 | 89.86 | 90.89 | 90.55 | 90.34 | 90.89 |
| YOLOv5s [41] | 91.4 | 83.3 | 87.3 | 91.6 | 90.7 | 92.75 | 91.3 | 91.6 | 94.4 |
| YOLOv8n [42] | 91.5 | 89.8 | 100 | 93.6 | 94.1 | 99.8 | 97.2 | 95.3 | 99.5 |
| DETR [43] | 98.1 | 91.0 | 95.8 | 94.4 | 94.1 | 95.8 | 98.3 | 97.3 | 99.0 |
| DPF | 98.6 | 94.1 | 100 | 94.5 | 94.1 | 92.7 | 98.3 | 97.3 | 99.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Chen, G. Rail Surface Defect Detection Based on Dual-Path Feature Fusion. Electronics 2024, 13, 2564. https://doi.org/10.3390/electronics13132564
Zhong Y, Chen G. Rail Surface Defect Detection Based on Dual-Path Feature Fusion. Electronics. 2024; 13(13):2564. https://doi.org/10.3390/electronics13132564
Chicago/Turabian StyleZhong, Yinfeng, and Guorong Chen. 2024. "Rail Surface Defect Detection Based on Dual-Path Feature Fusion" Electronics 13, no. 13: 2564. https://doi.org/10.3390/electronics13132564
APA StyleZhong, Y., & Chen, G. (2024). Rail Surface Defect Detection Based on Dual-Path Feature Fusion. Electronics, 13(13), 2564. https://doi.org/10.3390/electronics13132564






