Research on Forging Dimension Online Measuring System Based on Vibration Point Cloud Compensation
Abstract
1. Introduction
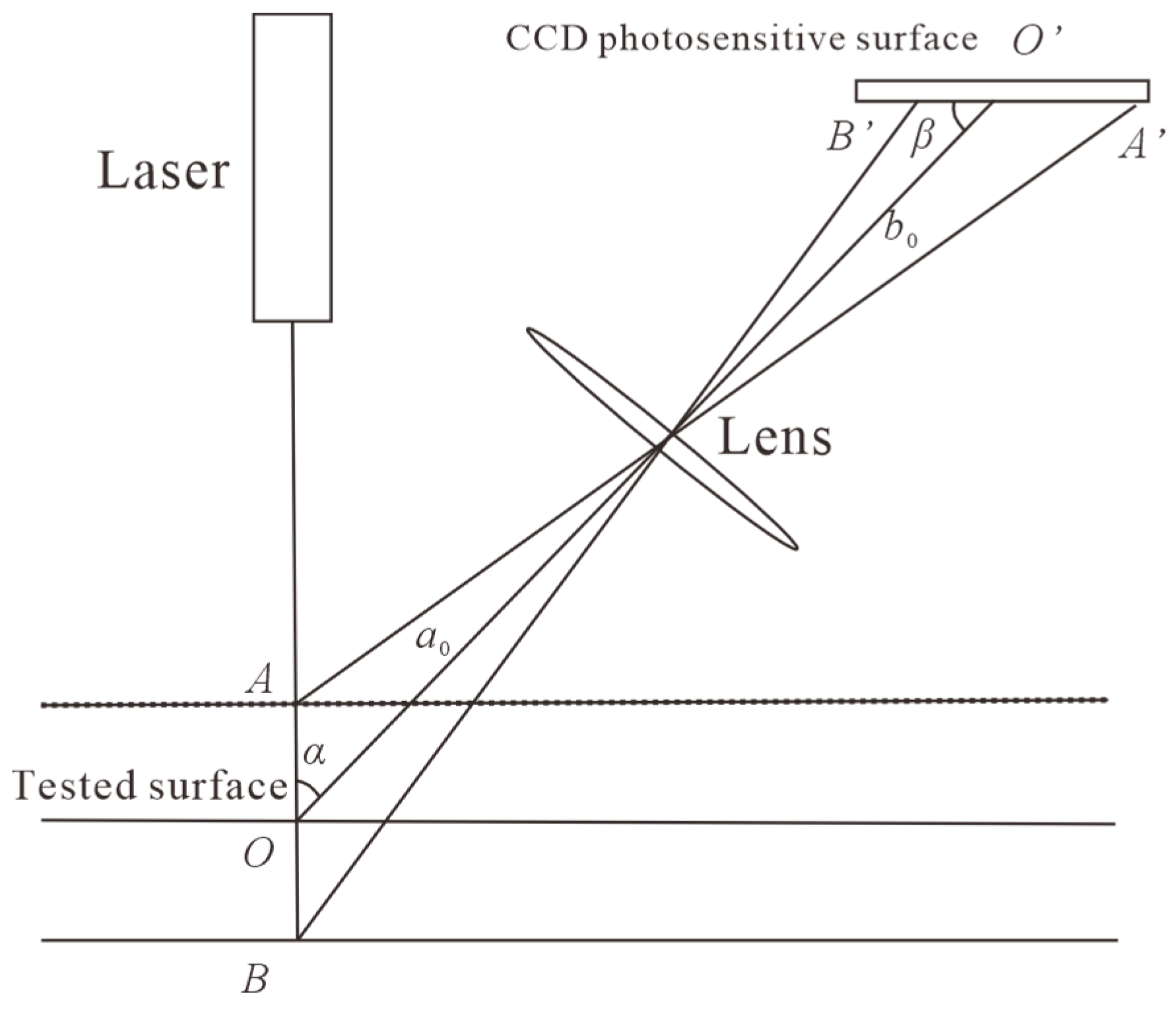
2. The Principle of Laser Triangulation Distance Measurement Technology
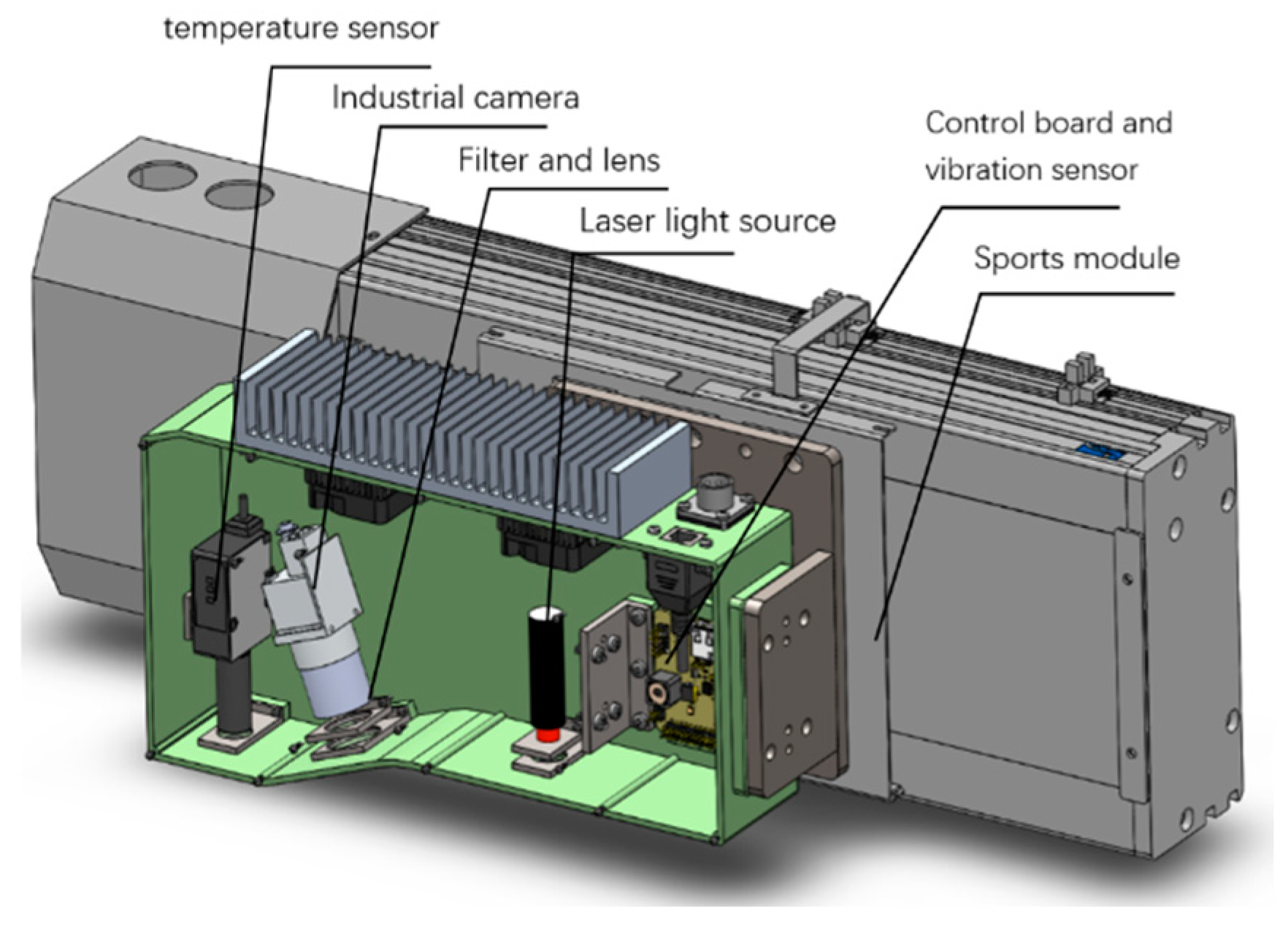
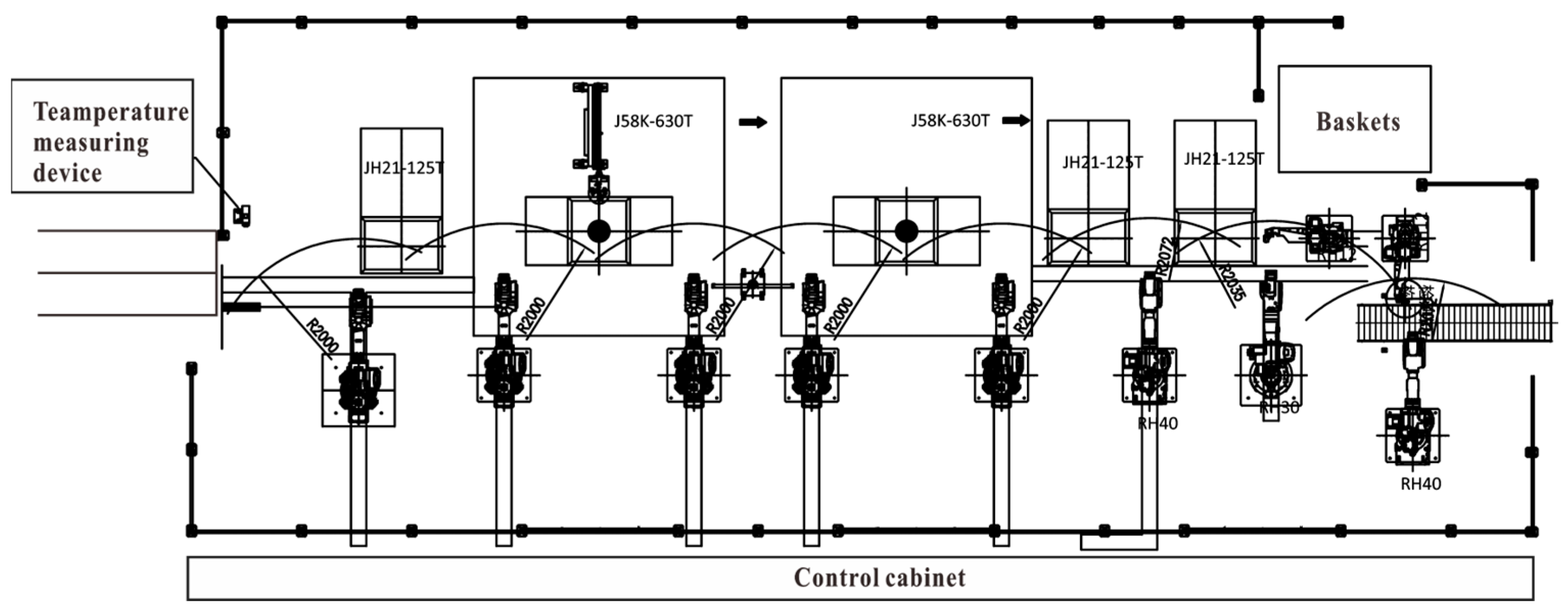
3. Construction of a Hot Dimensional Measurement Device for Forgings
3.1. Camera
3.2. Laser Light Source
3.3. Filters and Lenses
3.4. Vibration and Temperature Sensors
4. Algorithm Design
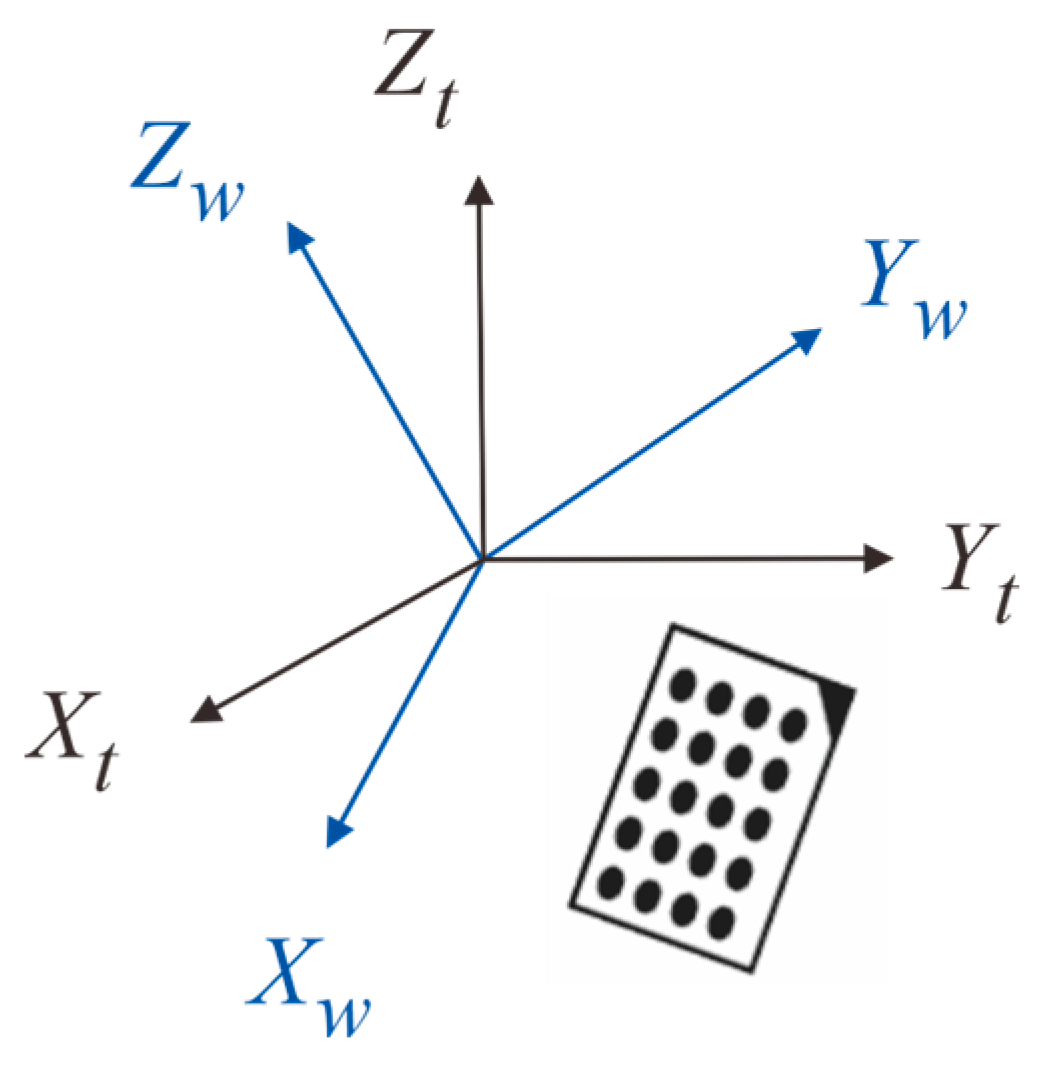
4.1. 3D Point Cloud Data Compensation for Forgings
4.2. Forging Detection Based on Surface Template Matching
4.2.1. Creating a Global Model of Forging Point Cloud
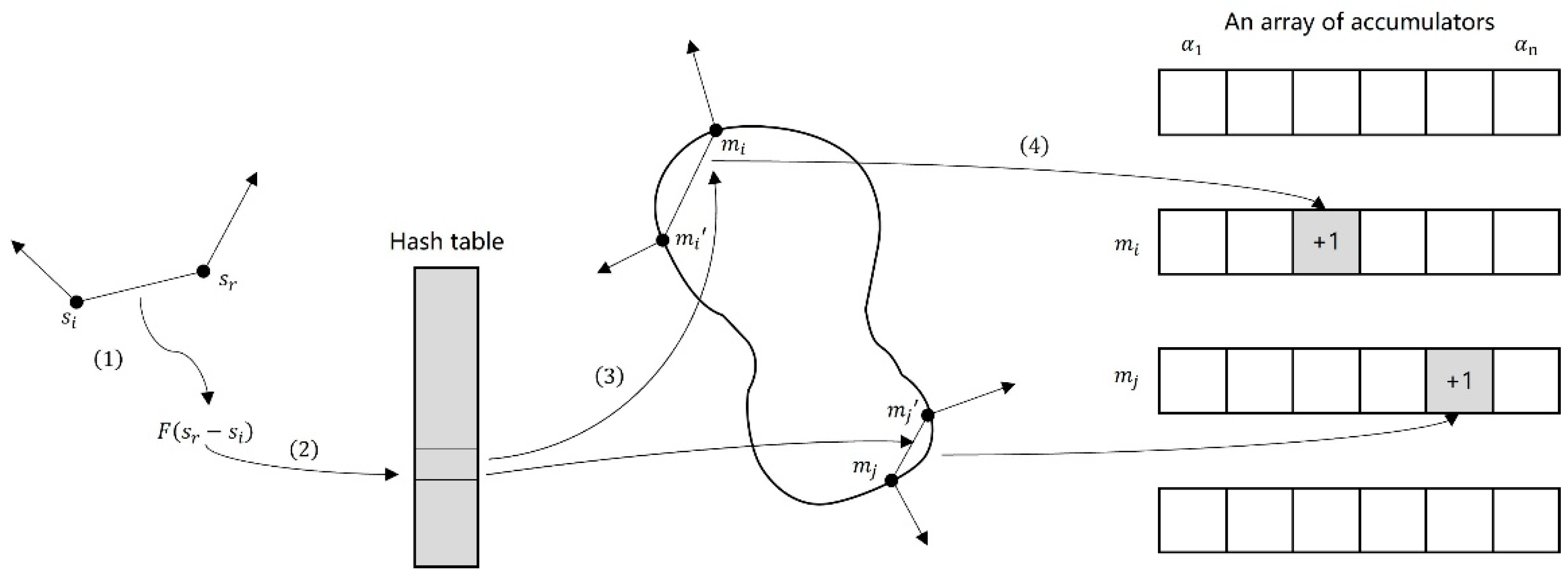
4.2.2. Selection of Reference Points for Forging Inspection
4.2.3. Forging Pose Correction
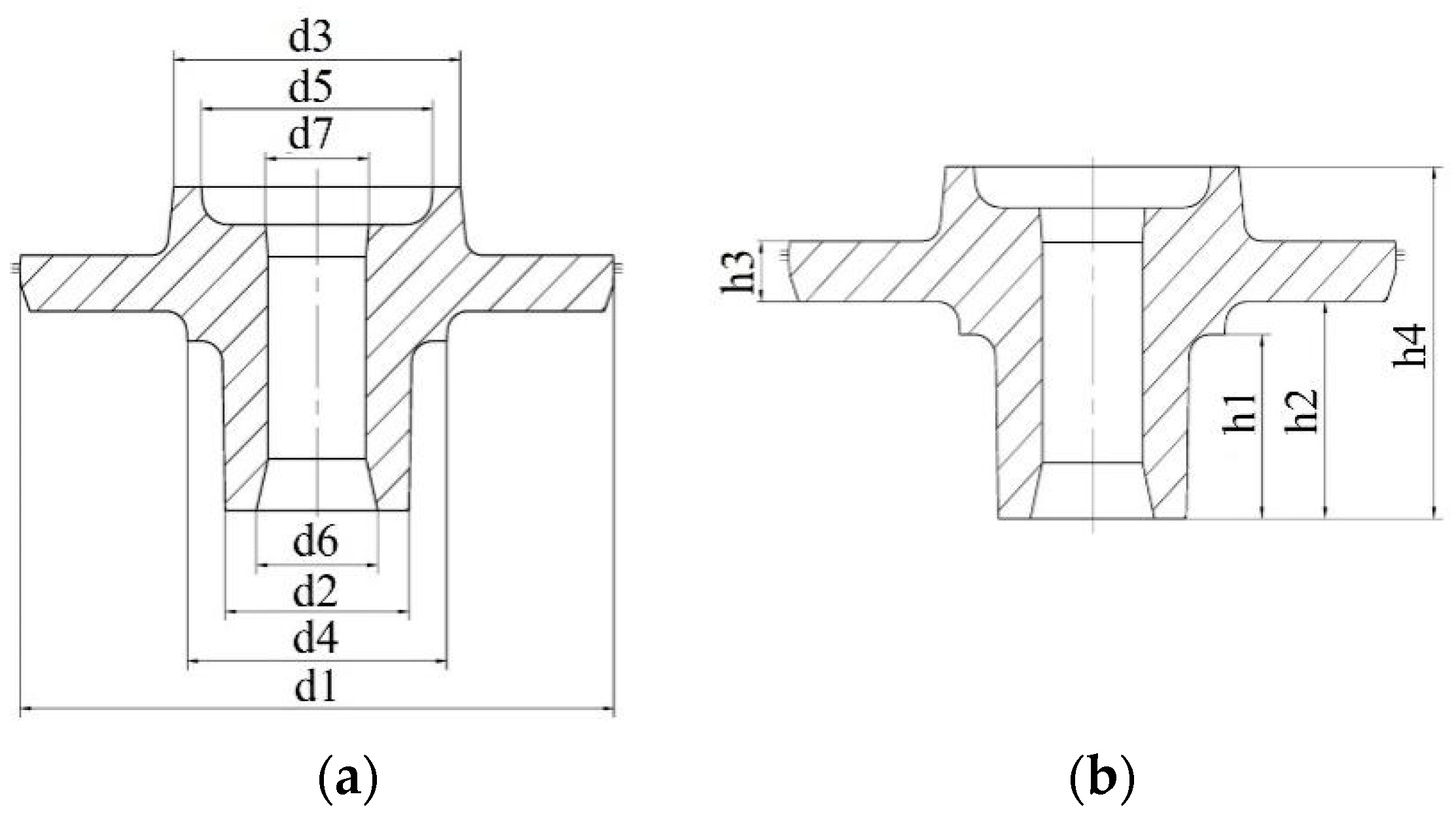
4.3. Measurement of Forging Dimensions
4.3.1. Point Cloud Fitting of Three-Layer Planes for Forgings
4.3.2. Edge Extraction of Forging Contour
4.3.3. Edge Fitting of Forging Contour
4.3.4. Obtaining Forging Dimensions
5. Experimental Setup
6. Experimental Testing and Analysis
7. Conclusions
- We achieved compensation for the deviation of the point cloud of the workpiece to be measured by integrating the vibration signal obtained from the built-in accelerometer and transforming the displacement offset under TCS to WCS through the rotation matrix, reducing the impact of forging machine vibration on the point cloud data of the forging;
- We use the Hough voting method to obtain the forging detection reference point based on the standard forging uniform sampling of the forging global model. We improve the integrity of the forging point cloud map by using the ICP algorithm to match the reference points and complete the forging pose correction;
- On the basis of compensating for point cloud data of forgings and correcting the pose of forgings, we achieve a series of diameter and height measurements of hub forgings through fitting the forging plane point cloud, extracting the contour edge of forgings, and fitting the forging edge. The measurement accuracy was significantly improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hawryluk, M.; Ziemba, J.; Sadowski, P. A review of current and new measurement techniques used in hot die forging processes. Meas. Control. 2017, 50, 74–86. [Google Scholar] [CrossRef]
- Hawryluk, M.; Ziemba, J. Possibilities of application measurement techniques in hot die forging processes. Measurement 2017, 110, 284–295. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Fu, X.; Zhang, F. Measurement and control technology of the size for large hot forgings. Measurement 2014, 49, 52–59. [Google Scholar] [CrossRef]
- Gao, H.; Wang, B.; Zuo, J. A Review of Online Detection Method for Thermal Geometric Parameters of Large Rings. Mach. Des. Manuf. Eng. 2019, 1, 93–96. [Google Scholar]
- Shen, J.; Xing, T.; Zhang, C. Cavity Detection Method of Hot State Axle Forging Based on Laser Technology. Optik 2022, 257, 168782. [Google Scholar] [CrossRef]
- Dworkin, S.B.; Nye, T.J. Image Processing for Machine Vision Measurement of Hot Formed Parts. J. Mater. Process. Technol. 2006, 174, 1–6. [Google Scholar] [CrossRef]
- Shen, J.; Xing, T. Detection Technology of Void Temperature Field inside Hot Hull Forgings. J. Coast. Res. 2020, 103, 397–401. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Fu, X. Detection analysis of interior void for hot axial forging based on the interior temperature field. Appl. Therm. Eng. 2016, 93, 43–49. [Google Scholar] [CrossRef]
- Zhang, Y.; Miao, S.; Fu, X.; Li, Q.; Gao, J. Online measuring method of radial section line for ring forgings. Int. J. Adv. Manuf. Technol. 2019, 101, 3035–3046. [Google Scholar] [CrossRef]
- Nellums, R.O.; Habbit, R.D.; Heying, M.R.; Pitts, T.A.; Sandusky, J.V. 3D scannerless LADAR for orbiter inspection. In Proceedings of the Spaceborne Sensors III, Kissimmee, FL, USA, 18 April 2006; pp. 147–163. [Google Scholar]
- Wu, Z.; Wei, X.; Song, L.; Zhu, X. Solution for vision occlusion based on binocular line-structured light. Optoelectron. Lett. 2021, 17, 432–437. [Google Scholar] [CrossRef]
- Lee, J.; Shin, H.; Lee, S. Development of a wide area 3D scanning system with a rotating line laser. Sensors 2021, 21, 3885. [Google Scholar] [CrossRef]
- Han, L. Research on Automated 3D Measurement for Online Inspection of Hot Forming Parts. Ph.D. Thesis, Huazhong University of Science & Technology, Wuhan, China, 2019. [Google Scholar]
- Liu, Y.; Wang, Z.; Liu, Q. Research on Aircraft Profile Digital Measurement Based on Fusion of Metrascan and Laser Radar. Mod. Manuf. Eng. 2019, 2, 36–40. [Google Scholar]
- Pan, X.; Zhang, L.; He, K. Method of Accuracy Analysis for Composite Material Surface Measurement by Lidar. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1398–1404. [Google Scholar]
- Lei, C.; Liu, Y. A Method for Measuring the Surface Shape of Dynomizing Optical Element Based on Binocular Structured Light 3D Measurement. Opt. Optoelectron. Technol. 2022, 1, 14–20. [Google Scholar]
- An, Z.; Wang, J. Surface Flatness Measurement of Workpiece Based on Line Laser and Template Matching. Control Eng. China 2018, 25, 341–345. [Google Scholar]
- Han, L.; Cheng, X.; Li, Z.; Zhong, K.; Shi, Y.; Jiang, H. A robot-driven 3D shape measurement system for automatic quality inspection of thermal objects on a forging production line. Sensors 2018, 18, 4368. [Google Scholar] [CrossRef]
- He, J.; Gao, F.; Wu, S.; Liu, R.; Zhao, X. Measure dimension of rotating large hot steel shell using pulse laser on PRRR robot. Measurement 2012, 45, 1814–1823. [Google Scholar] [CrossRef]
- Liao, Y.; Huang, W.; Zhang, R. Application of Intelligent Operation and Maintenance Technology in 2050 mm Hot Rolling Equipment. Bao-Steel Technol. 2019, 6, 31–37. [Google Scholar]
- Liu, W.; Feng, T.; Shi, Q. Hydraulic Shock Vibration and Positioning Control for Forging Manipulator Walking System. Forg. Stamp. Technol. 2019, 12, 99–103. [Google Scholar]
- Teng, H.; Han, J.; Wang, M. State Diagnosis of Automatic Tool Changer Positioning Accuracy Based on Vibration Characteristics. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 86–91, 95. [Google Scholar]
- Wang, Q.; He, F. A review of developments in the forging of connecting rods in China. J. Mater. Process. Technol. 2004, 151, 192–195. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, S.; Liu, Z.; Liu, C. Design and development of management and control system for intelligent die forging production line. In Proceedings of the 2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; pp. 230–233. [Google Scholar]
- Tombari, F.; Di Stefano, L. Object recognition in 3d scenes with occlusions and clutter by hough voting. In Proceedings of the 2010 Fourth Pacific-Rim Symposium on Image and Video Technology, Singapore, 14–17 November 2010; pp. 349–355. [Google Scholar]





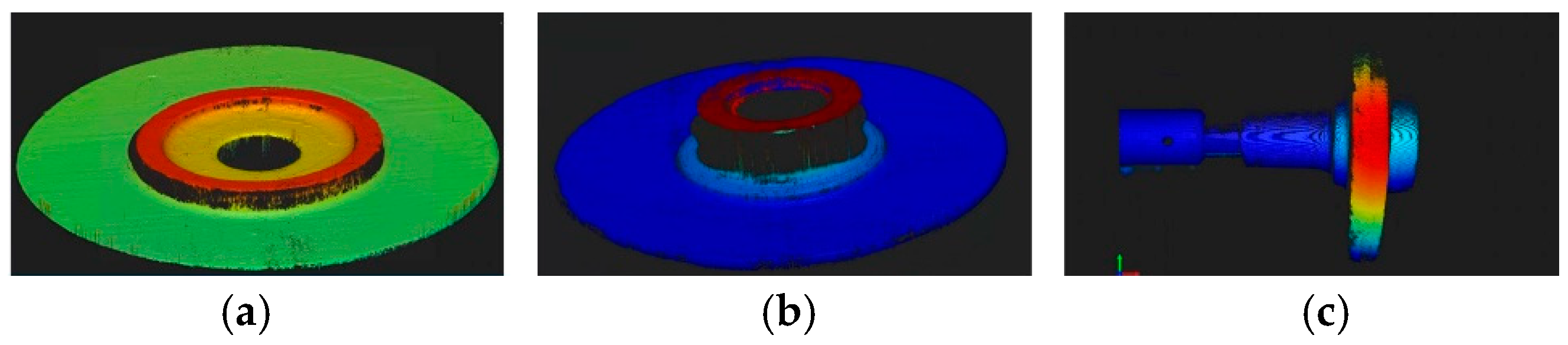
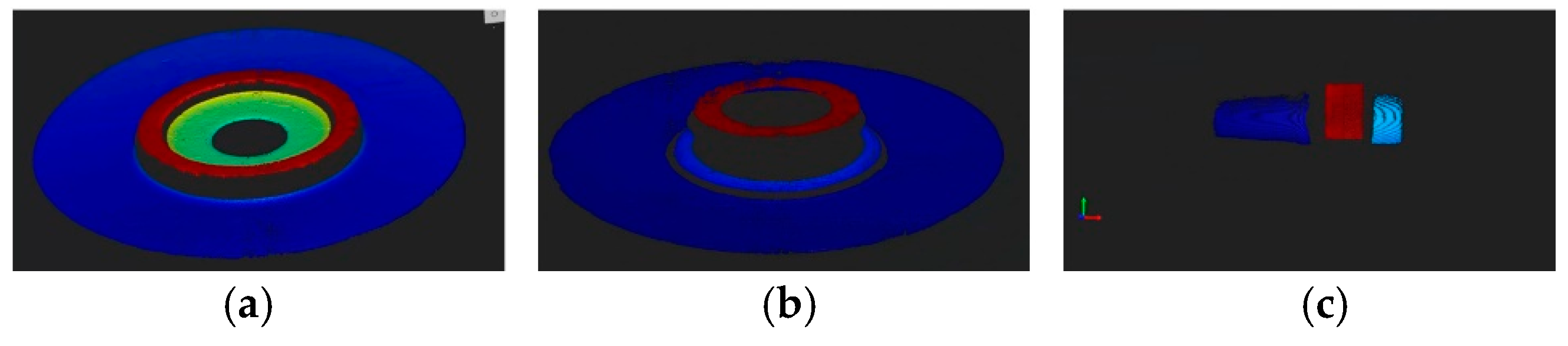


| Index | Before Compensation/mm | After Compensation/mm | Theoretical Value/mm | Error after Compensation/mm |
|---|---|---|---|---|
| 1 | 69.59 | 69.55 | 69.5 | 0.05 |
| 2 | 68.52 | 69.53 | 0.03 | |
| 3 | 69.40 | 69.43 | −0.07 | |
| 4 | 69.50 | 69.60 | 0.1 | |
| 5 | 70.1 | 69.41 | −0.09 | |
| 6 | 68.9 | 69.48 | −0.02 | |
| 7 | 70.0 | 69.50 | 0.00 | |
| 8 | 69.53 | 69.52 | 0.02 | |
| 9 | 69.41 | 69.52 | 0.02 | |
| 10 | 70.1 | 69.43 | −0.07 | |
| 11 | 68.6 | 69.42 | −0.08 | |
| 12 | 69.0 | 69.51 | 0.01 | |
| standard deviation | 0.52 | 0.056 | / | / |
| Scanning Surface | Parameter | Measurement/mm | Theoretical Value/mm | Error/mm |
|---|---|---|---|---|
| Front | Diameter 7 | 24.27 | 24.3 | −0.03 |
| Diameter 3 | 69.55 | 69.5 | 0.05 | |
| Diameter 5 | 54.62 | 54.6 | 0.02 | |
| Opposite | Diameter 1 | 138.43 | 138.4 | 0.03 |
| Diameter 4 | 62.47 | 62.5 | −0.03 | |
| Diameter 2 | 43.96 | 43.9 | 0.06 | |
| Diameter 6 | 27.74 | 27.7 | 0.04 | |
| Height 1 | 39.36 | 39.3 | 0.06 | |
| Height 2 | 48.25 | 48.3 | −0.05 | |
| Side 1 | Height 3 | 13.72 | 13.7 | 0.02 |
| Height 4 | 76.26 | 76.2 | 0.06 | |
| Side 2 | Height 3 | 13.66 | 13.7 | −0.04 |
| Height 4 | 76.25 | 76.2 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, S.; Zhang, B.; Han, X.; Yuan, M.; Xu, J.; Shan, D. Research on Forging Dimension Online Measuring System Based on Vibration Point Cloud Compensation. Electronics 2024, 13, 2494. https://doi.org/10.3390/electronics13132494
Bian S, Zhang B, Han X, Yuan M, Xu J, Shan D. Research on Forging Dimension Online Measuring System Based on Vibration Point Cloud Compensation. Electronics. 2024; 13(13):2494. https://doi.org/10.3390/electronics13132494
Chicago/Turabian StyleBian, Shaoshun, Bin Zhang, Xiuhong Han, Mingxin Yuan, Jiawei Xu, and Debin Shan. 2024. "Research on Forging Dimension Online Measuring System Based on Vibration Point Cloud Compensation" Electronics 13, no. 13: 2494. https://doi.org/10.3390/electronics13132494
APA StyleBian, S., Zhang, B., Han, X., Yuan, M., Xu, J., & Shan, D. (2024). Research on Forging Dimension Online Measuring System Based on Vibration Point Cloud Compensation. Electronics, 13(13), 2494. https://doi.org/10.3390/electronics13132494





