Multi-Objective Region Encryption Algorithm Based on Adaptive Mechanism

Abstract

The advancement of information technology has led to the widespread application of remote measurement systems, where information in the form of images or videos, serving as measurement results, is transmitted over networks. However, this transmission is highly susceptible to attacks, tampering, and disputes, posing significant risks to the trustworthy transmission of measurement results from instruments and devices. In recent years, many encryption algorithms proposed for images have focused on encrypting the entire image, resulting in resource waste. Additionally, most encryption algorithms are designed only for single-object-type images. Addressing these issues, this paper proposes a multi-object region encryption algorithm based on an adaptive mechanism. Firstly, an adaptive mechanism is employed to determine the strategy for adjusting the sampling rate of encryption objects, achieved through an encryption resource allocation algorithm. Secondly, an improved polygon segmentation algorithm is utilized to separate single-object regions from multi-object images, dynamically adjusting the sequence of encryption objects based on the adaptive mechanism. Finally, encryption is achieved using a chaos fusion XOR encryption algorithm. Experimental validation using instrument images demonstrates that the proposed algorithm offers high efficiency and security advantages compared to other mainstream image encryption algorithms.

1. Introduction

In recent years, with the development of science and technology and the widespread application of remote measurement systems, the problem of researchers having to complete instrument calibration tasks on site has been solved, greatly improving the efficiency of both factories and researchers. However, there are risks such as leakage, illegal theft, and tampering during the transmission of instrument images. Therefore, it is necessary to encrypt the instrument image data in order to protect its security [1,2]. In recent years, many scholars have proposed numerous encryption algorithms for image encryption problems [3,4,5,6,7]. Chaos theory is an evolutionary theory about a system transitioning from an ordered state to a disordered state. It analyzes irregular and unpredictable phenomena and their processes. It has characteristics such as sensitivity to initial conditions, randomness, and ergodicity [8], which can generate random chaotic sequences. Therefore, it is widely used in the field of image encryption [9,10,11,12,13,14]. Chen et al. [15] combined chaotic systems with compressive sensing, used SHA-3 to calculate the hash value of the preprocessed image, and designed a new mathematical model to calculate the key. The RSA algorithm encrypts the key, with no extra transmission. The experimental results show that the method can resist known plaintext attack and chosen plaintext attack. Wang et al. [16] proposed a new one-dimensional piecewise chaotic map, which is combined with Arnold scrambling and parallel compressive sensing to encrypt and compress double images. The ciphertext is embedded into the carrier image by using fast Fourier transform. It not only protects the image in content and vision, but also improves the transmission efficiency. However, the embedding and extraction of the image in this method is not lossless. In order to make the chaotic system have a wider chaotic range and more complex chaotic behavior, Liu et al. [17] proposed a new spatiotemporal chaotic model by combining the sine chaotic system and the coupled mapping lattice. The rules of DNA encoding are selected by the plaintext image information, and the 1D Fisher is extended to 3D Fisher. The improved algorithm can more completely scramble the base plane of the three-dimensional image, use the new DNA operation to achieve pixel diffusion, and finally achieve the goal of encryption. The experiment proves that this method can effectively resist various attacks, but there is room for improvement in encryption time. The above encryption algorithms encrypt the entire image, yet for most images, only a small portion contains important information. Encrypting the entire image largely wastes resources. Therefore, in recent years, there has been a growing number of encryption algorithms focusing on regions of interest in images [18,19,20,21]. Liu [22] proposed a method where the content owner divides the image into regions of interest and non-interest. They use Least Significant Bits(LSB)steganography to embed key information into the encrypted image. While this method protects the security of key information, it lacks accuracy and timeliness in delineating regions of interest. Shan et al. [23] proposed a method based on semantic segmentation, utilizing PSNet to segment scenes and select regions of interest. However, the recognition rate of this method needs improvement. Wang et al. [24] achieved encryption of regions of interest in medical images by binarizing the images using a threshold to determine the location of regions of interest. However, this method is more suitable for images where regions of interest are concentrated in the middle of the image. In [25], the Gray Level Co-occurrence Matrix and Faster R-CNN were combined to extract the region of interest of the image and select new features. In [26], You Only look Once (YOLOv2) was used to detect the region of interest of the image, which was encrypted by a new chaotic map. However, all of the above methods are only suitable for images with a single target. In recent years, in order to better fulfill the different tasks of encryption, an adaptive disambiguation method that combines the target image information to directly disambiguate the image pixels is proposed in [27], which employs adaptive disambiguation to change the image pixel values and effectively disambiguates the pixel positions. In [28], in order to consider the representative features of the image, a novel adaptive image encryption algorithm, PixAdapt, is proposed, which adaptively changes the parameters of the chaotic system, thereby optimizing theunified average changing intensity(UACI)value of the image. The above adaptive mechanism cannot solve the problem of rationally adjusting the encryption resources when they are limited. Therefore, in this paper, we propose a scheme for multi-objective region encryption, and can solve the problem of utilizing encryption resources as much as possible in the case of limited encryption resources, to complete the encryption of multiple objectives in the image.

The main contributions of this paper are as follows. (1) This paper proposes a new image encryption algorithm for images containing multiple objects, which correlates the priority of the multi-objective image with the hash value of the image and serves as the key. Compared with the traditional encryption algorithm that only targets a single object in the image, the ability of the encryption algorithm to resist the chosen plaintext attacks is enhanced, and the security of the encryption algorithm is improved. (2) Aiming at the problem that the overlapping regions of multiple objects extracted from YOLOv8 are encrypted multiple times, an improved polygonal segmentation algorithm is proposed, which effectively improves the efficiency of the encryption algorithm. (3) A new resource allocation algorithm is proposed for the situation of limited CPU encryption resources. The sampling rate of each part is adjusted according to the priority of the multi-objective image to realize efficient encryption of each extracted region of interest under the condition of limited encryption resources.

The rest of this article is organized as follows. Section 2 introduces the improved polygon segmentation algorithm, encryption resource allocation algorithm, and chaotic fusion XOR encryption algorithm. Section 3 introduces the encryption and decryption process, and Section 4 gives the experimental process and result analysis.

2. Adaptive Mechanism Encryption Algorithm

2.1. Improved Polygon Segmentation Algorithm

In order to solve the problem of rational encryption and decryption of multi-target objects, especially for the overlapping region of multiple targets, which can save a lot of CPU resource overhead, segmentation of detected irregularities is required. In this paper, the segmentation algorithm proposed by David Eppstein [29] is improved. The positions of overlapping parts of multi-target object images in the instrumentation image are united to form an irregular polygon. The irregular polygon has concave points, which provide important information about the internal structure of the polygon and can guide the segmentation algorithm in determining suitable segmentation locations. Therefore, the polygon is segmented into rectangles by searching for concave points, and after finding the concave points of the polygon, each concave point is used as a starting point for segmentation until the segmentation is complete.

During the segmentation process, there is an inevitable relationship between the position of the concave points and the direction of segmentation. If segmentation is performed in an arbitrary direction, it may result in a polygon being split into two polygons, necessitating an additional step to match the concave points of the two new polygons. Therefore, the best approach is to ensure that each segmentation results in one rectangle and one polygon. To achieve this segmentation method, it is necessary to determine the positional relationship between the current concave point and all concave points before each segmentation. If the current concave point is on the far left or right (the smallest or largest x-value), vertical segmentation can ensure that the result is one rectangle and one polygon (with the final result being two rectangles). If the current concave point is at the bottom or top (the smallest or largest y-value), horizontal segmentation can also achieve the aforementioned segmentation result. To simplify the aforementioned comparison process, a fixed-direction segmentation method can be adopted, which allows for the concave points to be sorted according to certain rules in advance, and then segmented in the specified direction. Sorting all concave points according to the rules where the smaller the x-value, the higher the priority, and the larger the y-value, the higher the priority, with x-priority being greater than y-priority, can meet all the vertical segmentation needs of the concave points. Similarly, sorting all concave points according to the rules where the larger the y-value, the higher the priority, and the smaller the x-value, the higher the priority, with y-priority being greater than x-priority, can meet all the horizontal segmentation needs of the concave points. This paper adopts a fixed-direction vertical segmentation scheme.

The implementation of the algorithm consists of three steps, which are uniting polygons, finding concave points, and segmenting and outputting rectangles. The pseudo-code of the algorithm is shown in Algorithm 1, and the result of the algorithm is shown in Figure 1.

Algorithm 1: Polygon segmentation Algorithm

Input:    yolov8 output rectangle yolo_res Output: The split rectangle list box_list 1.      input_box = [box[2:] for box in yolo_res] 2.      for i = 0 to len((input_box) do 3.      union_flage = false 4.      for j = i + 1 to len(input_box) do 5.      if input_ box [i] intersects input_rec [j] then 6.      Input_box[i] = input_box[i] and input_box[j] joint polygons 7.      Delete input_box[j] 8.      union_flage = true 9.      end if 10.    end for 11.    if not union_flage 12.    input_box[i] ->box_list 13.    Delete input_box[i] 14.    end if 15.    end for 16.    Dimples_list = [Look for the dimples of the polygon ploy for ploy in input_box]  // Finding concave vertices 17.    Dimples_list = [Sort the points in Dimples for Dimples in Dimples_list] 18.    for i = 0 to (len(input_box)) do 19.    for j = 0 to (len(Dimples_list[i])) do 20.    Vertical_lines = A vertical straight line passing through Dimples_list[i][j] 21.    intersections = Vertical_lines the intersection of the line and the polygon input_box[i] 22.    for k = 0 to (len(intersections))do 23.    Dividing_line = The line segment starts from Dimples_list[i][j] and ends at intersections[k] 24.    if Dividing_line does not intersect with the polygon input_box[i] 25.    if intersections[k] in the dimple set Dimples_list[i] 26.    Dimples_list[i].remove(intersections[k]) 27.    break 28.    end if 29.    end if 30.    end for 31.    res1, res2 = Splitting polygons with Dividing_line input_box[i] 32.    if res1 is rectangular then 33.    res1 -> box_list 34.    input_box[i] = res2 35.    else 36.    input_box[i] = res1 37.    res2 -> box_list 38.    end if 39.    end for 40.    end for

2.2. Encryption Resource Allocation Algorithm

The image from the instrument has the characteristics of high clarity, large volume, and high resolution. It is easy to encounter a shortage of encryption resources when encrypting it. In order to alleviate the pressure of resource scarcity, this paper proposes an adaptive multi-object region encryption algorithm for instrument images. Firstly, prioritize the detected multi-object regions. Taking three levels of priority as an example (level 1 is high, level 3 is low), set a threshold for CPU utilization. If the CPU utilization is less than or equal to threshold 0, it indicates that there are sufficient encryption resources and there is no need to adjust the sampling rate of the multi-target regions; if the CPU utilization is between threshold 0 and threshold 1, it means that the CPU usage is light at this time, so reduce the sampling rate of the region with priority level 3; if the CPU utilization is greater than threshold 1 but less than threshold 2, it means that moderate use by the CPU occurs at this time. Reduce the sampling rate of region images with priority levels 2 and 3. When CPU utilization exceeds threshold 2, it indicates severe use by the system and tightness in encryption resources. Lower the sampling rate for all priority area images. The pseudocode for the algorithm can be seen in Algorithm 2.

Algorithm 2: Encryption Resource Allocation Algorithm

Input:     Yolov8 Output yolo_res, The list of divided small rectangles box_list, En cryption category Priority class_priority, CPU usage threshold cpu_threshold Output:  An encrypted list out_box with encrypted properties 1.      Get CPU usage cpu_usage 2.      if cpu_usage < cpu_threshold[0] 3.      All categories are fidelity encrypted using yolo_res -> cpu_box_list 4.      else if cpu_usage < cpu_threshold[1] 5.      In addition to class_priority [2] adjust the sampling rate encryption, other fidelity encryption using yolo_res -> cpu_box_list 6.      else if cpu_usage < cpu_threshold[2] 7.      In addition to class_priority[1,2] adjust the sampling rate encryption, other fidelity encryption using yolo_res -> cpu_box_list 8.      else 9.      All categories are encrypted with adjusted sample rate using yolo_res -> cpu_box_list 10.    end if 11.    for i in range(len(box_list)) 12.    box_list[i].insert(0, 0) 13.    for i range(len(cpu_box_list)) 14.    if box_list[i] intersects with cpu_res[j] and cpu_box_list[j][0] == 1 15.    box_list[i][0] = 1 16.    end if 17.    end for 18.    end for

2.3. Chaotic Fusion XOR Encryption Algorithm

The algorithm combines PWLCM chaotic mapping [30], the Chen hyper-chaotic system, and DNA XOR encoding. PWLCM chaotic mapping refers to Piecewise Linear Chaotic map with a control parameter $\rho \in (0,1)$. The parameters for the Chen hyper-chaotic system are set as $a=36$, $b=3$, $c=28$, $d=16$, and $k=0.3$. The fourth-order Runge–Kutta method is employed to solve the equation system, yielding four chaotic sequences: E, F, G, and H. DNA XOR encoding utilizes eight encoding rules: ACGT, CATG, GTAC, TCGA, CTAG, AGCT, TGCA, and GATC.

Suppose that the size of the original color image P is $M\times N\times 3$, and the complete encryption process consists of the following steps.

Step 1: Calculate the hash value of the plain image by the SHA-512 algorithm, divide it into six groups, each a group of 20 hexadecimal data points, and generate the key formula as follows:

$$\begin{array}{l}{x}_i=hash[i\ast 20:i\ast 20+20]\\ m_i=hex2dec(x_i)/2^{90}\\ ke{y}_i=ke{y}_{i0}+m_i+pri(P)/10\end{array}$$

(1)

where $ke{y}_{i0}$ is the initial value of the key, $i=1,2,\dots ,6$, $\mathit{pri}\left(P\right)$ is the priority of the plain image.

Step 2: Convert the color image into a one-dimensional array, the length of which is $3\left(M\times N\right)$, input keys 1 2 into the PWLCM chaotic system iteratively to obtain a chaotic sequence D. In this paper, t = 500, and chaotic sequence D is used to sort the one-dimensional array and realize the scrambling of pixel values.

Step 3: Use the remaining four keys and the Chen hyperchaotic system to generate four pseudo-random sequences E, F, G, and H of size$t+3(M\times N)$. In order to avoid transient effects, the first t values are discarded here, and the XOR operation is performed on one-dimensional pixels using chaotic sequence E to change the pixel values and realize the diffusion of pixels. The operation is as follows:

$$\begin{array}{l}E=(E\times {10}^{15})\%255\\ pixels=pixel\hspace{0.17em}XO\mathrm{R}E\end{array}$$

(2)

Step 4: Divide the one-dimensional array after XOR into R, G, and B channels. Chaotic sequences $F(:\mathit{MN})$,$F(\mathit{MN}:2\mathit{MN})$, and $F(2\mathit{MN}:3\mathit{MN})$ were used to select DNA coding rules for each pixel value in the R, G, and B channels, respectively. In this paper, the first four encoding rules are adopted for encoding, and the last four encoding rules are adopted for decoding. The selection rules are as follows:

$$\begin{array}{l}{R}_{en}\_rule=F[:MN]\%4\\ G_{en}\_rule=F[MN:2MN]\%4\\ B_{en}\_rule=F[2MN:3MN]\%4\end{array}$$

(3)

Step 5: Convert each pixel in R, G, and B channels into a DNA base sequence and realize pixel diffusion through the DNA XOR operation. The chaotic sequence G determines the XOR object of each pixel. There are eight kinds of XOR objects for each pixel value to choose from. The selection rules and steps for DNA operation XOR are as follows:

$$\begin{array}{l}rule=G[i]\%8\\ pixel[i]=DNA\_XOR(pixel[i],rule)\end{array}$$

(4)

Step 6: Transform the base sequence into pixel values according to the last four coding rules of the DNA coding table. The chaotic sequence H determines the selection of decoding rules. The formula is as follows:

$$rule=H[i]\%4$$

(5)

The detailed steps are shown in Algorithm 3.

Decryption is the opposite process, so the algorithm is the inverse of Algorithm 3. The main steps are as follows:

Step 1: Obtain the key required for decryption. There are six keys in total. Input key 1 and key 2 into the PWLCM chaotic system for $[t+3(M\times N\left)\right]$ iterations and discard the first t times to obtain the chaotic sequence D. Input the remaining four keys into the Chen hyperchaotic system for $[t+3(M\times N\left)\right]$ iterations and discard the first t times to obtain the four chaotic sequences E, F, G, and H.

Step 2: Chaotic sequence H is used to encode the three-channel pixel values of R, G, and B of the ciphertext image, respectively. The encoding rules used in decryption are the last four, and the rules are selected as follows in Formula (5). The chaotic sequence G is used to determine the object of each pixel’s XOR, so there are also eight kinds of XOR objects to choose from for each pixel value. The selection rule and the DNA operation XOR operation method are shown in Formula (4). Chaotic sequence F is used to select DNA decoding rules for each pixel value in the R, G, and B channels. During decryption, the last four encoding rules are adopted for encoding and the first four encoding rules for decoding. The decoding rules are shown in Formula (3). Chaotic sequence E is used to perform XOR operations on pixels to realize the diffusion of pixels. The calculation method is shown in Formula (2).

Step 3: Use chaotic sequence D to sort the one-dimensional array and realize the scrambling of pixel values. Finally, the decrypted plaintext is obtained by merging R, G, and B channel data.

Algorithm 3: Chaotic fusion XOR encryption algorithm

Input:     Plain Image P Output:     Cipher Image C Key generation 1.       hash = SHA-512(P) 2.       $x_i=\mathit{int}(\mathit{hash}\left[20\times i:20\times i+20\right]{,16)/2}^{90}$ 3.       ${\mathit{key}}_i{=\mathit{key}}_{i0}+x_i+pri\left(P\right)/10$          //   Scrambling phase 4.       pixels = img.flatten()  // Convert to one dimensional array 5.       [valD,idxD] =sort(D) 6.       pixels = pixels(idxD)  // Chaotic sequence D scrambles pixels //   Diffusion stage 7.       $E=(E\times {10}^{15})\%255$ 8.       $\mathit{pixels}=\mathit{pixel} \oplus E$ 9.       R = [pixels(1), pixels(2),……pixels(MN)] 10.     G = [pixels(MN), pixels(MN + 1),……pixels(2MN)] 11.     B = [pixels(2MN), pixels(2MN + 1),……pixels(3MN)] 12.     rules = [‘ACGT’,‘CATG’,‘GTAC’,‘TCGA’]  // encoding rules 13.     $R_{\mathit{en}}\_\mathit{rule}=F\left[:\mathit{MN}\right]\%4$  //Chaotic sequence F implements the encoding of R, G, B three-channel pixel values 14.     $G_{\mathit{en}}\_\mathit{rule}=F\left[\mathit{MN}:2\mathit{MN}\right]\%4$ 15.     $B_{\mathit{en}}\_\mathit{rule}=F\left[2\mathit{MN}:3\mathit{MN}\right]\%4$ 16.     rules = [‘ACGT’,‘CATG’,‘GTAC’,‘TCGA’,‘CTAG’,‘AGCT’,‘TGCA’,‘GATC’] // 8 kinds of XOR objects 17.     $R_{\mathit{xor}}\_\mathit{rule}=G\left[:\mathit{MN}\right]\%8$   //Chaotic sequence G selects an XOR object for R, G, B three-channel base sequence 18.     $G_{\mathit{xor}}\_\mathit{rule}=G\left[\mathit{MN}:2\mathit{MN}\right]\%8$ 19.     $B_{\mathit{xor}}\_\mathit{rule}=G\left[2\mathit{MN}:3\mathit{MN}\right]\%8$ 20.     rules = [‘ACGT’,‘CATG’,‘GTAC’,‘TCGA’]  // decoding rules 21.     $R_{\mathit{de}}\_\mathit{rule}=H\left[:\mathit{MN}\right]\%4$  //Chaotic sequence H selects decoding rules for R, G, B three-channel base sequences 22.     $G_{\mathit{de}}\_\mathit{rule}=H\left[\mathit{MN}:2\mathit{MN}\right]\%4$ 23.     $B_{\mathit{de}}\_\mathit{rule}=H\left[2\mathit{MN}:3\mathit{MN}\right]\%4$ 24.     Cipher = np.arry(R + G + B).reshape(M,N,3)

3. Adaptive Mechanism Encryption and Decryption Process

3.1. Adaptive Mechanism Encryption Process

The multi-object region of interest encryption algorithm for an adaptive instrument image mainly includes three parts: segmentation of overlapping region image, allocation of encryption resources, chaotic fusion or encryption algorithm.

Step 1: Identify the multi-target objects in the input image through yolov8, read the CPU utilization, and determine the objects that need to reduce the sampling rate according to the CPU utilization threshold and the priority of the multi-target objects.

Step 2: Algorithm 1 was used to combine the positions of the multi-object graphics output by yolov8 into polygons, output the single area separately, and divide the overlapping area into a rectangular list. Algorithm 2 determines the image that needs to be adjusted. It dynamically adjusts the sampling rate for the encryption category according to the preset threshold based on the current CPU usage. When the CPU usage is high, it downsamples and encrypts the target category of low priority based on the dynamic adjustment policy to ensure stable and fast system running.

Step 3: The Chaotic Fusion XOR Encryption algorithm (Algorithm 3) encrypts the rectangular list generated in Step 2.

Step 4: Combined with Step 2 and Step 3, the ciphertext of the image that does not need to adjust the sampling rate is directly written to the area of interest. For the image that needs to adjust the sampling rate, the ciphertext sampling rate is adjusted back to the original size and then written to the area of interest. At the same time, the real ciphertext is stored in the area of the adjusted sampling rate.

Step 5: In order to ensure the security of the real ciphertext location of the key, the location of the region of interest, and the location of the adjusted sampling rate of some images, this paper uses the LSB algorithm [31] to concatenate the information of the key, the location of the region of interest, and the location of the adjusted sampling rate in the encrypted picture after steganography for decryption. The flowchart of the encryption process is shown in Figure 2, and the encryption algorithm is shown in Algorithm 4.

Algorithm 4: Adaptive mechanism encryption process

Input:     Image to be encrypted, box_list with image fidelity properties [Whether to adjust image, x, y, w, h] Output: Ciphertext with steganographic data content. 1.       for i = len(box_list)do 2.       img = input_img(box_list[i]) 3.       write_box.append(box_list[i][1]:[4]) // Save the pixel source area [x, y, w, h] 4.       if box_list[i][0] == 1 then  // Do not adjust the sampling rate 5.       write_box.append(box_list[i][1]:[4])   //[x, y, w1, h1] 6.       encrypt_img = Gets the encrypt_key from img and encrypts img with the encrypt_key 7.       write_key.append(encrypt_key) 8.       writes encrypt_img to the [x, y, w1, h1] region of out_img 9.       else then //Adjust sampling rate 10.     zip_rec = box_list[i][1]:[2] + [ box_list[i][3]/2] + [ box_list[i][4]/2] 11.     write_box.append(zip_rec)      //[x,y,w1,h1] 12.     img = img.resize(box_list[i][3]/2, box_list[i][4]/2) 13.     encrypt_img = Gets the encrypt_key from img and encrypts img with the encrypt_key 14.     write_key.append(encrypt_key) 15.     encode_back = encode_img.resize(box_list[i][3], box_list[i][4])   // Fill the background area 16.     Writes encode_back to the [x, y, w, h] region of out_img and encrypt_img to the [x, y, w1, h1] region 17.     end if 18.     end for 19.     Cipher image = LSB_write(write_box, write_key, out_img)

3.2. Adaptive Mechanism Decryption Process

The decryption process is the opposite process, which mainly includes LSB steganography reading, ciphertext decryption, and decrypting data write back (data save).

Step 1: LSB is used to read the steganographic key and the position of the region of interest [x, y, w, h] in ciphertext and adjust the real ciphertext position of some images [x, y, w1, h1] in the sampling rate. [x, y, w1, h1] is the encrypted data storage area, while [x, y, w, h] is the original encrypted data storage location (decrypted data should also be stored in this area).

Step 2: Read the data in the [x, y, w1, h1] field and decrypt it using the key. Obtain the decrypted image data.

Step 3: If w1 = w and h1 = h, the decrypted data are stored in the [x, y, w, h] region of the image; otherwise, the decrypted data are resized to $h\times w$ and then stored in the [x, y, w, h] region of the image. The decryption algorithm is shown in Algorithm 5.

Algorithm 5: Adaptive encryption algorithm decryption process

Input:    Cipher image Output: Plain image 1.       read_box,read_key = LSB_read(Cipher)   // Read the steganographic key and the location of the encryption region from the ciphertext 2.       for i = 0 to len(read_box) do 3.       img = input_img(read_box[$2\times i+1$])     // [x, y, w1, h1] 4.       decrypt_img = Decrypts img with key[i] 5.       if w1 = w and h1 = h then 6.                           out_img = img 7.       else 8.                           out_img = img.resize(read_box[$2\times i$][2], read_box[$2\times i$][3]) 9.       end if 10.     Save out_img to the region [x, y, w, h] of the image Cipher 11.     end for

4. Experiment

The security and efficiency of the proposed algorithm are evaluated in this section. Experimental conditions are shown in

Table 1. Experimental conditions.

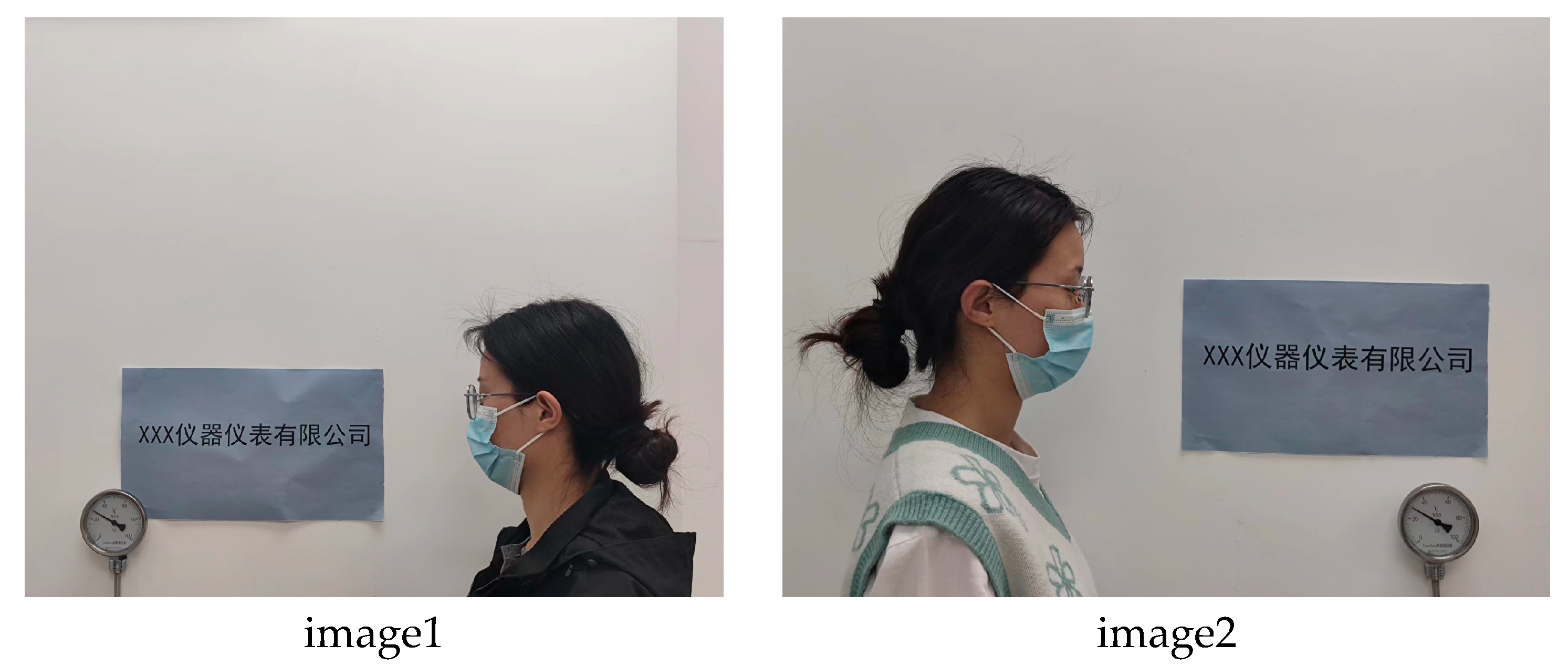
System	CPU	RAM	Software	Object Detection	Dataset	Model
Win11	Inter Core i7-11390H, CPU@3.40 GHz 3.42 GHz	16 GB	Pycharm Communit 2022	Yolov8	Self-built, including about 800 pictures of instruments	multi_encode.onnx

.

4.1. Experimental Process

In this paper, the CPU utilization thresholds are set as follows: threshold 1 = 30%, threshold 2 = 50%, and threshold 3 = 70%. The priority of multi-target objects is instruments, people, and billboards. The dataset used in this document is a private dataset, and the YOLOv8 model used in the experiment is multi_encode.onnx. To demonstrate the effectiveness of the adaptive mechanism encryption, we conducted experiments on images from the dataset under different CPU utilization conditions. Taking image1 in Figure 3 as an example, the experimental process is shown in Figure 4.

The experiment takes the input image from image1 in Figure 3, and after detection by YOLOv8, outputs the detection box with the category in the following format: [class number, x, y, w, h], where the category numbers are as follows: 0: billboards, 1: instrument, and 2: people. The detection results are shown in Figure 4A(b). Subsequently, the CPU utilization rate is read and compared with the preset threshold to determine whether different categories need to be downsampled and encrypted, with the output format being [Is the sampling rate adjusted?, x, y, w, h], where 0 indicates downsampling and 1 indicates preservation of fidelity. After that, the encryption area is fused and segmented, inheriting the attribute of whether to preserve fidelity. This is divided into two steps. First, the multi-rectangle fusion and segmentation are carried out to obtain all the regions of interest for encryption: [x, y, w, h], as shown in Figure 4A(c). Then, the segmentation results are compared with the segmentation input data. If the segmented small rectangle intersects with the area that needs to be encrypted with fidelity preservation, then this small block is the area for fidelity preservation encryption; otherwise, it needs to be downsampled, obtaining the position of the image that needs to be encrypted with adjusted sampling rate: [x, y, w1, h1]. By comparing w1 with w and h1 with h, it is determined whether downsampling encryption is needed. Moreover, this has the advantage that after encryption, [x, y, w, h] can serve as the source area for the actual encrypted data, and [x, y, w1, h1] can serve as the storage area for the actual encrypted data after encryption. Subsequently, the encryption process is carried out, reading the encryption area [x, y, w, h]. If w is equal to w1 and h is equal to h1, then encrypt directly, and save the encrypted data to the [x, y, w1, h1] position. If not equal, resize the data to$w1\times h1$ for encryption and save the encrypted data to the [x, y, w1, h1] position. It should be noted that if w1 ≠ w or h1 ≠ h, multiple saves are needed to ensure that the information in the area [x, y, w, h] of the original image is completely covered and refreshed, and the area [x, y, w1, h1] contains complete encrypted data. Subsequently, the key, the position of the region of interest, and the position of the image that needs to be encrypted with the adjusted sampling rate are steganographically written into the picture for decryption, as shown in Figure 4A(d).

During the decryption process, first read the key, the position of the region of interest [x, y, w, h], and the position of the image that needs to be decrypted with the adjusted sampling rate [x, y, w1, h1]. After reading the [x, y, w1, h1] area of the picture, decrypt it using the key. After decryption, determine whether w = w1 and h = h1. If the condition is met, directly save the decrypted data to the [x, y, w, h] area of the picture. If not, resize the decrypted data to $w\times h$, and then save the data to the [x, y, w, h] area. Encrypt and decrypt the image in environments with CPU utilization rates of 25%, 35%, 55%, and 75%. The decrypted images are shown in Figure 4A(e–h).

According to Figure 4, it is evident that when the current CPU utilization rate is less than threshold 1, no targets need downsampling encryption. When the current CPU utilization rate is greater than threshold 1 and less than threshold 2, only the lowest-priority ‘brand’ category is downsampled. When the current CPU utilization rate is greater than threshold 2 and less than threshold 3, only the highest-priority ‘instrument’ category is not downsampled. When the current CPU utilization rate is greater than threshold 3, all categories are downsampled.

4.2. Experimental Results

The key length for modern computers should exceed 2¹⁰⁰ in order to withstand exhaustive attacks [32]. The encryption algorithm proposed in this paper utilizes a total of six keys, and complies with the IEEE floating point standard, resulting in a calculation accuracy of 10⁻¹⁵. As a result, the key space of the algorithm is (10¹⁵)⁶ = 10⁹⁰, which exceeds 2¹⁰⁰ and thus provides robust resistance against various attack methods.

In order to withstand brute force attacks, a robust encryption algorithm should exhibit high sensitivity to the key. Even a slight change in the key for plaintext encryption should result in significant changes in the ciphertext. The evaluation indexes used are the number of pixels change rate (NPCR) and (UACI). The closer these values are to 99.6094% and 33.4635% [33], the greater the key sensitivity. Taking image2 in Figure 3 as an example, with regions of interest (ROIs) being people, clock, and board, respectively, changing one of the keys results in a specific change rate, as shown in

Table 2. NPCR and UACI of ROI images (%).

Image	NPCR			UACI
	R	G	B	R	G	B
clock	99.6323	99.6091	99.5718	33.3300	33.4198	33.2817
board	99.6283	99.5945	99.5978	33.4108	33.4391	33.5169
people	99.6198	99.6049	99.5923	33.4490	33.4290	33.5218

from experimental results. When decrypting the ciphertext, an attacker is unable to decipher it, even with any alteration to the key value. In our experiment, altering one of the keys resulted in a difference of 10⁻¹⁵ between the pre-change and post-change keys. Figure 5 illustrates decryption after randomly changing one of image 1’s keys while maintaining a change rate below threshold CPU utilization.

Secondly, the histogram of the image can visualize the statistical information of the image, which reflects the pixel intensity and distribution pattern of the image. In order to prevent the attacker from finding the relationship between the ciphertext and the plaintext image to break the encryption algorithm, the histogram of the encrypted ciphertext must be homogeneous and completely different from the histogram of the plaintext image. Figure 6 shows the histograms of three different ROI images in image2 in Figure 3 and the histograms of their ciphertexts.

The stronger the correlation between adjacent pixels of an image, the greater the possibility of information leakage. Therefore, the correlation of ciphertext images in horizontal, vertical, and diagonal directions should be as close to 0 as possible, so as to better prevent information leakage [34]. Assuming the image size is M, the correlation coefficient of its adjacent pixels is calculated as follows:

$$r_{xy}=\frac{M^2·E[(x-E_x)(y-E_y)]}{{\displaystyle \sum _{i=1}^m{(x_i-E_x)}^2·}{\displaystyle \sum _{j=1}^n{(y_j-E_y)}^2}}$$

(6)

$E_x=\frac{1}{N}\times {{\displaystyle \sum }}_{\mathrm{i}=1}^N{x}_i$,$x_i$,$y_i$ are adjacent pixels. A total of 3000 pairs of adjacent pixels are randomly selected in the ROI part of image 3, and their correlation coefficients are calculated in the horizontal, vertical, and diagonal directions, respectively.

Table 3. Correlation analysis.

Image	Direction	Plain Cropped Image			Encrypted Cropped Image
		R	G	B	R	G	B
	Horizontal	0.9932	0.9929	0.9280	−0.0039	−0.0045	−0.0204
people	Vertical	0.9940	0.9938	0.9931	0.0067	−0.0140	−0.0376
	Diagonal	0.9895	0.9902	0.9888	0.0057	−0.0044	−0.0023
	Horizontal	0.9819	0.9815	0.9782	−0.0154	−0.0159	−0.0151
clock	Vertical	0.9742	0.9742	0.9775	0.0324	−0.0377	−0.0399
	Diagonal	0.9746	0.9593	0.9595	−0.0064	−0.0082	−0.0277
	Horizontal	0.9539	0.9532	0.9598	−0.0227	−0.0010	0.0074
board	Vertical	0.9551	0.9555	0.9506	−0.0257	−0.0021	0.0089
	Diagonal	0.9199	0.9080	0.9154	−0.0096	−0.0197	−0.0080

shows that the algorithm is robust to statistical attacks.

Table 4. Correlation coefficients of Peppers (512 × 512) and Lena (512 × 512) for different encryption schemes.

Image		Horizontal	Vertical	Diagonal
Peppers	Ref. [8]	0.0012	−0.0017	0.0023
	Ref. [13]	0.0016	−0.0013	0.0011
	ours	−0.0066	−0.0095	−0.0084
Lena	Ref. [6]	−0.001	0.0025	−0.0067
	Ref. [14]	0.001045	0.001042	0.000325
	ours	−0.0170	−0.0200	−0.0047

shows the results of comparative experiments using Lena and Peppers with other algorithms.

Finally, the encryption efficiency is crucial to the encryption of instrument images, so in order to verify the effectiveness of the encryption scheme of adaptive instrument images, the time used to adjust the encryption resources according to CPU utilization and not adjust the encryption resources by using this algorithm was tested, as shown in

Table 5. Adaptive mechanism encryption and decryption time (The following are the times taken for encryption and decryption of four regions of interest ex-tracted from Figure 1 under different conditions).

Image	ROI Size	CPU Utilization	Encrypt Time (s)	Decrypt Time (s)
image1	$415\times 516$	unjustment	9.6843	10.3964
	$76\times 548$	(30%,50%)	8.9383	9.3633
	$27\times 139$	(50%,70%)	3.6093	3.3798
	$191\times 125$	>70%	2.9824	2.4863

. In order to verify the feasibility of the proposed encryption algorithm, the image “Lena” (256 × 256 pixels) is taken as an example. The algorithm was compared with the algorithms in

Table 6. Encryption time comparison of other algorithms.

Algorithm	Encryption Time	Decryption Time	Computer Configuration
Ref. [9]	3.4826	3.9547	A PC with Intel Core i7-11390H, CPU@3.40 GHz 3.42 GHz, 16 GB RAM, pycharm 2022 community
Ref. [7]	2.000	NA	A PC with Intel Core (TM) i5-4200U CPU @1.6 GHz, 8 GB RAM, MATLAB 2017(a)
Ref. [14]	0.9654	0.8181	A PC with AMD R7 5800H CPU 3.20 GHz, 16.0 GB RAM, MATLAB R2019a
Ours	0.4595	0.4643	A PC with Intel Core i7-11390H, CPU@3.40 GHz 3.42 GHz, 16 GB RAM, pycharm 2022 community

using this algorithm with a CPU utilization of about 50%, and the results show the effectiveness of the encryption algorithm in this paper.

Finally, we compare our algorithm with the current advanced similar algorithms, and the results are listed in

Table 7. The proposed work is compared with the latest algorithms (“✓” represents yes, “__” represents no).

Algorithm	Multi-Target Detection	Encryption Resource Adjustment	Dynamic Encryption Parameter	Adaptive Scrambling
Ref. [27]	__	__	__	✓
Ref. [28]	__	__	✓	__
Ours	✓	✓	__	__

.

5. Conclusions

Overall, the adaptive multi-object region encryption algorithm proposed in this paper effectively addresses the issue of dynamic encryption of multi-object images under limited encryption resources by fully utilizing available resources. The proposed encryption resource allocation algorithm determines the categories that need to adjust the sampling rate based on CPU utilization and the priority of the multi-target objects. The improved segmentation algorithm solves the problem of reasonable encryption and decryption for multi-target objects, especially in overlapping regions of multiple targets, significantly reducing CPU resource overhead. Finally, to ensure the security of the keys and other information, the LSB steganography algorithm is used to embed important information, such as keys and the locations of the regions of interest into the ciphertext. Experimental results demonstrate that this scheme is highly efficient and secure.