Joint Optimization of User Scheduling, Flight Path and Power Allocation in a UAV Secure Communication System

Abstract

In the future network, the data traffic increases rapidly and users’ communication service needs are diversified. The application of unmanned aerial vehicles (UAVs) in communication effectively relieves the pressure of ground communication equipment. However, the UAV-assisted communication also faces many challenges. Due to the broadcast and open characteristics of the UAV communication channel in the wireless network, it is easily subject to eavesdropping, so secure and efficient communication is hard to guarantee. In order to improve the security of the UAV communication system, this paper studies the secure communication system of a UAV as a base station to assist wireless network communication. In this system, the UAV, as an airborne mobile base station, transmits confidential information to multiple users on the ground, and there is an eavesdropper around the users. The optimization problem of joint user communication scheduling, UAV flight path, and power allocation is established to maximize the minimum secrecy rate of the system. Considering the constraints of user service quality, UAV flight path, and transmit power, the optimization problem is a nonconvex problem and the solution complexity is extremely high. Therefore, we propose an efficient iterative algorithm, jointly considering the block coordinate descent method and the successive convex approximation technique. Simulation results verify the correctness of the theoretical analysis, and further show that this scheme significantly improves the minimum secrecy rate of the system compared with other benchmark schemes.

1. Introduction

With advantages of low cost, high mobility, and rapid deployment, unmanned aerial vehicles (UAVs) have been widely utilized in the field of wireless communication, such as aerial base stations [1,2,3], wireless sensor networks [4,5,6], and aerial relay [7,8,9]. Although the line-of-sight (LoS) wireless link provides better communication quality in UAV communication, it also makes UAV transmission signals vulnerable to eavesdropping by illegal nodes on the ground, which will lead to the leakage of confidential information and the decline in communication quality. Therefore, determining how to ensure the security of information transmission in the UAV communication is a challenging task.

At present, UAV flight path design combined with physical layer security technology is deemed a promising solution. The authors of [10] studied a UAV-assisted relay wireless network with caching. Considering the presence of an eavesdropper (Eve), the maximum secrecy rate of the system was obtained by optimizing the UAV flight path. In [11], considering the security relay network with multiple Eves, the secrecy rate of the system was improved by jointly designing the transmission beamforming and artificial noise under the constraint of UAV transmit power. Based on [10,11], a jamming UAV was introduced to interfere with Eves in [12,13], and the secrecy rate of the system was improved by jointly optimizing the transmit power and flight paths of two UAVs. Furthermore, in [14], to counteract Eves, the authors proposed a scheme of combining UAV flight path optimization with transmit power control to maximize the average secrecy rate of the communication system. Nonorthogonal multiple access (NOMA), which is a promising technique, has also been introduced into the UAV security communication system. Thus, the authors proposed an NOMA-aided UAV communication scheme in [15], which used UAV together with the NOMA technique to generate artificial interference to ensure the system’s safety and improve the throughput of users. In [16], a UAV-enabled NOMA system was studied, and a joint power allocation and aerial jamming scheme was proposed to achieve reliable and secure communication in the presence of a malicious Eve. Due to the high transmit power for weak users in NOMA, a power allocation scheme for an NOMA-UAV network with circular flight path was proposed to maximize the sum rate of common users and ensure the safety of specific users in [17]. While improving the safe communication, the energy consumption of communication system should be reduced. In [18], a scenario of UAV-assisted joint sensing and communication system was considered, and the system safety and energy efficiency was maximized by optimizing the sensing and transmit time as well as the location of the UAV. The max–min optimization problem in secure communications has been studied. A cooperative UAV was introduced to send artificial noise to confuse malicious Eves in [19], and the worst-case secrecy rate of all time slots was maximized by jointly designing the 3D trajectory and time allocation of the UAV. In [20,21], the energy efficiency was maximized under the constraints of SOP (secrecy outage probability), phase shift, and transmission power while ensuring the worst-case security performance.

Although lots of works study the UAV relay security network, few works consider the UAV mobile base station security network. In [22], as an aerial platform, UAV communicated with ground users. The time to complete tasks was minimized by optimizing the flight path and communication resource allocation design of the UAV. In [23], the average transmit power consumed by users was minimized by dynamically optimizing user association and transmit power allocation in each time slot. In [24], the authors considered the coverage of UAV, heterogeneous QoS and backhaul link rate constraints, and optimized UAV flight path to maximize the total rate of ground users. They all only considered the situation that UAV was used as an air base station for communication, but ignored security issues. In addition, the system throughput was improved by optimizing the UAV flight path, but the communication quality of all ground users was not taken into account.

Different from the previous research, this paper considers the secure transmission scenario of a UAV as a mobile base station to assist wireless network communication, and studies how to comprehensively consider the wireless resource allocation and flight path optimization in the network to maximize the minimum secrecy rate of the system. The main contributions are summarized as follows:

•

A joint optimization scheme of user scheduling, UAV flight path, and transmit power control is proposed. In the proposed optimization scheme, firstly, the relationship between UAV position and air–ground communication channel is deeply analyzed, and a time-varying channel model is established. Then, the optimization problem of maximizing the minimum secrecy rate of the system is formulated.

•

Given that the objective function of the optimization problem is a multivariate nonconvex function, and the problem includes numerous nonconvex constraints, it presents significant challenges to solve directly. Therefore, the optimization problem is initially decomposed through a combination of variable substitution and the difference of convex method, resulting in several univariate optimization problems. Subsequently, each subproblem is tackled by alternating iteration, ultimately yielding the UAV flight path and resource allocation that achieve optimal performance.

•

The simulation results verify the effectiveness and feasibility of the proposed algorithm, and verify that the proposed scheme is superior to other benchmark schemes, which can effectively improve the minimum security rate of the system and ensure the quality of service of users.

2. System Model and Problem Formulation

The system model is shown in Figure 1. In the system, the UAV, as an air base station, uses time division multiple access (TDMA) mode to provide services for K users on the ground in the presence of an eavesdropper (Eve). The set of the K users is denoted by $\mathcal{K}\stackrel{\Delta }{=}\{1,2,\dots ,K\}$, and $\left|\mathcal{K}\right|=K$.

Without loss of generality, assume that the positions of the k-th user and Eve are ${\mathbf{w}}_k={\left[x_k,y_k,h_k\right]}^T$ and ${\mathbf{w}}_{\mathrm{e}}={\left[x_{\mathrm{e}},y_{\mathrm{e}},h_{\mathrm{e}}\right]}^{\mathit{T}}$, respectively, which can be ascertained by a Global Positioning System (GPS) device. Due to energy limitation, the UAV needs to fly between the initial and final positions to obtain energy supply. Here, we assume that the initial and final positions of the flight are predetermined as ${\mathbf{q}}_{\mathrm{I}}={\left[x_{\mathrm{I}},y_{\mathrm{I}},H\right]}^{\mathit{T}}$ and ${\mathbf{q}}_{\mathrm{F}}={\left[x_{\mathrm{F}},y_{\mathrm{F}},H\right]}^{\mathit{T}}$, respectively, where some charging piles are deployed. The UAV flies at a fixed height H within the limited time T due to power constraint, and its position at time t is expressed as ${\mathbf{q}}_{\mathrm{b}}\left(t\right)={\left[x\left[t\right],y\left[t\right],h\left[t\right]\right]}^{\mathit{T}}$, $0\le t\le T$. To simplify the following process, the preset flight period T is discretized into N equal-interval time slots, and the duration of a time slot is ${\delta }_t$. Herein, the slot ${\delta }_t$ should be small enough to ensure that the distance between the UAV and the ground node is approximately constant in any time slot. On this condition, the path of the UAV can be represented by a discrete sequence ${\mathbf{q}}_{\mathrm{b}}\left(n\right)={\left[x\left[n\right],y\left[n\right],h\left[n\right]\right]}^{\mathit{T}},n\in \{1,2,\dots ,N\}$. The flight path of the UAV has the following mobility constraints:

$${\mathbf{q}}_{\mathrm{b}}\left[1\right]={\mathbf{q}}_{\mathrm{I}},$$

(1)

$${\mathbf{q}}_{\mathrm{b}}\left[N\right]={\mathbf{q}}_{\mathrm{F}},$$

(2)

$${∥{\mathbf{q}}_{\mathrm{b}}[n+1]-{\mathbf{q}}_{\mathrm{b}}\left[n\right]∥}^2\le V^2,\mathit{n}=1,2,\cdots \mathit{N}-1,$$

(3)

where $V=v_{max}{\delta }_t$ represents the maximum distance that the UAV can move in a time slot.

The measurement results in [25] show that the LoS channel model provides a good approximation for the actual air-to-ground wireless channel, so we assume that the channels from the UAV to users and from the UAV to the Eve are linked by LoS. Furthermore, the Doppler effect caused by the UAV mobility is assumed to be well compensated at the receivers [26]. Therefore, at the n-th time slot, the UAV–user k and UAV–Eve power gains follow the free space path loss model, which can be expressed as

$$h_{\mathit{k}}\left[n\right]={\beta }_0{d}_{\mathit{k}}^{-2}\left[n\right]=\frac{{\beta }_0}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathit{k}}∥}^2},$$

(4)

and

$$h_{\mathrm{e}}\left[n\right]={\beta }_0{d}_{\mathrm{e}}^{-2}\left[n\right]=\frac{{\beta }_0}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2},$$

(5)

where ${\beta }_0$ is the power gain with a reference distance $d_0=1$ m, and $d_{\mathit{k}}\left[n\right]$ and $d_{\mathrm{e}}\left[n\right]$ represent distances from the UAV to the k-th user and from the UAV to the Eve at time slot n.

Considering that the UAV works in TDMA mode, at most, one user is arranged to communicate with the UAV in each time slot. A binary variable ${\alpha }_k\left[n\right]$ indicates whether the k-th user is served at time slot n, and ${\alpha }_k\left[n\right]=1$ indicates that the k-th user is served, otherwise ${\alpha }_k\left[n\right]=0$. According to the above scheduling scheme, it will yield the following constraints:

$$\sum _{k=1}^K{a}_k\left[n\right]\le 1,\forall n;$$

(6)

$$a_k\left[n\right]\in \left\{0,1\right\},\forall n,k.$$

(7)

Therefore, the achievable rates from the UAV to the k-th user and from the UAV to the Eve at time slot n are expressed as

$$\begin{array}{c}{R}_k\left[n\right]={\alpha }_k\left[n\right]{log}_2\left(1+\frac{p\left[n\right]·h_k\left[n\right]}{{\sigma }^2}\right)\hfill \\ ={\alpha }_k\left[n\right]{log}_2\left(1+\frac{p\left[n\right]·{\gamma }_0}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathit{k}}∥}^2}\right),\hfill \end{array}$$

(8)

and

$$\begin{array}{c}{R}_{\mathrm{e}}\left[n\right]={\alpha }_k\left[n\right]{log}_2\left(1+\frac{p\left[n\right]·h_{\mathrm{e}}\left[n\right]}{{\sigma }^2}\right)\hfill \\ ={\alpha }_k\left[n\right]{log}_2\left(1+\frac{p\left[n\right]·{\gamma }_0}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2}\right),\hfill \end{array}$$

(9)

where $p\left[n\right]$ is the UAV transmit power at time slot n, ${\gamma }_0=\frac{{\beta }_0}{{\sigma }^2}$ is the referenced signal-to-interference-plus-noise ratio, and ${\sigma }^2$ is the noise power at the receivers. In the practical communication system, the transmit power of the UAV needs to meet the constraints of both peak power and average power, namely,

$$0\le p\left[n\right]\le P_{max},n=1,\dots ,N,$$

(10)

$$\sum _{n=1}^{N}p\left[n\right]\le N\overline{P},n=1,\dots ,N,$$

(11)

where $P_{max}$ is the UAV’s maximum power and $\overline{P}$ is its average power.

To ensure the safety communication between the UAV and every ground user, our goal is to join the user scheduling $\mathbf{A}=\{{\alpha }_k\left[n\right],\forall k,n\}$, UAV flight path $\mathbf{Q}=\left\{{\mathbf{q}}_{\mathrm{b}}\left[n\right],\forall n\right\}$, and transmit power $\mathbf{P}=\left\{p\left[n\right],\forall n\right\}$ for N time slots to maximize the minimum secrecy rate among all users. The optimization problem is elaborated as follows:

$$\begin{array}{c}\underset{\mathbf{A},\mathbf{Q},\mathbf{P}}{max}\underset{k\in \mathcal{K}}{min}{\displaystyle \sum _{n=1}^N}(R_k\left[n\right]-R_{\mathrm{e}}\left[n\right])\hfill \end{array}$$

(12)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.0\le a_k\left[n\right]\le 1,\forall n,k,\hfill \\ \left(1\right),\left(2\right),\left(3\right),\left(6\right),\left(10\right),\left(11\right).\hfill \end{array}$$

(13)

To address the mixed-integer problem, binary variables are relaxed into continuous variables by introducing the inequality constraint. Note that in the optimization problem (12), many variables are coupled with each other, and the objective function is concave while nonconvex constraints are contained, so the problem is nonconvex, and it is usually difficult to solve optimally by traditional methods. In Section 3, an efficient algorithm is given to resolve problem (12).

3. Proposed Algorithm

In this section, for the multivariable nonconvex optimization problem, we combine variable substitution with the difference of convex function to decouple the optimization problem into several more easily handled subconvex optimization problems, and propose an efficient algorithm based on alternating optimization. Specifically, we firstly optimize A by fixing Q, P. Then, by keeping A, P, we optimize Q. Finally, we optimize P by fixing A, Q. The algorithm alternately optimizes the three subproblems until reaching convergence.

3.1. User Scheduling Optimization

For any given UAV flight path Q and transmit power P, we optimize user scheduling A by solving the following problem:

$$\begin{array}{c}\underset{\mathbf{A}}{max}\underset{k\in \mathcal{K}}{min}{\displaystyle \sum _{n=1}^N}(R_k\left[n\right]-R_{\mathrm{e}}\left[n\right])\\ \mathrm{s}.\mathrm{t}.\left(6\right),\left(13\right).\end{array}$$

(14)

Note that problem (14) is not convex, as the objective function in (14) is not concave. To solve the problem, we firstly introduce the relaxation variable $\mu$. Then, problem (14) can be transformed into

$$\begin{array}{c}\underset{\mathbf{A},\mu }{max}\mu \hfill \end{array}$$

(15)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\mu \le {\displaystyle \sum _{n=1}^N}(R_k\left[n\right]-R_{\mathrm{e}}\left[n\right]),\forall k,\\ \left(6\right),\left(13\right).\end{array}$$

(16)

It is assumed that there is a time slot $\tilde{n}\in \{1,\dots N\}$, where ${\alpha }_k\left[\tilde{n}\right]$ makes constraint (16) satisfy strict inequality and it is an optimal solution to problem (15). Then, we can always reduce ${\alpha }_k\left[n\right]$ without decreasing the objective value of (15), and find ${\tilde{\alpha }}_k\left[\tilde{n}\right]$, which satisfies ${\tilde{\alpha }}_k\left[\tilde{n}\right]<{\alpha }_k\left[\tilde{n}\right]$ so that constraint (16) satisfies the equation. Therefore, problem (15) and problem (14) are equivalent. At this time, problem (15) is convex, which can be solved by the existing CVX toolbox or interior point method [27].

3.2. Flight Path Optimization

Next, we optimize the flight path with user scheduling and transmit power fixed. The optimization problem is described as follows:

$$\begin{array}{c}\underset{\mathbf{Q}}{max}\underset{k\in \mathcal{K}}{min}{\displaystyle \sum _{n=1}^N}(R_k\left[n\right]-R_{\mathrm{e}}\left[n\right])\\ \mathrm{s}.\mathrm{t}.\left(1\right),\left(2\right),\left(3\right).\end{array}$$

(17)

Problem (17) is also nonconvex. Firstly, the relaxation variable $\tau$ is introduced. Then, to facilitate calculation, we define that ${\gamma }_{\mathrm{b}}\left[n\right]\stackrel{\Delta }{=}p\left[n\right]·{\gamma }_0$. Thus, problem (17) is reformulated as

$$\begin{array}{c}\underset{\mathbf{Q},\tau }{max}\tau \hfill \end{array}$$

(18)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\tau \le {\displaystyle \sum _{n=1}^N}{\alpha }_k\left[n\right]({\log }_2(1+\frac{{\gamma }_{\mathrm{b}}\left[n\right]}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathit{k}}∥}^2})\\ {\displaystyle -{\log }_2(1+\frac{{\gamma }_{\mathrm{b}}\left[n\right]}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2})),\forall k,}\\ \left(1\right),\left(2\right),\left(3\right).\end{array}$$

(19)

Similar to problem (15), there always exists an optimal solution for (18) so that the inequality constraint (19) satisfies the equation. Therefore, problems (17) and (18) are equivalent. Note that the second term in the right-hand-side of (19) is nonconcave in relation to ${\mathbf{q}}_{\mathrm{b}}\left[n\right]$. If the denominator inside the function is directly replaced by a relaxation variable, it will become the form of ${log}_2\left(1+x^{-1}\right)$, which does not follow the disciplined convex programming rules. To deal with this problem, slack variables $\mathbf{S}\stackrel{\Delta }{=}\left[S\left[1\right],S\left[2\right],\dots ,S\left[N\right]\right]$ are introduced and we further change problem (18) as

$$\begin{array}{c}\underset{\mathbf{Q},\mathbf{S},\tau }{max}\tau \hfill \end{array}$$

(20)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\tau \le {\displaystyle \sum _{n=1}^N}{\alpha }_k\left[n\right]({\widehat{R}}_k\left[n\right]-{\log }_2(1+{\gamma }_{\mathrm{b}}\left[n\right]e^{S\left[n\right]})),\hfill \end{array}$$

(21)

$$\begin{array}{c}{e}^{-S\left[n\right]}\le {∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2,\\ \left(1\right),\left(2\right),\left(3\right).\end{array}$$

(22)

It is obvious that ${\widehat{R}}_k\left[n\right]={\log }_2(1+\frac{{\gamma }_{\mathrm{b}}\left[n\right]}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_k∥}^2})$ and the second term in the right-hand-side of (21) is concave in relation to $S\left[n\right]$. In addition, similar to problem (18), there always exists an optimal solution that satisfies constraint (22) with equality. Hence, problem (20) is equivalent to problem (18). However, problem (20) is still difficult to solve since ${\widehat{R}}_k\left[n\right]$ in (21) is neither convex nor concave with respect to ${\mathbf{q}}_{\mathrm{b}}\left[n\right]$, and the right-hand-side of (22) is nonconcave with respect to ${\mathbf{q}}_{\mathrm{b}}\left[n\right]$.

Next, we solve problem (20) based on the successive convex approximation and this method continuously maximizes the objective value of (20) on its convex feasible region until the objective value converges. Specifically, considering the $(l+1)$-th iteration, herein, ${\mathbf{q}}_{\mathrm{b}}^l\left[n\right]$ is the UAV path variable obtained from the l-th iteration. ${\widehat{R}}_k\left[n\right]$ in (21) is convex with respect to ${∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_k∥}^2$. Depending on the property that the convex function’s first-order Taylor expansion at a given point is its global lower bound, we can obtain the lower bound ${\widehat{R}}_k^{\mathrm{lb}}\left[n\right]$ with the first-order Taylor expansion at ${∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_k∥}^2$. It is expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{R}}_k\left[n\right]={\log }_2(1+\frac{{\gamma }_b\left[n\right]}{{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_k∥}^2})\ge {\widehat{R}}_k^{\mathrm{lb}}\left[n\right],\hfill \end{array}\end{array}$$

(23)

where

$$\begin{array}{c}\hfill \begin{array}{c}{\widehat{R}}_k^{\mathrm{lb}}\left[n\right]\stackrel{\Delta }{=}-\frac{{\gamma }_{\mathrm{b}}\left[n\right]·{log}_{2}e}{\left({∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_k∥}^2\right)·({∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_k∥}^2+{\gamma }_{\mathrm{b}}\left[n\right])}\hfill \\ {\displaystyle \times ({∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_k∥}^2-{∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_k∥}^2)}\hfill \\ {\displaystyle +{log}_2\left(1+\frac{{\gamma }_{\mathrm{b}}\left[n\right]}{{∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_k∥}^2}\right).}\hfill \end{array}\end{array}$$

(24)

Since ${∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2$ in (22) is convex in relation to ${\mathbf{q}}_{\mathrm{b}}\left[n\right]$, we can get its lower bound with the first-order Taylor expansion at ${\mathbf{q}}_{\mathrm{b}}^l\left[n\right]$:

$$\begin{array}{c}\hfill \begin{array}{c}{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2\ge {∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2+2({\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_e{)}^T\times ({\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]).\hfill \end{array}\end{array}$$

(25)

After the above procedures, problem (20) can be replanned as

$$\begin{array}{c}\underset{\mathbf{Q},\mathbf{S},\tau }{max}\tau \hfill \end{array}$$

(26)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\tau \le {\displaystyle \sum _{n=1}^N}{\alpha }_k\left[n\right]({\widehat{R}}_k^{\mathrm{lb}}\left[n\right]-{\log }_2(1+{\gamma }_{\mathrm{b}}\left[n\right]e^{S\left[n\right]})),\hfill \end{array}$$

(27)

$$\begin{array}{c}{e}^{-S\left[n\right]}\le {∥{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}^2+2({\mathbf{q}}_{\mathrm{b}}^l\left[n\right]-{\mathbf{w}}_e{)}^T\times ({\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{q}}_{\mathrm{b}}^l\left[n\right]),\\ \left(1\right),\left(2\right),\left(3\right).\end{array}$$

(28)

Here, the objective function is linear, and constraints (1), (2), (3), (27), and (28) are all convex. Therefore, problem (26) is a convex optimization problem which can be solved through the interior point method or the existing CVX toolbox [27]. Note that constraints (27) and (28) imply constraints (21) and (22); thus, the solution obtained from problem (26) is also a feasible solution to problem (20). Hence, the objective value of problem (20) can be obtained by solving (26) in the $(l+1)$-th iteration, and must not be less than the corresponding objective value obtained in the l-th iteration.

3.3. Transmit Power Optimization

The transmit power is optimized by fixing the user scheduling and flight path. The optimization problem is written as

$$\begin{array}{c}\underset{\mathbf{P}}{max}\underset{k\in \mathcal{K}}{min}{\displaystyle \sum _{n=1}^N}(R_k\left[n\right]-R_{\mathrm{e}}\left[n\right])\\ \mathrm{s}.\mathrm{t}.\left(10\right),\left(11\right).\end{array}$$

(29)

Problem (29) is also nonconvex. Firstly, we define the following variables as ${\gamma }_1\left[n\right]=\frac{{\gamma }_0}{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathit{k}}∥}$, ${\gamma }_2\left[n\right]=\frac{{\gamma }_0}{∥{\mathbf{q}}_{\mathrm{b}}\left[n\right]-{\mathbf{w}}_{\mathrm{e}}∥}$, and then introduce the relaxation variable $\eta$. Problem (29) can be transformed into

$$\begin{array}{c}\underset{\mathbf{P},\eta }{max}\eta \hfill \end{array}$$

(30)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\eta \le {\displaystyle \sum _{n=1}^N}{\alpha }_k\left[n\right]({\log }_2(1+p\left[n\right]{\gamma }_1\left[n\right])-{\widehat{R}}_e\left[n\right]),\\ \left(10\right),\left(11\right),\end{array}$$

(31)

where ${\widehat{R}}_e\left[n\right]={\log }_2(1+p\left[n\right]{\gamma }_2\left[n\right])$.

Similar to problem (15), there always exists an optimal solution for (30) so that the inequality constraint (31) satisfies the equation. Therefore, problems (29) and (30) are equivalent. However, solving problem (30) is also challenging, as constraint (31) is nonconvex.

Then, we can solve the problem (30) by applying the successive convex approximation method. Note that ${\widehat{R}}_{\mathrm{e}}\left[n\right]$ in (31) is neither convex nor concave with respect to $p\left[n\right]$. Hence, we can obtain the upper bound ${\widehat{R}}_{\mathrm{e}}^{\mathrm{ub}}\left[n\right]$ with the first-order Taylor expansion at $p^l\left[n\right]$. It is expressed as follows,

$$\begin{array}{c}{\widehat{R}}_{\mathrm{e}}\left[n\right]={\log }_2(1+p\left[n\right]{\gamma }_2\left[n\right])\hfill \\ {\displaystyle \le \frac{{\gamma }_2\left[n\right]{log}_2\left(e\right)}{(1+p^l\left[n\right]{\gamma }_2\left[n\right])}(p\left[n\right]-p^l\left[n\right])}\hfill \\ {\displaystyle +{\log }_2(1+p^l\left[n\right]{\gamma }_2\left[n\right])}\hfill \\ {\displaystyle \stackrel{\Delta }{=}{\widehat{R}}_{\mathrm{e}}^{\mathrm{ub}}\left[n\right].}\hfill \end{array}$$

(32)

By replacing the term ${\widehat{R}}_{\mathrm{e}}\left[n\right]$ with its upper bound ${\widehat{R}}_{\mathrm{e}}^{\mathrm{ub}}\left[n\right]$, problem (30) is formulated as

$$\begin{array}{c}\underset{\mathbf{P},\eta }{max}\eta \hfill \end{array}$$

(33)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.\eta \le {\displaystyle \sum _{n=1}^N}{\alpha }_k\left[n\right]({\log }_2(1+p\left[n\right]{\gamma }_1\left[n\right])-{\widehat{R}}_{\mathrm{e}}^{\mathrm{ub}}\left[n\right]),\\ \left(10\right),\left(11\right).\end{array}$$

(34)

Since the first term in the right-hand-side of (34) is concave in relation to $p\left[n\right]$ while the second term in the right-hand-side of (34) is linear, problem (33) is a convex optimization problem which can be solved through the interior point method or the existing CVX toolbox [27]. Similar to Section 3.2, the objective value of problem (30) can be obtained by solving (33).

3.4. Overall Algorithm and Convergence

Based on the analysis of solving the above three subproblems, Algorithm 1 summarizes the proposed iterative optimization algorithm for solving problem (12), where $\epsilon$ is the introduced convergence threshold. If the difference between the solutions obtained by two successive iterations is less than this threshold, it can be considered that the solution obtained by Algorithm 1 meets the expected accuracy requirements.

Algorithm 1 Alternating iteration algorithm for problem (9).

1: Initialization: Set the initial flight path and transmit power, let $l=0$ and give accuracy tolerance $\epsilon$. 2: repeat: 3: Solve the problem (15) with the given ${\mathbf{Q}}^l$, ${\mathbf{P}}^l$ and obtain the optimal solution ${\mathbf{A}}^{l+1}$. 4: Solve the problem (26) with ${\mathbf{A}}^{l+1}$, ${\mathbf{P}}^l$ and obtain the optimal solution ${\mathbf{Q}}^{l+1}$. 5: Solve the problem (33) with ${\mathbf{A}}^{l+1}$, ${\mathbf{Q}}^{l+1}$ and obtain the optimal solution ${\mathbf{P}}^{l+1}$. 6: Updata $l=l+1$. 7: Until the objective value increases below the accuracy tolerance $\epsilon$.

Next, we discuss the convergence of Algorithm 1. Firstly, define $R_{\mathbf{Q}}^{\mathrm{lb},l}(\mathbf{A},\mathbf{Q},\mathbf{P})=R_{\mathbf{Q}}^l$ and $R_{\mathbf{P}}^{\mathrm{lb},l}(\mathbf{A},\mathbf{Q},\mathbf{P})=R_{\mathbf{P}}^l$, where $R_{\mathbf{Q}}^l$ and $R_{\mathbf{P}}^l$ are the objective values of problem (15) and problem (26) with respect to A, Q, and P. In step 3 of Algorithm 1, since the optimal solution of problem (15) is obtained for given ${\mathbf{Q}}^l$ and ${\mathbf{P}}^l$, we have

$$\begin{array}{c}R({\mathbf{A}}^l,{\mathbf{Q}}^l,{\mathbf{P}}^l)\le R({\mathbf{A}}^{l+1},{\mathbf{Q}}^l,{\mathbf{P}}^l),\hfill \end{array}$$

(35)

where $R(\mathbf{A},\mathbf{Q},\mathbf{P})$ is the minimum secrecy rate of all users. Then, for given ${\mathbf{A}}^{l+1}$, ${\mathbf{Q}}^l$ and ${\mathbf{P}}^l$ in step 4 of Algorithm 1, we have

$$\begin{array}{c}R({\mathbf{A}}^{l+1},{\mathbf{Q}}^l,{\mathbf{P}}^l)\stackrel{\left(a\right)}{=}{R}_{\mathbf{Q}}^{\mathrm{lb},l}({\mathbf{A}}^{l+1},{\mathbf{Q}}^l,{\mathbf{P}}^l)\hfill \\ \stackrel{\left(b\right)}{\le }{R}_{\mathbf{Q}}^{\mathrm{lb},l}({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^l)\hfill \\ \stackrel{\left(c\right)}{\le }R({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^l),\hfill \end{array}$$

(36)

where equation (a) holds because the first-order Taylor expansions in (23) and (25) strictly approximate the original function at a given local point, which means that problem (26) and problem (17) have the same objective value. The reason why inequality (b) holds is the same as that of (35). On the basis of given ${\mathbf{A}}^{l+1}$, ${\mathbf{Q}}^l$ and ${\mathbf{P}}^l$, problem (26) is solved to obtain the optimal solution. Inequality (c) holds because the objective value of problem (26) is the lower bound of the objective value of its original problem (17). Thirdly, for given ${\mathbf{A}}^{l+1}$, ${\mathbf{Q}}^{l+1}$ and ${\mathbf{P}}^l$ in step 5 of Algorithm 1, we have

$$\begin{array}{c}R({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^l)\stackrel{\left(a\right)}{=}{R}_{\mathbf{P}}^{\mathrm{lb},l}({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^l)\hfill \\ \stackrel{\left(b\right)}{\le }{R}_{\mathbf{P}}^{\mathrm{lb},l}({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^{l+1})\hfill \\ \stackrel{\left(c\right)}{\le }R({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^{l+1}),\hfill \end{array}$$

(37)

and the reason why (37) holds is similar to (36). Based on (35)–(37), we can obtain

$$\begin{array}{c}R({\mathbf{A}}^l,{\mathbf{Q}}^l,{\mathbf{P}}^l)\le R({\mathbf{A}}^{l+1},{\mathbf{Q}}^{l+1},{\mathbf{P}}^{l+1}),\hfill \end{array}$$

(38)

which shows that the objective value of problem (12) does not decrease after each iteration of Algorithm 1. Since the upper bound of the objective value for problem (12) is a finite value, the convergence of Algorithm 1 can be guaranteed. Additionally, since each subproblem is a standard convex optimization problem, we analyze the algorithm complexity based on interior point method [28], and the computational complexity of Algorithm 1 is $\mathrm{O}\left[K_{ite}\left(3{\left(N\right)}^{3.5}\right)\right]$, where $K_{ite}$ represents the number of iterations.

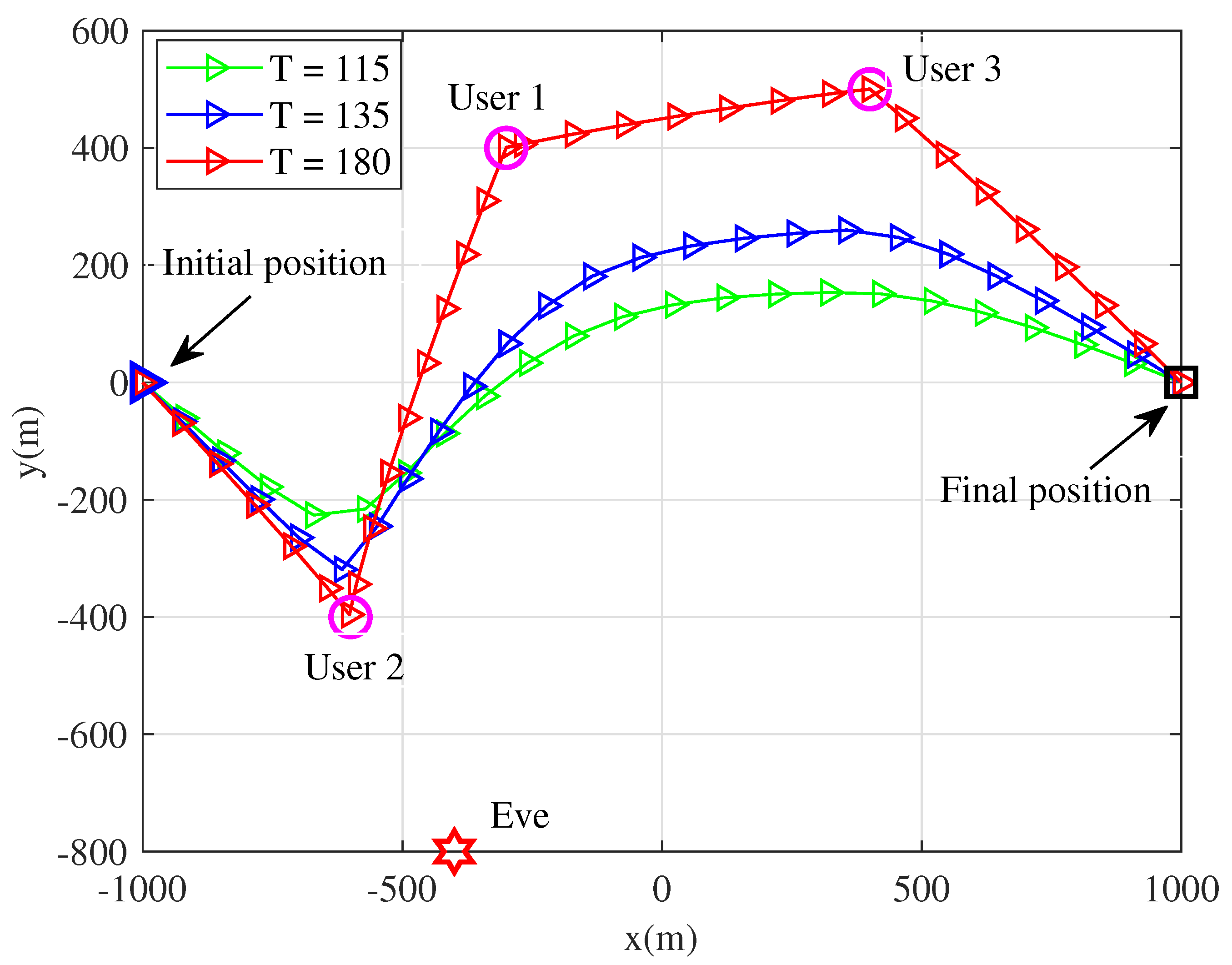
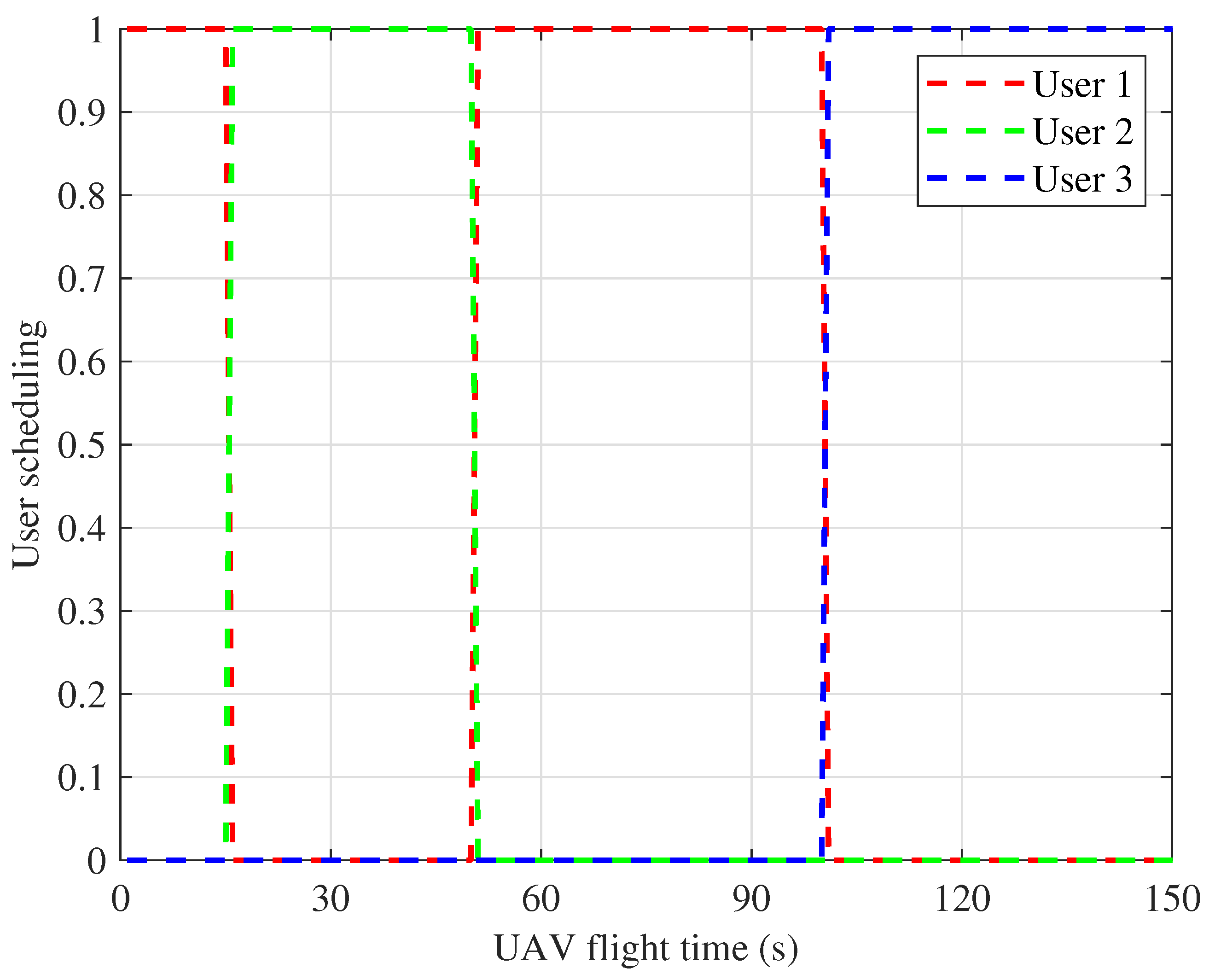
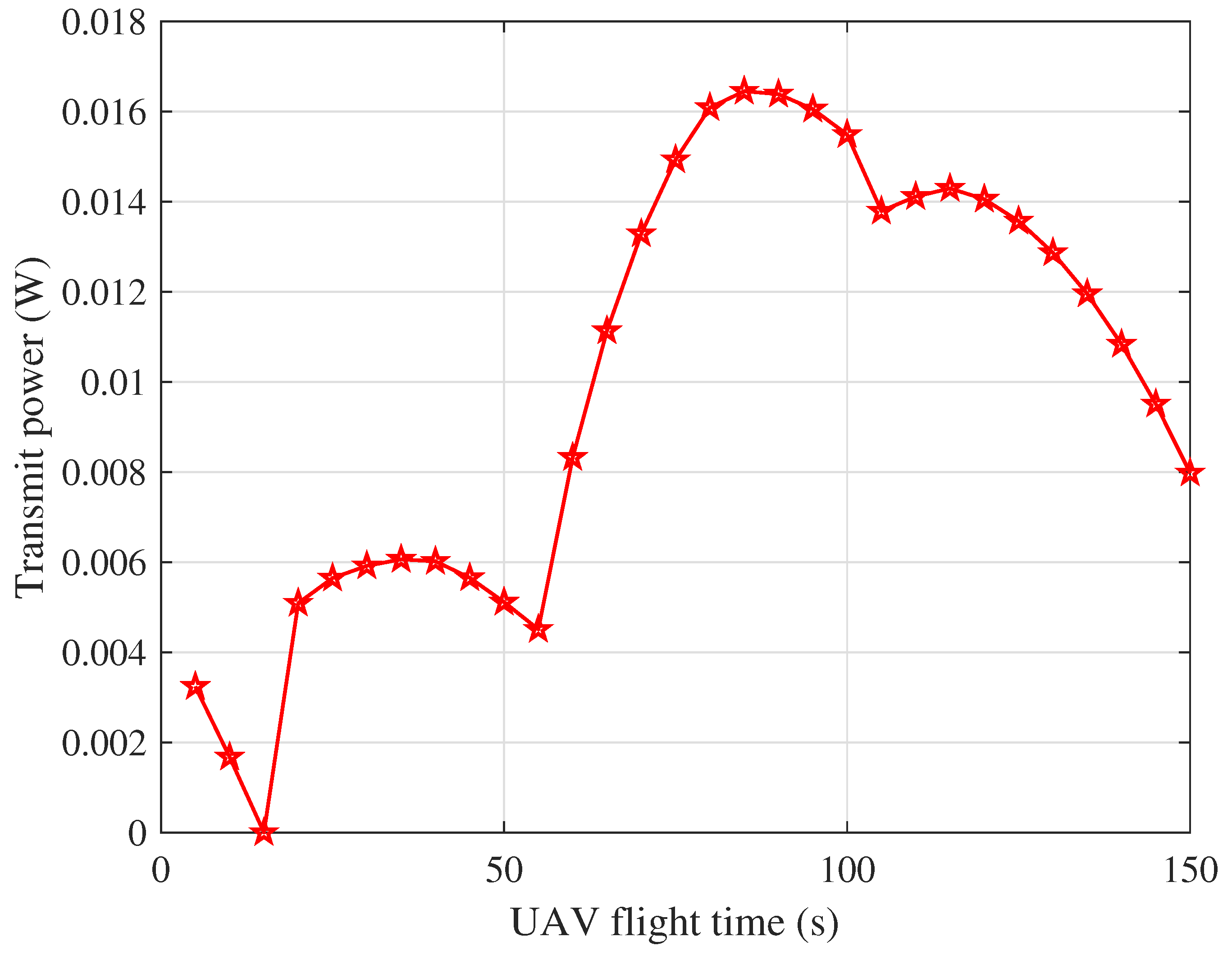
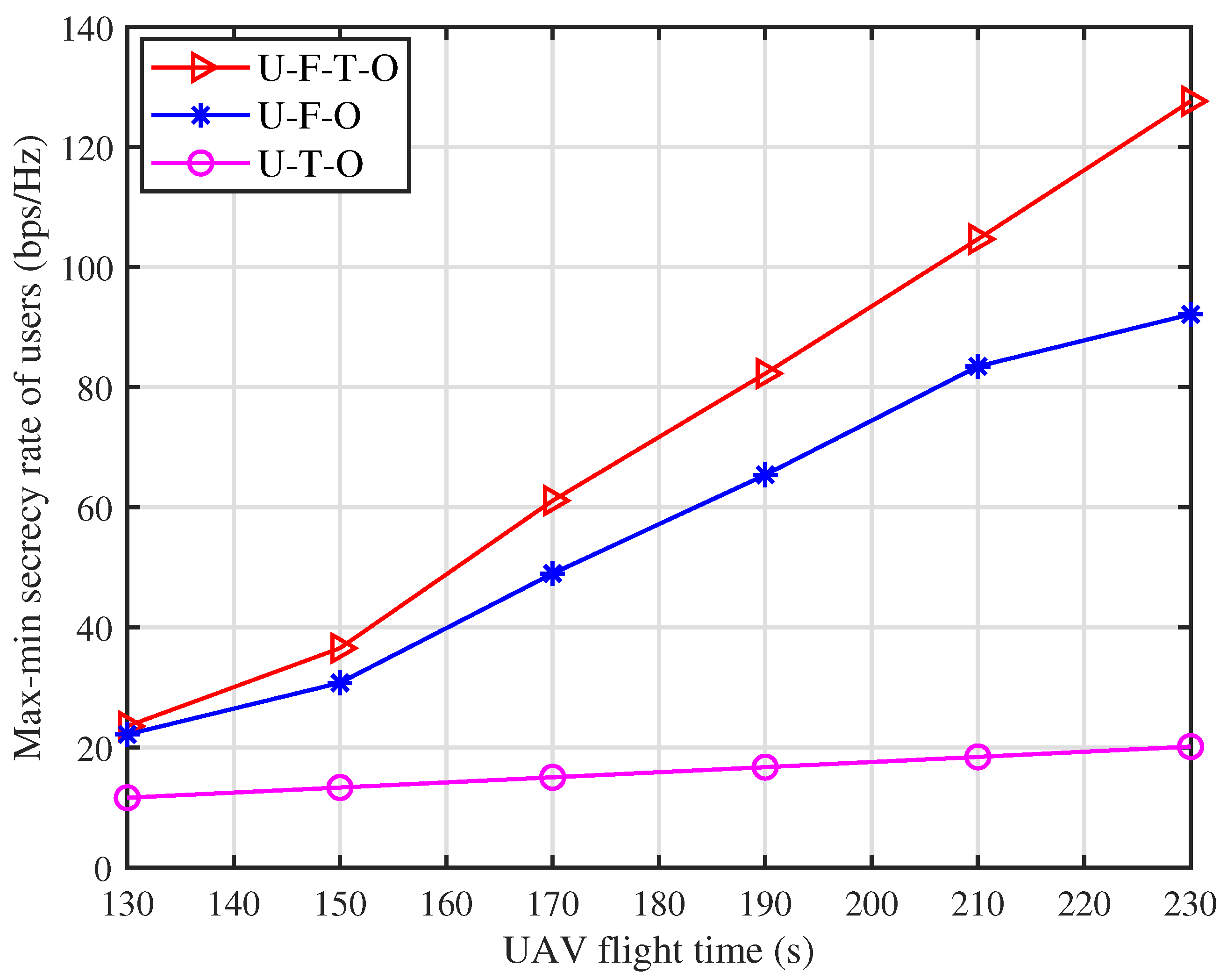
4. Numerical Results and Discussions

This section presents simulation results to demonstrate the performance of the proposed joint user scheduling, transmit power, and flight path optimization algorithm, which is denoted by “U-T-F-O”. To better verify its performance, it is compared with two benchmark schemes: user scheduling and flight path optimization with a fixed transmit power allocation (“U-F-O”) and joint user scheduling and transmit power optimization with a fixed flight path (“U-T-O”). In the “U-F-O” scheme, the UAV is assigned equal transmit power in each time slot, for example, $p\left[n\right]=\overline{\mathrm{P}}$. In the “U-F-O” scheme, the UAV flies along a straight line from the initial position to the final position.

In the simulation, suppose that there are three users distributed in a geographical area of $2\times 1.4\mathrm{k}{\mathrm{m}}^2$. We set Eve’s coordinates as ${(-400,-800,0)}^{\mathit{T}}$. The flight altitude is 50 m. We set the reference SNR ${\gamma }_0=80\mathrm{dB}$ at the reference distance $d_0=1$ m. The duration of a time slot is ${\delta }_t=5\mathrm{s}$. The maximum UAV flight speed is $v_{max}=20\mathrm{m}/\mathrm{s}$. The accuracy tolerance in Algorithm 1 is set to $\epsilon ={10}^{-3}$. Furthermore, let $p\left[n\right]=\overline{\mathrm{P}}$ and ${\mathrm{P}}_{max}=4\overline{\mathrm{P}}$.

Figure 2 shows the optimized flight paths obtained by the proposed algorithm for different flight time T when $\overline{\mathrm{P}}=10 \mathrm{dBm}$. With the increase in flight time, the optimized path will be closer to users to obtain better channel conditions to transmit information, but it will be as far away from the Eve as possible while being close to users. With the continuous increase of flight time, the UAV has more freedom to adjust its flight path, so that it can visit all users. If the flight time T is large enough, it will stay over the users for a certain period of time, because in its hovering position, the UAV can achieve the best balance between information leakage to the Eve and maximizing the achievable rate of users. In the case of flight time T = 180 s, the density of points on the flight path around each user is higher than that far away from the user. The reason is that when the UAV flies close to the user, it will slow down accordingly to obtain better communication conditions. In addition, with the increase in flight time, the flight path of the UAV becomes less smooth until it becomes a polyline passing through users on the ground, and the flight path of the UAV no longer changes with flight time.

Figure 3 shows the user scheduling when T = 150 s, $\overline{\mathrm{P}}=10\mathrm{dBm}$. As can be seen from Figure 3, at any moment, when the UAV provides a communication connection to a user, the user communication scheduling value is 1, while other users are not served, and the user communication scheduling value is 0. The scheduling order of users is user 1, user 2, user 1, and user 3, that is, the UAV communicates with user 1, user 2, user 1, and user 3 successively during the whole flight time. The reason is that due to the existence of the potential Eve, the UAV will select the appropriate user to serve according to the current channel conditions during the flight from the initial position to the final position, so as to obtain better communication quality, which shows the effectiveness of the proposed algorithm. In addition, it can be observed that the whole flight cycle of the UAV can be roughly divided into several time periods. During the flight time of 0–15 s and 51–100 s, the UAV provides services for user 1; during the time period of 16–50 s, the UAV provides services for user 2; and during the period of 101–150 s, the UAV provides services for user 3. The communication time for user 2 is slightly less, which is because user 2 is closer to the Eve. This schedule makes the secrecy rate among all users have the optimal balance, which reflects the fairness of the algorithm and can take into account the communication quality of all users.

Figure 4 describes the trend of the UAV transmit power changing with flight time under the joint optimization scheme when T = 150 s, $\overline{\mathrm{P}}=10\mathrm{dBm}$. At the beginning of the flight, the UAV transmit power has a decreasing trend, because the superiority of UAV-user 1 link’s channel quality over UAV-Eve link’s channel quality is diminishing. Then, when the UAV continues to provide services for each user according to the user’s scheduling order, the UAV transmit power first increases and then decreases, since in each period, the UAV first flies close to the user and then flies away from the user. When the UAV is approaching the user, the channel quality of the UAV-user link is superior to that of the UAV-Eve link. As this advantage is increasing, more power will be allocated. When the UAV flies away from the user, the advantage of the UAV-user link (that the channel quality is better than that of the UAV-Eve link) is decreasing, so the power allocated is less and less. In addition, the sum of UAV transmit power is different during the time of providing services for each user, since the distances of UAV-users and users-Eve are different.

In order to study the relationship between the max-min secrecy rate of users and the UAV flight time under different schemes, the simulation results of the three schemes are compared when $\overline{\mathrm{P}}=10\mathrm{dBm}$. As can be seen from Figure 5, the max-min secrecy rates of different schemes increase with the increase of flight time, and the “U-T-F-O” scheme achieves the best safety communication performance, followed by the “U-F-O” scheme, and the “U-T-O” scheme is the worst. This is because in the “U-T-O” scheme, the flight path of the UAV is not optimized, which leads to the communication channel conditions of the UAV not being optimized, so the maximum-minimum secrecy rate of the “U-T-O” scheme is the lowest, and the variation range with flight time is not large. In contrast, the “U-F-O” scheme and the “U-T-F-O” scheme take advantage of the mobility of the UAV, which makes the channel quality of the UAV-user link better than that of UAV-Eve’s link, and fully considers the balance between communication rate and eavesdropping rate, so the max-min secrecy rate is higher. Comparing the “U-F-O” scheme with “U-T-F-O” scheme, the order of the UAV accessing users is the same, but the joint optimization scheme has better secure communication performance. The reason is that the “U-T-F-O” scheme not only optimizes the flight path of the UAV, but also optimizes the power allocation of the UAV. This scheme can control the power allocation according to the current communication channel conditions after the flight path optimization.

5. Conclusions

This paper studied the multi-user secure communication system assisted by the UAV base station, and proposed a joint optimization algorithm of flight path planning and resource allocation. Firstly, the system model of a UAV secure communication network was analyzed, and the achievable rate from the UAV to the user and eavesdropping rate from the UAV to the Eve were deduced. Secondly, a joint optimization problem of user scheduling, UAV flight path, and transmit power control, with the goal of maximizing the minimum secrecy rate of the system, was established. Facing the nonconvex objective optimization problem, it was decomposed by combining variable substitution with the difference of convex function. Several single-variable optimization problems were obtained, and then the three subproblems were solved alternately by the block coordinate descent method. Finally, numerical results verified the correctness of the theoretical analysis, and showed that the proposed scheme is superior to other schemes in improving the minimum secrecy rate of the system, and can effectively improve the security of the system.