Application of Gray Wolf Particle Filter Algorithm Based on Golden Section in Wireless Sensor Network Mobile Target Tracking

Abstract

In order to address the issue of low tracking accuracy caused by particle depletion in the particle filter, a mobile target tracking algorithm tailored for wireless sensor networks (WSNs) is presented. This algorithm, based on the golden-section gray wolf particle filter (PF), represents a novel approach to target tracking. The algorithm’s originality lies in its ability to guide the particle swarm toward regions of higher weights, thereby striking a balance between global and local exploration capabilities. This not only alleviates issues related to sample depletion and local extrema but also enhances the diversity of the particle swarm, significantly improving tracking performance. To assess the effectiveness of the proposed algorithm, a series of simulation experiments were conducted, comparing it with the extended Kalman filter (EKF) and the standard PF algorithm. The experiments employed a constant velocity circular motion model (CM) for filtering and tracking. The root mean square error metric demonstrated a significant reduction in error of 57% and 37% in comparison to the extended Kalman filter (EKF) and the particle filter (PF), respectively. This serves to illustrate the superiority of our method in enhancing tracking accuracy.

1. Introduction

A wireless sensor network (WSN) is a sophisticated high-tech technology that employs wireless sensor devices to detect environmental data within a given environment. The data collected by these devices are then integrated in real time to form a network connection. This represents one of the most significant technical forms of the Internet of Things. This technology offers substantial support for applications such as target tracking.

Target tracking represents a significant application field and a highly active research area within the domain of wireless sensor networks. In scenarios such as traffic monitoring and war detection, target tracking technology plays a pivotal role. The placement of the target in an environment equipped with wireless sensors enables the real-time collection of data on the target’s movement. These data can then be combined with the control of the tracking system to estimate the position of the tracked target in real time, thereby achieving accurate tracking.

In order to ascertain the location of mobile nodes within a wireless sensor network, the most straightforward approach would be to equip each node with a Global Positioning System (GPS) or a China’s Beidou Navigation Satellite System (BDS) module. However, this appears to be an impractical project due to considerations of cost, limitations on node energy, and the specific deployment environment required for GPS. Consequently, only a select number of nodes typically obtain their coordinates through the use of GPS or by being pre-deployed at specific locations. The remaining nodes calculate their distance from the anchor nodes based on their ranging or connectivity information. They then employ techniques such as maximum likelihood estimation or triangulation to determine their positions.

Generally speaking, wireless sensor network (WSN) tracking algorithms can be divided into algorithmic localization and filtering prediction. Localization algorithms are divided into two categories: distance-based and distance-free. In distance-measurement-based methods, the coordinates of two nodes are estimated by measuring the distance and angle between them. The RSSI (received signal strength indication), TOA (time of arrival) [1], TDOA (time difference of arrival) [2], and AOA (angle of arrival) [3] are the most commonly used ranging techniques. These algorithms have high positioning accuracy but are limited by high measurement costs and power consumption and cannot be applied to some areas with harsh geographical environments. Algorithms that do not require distance measurement include APIT (approximate perfect point in tri-angulation test), DV, and Hop [4], which rely on connectivity information between nodes to estimate the distance between them. Although these algorithms reduce costs and power consumption, positioning accuracy is often poor. However, these algorithms often have a large time delay when facing target tracking and cannot track a target for a long time. As such, filtering algorithms often become an important method for determining target tracking. Filtering algorithms are often divided into Kalman filtering and particle filtering algorithms, with particle filtering having significant advantages over Kalman filtering. It is not limited by linear and Gaussian noise distributions and can flexibly handle nonlinear and non-Gaussian problems, making it more widely applicable. The particle filter adopts a recursive structure algorithm, which has high real-time processing efficiency. The recursive process of Bayesian filtering is achieved through nonparametric Monte Carlo simulation, thereby more accurately estimating the target state and performing well in the field of target tracking [5,6].

Nevertheless, in wireless sensor networks (WSNs), there is a prevalent issue of particle poverty in particle filtering tracking, which can result in a considerable increase in tracking errors. Particle poverty is most commonly observed during the filtering process when the particle set is unable to fully represent the posterior distribution of the target state. Over time, some particles may gradually lose their representativeness toward the target state, resulting in a decrease in the diversity of the particle set. This can result in inaccuracy in the estimation of the target position by the particle filtering algorithm, with the potential for the target to be completely lost. Particle impoverishment not only affects the accuracy of target tracking but may also result in a reduction in tracking stability, thereby rendering it challenging for wireless sensor networks to maintain continuous and effective target tracking.

Although the particle filter has the potential to be an effective method for target tracking, it also has some notable limitations. For instance, the tracking accuracy of the particle filter may be diminished due to particle degradation. Concurrently, when confronted with intricate dynamic models, the sampling and updating process of particles may become inefficacious and time-consuming, which impinges upon the real-time performance of the algorithm. Furthermore, the particle filter is also relatively constrained in its ability to address the uncertainty of the observed data, which is susceptible to noise interference. The motivation for developing the golden-section gray wolf particle filter maneuvering target tracking algorithm was to address the aforementioned issues. The objective of the proposed algorithm is to optimize the particle sampling and updating process, reduce particle degradation, and improve tracking accuracy and stability. This has been achieved by combining the advantages of the golden-section search and gray wolf optimization algorithms. Concurrently, the algorithm is capable of more effectively addressing the uncertainty of observed data, enhancing resilience to noise interference, and improving the efficiency of the algorithm’s operation while maintaining the tracking performance necessary for real-time applications.

The particle filter algorithm is based on the Monte Carlo method, which necessitates a significant number of particles to achieve the desired estimation accuracy; the greater the number of particles, the greater the time complexity of the algorithm. In order to maintain local diversity during the process of particle swarm optimization, this paper proposes an improvement to the particle filtering algorithm. The proposed improvement is designed to address the issue of particle impoverishment and to resolve the defect of particle degradation.

There are various development directions in the field of modern particle filtering, among which the swarm intelligent optimization particle filtering algorithm is a relatively new development direction. The main idea of the swarm intelligent particle filter method is to carry out repeated iterative optimization of the particle distribution, and low-weight particles in the particle swarm do not have the problem of abandonment, thus increasing the diversity of the particle iterative process and fundamentally solving the problem of particle impoverishment. Evolutionary problems and particle filters essentially obtain optimal solutions through an iterative process of evaluation, selection, and updating [6,7,8,9]. Therefore, many researchers have used evolutionary methods to solve particle filter problems. Jie Cao [10] and others proposed to combine the weighted dithering firefly algorithm and incomplete resampling to improve particle filtering and alleviate the problems of particle degradation and diversity exhaustion. However, the firefly algorithm is extremely easy to fall into the local optimum during the iteration process, which will verify the efficiency of particle filtering, which is often non-negligible in maneuvering target tracking. Liu Haitao [11] proposed an improved low-weight particle intelligent filtering (IPF) processing strategy based on a genetic algorithm to improve the filtering accuracy. While improving the filtering performance, low-weight particle intelligent filtering also faces the problem of underoptimization or overoptimization. Weigang Li et al. [12] proposed a new particle filtering method based on the improved gray wolf algorithm to improve the estimation accuracy of particle filtering, which has poorer search accuracy than the gray wolf algorithm in this paper, and it is extremely easy for the ordinary gray wolf algorithm to fall into the local optimum of the optimization algorithm. Chen Zhimin [13] proposed a new particle filtering algorithm based on the bat algorithm, which uses particles to represent individual bats and simulates the process of searching for prey by bat populations, thus improving the overall quality and distribution rationality of particles. Li Ji [14] combined the Harris hawk optimization algorithm with the hunting strategy and proposed a population intelligent optimization particle filtering method (EHHOPF) that effectively improves the system state estimation accuracy and filtering stability. The scalability of these algorithms may be limited as the size and complexity of the system increases. This is mainly due to the fact that intelligent algorithms require more computational resources and time when dealing with large-scale problems. All of the above methods improve the performance of the particle filtering algorithm, but most of them control the number of iterations of the intelligent algorithm through empirical values, which can easily lead to underoptimization or overoptimization, resulting in a decrease in estimation accuracy.

This illustrates the comprehensive research conducted on the utilization of intelligent optimization algorithms to enhance particle filtering. Consequently, it is also possible to utilize intelligent optimization particle filtering for the purpose of maneuvering target tracking. Nevertheless, the necessity for a system that can run quickly is often a prerequisite for the successful implementation of a maneuvering target tracking system. Consequently, the algorithms in question should be both simple and accurate.

Particle filtering has been demonstrated to possess unique advantages in applications within the field of target tracking. As a state estimation method based on Monte Carlo sampling, particle filtering approximates the probability distribution of the target state by a set of particles with weights, thereby enabling it to deal with nonlinear and non-Gaussian state estimation problems in complex environments. In a target tracking task, the state of the target may change dynamically with time and environment. This may include the updating of parameters such as position, velocity, and acceleration. Particle filtering is capable of tracking and predicting the motion trajectory of the target in real time by continuously and iteratively updating the position and weight of the particles, thereby achieving the fast and accurate tracking of maneuvering targets. In the tracking of maneuvering targets, the motion state of the target may change rapidly, necessitating the tracking system to possess the capacity for rapid response and accurate prediction. Particle filtering, in conjunction with intelligent optimization algorithms, enables rapid convergence to the vicinity of the true value of the target state, thereby facilitating the real-time tracking and prediction of maneuvering targets through information interaction between particles and the optimization of the update strategy. The particle filtering method, when combined with an intelligent optimization algorithm, can enhance the accuracy and efficiency of target tracking. Furthermore, it can address the uncertainty factors present in complex environments, such as noise interference and target occlusion. This results in a more reliable and stable target tracking system.

The gray wolf optimization algorithm represents a simplified and more robust approach to optimization. In addition to its intuitive nature, this algorithm is also straightforward to implement in program code. In contrast to other algorithms, the program code is relatively concise and can be readily employed to address a range of optimization issues [15]. Moreover, in contrast to some recently developed optimization algorithms, the gray wolf optimization algorithm has been employed in a diverse range of applications.

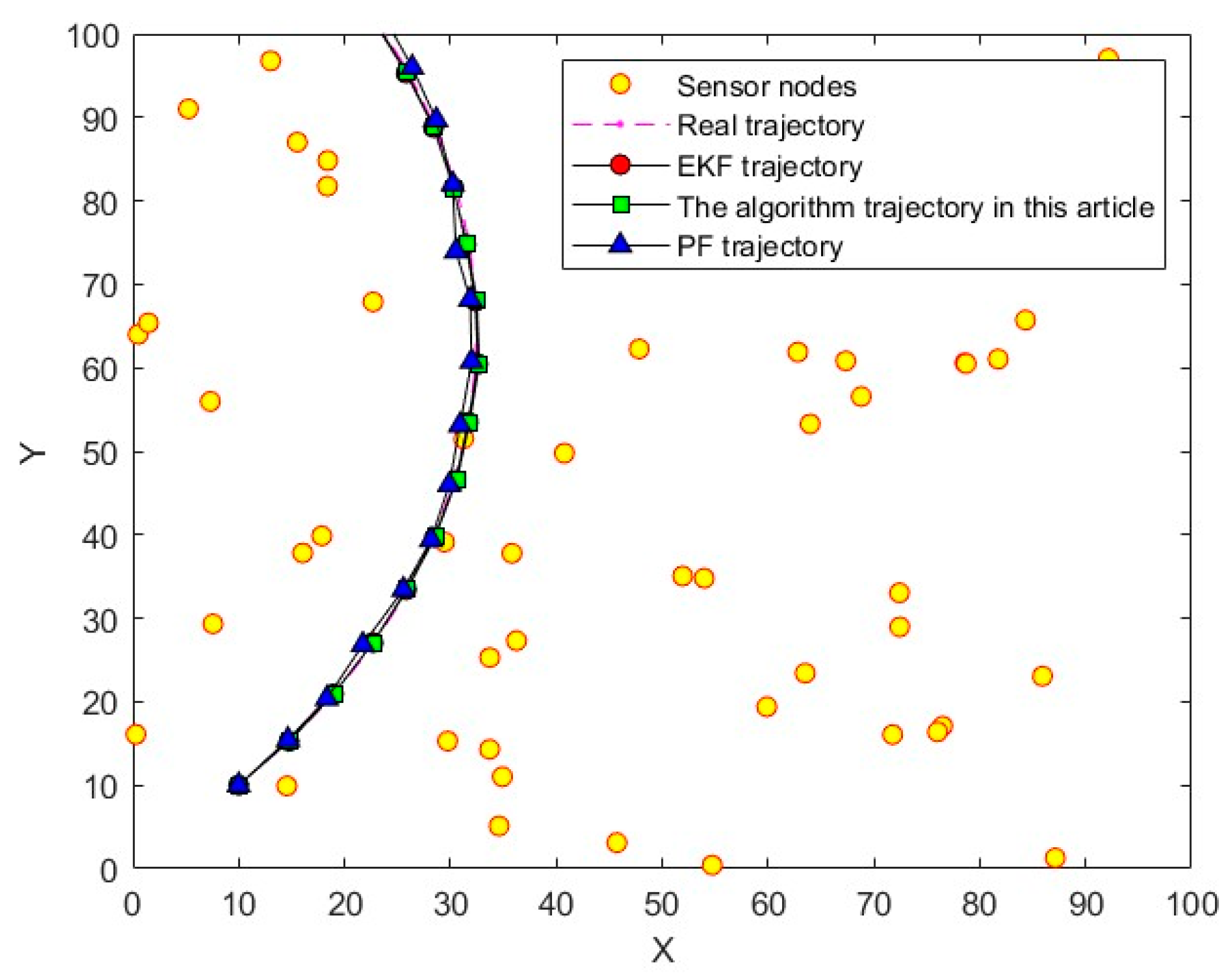
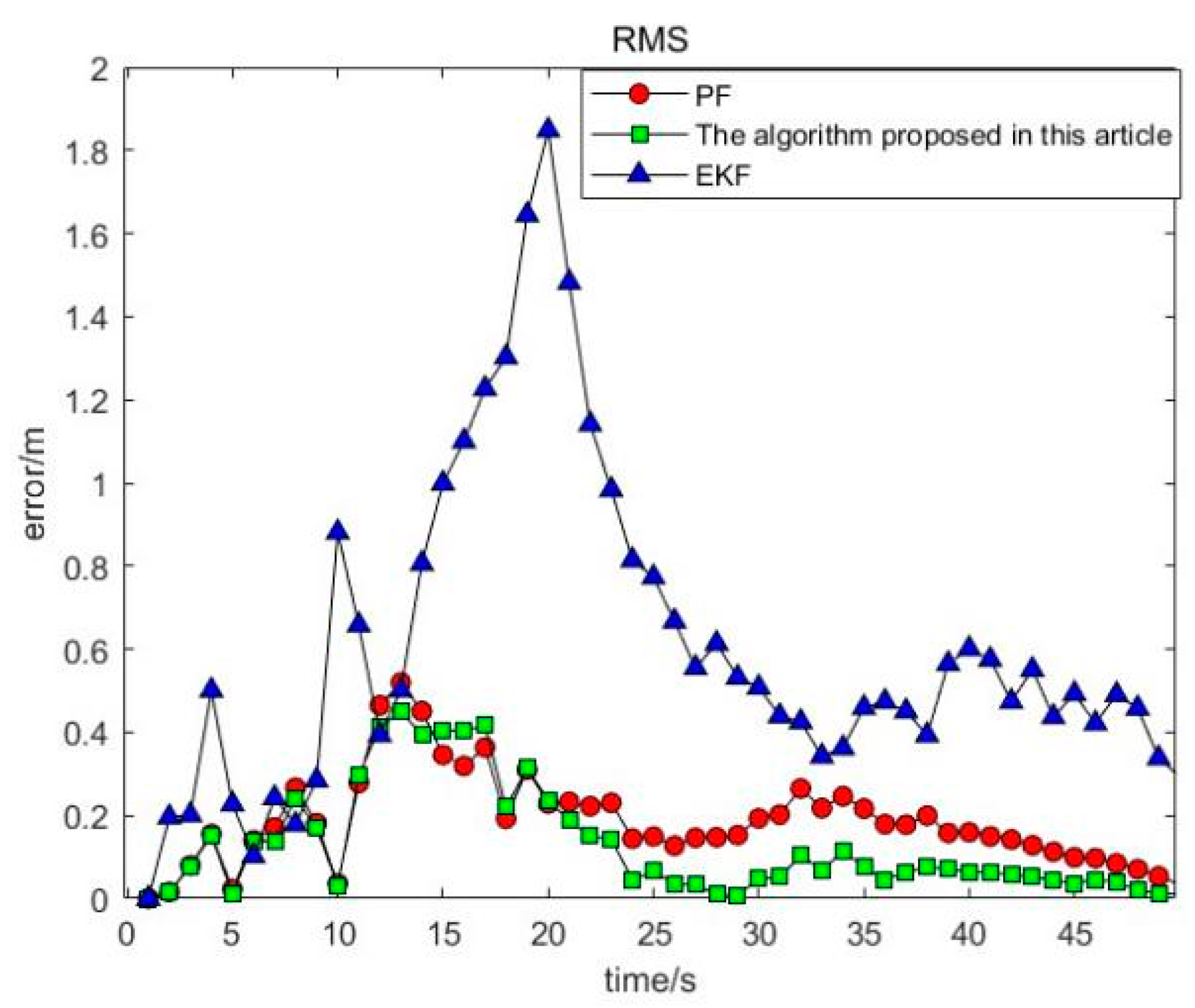
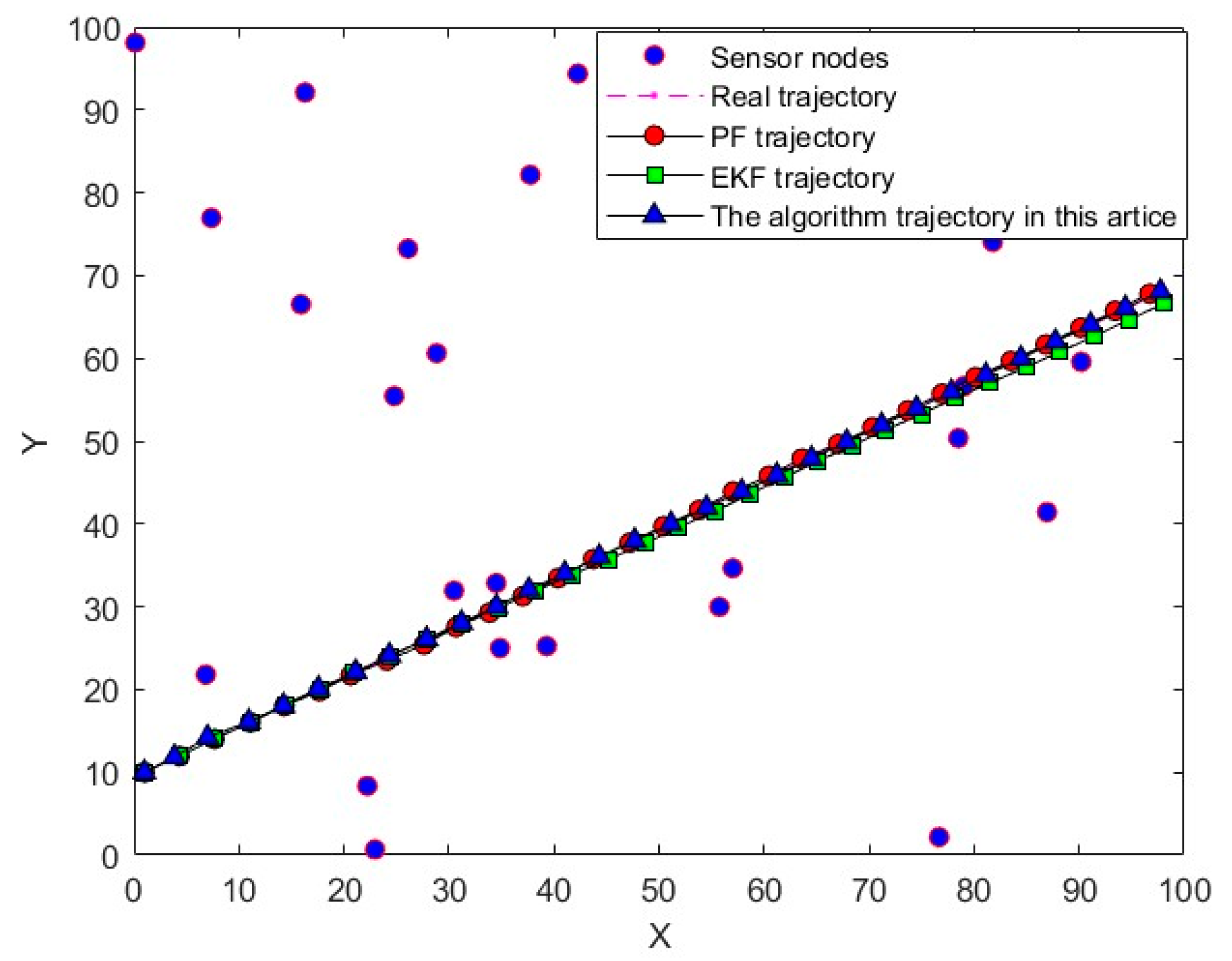
In this study, the gray wolf optimization algorithm, renowned for its simplicity, robustness, and ease of implementation, was further enhanced by integrating the golden ratio algorithm and introducing an adaptive adjustment strategy. This hybrid approach combines the global search capabilities of the gray wolf optimization algorithm with the local search precision of the golden ratio algorithm, thereby simulating the social behavior of gray wolves to strike a balance between global and local searches. To validate its performance, we designed experiments on benchmark optimization problems and applied the algorithm to real-world challenges, such as WSN maneuvering target tracking. The results demonstrate the effectiveness of this innovative fusion in efficiently solving complex optimization problems.

2. Particle Filter

In particle filtering, the posterior probability density is often approximated by randomly weighted random samples. Assuming there are N samples in particle filtering, ${x^{\prime }}_g\sim u(x_g|z_{1:g})$, Formula (1) describes the principle of particle filtering [16,17].

It is recommended that research manuscripts reporting large datasets that are deposited in a publicly available database specify where the data have been deposited and provide the relevant accession numbers. In the event that the accession numbers have not yet been obtained at the time of submission, this should be stated and the relevant information should be provided during the review process. Such information must be provided prior to publication.

$$u(x_g|z_{1:g})=\frac{1}{N}{\displaystyle \sum _{i=1}^n\delta (x_g-x_g^i)}$$

(1)

where $\delta$ is the delta function; in the particle filter algorithm, the state of a moving target is often predicted in real time using the posterior estimation density function. At the same time, according to the principle of important samples, the importance distribution function is used to obtain high-weight particles as important particles and low-weight particles as small-weight particles [18]. In the case of known sample distribution, the calculation of the weight corresponding to each particle individual is carried out using Formula (2), and the calculation of the posterior probability is carried out using Formula (3).

$$w_g^i\propto \frac{u(x_g^i)}{v(x_g^i)} \mathrm{and} u(x_g=x_g^i)=w_g^i$$

(2)

$$u(x_g|z_{1:g})={\displaystyle \sum _{i=1}^n{w}_g^i\delta (x_g-x_g^i)}$$

(3)

By substituting Equation (2) into Equation (4), the update process of the weighted particle set can be determined as follows:

$$w_g^i\propto w_{g-1}^i\frac{u(z_g|x_g^i)u(x_g^i|x_{g-1}^i)}{v(x_g^i|x_{g-1}^i\cdot z_g)}$$

(4)

The particle filtering algorithm is constituted by the application of Formulas (3) and (4). In order to maintain a reasonable distribution in particle filtering, the method of particle resampling is typically employed. This entails the duplication of particles with high weights and the deletion of particles with low weights [19,20,21,22,23]. Nevertheless, particle resampling may result in an increase in the repetition rate of particles with high weights and a decrease in particle diversity, which significantly impairs the accuracy of tracking. This paper introduces a golden-section gray wolf particle filtering algorithm, which guides particles in the particle filtering process to the interval with higher weight values. This effectively enhances the global and local exploration capabilities of the particles and reduces the impact of particle impoverishment, thereby further improving tracking performance.

3. Translation of the Golden-Section Gray Wolf Filter Algorithm

In particle filtering, resampling represents a pivotal step employed to address the issue of particle degradation [24]. The optimization of the resampling process through the utilization of the gray wolf optimization algorithm enables the selection of representative particles to be conducted in a more effective manner, thus avoiding oversampling or undersampling. Consequently, this results in an enhancement of the filtering performance and the accuracy of the filtering prediction.

3.1. Nonlinear Convergence Factor

The gray wolf algorithm exhibits robust optimization capabilities; however, the convergence factor of the gray wolf optimization algorithm declines linearly with the increase in iteration times. This may result in the algorithm becoming trapped in local optima. In the initial stages of the algorithm, the decay of the convergence factor is relatively low, which allows the wolf pack to move with a larger step size. This enables the algorithm to conduct a global search more effectively. As the number of iterations increases, the convergence factor declines, and the wolf pack’s movement step size diminishes. This enables a more precise local search, which ultimately leads to the identification of the optimal solution.

The convergence factor of the gray wolf algorithm can be enhanced in order to achieve a more balanced approach between global and local search, thereby enabling it to adapt more effectively to complex search processes [25]. Consequently, the algorithm’s capacity to optimize is enhanced. In comparison to alternative methodologies, the nonlinear convergence factor is capable of more effectively balancing global and local search while maintaining the algorithm’s overall simplicity. Particle filtering is more computationally intensive than other filtering algorithms. Consequently, this paper employs a relatively simple nonlinear convergence factor, which not only markedly balances the search process but also significantly reduces the algorithmic complexity [26,27].

In the gray wolf particle filtering algorithm, the nonlinear convergence factor plays a decisive role. This factor balances the global and local search capabilities of the algorithm by nonlinearly adjusting the search behavior during iterations. At the beginning of the algorithm, the nonlinear convergence factor allows the algorithm to descend at a slower rate, which enhances the global search of the solution space and helps the algorithm discover potential optimal solution regions. As the iterations progress, the convergence factor decreases, speeding up the convergence of the algorithm and improving the search accuracy. In the gray wolf particle filtering algorithm, the nonlinear convergence factor is also used to adjust the state update process of the particle swarm and control the diffusion and convergence speed of the particles, thus maintaining the diversity of the particles while improving the convergence speed and accuracy of the algorithm. This flexible and effective adjustment strategy makes the gray wolf particle filtering algorithm show excellent performance.

The expression of the nonlinear convergence factor is as follows:

$$a=\frac{e^{(\frac{t}{\max t}-1)}}{e-1}$$

(5)

The term “max t” in the equation refers to the maximum number of iterations.

3.2. Fusion of Golden Sine

In the context of the gray wolf optimization algorithm, during the iteration process, the alpha wolf assumes the position with the highest fitness value, thereby leading the entire gray wolf population in hunting. However, there is a notable absence of communication between individual gray wolves. The incorporation of the golden sine can effectively compensate for this deficiency in the optimization algorithm. The steps of the golden sine are as follows:

Step 1: The fitness value of each discovered wolf individual is calculated, and they are sorted in descending order based on their fitness values.

Step 2: Subsequently, the updated positions of each discovered wolf individual are calculated in accordance with the mathematical formula of the golden sine function. The golden sine function enables the magnitude of the position update to be determined based on the current iteration count and the ranking of the discovered wolf individual.

Step 3: The positions of each discovered wolf individual are updated based on the calculated updated positions.

Step 4: Following the updating of the positions of all discovered wolf individuals, the fitness value of each individual must be recalculated, and they must be sorted in descending order based on their fitness values.

Step 5: The aforementioned steps are repeated until the predefined iteration count is reached or the stipulated stopping condition is met.

The introduction of the golden sine function facilitates enhanced communication between discovered wolf individuals, enabling the entire population to more effectively search for positions with higher fitness values. This, in turn, enhances the performance and effectiveness of the algorithm.

The expression of the golden sine function is as follows:

$$\left\{\begin{array}{c}a=2-2\times \frac{t}{\max t}\\ b=1\\ r=\lambda \\ r_4=r\times 2\pi \\ r_5=r\times \pi \\ g=\frac{\sqrt{5}-1}{2}\\ X_1=a+(1-g)\times (b-a)\\ X_2=a+g\times (b-a)\end{array}\right.$$

(6)

In the equation above, $\max t$ is the maximum number of iterations, $\lambda$ is a random number between 0 and 1, and $g$ is the golden ratio.

3.3. Fusion of Golden-Section Gray Wolf Optimization Algorithm and Particle Filtering Algorithm

The golden-section gray wolf algorithm is a hybrid of the golden-section principle and the optimization strategies of the gray wolf algorithm. The algorithm is designed to identify optimal or satisfactory solutions to optimization problems through iterative search. This algorithm not only exhibits the characteristics of heuristic algorithms, which are constructed based on intuition or experience but also demonstrates enhanced global search capabilities and optimization performance through the integration of random strategies with local search.

The golden-section gray wolf algorithm represents an advanced optimization technique that combines the accuracy of the golden-section method with the group intelligence of the gray wolf optimization algorithm to form an efficient and powerful solution tool. The initial phase of the algorithm’s operation involves the gray wolf optimization algorithm rapidly identifying the region within the solution space of the problem that may contain the optimal solution, due to its exceptional global search capability. This is achieved by simulating the hunting behavior of gray wolf packs in nature, where information exchange and collaboration among individual gray wolves allows the algorithm to rapidly adapt to complex search environments.

Once the gray wolf algorithm has identified an approximate location for the optimal solution, the golden-section method employs its distinctive capabilities to refine the search process to a smaller area. The golden-section method determines the step size and range of the search by applying the golden-section ratio, thereby significantly enhancing the search accuracy of the algorithm while maintaining search efficiency. This degree of precision is of particular importance during the local search phase, as it enables the algorithm to identify the optimal or satisfactory solution to the problem with great accuracy.

In conclusion, the introduction of adaptive weight values has the potential to enhance the adaptability of global and local exploration, improve particle degeneration and local extremum problems, and increase the diversity of the particle swarm, thereby improving tracking performance. The algorithm displays enhanced adaptability and randomness. The repeated interaction of these two algorithms in iterative updates allows for improvement in particle diversity and the effective compression of particle scale while simultaneously enhancing computational efficiency and accuracy.

The particle filter resampling method of the golden-section gray wolf algorithm has the capacity to prevent particle degeneration and increase particle diversity while simultaneously stabilizing the scale of the particle set within a smaller range. Furthermore, it can enhance the computational accuracy of the particle filter algorithm and reduce the running time, thereby significantly enhancing real-time performance. To address the issue of particle degeneration in the particle filter algorithm, this paper employs the golden-section gray wolf optimization algorithm to replace the original resampling process within the particle filter algorithm. The implementation steps of the golden-section gray wolf particle filter are as follows:

Step 1: Set j = 0 as the starting point for the algorithm and perform the initial sampling according to the distribution p(x0). The generated N particles may be utilized as the initial samples for the particle filtering algorithm, where x_k(j) follows the importance density function as follows:

$$x_{{ }_k}(j)\_p(x_{{ }_k}(j)|x_{{ }_k}(j-1),z(j))$$

(7)

Step 2: Some particles are initialized in the particle filter algorithm and assigned initial weights in accordance with Equations (2) and (3).

Step 3: The golden-section gray wolf algorithm is used to identify particles. Firstly, the position of each particle in the search space must be determined in accordance with its weight. Subsequently, the positions of each particle are updated in accordance with the search strategy of the gray wolf algorithm.

(1) The initial particles for optimization are shown in Equation (8).

$$\left\{{ }_i(j)\right\}=\left\{x_g(j)\right\}(i=1,2,\cdots ,N)$$

(8)

(2) In the gray wolf algorithm based on the golden section, particle samples are added. In accordance with the aforementioned steps, a novel set of particles is generated with each iteration update. Consequently, the outcome of each iteration is contingent upon the results of the previous iteration. The fitness function is employed to compute the fitness value of the filtering parameters generated in the current iteration. The fitness function employed in this algorithm is based on the golden-section gray wolf algorithm.

$$f(x_{{ }_g}^i)=\exp \left(-\frac{1}{2R}|z_g-z_{{ }_g}^i|\right)$$

(9)

where $z_{{ }_g}^i$ is the corresponding observation values, and R is noise variance.

(3) The golden-section gray wolf algorithm is employed in the resampling process of particle filtering.

(4) The importance weights of the particles are calculated once more, and the data are normalized.

$${\overline{\omega }}_i(g)=\frac{{\omega }_i(g)}{{\displaystyle \sum _{g=0}^N{\omega }_i(g)}}$$

(10)

(5) The mean of the particles is calculated following the application of the golden-section gray wolf particle filter.

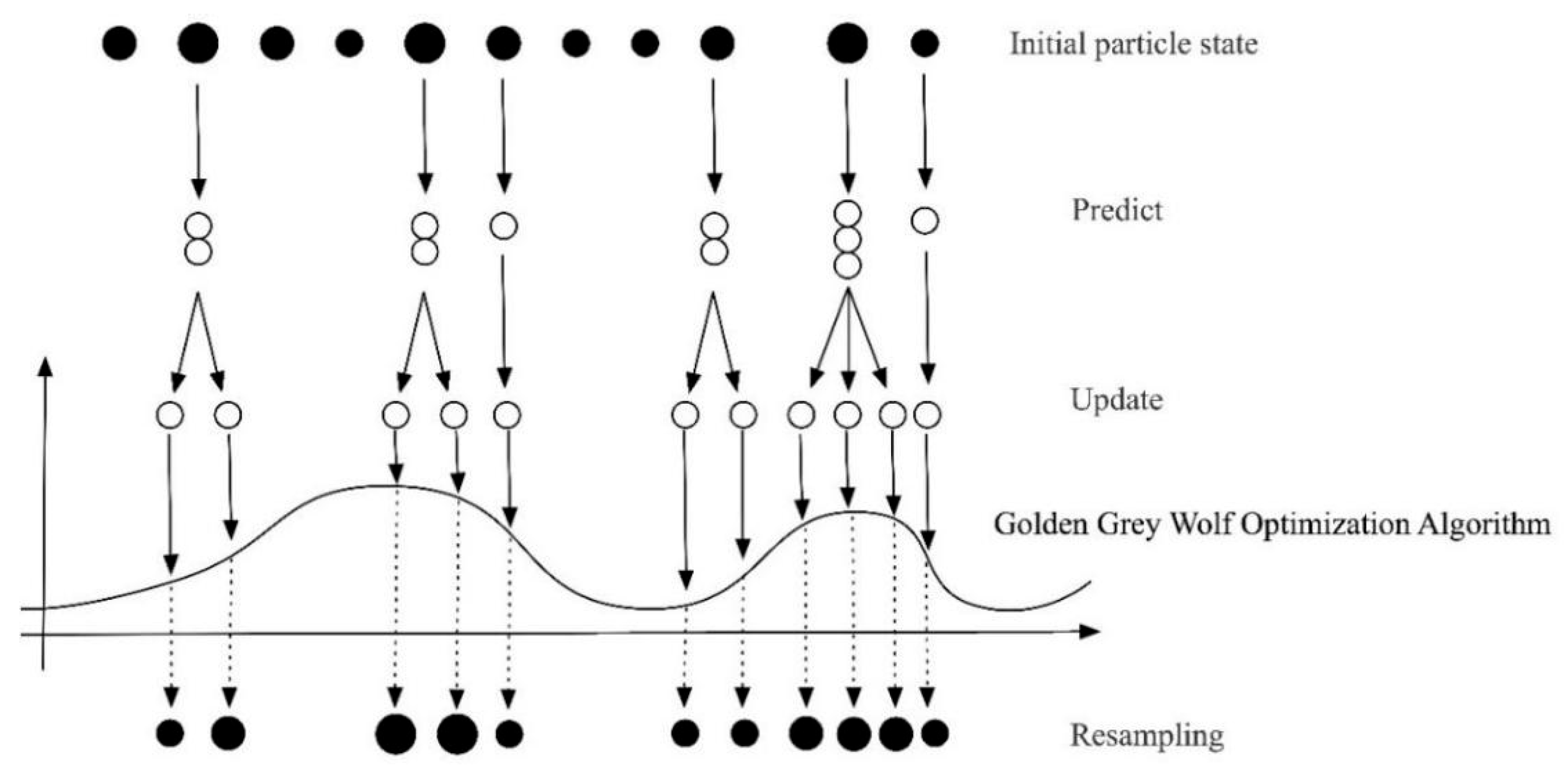
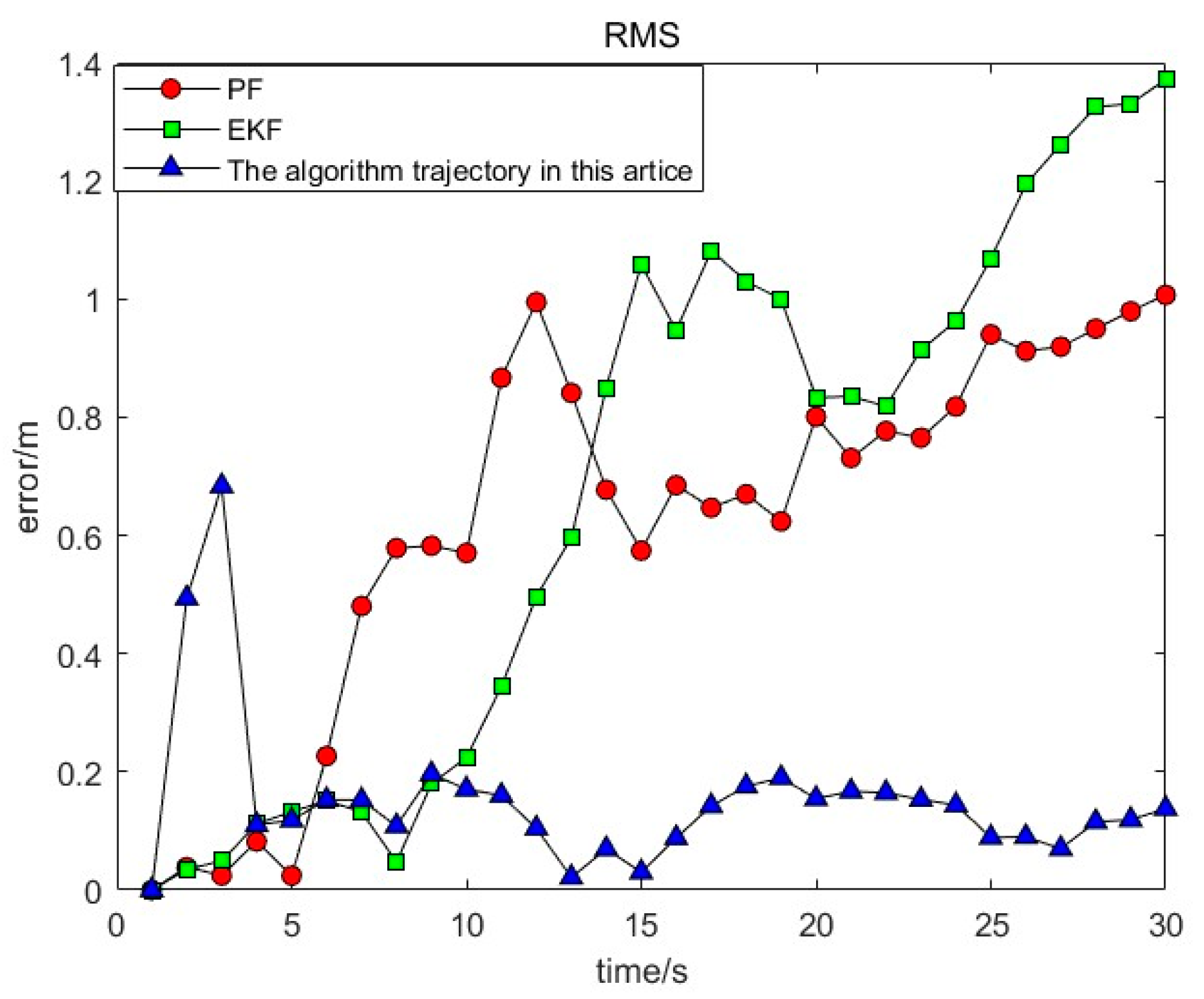
In terms of the convergence of the algorithm proposed in this article, each repetition of the algorithm generates the optimal position for the population, thereby enabling the random algorithm to achieve convergence. Following a number of iterations, the proposed algorithm improves the state of the population sequence of gray wolf positions, reaching the optimal state position. Consequently, the potential for an infinite search for the global optimum is eliminated. Consequently, the algorithm proposed in this article will converge to the global optimum. The schematic diagram of the golden-section gray wolf particle filter is presented below Figure 1.

4. Simulation and Evaluation

4.1. Basic Performance Testing

4.1.1. Filtering Performance Testing

In order to ascertain the efficacy of the proposed filtering algorithm, a comparative experiment was conducted between the GWO-PF algorithm and the proposed algorithm. The selected filtering model is based on a univariate dynamic changing model, with the state equation and observation equation presented below.

$$x(u)=0.5x(u-1)+\frac{25x(u-1)}{1+{\left[x(u-1)\right]}^2}+8\cos [1.2(u-1)]+\omega (u)$$

(11)

$$z(u)=\frac{x{(u)}^2}{20}+v(u)$$

(12)

In this equation, w(u) and v(u) represent zero-mean Gaussian noises, and X(u) denotes the state of the system at time u, while Z(u) represents the measurement value of the system at time u. The initial state is x = 1. The parameter distribution from left to right is set to N = 100, Q = 1, and R = 1; N = 200, Q = 2, and R = 1; and N = 200, Q = 1, and R = 1. The comparison of filtering effects is shown in Figure 2.

The proposed algorithm is enhanced by incorporating elements of the gray wolf optimization algorithm. In comparison to the particle filtering algorithm of gray wolf optimization, the algorithm presented in this paper demonstrates enhanced global and local search and optimization capabilities, as evidenced by the comparative test of filtering effectiveness. This improvement enables a more accurate prediction of the state value of maneuvering targets in maneuvering target tracking. The proposed algorithm is well suited to the task of fast and accurate prediction, such as radar and wireless sensor target tracking.

4.1.2. Optimizing Algorithm Performance Testing

In order to assess the optimization performance of IGWO, we chose twenty standard test functions from the CEC Benchmark, as presented in

Table 1. Benchmark test functions.

Number	Name	Search Range	Dimension	Optimal Value
F1	Sphere	[−100,100]	30	0
F2	Schwefel’s Problem 2.22	[−10,10]	30	0
F3	Schwefel’s Problem 1.2	[−100,100]	30	0
F6	Step Function	[−100,100]	30	0
F8	Schwefel’s Problem 2.26	[−500,500]	30	0
F10	Ackley’s Function	[−32,32]	30	0
F14	S-H Camel-Back Function	[−5,5]	2	−1.0306
F18	Shekel’s Family	[0,10]	4	−10.1532

. The four functions, each with distinct features, permit a comprehensive analysis of IGWO’s optimization abilities. The population size was set to 30, and the number of iterations was set to 200. A comparison was conducted between the dragonfly optimization algorithm (DBO), the gray wolf optimization algorithm (GWO), the whale optimization algorithm (WOA), the northern goshawk optimization algorithm (NGO), and the proposed algorithm [28,29,30]. A total of 30 independent simulations of the test function were conducted, and the resulting experimental data were compiled. A comparison of the aforementioned optimization algorithms is presented in Figure 3 and Figure 4.

The final fitness convergence comparison curves indicate that IGWO demonstrates the fastest convergence speed for the F1 function, thus demonstrating superior fitness simultaneously. Similarly, the outcomes for the F2 to F3 functions closely resemble those of the F1 function, thereby corroborating the superior performance of IGWO. Figure 4 illustrates that, although IGWO does not achieve the absolute best performance, its convergence speed and fitness consistently rank within the top three. With regard to the F20 functions, IGWO continues to demonstrate its superiority.

In comparison to other algorithms, the gray wolf optimization algorithm exhibits significant advantages in solving optimization problems. This is due to its balanced approach to global and local search, rapid convergence speed, ability to avoid falling into local optima, robust performance, and ease of implementation. These characteristics render the algorithm more reliable, flexible, and efficient in practical applications.

4.2. Mobile Target Tracking Test

The text primarily concerns the performance testing of the constant speed turning motion model [31,32]. The motion state equation of the constant speed turning motion model is as follows:

$$F=\left[\begin{array}{cccc}1& \frac{\sin \Omega \Delta t}{\Omega }& 0& \frac{1-\cos \Omega \Delta t}{\Omega }\\ 0& \cos \Omega \Delta t& 0& -\sin \Omega \Delta t\\ 0& \frac{1-\cos \Omega \Delta t}{\Omega }& 0& \frac{\sin \Omega \Delta t}{\Omega }\\ 0& \sin \Omega \Delta t& 0& \cos \Omega \Delta t\end{array}\right]$$

(13)

$$G_k=\left[\begin{array}{c}\begin{array}{cc}\frac{\Delta t_k^2}{2}& 0\\ \Delta t_k& 0\end{array}\\ \begin{array}{cc}0& \frac{\Delta t_k^2}{2}\\ 0& \Delta t_k\end{array}\end{array}\right]$$

(14)

$$x_{k+1}=F{x}_k+G{w}_k$$

(15)

The variable “w_k” in the equation represents the system noise in the state equation.

The observation model used by the sensors in the WSN is as follows:

$$z_i=\left(1+{\gamma }_i\right)r_i+n_i=r_i+u_i$$

(16)

$$r_i=\sqrt{{\left(x-x^i\right)}^2+{\left(y-y^i\right)}^2}$$

(17)

This equation represents the position of the target (x, y) at time t, where (xⁱ, yⁱ) is the position of sensor i, and u_i is the random noise generated with covariance Q.

4.2.1. WSN Ranging Model Modelin

A total of 30 sensors were randomly deployed in a wireless sensor network monitoring area of 100 m × 100 m. The communication radius of the sensors was set to 30 m. The sampling period was set to 0.1 s, and the number of samples was set to 50. In the filtering algorithm, the environmental noise was set to diag[(0.5,0.5)] and the observation noise was set to 10.

In the gray wolf optimization algorithm with golden section, the population size M was set to 30, and the maximum number of iterations was set to 50.

The efficacy of target tracking algorithms is typically gauged by the magnitude of tracking accuracy, which is typically represented by the average square root error. We employed three algorithms, namely the PF algorithm, the EKF algorithm, and the UKF algorithm, to assess their performance by calculating the average square root error and comparing their curves. In the simulation experiment, the root mean square error (RMSE) was employed as a measure of tracking performance, with the following Formula:

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N\sqrt{{\left(\tilde{x}-x\right)}^2+{\left(\tilde{y}-y\right)}^2}}}$$

(18)

In the above equation, RMSE represents the normalized average positioning error of the nodes, $(\stackrel{⌢}{x},\stackrel{⌢}{y})$ represents the estimated coordinates at time t, and $(x,y)$ represents the actual coordinates of the unknown nodes.

4.2.2. WSN Trace Test Results

The initial value of the trajectory in the X direction was set to 10 m, and the initial value in the Y direction was set to 10 m. The initial velocities in the X direction and Y direction were set to 5 m/s and 0.122, respectively. Once the target model was established, and the initial conditions for simulation were set, the trajectory was tracked using the algorithm proposed in this paper. Figure 5 depicts the trajectory comparison graph. To validate the efficacy of the algorithm, 100 repeated experiments were conducted using this algorithm, the PF algorithm, and the EKF algorithm for the tracking of a maneuvering target. The root mean square error (RMSE) was employed as the performance evaluation metric.

Table 2. Comparison of tracking errors.

	Location RMSE (m)	X Location RMSE (m)	Y Location RMSE (m)
UKF	0.8016	0.4972	0.4131
EKF	0.7009	0.4862	0.4039
PF	0.4576	0.2270	0.3124
The algorithm trajectory in this article	0.3037	0.1571	0.1529

presents a comparison of the tracking errors of the three algorithms. The simulation results indicate that, in terms of tracking accuracy and error, the order of superiority of the algorithms is as follows: the algorithm proposed in this paper, the PF algorithm, and the EKF algorithm.

Figure 5 illustrates the comparison of the target tracking trajectory in two-dimensional space. Figure 5 and Table 2 demonstrate that the tracking trajectory of the algorithm in this paper is nearly identical to the true trajectory. The root mean square error of tracking is 0.3037. Consequently, it can be concluded that the algorithm in question is an effective means of tracking nonlinear model targets.

Table 2 and Figure 6 illustrate that particle filtering is more effective than the PF and EKF algorithms in handling complex motion situations, such as nonlinearity, through Monte Carlo sampling. Furthermore, it has a broader range of applications and higher tracking accuracy. The proposed algorithm exhibits excellent tracking performance. The incorporation of the enhanced gray wolf strategy enables the algorithm to achieve the performance of a larger number of particles with a smaller number of particles. When the number of particles is held constant, the tracking performance of the proposed algorithm is superior to that of the particle filtering algorithm.

Figure 7 demonstrates that the incorporation of the enhanced gray wolf strategy significantly enhances the tracking efficacy of the particle filtering algorithm. Concurrently, the enhanced algorithm exhibits a reduced reliance on the positional predictions of the preceding stage during the tracking of maneuvering targets, resulting in diminished fluctuations in the prediction outcomes and optimal tracking stability and precision. The experimental results demonstrate the effectiveness of the proposed golden-section gray wolf particle filtering algorithm for WSN target tracking. Particle resampling is enhanced in the golden-section gray wolf optimization particle filtering algorithm, and the fitness function of particles is redefined based on the most recent sensor observations. This results in the algorithm guiding particles to move toward higher random areas on a global scale, effectively adjusting the exploration capabilities of both global and local search. The proposed algorithm is demonstrated to exhibit superior tracking performance in both the X and Y directions in comparison to the PF and RSSI algorithms. This is attributed to the algorithm’s capacity to address the issues related to particle impoverishment and local extremum problems, as well as to enhance the diversity of the particle swarm, thereby improving tracking performance.

In order to verify that the algorithm proposed in this paper still has a good tracking effect under the linear motion model, the uniformly variable linear motion model was chosen. The initial value of the X direction and Y direction of the target trajectory was set as 0 m, the initial value of the Y direction was set as 10 m, and the initial value of the velocity in the X direction and Y direction was set as 3 m/s. The acceleration was 1 m/s. The equations of motion state of the uniformly variable linear motion model are shown as follows:

$$F=\left[\begin{array}{cccccc}1& T& \frac{1}{2}{T}^2& 0& 0& 0\\ 0& 1& T& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& T& \frac{1}{2}{T}^2\\ 0& 0& 0& 0& 1& T\\ 0& 0& 0& 0& 0& 1\end{array}\right]$$

(19)

where T is the sampling interval.

The experimental results are shown in Figure 8 and Figure 9.

From the detailed comparison and presentation in Figure 8 and Figure 9, we can clearly observe that the algorithm proposed in this paper demonstrates excellent tracking performance in linear maneuvering target tracking tasks. This indicates that the algorithm proposed in this paper can not only adapt to the complex nonlinear tracking environment but also has a good tracking performance in the uncomplicated linear tracking environment.

Given the severely constrained connectivity resources of wireless sensor networks, it is insufficient to consider tracking accuracy as the sole indicator of algorithmic efficacy when designing algorithms. The complexity of the tracking algorithm is also a crucial factor in the effectiveness of the tracking algorithm. In contrast to traditional intelligent optimization-enhanced particle filtering algorithms, the algorithm presented in this paper employs the golden ratio to approximate the roots of nonlinear equations. One of the advantages of this method is its rapid convergence, which greatly reduces the complexity of the optimization algorithm, especially in the vicinity of the roots. The gray wolf algorithm is enhanced by an improved convergence factor, which achieves a more balanced approach between global and local search. This results in greater effectiveness in adapting to complex search processes and a notable reduction in algorithmic complexity, thereby improving tracking performance in applicable scenarios.

4.3. Mobile Target Tracking Test

In this paper, four filtering algorithms, namely the PF algorithm, the UKF algorithm, the EKF algorithm, and the algorithm proposed in this paper, were each subjected to 100 simulated experiments. The results of this comparison are presented in Figure 10, which shows the timeliness comparison table of the four algorithms. The incorporation of an adjustment factor into the gray wolf optimization algorithm results in the algorithm proposed in this paper demonstrating the most optimal timeliness.

In view of the severely constrained connectivity resources of wireless sensor networks, it is not sufficient to consider tracking accuracy as the sole indicator of the efficacy of algorithms when designing them. The complexity of the tracking algorithm is also a crucial factor in determining the effectiveness of the tracking algorithm. In contrast to traditional intelligent optimization algorithms, the algorithm presented in this paper employs the golden ratio to approximate the roots of nonlinear equations. One of the advantages of this method is its rapid convergence, which greatly reduces the complexity of the optimization algorithm, especially in the vicinity of the roots. The enhanced convergence factor of the gray wolf algorithm enables a more balanced approach between global and local search, rendering it more adept at adapting to complex search processes and significantly reducing its complexity. Consequently, this enhances its tracking performance in applicable scenarios.

The golden-section gray wolf algorithm shows its unique optimization ability and scalability when dealing with the complex computational problems faced by filtering algorithms in wireless sensor networks. First, in the design of the algorithm, the proposed algorithm is capable of automatically adjusting key parameters, such as the golden-section ratio and the convergence factor of the gray wolf algorithm, in different iteration stages and search environments by introducing a parameter adaptive adjustment strategy, so as to ensure that the algorithm always stays in the optimal search state. This adaptive mechanism greatly improves the algorithm’s ability to adapt to different problems and scenarios. In terms of search strategy, the proposed method ensures that the algorithm can avoid falling into the local optimal solution while maintaining the search efficiency by balancing the local search and global search. Different individuals in the gray wolf algorithm undertake different search tasks; some are responsible for global search, while others perform local fine search, and this collaborative work makes the algorithm cover the solution space more comprehensively in the search process.

In addition, the golden-section gray wolf algorithm introduces a heuristic strategy that combines the properties of the problem and prior knowledge to provide guidance for the search process. This heuristic strategy helps the algorithm to find the approximate or optimal solution to the problem faster, and it especially excels in dealing with complex nonlinear problems. Meanwhile, in terms of scalability, the algorithm adopts a modularized design, which divides the algorithm into several independent modules, each of which is responsible for handling a specific task. Also, the algorithm fusion strategy enables the algorithm to be used in conjunction with other optimization algorithms to solve complex problems.

5. Conclusions and Future Direction

In order to address the issue of low tracking accuracy caused by particle depletion in particle filters, a mobile target tracking algorithm for wireless sensor networks (WSNs) based on the golden-section gray wolf particle filter (PF) is proposed. The algorithm guides the particles in the filtering process toward intervals with higher weight values, thereby enhancing their exploration capability and reducing the impact of particle impoverishment. Moreover, this method can enhance the diversity of particle groups, thereby improving tracking performance. The efficacy of this algorithm was demonstrated through filtering and tracking using the constant velocity circular motion model (CM) and compared with the EKF algorithm and PF algorithm to obtain the mean square error curve of the position. Upon analysis of the results, it is evident that the proposed golden-section gray wolf particle filter algorithm offers a significant improvement in tracking accuracy. The algorithm’s capacity to direct particles toward regions of greater weight effectively balances global and local exploration, overcoming the challenges posed by sample scarcity. Furthermore, the increased diversity of the particle swarm contributes to enhanced tracking performance. However, this algorithm is only applicable to scenarios with relatively small environmental areas. Future research will concentrate on reducing the algorithm’s complexity and conserving energy on nodes while maintaining tracking accuracy in large scenarios. This will allow the network to function for a longer period. Although the golden-section-based gray wolf particle filtering algorithm significantly enhances the accuracy of tracking in mobile target tracking for wireless sensor networks, it still exhibits limitations in certain respects. Firstly, the algorithm’s computational complexity and resource consumption may be excessive when applied to large-scale environments, which limits its applicability in a wider range of scenarios. Given the fact that nodes in WSNs typically have limited computational power and energy resources, the high complexity of the algorithm may result in the nodes consuming energy at an accelerated rate, which could ultimately impact the lifespan of the entire network. This issue was incorporated into the summary section “Conclusions and Future Direction”.

In response to the advantages demonstrated by the golden-section-based gray wolf particle filtering algorithm in mobile target tracking for wireless sensor networks and its computational complexity and energy consumption problems in large-scale environments, future research will focus on the optimization of the algorithm and the exploration of energy-saving strategies. Further research will be conducted with the objective of reducing the complexity of the algorithms and improving their applicability in large-scale environments. Furthermore, intelligent node scheduling mechanisms will be developed with the objective of facilitating more efficient distributed processing and adaptive energy saving. The objective of these research programs is to ensure the accuracy of tracking while extending the lifetime of WSNs and to promote their application and development in a wider range of fields.