Color Image Encryption Based on a Novel Fourth-Direction Hyperchaotic System

Abstract

Neuromorphic computing draws inspiration from the brain to design energy-efficient hardware for information processing, enabling highly complex tasks. In neuromorphic computing, chaotic phenomena describe the nonlinear interactions and dynamic behaviors. Chaotic behavior can be utilized in neuromorphic computing to accomplish complex information processing tasks; therefore, studying chaos is crucial. Today, more and more color images are appearing online. However, the generation of numerous images has also brought about a series of security issues. Ensuring the security of images is crucial. We propose a novel fourth-direction hyperchaotic system in this paper. In comparison to low-dimensional chaotic systems, the proposed hyperchaotic system exhibits a higher degree of unpredictability and various dynamic behaviors. The dynamic behaviors include fourth-direction hyperchaos, third-direction hyperchaos, and second-direction hyperchaos. The hyperchaotic system generates chaotic sequences. These chaotic sequences are the foundation of the encryption scheme discussed in this paper. Images are altered by employing methods such as row and column scrambling as well as diffusion. These operations will alter both the pixel values and positions. The proposed encryption scheme has been analyzed through security and application scenario analyses. We perform a security analysis to evaluate the robustness and weaknesses of the encryption scheme. Moreover, we conduct an application scenario analysis to help determine the practical usability and effectiveness of the encryption scheme in real-world situations. These analyses demonstrate the efficiency of the encryption scheme.

1. Introduction

The swift advancement of artificial intelligence and supercomputing technology has greatly enhanced computational efficiency [1,2,3,4,5,6,7,8]. In the increasingly advanced digital world, image encryption is becoming more and more important. The proposal of neural networks and neuromorphic computing also magnifies this issue [9,10,11,12,13,14,15,16]. Therefore, ensuring the security of images on the Internet has become critical [17]. In neuromorphic computing, chaos is involved in the interactions among neurons. This chaotic behavior can be used to perform complex information processing tasks, such as remote heart rate measurement [18]. Chaotic systems have high complexity and randomness and can produce pseudorandom sequences [19,20]. Additionally, it is suitable to utilize chaotic systems for secure image transmission. Chaos systems exhibit a significant level of complexity; minor adjustments to the parameters in the system have the potential to result in significant changes in the behavior of system [21,22].

In recent years, there has been a proliferation of encryption schemes put forth in academic papers. Progress in this area has primarily followed two main paths. The first path involves the development of innovative chaotic systems and their application in encryption schemes [23]. For example, Liu et al. introduced a novel fourth-order chaotic system to enhance the security of medical images [24]. Similarly, Zhu et al. conducted a study on the utilization of a composite chaotic system that integrates sinusoidal and polynomial functions for the encryption of images [25]. Gao et al. proposed an efficient encryption method utilizing single-channel encryption and chaotic systems [26]. Moreover, Zhu et al. presented a set of multi-cavity hyperchaotic maps in m dimensions [27]. Jin et al. also contributed to this field by introducing a distinctive complex system with a hyperchaotic fractional order and investigating its synchronization properties [28]. Promising results have been obtained recently in various studies of neural networks and memristor-based hyperchaotic systems [29,30,31,32,33].

A second manner of proposing new encryption schemes is from the perspective of practical applications. For example, Lin et al. introduced a rapid image encryption method designed for embedded systems by incorporating mixed-sequence systems and the decorrelation operation [34]. Zhu et al. proposed a three-dimensional bit-level image encryption scheme utilizing the Rubik’s cube method [17]. Kamal et al. introduced a novel image encryption method for grayscale and color medical images by employing an innovative image splitting approach focused on image blocks [35]. Wang et al. employed hash tables, Hilbert curves, and hyperchaotic synchronization to encrypt color images [36].

However, using low-dimensional chaotic systems to encrypt images is insecure [23,26]. The limited key space inherent in low-dimensional chaotic systems makes them vulnerable to brute force attacks.

In order to address these issues, high-dimensional hyperchaotic systems can be utilized instead of hyperchaotic systems with low dimensions. Hyperchaotic systems have at least two positive Lyapunov exponents. Positive Lyapunov exponents suggest that the system is significantly more sensitive and complex in various directions, exhibiting exponential growth in complexity [37,38,39]. Increasing the dimension of the system and adding more nonlinear terms will make the dynamics more complex. High-dimensional hyperchaotic systems are typically seen as better for encrypting images than low-dimensional chaotic systems [40].

In this work, a tenth-order hyperchaotic system is proposed based on nth-order ordinary differential equations proposed by Liu et al. [41]. The dynamic behavior of the system is highly complex, including fourth-direction hyperchaos, third-direction hyperchaos, and second-direction hyperchaos. Using this hyperchaotic system for image encryption can address the issues encountered in low-dimensional chaotic systems. Having a larger key space enhances the ability of encryption scheme to withstand brute force attacks. Due to high level of randomness in hyperchaotic systems, the distribution of pixels in encrypted images also shows a high level of randomness. As a result, the majority of the initial data can still be retrieved from the encrypted image, even after undergoing cropping attacks.

The major contributions of this work are outlined below:

• This paper presents an innovative encryption scheme that employs a fourth-direction (4D) hyperchaotic system. The encryption process involves the utilization of row and column scrambling as well as diffusion.
• A novel 4D hyperchaotic system is presented in this paper. Through dynamic analysis, it is found to exhibit highly complex dynamic characteristics. These dynamic characteristics include fourth-direction hyperchaos, third-direction hyperchaos, and second-direction hyperchaos.
• The encryption scheme under consideration has been evaluated and compared with other encryption methods based on criteria such as information entropy, histogram analysis, key sensitivity, pixel correlation, and key space. It has been confirmed in its ability to resist both cropping attacks and differential attacks, indicating its robust security characteristics. Moreover, a brief examination of the potential application scenarios for the proposed encryption scheme has been conducted.

The structure of this paper is as follows: Section 2 introduces encryption and decryption methods; Section 3 discusses a new 4D hyperchaotic system and its behavior; Section 4 delves into encryption and decryption processes by using the characteristics of the 4D hyperchaotic system and its dynamics; and Section 5 presents the experimental results and a thorough security analysis. Lastly, Section 6 provides a summary of the research presented in this paper.

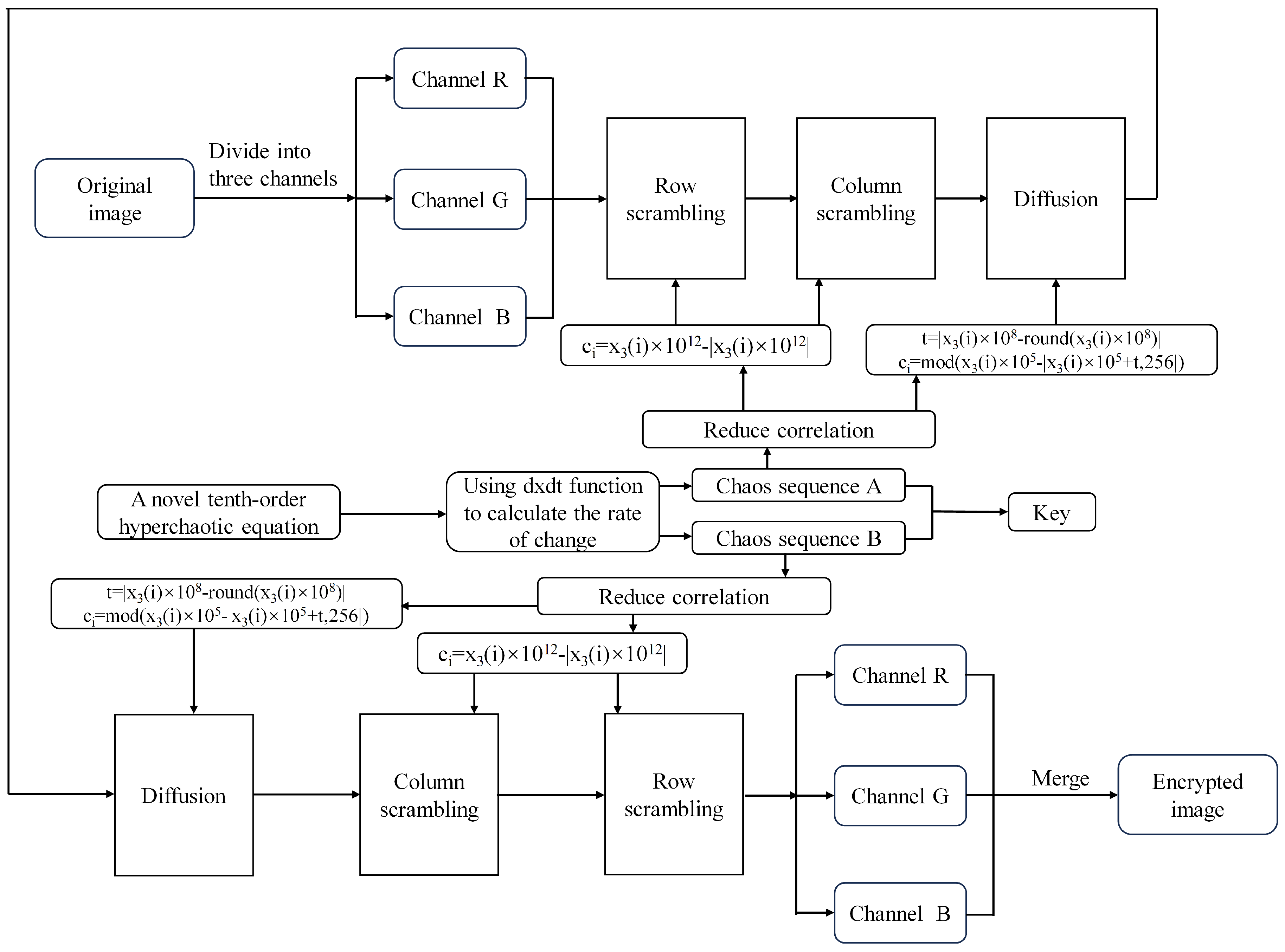
2. Overview of Encryption and Decryption Schemes

The encryption scheme comprises two encryption iterations, with the decryption process being the opposite of the encryption process. Four chaotic sequences are generated through the hyperchaotic system described in Section 3, and these sequences are employed in both the encryption and decryption processes.

The chaotic sequence denoted as $c_1$ is applied for both row and column scrambling, while the chaotic sequence $c_2$ is employed for diffusion in the first encryption round. During the second encryption round, the chaotic sequence $c_3$ is utilized for diffusion, whereas the chaotic sequence $c_4$ is utilized for both column and row scrambling. In the row scrambling process, the image pixels are transformed into a linear sequence based on row-major order and subsequently rearranged in accordance with the sequence provided by the chaotic sequence. Similarly, in column scrambling, the image pixels are converted into a linear sequence following column-major order and then rearranged according to the chaotic sequence. Additionally, the diffusion operation involves executing an XOR operation between the chaotic sequence and the pixel value of the image.

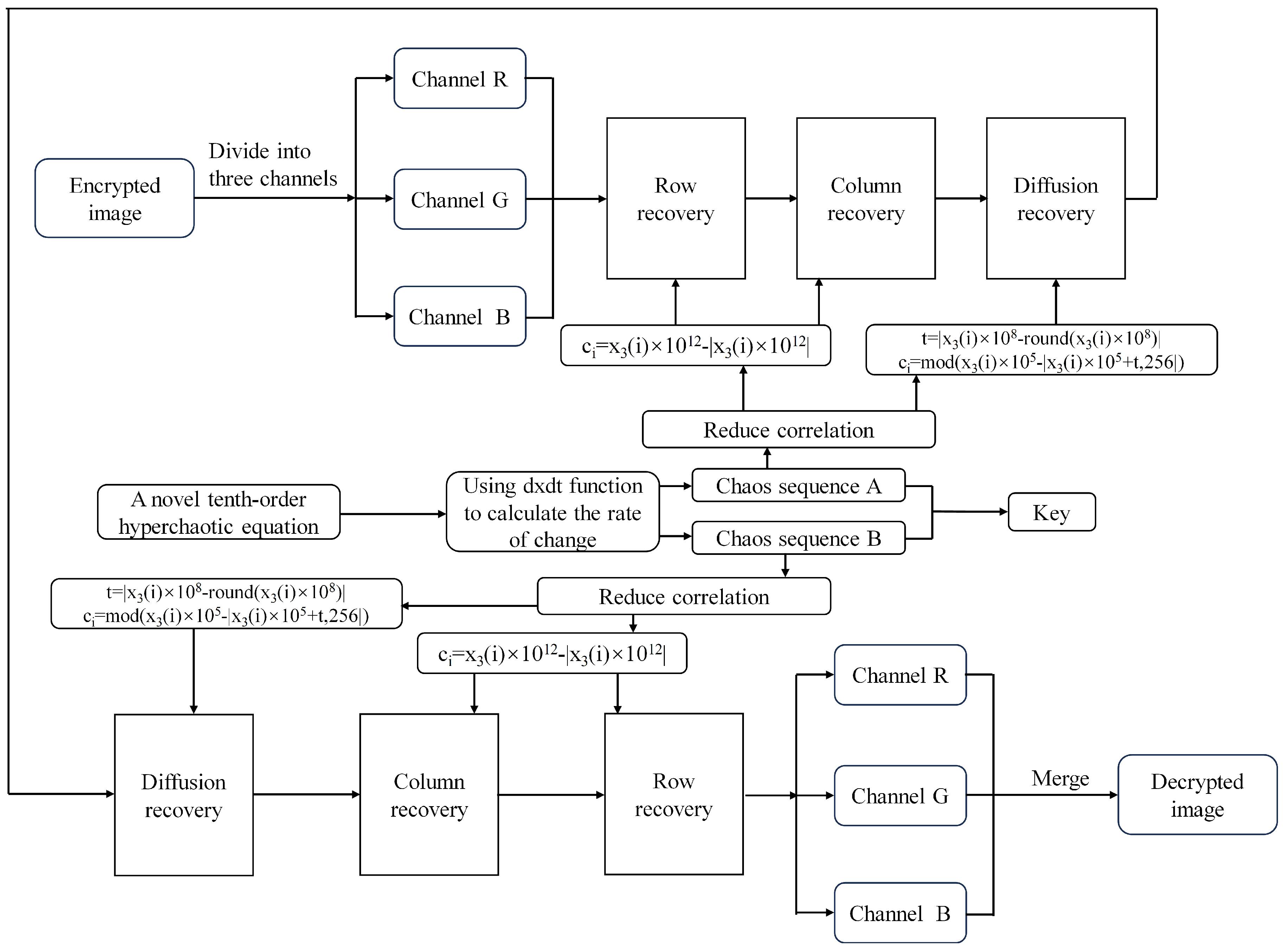
The decryption process consists of two decryption rounds and is the complete opposite of the encryption process.

3. A Novel 4D Hyperchaotic System and Its Dynamic Behavior

3.1. Equations Describing a Novel 4D Hyperchaotic System

Reference [41] proposed an nth-order chaotic system. Equation (1) represents the chaotic system when $n=10$.

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2-x_1\hfill \\ \hfill {\dot{x}}_2& =x_3-x_2\hfill \\ \hfill {\dot{x}}_3& =x_4-x_3\hfill \\ \hfill {\dot{x}}_4& =x_5-x_4\hfill \\ \hfill {\dot{x}}_5& =x_6-x_5\hfill \\ \hfill {\dot{x}}_6& =x_7-x_6\hfill \\ \hfill {\dot{x}}_7& =x_8-x_7\hfill \\ \hfill {\dot{x}}_8& =x_9\hfill \\ \hfill {\dot{x}}_9& =x_{10}\hfill \\ \hfill {\dot{x}}_{10}& =-x_{10}-\rho \left(e^{\frac{x_9}{\varphi }}\right)+ϵ\left(e^{-\frac{x_9}{\varphi }}\right)-10·(x_8+x_7+x_6\hfill \\ \hfill & +x_5+x_4+x_3+x_2-\frac{1}{200}·x_1)\hfill \end{array}\right.$$

(1)

To derive a novel 4D hyperchaotic system, modifications need to be made based on Equation (1). Some nonlinear terms are coupled into Equation (1), increasing the complexity of the system. Through adjusting parameters and analyzing the dynamics of the system, a novel 4D hyperchaotic system is proposed.

The novel 4D hyperchaotic system is described as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2·x_7-m_1·x_1·x_2\hfill \\ \hfill {\dot{x}}_2& =m_2·x_3·x_4-m_3·x_2^2\hfill \\ \hfill {\dot{x}}_3& =m_4·x_4^2-m_5·x_3·x_4\hfill \\ \hfill {\dot{x}}_4& =m_6·x_5·x_2-m_7·\mathrm{sign}\left(x_4\right)\hfill \\ \hfill {\dot{x}}_5& =m_8·x_6·x_7-x_5\hfill \\ \hfill {\dot{x}}_6& =m_9·\mathrm{sign}\left(x_7\right)-m_{10}·x_6\hfill \\ \hfill {\dot{x}}_7& =x_8-m_{11}·x_7\hfill \\ \hfill {\dot{x}}_8& =m_{12}·x_9\hfill \\ \hfill {\dot{x}}_9& =m_{13}·x_{10}\hfill \\ \hfill {\dot{x}}_{10}& =-\left(c\right)·x_{10}-\rho \left(e^{\frac{x_9}{\varphi }}\right)+ϵ\left(e^{-\frac{x_9}{\varphi }}\right)-m_{14}(·x_8+·x_7+·x_6\hfill \\ \hfill & +·x_5+·x_4+·x_3+·x_2)-m_{15}·x_1\hfill \end{array}\right.$$

(2)

where $\mathit{c}$ ∈ [0.2, 2], $\mathit{c}$, $\rho$, and $\varphi$ are control parameters, while the remaining parameters are regarded as constant parameters. These parameters determine the dynamic behaviors of the hyperchaotic system, and setting the initial values of the variables is essential.

When ($m_1,m_2,m_3,m_4,m_5,m_6,m_7,m_8,m_9,m_{10},m_{11},m_{12},m_{13},m_{14},m_{15}$) = (0.301, 0.3, 0.3, 1.4, 0.4, 1.8, 0.88, 1.1, 1.2, 0.98, 0.6, 1.8, 1.2, 10, 0.05), the hyperchaotic system is described as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2·x_7-0.301·x_1·x_2\hfill \\ \hfill {\dot{x}}_2& =0.3·x_3·x_4-0.3·x_2^2\hfill \\ \hfill {\dot{x}}_3& =1.4·x_4^2-0.4·x_3·x_4\hfill \\ \hfill {\dot{x}}_4& =1.8·x_5·x_2-0.88·\mathrm{sign}\left(x_4\right)\hfill \\ \hfill {\dot{x}}_5& =1.1·x_6·x_7-x_5\hfill \\ \hfill {\dot{x}}_6& =1.2·\mathrm{sign}\left(x_7\right)-0.98·x_6\hfill \\ \hfill {\dot{x}}_7& =x_8-0.6·x_7\hfill \\ \hfill {\dot{x}}_8& =1.8·x_9\hfill \\ \hfill {\dot{x}}_9& =1.2·x_{10}\hfill \\ \hfill {\dot{x}}_{10}& =-\left(c\right)·x_{10}-\rho \left(e^{\frac{x_9}{\varphi }}\right)+ϵ\left(e^{-\frac{x_9}{\varphi }}\right)-10(·x_8+·x_7+·x_6\hfill \\ \hfill & +·x_5+·x_4+·x_3+·x_2)-0.05·x_1\hfill \end{array}\right.$$

(3)

The control parameters are $\rho =6\times {10}^{-7}$, $\varphi =0.026$, $ϵ=6\times {10}^{-7}$, $c=1$, and the initial values of the variables are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).

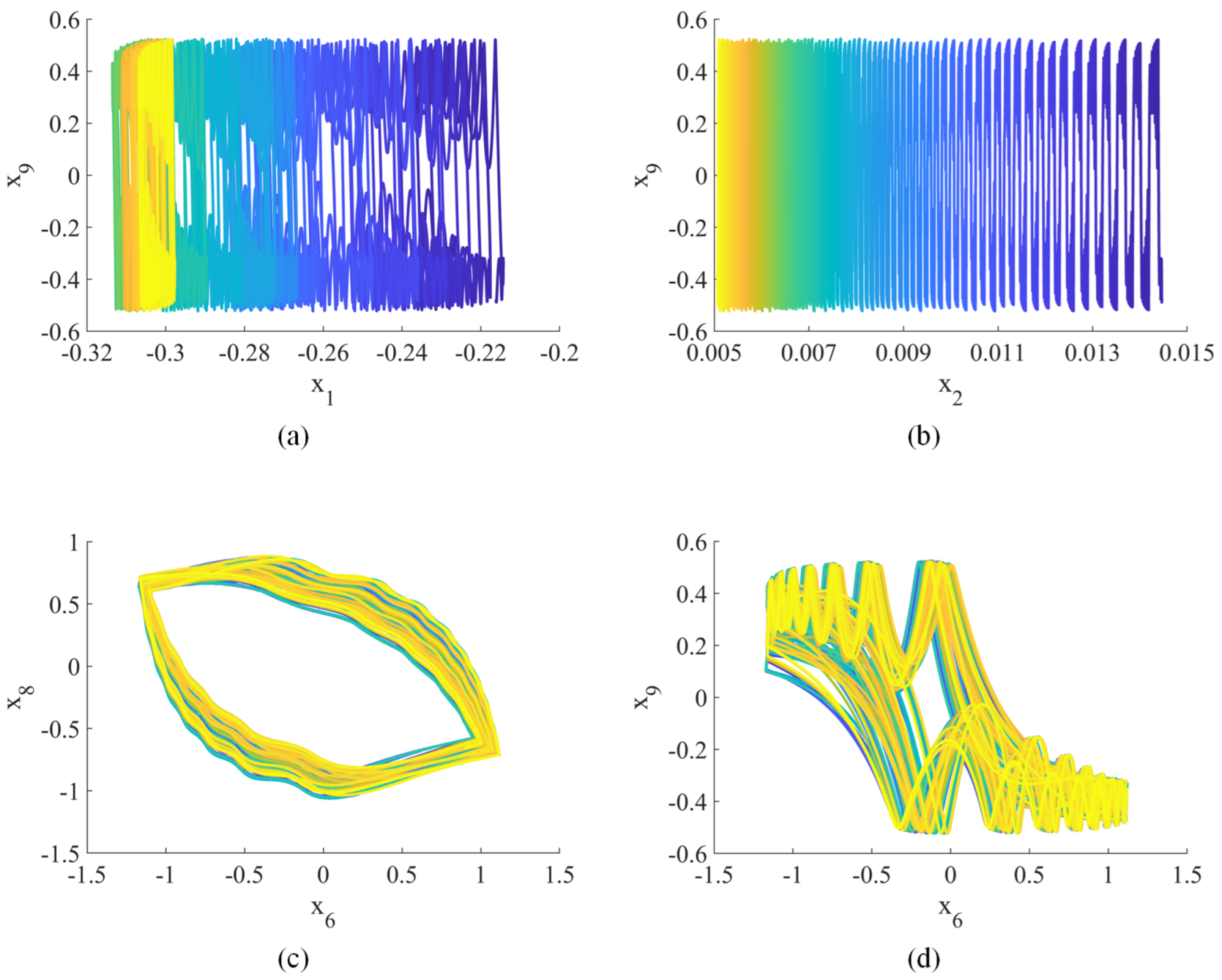
When $c=1$, the Lyapunov exponents (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$, ${\lambda }_9$, ${\lambda }_{10}$) = (0.25, 0.24, 0.19, 0.09, 0, −0.14, −0.76, −0.93, −0.98, −1.21), indicating hyperchaotic behavior [42]. Figure 1, Figure 2 and Figure 3 show the hyperchaotic attractor. These attractors are observed when the variables all have initial values of 0.1.

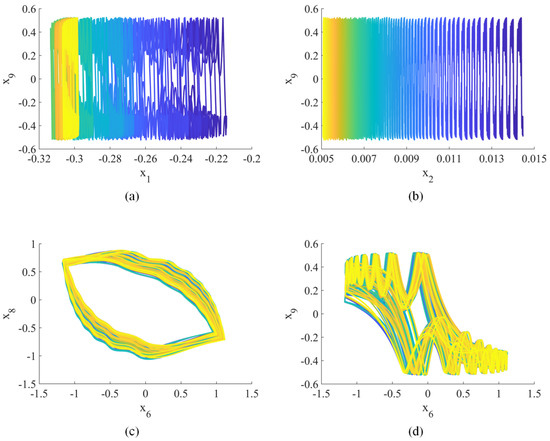
Figure 1. Hyperchaotic attractor (2D phase plane): (a) $x_1$–$x_9$; (b) $x_2$–$x_9$; (c) $x_6$–$x_8$; (d) $x_6$–$x_9$.

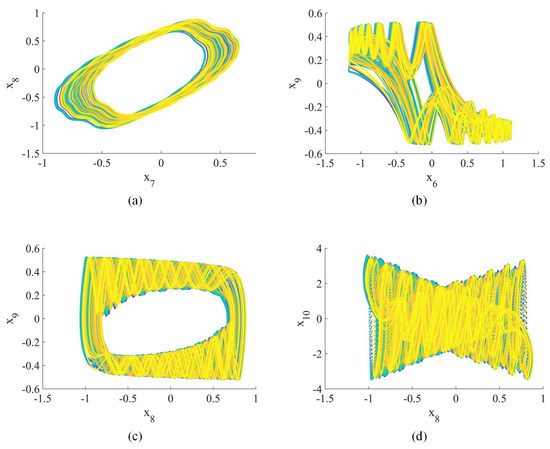
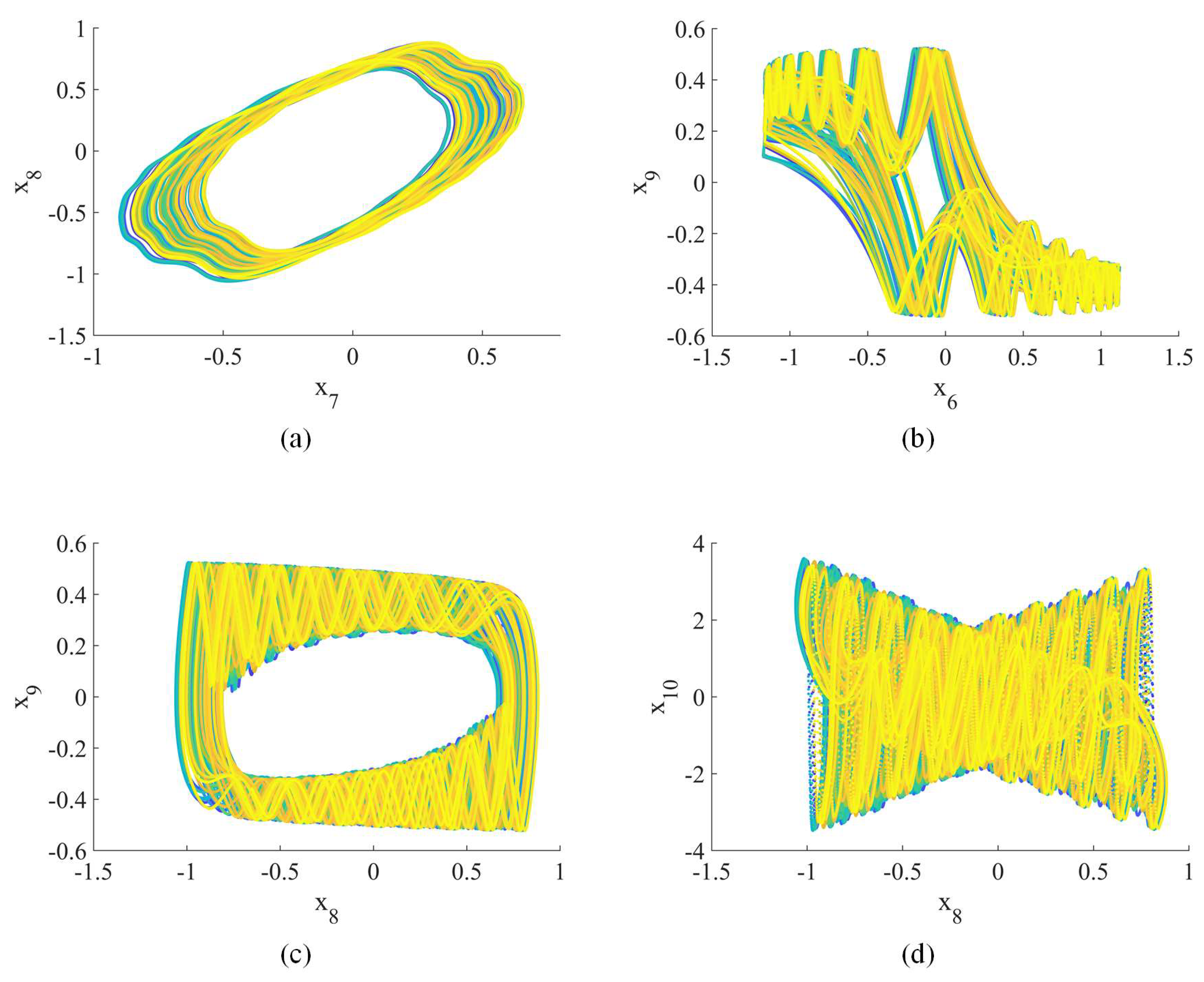
Figure 2. Hyperchaotic attractor (2D phase plane): (a) $x_7$–$x_8$; (b) $x_6$–$x_9$; (c) $x_8$–$x_9$; (d) $x_8$–$x_{10}$.

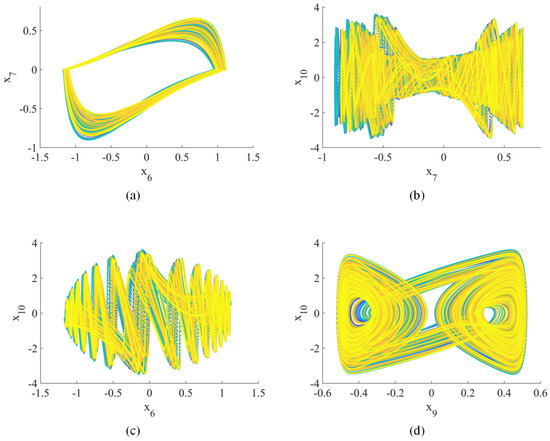
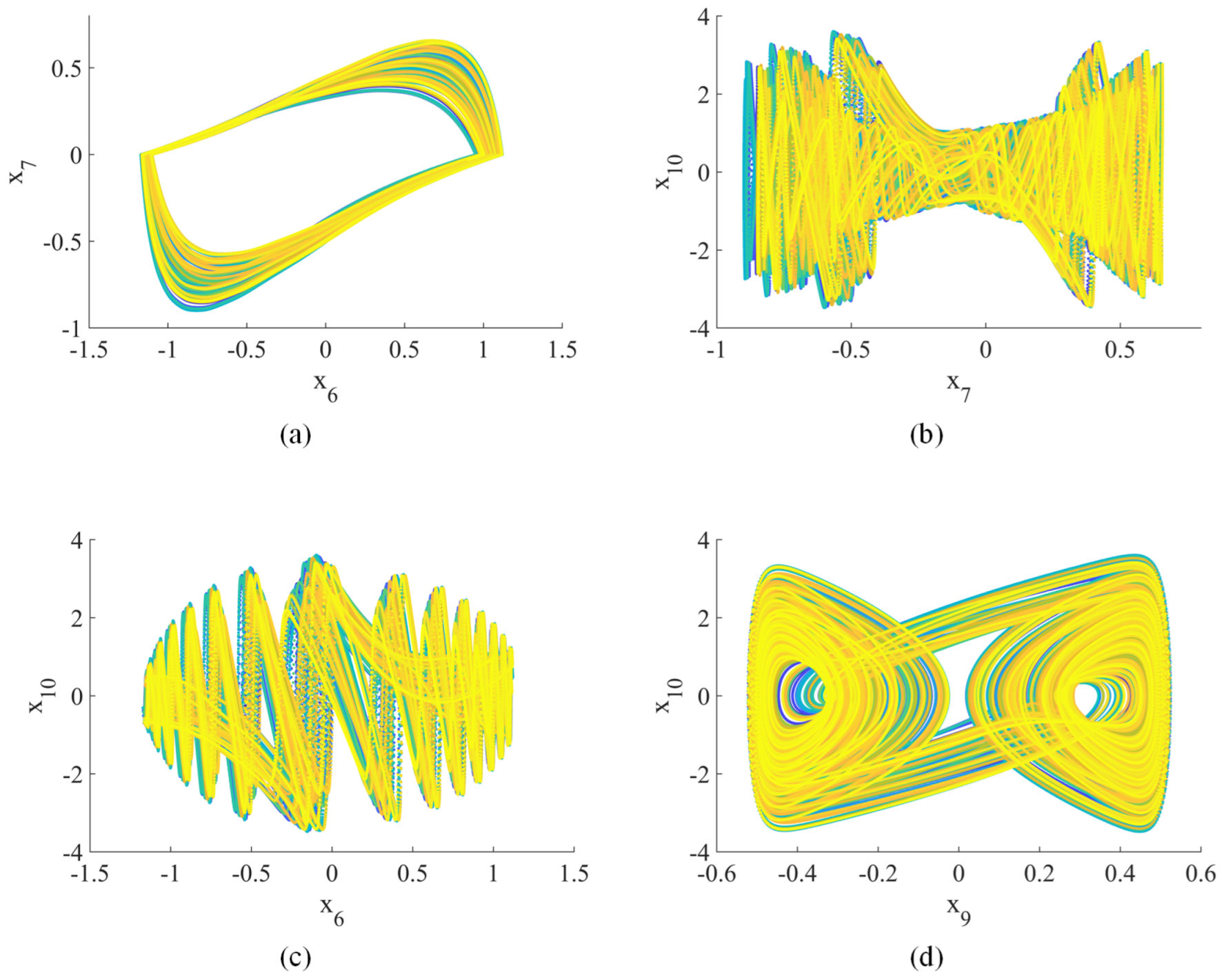
Figure 3. Hyperchaotic attractor (2D phase plane): (a) $x_6$–$x_7$; (b) $x_7$–$x_{10}$; (c) $x_6$–$x_{10}$; (d) $x_9$–$x_{10}$.

3.2. Dynamic Behavior of the 4D Hyperchaotic System

The sign of the Lyapunov exponent is essential for classifying the behavior of systems. It is a unique tool to distinguish chaotic from hyperchaotic and quantify local dynamic stability [43]. Analyzing Lyapunov exponents can provide us with profound insights into the behavior of the hyperchaotic system.

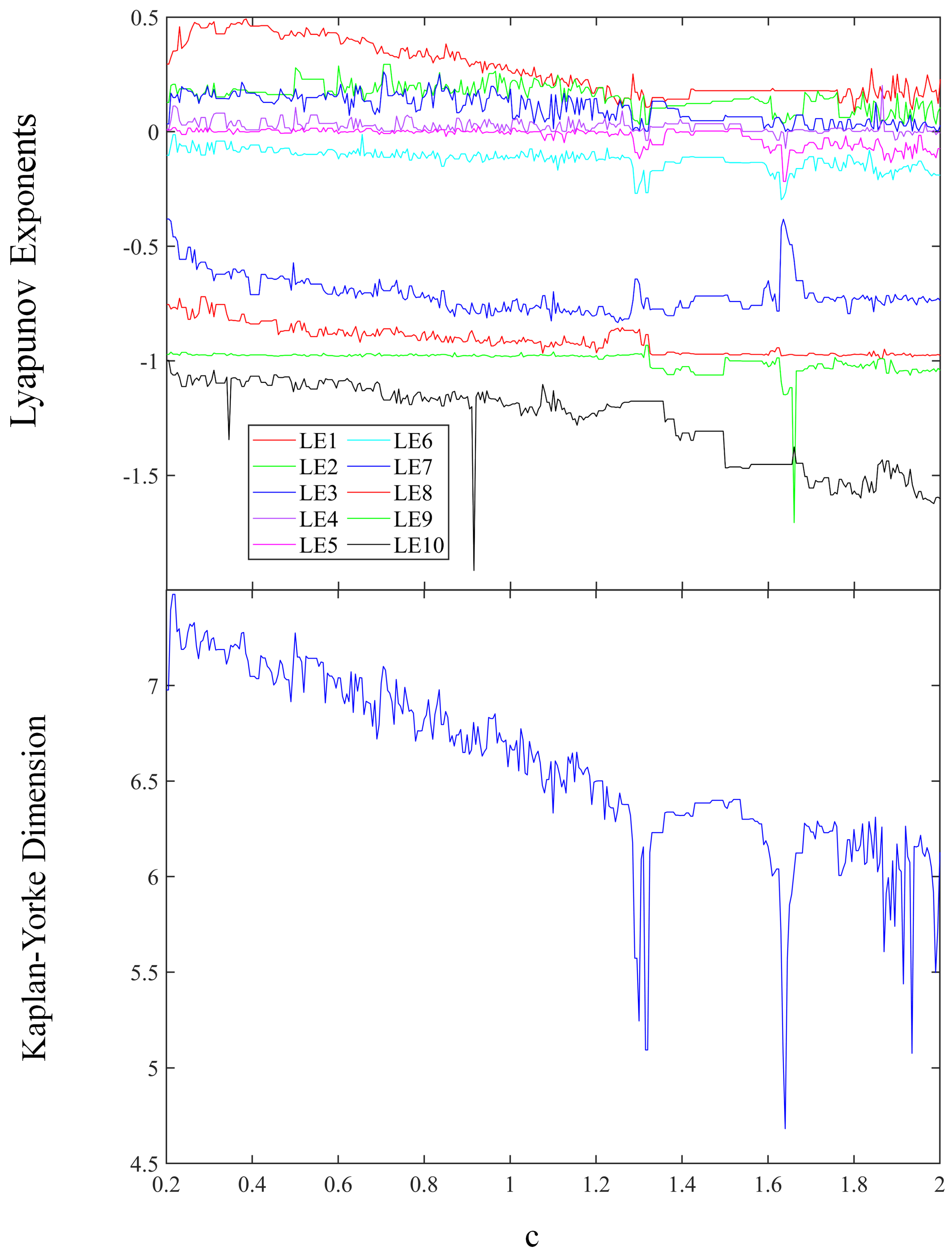
The Kaplan–Yorke dimension and Lyapunov exponent spectrum are depicted in Figure 4 for values of c within the interval [0.2, 2]. In Figure 4, ten lines of different colors represent ten different Lyapunov exponents. The largest Lyapunov exponent is depicted by the red line, with the subsequent largest exponent shown by the green line. The third largest exponent is indicated by the dark blue line, and the fourth largest exponent is represented by the mauve line. When the first four Lyapunov exponents exhibit positive values, the system demonstrates characteristics of a hyperchaotic attractor. For values of parameter c in the range 0.2 to 1.63, four Lyapunov exponents are positive. In contrast, for values of c ranging from 1.63 to 2, three Lyapunov exponents are positive.

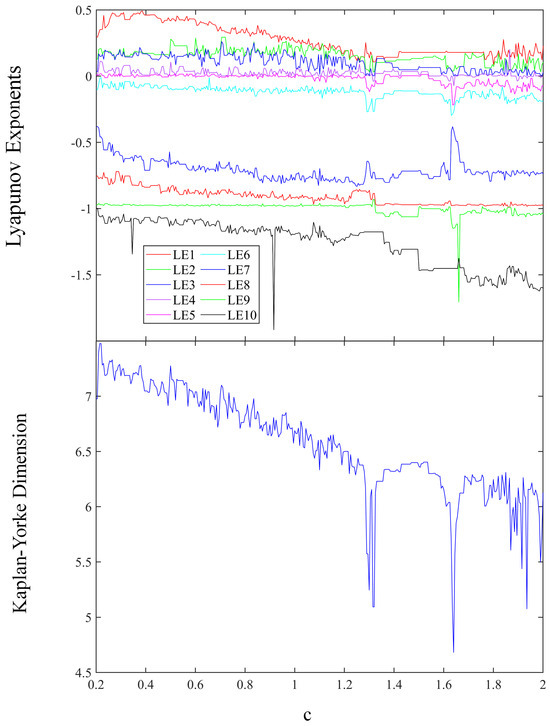
Figure 4. The Lyapunov exponent spectrum and Kaplan−Yorke dimension.

To evaluate the complexity of hyperchaotic systems and characterize the dimension of their attractors, it is essential to calculate the Kaplan–Yorke dimension. The Kaplan–Yorke dimension can be calculated through the utilization of a specific mathematical formula:

$$\begin{array}{cc}\hfill D_{KY}& =D+\frac{{\sum }_{i=1}^{D}L{E}_i}{\left|L{E}_D\right|}\hfill \end{array}$$

(4)

In Equation (4), the term $D_{KY}$ represents the Kaplan–Yorke dimension. The ${\sum }_{i=1}^{D}L{E}_i$ denotes the sum of Lyapunov exponents from 1 to D, and D is less than N (the number of Lyapunov exponents). There exists a maximum integer D for which ${\sum }_{i=1}^{D}L{E}_i$ is positive, and there exists an integer $D+1$ for which ${\sum }_{i=1}^{D+1}L{E}_i$ is negative, and $L{E}_D$ represents the D-th Lyapunov exponent.

When the parameter c falls within the interval of [0.2, 2], the estimated range for the Kaplan–Yorke dimension is approximately between 4.62 and 7.45.

In a chaotic system, the equilibrium point refers to a specific stable state. Equilibrium points play an important role in enhancing our comprehension of the dynamics exhibited by chaotic systems.

Let ${\dot{x}}_1={\dot{x}}_2={\dot{x}}_3={\dot{x}}_4={\dot{x}}_5={\dot{x}}_6={\dot{x}}_7={\dot{x}}_8={\dot{x}}_9={\dot{x}}_{10}=0$ in Equation (3), that is:

$$\left\{\begin{array}{cc}\hfill 0& =x_2·x_7-0.301·x_1·x_2\hfill \\ \hfill 0& =0.3·x_3·x_4-0.3·x_2^2\hfill \\ \hfill 0& =1.4·x_4^2-0.4·x_3·x_4\hfill \\ \hfill 0& =1.8·x_5·x_2-0.88·\mathrm{sign}\left(x_4\right)\hfill \\ \hfill 0& =1.1·x_6·x_7-x_5\hfill \\ \hfill 0& =1.2·\mathrm{sign}\left(x_7\right)-0.98·x_6\hfill \\ \hfill 0& =x_8-0.6·x_7\hfill \\ \hfill 0& =1.8·x_9\hfill \\ \hfill 0& =1.2·x_{10}\hfill \\ \hfill 0& =-\left(c\right)·x_{10}-\rho \left(e^{\frac{x_9}{\varphi }}\right)+ϵ\left(e^{-\frac{x_9}{\varphi }}\right)-10(·x_8+·x_7+·x_6\hfill \\ \hfill & +·x_5+·x_4+·x_3+·x_2)-0.05·x_1\hfill \end{array}\right.$$

(5)

When the values of $\rho$, $\varphi$, $ϵ$, and c are specified as $6\times {10}^{-7}$, $0.026$, $6\times {10}^{-7}$, and 1, respectively, the equilibrium point (0, 0, 0, 0, 0, 0, 0, 0, 0, 0) is identified. To assess the stability of the equilibrium point, it is necessary to acquire the relevant Jacobian matrix. The Jacobian matrix is a matrix consisting of the first-order partial derivatives of a function with multiple variables. The Jacobian matrix is expressed as $f^{\prime }\left(x\right)$. Through the Jacobian matrix, ten eigenvalues can be calculated.

$$\begin{array}{c}\hfill f^{\prime }\left(x\right)=\frac{\partial f}{\partial x}=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \cdots & \frac{\partial f_1}{\partial x_{10}}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \cdots & \frac{\partial f_2}{\partial x_{10}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_{10}}{\partial x_1}& \frac{\partial f_{10}}{\partial x_2}& \cdots & \frac{\partial f_{10}}{\partial x_{10}}\end{array}\right]\end{array}$$

(6)

In dynamical systems, eigenvalues describe the stability of the system near its equilibrium point. The ten eigenvalues are as follows:

$$\begin{array}{cc}\hfill {\lambda }_1& =-0.00030913,\hfill \\ \hfill {\lambda }_2& =(-0.00009904+0.00028896i),\hfill \\ \hfill {\lambda }_3& =(-0.00009904-0.00028896i),\hfill \\ \hfill {\lambda }_4& =(0.00024071+0.00017865i),\hfill \\ \hfill {\lambda }_5& =(0.00024071-0.00017865i),\hfill \\ \hfill {\lambda }_6& =0,\hfill \\ \hfill {\lambda }_7& =0,\hfill \\ \hfill {\lambda }_8& =0,\hfill \\ \hfill {\lambda }_9& =-8.8,\hfill \\ \hfill {\lambda }_{10}& =-0.00001.\hfill \end{array}$$

(7)

Corresponding to the eigenvalues of ${\lambda }_2$ and ${\lambda }_3$, ${\lambda }_4$ and ${\lambda }_5$ exhibit a complex conjugate relationship. The real parts of ${\lambda }_4$ and ${\lambda }_5$ are positive, while the real parts of ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_9$, and ${\lambda }_{10}$ are negative.

In a dynamic system, the presence of a positive eigenvalue indicates instability in the corresponding direction, potentially leading to instability within the system. A negative eigenvalue shows stability in that direction and helps the system maintain equilibrium. If the eigenvalue is zero, the system may have one or more degrees of freedom without a definite direction of stability.

Among the ten eigenvalues analyzed, it is noteworthy that two of them have positive real parts, indicating that the system will move away from the equilibrium point rather than return to it. Additionally, five eigenvalues have negative real parts. This shows that a slight disturbance in the system near the equilibrium point will lead to a gradual decrease in the system state in that direction, ultimately returning to the equilibrium point. Additionally, there are three eigenvalues that are equal to zero. The state change in this direction cannot be determined. The linear change is relatively slow, making it impossible to ascertain whether it is stable or unstable.

Divergence describes whether a vector field is “convergent” or “divergent” at a specific point. If the divergence of a vector field at a certain point is positive, it shows that the vectors around this specific point mainly point towards this point. In other words, more fluid or matter converges toward the certain point, suggesting that the point is a “convergence point”. In other words, more fluid or matter converges toward that point, suggesting that the point is a “convergence point”. On the contrary, if the divergence of a vector field at a certain point is negative, it shows that the vectors around the point mainly point away from it. If the divergence is zero, it means that the fluid or material around the point does not converge or diverge; in other words, the point is a “stable point”. In this system, the divergence equation is as follows:

$$\begin{array}{c}\hfill \nabla ·\mathbf{F}=\sum _{i=1}^{10}\frac{\partial {\dot{x}}_i}{\partial x_i}\end{array}$$

(8)

According to Equation (8), the calculated result is −8.8. In general, the hyperchaotic system is commonly found to exhibit a negative divergence, indicating its inherent divergent characteristics [44].

4. Detailed Encryption and Decryption Schemes

Four pseudorandom sequences generated by the innovative 4D hyperchaotic system are used for encrypting images. The chaotic sequence denoted as $c_1$ is applied for both row and column scrambling, whereas the sequence $c_2$ is employed for diffusion during the first encryption round. In the second encryption round, the sequence $c_3$ is utilized for diffusion, while $c_4$ is employed for scrambling both rows and columns. The encryption and decryption processes are delineated in Algorithms 1 and 2, correspondingly. The generation processes of $c_1$, $c_2$, $c_3$, and $c_4$ are expounded in Algorithms 3, 4, 5 and 6, respectively.

The definitions of the variables in Algorithms 1 and 2 are outlined as follows:

• $Org\_Img$: Pixel matrix of the original image.
• $En\_Img$: Pixel matrix of the encrypted image.
• $1st\_row$: The result of the first row scrambling.
• $1st\_column$: The result of the first column scrambling.
• $1st\_diffusion$: The result of the first diffusion.
• $2nd\_row$: The result of the second row scrambling.
• $2nd\_column$: The result of the second column scrambling.
• $2nd\_diffusion$: The result of the second diffusion.
• $1st\_encryption$: The result of the first encryption.

Algorithm 1 Pseudocode of the encryption process

Input value: $Org\_Img$ Output value: $En\_Img$ 1: $Average\_pixel\_value\leftarrow \mathrm{mean}2(Org\_Img)\times {10}^{-9}$ 2: $y_1=y_2=y_3=y_4=y_5=y_6=y_7=y_8=y_9=y_{10}=0.1$ 3: $y_1\left(1\right)\leftarrow y_1\left(1\right)+Average\_pixel\_value$ 4: $c_1\leftarrow \mathrm{SEQA}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 5: $c_2\leftarrow \mathrm{SEQB}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 6: $1st\_row\leftarrow \mathrm{row}\_\mathrm{scrambling}$($Org\_Img$, $c_1$) 7: $1st\_column\leftarrow \mathrm{column}\_\mathrm{scrambling}$($1st\_row$, $c_1$) 8: $1st\_diffusion\left(1st\_encryption\right)\leftarrow \mathrm{diffusion}($$1st\_column$, $c_2$) 9: $y_1=y_2=y_3=y_4=y_5=y_6=y_7=y_8=y_9=y_{10}=0.1$ 10: $y_1\left(1\right)\leftarrow y_1\left(1\right)+Average\_pixel\_value$ 11: $c_3\leftarrow \mathrm{SEQC}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 12: $c_4\leftarrow \mathrm{SEQD}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 13: $2nd\_diffusion\leftarrow \mathrm{diffusion}($$1st\_diffusion$, $c_4$) 14: $2nd\_column\leftarrow \mathrm{column}\_\mathrm{scrambling}$($2nd\_diffusion$, $c_3$) 15: $2nd\_row\left(En\_Img\right)\leftarrow \mathrm{row}\_\mathrm{scrambling}$($2nd\_column$, $c_3$)

Algorithm 2 Pseudocode of the decryption process

Input value: $En\_Img$ Output value: $Org\_Img$ 1: $y_1=y_2=y_3=y_4=y_5=y_6=y_7=y_8=y_9=y_{10}=0.1$ 2: $y_1\left(1\right)\leftarrow y_1\left(1\right)+Average\_pixel\_value$ 3: $c_3\leftarrow \mathrm{SEQC}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 4: $c_4\leftarrow \mathrm{SEQD}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 5: $1st\_row\leftarrow \mathrm{row}\_\mathrm{scrambling}$($En\_Img$, $c_3$) 6: $1st\_column\leftarrow \mathrm{column}\_\mathrm{scrambling}$($1st\_row$, $c_3$) 7: $1st\_diffusion\left(1st\_encryption\right)\leftarrow \mathrm{diffusion}($$1st\_column$, $c_4$) 8: $y_1=y_2=y_3=y_4=y_5=y_6=y_7=y_8=y_9=y_{10}=0.1$ 9: $y_1\left(1\right)\leftarrow x_1\left(1\right)+Average\_pixel\_value$ 10: $c_1\leftarrow \mathrm{SEQA}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 11: $c_2\leftarrow \mathrm{SEQB}(y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10})$ 12: $2nd\_diffusion\leftarrow \mathrm{diffusion}($$1st\_encryption$, $c_2$) 13: $2nd\_column\leftarrow \mathrm{column}\_\mathrm{scrambling}$($2nd\_diffusion$, $c_1$) 14: $2nd\_row\left(Org\_Img\right)\leftarrow \mathrm{row}\_\mathrm{scrambling}$($2nd\_column$, $c_1$)

Algorithm 3 SEQA

1: function SEQA($y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10}$) 2:     for $k=1$ to $m\times n$ do 3:         $$\begin{gathered} [d{y}_1,d{y}_2,d{y}_3,d{y}_4,d{y}_5,d{y}_6,d{y}_7,d{y}_8,d{y}_9,d{y}_{10}] \\ \leftarrow \mathrm{Runge}–\mathrm{Kutta}(y_1\left(k\right),y_2\left(k\right),y_3\left(k\right),y_4\left(k\right),y_5\left(k\right),y_6\left(k\right),y_7\left(k\right),y_8\left(k\right),y_9\left(k\right),y_{10}\left(k\right)) \end{gathered}$$ 4:         $y_1(k+1)\leftarrow y_1\left(k\right)+d{y}_1$ 5:         $y_2(k+1)\leftarrow y_2\left(k\right)+d{y}_2$ 6:         $y_3(k+1)\leftarrow y_3\left(k\right)+d{y}_3$ 7:         $y_4(k+1)\leftarrow y_4\left(k\right)+d{y}_4$ 8:         $y_5(k+1)\leftarrow y_5\left(k\right)+d{y}_5$ 9:         $y_6(k+1)\leftarrow y_6\left(k\right)+d{y}_6$ 10:       $y_7(k+1)\leftarrow y_7\left(k\right)+d{y}_7$ 11:       $y_8(k+1)\leftarrow y_8\left(k\right)+d{y}_8$ 12:       $y_9(k+1)\leftarrow y_9\left(k\right)+d{y}_9$ 13:       $y_{10}(k+1)\leftarrow y_{10}\left(k\right)+d{y}_{10}$ 14:       $s_k=\left|y_3\left(k\right)\times {10}^{12}-\mathrm{floor}(y_3\left(k\right)\times {10}^{12})\right|$ 15:     end for 16:     $[z1,c]=\mathrm{sort}\left(s\right);$ 17:     return c 18: end function

Encryption Algorithm:

<1>

Determine the key by computing the mean value of pixels in the original image.

<2>

Divide the individual pixels in the original image based on three distinct color channels: red, green, and blue.

<3>

Calculate $c_1$ by applying mathematical operations to the chaotic sequence A following Algorithm 3.

<4>

Calculate $c_2$ through sequence B according to Algorithm 4.

<5>

Calculate $c_3$ through sequence C according to Algorithm 5.

<6>

Calculate $c_4$ through sequence D according to Algorithm 6.

<7>

Rearrange the three channels by applying row scrambling using sequence $c_1$ as described in <3>.

<8>

Rearrange the three channels by applying column scrambling using sequence $c_1$ as described in <3>.

<9>

Diffuse the three channels by employing the sequence denoted as $c_2$ as described in <4>.

<10>

Integrate the three channels to generate the first round encryption image.

<11>

Diffuse the three channels by employing the sequence denoted as $c_4$ as described in <6>.

<12>

Rearrange the three channels by applying column scrambling using sequence $c_3$ as described in <5>.

<13>

Rearrange the three channels by applying row scrambling using sequence $c_3$ as described in <5>.

<14>

Integrate the three channels to generate the second round encryption image.

Algorithm 4 SEQB

1: function SEQB($y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10}$) 2:     for $k=1$ to $m\times n$ do 3:         $$\begin{gathered} [d{y}_1,d{y}_2,d{y}_3,d{y}_4,d{y}_5,d{y}_6,d{y}_7,d{y}_8,d{y}_9,d{y}_{10}] \\ \leftarrow \mathrm{Runge}–\mathrm{Kutta}(y_1\left(k\right),y_2\left(k\right),y_3\left(k\right),y_4\left(k\right),y_5\left(k\right),y_6\left(k\right),y_7\left(k\right),y_8\left(k\right),y_9\left(k\right),y_{10}\left(k\right)) \end{gathered}$$ 4:         $y_1(k+1)\leftarrow y_1\left(k\right)+d{y}_1$ 5:         $y_2(k+1)\leftarrow y_2\left(k\right)+d{y}_2$ 6:         $y_3(k+1)\leftarrow y_3\left(k\right)+d{y}_3$ 7:         $y_4(k+1)\leftarrow y_4\left(k\right)+d{y}_4$ 8:         $y_5(k+1)\leftarrow y_5\left(k\right)+d{y}_5$ 9:         $y_6(k+1)\leftarrow y_6\left(k\right)+d{y}_6$ 10:       $y_7(k+1)\leftarrow y_7\left(k\right)+d{y}_7$ 11:       $y_8(k+1)\leftarrow y_8\left(k\right)+d{y}_8$ 12:       $y_9(k+1)\leftarrow y_9\left(k\right)+d{y}_9$ 13:       $y_{10}(k+1)\leftarrow y_{10}\left(k\right)+d{y}_{10}$ 14:       $s_k=\left|y_3\left(k\right)\times {10}^8-\mathrm{round}(y_3\left(k\right)\times {10}^8)\right|$ 15:       $c_k=\mathrm{mod}\left(y_2\left(k\right)\times {10}^{12}-\lfloor y_2\left(k\right)\times {10}^{12}\rfloor +s_k,256\right)$ 16:     end for 17:     $c\left(k\right)=\mathrm{fix}\left(c\right(k\left)\right);$ 18:     return c 19: end function

Algorithm 5 SEQC

1: function SEQC($y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10}$) 2:     for $k=1$ to $m\times n\times 10$ do 3:         $$\begin{gathered} [d{y}_1,d{y}_2,d{y}_3,d{y}_4,d{y}_5,d{y}_6,d{y}_7,d{y}_8,d{y}_9,d{y}_{10}] \\ \leftarrow \mathrm{Runge}–\mathrm{Kutta}(y_1\left(k\right),y_2\left(k\right),y_3\left(k\right),y_4\left(k\right),y_5\left(k\right),y_6\left(k\right),y_7\left(k\right),y_8\left(k\right),y_9\left(k\right),y_{10}\left(k\right)) \end{gathered}$$ 4:         $y_1(k+1)\leftarrow y_1\left(k\right)+d{y}_1$ 5:         $y_2(k+1)\leftarrow y_2\left(k\right)+d{y}_2$ 6:         $y_3(k+1)\leftarrow y_3\left(k\right)+d{y}_3$ 7:         $y_4(k+1)\leftarrow y_4\left(k\right)+d{y}_4$ 8:         $y_5(k+1)\leftarrow y_5\left(k\right)+d{y}_5$ 9:         $y_6(k+1)\leftarrow y_6\left(k\right)+d{y}_6$ 10:       $y_7(k+1)\leftarrow y_7\left(k\right)+d{y}_7$ 11:       $y_8(k+1)\leftarrow y_8\left(k\right)+d{y}_8$ 12:       $y_9(k+1)\leftarrow y_9\left(k\right)+d{y}_9$ 13:       $y_{10}(k+1)\leftarrow y_{10}\left(k\right)+d{y}_{10}$ 14:       if $\mathrm{mod}(k,10)=0$ then 15:            $s_k=\left|y_8\left(k\right)\times {10}^8-\mathrm{floor}(y_8\left(k\right)\times {10}^8)\right|$ 16:       end if 17:     end for 18:     $[z1,c]=\mathrm{sort}\left(s\right);$ 19:     return c 20: end function

Algorithm 6 SEQD

1: function SEQD($y_1,y_2,y_3,y_4,y_5,y_6,y_7,y_8,y_9,y_{10}$) 2:     for $k=1$ to $m\times n\times 10$ do 3:         $$\begin{gathered} [d{y}_1,d{y}_2,d{y}_3,d{y}_4,d{y}_5,d{y}_6,d{y}_7,d{y}_8,d{y}_9,d{y}_{10}] \\ \leftarrow \mathrm{Runge}–\mathrm{Kutta}(y_1\left(k\right),y_2\left(k\right),y_3\left(k\right),y_4\left(k\right),y_5\left(k\right),y_6\left(k\right),y_7\left(k\right),y_8\left(k\right),y_9\left(k\right),y_{10}\left(k\right)) \end{gathered}$$ 4:         $y_1(k+1)\leftarrow y_1\left(k\right)+d{y}_1$ 5:         $y_2(k+1)\leftarrow y_2\left(k\right)+d{y}_2$ 6:         $y_3(k+1)\leftarrow y_3\left(k\right)+d{y}_3$ 7:         $y_4(k+1)\leftarrow y_4\left(k\right)+d{y}_4$ 8:         $y_5(k+1)\leftarrow y_5\left(k\right)+d{y}_5$ 9:         $y_6(k+1)\leftarrow y_6\left(k\right)+d{y}_6$ 10:       $y_7(k+1)\leftarrow y_7\left(k\right)+d{y}_7$ 11:       $y_8(k+1)\leftarrow y_8\left(k\right)+d{y}_8$ 12:       $y_9(k+1)\leftarrow y_9\left(k\right)+d{y}_9$ 13:       $y_{10}(k+1)\leftarrow y_{10}\left(k\right)+d{y}_{10}$ 14:       if $\mathrm{mod}(k,10)=0$ then 15:            $s_k=\left|y_3\left(k\right)\times {10}^8-\mathrm{round}(y_3\left(k\right)\times {10}^8)\right|$ 16:            $c_k=\mathrm{mod}\left(y_3\left(k\right)\times {10}^{12}-\lfloor y_3\left(k\right)\times {10}^{12}\rfloor +s_k,256\right)$ 17:       end if 18:     end for 19:     $c\left(k\right)=\mathrm{fix}\left(c\right(k\left)\right);$ 20:     return c 21: end function

Decryption Algorithm:

<1>

Rearrange the three channels by applying row scrambling using sequence $c_3$.

<2>

Rearrange the three channels by applying column scrambling using sequence $c_3$.

<3>

Diffuse the three channels by employing the sequence denoted as $c_4$.

<4>

Integrate the three channels to generate the first round encryption image.

<5>

Diffuse the three channels by employing the sequence denoted as $c_2$.

<6>

Rearrange the three channels by applying column scrambling using sequence $c_1$.

<7>

Rearrange the three channels by applying row scrambling using sequence $c_1$.

<8>

Integrate the three channels to generate the second round encryption image.

The encryption and decryption processes are illustrated in Figure 5 and Figure 6.

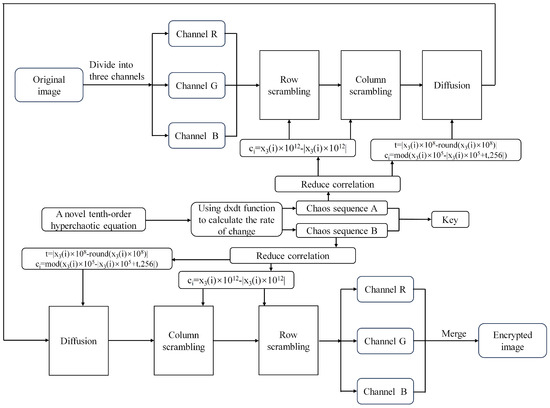
Figure 5. The process of encrypting an image.

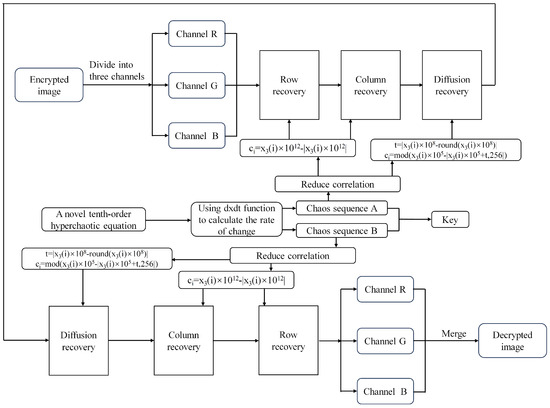
Figure 6. The process of decrypting an image.

5. Experiments with Related Security Analysis

5.1. Encryption Results

Color image encryption includes rearranging rows and columns as well as diffusing pixel values within the image. By incorporating two encryption rounds and utilizing four chaotic sequences, the encryption process is designed to enhance complexity and subsequently improve encryption effectiveness. The resulting encrypted image exhibits a highly chaotic and complex pixel arrangement, rendering it infeasible to recover any original data from the encrypted result.

The outcomes of encrypting and decrypting images utilizing the suggested encryption and decryption schemes are illustrated in Figure 7. Column (i) of Figure 7 shows the final encryption results. Through the examination of encrypted images, it is evident that no discernible data pertaining to the original images can be derived. This highlights how the encryption system effectively safeguards the security of images.

Figure 7. Encryption and decryption results: (a) nine original images; (b) nine decrypted images of red channel; (c) nine decrypted images of green channel; (d) nine decrypted images of blue channel; (e) nine decrypted images; (f) nine encrypted images of red channel; (g) nine encrypted images of green channel; (h) nine encrypted images of blue channel; (i) nine encrypted images.

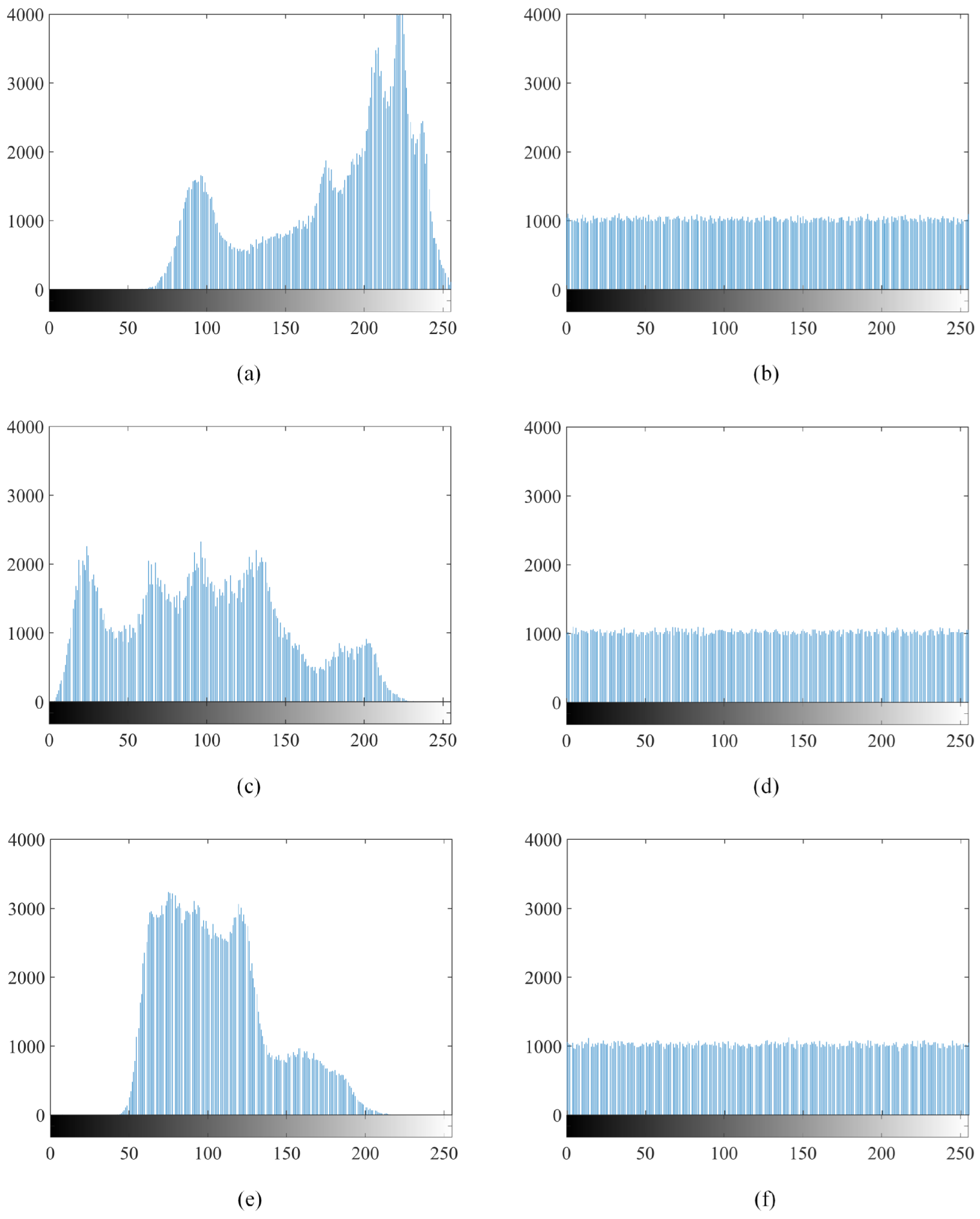
5.2. Histogram Analysis

A histogram is a representation that shows how often data points occur [45]. The image histogram illustrates the spread of pixels across different brightness levels within an image. The following section displays the histogram of a color image that has been encrypted. The horizontal axis represents the spectrum of tonal differences, while the vertical axis shows the number of pixels associated with each tone. A histogram displaying a uniform distribution indicates that the occurrence of individual pixel values is approximately equal in probability. Consequently, such uniformity enhances the image’s resistance against statistical analysis, as it becomes challenging for attackers to deduce information about the original image. The increased complexity makes it difficult for attackers to anticipate the original image’s information by analyzing the statistical characteristics of the encrypted image.

To evaluate encrypted images, the variance of the histogram can be used as a method of measuring the histogram. A lower variance value signifies a higher level of uniformity in encrypted result. The equation for the computation of histogram variance is outlined as follows:

$$\begin{array}{c}\hfill \mathrm{var}\left(\mathrm{X}\right)=\frac{1}{k^2}\sum _{i=1}^k\sum _{j=1}^k{(x_i-x_j)}^2\end{array}$$

(9)

The variance of the histogram is denoted by X. The variables $x_j$ and $x_i$ denote the pixel values of positions j and i in a single channel. In this study, an analysis using histograms was conducted on the image titled “Jetplane”. Table 1 presents the variance values of the image across the three channels. The variance values observed in the encrypted image were significantly lower than those in the original image across all three color channels. The difference suggests a more consistent spread of pixel values in the encrypted image, effectively hiding the original image’s structure and features. Therefore, it is impossible for an attacker to extract any useful information from the encrypted image just by observation.

Table 1. Variances of image “Jetplane” in three channels.

Channel	Variance of the Original “Jetplane”	Variance of the Encrypted “Jetplane”
Red	1,473,469	262,656
Green	1,804,092	262,656
Blue	3,220,626	262,670

The comparison between the histograms of the original “Jetplane” and the encrypted “Jetplane” is shown in Figure 8. The histograms depicted in (b), (d), and (f) indicate that the histogram of the encrypted “Jetplane” exhibits a closer resemblance to a uniform distribution. Consequently, the analysis suggests the effectiveness of the proposed encryption scheme.

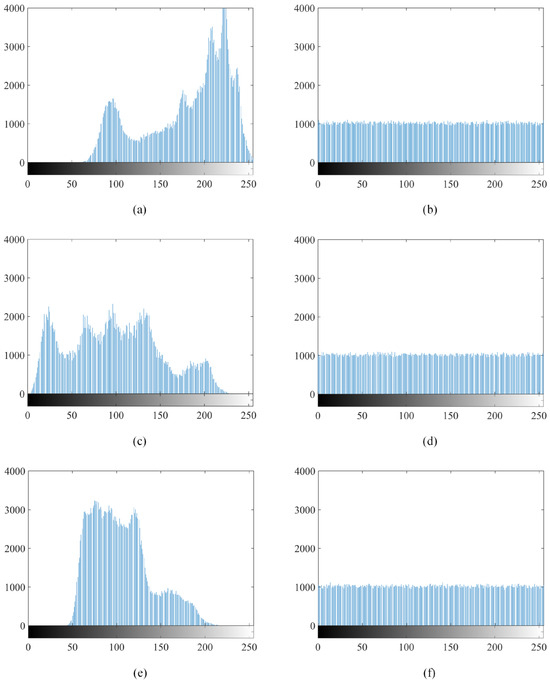
Figure 8. Comparison of the histograms: (a) the distribution of pixels within red channel of original “Jetplane”; (b) the distribution of pixels within red channel of encrypted “Jetplane”; (c) the distribution of pixels within green channel of original “Jetplane”; (d) the distribution of pixels within green channel of encrypted “Jetplane”; (e) the distribution of pixels within blue channel of original “Jetplane”; (f) the distribution of pixels within blue channel of encrypted “Jetplane”.

5.3. Key Space Analysis

In image encryption, the term “key space” denotes the collection of all keys that can be employed in the encryption process. This concept is instrumental in assessing the security level and the quantity of keys associated with a particular encryption method. An effective encryption scheme is characterized by a substantial key space, as this feature enhances the complexity of discovering a valid key through brute force. A key space of significant magnitude is imperative for safeguarding the security integrity of the encryption scheme.

If the resolution is determined to be ${10}^{15}$, the range of the attraction domain for variable $x_1$ is $x_1\in [-0.3135,-0.2143]$. There are $0.0992\times {10}^{15}=0.0992\times {10}^{15}$ kinds of choices. For the variables ranging from $x_2$ to $x_{10}$, the number of choices available is outlined in Table 2.

Table 2. Variables and the quantity of choices.

Variables	Quantity of Choices
$x_2$	$0.0094\times {10}^{15}$
$x_3$	$0.0013\times {10}^{15}$
$x_4$	$0.0005\times {10}^{15}$
$x_5$	$0.6329\times {10}^{15}$
$x_6$	$2.2924\times {10}^{15}$
$x_7$	$1.5574\times {10}^{15}$
$x_8$	$1.9437\times {10}^{15}$
$x_9$	$1.0475\times {10}^{15}$
$x_{10}$	$7.0864\times {10}^{15}$

The control variables contribute to the formation of a key space, which is $0.0992\times {10}^{15}\times 0.0094\times {10}^{15}\times 0.0013\times {10}^{15}\times 0.0005\times {10}^{15}\times 0.6329\times {10}^{15}\times 2.2924\times {10}^{15}\times 1.5574\times {10}^{15}\times 1.9437\times {10}^{15}\times 1.0475\times {10}^{15}\times 7.0864\times {10}^{15}=1.976\times {10}^{142}$. By focusing on the control variable c in Equation (3), it becomes feasible to ascertain the key space. It is $1.976\times {10}^{142}\times 2.88\times {10}^{15}=5.691\times {10}^{157}$. When analyzing the hyperchaotic system and only considering first-order terms with a coefficient of 1, the phase space is estimated to be $6.4\times {10}^{432}$. The aforementioned computation demonstrates the phase space following a single encryption iteration. Moreover, given that this encryption scheme entails two encryption rounds, the phase space is expected to be expanded twofold. The key space expands to $6.4\times {10}^{432}\times 6.4\times {10}^{432}=4.096\times {10}^{865}\approx 2^{877}$. It is worth noting that the calculations for key space above are not comprehensive. The effective key space of this system exceeds $2^{877}$ by a significant margin.

Table 3 compares the key space of the image encryption scheme proposed in this study with various other encryption methods, and the encryption scheme proposed in this paper exhibits the largest key space. The analysis shows that the proposed encryption scheme has a large enough key space to resist brute force attacks effectively.

Table 3. Comparison of key space.

Encryption Scheme	Key Space
Proposed Encryption Scheme	>2877
Reference [35]	>2116
Reference [46]	>2478
Reference [47]	>2219
Reference [48]	>2604
Reference [49]	>2554
Reference [50]	>2372

5.4. Correlation Analysis

Natural images exhibit a significant level of correlation among pixels, whether they are oriented vertically, horizontally, or diagonally. A successful encryption scheme should guarantee that the encrypted image, which has decreased pixel correlation, is resistant against encryption attacks that rely on statistical analysis [51]. Adjacent pixel correlation refers to the quantification of the association among pixel values that are in close proximity to each other within an image. A low correlation can be considered to be an indication of the effectiveness of the encryption scheme. The correlation among pixels in the encrypted image tends towards zero, suggesting an enhancement in the randomness and independence of pixel values. Consequently, encrypted images display a seemingly random distribution of pixels, thereby thwarting attempts by attackers to decrypt it through basic statistical analyses or pattern recognition techniques.

The correlation is determined through the utilization of the subsequent mathematical Equations [52]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathrm{E}\left(m\right)& =\frac{1}{M}\sum _{i=1}^M{m}_i\hfill \\ \hfill \mathrm{D}\left(m\right)& =\frac{1}{M}\sum _{i=1}^M{(m_i-E\left(m\right))}^2\hfill \\ \hfill \mathrm{cov}(m,n)& =\frac{1}{M}\sum _{i=1}^M(x_i-E\left(m\right))(y_i-E\left(n\right))\hfill \\ \hfill {\mathrm{r}}_{xy}& =\frac{\mathrm{cov}(m,n)}{\sqrt{\mathrm{D}\left(m\right)·\mathrm{D}\left(n\right)}}\hfill \end{array}\right.\end{array}$$

(10)

Table 4 below displays the outcomes of a correlation analysis conducted on pixel values from eight images. The data in Table 4 indicate that correlation value of encrypted images approaches zero, suggesting a minimal correlation among individual pixel values within images. This lack of correlation is ascribed to the disturbance in the pixel arrangement of the original image, leading to the encrypted image manifesting as random noise. Furthermore, Table 5 provides a comparative analysis of correlation values obtained from the proposed encryption scheme in contrast to other encryption schemes. The comparison indicates that the encryption performance of the proposed scheme is similar to that of existing methods in relation to correlation. Therefore, the proposed encryption scheme demonstrates a significant degree of effectiveness.

Table 4. Correlation coefficients among eight images.

Image	Original Image			1st Round Encryption			2nd Round Encryption
	Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
Monkey	R 0.9123	0.8625	0.8505	0.0045	0.0004	−0.0002	−0.0001	−0.0016	−0.0001
	G 0.8628	0.7811	0.7496	−0.0003	−0.0045	0.0045	−0.0037	−0.0008	−0.0014
	B 0.8965	0.8712	0.8314	−0.0001	−0.0021	0.0016	−0.0051	−0.0046	−0.0018
Mountain	R 0.8417	0.8556	0.7818	−0.0005	0.0006	−0.0022	0.0029	−0.0026	0.0022
	G 0.7543	0.7802	0.6769	0.0018	0.0007	−0.0005	−0.0010	−0.0029	0.0022
	B 0.6754	0.7083	0.5842	0.0015	0.0032	−0.0023	0.0008	0.0030	0.0035
Ice	R 0.9194	0.8997	0.8538	0.0012	0.0002	−0.0042	−0.0001	0.0001	−0.0012
	G 0.9189	0.9102	0.8596	−0.0033	−0.0018	−0.0013	0.0006	0.0028	−0.0016
	B 0.8957	0.8888	0.8367	−0.0017	−0.0001	0.0017	0.0015	0.0049	−0.0024
Apartment	R 0.9552	0.9591	0.9252	−0.0008	0.0005	−0.0003	0.0002	−0.0032	0.0015
	G 0.9405	0.9445	0.8951	−0.0001	0.0011	0.0014	0.0005	0.0030	0.0021
	B 0.9728	0.9691	0.9456	0.0032	−0.0008	−0.0032	−0.0004	0.0022	0.0019
Lake	R 0.9713	0.9697	0.9534	0.0018	−0.0004	0.0009	0.0021	0.0014	−0.0014
	G 0.9718	0.9666	0.9534	−0.0005	0.0003	−0.0002	0.0029	0.0020	0.0011
	B 0.9713	0.9697	0.9534	−0.0022	0.0010	0.0010	0.0015	−0.0006	0.0037
spatter	R 0.9938	0.9953	0.9898	0.0019	0.0008	−0.0006	0.0017	−0.0005	−0.0040
	G 0.9812	0.9872	0.9713	0.0019	0.0008	−0.0006	0.0031	−0.0047	0.0022
	B 0.9826	0.9792	0.9653	0.0004	0.0007	−0.0024	0.0040	−0.0024	−0.0004
Earth	R 0.9695	0.9737	0.9518	−0.0013	−0.0048	0.0020	−0.0001	−0.0012	0.0024
	G 0.9683	0.9734	0.9492	0.0022	−0.0012	0.0013	−0.0002	−0.0033	−0.0004
	B 0.9572	0.9623	0.9337	0.0016	0.0012	−0.0002	0.0041	−0.0019	−0.0049
Jetplane	R 0.9738	0.9593	0.9382	0.0019	0.0019	0.0019	−0.0035	0.0023	−0.0022
	G 0.9596	0.9691	0.9356	0.0005	0.0006	0.0013	−0.0036	−0.0010	0.0016
	B 0.9673	0.9431	0.9249	−0.0006	0.0001	0.0019	0.0007	0.0011	0.0004

Table 5. Comparison in terms of pixel correlation.

Encryption Scheme	Horizontal	Vertical	Diagonal
Proposed Encryption Scheme	0.0013	−0.0021	−0.0010
Reference [35]	−0.0093	0.0025	−0.0024
Reference [53]	−0.0012	0.0099	−0.0032
Reference [54]	0.0027	0.0015	0.0019
Reference [55]	0.0023	−0.0010	0.0009

As indicated in Table 4, the original image exhibits a strong correlation coefficient, whereas the encrypted image demonstrates a correlation coefficient that approaches zero [56].

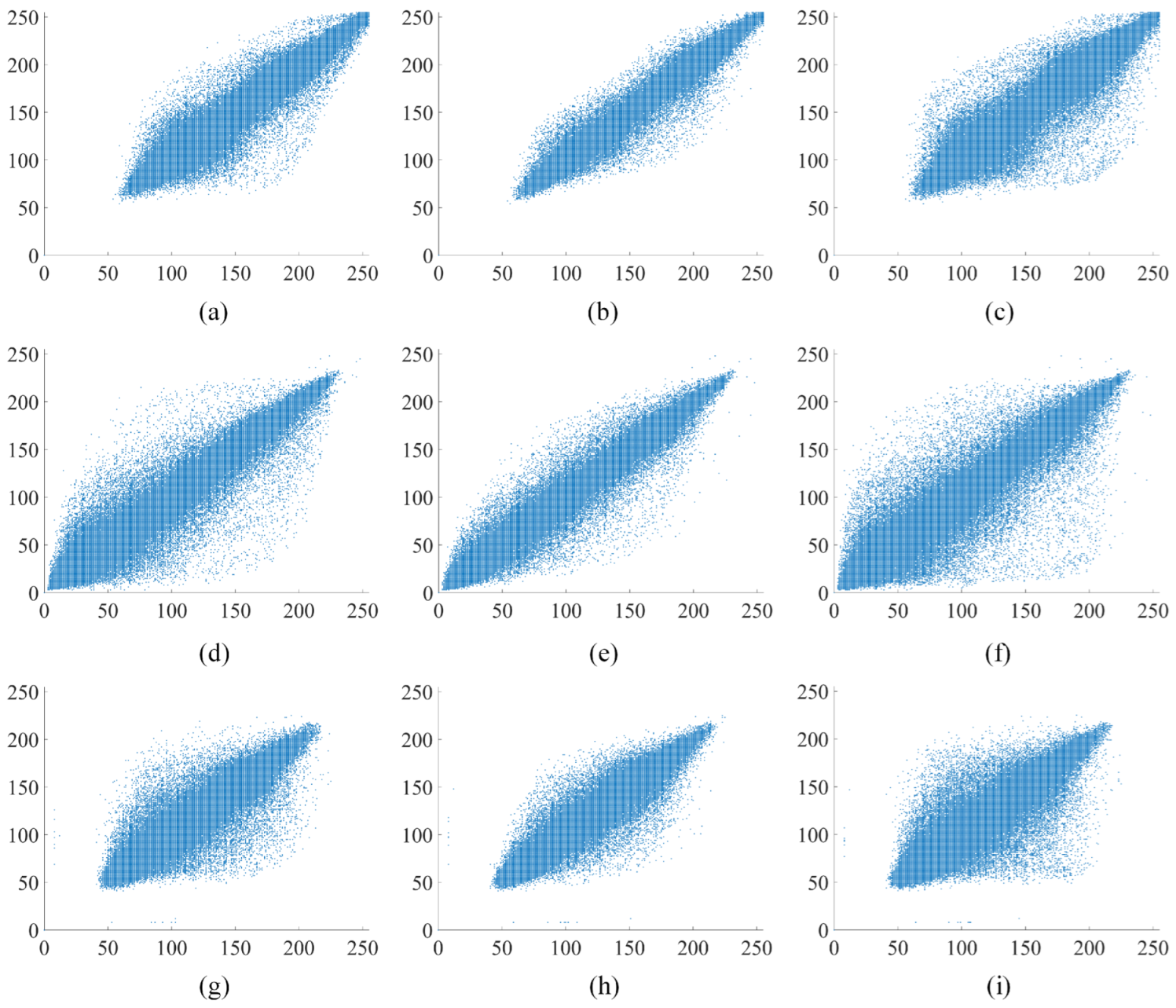
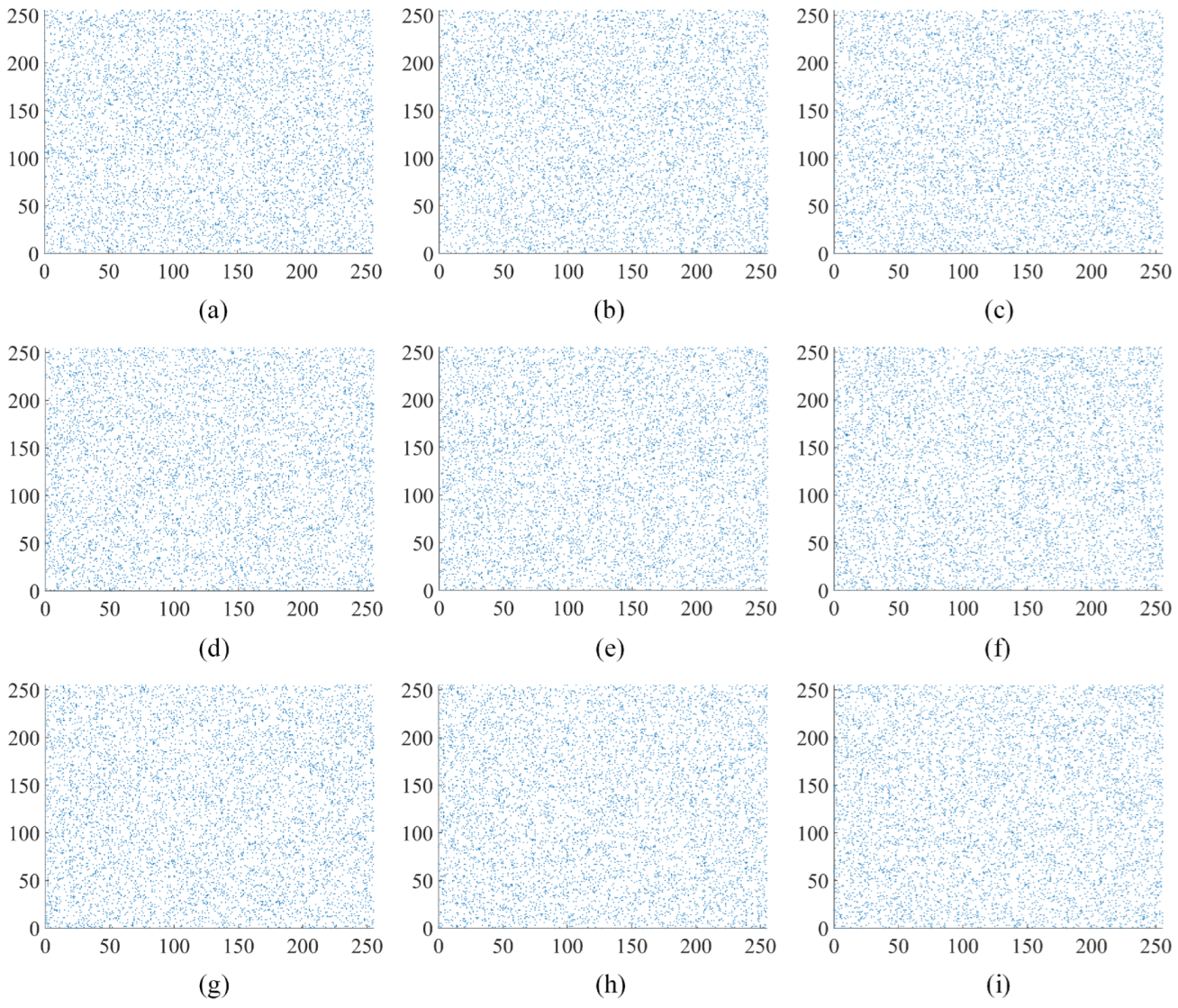
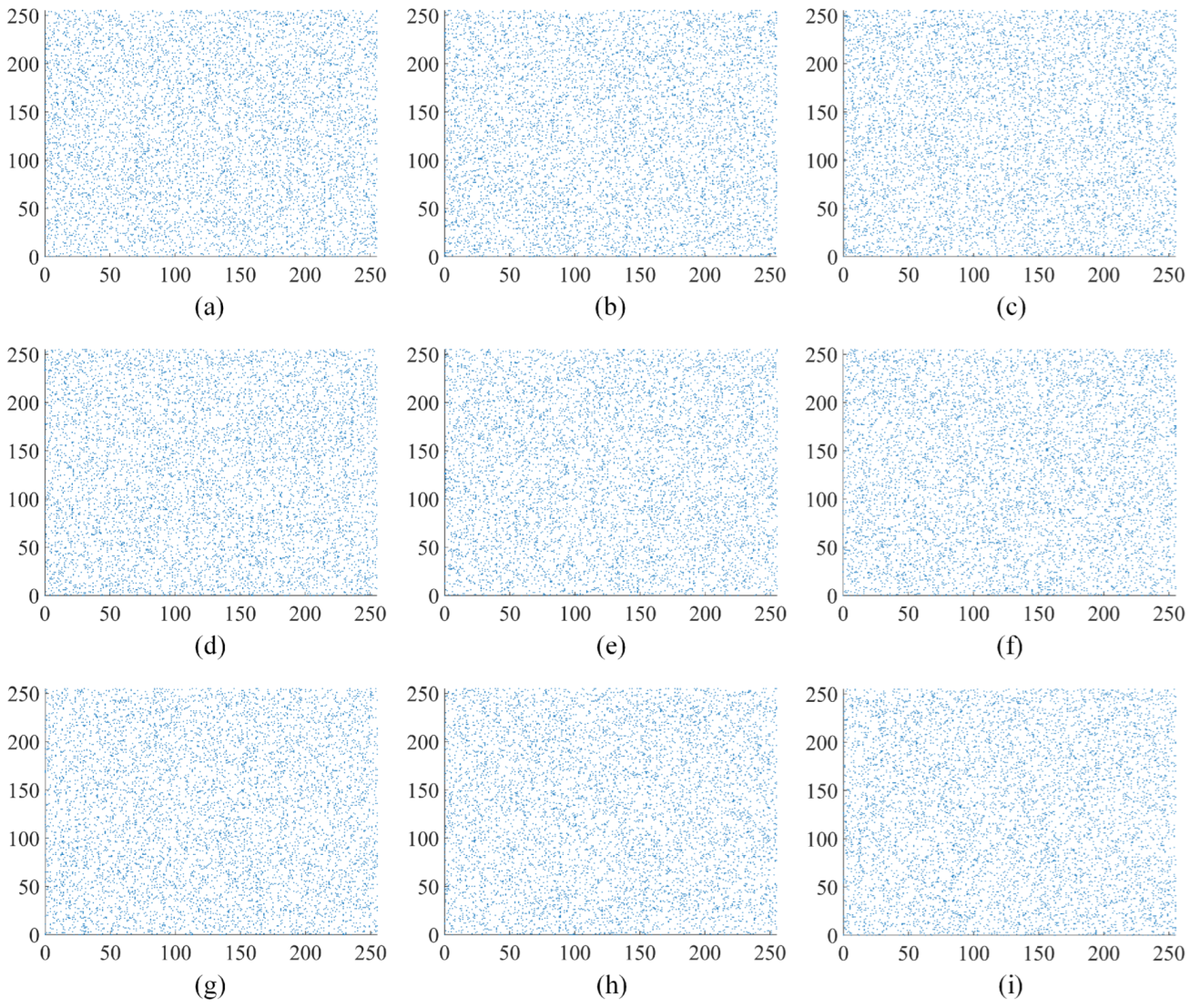
The analysis of pixel correlations in the image is performed in vertical, horizontal, and diagonal directions using the image “Apartment” as an example. The original “Apartment” image, the first round encryption of the “Apartment” image, and the second round encryption of the “Apartment” image are depicted in Figure 9, Figure 10 and Figure 11, respectively. Figure 10 and Figure 11 illustrate the outcomes of selecting every sixth point at regular intervals. The original “Apartment” image, as shown in Figure 9, exhibits a high degree of correlation among pixels in the vertical, horizontal, and diagonal orientations, with a predominant alignment along the $y=x$ line. Conversely, Figure 10 and Figure 11 reveal that pixel points of the encrypted “Apartment” image are dispersed throughout the entire image area, indicating a diminished correlation between pixels. The comparison highlights a significantly reduced correlation between pixels in the encrypted “Apartment’ image’. This prevents attackers from reconstructing the original image by analyzing the relationships between pixels.

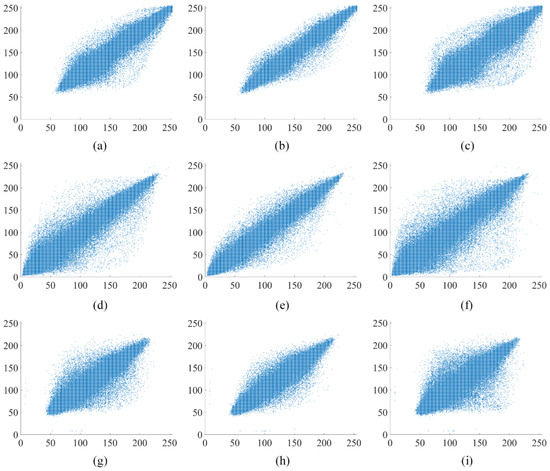
Figure 9. Analysis of correlation in the original “Apartment” image: (a) the horizontal orientation within red channel of “Apartment”; (b) the vertical orientation within red channel of “Apartment”; (c) the diagonal orientation within red channel of “Apartment”; (d) the horizontal orientation within green channel of “Apartment”; (e) the vertical orientation within green channel of “Apartment”; (f) the diagonal orientation within green channel of “Apartment”; (g) the horizontal orientation within blue channel of “Apartment”; (h) the vertical orientation within blue channel of “Apartment”; (i) the diagonal orientation within blue channel of “Apartment”.

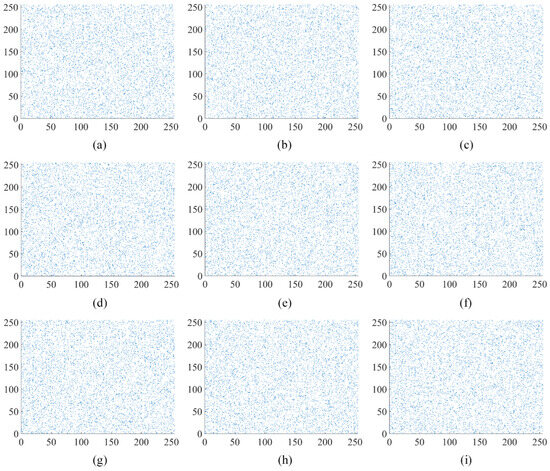
Figure 10. Analysis of correlation after the first round of encryption in “Apartment”: (a) the horizontal orientation within red channel of “Apartment”; (b) the vertical orientation within red channel of “Apartment”; (c) the diagonal orientation within red channel of “Apartment”; (d) the horizontal orientation within green channel of “Apartment”; (e) the vertical orientation within green channel of “Apartment”; (f) the diagonal orientation within green channel of “Apartment”; (g) the horizontal orientation within blue channel of “Apartment”; (h) the vertical orientation within blue channel of “Apartment”; (i) the diagonal orientation within blue channel of “Apartment”.

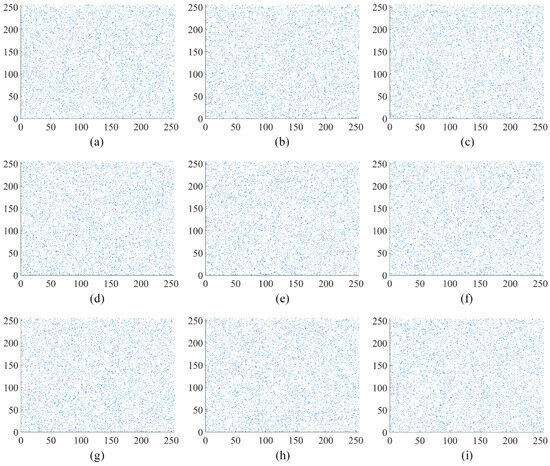
Figure 11. Analysis of correlation after the second round encryption in “Apartment”: (a) the horizontal orientation within red channel of “Apartment”; (b) the vertical orientation within red channel of “Apartment”; (c) the diagonal orientation within red channel of “Apartment”; (d) the horizontal orientation within green channel of “Apartment”; (e) the vertical orientation within green channel of “Apartment”; (f) the diagonal orientation within green channel of “Apartment”; (g) the horizontal orientation within blue channel of “Apartment”; (h) the vertical orientation within blue channel of “Apartment”; (i) the diagonal orientation within blue channel of “Apartment”.

5.5. Information Entropy Analysis

Information entropy is frequently used in image encryption to measure the amount of uncertainty related to information. Within image encryption, entropy is a measure of the disorder of image pixels. Enhanced encryption performance is typically associated with a higher level of disorder among pixels in the encrypted image. Consequently, in image encryption, information entropy of an encrypted image is expected to closely approach the maximum value, which is 8 [57]. Information entropy can be determined using the subsequent equation:

$$\begin{array}{c}\hfill H\left(X\right)=-\sum _{i=1}^{n}p\left(x_i\right){log}_{2}p\left(x_i\right)\end{array}$$

(11)

In Equation (11), $H\left(X\right)$ represents the information entropy of the random variable X. The probability $p\left(x_i\right)$ represents the probability of the random variable X assuming the value $x_i$. Table 6 compares the information entropy of original and encrypted images for eight images, showing that the information entropy of the encrypted images closely approximates the expected theoretical value. Table 7 contrasts the information entropy of encrypted images utilizing various encryption methods. The information entropy associated with the proposed encryption scheme aligns closely with the optimal value of 8, surpassing the outcomes of other encryption methods. Consequently, the proposed encryption scheme is deemed to possess a high level of security.

Table 6. Information entropy of eight images.

Image	Original Image	1st Round Encrypted	2nd Round Encrypted	Ideal Value
Monkey	7.1073	7.9998	7.9998	8
Radar	7.5787	7.9998	7.9998	8
Ice	7.3983	7.9997	7.9997	8
Apartment	7.4858	7.9998	7.9998	8
Lake	7.7622	7.9998	7.9998	8
spatter	7.2428	7.9998	7.9998	8
Earth	7.3983	7.9997	7.9997	8
Jetplane	6.6639	7.9997	7.9997	8

Table 7. Comparison in terms of information entropy.

Encryption Scheme	Information Entropy
Proposed Encryption Scheme	7.9998
Reference [35]	7.9993
Reference [58]	7.9993
Reference [50]	7.9821
Reference [48]	7.9971
Reference [59]	7.9966

5.6. Key Sensitivity Analysis

The term “key sensitivity” refers to the phenomenon where slight alterations in the initial key can result in notable variations in the keys produced by the iterative function. A minor adjustment in the key can lead to a substantial transformation in encrypted images. Key sensitivity is a crucial feature in image encryption to guarantee data security, and it is used to assess the importance of an encryption scheme.

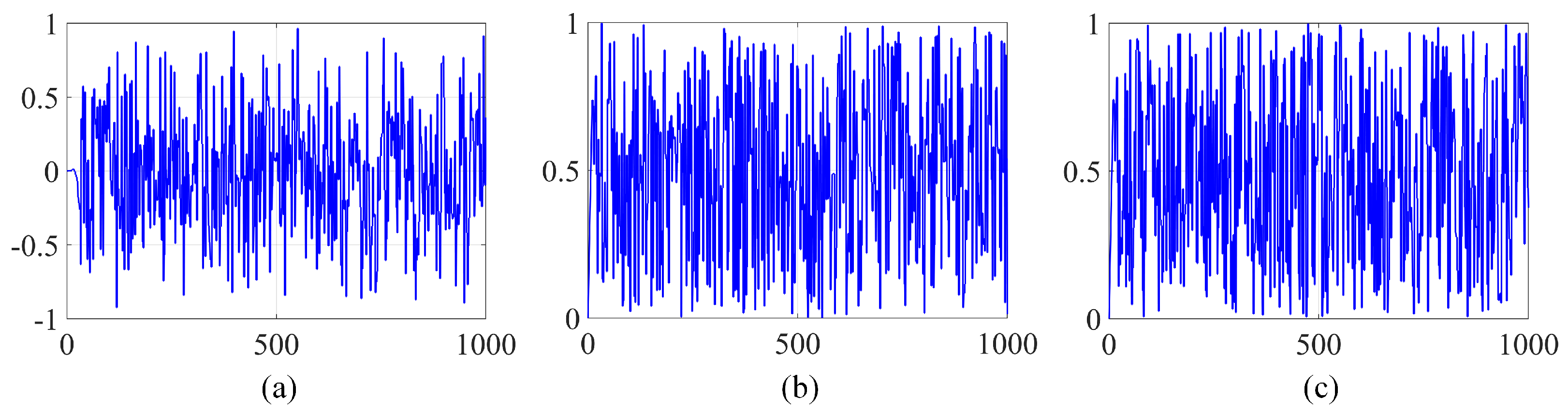
In order to illustrate the importance of sensitivity, we conducted an experiment where we encrypted an image using keys that were only slightly different. Specifically, we introduced a minute increment of ${10}^{-14}$ to the original key during this process. Figure 12 illustrates the waveform for c in Equation (3) and $c+\Delta c$, along with their changing difference over time. After subtracting images encrypted with different keys, it is apparent from the data presented in Figure 13 that the resulting images display significant differences.

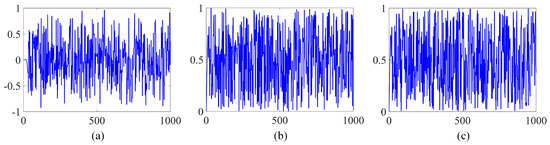
Figure 12. (a) the value of $\Delta c$; (b) the value of $c+\Delta c$; (c) the value of c.

Figure 13. Analysis of key sensitivity: (a) the discrepancy within red channel; (b) the discrepancy within green channel; (c) the discrepancy within blue channel; (d) the discrepancy within three channels.

Key sensitivity analysis in image encryption schemes is commonly assessed using two main metrics: NPCR and UACI. The two metrics are crucial in evaluating the effectiveness and robustness of image encryption methods. These metrics are formally defined as part of the evaluation process. These indicators are defined as [60]:

$$\begin{array}{cc}\hfill \mathbf{NPCR}& =\frac{1}{N\times M}\sum _{i=1}^N\sum _{j=1}^M{\delta }_{i,j}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \mathbf{UACI}& =\frac{1}{255\times N\times M}\sum _{i=1}^N\sum _{j=1}^M|E_{i,j}-F_{i,j}|\hfill \end{array}$$

(13)

The variables M and N correspond to the width and height of the image, and ${\delta }_{i,j}$ signifies the alteration in pixel intensity at coordinates $(i,j)$. $E_{i,j}$ is the pixel value of the original image at the coordinates $(i,j)$, while $F_{i,j}$ is the pixel value of the encrypted image at the same location.

The theoretical values for UACI and NPCR are reported as 33.4635% and 99.6043%, respectively [61]. The results presented in Table 8 and Table 9 demonstrate a high level of concordance with the theoretical values, suggesting robust key sensitivity in the proposed encryption scheme.

Table 8. Analysis of the key sensitivity in terms of NPCR.

Image	NPCR (%) Ideal Value: 99.60
	R	G	B
Monkey	99.5972	99.5983	99.6029
Mountain	99.6017	99.6075	99.6159
Boat	99.6006	99.5960	99.5972
Apartment	99.6132	99.6143	99.6044
Lake	99.5953	99.6071	99.6140
spatter	99.5934	99.5934	99.6086
Earth	99.5934	99.6123	99.5934
Jetplane	99.6140	99.6158	99.6075

Table 9. Analysis of the key sensitivity in terms of UACI.

Image	UACI (%) Ideal Value: 33.46 (%)
	R	G	B
Monkey	33.4656	33.4756	33.4610
Mountain	33.4671	33.4670	33.4788
Boat	33.4581	33.4607	33.4779
Apartment	33.4675	33.4680	33.4658
Lake	33.4721	33.4619	33.4553
spatter	33.4695	33.4635	33.4720
Earth	33.4643	33.4529	33.4711
Jetplane	33.4677	33.4611	33.4769

5.7. Differential Attack

Differential attack refers to an attack method that utilizes the differences between pixels in an image to crack the encryption scheme. Aiming to mitigate risks of differential attacks, robust encryption methods should demonstrate a heightened response to variations in plaintext. Even a slight alteration in the pixel values of the original image can cause significant changes in a generated encrypted image. In this study, encryption was performed by adjusting the top-left corner pixel value in the original image “Boat”. The analysis revealed a notable difference between the resulting encrypted “Boat” image and the original encrypted “Boat” image. The outcomes are illustrated in Figure 14.

Figure 14. Analysis of differential attack: (a) the difference within red channel; (b) the difference within green channel; (c) the difference within blue channel; (d) the difference within three channels.

The NPCR and UACI of differential attacks are detailed in Table 10 and Table 11, respectively. Table 12 compares the UACI and NPCR values calculated from the proposed encryption scheme with those obtained from other encryption schemes. The NPCR and UACI values presented in Table 10 and Table 11 closely approximate the ideal values, indicating that the proposed encryption scheme is proficient in mitigating against differential attacks.

Table 10. Analysis of the differential attack in terms of NPCR.

Image	NPCR (%) Ideal Value: 99.60
	R	G	B	Average
Monkey	99.5998	99.5961	99.6127	99.6029
Radar	99.5930	99.6177	99.6159	99.6089
Ice	99.6181	99.6071	99.6147	99.6133
Apartment	99.6155	99.6044	99.6108	99.6102
Lake	99.6113	99.6189	99.6075	99.6126
spatter	99.6181	99.6132	99.6059	99.6124
Earth	99.6197	99.6168	99.5964	99.6110
Jetplane	99.6154	99.6107	99.5995	99.6085

Table 11. Analysis of the differential attack in terms of UACI.

Image	UACI (%) Ideal Value: 33.46
	R	G	B	Average
Monkey	33.4645	33.4675	33.4741	33.4687
Radar	33.4694	33.4647	33.4638	33.4660
Ice	33.4727	33.4637	33.4728	33.4697
Apartment	33.4692	33.4623	33.4751	33.4689
Lake	33.4638	33.4687	33.4747	33.4691
spatter	33.4637	33.4698	33.4742	33.4692
Earth	33.4786	33.4765	33.4781	33.4777
Jetplane	33.4665	33.4673	33.4673	33.4670

Table 12. Comparison of NPCR and UACI in terms of differential attack.

Encryption Scheme	NPCR (%)	UACI (%)
Proposed Encryption Scheme	99.6100	33.4695
Reference [35]	99.6065	33.4595
Reference [55]	99.5320	33.4500
Reference [62]	99.5855	30.3873

5.8. Cropping Attack

During the data transfer process, the encrypted image may become corrupted. A robust encryption scheme should be capable of withstanding partial data loss during transmission. If the encrypted image is partially damaged, an excellent encryption should recover the image as much as possible through decryption [63].

Figure 15 illustrates that even with data loss rates of 12.5%,12.5%, 25%, 37.5%, 50%, and 62.5%, the images that have been decrypted exhibit a strong resemblance to the original image, effectively preserving important information. The results indicate that the encryption scheme is capable of withstanding cropping attacks.

Figure 15. Analysis of cropping attacks in four different images.

5.9. Comparison with Existing Methods

In this section, a thorough evaluation is carried out to compare the proposed encryption scheme with current encryption schemes, focusing on aspects related to security and application scenarios.

In the realm of security, the encryption scheme in this paper is evaluated in comparison to established encryption schemes by examining factors such as information entropy, correlation coefficient, key space, UACI, and NPCR. The encryption scheme demonstrates superior performance, as evidenced by the preceding evaluation and comparison.

The encryption scheme is applicable to the medical field, as evidenced by Liu et al. in their utilization of a chaos-based encryption method for medical images [64]. Encryption schemes intended for medical applications are required to adhere to specific criteria, such as ensuring robust security measures and maintaining data integrity. The proposed encryption scheme exhibits potential for application in medical contexts, as indicated by the assessment of factors including histograms, key space, key sensitivity, and pixel correlation.

6. Conclusions

In this study, a novel color image encryption scheme that employs a 4D hyperchaotic system is presented. The scheme involves the generation of four chaotic sequences for two encryption rounds, thereby enhancing the pseudorandomness and unpredictability of the encrypted images. The hyperchaotic system utilized in this method outperforms low-dimensional chaotic systems in terms of key space efficiency. Moreover, in comparison to existing encryption methods, the proposed scheme offers a larger key space, thereby improving its resistance against both differential and cropping attacks. Evaluation metrics, including entropy, pixel correlation, NPCR, and UACI values, demonstrate a close alignment of the encrypted images with ideal values. The encryption scheme demonstrates notable effectiveness in preserving the security of color images.