Abstract
An integrated energy system (IES) plays a key role in transforming energy consumption patterns and solving serious environmental and economic problems. However, the abundant optional schemes and the complex coupling relationship among each piece of equipment make the optimization of an IES very complicated, and most of the current literature focuses on optimization of a specific system. In this work, a simulation-based two-step decoupling method is proposed to simplify the optimization of an IES. The generalized IES is split into four subsystems, and a two-layer optimization method is applied for optimization of the capacity of each piece of equipment. The proposed method enables fast comparison among abundant optional configurations of an IES, and it is applied to a hospital in Beijing, China. The optimized coupling system includes the gas-fired trigeneration system, the GSHP, and the electric chiller. Compared with the traditional distributed systems, the emission reduction rate of CO2 and NOX for the coupling system reaches 153.8% and 314.5%, respectively. Moreover, the primary energy consumption of the coupling system is 82.67% less than that of the traditional distributed energy system, while the annual cost is almost at the same level.
1. Introduction
Serious environmental and economic problems have been caused by the overconsumption of fossil fuels, and the transformation of energy consumption patterns has been promoted for the past decade [1,2,3,4,5]. Compared with traditional energy systems, an integrated energy system (IES) has obvious advantages in terms of improving energy utilization efficiency and reducing pollution emission [6,7,8,9]. It couples various forms of energy into a single system and usually incorporates energy generation, conversion, distribution, and consumption sectors. Acting as a significant part in the future energy system, it can also improve the economic benefits of the energy system [10,11,12,13].
To achieve an efficient performance of an IES, the system design should be conducted with care during the planning stage. The modeling of an IES is the first step to solving the design problem, which acts as a basis of quantifying energy flow between various devices [14,15]. Abundant research has focused on modeling IESs [16,17,18,19,20,21,22]. Qin et al. proposed a matrix modeling method based on graph theory for multi-energy flows of IESs [23]. Similarly, an energy internet model was proposed by Sun et al., coupling power, gas, and thermal networks, and an extended Newton–Raphson method was adopted to calculate multi-energy flow [24]. Moreover, Qin et al. proposed a generalized quasi-dynamic model for electric–heat coupling integrated energy systems which considered the heat dynamic process, the meshed network topology, multiple DERs, and variable mass flow simultaneously [25]. The above studies applied the Energy Network Theory, which is usually applied in an IES at the regional level. For community or district levels, where an IES is located close to users, the energy transmission limits can be neglected because of short-distance transmission. In this case, the energy flows in an IES can be modeled with the concept of an energy hub (EH) [26,27]. This method can model the distribution, transformation, and storage of various types of energy flows, as well as the coupling relationship among all devices throughout the system [28,29,30,31,32]. For a specific integrated system, the working condition of each component and the relationship between the energy input and output at a given moment can be calculated by applying the matrix equation corresponding to the system and the mathematical models of each component in the system [33,34].
Transient simulation, which enables the comparison of a large number of optional schemes for an IES with less time and labor, applies this concept [35,36,37,38]. For example, to better analyze the nearly zero-energy buildings, Ferrara et al. proposed an optimization method based on simulation, in which the TRNSYS simulation platform and the GenOpt optimization program are coupled [39]. It is validated that such a method is suitable for dealing with the configuration design problem for an IES. Moreover, another important advantage of transient simulation is that the dynamic working conditions of each component in the system can be modeled accurately. The meteorological parameters and the energy demands change continuously in reality, which means the loads also change all the time [40]. The transient simulations can model the changes in energy loads and facilitate the solution of the dynamic balance between supply and demand at each time point. Therefore, the results obtained by using this method are more accurate.
System optimization is a key issue in designing an IES. Many scholars have conducted research on the optimization problem for a specific IES [41,42,43,44,45,46,47,48]. For example, Wu et al. presented a mixed linear programming model of an IES with electricity and hot water interchanges, and the robustness of the optimization model was validated by a low-carbon community [41]. In addition, Mohammad et al. proposed a mixed-integer linear programming model to determine the optimal capacity of each component in various systems [49]. Furthermore, some algorithms, including the genetic algorithm and particle swarm optimization, have been proposed and improved, and the optimization efficiency has been promoted [50,51,52,53,54].
However, such investigations focus on specific energy systems and do not consider the configuration design. The involvement of energy generation units, energy transmission units, energy storage units, and energy utilization units causes the configuration design of an IES to become an extremely complex problem [55,56]. The system’s configuration is usually diversified, which makes it difficult to design the configuration of an IES in the most appropriate way [57,58]. In addition, the complex coupling relationship among system components makes it more complicated. For example, the electric chiller that generates cooling energy operates based on the power obtained from the main grid or the distributed power equipment. Furthermore, the absorption chiller uses the heat generated from equipment like gas turbines. Although the novel optimization algorithms have promoted the optimization efficiency, the optimization problem of an IES is still far from being well addressed.
In this work, a two-step decoupling method is proposed to solve the optimization problem. A generalized IES structure is established, and it is decoupled by splitting it into four subsystems, including a gas-fired trigeneration subsystem, a heating subsystem, a cooling subsystem, and a power subsystem. The relationship among the four subsystems is established through transfer functions written by MATLAB 2022. In this way, the optional schemes for an IES can be preliminarily screened out based on external conditions, such as meteorological parameters, geological conditions, resource distributions, and so on. Then, for a specific IES, a two-layer optimization method is combined with transient simulation to determine the capacity of each piece of equipment. As the trigeneration subsystem provides heat, cooling, and power at the same time, it is strongly coupled with other subsystems. Therefore, the capacity of the gas turbine is taken as the first layer of the optimization variable. For each case of the gas turbine’s capacity, the heating load, cooling load, and electricity load are adjusted on the basis of the amount of energy that can be provided by the gas turbine. Then, the capacity of other pieces of equipment in the other three subsystems are optimized. In this way, the system is decoupled and the complicated optimization problem of an IES is largely simplified.
This paper is organized as follows. In Section 2, a generalized IES is established and split into four subsystems that are coupled with each other. The model of each subsystem is established for transient simulation. Then, the two-layer optimization method is introduced. In Section 3, a specific IES in Beijing, China, is analyzed based on the proposed method. In Section 4, some conclusions are presented which can give a better understanding of the content and innovation of our research.
2. Materials and Methods
2.1. The Decoupling of a Generalized Structure of an IES
A typical model of an integrated energy system usually consists of many interconnected source, load, and storage nodes. Energy sources, including solar energy, biomass energy, natural gas, and electricity, enter the system and are converted to user-demanded energy, such as heat, cooling, and electricity. Modeling an integrated energy system is the basis for the optimization of the system’s configuration and operation mode. A generalized structure of a grid-interactive integrated energy system is established, as shown in Figure 1.
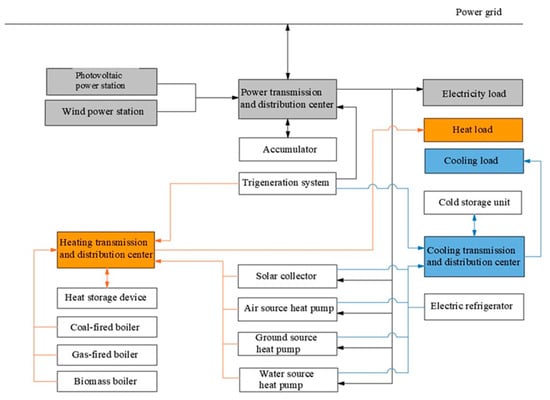
Figure 1.
A generalized structure of a grid-interactive integrated energy system.
It is illustrated that the heat distribution center, cooling distribution center, and power distribution center coexist in this generalized structure. Heat input into the heat distribution center can be provided by various forms of energy sources, including a gas-fired trigeneration system, various types of boilers, various types of heat pumps, a solar energy collector, and heat storage equipment. The output of the center is connected to the heating load as well as to the heat storage equipment. Similarly, the cooling input entered into the cooling distribution center can be supplied from a gas-fired trigeneration system, electric chiller, and various types of heat pumps. At the same time, the output is connected to the cooling load and the cooling storage system. In addition, electricity input into the power distribution center can be provided by a gas-fired trigeneration system, cogeneration system, photovoltaic power, wind power, electricity storage equipment, as well as a power grid. Additionally, electricity provided by the center is distributed to the electricity load, various types of heat pumps, the electric chiller, the electricity storage equipment, and the power grid.
This generalized structure of a grid-interactive integrated energy system considers many types of energy supply equipment and energy conversion equipment. In order to simplify the coupling relationship among each component, the generalized structure is split into four subsystems that are coupled together, including a gas-fired trigeneration subsystem, a heating subsystem, a cooling subsystem, and a power subsystem. Additionally, the coupling relationship among subsystems is established by using MATLAB software (version 2022).
A schematic illustration of the gas-fired trigeneration system is shown in Figure 2. A typical form of the system includes a combustion gas turbine, an electric generator, a heat recovery steam generator (HRSG), an absorption chiller, and a gas/water heat exchanger. The residual heat from the exhaust gas is used to drive the absorption chiller and provide cooling energy in summer, while it generates the heating load in winter by using the gas/water heat exchanger.
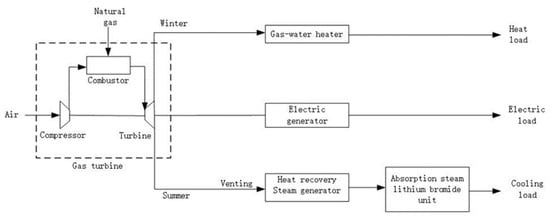
Figure 2.
A schematic illustration of the gas-fired trigeneration system.
Moreover, the heating system is displayed in Figure 3. This subsystem considers various heat sources, except the exhaust heat produced by the gas-fired trigeneration system. In this heating system, the solar collector is connected to the water tank, and hot water provided by the tank is directly transported to the heat user if the water temperature satisfies the user’s demand; otherwise, it is transported into the inlet of the other heat source equipment, including the ASHP, GSHP, SSHP, and biomass boiler. The low-temperature water from the tank will be further heated in the equipment and then provided to the heat user. In this case, the storage temperature can be maintained at a low level to improve energy efficiency.
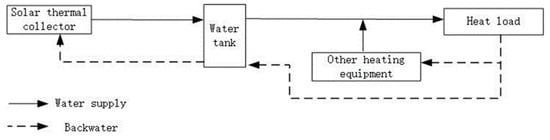
Figure 3.
A schematic illustration of the heating system.
Furthermore, a schematic illustration of the cooling system is shown in Figure 4. This subsystem includes different kinds of cooling equipment, except cooling provided by an absorption chiller within the gas-fired trigeneration system. The equipment that can be used in this subsystem includes an electric chiller and various types of heat pumps. The chiller and heat pumps are usually connected in parallel to the system.
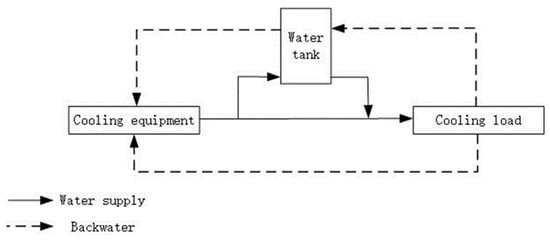
Figure 4.
A schematic illustration of the cooling system.
In addition, Figure 5 demonstrates the electric subsystem, which mainly considers photovoltaic power, wind power, and the power grid as optional power sources, in contrast to the trigeneration system. In some cases, the system needs to be equipped with an AC/DC inverter for AC users.
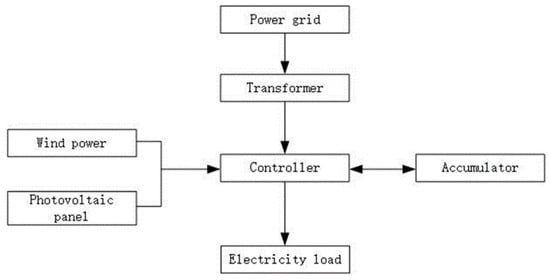
Figure 5.
A schematic illustration of the electric system.
These four subsystems can be established on the TRNSYS platform separately. Then, the coupling relationship among the subsystems is represented by transfer functions, which are written by using MATLAB software (version 2022). In order to simplify the coupling relationship between the heating system and the cooling system, some equipment can both exist within the heating and cooling systems, such as heat pumps and water tanks. It should be noted that they are actually the same equipment, and they should not be counted twice when calculating investment in the optimization process.
2.2. Mathematical Models of the Subsystems
The mathematical models of the four subsystems are established, which is the basis for transient simulation. For the gas-fired trigeneration subsystem, the mathematical model of the gas turbine can be established based on the relationship between the generated electricity and the exhaust heat from the discharged smoke. The generated electricity from the gas turbine can be calculated by Equation (1) as follows:
where EGE,i represents the electricity generated by the gas turbine at time i, kJ/h; GGE,i denotes the calorific value of natural gas at time i, kJ/h; ηGE,i is the efficiency of the gas turbine at time i.
The exhaust heat from the discharged smoke is calculated by Equation (2) below:
where represents the exhaust heat from the discharged smoke at time i, kJ/h; ηRE,i is the recovery efficiency of the gas turbine at time i. In addition, the generated electricity is calculated by Equation (3):
where Tm,i represents the outdoor dry bulb temperature at time i, °C.
For the heating subsystem and the cooling subsystem, the commonly used equipment include the solar thermal collector, heat pumps, and various types of boilers. For the solar thermal collector, the Hottel–Whillier equation is used to calculate the solar collector efficiency, as shown in Equation (4):
where A is the total area of the collector array, m2; FR is the total thermal efficiency factor of the collector; IT is the total radiation of the solar collector, kJ/(H·m2); m is the flow rate under the operating conditions, kg/h; Ta is the ambient temperature, °C; Ti is the inlet temperature of the collector, °C; UL is the total heat loss coefficient per unit area of the collector, kJ/(h·m2·K); α is the shortwave absorptivity of the heat-absorbing plate; τ is the shortwave transmittance of the collector; and τα is the shortwave transmittance of the collector in the vertical incidence of the sun.
For the air-source heat pump (ASHP), the actual heating load can be calculated by Equation (5):
where m is the water flow of heat pump, kg/h; cP is the specific heat capacity of water, taken as 4.190 kJ/(kg × K). In addition, the heating load and the power consumption are used to calculate the actual COP, as shown in Equation (6):
where COPC is the COP under nominal working conditions; COPr is the ratio of the COP on the performance curve provided by the manufacturer to the COP under nominal working conditions; CAPC is the heating capacity under nominal working conditions; CAPr is the ratio of the heating capacity on the performance curve provided by the manufacturer to the heating capacity under nominal working conditions; Fflp is the ratio of the partial load rate to the rated power of the equipment.
For the ground-source heat pump (GSHP), the heat transfer of the ground heat exchanger is analyzed by the heat conduction model, which is regarded as cylinder in numerical calculations. The two-dimensional non-steady-state heat conduction differential equation is shown in Equation (7) below:
where, is the thermal diffusivity m2/s; k represents the soil thermal conductivity w/(k·m); is the geothermal specific heat J/(m3·k). Usually, the finite control volume method can be applied to solve the above equation.
For the boilers, the output power can be calculated by Equation (8):
where QB,i is the output power of the boiler at time i, kW; ηB is the thermal efficiency of the boiler; ηC is the combustion efficiency of the fuel; Qf,i denotes the calorific value of the fuel at time i, kJ.
For the power subsystem, the output power of the photovoltaic panel can be calculated by Equation (9):
where PPV denotes the output power of the photovoltaic panel, kW; fPV represents the power derating factor, taken as 0.9; PPV,R is the peak output power of the photovoltaic panel, kW; GT is the actual illuminance, kW/m2; GT,STC denotes the illuminance under the standard condition, commonly taken as 1 kW/m2; αP is the temperature power coefficient, %/°C; Tcell is the surface temperature of the photovoltaic panel, °C; and Tcell,STC represents the surface temperature of the photovoltaic panel under the standard condition, and it is usually taken as 25 °C.
For the wind turbine, the output power can be calculated by Equation (10):
where PWT(vi) is the output power of the wind turbine when the wind speed is vi, kW.
2.3. A Two-Layer Optimization Method
For a specific IES, transient simulation is combined with a two-layer optimization method to determine the capacity of each piece of equipment in the system. The TRNSYS modeling platform is powerful for conducting transient simulation of an energy system. The operation mode should be preset before transient simulation. Commonly, if the gas-fired trigeneration system is selected, the capacity of the gas turbine can be determined either by the maximum heating load or the maximum electricity load. The operation mode of the former case is called “following the heating load mode”, while the latter is called “following the power load mode”. In this study, the “mixed mode” is applied, indicating that the capacity of the gas turbine is not preset to meet any type of load, instead, it is also determined through optimization. Therefore, the generated electricity could exceed the required load. Since the integrated energy system is usually grid-interactive, the electricity generated by the gas turbine can be transmitted to the grid.
As the trigeneration system is energy-efficient, the gas turbine is operated in a highly efficient operating range in each case. Then, the operation strategies of other subsystems should be determined. The sequence of each piece of equipment for the subsystems is determined by the operating cost. For the heating subsystem, cooling subsystem, and power subsystem, the sequence of operation for all possible pieces of equipment is listed in Table 1 below.

Table 1.
The sequence of operation for the equipment in the three subsystems.
The priority of the biomass boiler and the ASHP is the same in most cases. However, the performance of the ASHP varies as the outdoor temperature changes, and the priority of these two pieces of equipment should be determined based on the actual operation cost.
Then, a two-layer optimization method is applied. As the trigeneration subsystem provides heat, cooling, and power at the same time, it is strongly coupled with the other subsystems. Therefore, the capacity of the gas turbine is taken as the first layer of the optimization variable. For each case of the gas turbine’s capacity, the heating load, cooling load, and electricity load are adjusted based on the amount of energy that can be provided by the gas turbine. Then, the energy balance between the residual loads and the energy provided by the other subsystems is taken as the constraint for the optimization process. The constraints are listed in Equations (11)–(14):
where Qres,h, Qres,c, and Qres,e represent the residual heat load, cooling load, and electricity load, respectively. Qh,i, Qc,i, and Qe,i denote the actual heating power, cooling power, and electric power of the i-th piece of equipment, respectively. In addition, Qequ,i indicates the actual power of the i-th piece of equipment, and Qequ,c denotes the rated power of the i-th piece of equipment. It should be noted that the above constraints only consider energy balance and the limitation of the equipment capacity; in some practical cases, more constraints should be considered. For example, if the accommodation space for a gas turbine is limited, there should be a constraint of the gas turbine’s capacity.
Moreover, for the objective optimization function, many factors should be taken into account, including economy, energy consumption, and pollutant emissions. The objective optimization function is denoted as F, which is obtained from the weighted summation of the annual cost-saving rate, primary energy-saving rate, and shadow cost-saving rate of environmental pollutants. The objective optimization function can be calculated by Equation (15) as follows:
where M1, M2, and M3 represent the annual cost-saving rate, primary energy-saving rate, and shadow cost-saving rate of environmental pollutants, respectively. α, β, and γ represent the weighting coefficients of the three factors. Taking the equipment capacity as the optimization variable, optimization can be achieved under the constraint of power balance. M1 can be calculated by Equations (16)–(20) as follows:
where ATC is the annual cost, yuan; Cc is the annualized value of investment of each piece of equipment, yuan; Cf is the operation cost of the IES, yuan; Cm is the annual maintenance cost of the IES, yuan; P is the total investment, yuan; i is the annual interest rate, 6.5%; n is the operating life, 20 years; cg is the price of the natural gas, yuan/m3; VGE,i is the natural gas consumed by the gas turbine, m3; VGB,i is the natural gas consumed by the gas boiler, m3; ce,sell is the feed-in tariff, yuan/kWh; ce,buy is the power purchase price, yuan/kWh; is the proportionality coefficient, which is taken as 0.03; ATCX is the annual cost of the IES; and ACT0 is the annual cost of a benchmark system.
The primary energy consumption of the system is the sum of the primary energy converted from the power consumption, gas consumption, coal consumption, and biomass consumption. M2 can be calculated by Equations (21) and (22):
where PEC is the primary energy consumption of the IES, kJ; ηgrid,i is the average power supply efficiency of a power plant, which is taken as 0.92; CVg is the calorific value of natural gas, taken as 35,588 kJ/m3; CVc represents the calorific value of coal, and it is taken as 16,743 kJ/kg; mBB,i is the biomass consumption at the time i, kg/h; ηe is the transmission efficiency of the grid, taken as 0.35; PECX and PEC0 represent the PEC value of the IES and the benchmark system, respectively.
It is known that an IES could generate various environmental pollutants, including CO2, NOX, and SO2. Since different pollutant emissions have different impacts on the environment, a unified standard is needed to evaluate the environmental impacts caused by various pollutants. The shadow cost is adopted in this study to quantify the impact of various pollutants. This indicator means the cost of treating the emitted pollutants. In this way, the impacts of different pollutants can be quantified and compared. The shadow cost of environmental pollutants can be calculated by Equations (23) and (24) as follows:
where PSC represents the shadow cost of environmental pollutants, yuan; TC is the shadow cost of CO2, yuan/t; CDE is the emission amount of CO2, t; TN is the shadow cost of NOX, yuan/t; NOE is the emission amount of NOX, t; TS is the shadow cost of SO2, yuan/t; SOE is the emission amount of SO2, t. PSCX and PSC0 denote the PSC value of the IES and the benchmark system, respectively. The values of TC, TN, and TS are taken as 20.83, 8006.84, and 7843.16, respectively.
In order to consider the environmental impacts caused by the IES, the amount of various pollutant emissions produced by the IES should be calculated accurately. The power emission factor is introduced to link the amount of pollutant emissions and the generated electricity. If the generated electricity exceeds the load, the extra electricity will be transmitted to the grid; in this case, the environmental impacts caused by the on-grid electricity should not be counted.
Moreover, the sources of CO2 emissions of an IES mainly include the burning of coal and gas, the power obtained from the grid, as well as the leakage of the refrigerating fluid [59]. The calculation of the CDE of an IES is shown in Equation (25):
where CDE is the CO2 emission amount, t; VANG is the natural gas consumption each year, GJ/a; CENG denotes the emission coefficient of natural gas, taken as 58.5 kg/GJ; CMEF is the emission coefficient of methane, taken as 1.4 kg/TJ; CNEF denotes the N2O emission coefficient, taken as 2.3 kg/TJ. EGWP, CH4 and EGWP, MN denote the global warming potential of methane and N2O, respectively. The values are 21 and 310, respectively. In addition, CMLR is the leakage rate of methane, taken as 0.3 kg/GJ; θ denotes the power loss and its value can be taken as 8%; Cefy is the power emission factor, taken as 0.90255 t/MVh; Qmax is the maximum cooling load of the electric chiller, kW; QFV0 represents the unit amount of refrigerant charge, taken as 464 kg; CER is the leakage rate of the refrigerant and the value is 5%; and mB is the amount of coal consumption in the IES, t.
The NOX emissions of the system are calculated according to the emission factors of different pieces of equipment in the system. The sources of NOX emission and the corresponding emission factors are listed in Table 2 [60,61]. Moreover, the SO2 emissions in an IES mainly come from the consumed coal. Furthermore, if the electricity produced by the system comes from a coal-fired thermal power plant, this portion of electricity should be converted to the amount of coal consumed to calculate the SO2 emissions. The amount of SO2 emissions can be calculated based on Equation (26):
where SOE denotes the SO2 emission amount of the IES, kg; S indicates the sulfur content. Usually, this value can be taken as 0.6~1.5%.

Table 2.
The NOX emission factors [60,61].
Furthermore, the GenOpt optimization program coupled with the TRNSYS software (version 17) is used to optimize the capacity of each piece of equipment. The optimization process is shown in Figure 6. For each case of the gas turbine’s capacity, the initial configuration, i.e., the capacity of each piece of equipment in the other three subsystems, is randomly generated. Then, the objective function F is calculated. A new population can be generated using the genetic algorithm, and the process is iterated 200 times to obtain the best solution for the present case. Finally, the best solutions of various cases are compared, and the final scheme is obtained. In this way, the complicated optimization problem of an IES is largely simplified, and the speed of the optimization calculation is improved.
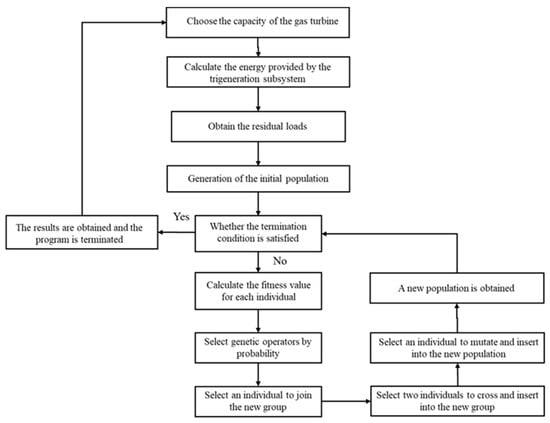
Figure 6.
A schematic illustration of the optimization process.
3. Results and Discussion
The proposed design method for a grid-interactive integrated energy system is applied in a hospital in Qinghe District, Beijing, China. The hospital includes many functional areas such as the emergency department, outpatient department, and inpatient department, which are in operation throughout the day. The hospital has a total floor area of 75,337 m2, of which about 64,000 m2 are air-conditioned. In order to compare the integrated energy system with traditional energy systems, only the loads in the heating and cooling seasons are considered. Additionally, the power consumed by the equipment in the system is taken as the power load. The heating season in Beijing is from November 15 to March 15 of the following year, that is, 0–1776 h and 7656–8760 h each year. The cooling season is from June 15 to September 15, which is 3961–6192 h each year. DeST software (version 2.0) is applied to obtain the exact heating load and cooling load throughout the year, which are shown in Figure 7. To distinguish it from the cooling load, the heating load is represented by a negative value. It is shown that the maximum heating load is 4916 kW and the maximum cooling load is 7975 kW.
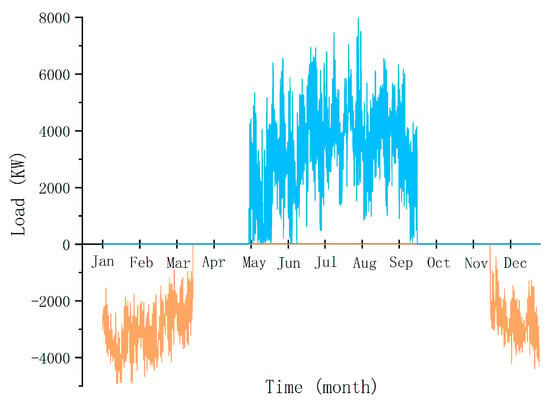
Figure 7.
The dynamic heat and cooling load throughout the year.
The optional equipment that could apply to this hospital are screened out at first. As the hospital can use natural gas supplied by the gas network conveniently, the trigeneration subsystem is selected in the energy system. Moreover, the GSHP is found to be suitable to undertake the heating load for this specific project. Furthermore, it is illustrated that the maximum cooling load is much higher than the maximum heating load. In order to avoid energy waste, the electric chiller acts as an auxiliary piece of equipment to complement the residual cooling load. Therefore, the heating subsystem includes the GSHP, and the cooling subsystem includes the GSHP as well as the electric chiller. As the system is grid-interactive, the excess power supplied by the trigeneration system can be sold to the grid.
Various schemes of the IES in this project can be built on the TRNSYS platform for transient simulation. According to the sequence of operation, as described in the previous section, the gas-fired trigeneration subsystem is operated at first. In the heating season, the exhaust gas of the gas turbine is used for heating. The GSHP undertakes the heating load; in the cooling season, both the GSHP and the electric chiller complement the residual cooling load. Therefore, two energy balance equations, as shown in Equations (27) and (28), can be established:
where is the rated heating power of the GSHP; is the rated heating power of the gas/water heat exchanger; , , and are the rated cooling power of the GSHP, the absorption chiller, and the electric chiller, respectively; is the maximum heating load, while is the maximum cooling load. Therefore, the optimization variable is the capacity of the gas turbine in this case.
In order to prevent the subjective selection of weighting coefficients from affecting the optimization results, different values of weighting coefficients are selected for optimization, as shown in Table 3 below.

Table 3.
Different values of weighting coefficients.
The price of each piece of equipment used in the calculation is shown in Table 4. The natural gas price for power generation is taken as 2.39 CNY/m3, while that for heating and cooling supply is 2.49 CNY/m3. Moreover, the on-grid tariff of natural gas is 0.65 CNY/kWh. Furthermore, the price of sharp electricity, peak electricity, shoulder electricity, and off-peak electricity is 1.440 CNY/kWh, 1.310 CNY/kWh, 0.785 CNY/kWh, and 0.311 CNY/kWh, respectively.

Table 4.
The price of each piece of equipment used in the calculation.
Figure 8 shows the system’s configuration for different values of the gas turbine’s capacity. The maximum value corresponds to the capacity of the gas turbine that can completely undertake the maximum heating load, and the GSHP is eliminated. It is indicated that the capacity of the absorption chiller decreases linearly as the capacity of the gas turbine increases. In addition, the capacity of the electric chiller fluctuates around 3000 to 4000 kW, because it is mainly used to complement the residual cooling load.
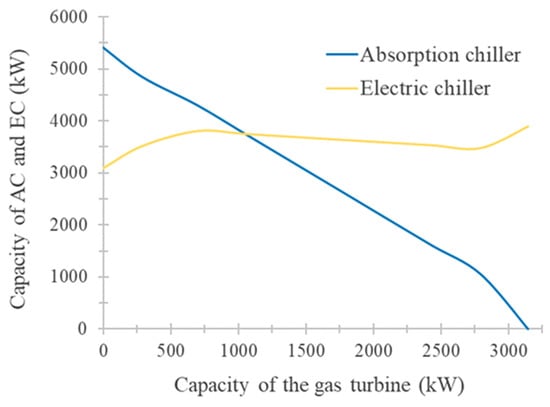
Figure 8.
The system’s configuration for different values of the gas turbine’s capacity.
Moreover, the parameters associated with system performance are shown in Figure 9. Both the operation cost and the income from the on-grid electricity reduce as the capacity of the gas turbine increases. A reduction in the GSHP’s capacity leads to a smaller power consumption of the system, thereby increasing the on-grid electricity. Moreover, the operation cost of the GSHP is mainly from the consumed electricity, which is much lower than the cost of natural gas used in the gas turbine. However, the income from the on-grid electricity produced by the gas turbine can offset a large proportion of the operation cost. Thus, the annual cost remains almost the same as the capacity of the gas turbine increases. Furthermore, the primary energy consumption and the shadow cost of environmental pollutants show opposite trends as the capacity of the gas turbine increases. The higher the capacity of the gas turbine, the more gas it consumes. Therefore, the primary energy consumption reaches its peak when the gas turbine can undertake the maximum heating load. Additionally, the impact of the on-grid electricity needs to be subtracted when calculating the shadow cost of environmental pollutants. The more on-grid electricity there is, the smaller the shadow cost of environmental pollutants. Figure 10 summarizes the relationship between the objective optimization function F and the capacity of the gas turbine for various cases. It is illustrated that the maximum F corresponds to a gas turbine capacity of 2790 kW in most cases, indicating the most suitable configuration of the integrated energy system.
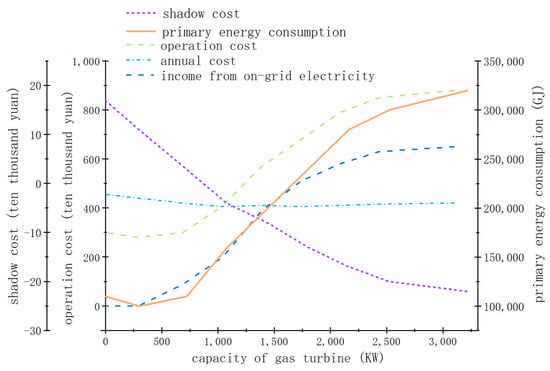
Figure 9.
The system’s performance for different values of the gas turbine’s capacity.
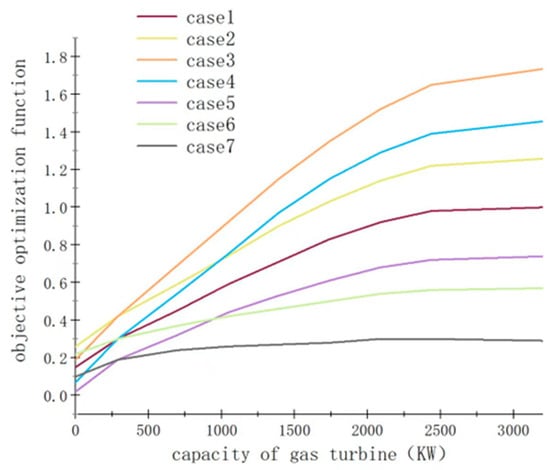
Figure 10.
The relationship between F and the capacity of the gas turbine for various cases.
A comparison of the cooling load and the heating load borne by each piece of equipment for the most suitable configuration is shown in Figure 11 and Figure 12, respectively. It is illustrated that the trigeneration subsystem undertakes a large part of the cooling load and most of the heating load, while the GSHP bears only a small part of the heating load. Because of the greater cooling load compared with the heating load, the electric chiller also replenishes a certain amount of cold energy.
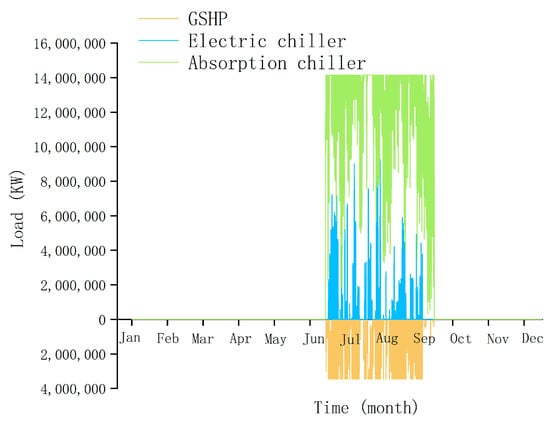
Figure 11.
The cooling load contributed by each piece of equipment.
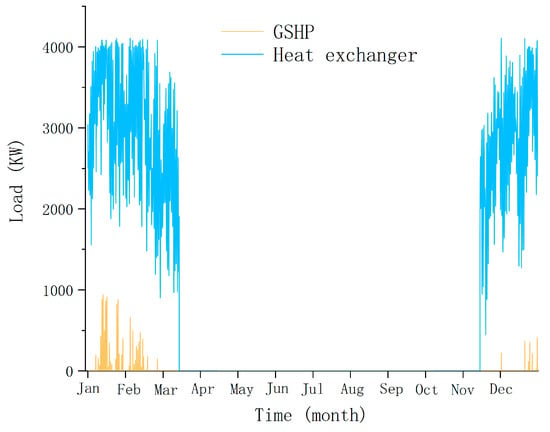
Figure 12.
The heating load contributed by each piece of equipment.
In order to demonstrate the advantages of the integrated energy system, the coupled system is compared with the traditional distributed system and the separate GSHP system. The annual cost, primary energy consumption, and pollutant emissions of the three systems are obtained from the simulation, as shown in Table 5. The optimized integrated energy system can help reduce the annual cost and energy consumption, and is also environmentally friendly. Since most of the generated power from the coupled system is on-grid, it should be deducted in the calculation of pollutant emissions; so, the coupled system can significantly reduce carbon dioxide and nitrogen oxide emissions. Compared with the separate GSHP system and the traditional distributed energy system, the emission reduction rate of NOX reaches 311.8% and 314.5%, respectively. Similarly, the reduction rate of CO2 emissions is 158% and 153.8%, respectively. Moreover, the annual cost of the coupled system is much lower than that of the separate GSHP system, and is comparative to the traditional distributed energy system. Furthermore, the primary energy consumption of the coupled system is 82.67% less than that of the traditional distributed energy system, indicating a great potential in reducing traditional energy consumption.

Table 5.
A comparison of the coupled system with the separate GSHP system and the traditional distributed energy system.
4. Conclusions
In this study, a simulation-based two-step decoupling method is proposed to simplify the optimization of an IES. A generalized IES structure is established, which includes various types of energy equipment related to generation, transmission, storage, and utilization. It is decoupled into four subsystems, including a trigeneration subsystem, a heating subsystem, a cooling subsystem, and a power subsystem. Then, a two-layer optimization method is applied to simplify the capacity optimization problem. The capacity of the gas turbine is taken as the first layer of the variable, and the capacity of the equipment in the other subsystems is taken as the second layer of the variable. In this way, a fast comparison among abundant optional configurations of an IES is enabled, and a hospital in Beijing, China, is analyzed based on the proposed method. The optimized coupling system includes the gas-fired trigeneration system, the GSHP, and the electric chiller. The relationship between the objective optimization function F and the capacity of the gas turbine is calculated and plotted. In this IES, the trigeneration subsystem undertakes a large part of the cooling load and most of the heating load. Because of the greater cooling load compared with the heating load, both the GSHP and the electric chiller bear a certain amount of cold energy. Compared with the traditional distributed systems, the reduction rate of CO2 and NOX emissions for the coupling system reaches 153.8% and 314.5%, respectively. Moreover, the primary energy consumption of the coupling system is 82.67% less than that of the traditional distributed energy system, while the annual cost is almost at the same level. Therefore, the optimized IES has obvious advantages compared with the GSHP system and the traditional distributed system in terms of the economy, energy savings, and environmental benefits.
Author Contributions
Conceptualization, L.Z. and J.G.; methodology, X.Y.; software, X.Y.; validation, G.H.; formal analysis, N.L. investigation, D.R.; resources, D.R.; data curation, J.W.; writing—original draft preparation, L.Z.; writing—review and editing, J.G.; supervision, J.G.; funding acquisition, L.Z. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China, grant number 52204039; the Key R&D Program (Soft Science Project), Shandong Province, grant number 2022RZB07055; the Key R&D Program (Competitive Innovation Platform), Shandong Province, grant number 2022CXPT051; and the Natural Science Foundation of Shandong Province, grant number ZR2022QB046.
Data Availability Statement
The data presented in this study are available in this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Song, C.; Jing, W.; Zeng, P.; Rosenberg, C. An analysis on the energy consumption of circulating pumps of residential swimming pools for peak load management. Appl. Energy 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy management and operational planning of a microgrid with a PV-based active generator for smart grid applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Gao, Z.; Zhang, Y. Wettability controlling effects on the fluid occurrence and flow in shale gas reservoirs: Present problems and new sights. Capillarity 2023, 9, 25–31. [Google Scholar] [CrossRef]
- Tu, Y.; Zhang, Y.; Dong, Y.; Ma, Y. Adsorption and desorption characteristics of coal seam gas under infrared radiation. Capillarity 2023, 8, 53–64. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Z.; Mandapaka, P.V.; Lo, E.Y. Risk-averse restoration of coupled power and water systems with small pumped-hydro storage and stochastic rooftop renewables. Appl. Energy 2023, 339, 120953. [Google Scholar] [CrossRef]
- Farrokhifar, M.; Nie, Y.; Pozo, D. Energy systems planning: A survey on models for integrated power and natural gas networks coordination. Appl. Energy 2020, 262, 114567. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Li, Z.; Chen, W.; Cai, Y. Distributed sensing and cooperative estimation/detection of ubiquitous power internet of things. Prot. Control Mod. Power Syst. 2019, 4, 13. [Google Scholar] [CrossRef]
- Liserre, M.; Sauter, T.; Hung, J.Y. Future energy systems: Integrating renewable energy sources into the smart power grid through industrial electronics. IEEE Ind. Electron. Mag. 2010, 4, 18–37. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Sampath, L.P.M.I.; Yang, J.; Nguyen, H.D.; Gooi, H.B.; Liang, R.; Gong, D. Blockchain-Enabled Carbon and Energy Trading for Network-Constrained Coal Mines with Uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 1634–1647. [Google Scholar] [CrossRef]
- Khalilpour, K.R.; Vassallo, A. A generic framework for distributed multi-generation and multi-storage energy systems. Energy 2016, 114, 798–813. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, Z.; Sun, G.; Cheung, K.W.; Zang, H.; Chen, S. A robust optimization approach for integrated community energy system in energy and ancillary service markets. Energy 2018, 148, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Yu, H.; Li, R.; Song, S. Energy Management for Smart Multi-Energy Complementary Micro-Grid in the Presence of Demand Response. Energies 2018, 11, 974. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wang, P.; Xiao, G. Coordinated preparation and recovery of a post-disaster Multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energy 2023, 336, 120736. [Google Scholar] [CrossRef]
- Riaz, M.; Ahmad, S.; Naeem, M. Joint energy management and trading among renewable integrated microgrids for combined cooling, heating, and power systems. J. Build. Eng. 2023, 75, 106921. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wang, P.; Xiao, G. Restoration of Multi Energy Distribution Systems With Joint District Network Recon Figuration by a Distributed Stochastic Programming Approach. IEEE Trans. Smart Grid 2023, 15, 2667–2680. [Google Scholar] [CrossRef]
- Quelhas, A.; Gil, E.; McCalley, J.D.; Ryan, S.M. A multiperiod generalized network flow model of the U.S. integrated energy system: Part I—Model description. IEEE Trans. Power Syst. 2007, 22, 829–836. [Google Scholar] [CrossRef]
- Zhu, M.; Xu, C.; Dong, S.; Tang, K.; Gu, C. An integrated multi-energy flow calculation method for electricity-gas-thermal integrated energy systems. Prot. Control Mod. Power Syst. 2021, 6, 5. [Google Scholar] [CrossRef]
- Li, J.; Li, D.; Zheng, Y.; Yao, Y.; Tang, Y. Unified modeling of regionally integrated energy system and application to optimization. Int. J. Electr. Power Energy Syst. 2022, 134, 107377. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C.R. A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- He, C.; Dai, C.; Wu, L.; Liu, T. Robust network hardening strategy for enhancing resilience of integrated electricity and natural gas distribution systems against natural disasters. IEEE Trans. Power Syst. 2018, 33, 5787–5798. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 2015, 101, 579–591. [Google Scholar] [CrossRef]
- Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Optimal design of CHP-based microgrids: Multiobjective optimisation and life cycle assessment. Energy 2015, 85, 181–193. [Google Scholar] [CrossRef]
- Qin, C.; Wang, L.; Han, Z.; Zhao, J.; Liu, Q. Weighted directed graph based matrix modeling of integrated energy systems. Energy 2021, 214, 118886. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, Y. Multi-Energy Flow Calculation Method for We-Energy Based Energy Internet. In Proceedings of the 1st IEEE International Conference on Energy Internet, ICEI 2017, Beijing, China, 17–21 April 2017; pp. 30–35. [Google Scholar] [CrossRef]
- Qin, X.; Sun, H.; Shen, X.; Guo, Y.; Guo, Q.; Xia, T. A generalized quasi-dynamic model for electric-heat coupling integrated energy system with distributed energy resources. Appl. Energy 2019, 251, 113270. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Beigvand, S.D.; Abdi, H.; La Scala, M. A general model for energy hub economic dispatch. Appl. Energy 2017, 190, 1090–1111. [Google Scholar] [CrossRef]
- Hao, R.; Ai, Q.; Jiang, Z. Bilayer game strategy of regional integrated energy system under multi-agent incomplete information. J. Eng. 2019, 2019, 1285–1291. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Zeng, M.; Yu, H.; Li, F.; Zhang, F. Optimal scheduling of the RIES considering time-based demand response programs with energy price. Energy 2018, 164, 773–793. [Google Scholar] [CrossRef]
- Gao, Y.; Ai, Q. Hierarchical Coordination Control for Interconnected Operation of Electric-thermal-gas Integrated Energy System with Micro-energy Internet Clusters. IEEE J. Emerg. Sel. Top. Power Electron. 2018. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, X. Failure probability estimation of gas supply using the central moment method in an integrated energy system. Appl. Energy 2018, 219, 1–10. [Google Scholar] [CrossRef]
- Ma, W.; Fang, S.; Liu, G. Hybrid optimization method and seasonal operation strategy for distributed energy system integrating CCHP, photovoltaic and ground source heat pump. Energy 2017, 141, 1439–14555. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, W.; Liu, F.; Wu, Q.; Mei, S. Analyzing and validating the economic efficiency of managing a cluster of energy hubs in multi-carrier energy systems. Appl. Energy 2018, 230, 403–416. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klöckl, B.; Andersson, G.; Fröhlich, K. The Energy Hub—A Powerful Concept for Future Energy Systems. In Proceedings of the Third Annual Carnegie Mellon Conference on the Electricity Industry, Pittsburgh, PA, USA, 13–14 March 2007. [Google Scholar]
- Evins, R.; Pointer, P.; Vaidyanathan, R.; Burgess, S. A case study exploring regulated energy use in domestic buildings using design-of-experiments and multi-objective optimization. Build. Environ. 2012, 54, 126–136. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Ferrara, M.; Fabrizio, E.; Virgone, J.; Filippi, M. A simulation-based optimization method for cost-optimal analysis of nearly Zero Energy Buildings. Energy Build. 2014, 84, 442–457. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Wu, Q.; Ren, H.; Gao, W.; Ren, J. Modeling and optimization of distributed energy supply network with power and hot water interchanges. Appl. Therm. Eng. 2016, 94, 635–643. [Google Scholar] [CrossRef]
- Lorestani, A.; Ardehali, M. Optimal integration of renewable energy sources for autonomous tri-generation combined cooling, heating and power system based on evolutionary particle swarm optimization algorithm. Energy 2018, 145, 839–855. [Google Scholar] [CrossRef]
- Li, Y.; Liang, W.; Tan, R. Optimal design of installation capacity and operation strategy for distributed energy system. Appl. Therm. Eng. 2017, 125, 756–766. [Google Scholar] [CrossRef]
- Urbanucci, L.; Testi, D. Optimal integrated sizing and operation of a CHP system with Monte Carlo risk analysis for long-term uncertainty in energy demands. Energy Convers. Manag. 2018, 157, 307–316. [Google Scholar] [CrossRef]
- Guo, L.; Liu, W.J.; Cai, J.J.; Hong, B.W.; Wang, C.S. A two-stage optimal planning and design method for combined cooling, heat and power microgrid system. Energy Convers. Manag. 2013, 74, 433–445. [Google Scholar] [CrossRef]
- Li, B.; Roche, R.; Paire, D.; Miraoui, A. Optimal sizing of distributed generation in gas/electricity/heat supply networks. Energy 2018, 151, 675–688. [Google Scholar] [CrossRef]
- Yousefi, H.; Ghodusinejad, M.H.; Noorollahi, Y. GA/AHP-based optimal design of a hybrid CCHP system considering economy, energy and emission. Energy Build. 2017, 138, 309–317. [Google Scholar] [CrossRef]
- Li, M.; Lu, Z.; Kang, Z.; Ban, L.; Cong, H.; Lu, Y. Investigation of an air-cooled double-channel photovoltaic/thermal system with integrated thermal energy storage. J. Build. Eng. 2023, 77, 107539. [Google Scholar] [CrossRef]
- Ameri, M.; Besharati, Z. Optimal design and operation of district heating and cooling networks with CCHP systems in a residential complex. Energy Build. 2016, 110, 135–148. [Google Scholar] [CrossRef]
- Wei, F.; Wu, Q.; Jing, Z.; Chen, J.; Zhou, X. Optimal unit sizing for small-scale integrated energy systems using multi-objective interval optimization and evidential reasoning approach. Energy 2016, 111, 933–946. [Google Scholar] [CrossRef]
- Zhang, L.; Kuang, J.; Sun, B.; Li, F.; Zhang, C. A two-stage operation optimization method of integrated energy systems with demand response and energy storage. Energy 2020, 208, 118423. [Google Scholar] [CrossRef]
- Qin, C.; Yan, Q.; He, G. Integrated energy systems planning with electricity, heat and gas using particle swarm optimization. Energy 2019, 188, 116044. [Google Scholar] [CrossRef]
- Tan, Z.; Yang, S.; Lin, H.; De, G.; Ju, L.; Zhou, F. Multi-scenario operation optimization model for park integrated energy system based on multi-energy demand response. Sustain. Cities Soc. 2020, 53, 101973. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Huang, Y.; Yu, H.; Du, R.; Zhang, F.; Zhang, F.; Zhu, J. Optimal Scheduling of the Regional Integrated Energy System Considering Economy and Environment. IEEE Trans. Sustain. Energy 2019, 10, 1939–1949. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Lee, W.-J.; Yan, H.; Li, D. The optimal structure planning and energy management strategies of smart multi energy systems. Energy 2018, 160, 122–141. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Zhao, N.; Gu, W. Low-carbon planning and optimization of the integrated energy system considering lifetime carbon emissions. J. Build. Eng. 2024, 82, 108178. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Ouyang, M. Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Tan, Z.; De, G.; Li, M.; Lin, H.; Yang, S.; Huang, L.; Tan, Q. Combined electricity-heat-cooling-gas load forecasting model for integrated energy system based on multi-task learning and least square support vector machine. J. Clean. Prod. 2020, 248, 119252. [Google Scholar] [CrossRef]
- Shao, Y.; Chen, B.; Xiao, H.; Qin, F.G.F. Discussion on Performance Evaluation Method of Distributed Combined Cooling, Heating, and Power System. J. Therm. Sci. 2019, 28, 1212–1220. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Niu, Y. A high proportion of new energy access–combined cooling, heating, and power system planning method. Int. J. Energy Res. 2019, 43, 7942–7955. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).