Pedestrian Trajectory Prediction Based on an Intention Randomness Influence Strategy
Abstract
1. Introduction
- We propose a random intention vector construction strategy that combines historical trajectory information with random factors, where the aim is to predict a trajectory by directly considering the direction and speed changes caused by the changes in a pedestrian’s own intentions.
- We designed an intention change probability based on the fitting error induced by the historical trajectory of the pedestrian and introduce an intention loss function to self-update the intention change probability, ensuring that the process of modeling the trajectory change caused by the randomness of pedestrian movement is targeted.
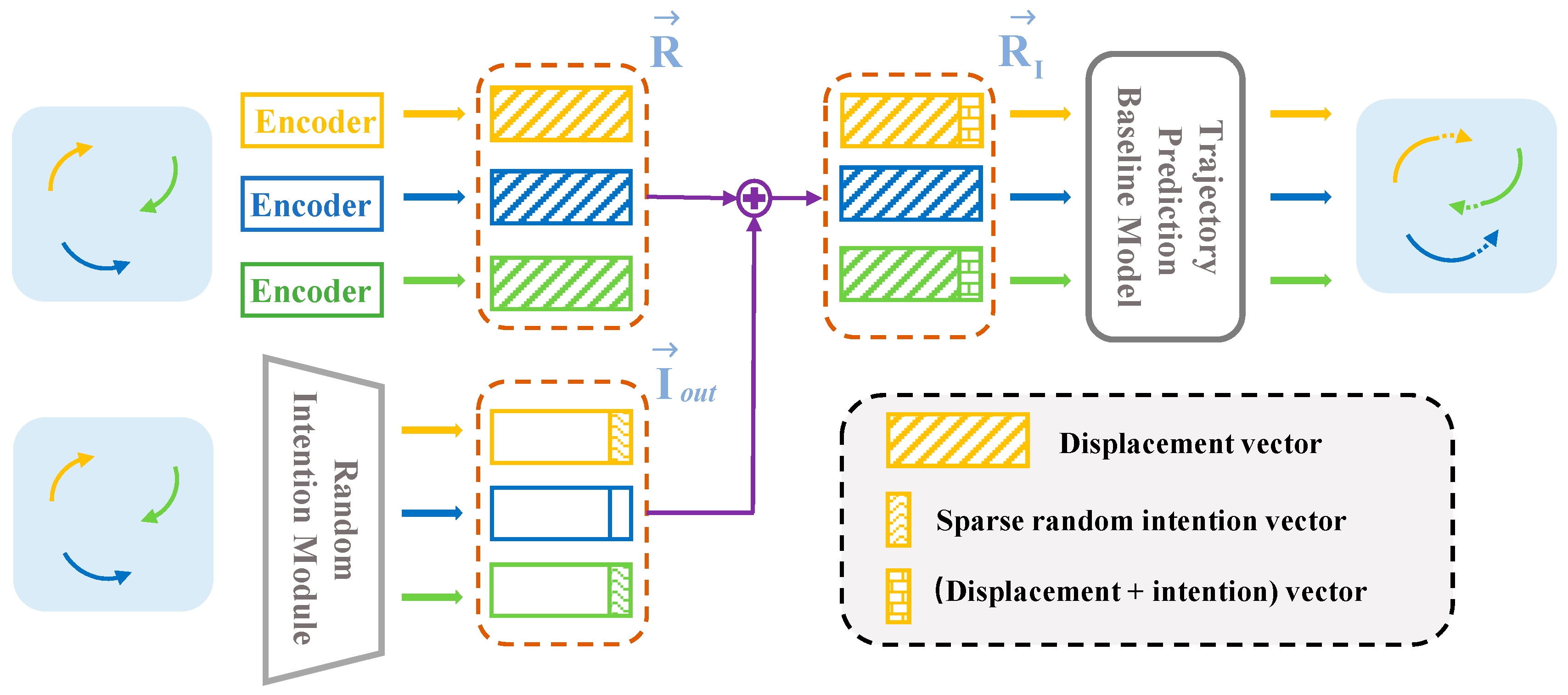
- The proposed intention vector construction method can be embedded into all trajectory prediction benchmark methods as a plug-in module to supplement the pedestrian randomness modeling process to improve the pedestrian trajectory prediction accuracies of the benchmark methods.
2. Related Work
2.1. Pedestrian Trajectory Prediction
2.2. Intention Prediction
3. Methods
3.1. Problem Definition
3.2. Construction of a Random Intention Vector and Intention Change Probabilities
3.2.1. Constructing the Random Intention Vector
3.2.2. Constructing the Intention Change Probability
3.3. Intention Loss Function
3.4. Sparse Intention
3.5. Implementation Details
4. Experiments
4.1. Datasets and Evaluation Metrics
4.2. Quantitative Evaluation
4.3. Visualization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadeghian, A.; Kosaraju, V.; Sadeghian, A.; Hirose, N.; Rezatofighi, H.; Savarese, S. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Amirian, J.; Hayet, J.B.; Pettré, J. Social ways: Learning multi-modal distributions of pedestrian trajectories with gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Huang, Y.; Bi, H.; Li, Z.; Mao, T.; Wang, Z. STGAT: Modeling Spatial-Temporal Interactions for Human Trajectory Prediction. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6271–6280. [Google Scholar]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-stgcnn: A social spatio-temporal graph convolutional neural network for human trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Shi, L.; Wang, L.; Long, C.; Zhou, S.; Zhou, M.; Niu, Z.; Hua, G. SGCN: Sparse graph convolution network for pedestrian trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Sun, J.; Jiang, Q.; Lu, C. Recursive social behavior graph for trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 660–669. [Google Scholar]
- Xu, P.; Hayet, J.B.; Karamouzas, I. Socialvae: Human trajectory prediction using timewise latents. In Computer Vision—ECCV 2022, Proceedings of the European Conference, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Mehran, R.; Oyama, A.; Shah, M. Abnormal crowd behavior detection using social force model. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Yamaguchi, K.; Berg, A.C.; Ortiz, L.E.; Berg, T.L. Who are you with and where are you going? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.-F.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Gupta, A.; Johnson, J.; Li, F.-F.; Savarese, S.; Alahi, A. Social GAN: Socially Acceptable Trajectories with Generative Adversarial Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2255–2264. [Google Scholar]
- Zhang, P.; Xue, J.; Zhang, P.; Zheng, N.; Ouyang, W. Social-aware pedestrian trajectory prediction via states refinement LSTM. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2742–2759. [Google Scholar] [CrossRef] [PubMed]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16; Springer: Cham, Switzerland, 2020; pp. 683–700. [Google Scholar]
- Song, X.; Chen, K.; Li, X.; Sun, J.; Hou, B.; Cui, Y.; Zhang, B.; Xiong, G.; Wang, Z. Pedestrian trajectory prediction based on deep convolutional LSTM network. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3285–3302. [Google Scholar] [CrossRef]
- Zamboni, S.; Kefato, Z.T.; Girdzijauskas, S.; Norén, C.; Dal Col, L. Pedestrian trajectory prediction with convolutional neural networks. Pattern Recognit. 2022, 121, 108252. [Google Scholar] [CrossRef]
- Kosaraju, V.; Sadeghian, A.; Martín-Martín, R.; Reid, I.; Rezatofighi, H.; Savarese, S. Social-bigat: Multimodal trajectory forecasting using bicycle-gan and graph attention networks. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Xin, L.; Wang, P.; Chan, C.Y.; Chen, J.; Li, S.E.; Cheng, B. Intention-aware long horizon trajectory prediction of surrounding vehicles using dual LSTM networks. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1441–1446. [Google Scholar]
- Chen, J.; Tang, C.; Xin, L.; Li, S.E.; Tomizuka, M. Continuous decision making for on-road autonomous driving under uncertain and interactive environments. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1651–1658. [Google Scholar]
- Kelley, R.; Tavakkoli, A.; King, C.; Nicolescu, M.; Nicolescu, M.; Bebis, G. Understanding human intentions via hidden markov models in autonomous mobile robots. In Proceedings of the 3rd ACM/IEEE International Conference on Human Robot Interaction, Amsterdam, The Netherlands, 12–15 March 2008; pp. 367–374. [Google Scholar]
- Vasquez, D.; Fraichard, T.; Laugier, C. Incremental learning of statistical motion patterns with growing hidden markov models. IEEE Trans. Intell. Transp. Syst. 2009, 10, 403–416. [Google Scholar] [CrossRef]
- Keller, C.G.; Gavrila, D.M. Will the pedestrian cross? a study on pedestrian path prediction. IEEE Trans. Intell. Transp. Syst. 2013, 15, 494–506. [Google Scholar] [CrossRef]
- Schneemann, F.; Heinemann, P. Context-based detection of pedestrian crossing intention for autonomous driving in urban environments. In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2243–2248. [Google Scholar]
- Dendorfer, P.; Osep, A.; Leal-Taixé, L. Goal-gan: Multimodal trajectory prediction based on goal position estimation. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Dendorfer, P.; Elflein, S.; Leal-Taixé, L. Mg-gan: A multi-generator model preventing out-of-distribution samples in pedestrian trajectory prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Motreal, BC, Canada, 11–17 October 2021; pp. 13158–13167. [Google Scholar]
- Pellegrini, S.; Ess, A.; Schindler, K.; van Gool, L. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 261–268. [Google Scholar]
- Lerner, A.; Chrysanthou, Y.; Lischinski, D. Crowds by Example. Comput. Graph. Forum 2007, 26, 655–664. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Hasegawa, T.; Nagai, M. Motion planning and control of autonomous driving intelligence system based on risk potential optimization framework. Int. J. Automot. Eng. 2016, 7, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Robicquet, A.; Sadeghian, A.; Alahi, A.; Savarese, S. Learning social etiquette: Human trajectory understanding in crowded scenes. In Computer Vision—ECCV 2016, Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VIII 14; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Mohamed, A.; Zhu, D.; Vu, W.; Elhoseiny, M.; Claudel, C. Social-implicit: Rethinking trajectory prediction evaluation and the effectiveness of implicit maximum likelihood estimation. In Computer Vision—ECCV 2022, Proceedings of the European Conference, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Li, J.; Ma, H.; Tomizuka, M. Conditional generative neural system for probabilistic trajectory prediction. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macao, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6150–6156. [Google Scholar]
- Zhang, L.; She, Q.; Guo, P. Stochastic trajectory prediction with social graph network. arXiv 2019, arXiv:abs/1907.10233. [Google Scholar]
- Liang, J.; Jiang, L.; Niebles, J.C.; Hauptmann, A.G.; Li, F.-F. Peeking into the future: Predicting future person activities and locations in videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Yu, C.; Ma, X.; Ren, J.; Zhao, H.; Yi, S. Spatio-temporal graph transformer networks for pedestrian trajectory prediction. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XII 16; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Mangalam, K.; Girase, H.; Agarwal, S.; Lee, K.H.; Adeli, E.; Malik, J.; Gaidon, A. It is not the journey but the destination: Endpoint conditioned trajectory prediction. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Monti, A.; Bertugli, A.; Calderara, S.; Cucchiara, R. Dag-net: Double attentive graph neural network for trajectory forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2551–2558. [Google Scholar]




| Notation | Description |
|---|---|
| Past trajectory of agent | |
| Interaction information of agent | |
| Trajectory prediction network | |
| Future trajectory of agent | |
| Total number of agents in a scene | |
| A coordinate component of the displacement of frame 8 | |
| A vector of random numbers sampled from a standard normal distribution | |
| Learnable weights and bias in a Linear model | |
| Learnable parameters in a custom Linear* model | |
| A random intention vector that combines coordinate components and random number factors | |
| Initialized fitting error vector with values between 0 and 1 | |
| A learnable vector that represents the probability of each pedestrian’s intention to change | |
| The true value of the intention change probability obtained from the fitting error of the future trajectory | |
| The output of the sparse intention module—a sparse random intention vector | |
| Random number between 0 and 1 | |
| The probability of the intention of agent changing | |
| The final output of the module obtained by splicing with zero vectors | |
| The displacement vector obtained by encoding the historical trajectory of a pedestrian | |
| Displacement vectors that superimpose intention changes |
| Baseline 1 | Performance (ADE/FDE) | |||||
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| Social LSTM [10] | 1.09/2.35 | 0.86/1.91 | 0.41/0.88 | 0.52/1.11 | 0.61/1.31 | 0.70/1.52 |
| SGAN [11] | 0.87/1.62 | 0.67/1.37 | 0.35/0.68 | 0.42/0.84 | 0.76/1.52 | 0.61/1.21 |
| SoPhie [1] | 0.70/1.43 | 0.76/1.67 | 0.30/0.63 | 0.38/0.78 | 0.54/1.24 | 0.54/1.15 |
| CGNS [30] | 0.62/1.40 | 0.70/0.93 | 0.32/0.59 | 0.35/0.71 | 0.48/1.22 | 0.49/0.97 |
| STSGN [31] | 0.75/1.63 | 0.63/1.01 | 0.30/0.65 | 0.26/0.57 | 0.48/1.08 | 0.48/0.99 |
| PITF [32] | 0.73/1.65 | 0.30/0.59 | 0.38/0.81 | 0.31/0.68 | 0.60/1.27 | 0.46/1.00 |
| Social-BiGAT [16] | 0.69/1.29 | 0.49/1.01 | 0.30/0.62 | 0.36/0.75 | 0.55/1.32 | 0.48/1.00 |
| STAR [33] | 0.56/1.11 | 0.26/0.50 | 0.41/0.90 | 0.31/0.71 | 0.52/1.15 | 0.41/0.87 |
| STGCNN [4] | 0.64/1.11 | 0.49/0.85 | 0.34/0.53 | 0.30/0.48 | 0.44/0.79 | 0.44/0.75 |
| Conv2D-tobs-NR-Ks5 [15] | 0.56/1.11 | 0.24/0.46 | 0.46/0.99 | 0.35/0.75 | 0.58/1.23 | 0.44/0.91 |
| SGCN [5] | 0.63/1.03 | 0.32/0.55 | 0.29/0.53 | 0.25/0.45 | 0.37/0.70 | 0.37/0.65 |
| SGCN * | 0.71/1.34 | 0.29/0.54 | 0.27/0.48 | 0.24/0.43 | 0.38/0.70 | 0.38/0.70 |
| Intention-SGCN | 0.64/0.83 | 0.28/0.46 | 0.27/0.47 | 0.24/0.42 | 0.38/0.73 | 0.36/0.58 |
| Baseline 2 | Performance (ADE/FDE) | |||||
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| STGAT [3] | 0.65/1.12 | 0.35/0.66 | 0.34/0.69 | 0.29/0.60 | 0.52/1.10 | 0.43/0.83 |
| STGAT * | 0.80/1.42 | 0.37/0.70 | 0.33/0.66 | 0.29/0.61 | 0.55/1.17 | 0.47/0.91 |
| Intention-STGAT | 0.68/1.18 | 0.37/0.70 | 0.32/0.66 | 0.30/0.61 | 0.54/1.14 | 0.44/0.86 |
| Baseline 3 | Performance (ADE/FDE) | |||||
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| PECNet [34] | 0.54/0.87 | 0.18/0.24 | 0.22/0.39 | 0.17/0.30 | 0.35/0.60 | 0.29/0.48 |
| Trajectron++ [13] | 0.54/0.94 | 0.16/0.28 | 0.21/0.42 | 0.16/0.31 | 0.28/0.55 | 0.27/0.50 |
| Social-Implicit [29] | 0.66/1.44 | 0.20/0.36 | 0.25/0.50 | 0.22/0.43 | 0.31/0.60 | 0.33/0.67 |
| SVAE [7] | 0.49/0.77 | 0.15/0.24 | 0.19/0.37 | 0.15/0.28 | 0.25/0.47 | 0.25/0.43 |
| SVAE * | 0.50/0.85 | 0.15/0.23 | 0.20/0.37 | 0.16/0.29 | 0.25/0.48 | 0.25/0.44 |
| Intention-SVAE | 0.50/0.75 | 0.16/0.23 | 0.20/0.37 | 0.15/0.29 | 0.26/0.49 | 0.25/0.43 |
| Method | Social-Ways [2] | DAG-Net [35] | Social-Implicit [29] | SVAE * | Intention-SVAE |
|---|---|---|---|---|---|
| ADE | 0.62 | 0.53 | 0.47 | 0.33 | 0.33 |
| FDE | 1.16 | 1.04 | 0.89 | 0.53 | 0.51 |
| Performance (ADE/FDE) | ||||||
|---|---|---|---|---|---|---|
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| SGCN * (baseline) | 0.71/1.34 | 0.29/0.54 | 0.27/0.48 | 0.24/0.43 | 0.38/0.70 | 0.38/0.70 |
| Intention-SGCN-X | 0.71/1.23 | 0.30/0.53 | 0.27/0.50 | 0.24/0.43 | 0.38/0.74 | 0.38/0.68 |
| Intention-SGCN-XY | 0.66/1.18 | 0.28/0.50 | 0.28/0.50 | 0.24/0.44 | 0.39/0.73 | 0.37/0.67 |
| Intention-SGCN-Y (ours) | 0.64/0.83 | 0.28/0.46 | 0.27/0.47 | 0.24/0.42 | 0.38/0.73 | 0.36/0.58 |
| Performance (ADE/FDE) | ||||||
|---|---|---|---|---|---|---|
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| SGCN * (baseline) | 0.71/1.34 | 0.29/0.54 | 0.27/0.48 | 0.24/0.43 | 0.38/0.70 | 0.38/0.70 |
| Intention-SGCN1 | 0.70/1.37 | 0.28/0.46 | 0.27/0.50 | 0.23/0.41 | 0.39/0.67 | 0.37/0.68 |
| Intention-SGCN2 | 0.65/1.21 | 0.26/0.43 | 0.27/0.48 | 0.23/0.42 | 0.37/0.69 | 0.36/0.65 |
| Intention-SGCN3 (ours) | 0.64/0.83 | 0.28/0.46 | 0.27/0.47 | 0.24/0.42 | 0.38/0.73 | 0.36/0.58 |
| Performance (ADE/FDE) | ||||||
|---|---|---|---|---|---|---|
| ETH | HOTEL | ZARA1 | ZARA2 | UNIV | AVG | |
| SGCN * (baseline) | 0.71/1.34 | 0.29/0.54 | 0.27/0.48 | 0.24/0.43 | 0.38/0.70 | 0.38/0.70 |
| Intention-SGCN w/o RBLL | 0.65/1.10 | 0.30/0.53 | 0.27/0.49 | 0.24/0.43 | 0.38/0.72 | 0.37/0.65 |
| Intention-SGCN w/o RNF | 0.66/1.18 | 0.32/0.56 | 0.27/0.49 | 0.24/0.43 | 0.41/0.75 | 0.38/0.68 |
| Intention-SGCN w/o POI | 0.64/0.92 | 0.33/0.60 | 0.27/0.50 | 0.25/0.45 | 0.39/0.74 | 0.37/0.64 |
| Intention-SGCN (ours) | 0.64/0.83 | 0.28/0.46 | 0.27/0.47 | 0.24/0.42 | 0.38/0.73 | 0.36/0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Zhang, L.; Chen, J.; Deng, Y.; Liu, J. Pedestrian Trajectory Prediction Based on an Intention Randomness Influence Strategy. Electronics 2024, 13, 2008. https://doi.org/10.3390/electronics13112008
Deng Y, Zhang L, Chen J, Deng Y, Liu J. Pedestrian Trajectory Prediction Based on an Intention Randomness Influence Strategy. Electronics. 2024; 13(11):2008. https://doi.org/10.3390/electronics13112008
Chicago/Turabian StyleDeng, Yingjian, Li Zhang, Jie Chen, Yu Deng, and Jing Liu. 2024. "Pedestrian Trajectory Prediction Based on an Intention Randomness Influence Strategy" Electronics 13, no. 11: 2008. https://doi.org/10.3390/electronics13112008
APA StyleDeng, Y., Zhang, L., Chen, J., Deng, Y., & Liu, J. (2024). Pedestrian Trajectory Prediction Based on an Intention Randomness Influence Strategy. Electronics, 13(11), 2008. https://doi.org/10.3390/electronics13112008






