1. Introduction
Computed tomography (CT), which uses an X-ray beam to scan a certain region of the human body, is a widely utilized medical imaging technique, due to its high-resolution output and rapid scanning capability. Unfortunately, the widespread use of CT has sparked concerns about the potential carcinogenic and genetic risks associated with X-ray exposure [
1,
2]. In response, the last decade has shifted towards minimizing radiation doses in CT scans, adhering to the As Low As Reasonably Achievable (ALARA) principle to mitigate safety hazards [
3]. However, this reduction in radiation dose inherently increases noise in the resulting CT images [
3]. This noise amplification negatively affects image quality, which poses a challenge to the diagnostic reliability of using the images. In essence, the lower the radiation dose, the greater the noise, and consequently, the less the clinical diagnostic value of CT images [
4].
Several denoising algorithms have been developed to address challenges in improving image quality in low-dose CT (LDCT). These can be broadly classified into three types: sinogram filtration, iterative reconstruction, and image post-processing. Sinogram filtration methods [
5,
6,
7] operate on the raw data before image reconstruction, benefiting from the well-known noise properties in this domain. However, they often lead to edge blurring or a loss of resolution, and access to sinogram data may not be available to all researchers. Iterative reconstruction methods [
8,
9,
10] aim to optimize an objective function that combines the statistical characteristics of sinogram data with prior image information. Despite achieving impressive results, these methods are limited by long processing times and the requirement for dedicated hardware, hindering their clinical use. Lastly, image post-processing methods [
11,
12,
13] focus on the suppression of noise in reconstructed images. This approach, unlike the others, faces challenges in accurately determining the noise distribution within the image domain, complicating the achievement of an optimal balance between noise reduction performance and structural detail preservation.
The advent of deep learning, particularly the success of convolutional neural networks (CNNs) in computer vision, has sparked significant advancements in LDCT denoising. Many CNN-based methods, focussing primarily on image post-processing, training end-to-end networks in a supervised manner to learn mappings from LDCT to normal-dose CT (NDCT) images, using a predefined loss function for optimisation. Chen et al. [
14] were among the first to demonstrate that a basic CNN could estimate the value of the NDCT Hounsfield Unit (HU) from LDCT patches. Gondara [
15] also validated the effectiveness of the CNN-based encoder–decoder structure in medical image denoising. Furthermore, the RED-CNN model proposed by Chen et al. [
16], incorporating shortcut connections in a residual encoder–decoder convolutional neural network, surpassed existing traditional image processing methods in Structural Similarity Index Measure (SSIM) and Peak Signal-to-Noise Ratio (PSNR), which were up to 0.0514 and 4.0802 dB, respectively. Additionally, to alleviate the requirement of paired LDCT and NDCT images, the exploration of unsupervised learning in LDCT denoising has been notable. Yang et al. [
17] employed a generative adversarial network with the Wasserstein distance (WGAN) and perceptual loss to enhance denoised image quality and reduce over-smoothing. Kang et al. [
18] introduced a CycleGAN-based approach using unpaired LDCT and NDCT images for training. In addition, Lee et al. [
19] introduced an additional noise extractor network based on CycleGAN [
20] to cooperate with its generators and obtained excellent results. However, a limitation of CNN-based models is their reliance on cascaded convolutional layers for high-level feature extraction focusing on local regions, restricting their ability to capture global contextual information due to the limited receptive fields of the convolution operation. This limitation hampers their efficiency in modelling structural similarity across the whole images [
21].
In recent years, vision Transformers have gained significant traction in computer vision, demonstrating remarkable achievements [
22,
23,
24]. The core of these Transformers, the self-attention unit, excels at extracting long-range dependencies by computing interactions between any two positions in the input sequence, outperforming CNN models in some extent. Vision Transformers have been increasingly applied to image restoration tasks. For instance, SwinIR [
25] successfully adapted the shifted window self-attention mechanism from the Swin Transformer [
26] for image restoration with an average PSNR of over 30 dB across several datasets. Uformer [
27] utilized non-overlapping window-based self-attention and depth-wise convolution in its feed-forward network, efficiently capturing local context. In the realm of LDCT denoising, several innovative approaches have been developed. Eformer [
28] combined a network similar to Uformer with an edge enhancement module, effectively enhancing image quality. CTformer [
29] introduced the first dedicated Transformer for LDCT denoising, employing dilation and cyclic shift in Token2Token to broaden the receptive field and gather more extensive contextual information from feature maps. These advancements underscore the Transformers’ superiority in this domain. However, their self-attention mechanism leads to a significant drawback—excessive GPU memory consumption, particularly when processing high-resolution images like CT scans. This results in extended processing times and heightened equipment demands.
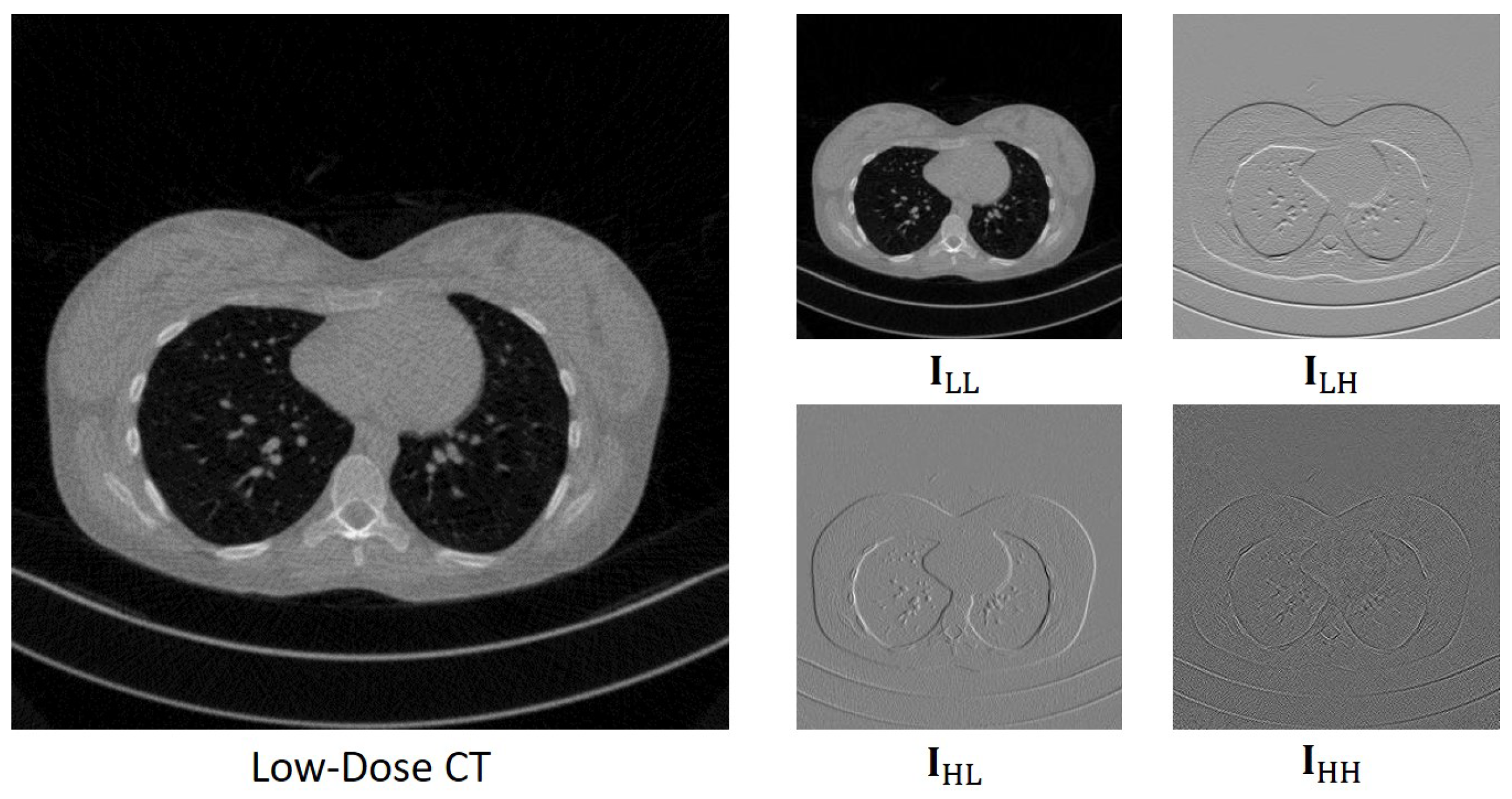
To optimize the performance of the Transformer without the constraints of GPU memory, a viable solution is to use low-resolution images, since it reduces the device resource consumption of the models. The wavelet transform, a prevalent technique in image processing, offers a reversible method to halve image size by decomposing signals into different frequency bands, achieving this without any loss of information and thereby reducing computational resource demands. Another significant advantage of the wavelet transform is the ease of handling sub-band signals separately and effectively. Integrating the wavelet transform with deep learning has already shown impressive results in several studies. Bae et al. [
30] demonstrated the effectiveness of learning on wavelet sub-bands, introducing the wavelet residual network for image restoration. Guo et al. [
31] developed a deep wavelet super-resolution network to retrieve missing details in wavelet sub-bands between low and high-resolution images. Similarly, Liu et al. [
32] proposed the multi-level wavelet-CNN (MWCNN) for image restoration, utilizing multi-level wavelet transform for various tasks and obtaining a PSNR of over 32 dB with a run time of less than 0.1 s. In the context of image denoising, the decomposition of noise along with the image allows for tailored noise suppression methods in different sub-bands. Such an approach is anticipated to surpass traditional noise reduction methods that operate directly in the image domain.
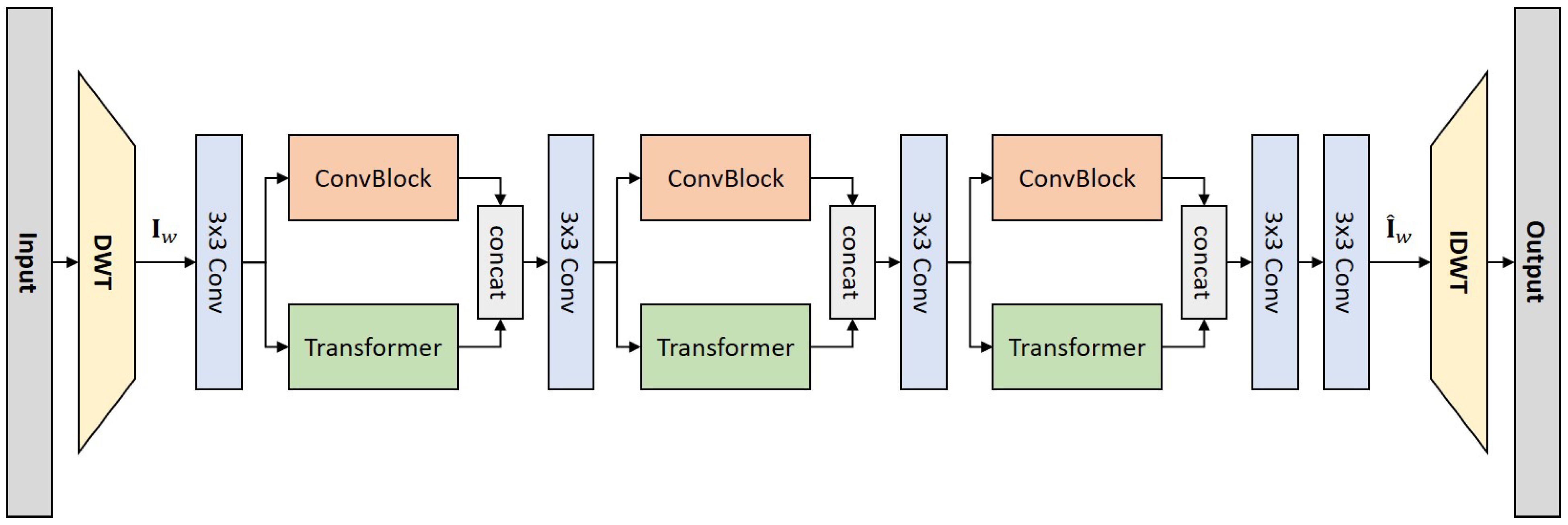
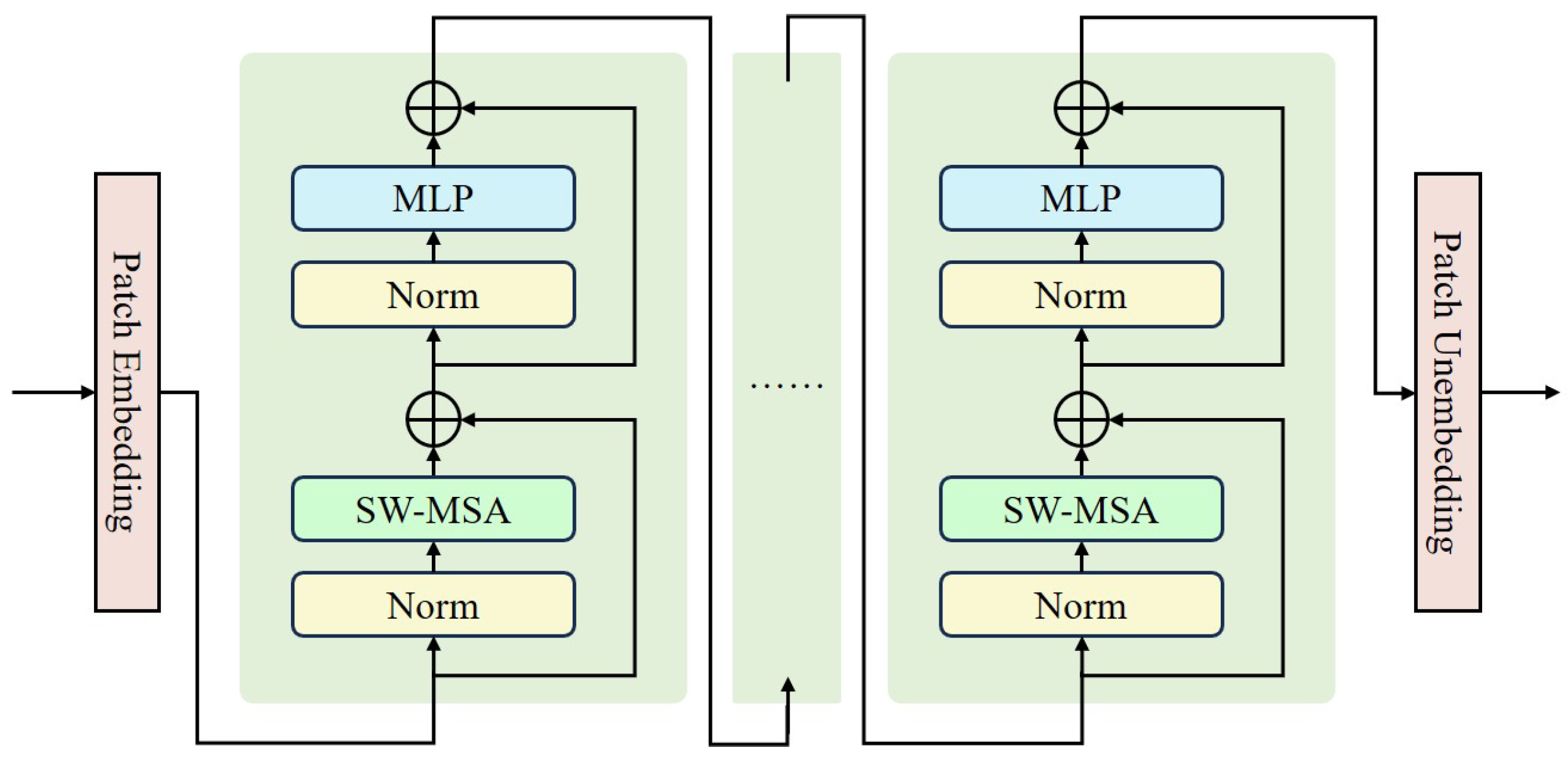
In this work, we leverage the wavelet transform as the sampling framework and attenuate noise in the wavelet domain. Drawing inspiration from previous LDCT denoising research, we introduce a novel denoising network that synergizes the strengths of both CNNs and Transformers. Our approach employs the discrete wavelet transform (DWT) for image downsampling and the inverse discrete wavelet transform (IDWT) for upsampling. The network architecture features dual forward denoising streams, which effectively combine the local feature extraction capability of the convolution operation with the fine-grained information connectivity modelling prowess of Transformers. This integration allows for the extraction of CT image features at various levels. Trained under a specifically designed dual-domain loss function, our proposed network, termed WaveletDFDS-Net, demonstrates enhanced performance in exquisite detail restoration, effectively utilizing the complementary advantages of CNNs and Transformers in the context of LDCT denoising. In summary, this paper introduces the following key contributions to LDCT denoising:
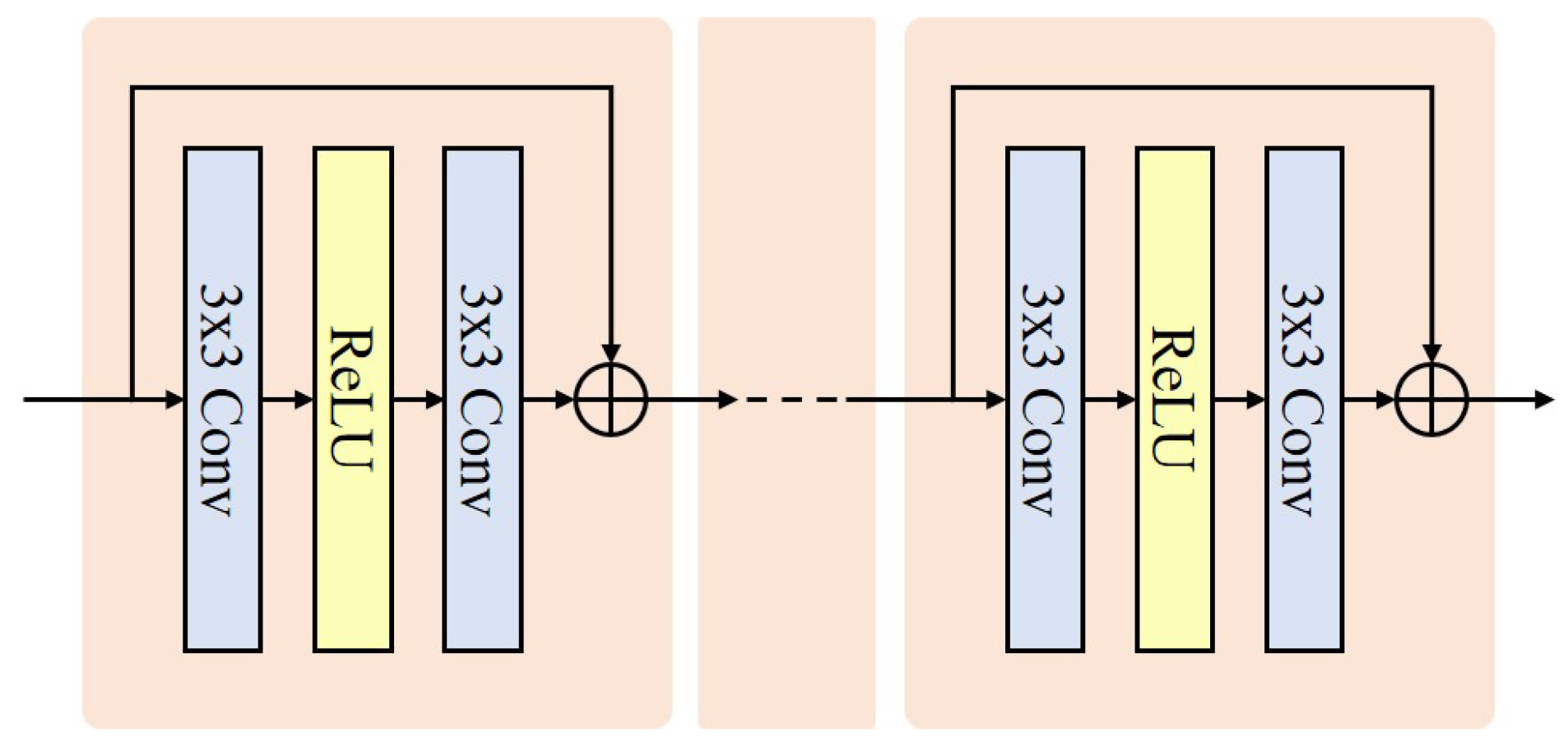
Development of WaveletDFDS-Net: We propose WaveletDFDS-Net, which harnesses the local feature extraction capabilities of the convolution operation and the pixel-level information encoding strength of Transformers and reduces noise in the wavelet domain. This network is designed to efficiently extract LDCT image wavelet features from various levels in parallel, leading to more effective noise suppression in LDCT images and fewer computing resource requirements.
Dual-domain compound loss function: An efficient dual-domain compound loss function has been formulated to train WaveletDFDS-Net. This function incorporates an additional wavelet domain loss as an auxiliary component to the image domain loss, aiming to achieve high-fidelity detail restoration in the denoising process.
Superior experimental outcomes: Our experimental evaluations demonstrate that the proposed method outperforms existing well-known denoising techniques. WaveletDF DS-Net not only shows improved performance metrics but also produces images of higher quality, underlining its effectiveness in LDCT denoising applications.
The remainder of this paper is structured as follows:
Section 2 provides a comprehensive description of the proposed WaveletDFDS-Net and the dual-domain compound loss mechanism.
Section 3 outlines the experimental setup, presents the outcomes of various ablation studies, and compares experimental results. The paper concludes with
Section 5, summarizing the key findings and contributions of this research.
4. Discussion
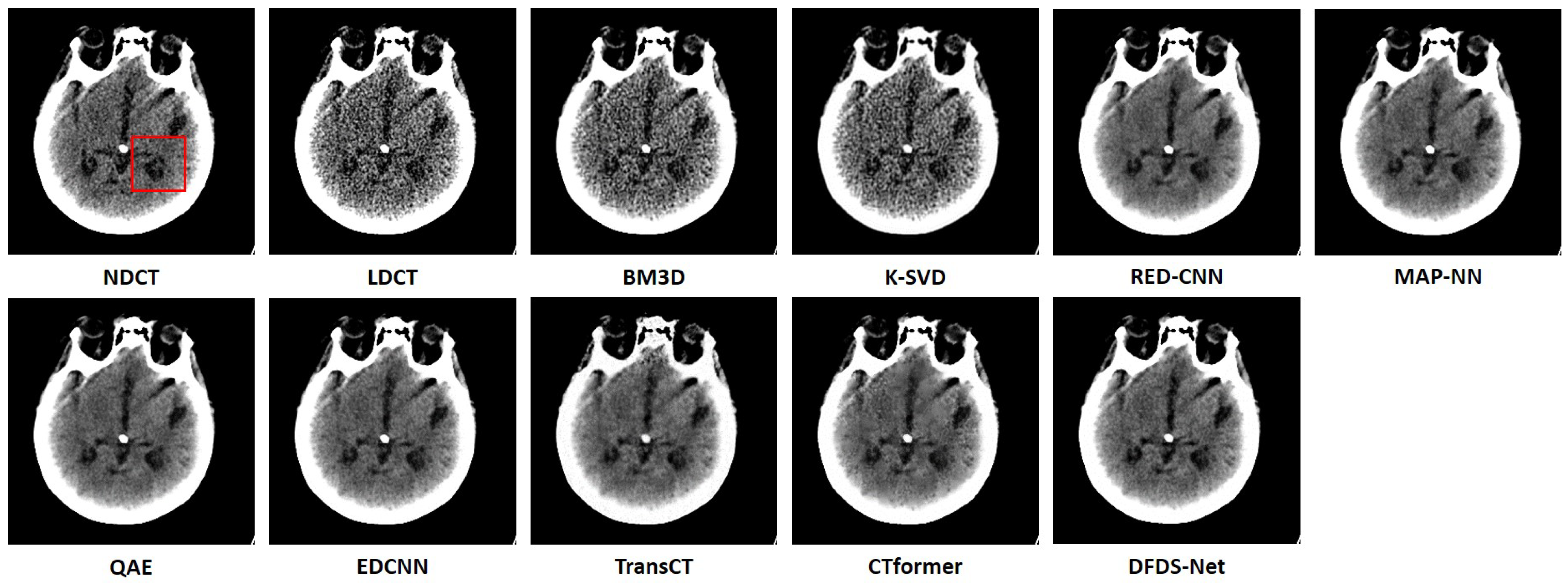
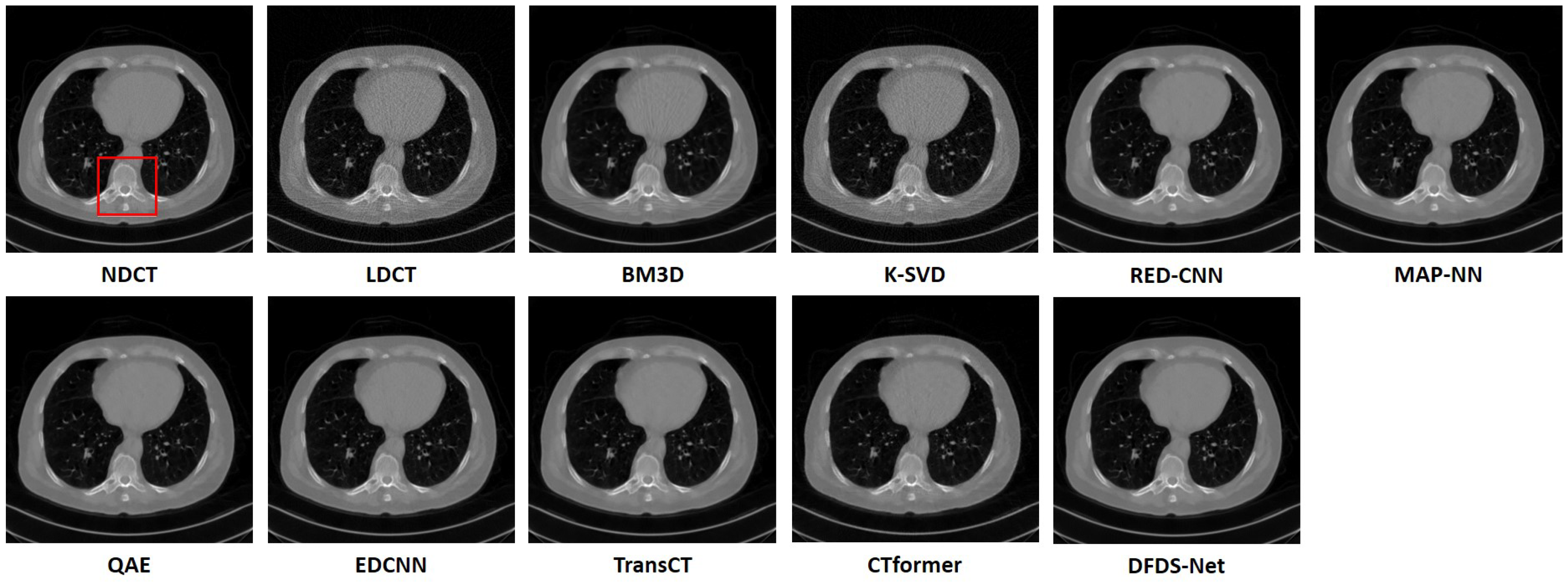
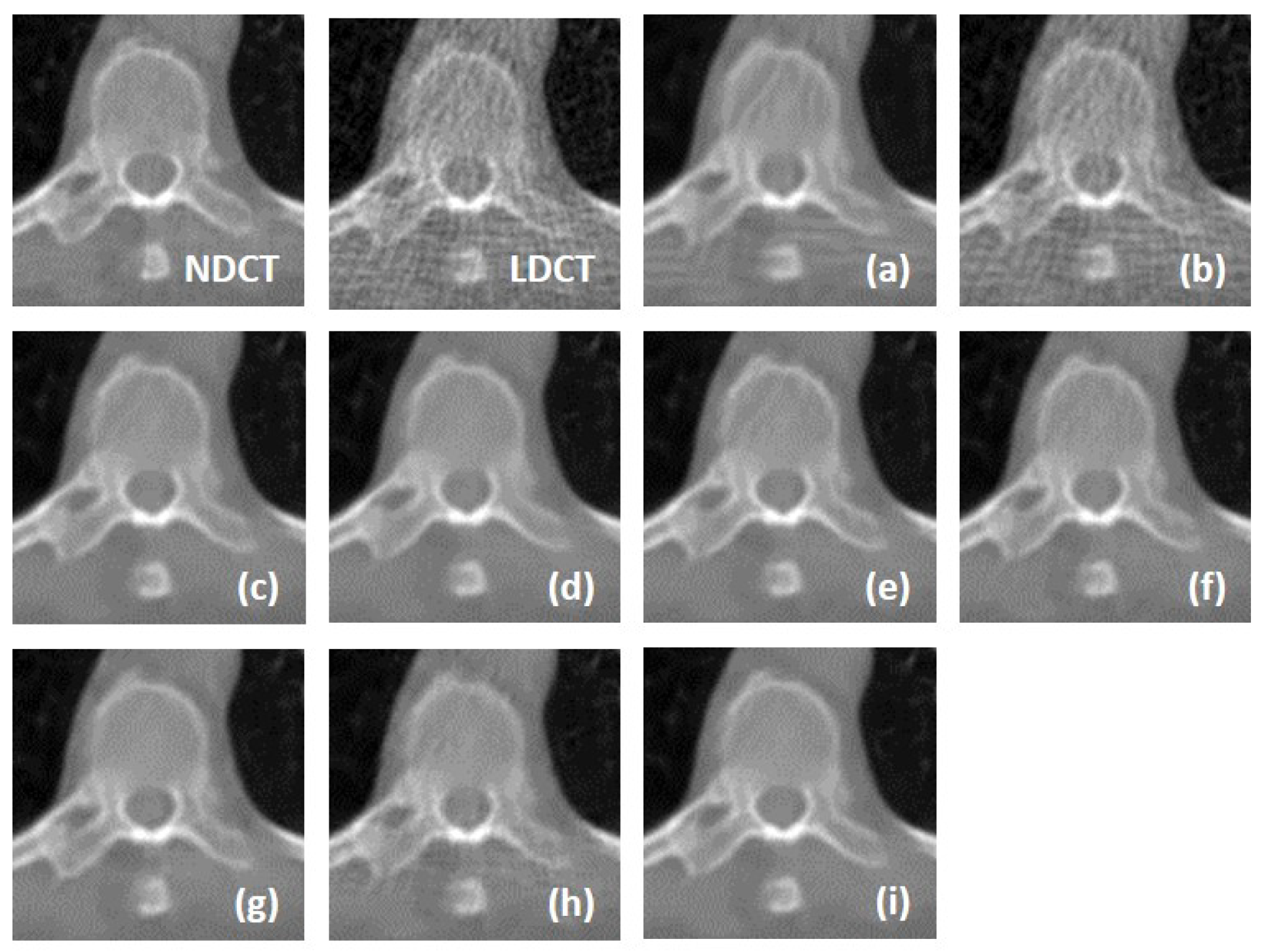
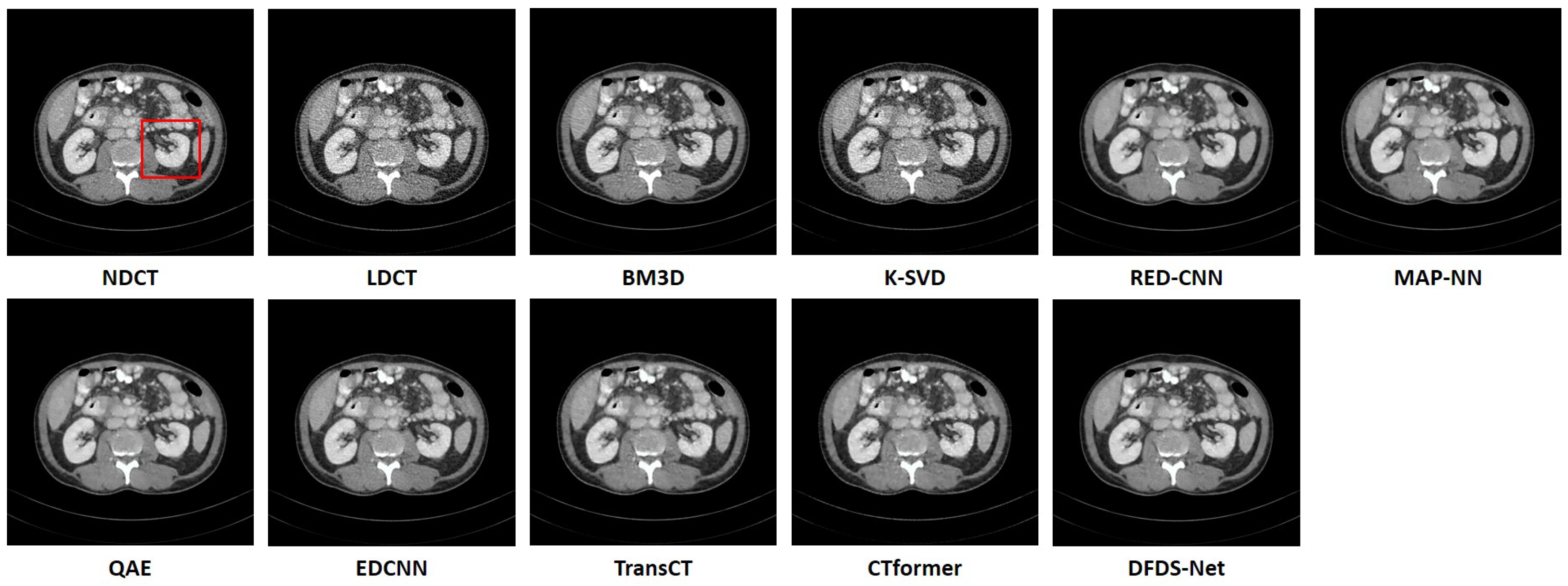
We fully compared the efficiency and performance of WaveletDFDS-Net with several well-known LDCT denoising methods and quantitatively and visually presented the experimental results in the above sections. As one of the classical image-denoising algorithms, BM3D groups patches by searching for similar regions in the image and performs collaborative filtering by the group to reduce noise. Although excellent achievements on natural image tasks have been obtained, the drawbacks are also obvious. For images with uneven noise distribution or pixels entangled with noise, BM3D has a limited denoising effect, whose results always suffer from noise residue or blurring. Similarly, classically, K-SVD is a dictionary learning method that applies an SVD decomposition of images and selects the term with the minimum error as the updated dictionary parameter to iteratively optimize until the noise level converges. However, in our case, since the noise of LDCT was introduced in the projection domain and converted into a more complex distribution in the image domain, the capacity of the SVD decomposition was insufficient, resulting in a minimum noise reduction effect of K-SVD in our experiments.
Different from the above two methods, the deep learning strategy had a more powerful denoising ability. RED-CNN, as an early model, constructs an encoder–decoder structure with residual connections that demonstrated far better performance than K-SVD and BM3D through end-to-end training, as shown in the experimental results in
Table 6. MAP-NN adaptively performs progressive noise reduction by looping through a convolutional network and takes a discriminator as one of the supervisors to train its network. These improvements contribute to increased evaluation metrics. Based on Red-CNN, QAE employs quadratic neurons (executing a quadratic operation on the input data) instead of the original inner product for high-order nonlinear sparse representation with a reasonable model complexity. As the efficiency shown in
Table 5 and performance shown in
Table 6, QAE comprehensively outperformed RED-CNN. EDCNN focuses on the extraction of image edge information and introduces an edge enhancement module in the first layer of the dense connection network to improve the effect of image edge restoration. Our experiments confirmed that EDCNN restored clearer boundaries of distinct organs than other models. However, all of these methods were inferior to WaveletDFDS-Net in denoising performance due to the inherent receptive field limitations of convolution.
TransCT and CTformer are two kinds of Transformer-based LDCT noise reduction models; the former separates the high-frequency content and low-frequency content of LDCT images and then mainly denoises the high-frequency part, while the latter designs a token-to-token learning strategy that encompasses local contextual information via token rearrangement rather than convolution operation. Although neither requires much computing resources, the performance is not satisfactory. Obviously, even though Transformer has the long-range feature extraction capabilities that CNN lacks, it does not reach its potential if it is used incorrectly. In contrast to these comparison methods, WaveletDFDS-Net builds two parallel branches based on Transformer and convolution operations, respectively, to learn the noise distribution at the fine-gained level and local coarse level on multiple wavelet bands to improve noise reduction performance in a cooperative manner. WaveletDFDS-Net shows promising potential to avoid the misrepresentation of anatomical structures in images and ultimately lead to better patient outcomes through more accurate diagnoses and treatments.
While the proposed methods demonstrate superior denoising capabilities, some aspects could be improved. Firstly, the concurrent architecture of CNNs and Transformers does not fully exploit the synergistic potential between these technologies, resulting in modest improvements in efficiency and experimental metrics. Secondly, the training of WaveletDFDS-Net relies on a supervised learning strategy requiring a substantial dataset of paired LDCT and NDCT images, which are challenging to acquire in real-world clinical settings, thus restricting practical applicability.