Unsupervised Anomaly Detection of Intermittent Demand for Spare Parts Based on Dual-Tailed Probability
Abstract
1. Introduction
2. Background
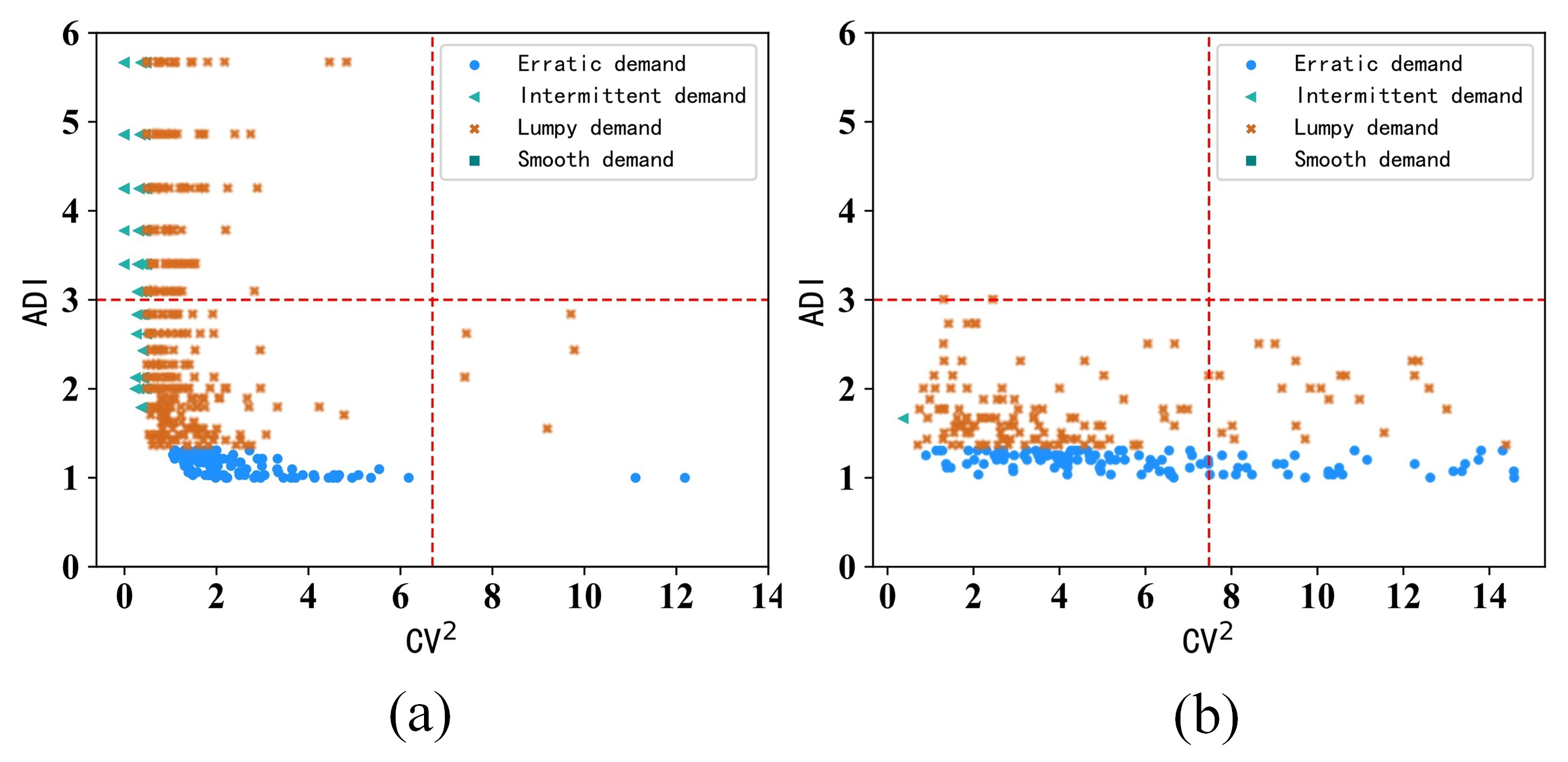
2.1. Demand Patterns
- (1)
- Stable demand (): this category of demand is relatively stable with few zero demand periods.
- (2)
- Unstable demand (): the demand is unstable with high variability and occurs frequently.
- (3)
- Intermittent demand (): the demand is irregular and scattered, but relatively stable.
- (4)
- Blocky demand (): this category has a random demand pattern, with a large number of time periods having no demand and the demands varying greatly from period to period, accompanied by a significant number of zero demand stages.
2.2. Multi-Way Delay Embedding Transform
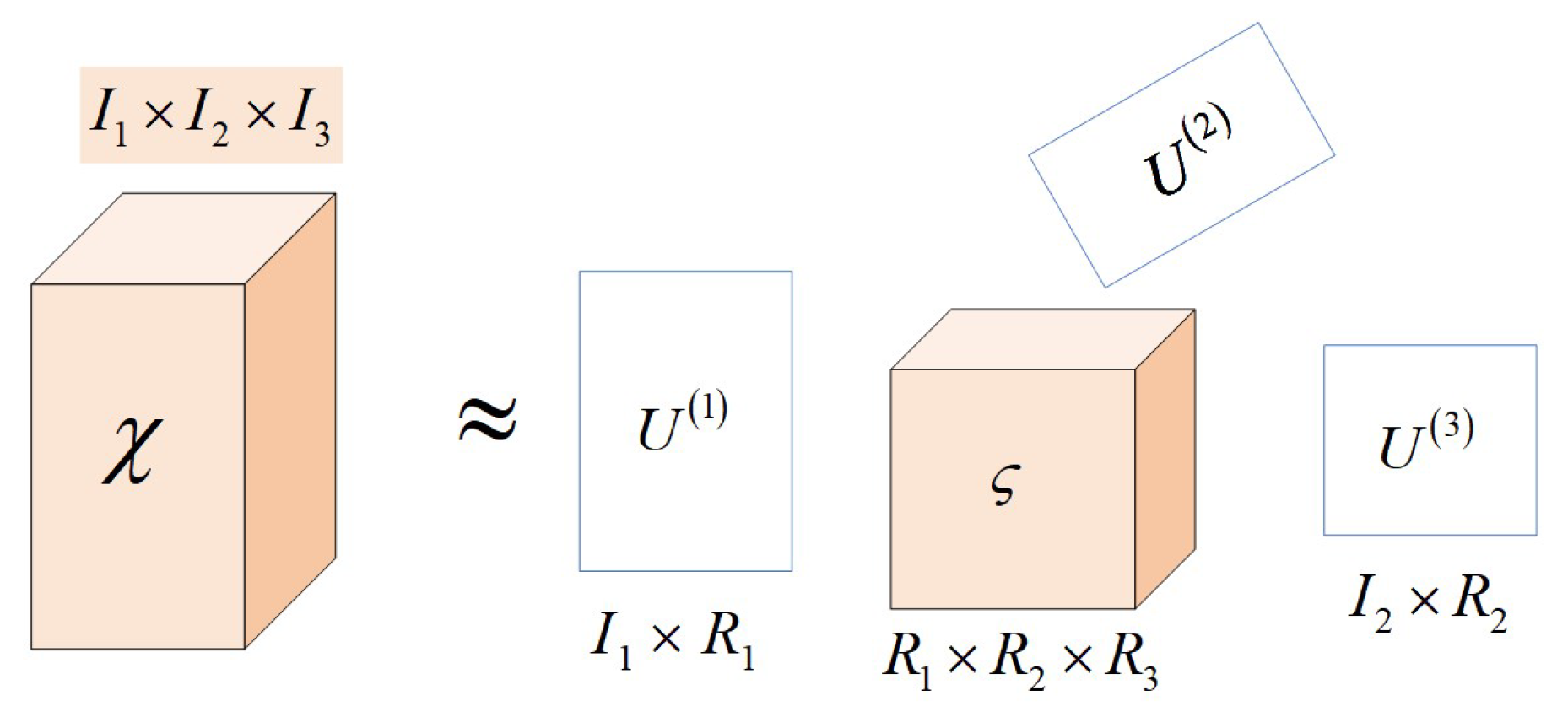
2.3. Tucker Tensor Decomposition
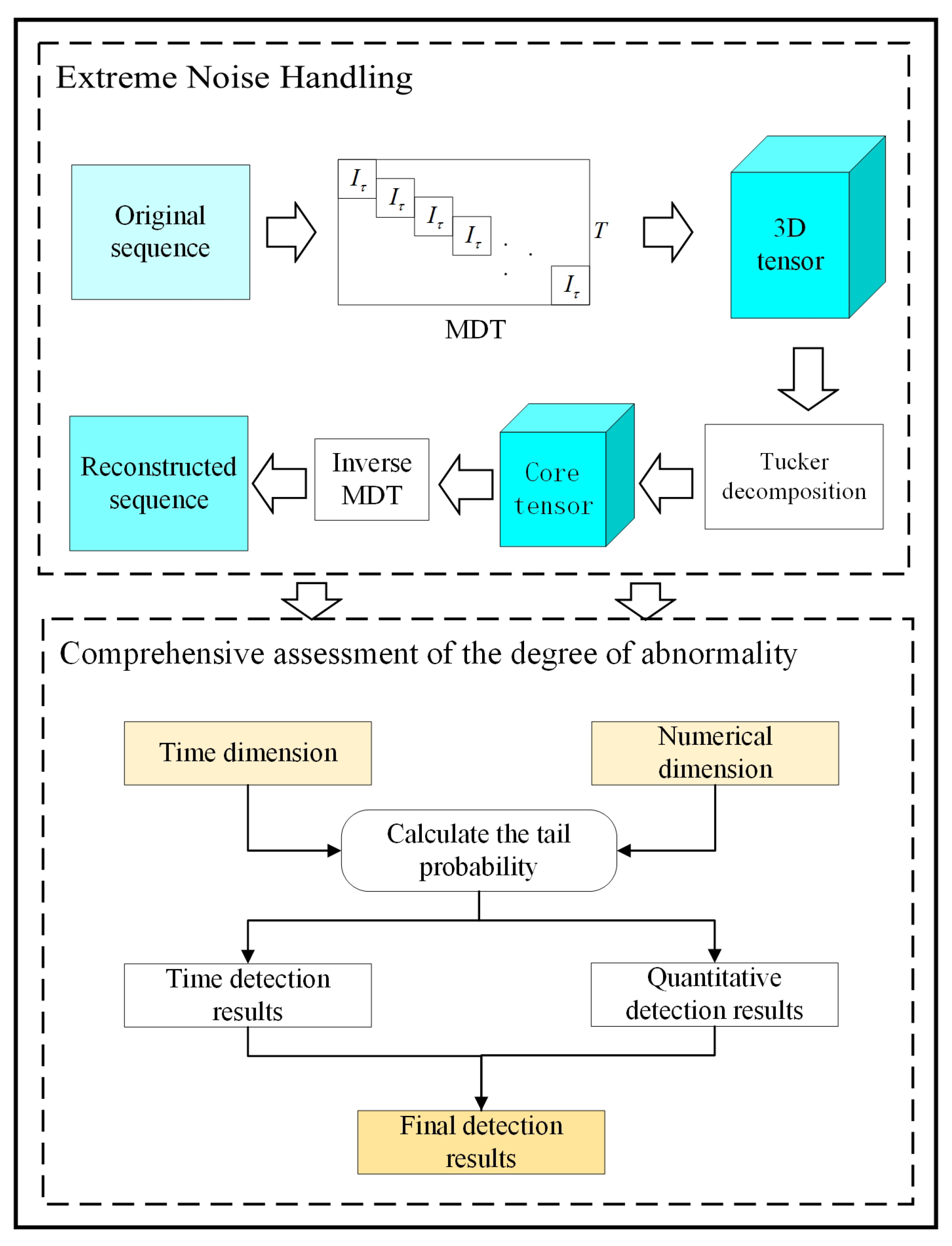
3. The Proposed Method
3.1. Data Pre-Processing
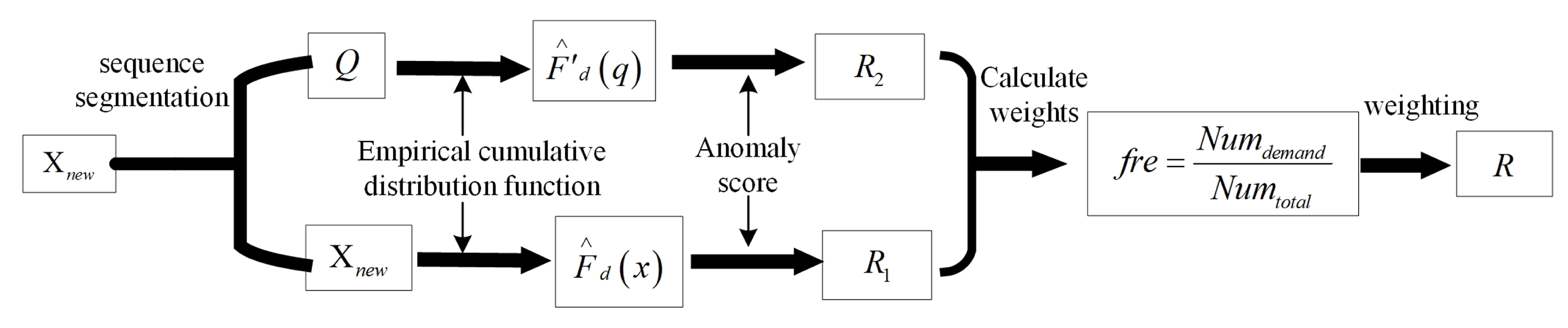
3.2. Anomaly Detection Based on Dual-Tailed Probability
| Algorithm 1: Unsupervised anomaly detection of intermittent demand for spare parts based on dual-tailed probability. |
| Input: An SPD sequence . |
| Output: Detected anomalous demands . |
| Step1: Run Tucker tensor decomposition to obtain the reconstructed sequence by Equation (12). |
| Step2: Split X to obtain a sequence of non-zero demand quantity , and perform the following steps for X and Q: |
| (1) Calculate the empirical left-tailed cumulative distribution function and the empirical right-tailed cumulative distribution function by Equations (13) and (14), approximated as the tail probability. |
| (2) Calculate by Equation (17) the outlier score for each data point in X and for each data point in Q. |
| Step3: Obtain the anomaly detection results and on X and Q based on the relative values of and . Calculate the final result R by Equation (19). |
4. Experimental Results
4.1. Dataset Introduction
4.2. Evaluation Metric
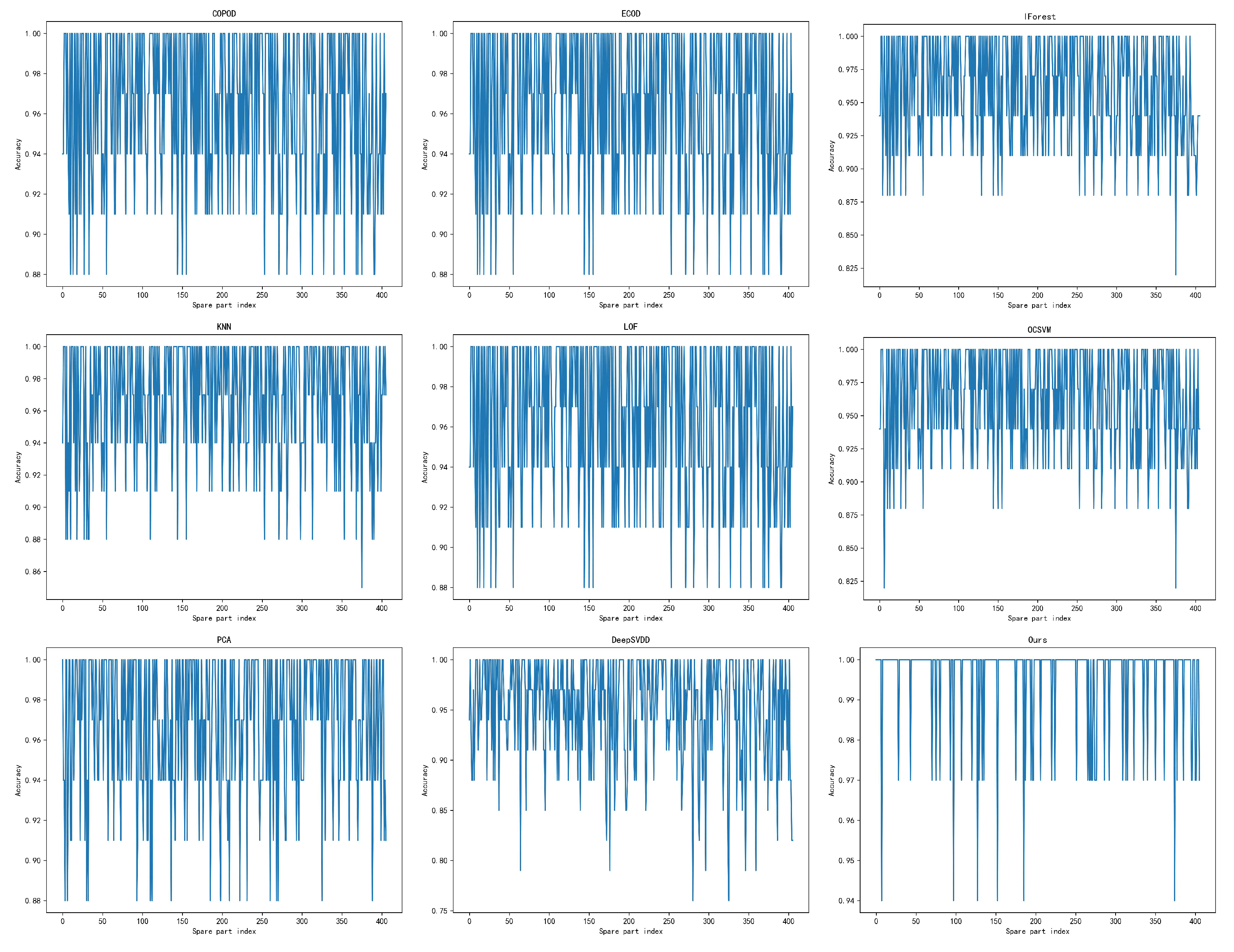
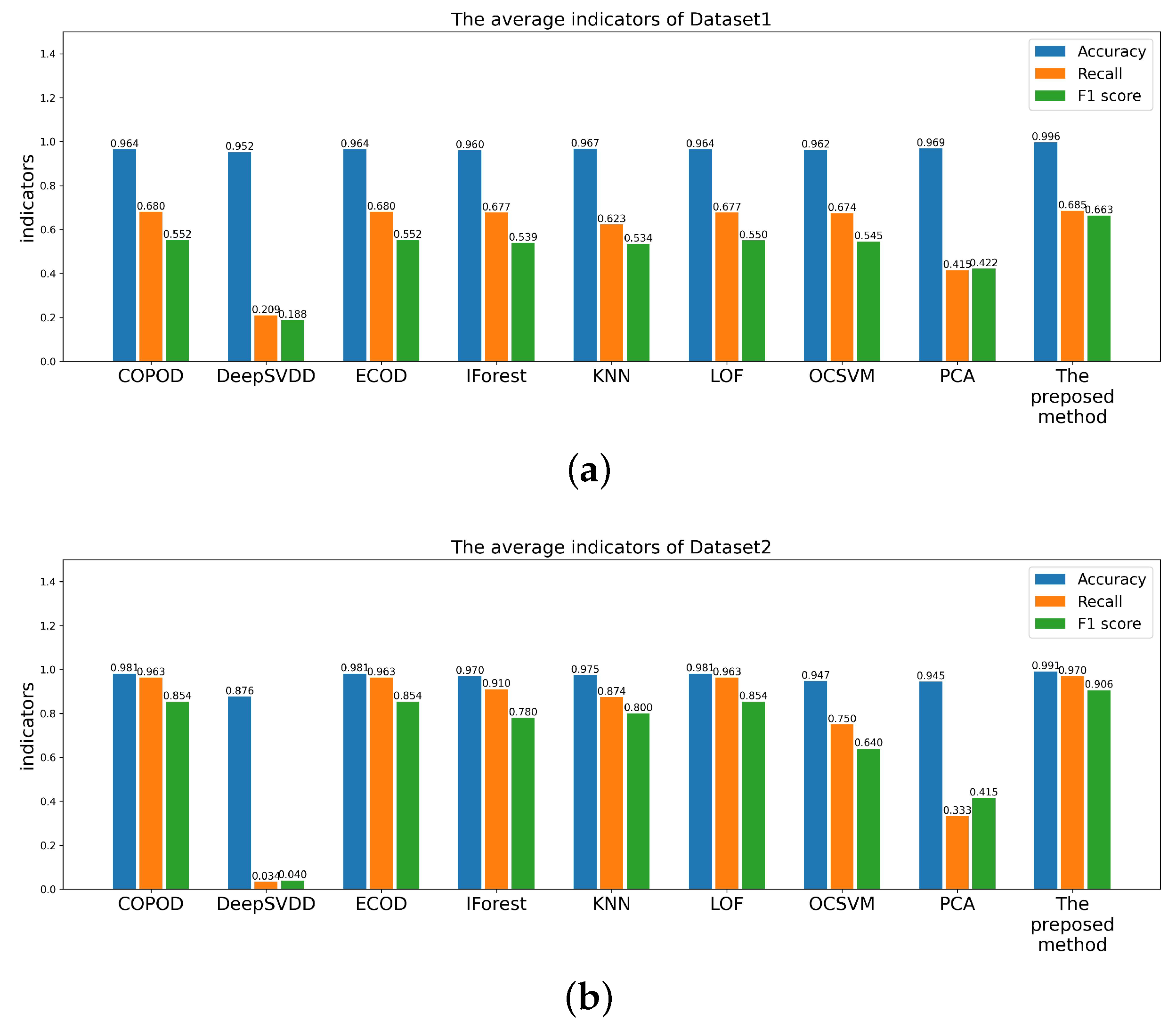
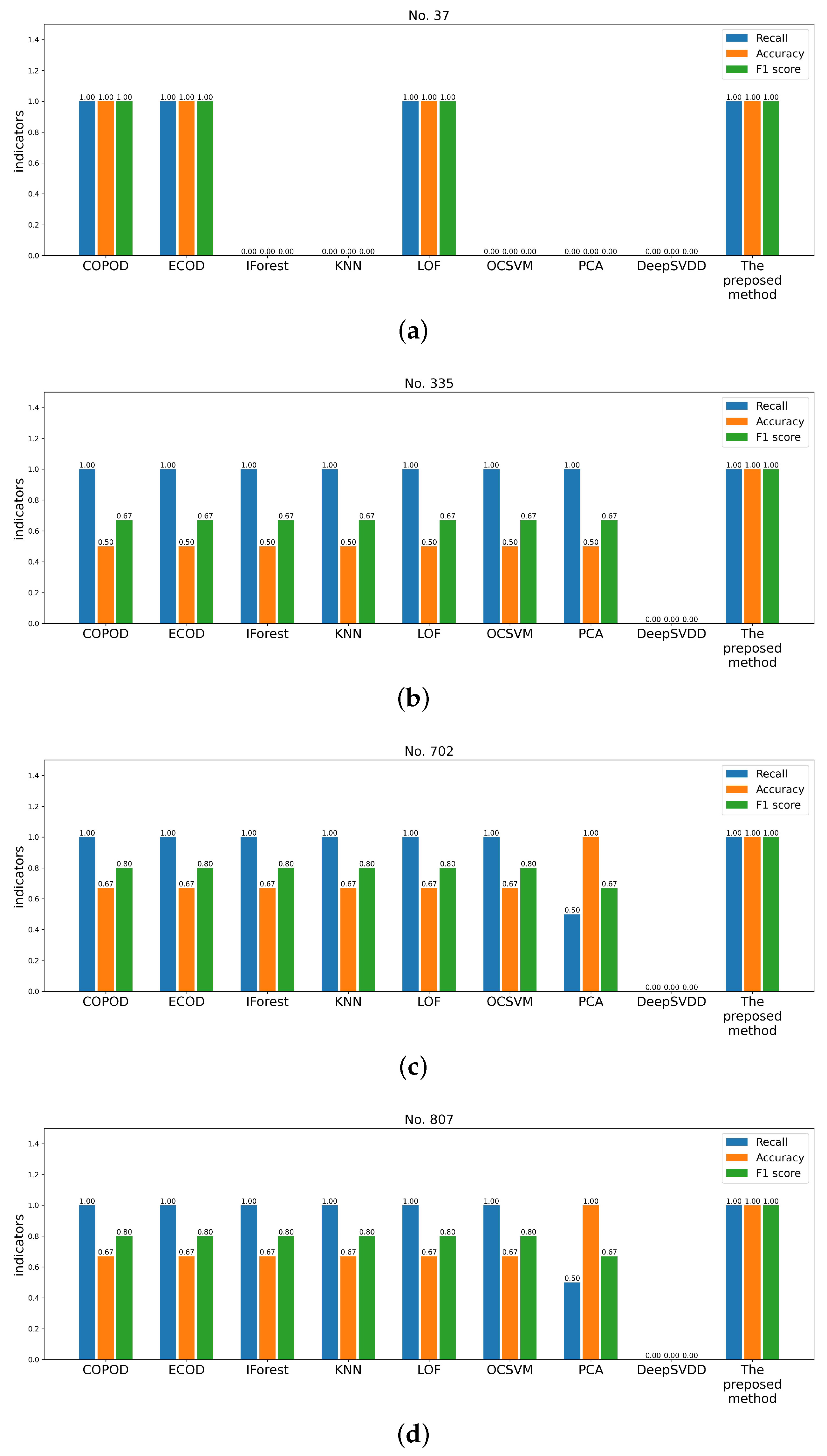
4.3. Comparative Experiment
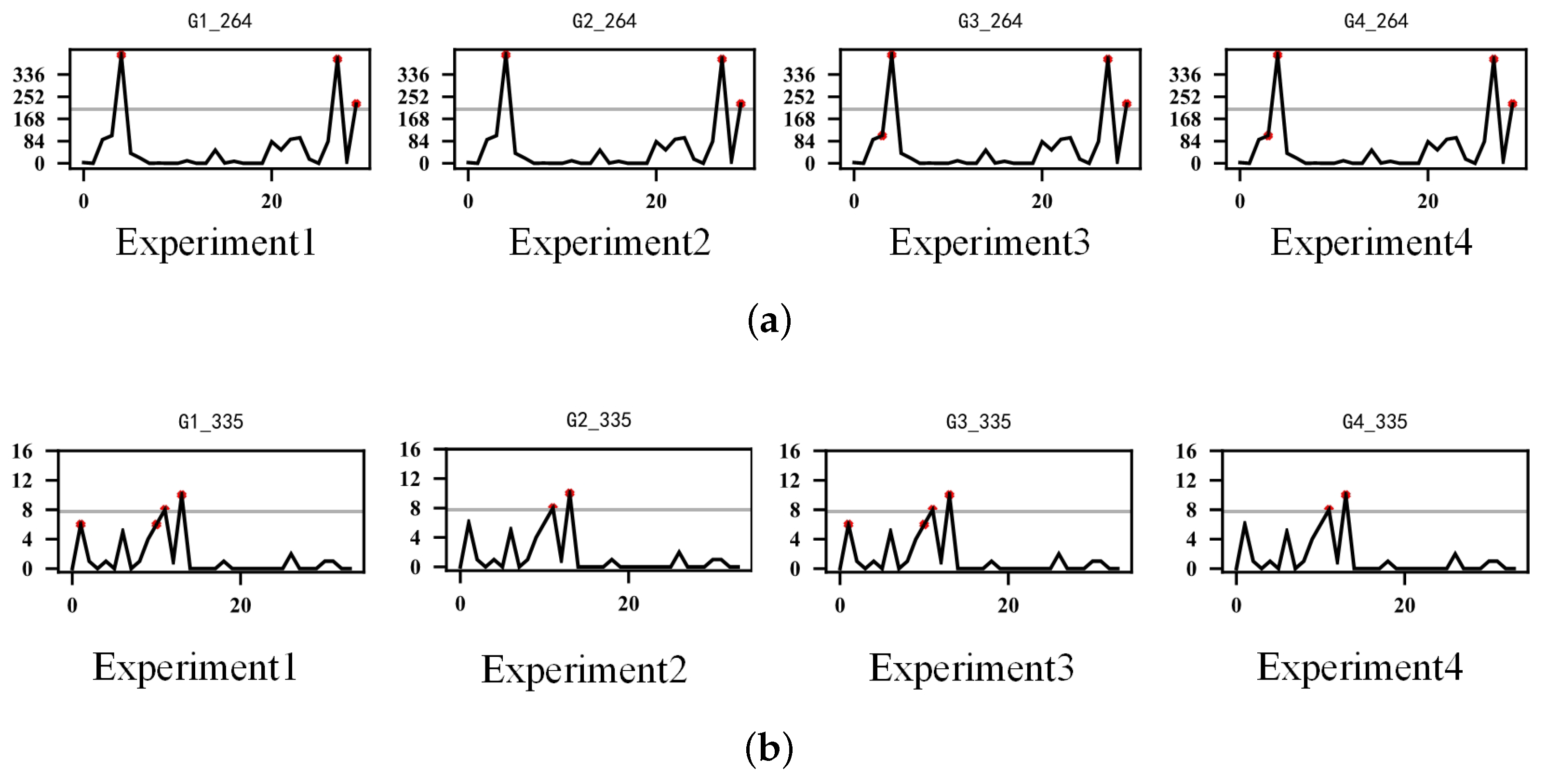
4.4. Ablation Experiment
5. Conclusions
- (1)
- The dual-tailed probability is suitable to detect anomalous demand from real-world SPD sequences since it does not require label information. Both false alarms and missing alarms can be effectively recognized in unsupervised mode, which can broaden the application range.
- (2)
- The proposed method has a very low computational cost by avoiding complex model training like deep learning techniques. A fast anomaly-detection method is of great importance to practical applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bao, Y.; Wang, W.; Zou, H. SVR-based method forecasting intermittent demand for service parts inventories. In Proceedings of the Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing: 10th International Conference, RSFDGrC 2005, Regina, SK, Canada, 31 August–3 September 2005; Proceedings, Part II 10. Springer: Berlin/Heidelberg, Germany, 2005; pp. 604–613. [Google Scholar]
- Van Horenbeek, A.; Buré, J.; Cattrysse, D.; Pintelon, L.; Vansteenwegen, P. Joint maintenance and inventory optimization systems: A review. Int. J. Prod. Econ. 2013, 143, 499–508. [Google Scholar] [CrossRef]
- Moore, J.R., Jr. Forecasting and scheduling for past-model replacement parts. Manag. Sci. 1971, 18, B-200. [Google Scholar] [CrossRef]
- Saaksvuori, A.; Immonen, A. Product Lifecycle Management Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 427–438. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep one-class classification. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4393–4402. [Google Scholar]
- Laptev, N.; Amizadeh, S.; Flint, I. Generic and scalable framework for automated time-series anomaly detection. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1939–1947. [Google Scholar]
- Yaacob, A.H.; Tan, I.K.; Chien, S.F.; Tan, H.K. Arima based network anomaly detection. In Proceedings of the 2010 Second International Conference on Communication Software and Networks, Singapore, 26–28 February 2010; pp. 205–209. [Google Scholar]
- Bontemps, L.; Cao, V.L.; McDermott, J.; Le-Khac, N.A. Collective anomaly detection based on long short-term memory recurrent neural networks. In Proceedings of the Future Data and Security Engineering: Third International Conference, FDSE 2016, Can Tho City, Can Tho City, Vietnam, 23–25 November 2016; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2016; pp. 141–152. [Google Scholar]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Garg, A.; Zhang, W.; Samaran, J.; Savitha, R.; Foo, C.S. An evaluation of anomaly detection and diagnosis in multivariate time series. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2508–2517. [Google Scholar] [CrossRef] [PubMed]
- Deldari, S.; Smith, D.V.; Xue, H.; Salim, F.D. Time series change point detection with self-supervised contrastive predictive coding. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 3124–3135. [Google Scholar]
- Socher, R.; Pennington, J.; Huang, E.H.; Ng, A.Y.; Manning, C.D. Semi-supervised recursive autoencoders for predicting sentiment distributions. In Proceedings of the 2011 Conference on Empirical Methods in Natural Language Processing, Edinburgh, UK, 27–29 July 2011; pp. 151–161. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Park, D.; Hoshi, Y.; Kemp, C.C. A multimodal anomaly detector for robot-assisted feeding using an lstm-based variational autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, K.; Wu, X. LSTM-based VAE-GAN for time-series anomaly detection. Sensors 2020, 20, 3738. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Chen, D.; Goh, J.; Ng, S.k. Anomaly detection with generative adversarial networks for multivariate time series. arXiv 2018, arXiv:1809.04758. [Google Scholar]
- Li, D.; Chen, D.; Jin, B.; Shi, L.; Goh, J.; Ng, S.K. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 703–716. [Google Scholar]
- Fan, L.; Zhang, J.; Mao, W.; Cao, F. Unsupervised Anomaly Detection for Intermittent Sequences Based on Multi-Granularity Abnormal Pattern Mining. Entropy 2023, 25, 123. [Google Scholar] [CrossRef] [PubMed]
- Schmidl, S.; Wenig, P.; Papenbrock, T. Anomaly detection in time series: A comprehensive evaluation. Proc. Vldb Endow. 2022, 15, 1779–1797. [Google Scholar] [CrossRef]
- Li, G.; Jung, J.J. Deep learning for anomaly detection in multivariate time series: Approaches, applications, and challenges. Inf. Fusion 2023, 91, 93–102. [Google Scholar] [CrossRef]
- Kim, J.; Kang, H.; Kang, P. Time-series anomaly detection with stacked Transformer representations and 1D convolutional network. Eng. Appl. Artif. Intell. 2023, 120, 105964. [Google Scholar] [CrossRef]
- Ren, H.; Xu, B.; Wang, Y.; Yi, C.; Huang, C.; Kou, X.; Xing, T.; Yang, M.; Tong, J.; Zhang, Q. Time-series anomaly detection service at microsoft. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 3009–3017. [Google Scholar]
- Bashar, M.A.; Nayak, R. TAnoGAN: Time series anomaly detection with generative adversarial networks. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, Australia, 1–4 December 2020; pp. 1778–1785. [Google Scholar]
- Boukhtouta, A.; Jentsch, P. Support vector machine for demand forecasting of canadian armed forces spare parts. In Proceedings of the 2018 6th International Symposium on Computational and Business Intelligence (ISCBI), Basel, Switzerland, 27–29 August 2018; pp. 59–64. [Google Scholar]
- Yokota, T.; Erem, B.; Guler, S.; Warfield, S.K.; Hontani, H. Missing slice recovery for tensors using a low-rank model in embedded space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8251–8259. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Botta, N.; Ionescu, C.; Hu, X. COPOD: Copula-based outlier detection. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 1118–1123. [Google Scholar]
- Croston, J.D. Forecasting and stock control for intermittent demands. J. Oper. Res. Soc. 1972, 23, 289–303. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Hu, X.; Botta, N.; Ionescu, C.; Chen, G. Ecod: Unsupervised outlier detection using empirical cumulative distribution functions. IEEE Trans. Knowl. Data Eng. 2022, 35, 12181–12193. [Google Scholar] [CrossRef]
- Shyu, M.L.; Chen, S.C.; Sarinnapakorn, K.; Chang, L. A novel anomaly detection scheme based on principal component classifier. In Proceedings of the IEEE Foundations and New Directions of Data Mining Workshop, Melbourne, FL, USA, 19–22 November 2003; pp. 172–179. [Google Scholar]
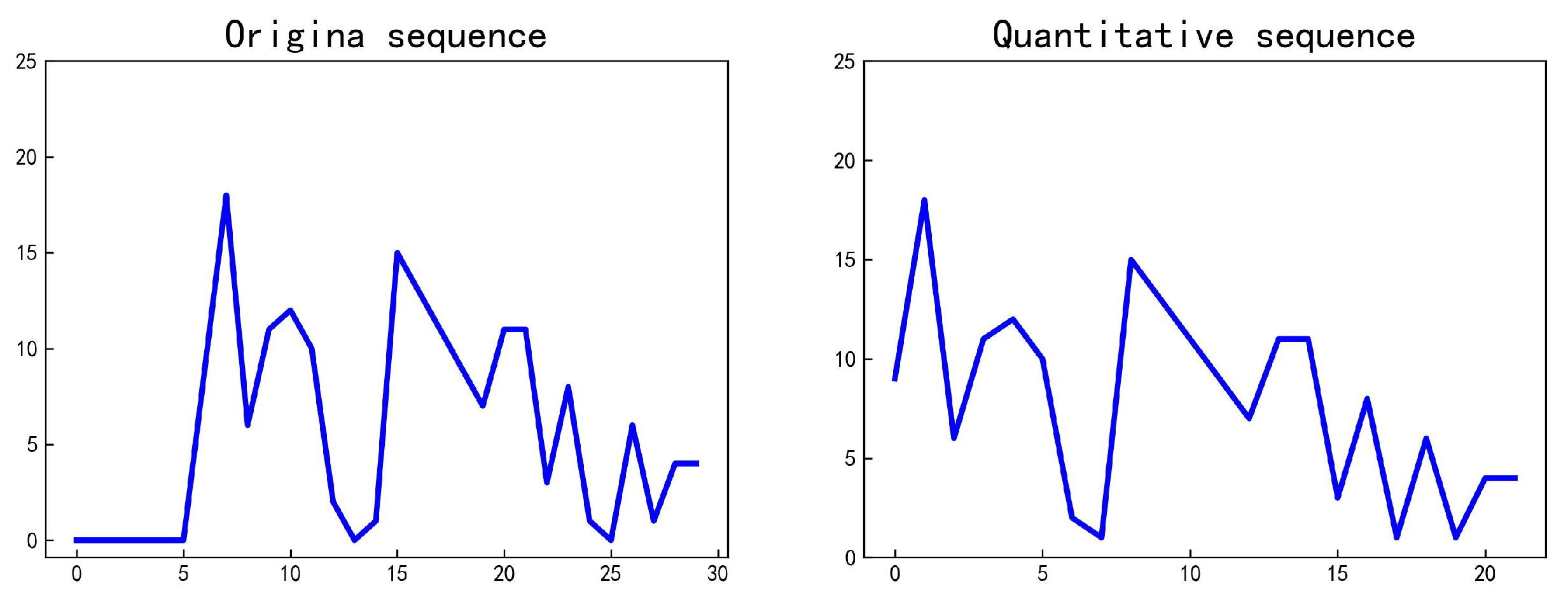





| Original Sequence | Sequence after Segmentation | Category of Sequence | |
|---|---|---|---|
| 0.733 | 1.000 | Unstable sequence | |
| 0.878 | 0.373 | Stable sequence |
| Type | Name |
|---|---|
| Probability Model | COPOD [32] |
| Probability Model | ECOD [34] |
| Probability Model | PCA [35] |
| Partition-Based Method | IForest [8] |
| Distance-Based Method | KNN [7] |
| Density-Based Method | LOFs [6] |
| Classification-Based Method | OCSVM [5] |
| Deep Learning Method | DeepSVDD [9] |
| Dataset | COPOD | ECOD | IForest | KNN | LOFs | OCSVM | PCA | DeepSVDD | Proposed Method |
|---|---|---|---|---|---|---|---|---|---|
| Dataset 1 | 0.4548 | 0.4538 | 85.608 | 1.7463 | 1.7154 | 2.2751 | 1.7513 | 1064.5993 | 1.131 |
| Dataset 2 | 0.2204 | 0.1865 | 50.1218 | 0.9828 | 0.8273 | 0.6951 | 1.166 | 449.343 | 0.4708 |
| Group | Fixed Part | Implementation |
|---|---|---|
| Experiment 1 | Remove sequence segmentation and tensor decomposition | The original SPD sequences are dealt with only by COPOD |
| Experiment 2 | Remove tensor decomposition | The original SPD sequences and the non-zero quantity sequences are dealt with by COPOD. |
| Experiment 3 | Remove sequence segmentation | The sequences after tensor decomposition are dealt with by COPOD. |
| Experiment 4 | None | The proposed method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, K.; Ren, Y.; Li, F.; Mao, W.; Liu, Y. Unsupervised Anomaly Detection of Intermittent Demand for Spare Parts Based on Dual-Tailed Probability. Electronics 2024, 13, 195. https://doi.org/10.3390/electronics13010195
Hong K, Ren Y, Li F, Mao W, Liu Y. Unsupervised Anomaly Detection of Intermittent Demand for Spare Parts Based on Dual-Tailed Probability. Electronics. 2024; 13(1):195. https://doi.org/10.3390/electronics13010195
Chicago/Turabian StyleHong, Kairong, Yingying Ren, Fengyuan Li, Wentao Mao, and Yangshuo Liu. 2024. "Unsupervised Anomaly Detection of Intermittent Demand for Spare Parts Based on Dual-Tailed Probability" Electronics 13, no. 1: 195. https://doi.org/10.3390/electronics13010195
APA StyleHong, K., Ren, Y., Li, F., Mao, W., & Liu, Y. (2024). Unsupervised Anomaly Detection of Intermittent Demand for Spare Parts Based on Dual-Tailed Probability. Electronics, 13(1), 195. https://doi.org/10.3390/electronics13010195







