Vardiational Bayesian Hybrid Multi-Bernoulli and CPHD Filters for Superpositional Sensors
Abstract
1. Introduction
2. Background
2.1. Problem Formulation
2.2. Hybrid Multi-Bernoulli/CPHD (HMB-CPHD) Filter for Superpositional Sensors
- (1)
- Prediction Step
- (2)
- Update Step
2.3. The Variational Bayesian Inference
3. Robust HMB-CPHD Filter for Superpositional Sensors with Unknown Noise Covariance
3.1. GM Implementations for the Original HMB-CPHD Method
- (1)
- Prediction Step
- (2)
- Update Step
3.2. The Proposed Method
| Algorithm 1: Pseudocode for Gaussian mixture implementation of VB-HMB-CPHD filter |
 |
4. Simulations
4.1. Simulation Scene Setup
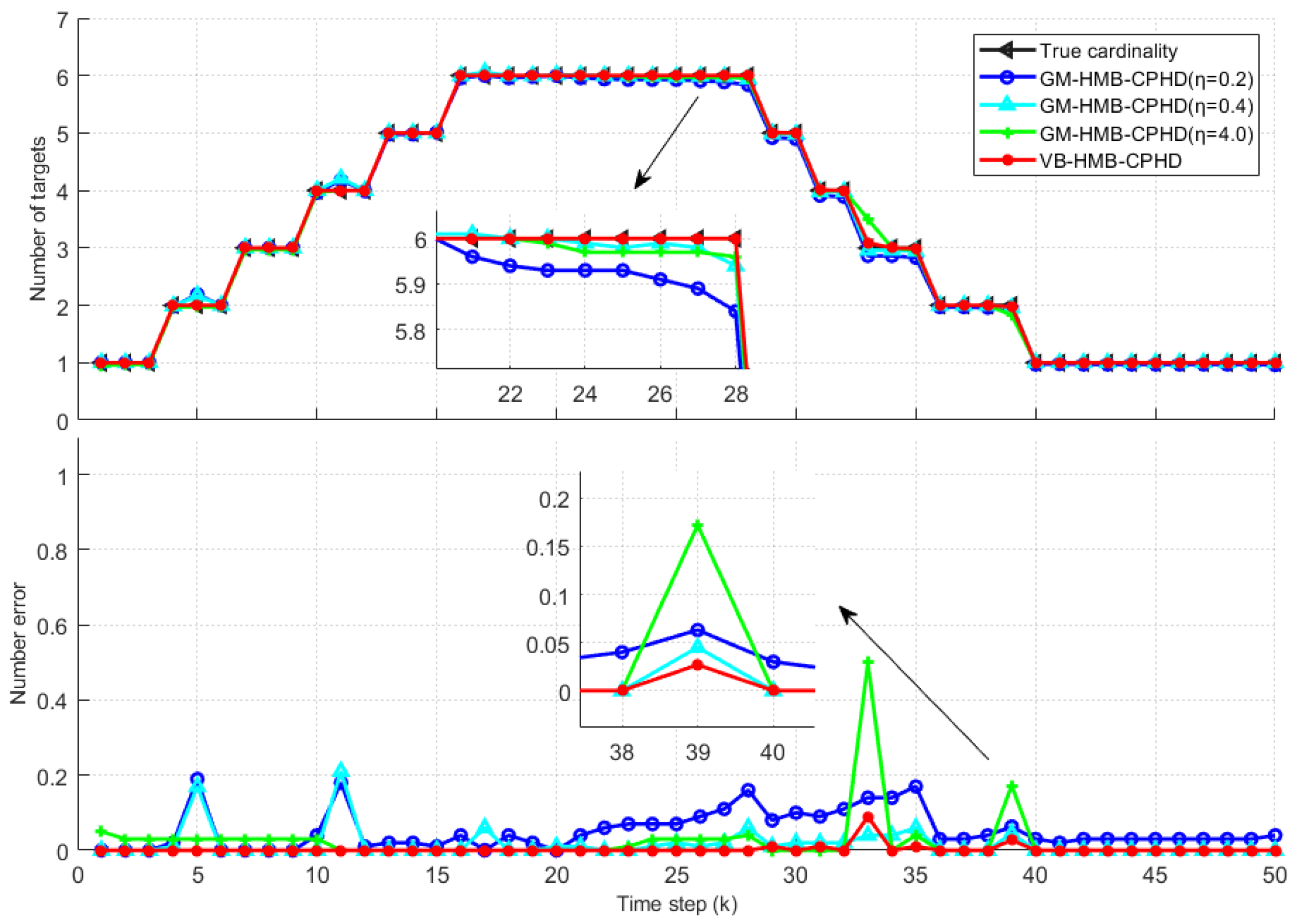
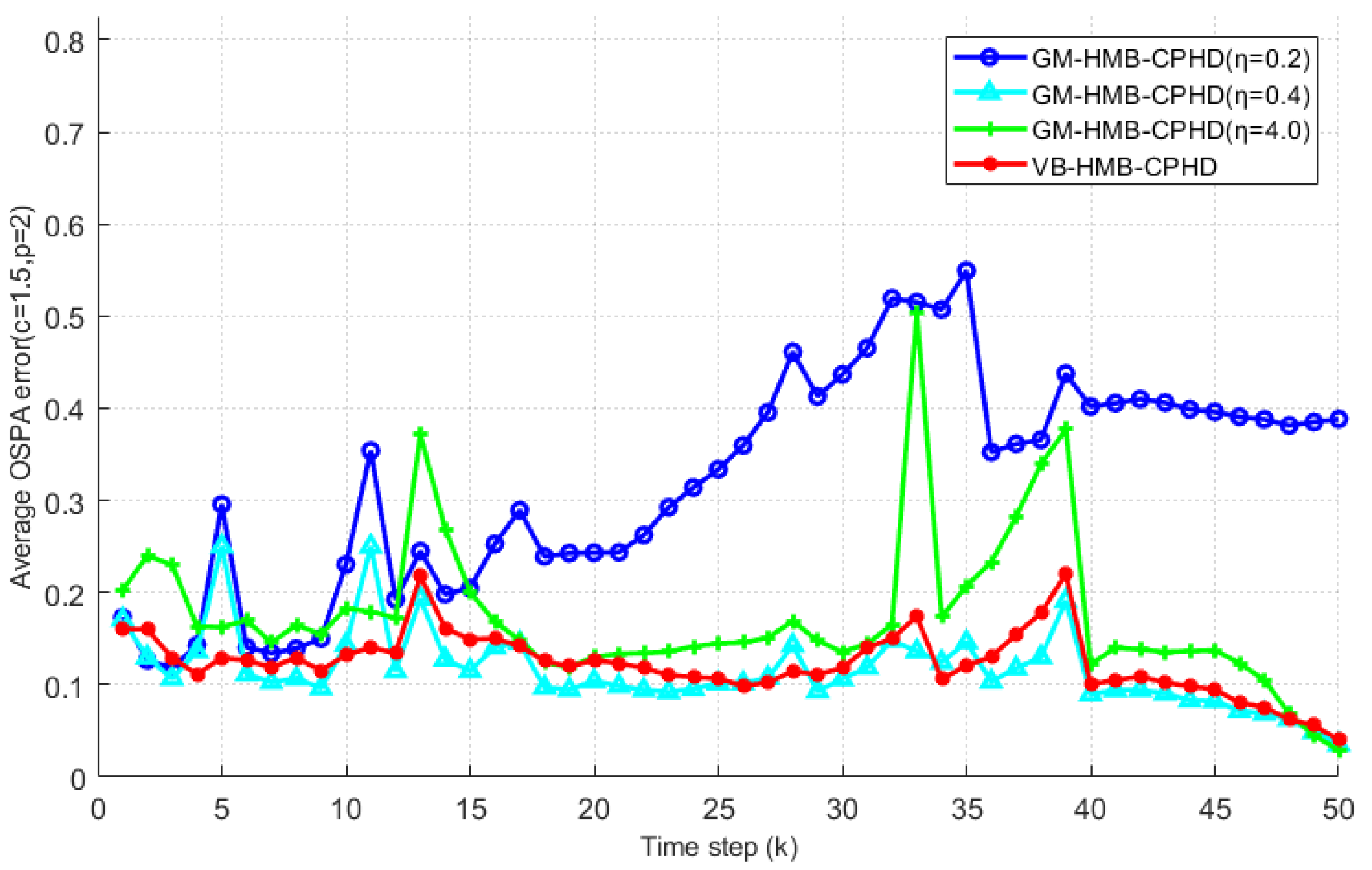
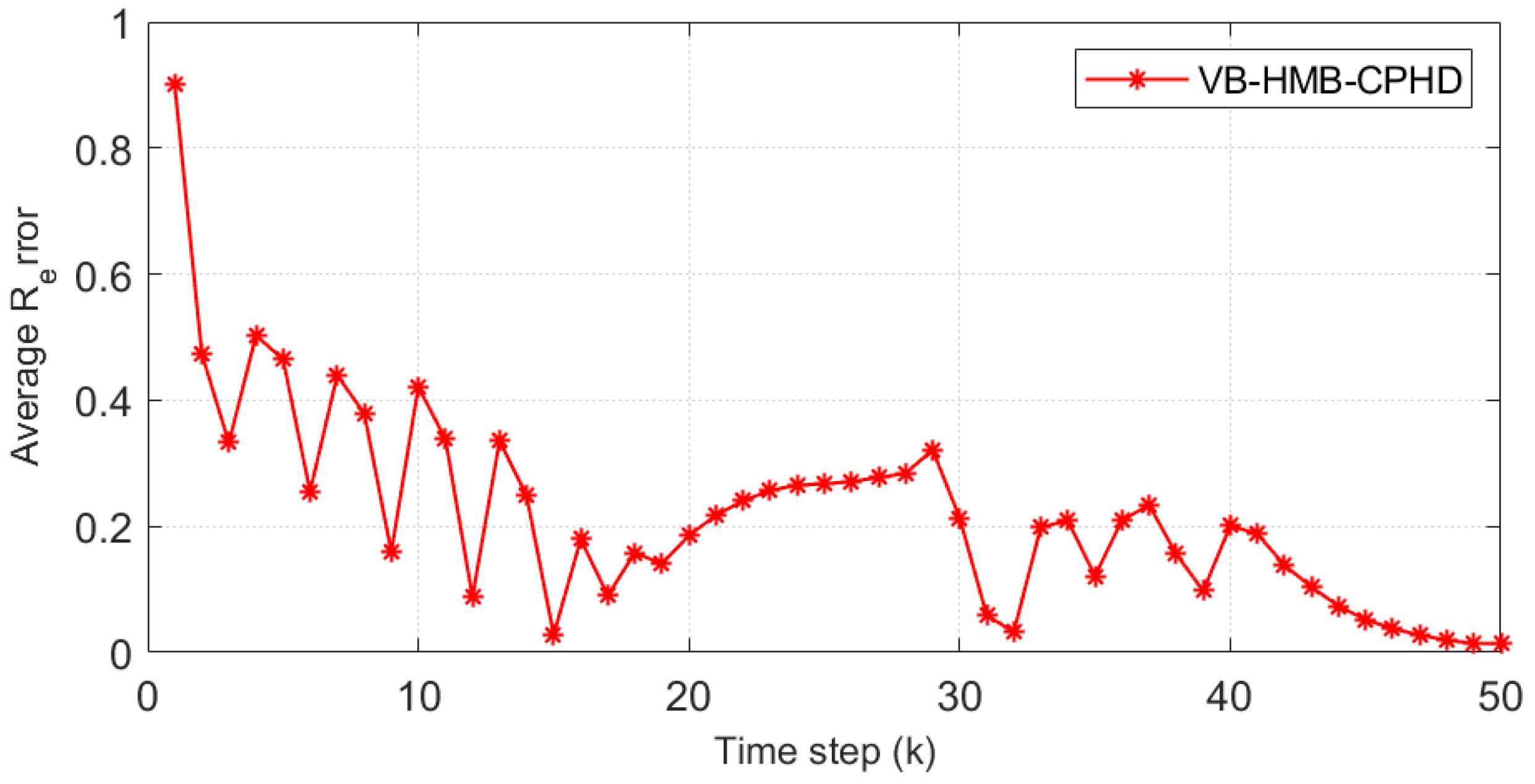
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cf, A.; Fd, A.; Yl, A.; Jin, J.A.; Chen, F.B. Learning dynamic regression with automatic distractor repression for real-time UAV tracking. Eng. Appl. Artif. Intell. 2021, 98, 104116. [Google Scholar]
- Ali, M.A.H.; Mailah, M. Path planning and control of mobile robot in road environments using sensor fusion and active force control. IEEE Trans. Veh. Technol. 2019, 68, 2176–2195. [Google Scholar] [CrossRef]
- Aftab, W.; Mihaylova, L. A learning Gaussian process approach for maneuvering target tracking and smoothing. IEEE Trans. Aerosp. Electron. Syst. 2019, 57, 278–292. [Google Scholar] [CrossRef]
- Shi, K.; Shi, Z.; Yang, C.; He, S.; Chen, A. Road-map aided GM-PHD filter for multi-vehicle tracking with automotive radar. IEEE Trans. Industr Inform. 2021, 18, 97–108. [Google Scholar] [CrossRef]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Oceanic Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef]
- Musicki, D.; Evans, R. Joint Integrated probabilistic data association: JIPDA. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1093–1099. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2009, 19, 5–18. [Google Scholar] [CrossRef]
- Mahler, R.; Ebrary, I. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Mahler, R. CPHD filters for superpositional sensors. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 2–6 August 2009; Volume 7445. [Google Scholar]
- Masnadi-Shirazi, A.; Bhaskar, R.D. A covariance-based superpositional CPHD filter for multisource DOA tracking. IEEE Trans. Signal Process. 2018, 66, 309–323. [Google Scholar] [CrossRef]
- Hlinka, O.; Sluciak, O.; Hlawatsch, F.; Djuric, P.M.; Rupp, M. Likelihood consensus and its application to distributed particle filtering. IEEE Trans. Signal Process. 2012, 60, 4334–4349. [Google Scholar] [CrossRef]
- Wilson, J.; Patwari, N. Radio tomographic imaging with wireless networks. IEEE Trans. Mob. Comput. 2010, 9, 621–632. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M.; Mahler, R. Computationally-tractable approximate PHD and CPHD filters for superpositional sensors. IEEE J. Sel. Top. Signal Process. 2013, 7, 410–420. [Google Scholar] [CrossRef]
- Hauschildt, D. Gaussian mixture implementation of the cardinalized probability hypothesis density filter for superpositional sensors. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–8. [Google Scholar]
- Nannuru, S.; Coates, M. Multi-Bernoulli filter for superpositional sensors. In Proceedings of the International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 368–371. [Google Scholar]
- Nannuru, S.; Coates, M. Particle filter implementation of the multi-Bernoulli filter for superpositional sensors. In Proceedings of the 2013 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), St. Martin, France, 15–18 December 2013; pp. 368–371. [Google Scholar]
- Nannuru, S.; Coates, M. Hybrid multi-Bernoulli and CPHD filters for superpositional sensors. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2847–2863. [Google Scholar] [CrossRef]
- Djuric, P.M.; Miguez, J. Sequential particle filtering in the presence of additive Gaussian noise with unknown parameters. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; pp. 1621–1624. [Google Scholar]
- Li, W.; Jia, Y.; Du, J.; Zhang, J. PHD filter for multi-target tracking with glint noise. Signal Process. 2014, 94, 48–56. [Google Scholar] [CrossRef]
- Li, C.; Rong, W.; Hu, Y.; Wang, J. Cardinalised probability hypothesis density tracking algorithm for extended objects with glint noise. IET Sci. Meas. Technol. 2016, 10, 528–536. [Google Scholar] [CrossRef]
- Hao, Q.; Gaoming, H.; Jun, G. Variational Bayesian labeled multi-Bernoulli filter with unknown sensor noise statistics. Chinese J. Aeronaut. 2016, 29, 1378–1384. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Leung, H.; Shen, K.; Li, M. The labeled multi-Bernoulli filter for multitarget tracking with glint noise. IEEE Trans Aerosp. Electron. Syst. 2019, 55, 2253–2268. [Google Scholar] [CrossRef]
- Vo, B.N.; Ma, W.K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp Electron Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Hartikainen, S. Variational Bayesian adaptation of noise covariances in non-linear Kalman filtering. In Proceedings of the International Workshop on Machine Learning for Signal Processing, Southampton, UK, 22–25 September 2013; pp. 1–6. [Google Scholar]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Automat. Contr. 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Sarkka, S.; Hartikainen, J. Non-linear noise adaptive Kalman filtering via variational Bayes. In Proceedings of the 2013 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Southampton, UK, 22–25 September 2013; pp. 1–6. [Google Scholar]
- Li, G.; Wei, P.; Li, Y.; Gao, L.; Zhang, H. A robust fast LMB Filter for superpositional sensors. Signal Process. 2020, 174, 107606. [Google Scholar] [CrossRef]
- Li, Y.; Xi, C.; Coates, M.; Bo, Y. Sequential monte carlo radio-frequency tomographic tracking. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3976–3979. [Google Scholar]
- Nannuru, S.; Li, Y.; Coates, M.; Yang, B. Multi-target device-free tracking using radio frequency tomography. In Proceedings of the 2011 Seventh International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Adelaide, SA, Australia, 6–9 December 2011; pp. 508–513. [Google Scholar]
- Nannuru, S.; Li, Y.; Zeng, Y.; Coates, M.; Yang, B. Radio-frequency tomography for passive indoor multitargettracking. IEEE Trans. Mob Comput. 2013, 12, 2322–2333. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential monte carlo methods for multi-target filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhang, H.; Li, G.; Li, W. Vardiational Bayesian Hybrid Multi-Bernoulli and CPHD Filters for Superpositional Sensors. Electronics 2023, 12, 2083. https://doi.org/10.3390/electronics12092083
Xu W, Zhang H, Li G, Li W. Vardiational Bayesian Hybrid Multi-Bernoulli and CPHD Filters for Superpositional Sensors. Electronics. 2023; 12(9):2083. https://doi.org/10.3390/electronics12092083
Chicago/Turabian StyleXu, Wenjie, Huaguo Zhang, Gaiyou Li, and Wanchun Li. 2023. "Vardiational Bayesian Hybrid Multi-Bernoulli and CPHD Filters for Superpositional Sensors" Electronics 12, no. 9: 2083. https://doi.org/10.3390/electronics12092083
APA StyleXu, W., Zhang, H., Li, G., & Li, W. (2023). Vardiational Bayesian Hybrid Multi-Bernoulli and CPHD Filters for Superpositional Sensors. Electronics, 12(9), 2083. https://doi.org/10.3390/electronics12092083






