A Polar Moving Base Alignment Based on Backtracking Scheme
Abstract
1. Introduction
2. The Polar Coarse and Fine Alignment Methods
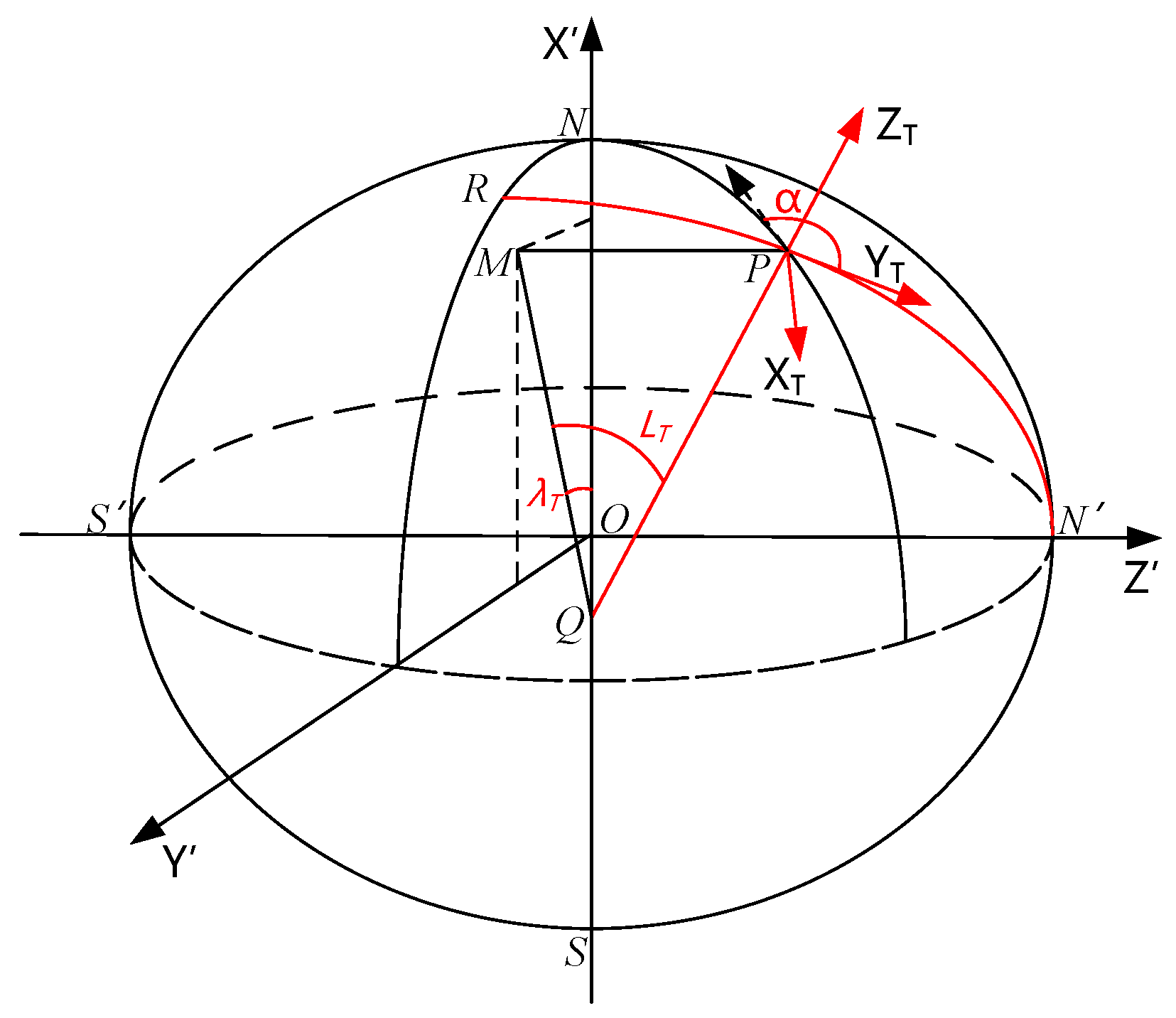
2.1. Transverse Earth Model and the Definition of Transverse Frame
- The Earth-Centered inertial frame, : the origin, , is at the center of the Earth, the axis points towards the vernal equinox, and the axis points towards the North Pole;
- Earth-Fixed frame, : the origin, , is at the center of the Earth, the axis points to the prime meridian, and the axis points to the North Pole;
- The transverse Earth frame, : the origin, , is at the center of the Earth, the axis points to the transverse prime meridian, and the axis points to the transverse North Pole;
- The transverse geographic frame, : the origin, , is the center of the mass of the carrier. The axis points to the north in the transverse direction, and the axis is perpendicular to the local transverse plane and points to the sky;
- The body frame, : The origin, , is at the center of the mass of the body. The axis points to the right of the body, the axis points forward along the longitudinal axis, and the axis points upward along the body axis;
- The initial transverse inertial frame, : the origin, , is at the center of the Earth, the axis points to the transverse North Pole, and the axis is parallel to the in the transverse equatorial plane;
- The initial transverse Earth frame, : the frame, , at the initial moment;
- The initial transverse geographic frame, : the frame, , at the initial moment;
- The initial body frame, : at the initial moment, the frame, , coincides with the frame, , and after the alignment begins, the frame, , remains fixed and does not move with the body.
2.2. The Inertial Frame Coarse Alignment Algorithm Aided by the Based on the Transverse Earth Model
2.3. The Polar Fine Alignment Method Assisted by DVL under Large Azimuth Misalignment
2.4. The Polar Fine Alignment Method Assisted by DVL under Small Misalignment
3. The Polar Backtracking Alignment Method
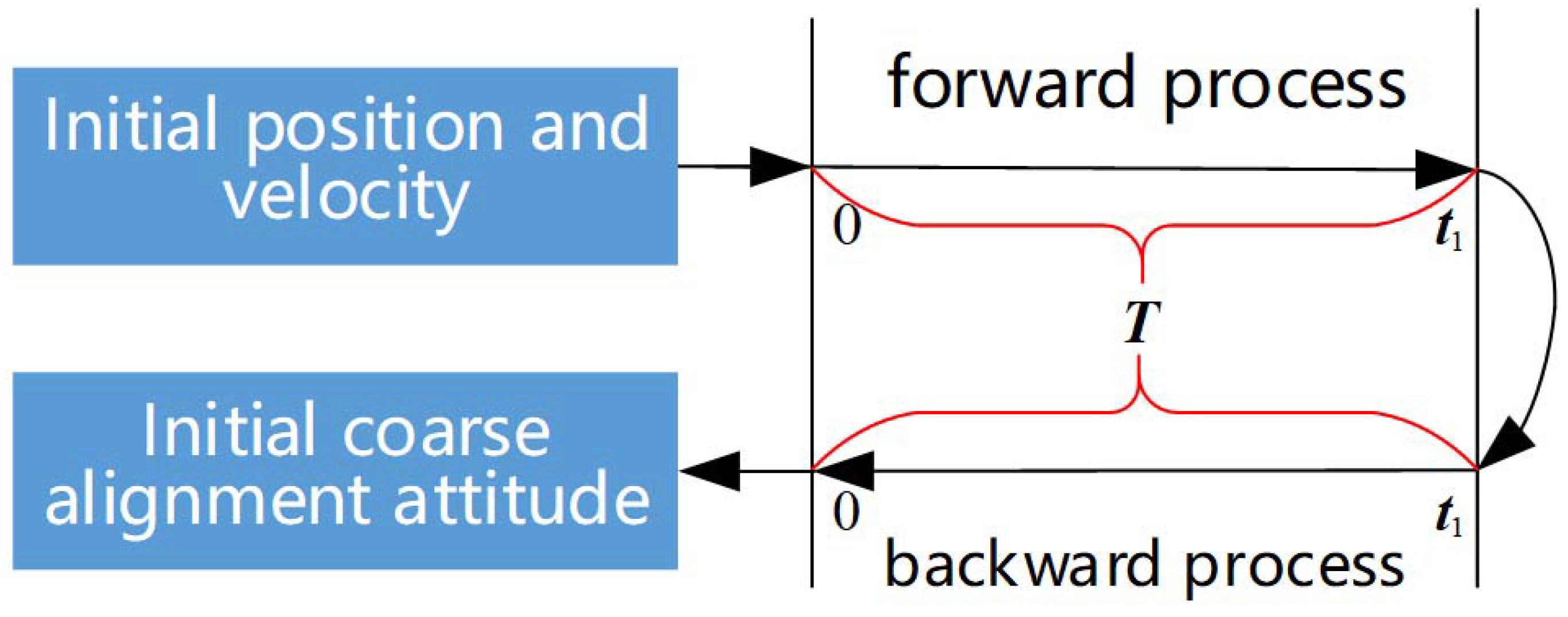
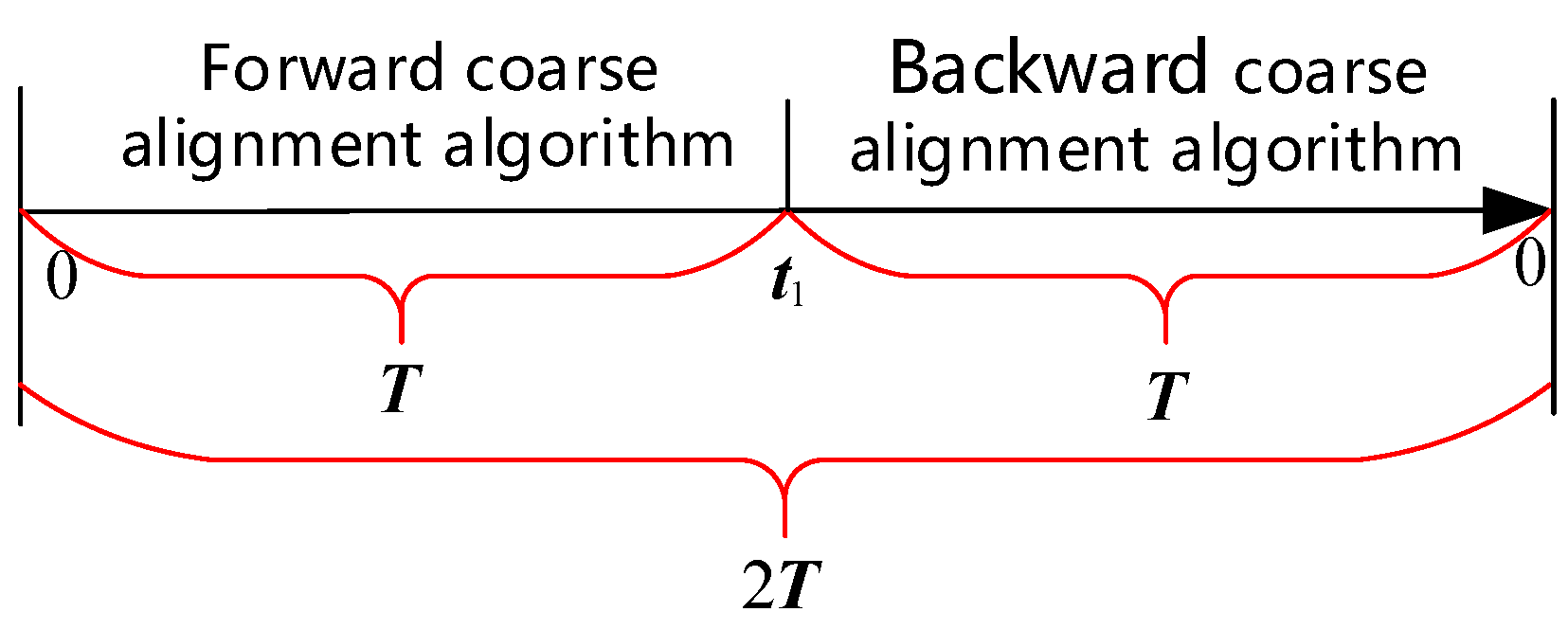
3.1. The Polar Backtracking Coarse Alignment Method
- Use the inertial frame coarse alignment algorithm in Section 2.2 to complete the forward coarse alignment and store the parameters in and , the gyroscope, the accelerometer, and the DVL data as the forward data;
- Use the partially stored data in the forward process to simulate the data required for the backward coarse alignment process, as detailed in Table 1;
- Continue the forward coarse alignment process and use Equations (41)–(43) to perform the backward coarse alignment. Finally, the initial attitude matrix, , can be directly obtained.
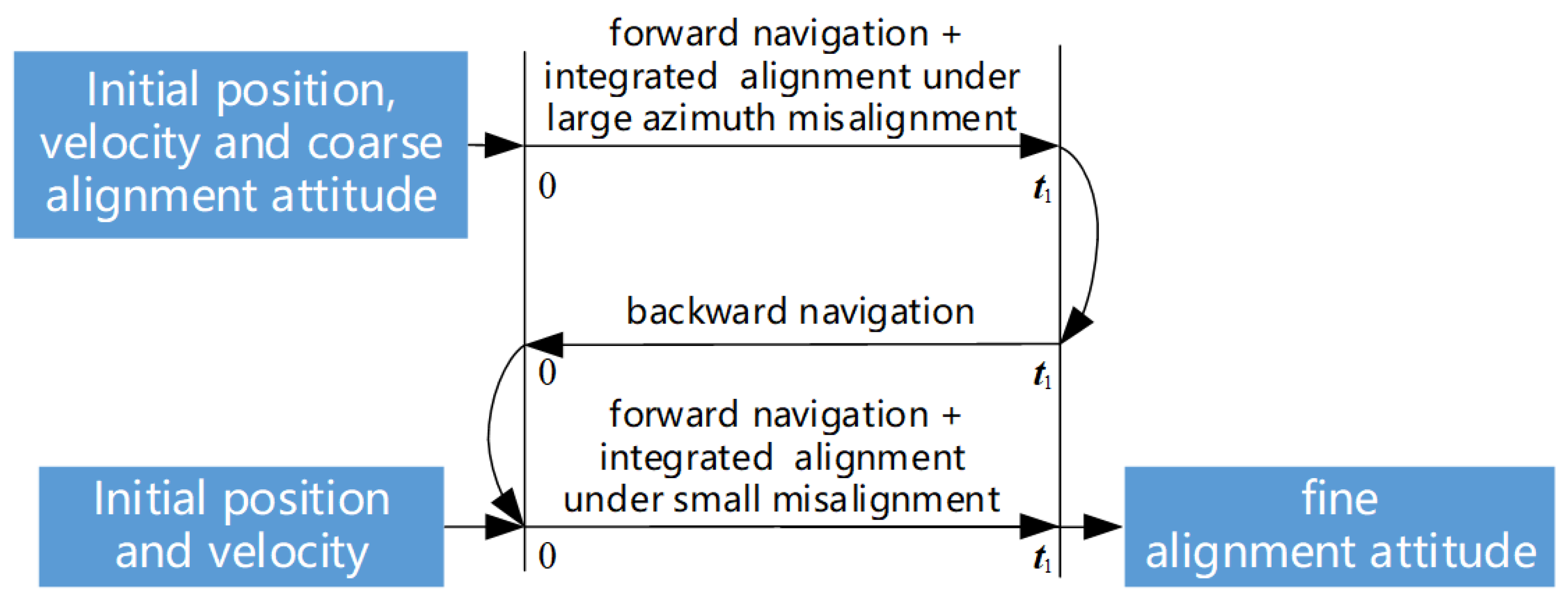
3.2. The Polar Backtracking Fine Alignment Method
- Use Equations (50)–(53) and the algorithm in Section 2.3 to perform forward navigation and achieve the polar integrated fine alignment under the large misalignment;
- Utilize the data required for the backward navigation process generated through forward data simulation, and use the initial navigation parameters estimated for the forward navigation process, which consist of the attitude, velocity, and position at the final time, to perform backward navigation with Equations (55)–(58);
- Using the known initial position and velocity at the starting time for the forward navigation process, the attitude obtained from the backward navigation process at the final time is employed as the initial attitude for the forward navigation process. Equations (50)–(53) and the algorithm in Section 2.4 are then used to perform forward navigation and achieve a precise alignment of the small misalignment angle combination, resulting in the attitude matrix, , at the final time and completing the alignment of the dynamic base.
4. Experimental Results and Analysis
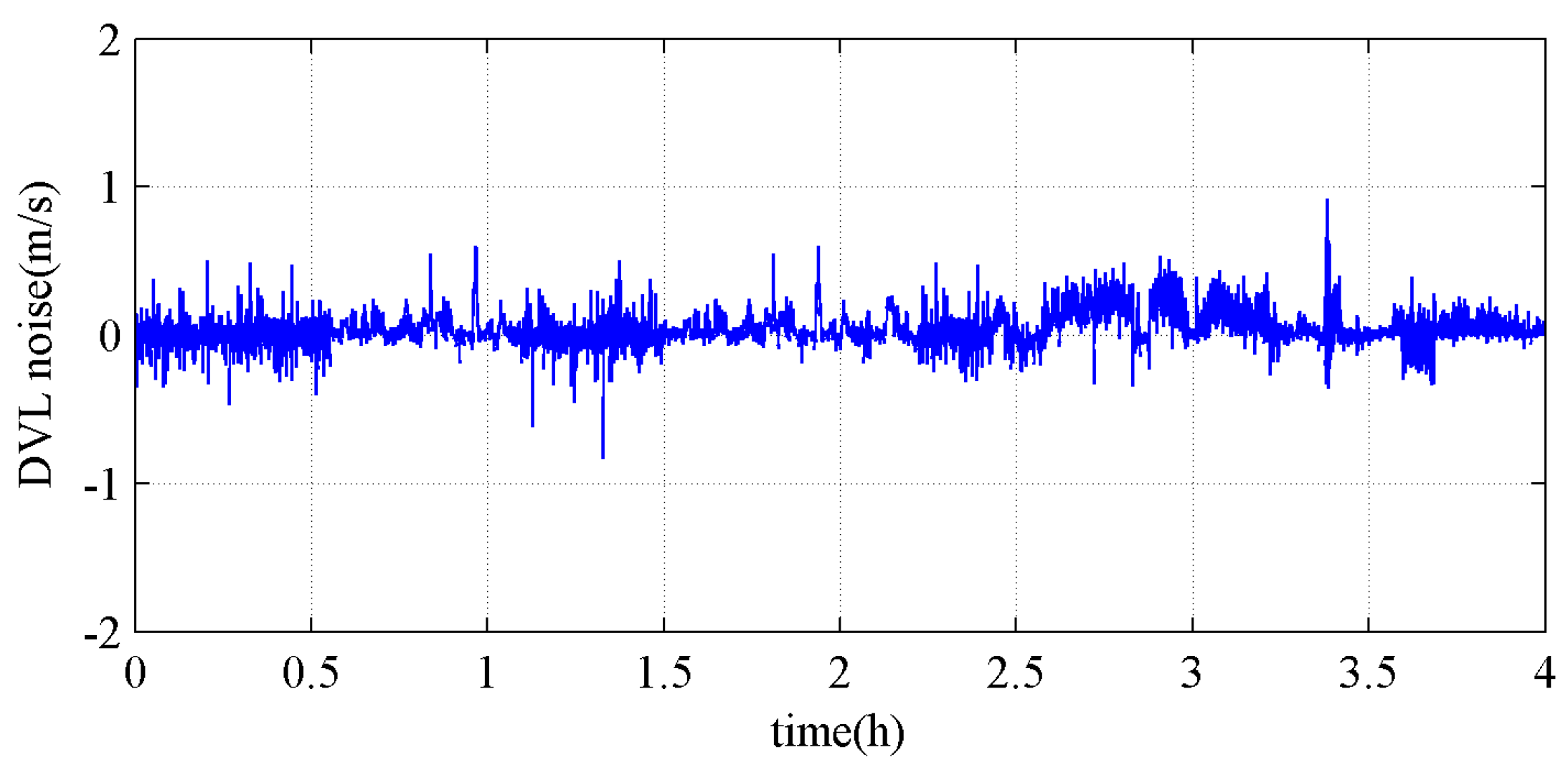
4.1. Semi-Physical Experimental Conditions
- (1)
- The navigation parameters in the mid-latitude region:
- (2)
- The navigation parameters in the polar region:
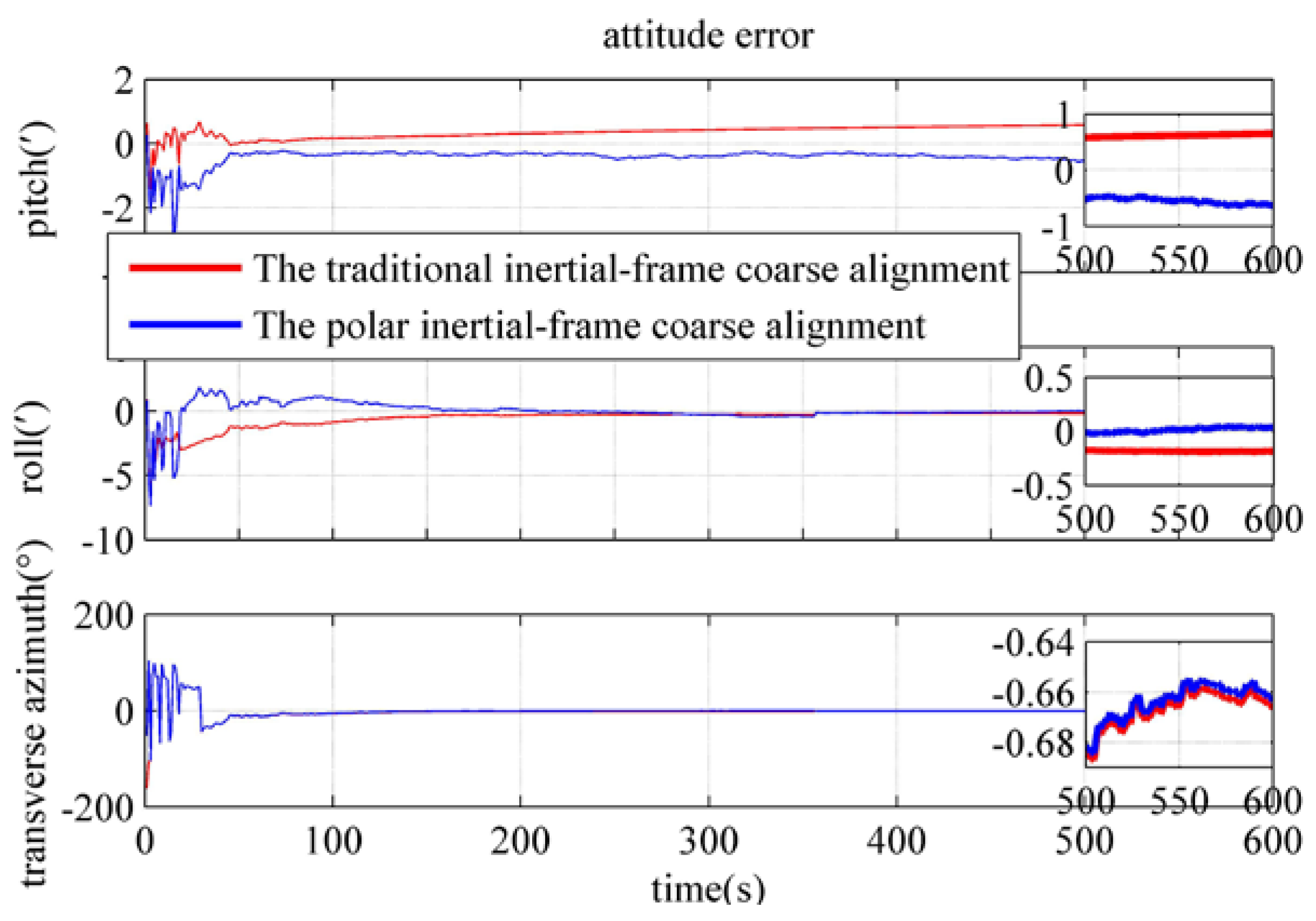
4.2. Performance Verification of the Inertial Frame Coarse Alignment Algorithm under the Transverse Earth Model
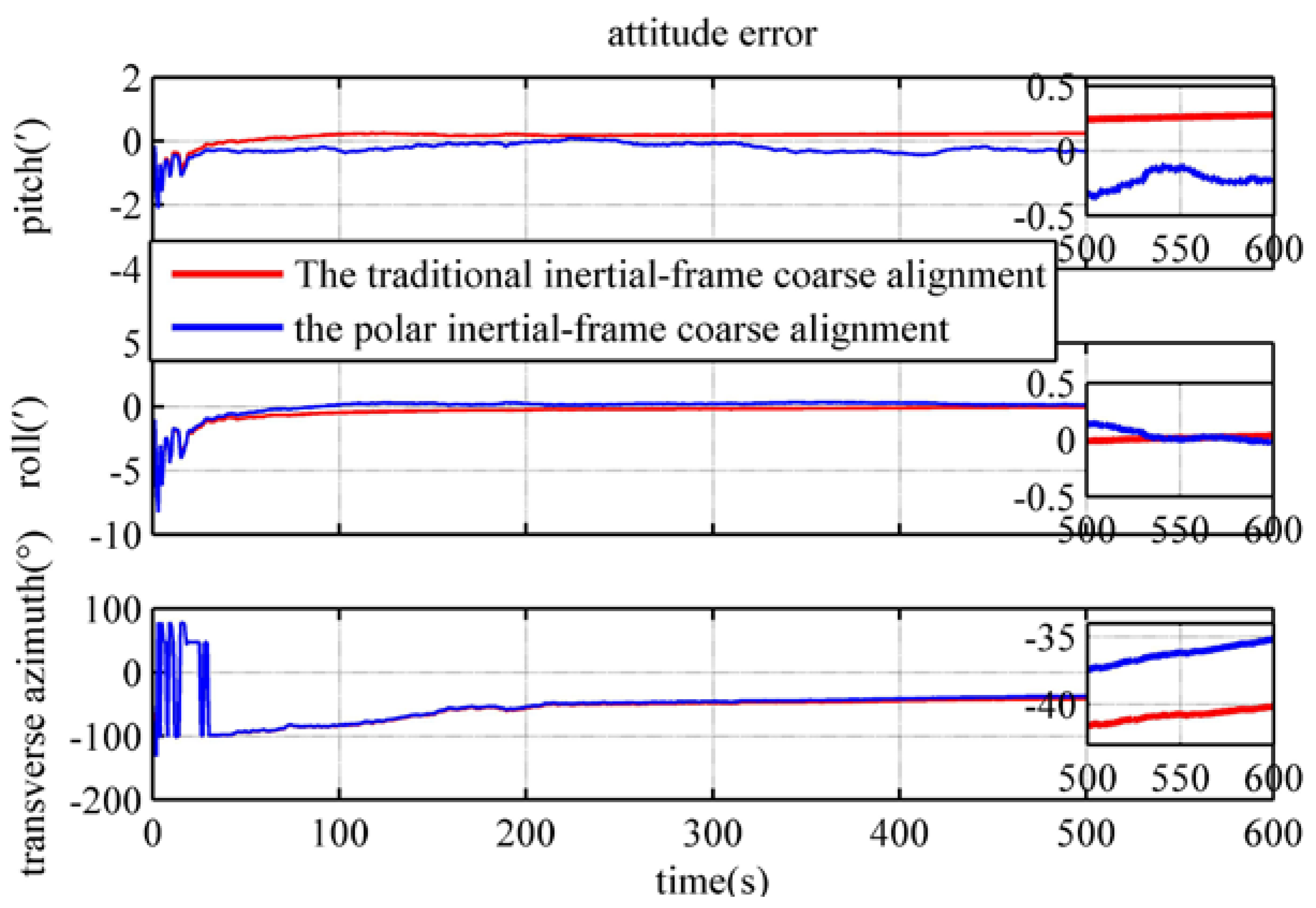
4.3. Performance Verification of the Polar Backtracking Coarse Alignment Algorithm
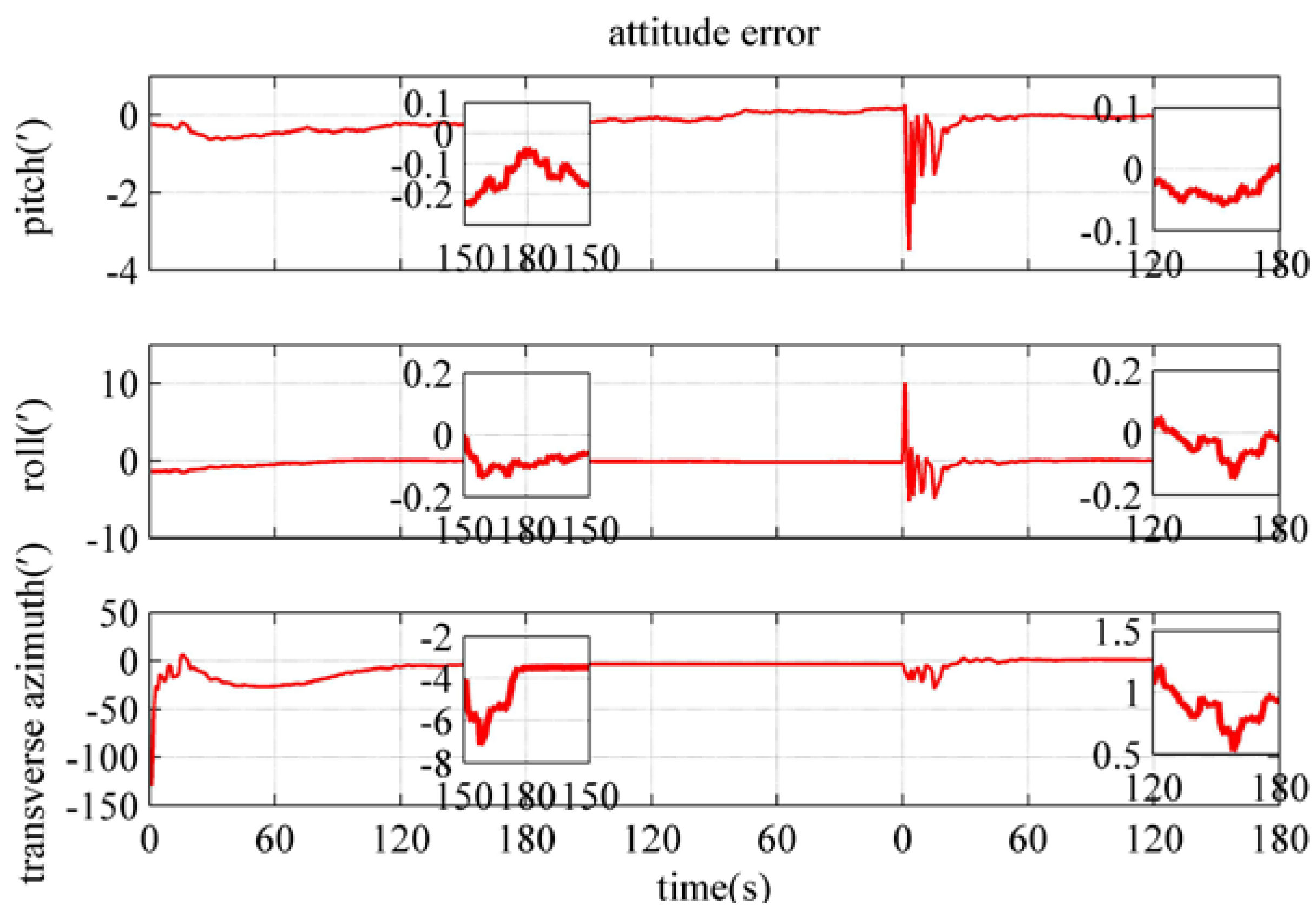
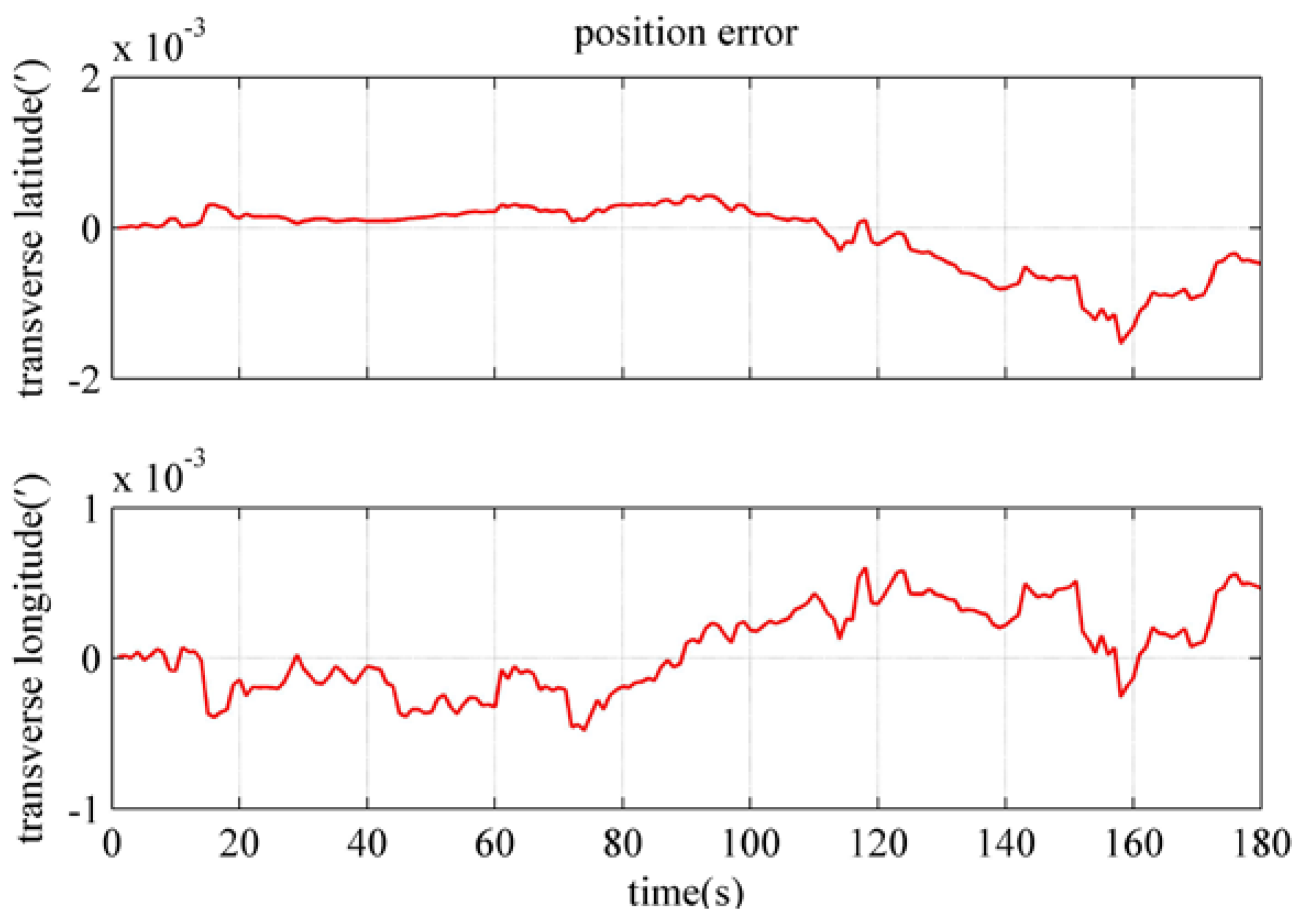
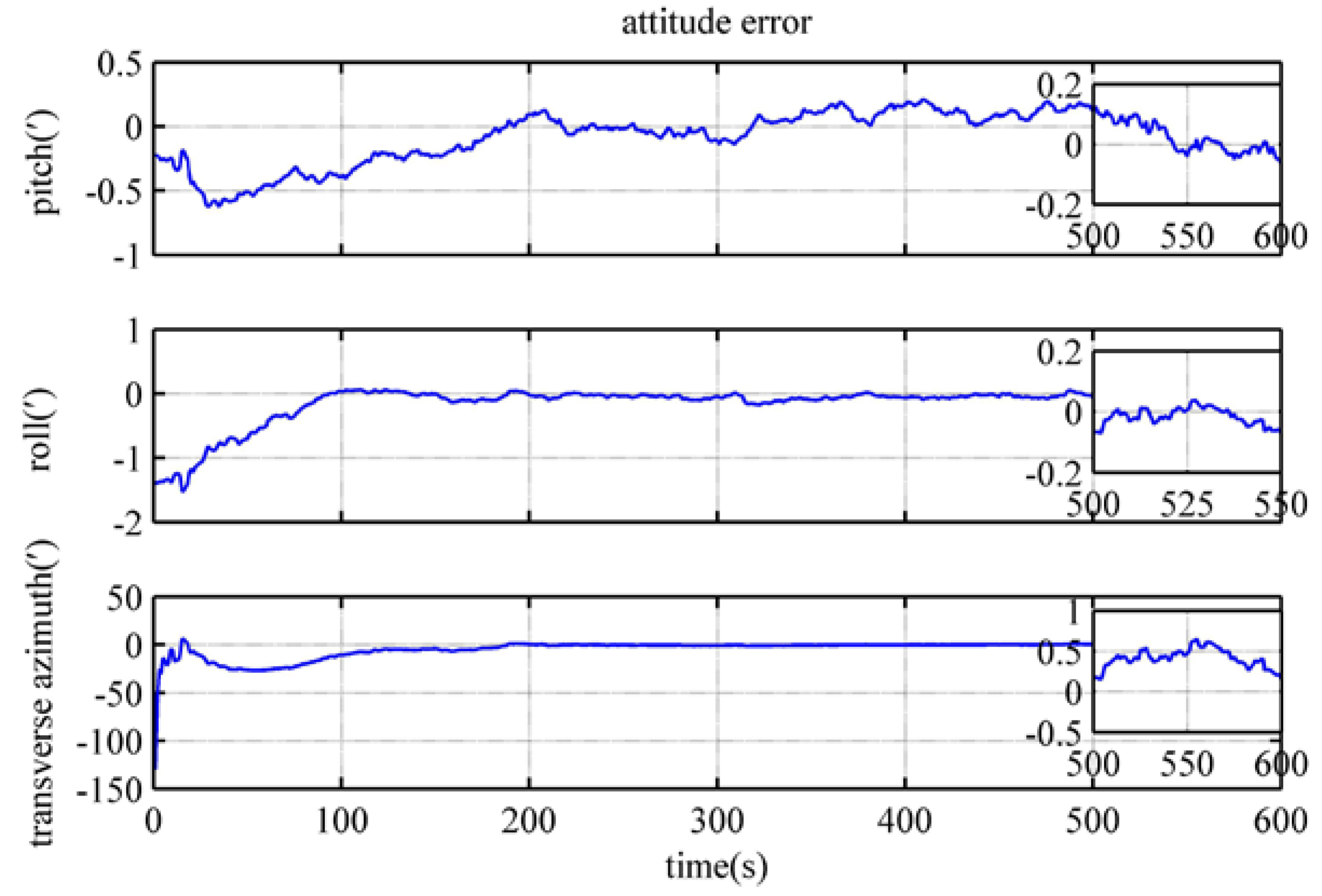
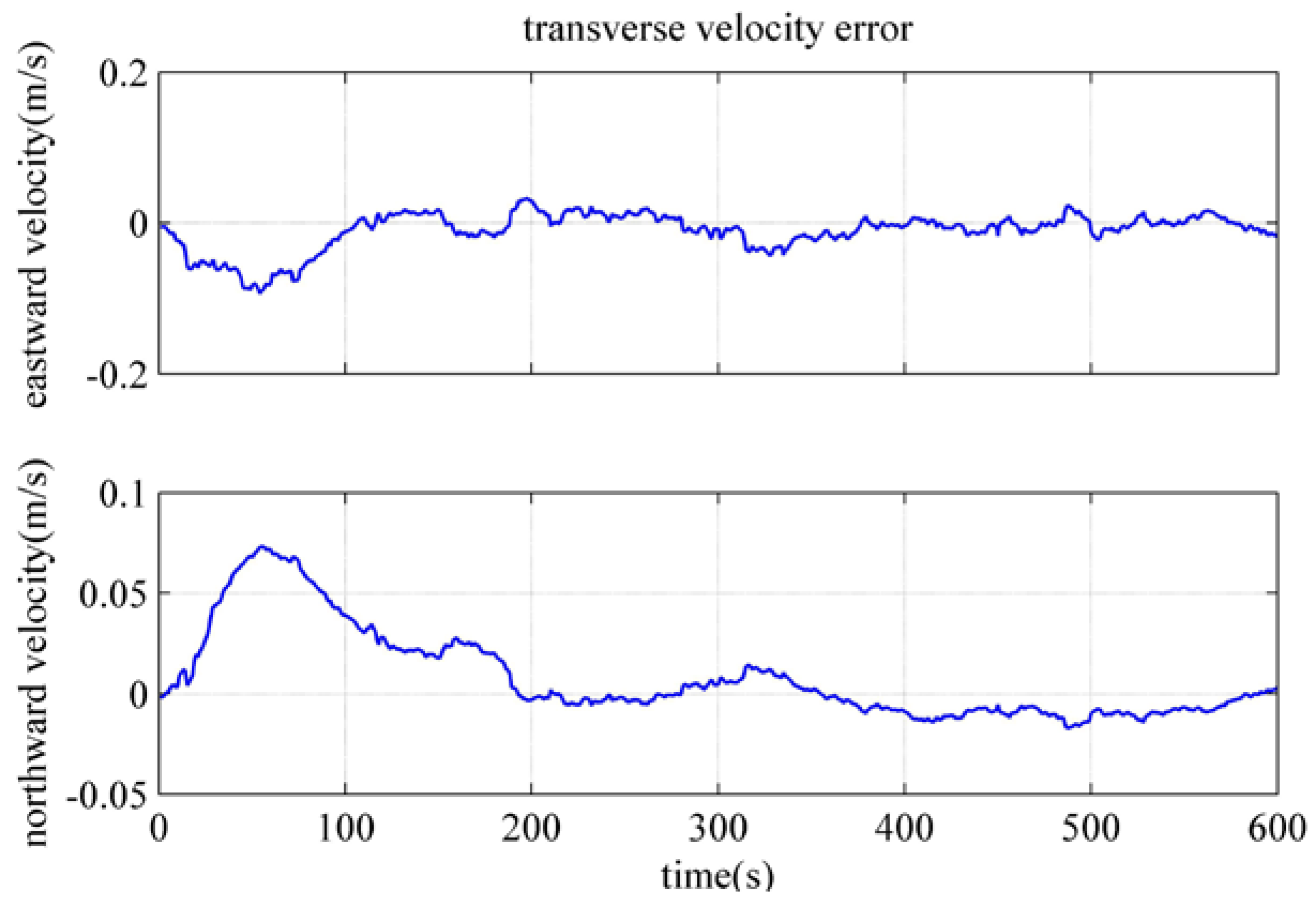
4.4. Performance Verification of the Polar Backtracking Fine Alignment Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Berkman, P.A.; Vylegzhanin, A.N. Environmental Security in the Arctic Ocean; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cheng, J.; Liu, J.; Zhao, L. Survey on polar marine navigation and positioning system. Chin. J. Ship Res. 2021, 16, 16–29. [Google Scholar]
- Zhou, J.; Nie, X.; Lin, J. A novel laser doppler velocimeter and its integrated navigation system with strapdown inertial navigation. Opt. Laser Technol. 2014, 64, 319–323. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Zhang, T.; Hu, G. An improved initial alignment method for sins/gps integration with vectors subtraction. IEEE Sens. J. 2021, 21, 18256–18262. [Google Scholar] [CrossRef]
- Liu, M.; Li, G.; Gao, Y. Improved polar inertial navigation algorithm based on pseudo INS mechanization. Aerosp. Sci. Technol. 2018, 77, 105–116. [Google Scholar] [CrossRef]
- Cai, J.; Cheng, J.; Zhong, S. An Innovative Polar Rapid Transfer Alignment Aided by Doppler Velocity Log For Marine Vessels. In Proceedings of the 2019 European Navigation Conference, Warsaw, Poland, 9–12 April 2019. [Google Scholar]
- Luo, L.; Huang, Y.; Zhang, Z.; Zhang, Y. A New Kalman Filter-Based In-Motion Initial Alignment Method for DVL-Aided Low-Cost SINS. IEEE Trans. Veh. Technol. 2021, 70, 331–343. [Google Scholar]
- Xu, X.; Guo, Z.; Yao, Y.; Zhang, T. Robust Initial Alignment for SINS/DVL Based on Reconstructed Observation Vectors. IEEE/ASME Trans. Mechatron. 2020, 25, 1659–1667. [Google Scholar] [CrossRef]
- Pei, F.; Yang, S.; Yin, S. In-Motion Initial Alignment Using State-Dependent Extended Kalman Filter for Strapdown Inertial Navigation System. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, S.; Xu, Z. Velocity-based optimization-based alignment (VBOBA) of low-end MEMS IMU/GNSS for low dynamic applications. IEEE Sens. J. 2020, 20, 5527–5539. [Google Scholar] [CrossRef]
- Xu, J.; He, H.; Qin, F. A novel autonomous initial alignment method for strapdown inertial navigation system. IEEE Trans. Instrum. Meas 2017, 66, 2274–2282. [Google Scholar] [CrossRef]
- Ouyang, W.; Wu, Y. Optimization-based strapdown attitude alignment for high-accuracy systems: Covariance analysis with applications. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4053–4069. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Gong, J. Double-velocity inertial-frame alignment algorithm with pseudo INS modeling in polar regions. J. Syst. Eng. Electron. 2022, 44, 1677–1684. [Google Scholar]
- Yao, Y.; Xu, X.; Li, Y.; Liu, Y.; Sun, J. Transverse navigation under the ellipsoidal earth model and its performance in both polar and non-polar areas. J. Navig. 2016, 69, 335–352. [Google Scholar] [CrossRef]
- Cai, J.; Cheng, J.; Liu, J.; Wang, Z.; Xu, Y. A polar rapid transfer alignment assisted by the improved polarized-light navigation. IEEE Sens. J. 2022, 22, 2508–2517. [Google Scholar] [CrossRef]
- Wu, Y.; He, C.; Liu, G. On inertial navigation and attitude initialization in polar areas. Satell. Navigat 2020, 1, 4. [Google Scholar]
- Liu, J.; Zhao, L.; Qi, B.; Cheng, J.; Cai, J. A new polar integrated alignment algorithm with the aids of DVL and the improved polarized-light navigation. In Proceedings of the Name of the 2022 5th International Symposium on Autonomous Systems. (ISAS), Hangzhou, China, 8–10 April 2022. [Google Scholar]
- Yan, Z.; Wang, L.; Wang, T.; Zhang, H.; Yang, Z. Polar transversal initial alignment algorithm for UUV with a large misalignment angle. Sensors 2018, 18, 3231. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, J.; Cai, J.; Xu, Y. A Polar Integrated Alignment Assisted by DVL Under Large Azimuth Misalignment. IEEE Sens. J. 2023, 23, 5962–5973. [Google Scholar] [CrossRef]
- Wen, Z.; Yang, G.; Cai, Q. Odometer aided SINS in-motion alignment method based on backtracking scheme for large misalignment angles. IEEE Access 2020, 8, 7937–7948. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, G.; Cai, Q. A robust in-motion attitude alignment method for odometer-aided strapdown inertial navigation system. Rev. Sci. Instrum. 2020, 91, 125006. [Google Scholar] [CrossRef]
- Wang, D.S.; He, G.Y.; Jiang, X.H. In-motion Alignment Scheme Based on Reverse Kalman Filter. J. Chin. Inertial Technol. 2020, 28, 721–728. [Google Scholar]
- Lin, Y.; Miao, L.; Zhou, Z. A high-accuracy initial alignment method based on backtracking process for strapdown inertial navigation system. Measurement 2022, 201, 111712. [Google Scholar] [CrossRef]
- Wahba, G. A least squares estimate of satellite attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Yan, G.; Chen, R.; Guo, K. Equivalence analysis between SVD and QUEST for multi-vector attitude determination. J. Chin. Inertial Technol. 2019, 27, 568–572. [Google Scholar]





| Initialization | The Forward Process | The Backward Process | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | … | … | |||||
| … | … | |||||||
| … | … | |||||||
| … | … | |||||||
| … | … | |||||||
| Algorithm | Estimation Error | Mid-Latitude | Polar |
|---|---|---|---|
| The polar inertial frame coarse alignment based on the transverse Earth model | Pitch/(′) | −0.6292 | −0.2342 |
| Roll/(′) | 0.0323 | −0.0256 | |
| Transverse azimuth/(°) | −0.6614 | −35.16 | |
| The traditional inertial frame coarse alignment | Pitch/(′) | 0.6503 | 0.2747 |
| Roll/(′) | −0.1848 | −0.0372 | |
| Transverse azimuth/(°) | −0.6665 | −40.15 |
| Algorithm | Pitch/(′) | Roll/(′) | Transverse Azimuth/(°) |
|---|---|---|---|
| The inertial frame coarse alignment based on the transverse Earth model | 0.2522 | −0.3251 | −59.86 |
| The polar backtracking coarse alignment | −0.0084 | −0.1285 | −35.37 |
| Algorithm | The Polar Backtracking Fine Alignment | The Polar-Integrated Fine Alignment | |
|---|---|---|---|
| Alignment time/(s) | 180 | 180 | 600 |
| Pitch error/(′) | 0.0072 | −0.0466 | −0.0662 |
| Roll error/(′) | −0.0230 | −0.1081 | −0.0700 |
| Transverse azimuth error/(′) | 0.9251 | −3.502 | 0.1408 |
| Transverse eastward velocity error/(m/s) | −8.400 × 10−3 | −0.0189 | −0.0184 |
| Transverse northward velocity error/(m/s) | 2.879 × 10−4 | −0.0200 | 0.0029 |
| Transverse latitude error/(′) | 4.765 × 10−4 | 7.284 × 10−4 | 4.297 × 10−4 |
| Transverse longitude error/(′) | 4.628 × 10−4 | 1.844 × 10−4 | 2.464 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Liu, J.; Wang, Y.; Cai, J. A Polar Moving Base Alignment Based on Backtracking Scheme. Electronics 2023, 12, 2037. https://doi.org/10.3390/electronics12092037
Cheng J, Liu J, Wang Y, Cai J. A Polar Moving Base Alignment Based on Backtracking Scheme. Electronics. 2023; 12(9):2037. https://doi.org/10.3390/electronics12092037
Chicago/Turabian StyleCheng, Jianhua, Jiaxin Liu, Yu Wang, and Jing Cai. 2023. "A Polar Moving Base Alignment Based on Backtracking Scheme" Electronics 12, no. 9: 2037. https://doi.org/10.3390/electronics12092037
APA StyleCheng, J., Liu, J., Wang, Y., & Cai, J. (2023). A Polar Moving Base Alignment Based on Backtracking Scheme. Electronics, 12(9), 2037. https://doi.org/10.3390/electronics12092037







