A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer
Abstract
1. Introduction
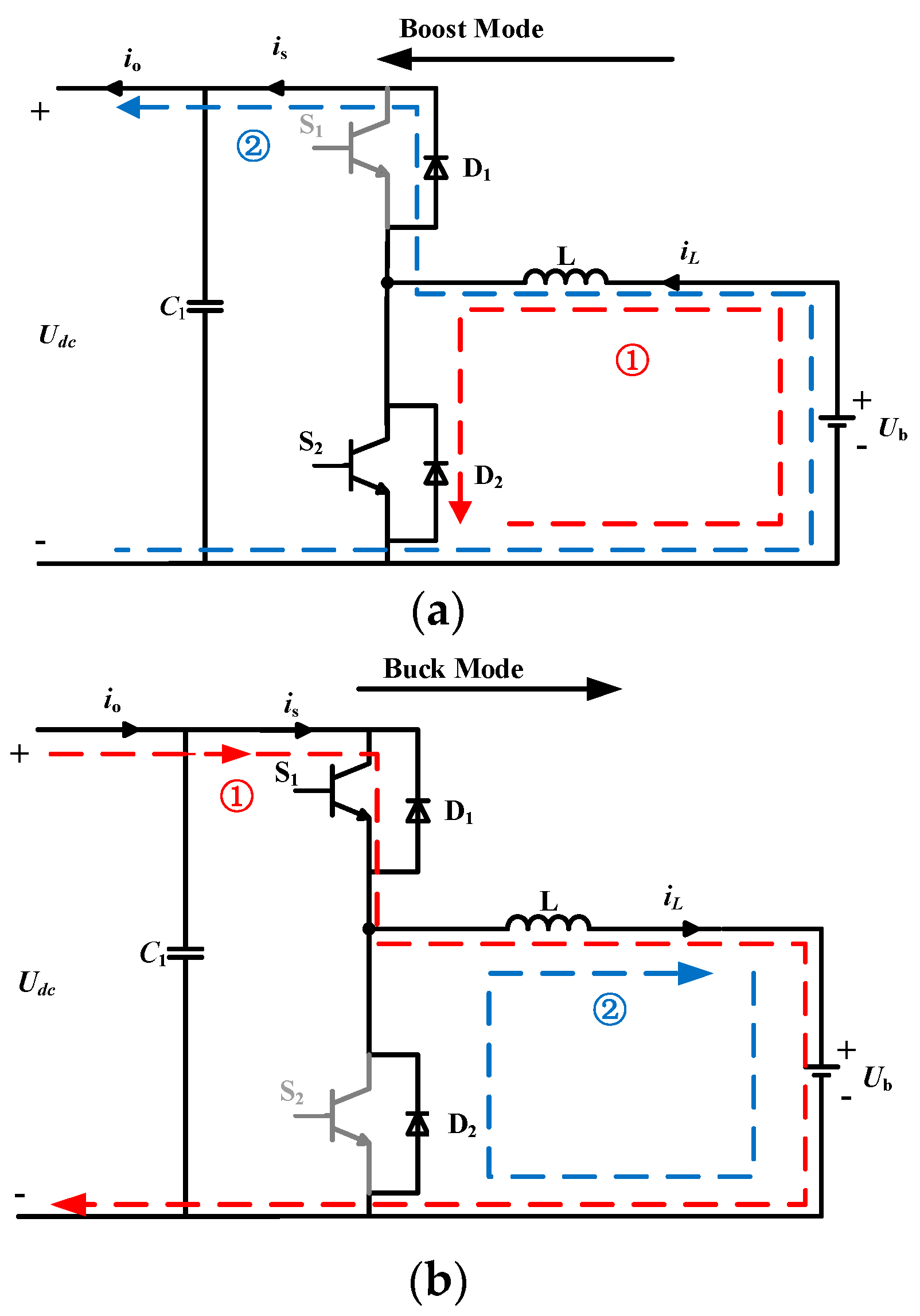
2. System Structure and Modeling
2.1. Boost Mode
2.2. Buck Mode
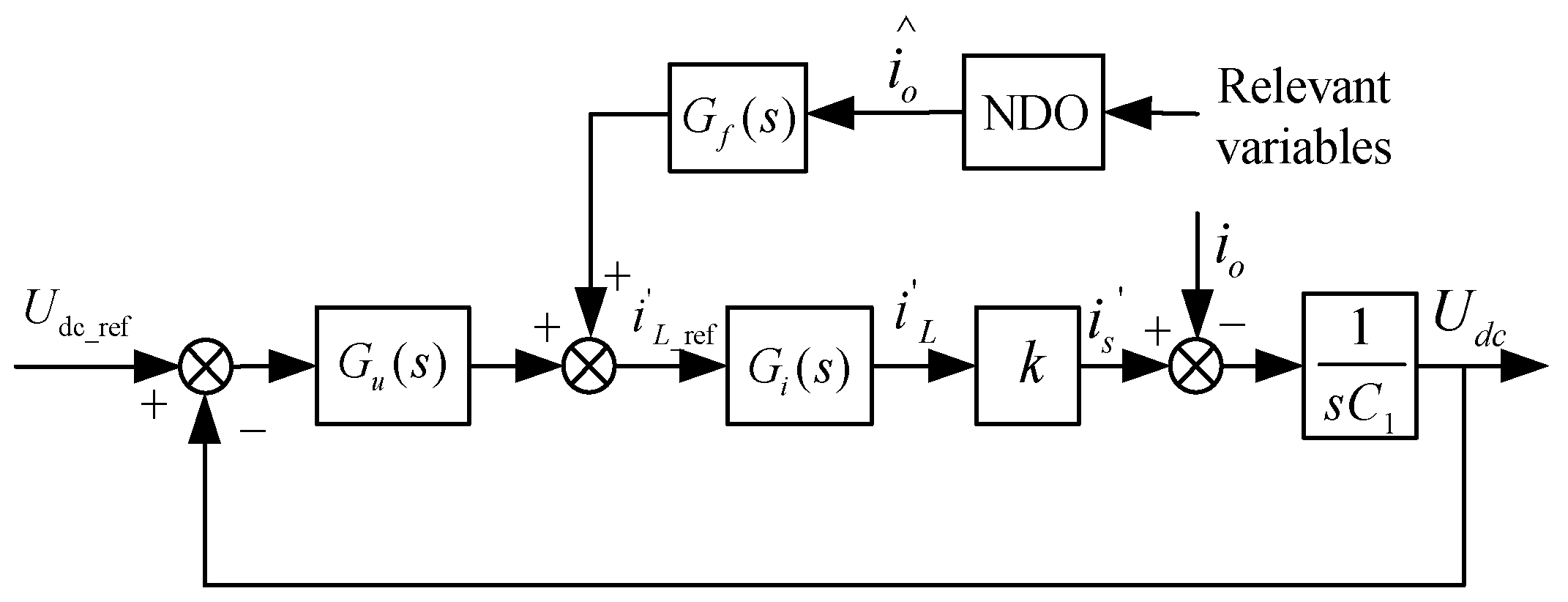
3. Continuous Control Set Predictive Current Control Based on Nonlinear Disturbance Observer
3.1. Continuous Control Set Predictive Current Control Method
3.1.1. The Design of CCS-PCC Controller in Boost Mode
3.1.2. The Design of CCS-PCC Controller in Buck Mode
3.2. Analysis of DC Bus Voltage Based on NDO
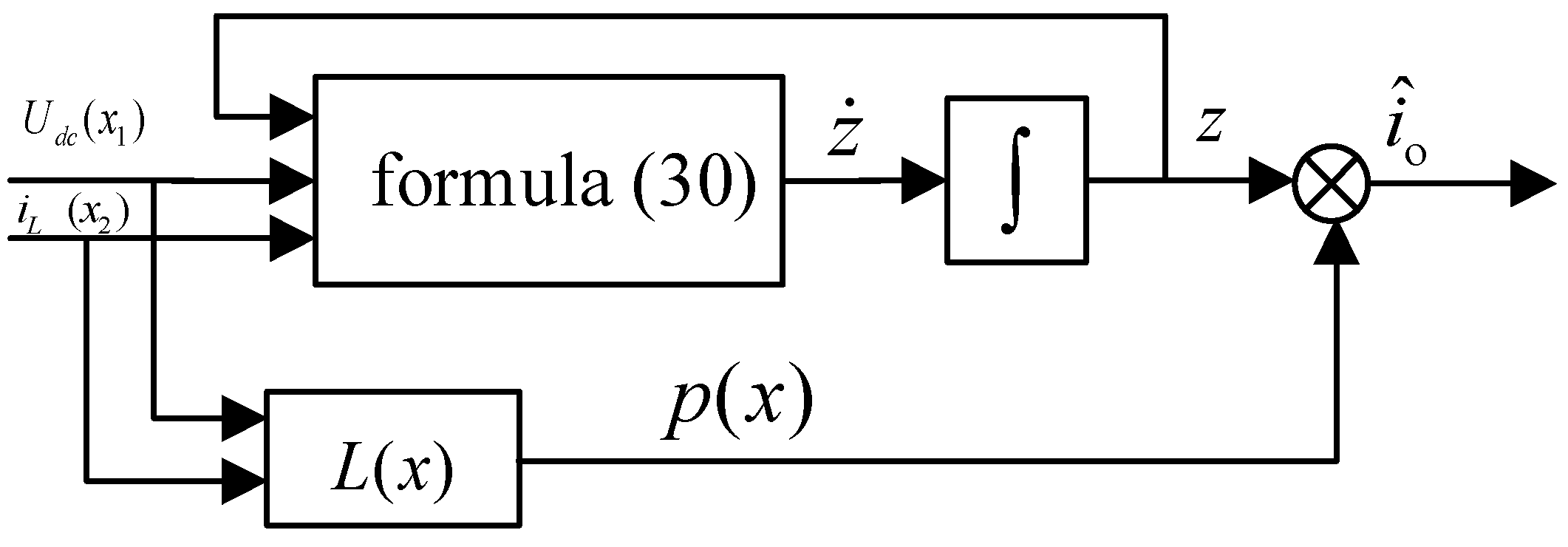
3.3. Design of Nonlinear Disturbance Observer
4. Simulation Results
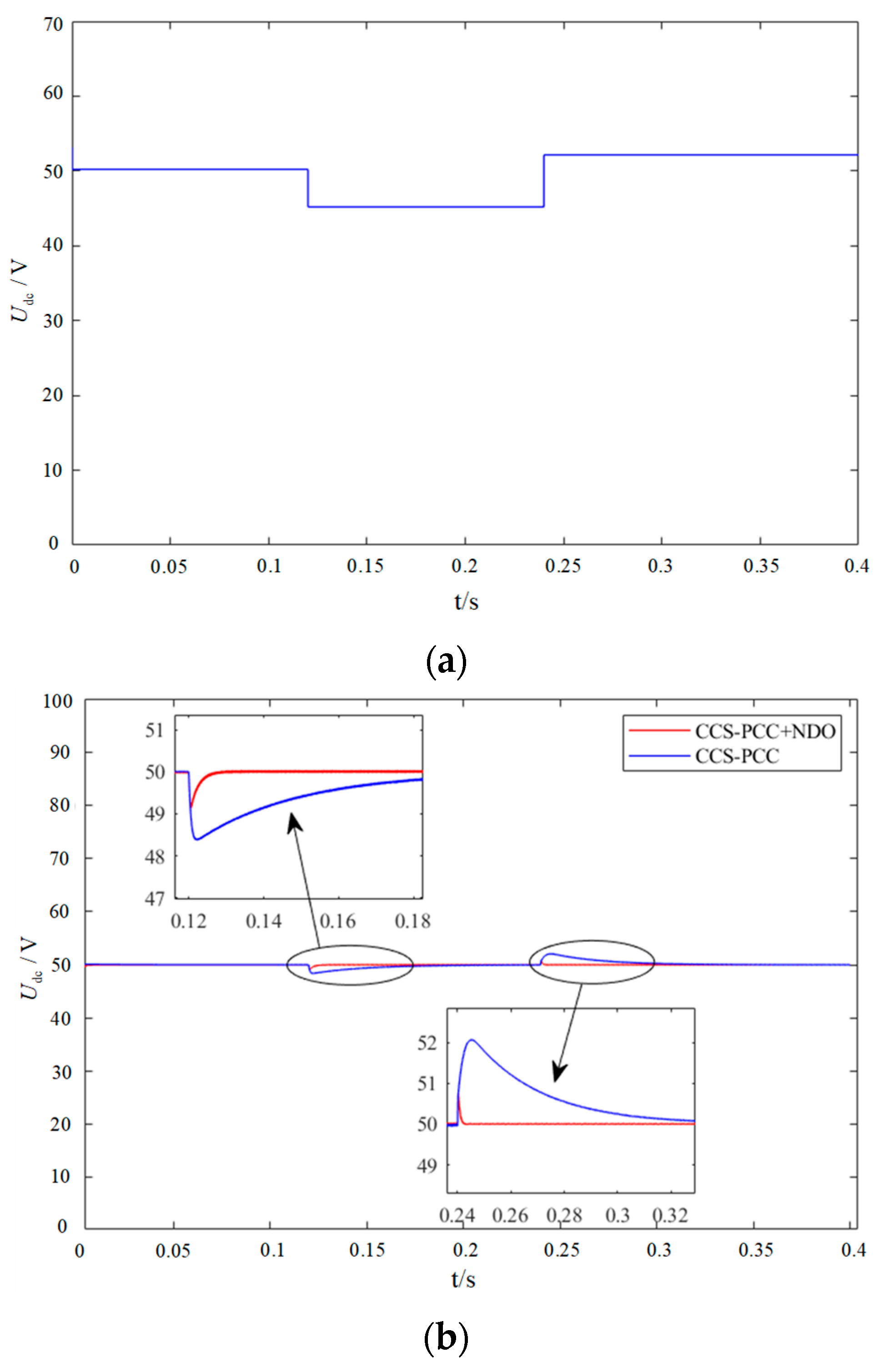
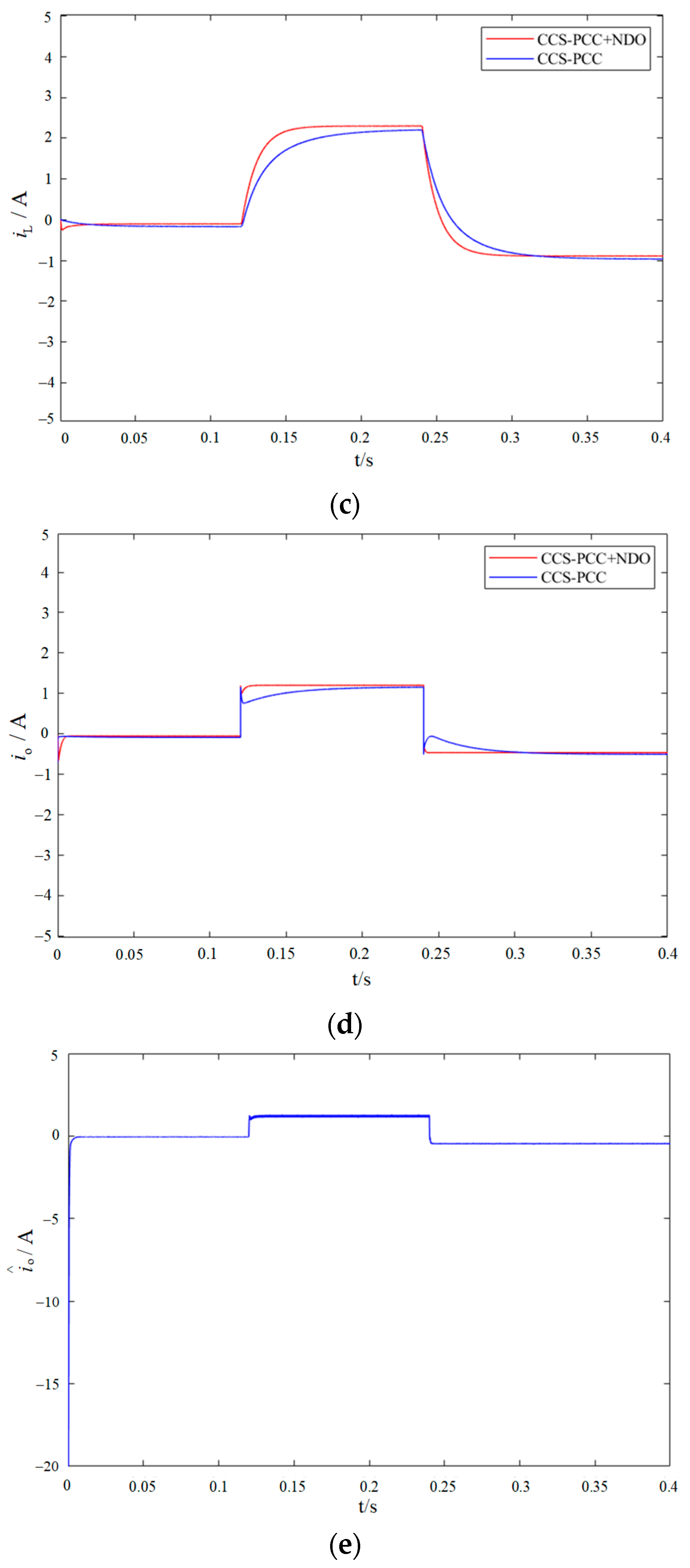
4.1. Dynamic Performance Verification with a Step Load
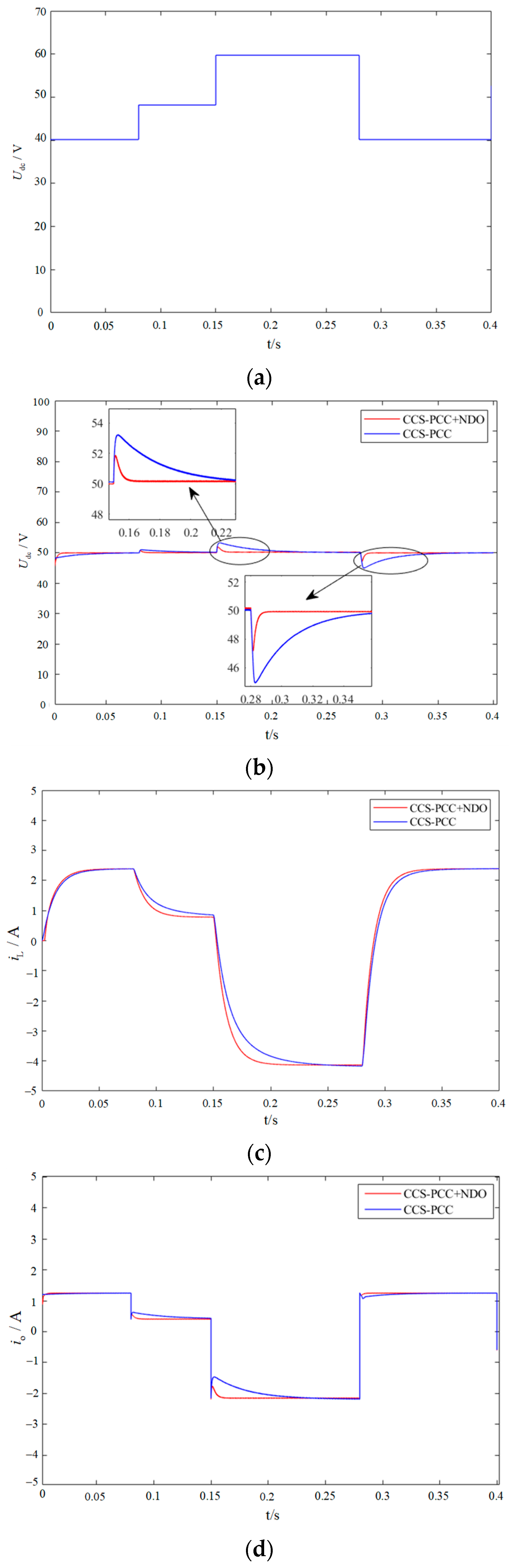
4.2. Dynamic Performance Verification with Photovoltaic Power Output Voltage Fluctuation
5. Experimental Results
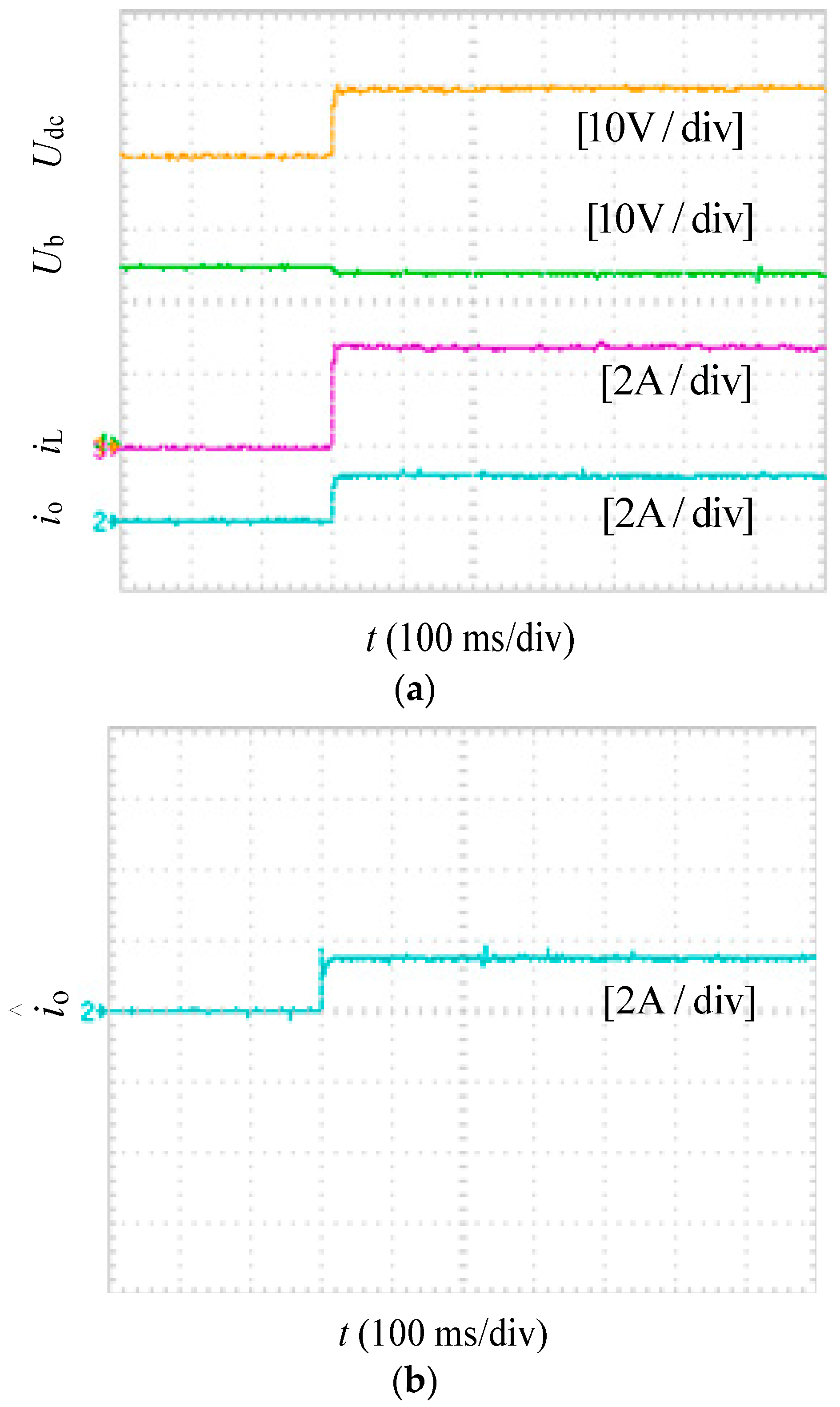
5.1. Correctness Verification of CCS-PCC+NDO in Different Operation Modes
5.1.1. Boost Mode
5.1.2. Buck Mode
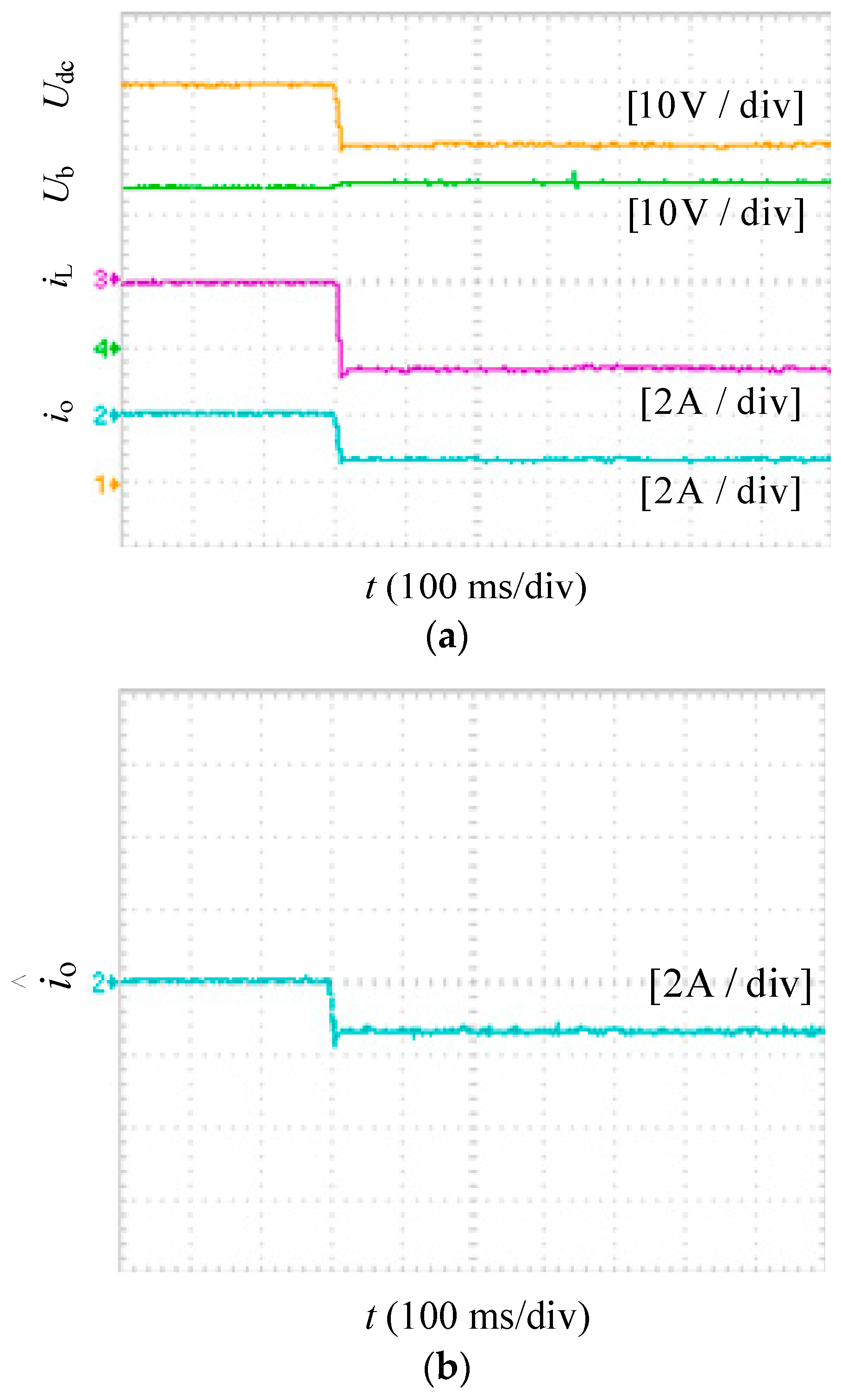
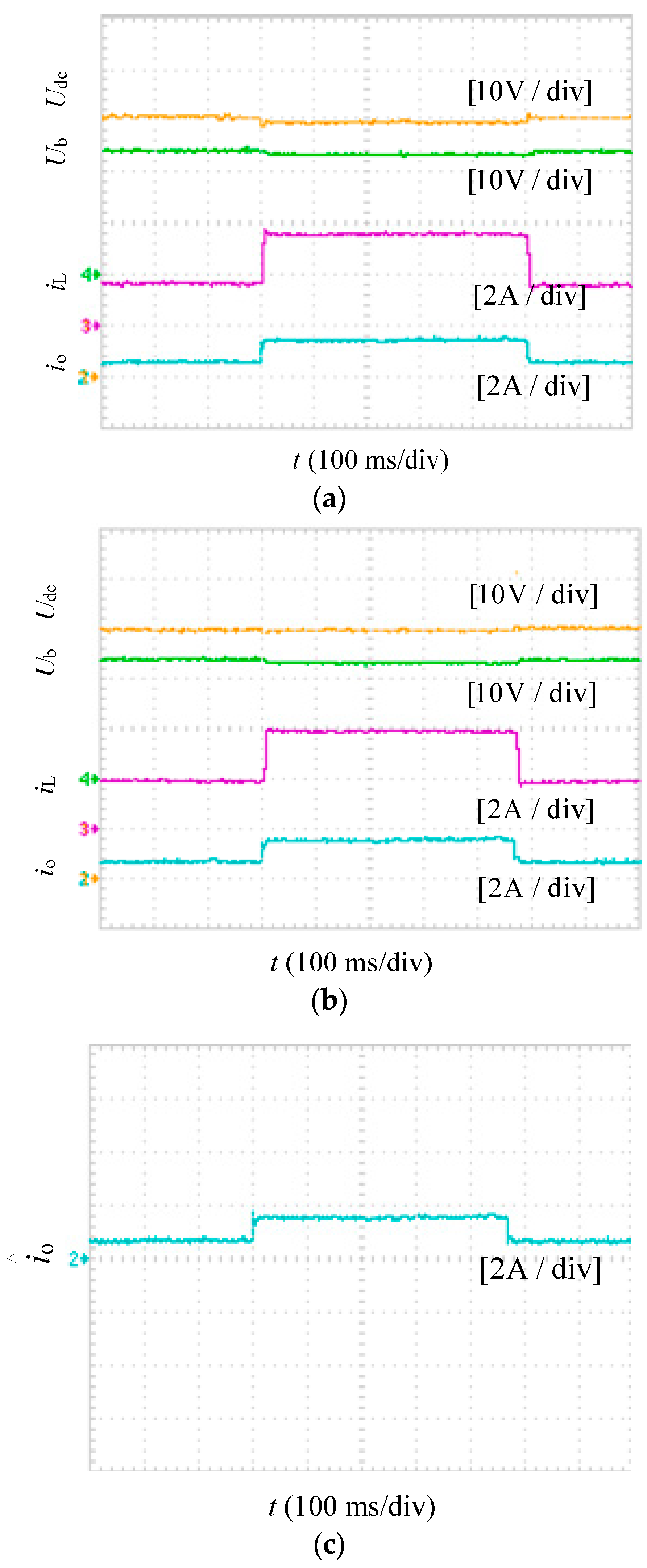
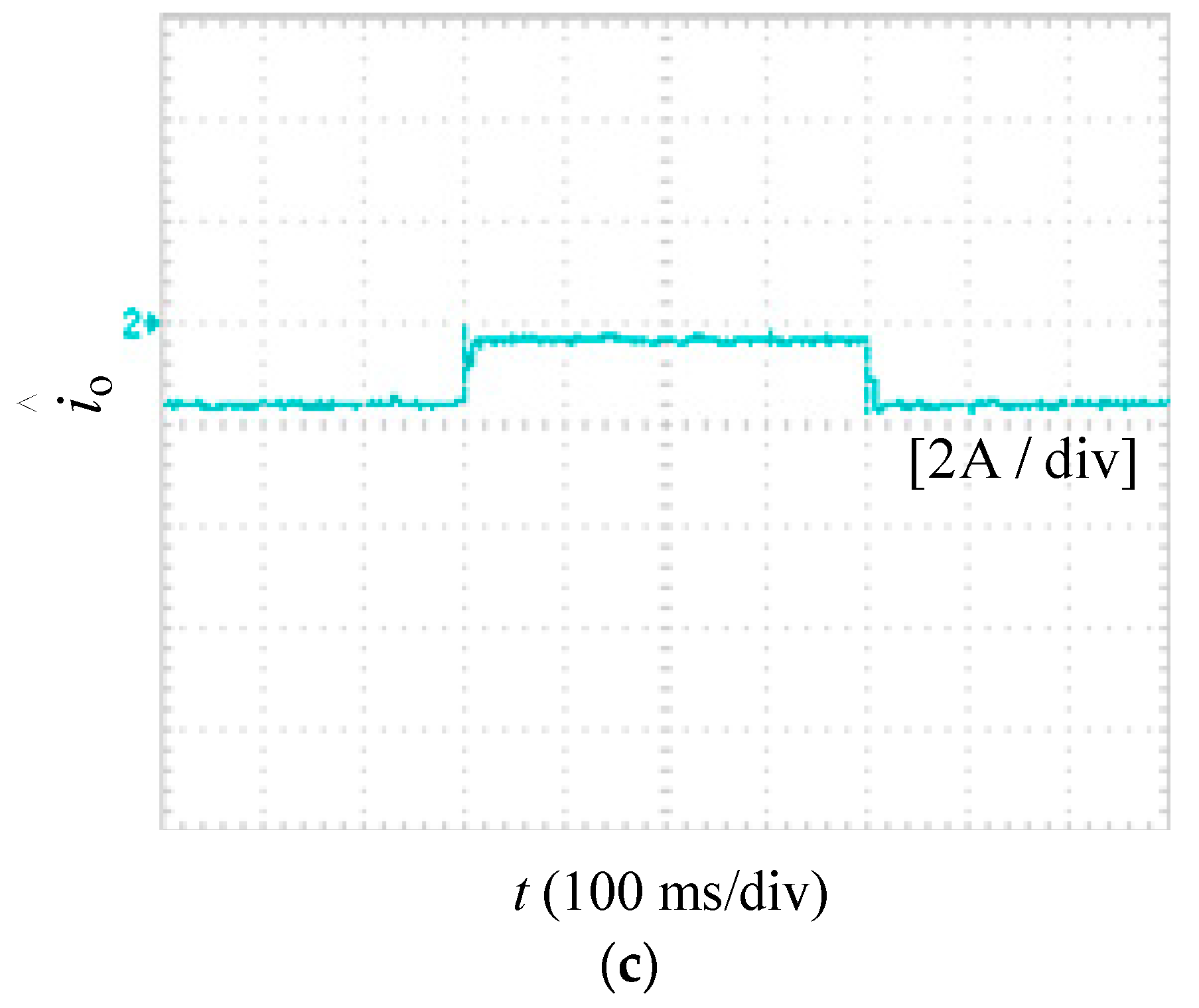
5.2. Dynamic Performance Verification with a Step Load
5.2.1. Boost Mode
5.2.2. Buck Mode
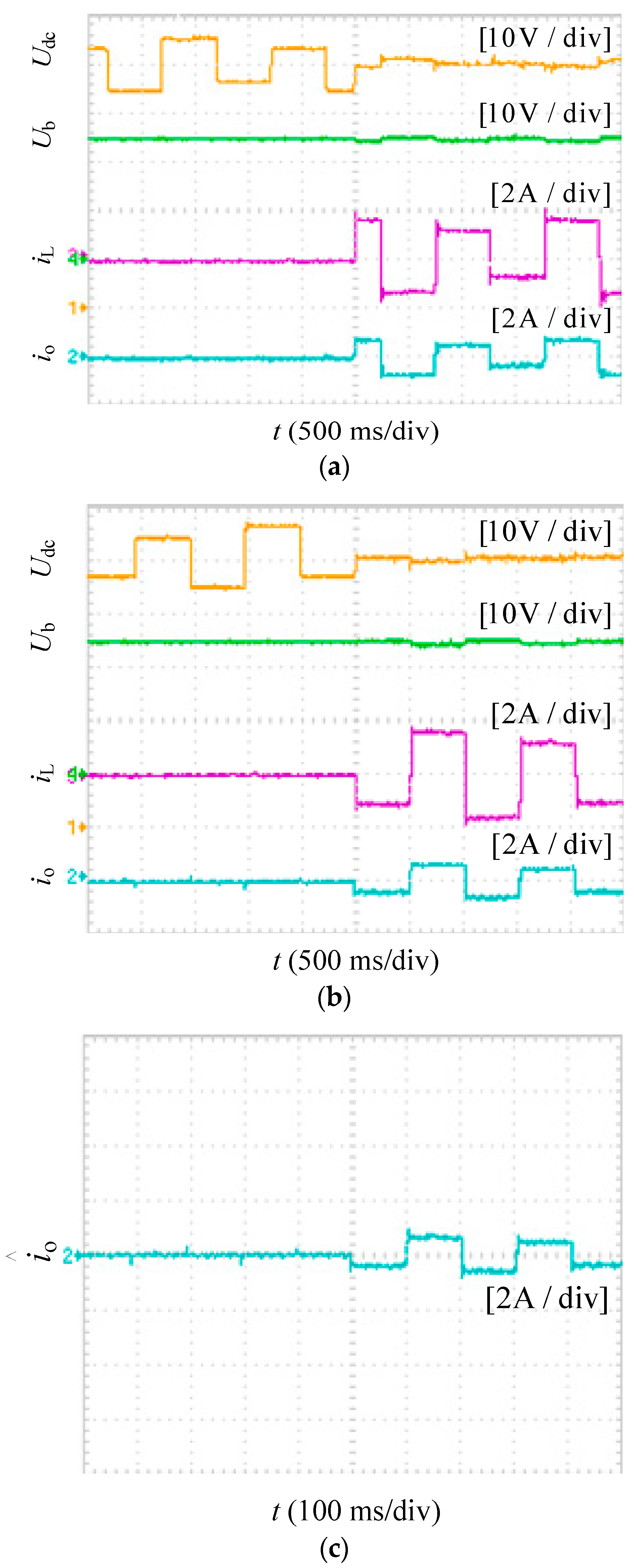
5.2.3. Different Modes Switch
5.3. Performance Verification with Photovoltaic Power Output Voltage Fluctuation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rana, M.M.; Uddin, M.; Sarkar, M.R.; Shafiullah, G.M.; Mo, H.; Atef, M. A review on hybrid photovoltaic–Battery energy storage system: Current status, challenges, and future directions. J. Energy Storage 2022, 51, 104597. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Guo, L.; Li, Y.W. A Nonlinear-Disturbance-Observer-Based DC-Bus Voltage Control for a Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2014, 29, 6162–6177. [Google Scholar] [CrossRef]
- Buticchi, G.; Costa, L.; Liserre, M. Improving System Efficiency for the More Electric Aircraft: A Look at DC/DC Converters for the Avionic Onboard DC Microgrid. IEEE Ind. Electron. Mag. 2017, 11, 26–36. [Google Scholar] [CrossRef]
- Subha, R.; Himavathi, S. Active power control of a photovoltaic system without energy storage using neural network-based estimator and modified P&O algorithm. IET Gener. Transm. Distrib. 2018, 12, 927–934. [Google Scholar]
- Hajebrahimi, H.; Kaviri, S.M.; Eren, S.; Bakhshai, A. A New Energy Management Control Method for Energy Storage Systems in Microgrids. IEEE Trans. Power Electron. 2020, 35, 11612–11624. [Google Scholar] [CrossRef]
- Gu, Y.; Xiang, X.; Li, W.; He, X. Mode-Adaptive Decentralized Control for Renewable DC Microgrid with Enhanced Reliability and Flexibility. IEEE Trans. Power Electron. 2014, 29, 5072–5080. [Google Scholar] [CrossRef]
- Prabhakaran, P.; Goyal, Y.; Agarwal, V. Novel Nonlinear Droop Control Techniques to Overcome the Load Sharing and Voltage Regulation Issues in DC Microgrid. IEEE Trans. Power Electron. 2018, 33, 4477–4487. [Google Scholar] [CrossRef]
- Xu, Q.; Vafamand, N.; Chen, L.; Dragicevic, T.; Xie, L.; Blaabjerg, F. Review on Advanced Control Technologies for Bidirectional DC/DC Converters in DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1205–1221. [Google Scholar] [CrossRef]
- Wu, Y.-E.; Ke, Y.-T. A Novel Bidirectional Isolated DC-DC Converter with High Voltage Gain and Wide Input Voltage. IEEE Trans. Power Electron. 2021, 36, 7973–7985. [Google Scholar] [CrossRef]
- Molavi, N.; Adib, E.; Farzanehfard, H. Soft-switching bidirectional DC–DC converter with high voltage conversion ratio. IET Power Electron. 2018, 11, 33–42. [Google Scholar] [CrossRef]
- Rezvanyvardom, M.; Mirzaei, A. Zero-Voltage Transition Nonisolated Bidirectional Buck–Boost DC–DC Converter with Coupled Inductors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3266–3275. [Google Scholar] [CrossRef]
- Santra, S.B.; Chatterjee, D.; Siwakoti, Y.P. Coupled Inductor Based Soft Switched High Gain Bidirectional DC-DC Converter with Reduced Input Current Ripple. IEEE Trans. Ind. Electron. 2023, 70, 1431–1443. [Google Scholar] [CrossRef]
- Mukherjee, N.; Strickland, D. Control of Cascaded DC–DC Converter-Based Hybrid Battery Energy Storage Systems—Part II: Lyapunov Approach. IEEE Trans. Ind. Electron. 2016, 63, 3050–3059. [Google Scholar] [CrossRef]
- Cornea, O.; Andreescu, G.-D.; Muntean, N.; Hulea, D. Bidirectional Power Flow Control in a DC Microgrid through a Switched-Capacitor Cell Hybrid DC–DC Converter. IEEE Trans. Ind. Electron. 2017, 64, 3012–3022. [Google Scholar] [CrossRef]
- Kumar, V.; Mohanty, S.R.; Kumar, S. Event Trigger Super Twisting Sliding Mode Control for DC Micro Grid with Matched/Unmatched Disturbance Observer. IEEE Trans. Smart Grid 2020, 11, 3837–3849. [Google Scholar] [CrossRef]
- Mosayebi, M.; Sadeghzadeh, S.M.; Gheisarnejad, M.; Khooban, M.H. Intelligent and Fast Model-Free Sliding Mode Control for Shipboard DC Microgrids. IEEE Trans. Transp. Electrif. 2021, 7, 1662–1671. [Google Scholar] [CrossRef]
- Hassan, M.A.; He, Y. Constant Power Load Stabilization in DC Microgrid Systems Using Passivity-Based Control with Nonlinear Disturbance Observer. IEEE Access 2020, 8, 92393–92406. [Google Scholar] [CrossRef]
- Melath, G.; Hussain, M.N.; Agarwal, V. A Nonlinear Adaptive Backstepping Controller for Stabilizing the DC Bus Voltage of an Islanded Hybrid Microgrid. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 538–548. [Google Scholar] [CrossRef]
- Wang, F.; Mei, X.; Rodriguez, J.; Kennel, R. Model predictive control for electrical drive systems—An overview. CES Trans. Electr. Mach. Syst. 2017, 1, 219–230. [Google Scholar] [CrossRef]
- Sun, C.; Sun, D.; Chen, W.; Nian, H. Improved Model Predictive Control with New Cost Function for Hybrid-Inverter Open-Winding PMSM System Based on Energy Storage Model. IEEE Trans. Power Electron. 2021, 36, 10705–10715. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Wei, X.; Liang, Z.; Kennel, R.; Rodriguez, J. Space-Vector-Optimized Predictive Control for Dual Three-Phase PMSM with Quick Current Response. IEEE Trans. Power Electron. 2022, 37, 4453–4462. [Google Scholar] [CrossRef]
- Abu-Ali, M.; Berkel, F.; Manderla, M.; Reimann, S.; Kennel, R.; Abdelrahem, M. Deep Learning-Based Long-Horizon MPC: Robust, High Performing, and Computationally Efficient Control for PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 12486–12501. [Google Scholar] [CrossRef]
- Bauersfeld, L.; Spannagl, L.; Ducard, G.J.J.; Onder, C.H. MPC Flight Control for a Tilt-Rotor VTOL Aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Baier, C.R.; Ramirez, R.O.; Marciel, E.I.; Hernandez, J.C.; Melin, P.E.; Espinosa, E.E. FCS-MPC without Steady-State Error Applied to a Grid-Connected Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2021, 36, 11785–11799. [Google Scholar] [CrossRef]
- Salem, A.; Abido, M.A.; Blaabjerg, F. Common-Mode Voltage Mitigation of Dual T-Type Inverter Drives Using Fast MPC Approach. IEEE Trans. Ind. Electron. 2022, 69, 7663–7674. [Google Scholar] [CrossRef]
- Bouaouaou, H.; Lalili, D.; Boudjerda, N. Model predictive control and ANN-based MPPT for a multi-level grid-connected photovoltaic inverter. Electr. Eng. 2022, 104, 1229–1246. [Google Scholar] [CrossRef]
- Wei, Q.; Wu, B.; Xu, D.; Zargari, N.R. Model Predictive Control of Capacitor Voltage Balancing for Cascaded Modular DC–DC Converters. IEEE Trans. Power Electron. 2017, 32, 752–761. [Google Scholar] [CrossRef]
- Vafamand, N.; Yousefizadeh, S.; Khooban, M.H.; Bendtsen, J.D.; Dragicevic, T. Adaptive TS Fuzzy-Based MPC for DC Microgrids with Dynamic CPLs: Nonlinear Power Observer Approach. IEEE Syst. J. 2019, 13, 3203–3210. [Google Scholar] [CrossRef]
- Yang, H.; Chao, K.; Sun, X.; Zhang, Q.; Ren, B.; Yang, M. Robust Predictive Current Control for Photovoltaic Energy Storage System Based on Second-order Tracking Differentiator. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2065–2070. [Google Scholar]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Vazquez, S. Enhanced Switching Frequency Control in FCS-MPC for Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 2470–2479. [Google Scholar] [CrossRef]
- Liu, C.; Xing, X.; Du, C.; Zhang, B.; Zhang, C.; Blaabjerg, F. An Improved Model Predictive Control Method Using Optimized Voltage Vectors for Vienna Rectifier with Fixed Switching Frequency. IEEE Trans. Power Electron. 2023, 38, 358–371. [Google Scholar] [CrossRef]
- Wang, D.; Shen, Z.J.; Yin, X.; Tang, S.; Liu, X.; Zhang, C.; Wang, J.; Rodriguez, J.; Norambuena, M. Model Predictive Control Using Artificial Neural Network for Power Converters. IEEE Trans. Ind. Electron. 2022, 69, 3689–3699. [Google Scholar] [CrossRef]
- Guler, N.; Biricik, S.; Bayhan, S.; Komurcugil, H. Model Predictive Control of DC–DC SEPIC Converters with Autotuning Weighting Factor. IEEE Trans. Ind. Electron. 2021, 68, 9433–9443. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Gamage, D.; Ukil, A. Model Predictive Control Based Dynamic Power Loss Prediction for Hybrid Energy Storage System in DC Microgrids. IEEE Trans. Ind. Electron. 2022, 69, 8080–8090. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Wu, W.; Ma, J.; Fang, Y.; Peng, Z.; Wang, D.; Rodriguez, J. Event-Triggered ESO-Based Robust MPC for Power Converters. IEEE Trans. Ind. Electron. 2023, 70, 2144–2152. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, L.Y.; Wang, C.; Jiang, J.; Jiang, C.; Duan, C. Adaptive Feedforward Compensation for Voltage Source Disturbance Rejection in DC–DC Converters. IEEE Trans. Control Syst. Technol. 2018, 26, 344–351. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, W.X.; Li, S.; Wu, B.; Cheng, M. Design of a Prediction-Accuracy-Enhanced Continuous-Time MPC for Disturbed Systems via a Disturbance Observer. IEEE Trans. Ind. Electron. 2015, 62, 5807–5816. [Google Scholar] [CrossRef]
- Lin, X.; Guo, L.; Feng, Y.; Wang, C.; Lin, M. A Nonlinear Disturbance Observer Based DC Bus Voltage Control for a DC microgrid. Proc. CSEE 2016, 36, 350–359. [Google Scholar]
- Li, S.; Yang, J. Robust Autopilot Design for Bank-to-Turn Missiles using Disturbance Observers. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 558–579. [Google Scholar] [CrossRef]








| Simulation Parameters | Value |
|---|---|
| Given DC bus voltage (V) | 50 |
| Batteries’ terminal voltage (V) | 24 |
| Inductor (mH) | 2.5 |
| Capacitor of DC bus (μF) | 470 |
| DC load (Ω) | 40 |
| Observer gain () | −0.75 |
| Sampling frequency (kHz) | 20 |
| Experiment Parameters | Value |
|---|---|
| Given DC bus voltage (V) | 50 |
| Batteries’ terminal voltage (V) | 24 |
| Capacitor of DC bus (μF) | 470 |
| Inductor (mH) | 2.5 |
| DC load (Ω) | 40 |
| Sampling frequency (kHz) | 20 |
| Load | 40 Ω → 20 Ω | 20 Ω → 40 Ω | ||
|---|---|---|---|---|
| Control Strategy | CCS-PCC | CCS-PCC+NDO | CCS-PCC | CCS-PCC+NDO |
| Overshoot | 4.2% (2.1 V) | 3.2% (1.6 V) | 1.8% (0.9 V) | 1.6% (0.8 V) |
| Settling time | 0.016 s | 0.014 s | 0.010 s | 0.009 s |
| Steady-state error | 0.9 V | 0.2 V | 0.4 V | 0.3 V |
| Load | 40 Ω → 20 Ω | 20 Ω → 40 Ω | ||
|---|---|---|---|---|
| Control Strategy | CSS-PCC | CSS-PCC+NDO | CSS-PCC | CSS-PCC+NDO |
| Overshoot | 3.8% (1.9 V) | 3.2% (1.6 V) | 4.4% (2.2 V) | 2% (1 V) |
| Settling time | 0.018 s | 0.010 s | 0.012 s | 0.010 s |
| Steady-state error | 0.8 V | 0.5 V | 0.7 V | 0.2 V |
| Load | 40 Ω → 17 Ω | |
|---|---|---|
| Control Strategy | CSS-PCC | CSS-PCC+NDO |
| Overshoot | 4.6% (2.3 V) | 1.6% (0.8 V) |
| Settling time | 0.016 s | 0.008 s |
| Steady-state error | 1.1 V | 0.3 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Long, H.; Zhang, Q.; Sun, X. A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer. Electronics 2023, 12, 1985. https://doi.org/10.3390/electronics12091985
Yang H, Long H, Zhang Q, Sun X. A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer. Electronics. 2023; 12(9):1985. https://doi.org/10.3390/electronics12091985
Chicago/Turabian StyleYang, Hui, Huachuan Long, Qi Zhang, and Xiangdong Sun. 2023. "A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer" Electronics 12, no. 9: 1985. https://doi.org/10.3390/electronics12091985
APA StyleYang, H., Long, H., Zhang, Q., & Sun, X. (2023). A Robust CCS Predictive Current Control for Photovoltaic Energy Storage System Based on a Nonlinear Disturbance Observer. Electronics, 12(9), 1985. https://doi.org/10.3390/electronics12091985






