Improved Reconstruction Algorithm of Wireless Sensor Network Based on BFGS Quasi-Newton Method

Abstract

Aiming at the problems of low reconstruction rate and poor reconstruction precision when reconstructing sparse signals in wireless sensor networks, a sparse signal reconstruction algorithm based on the Limit-Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) quasi-Newton method is proposed. The L-BFGS quasi-Newton method uses a two-loop recursion algorithm to find the descent direction d_k directly by calculating the step difference between m adjacent iteration points, and a matrix H_k approximating the inverse of the Hessian matrix is constructed. It solves the disadvantages of BFGS requiring the calculation and storage of H_k, reduces the algorithm complexity, and improves the reconstruction rate. Finally, the experimental results show that the L-BFGS quasi-Newton method has good experimental results for solving the problem of sparse signal reconstruction in wireless sensor networks.

1. Introduction

A wireless sensor network (WSN) is a wireless network composed of a large number of sensor nodes. Each sensor node needs to collect a large amount of data and transmit it to the sink node. Traditional data acquisition and transmission methods will cause huge energy consumption and reduce the service life of nodes [1]. If the collected data is compressed before transmission, the energy consumption can be greatly reduced and the node life can be prolonged. However, the traditional Nyquist sampling frequency is too high, resulting in excess energy consumption. To solve the problem that Nyquist’s sampling frequency is too high. Jose et al. proposed to apply the compressed sensing (CS) [2] theory to wireless sensor networks. The CS theory shows that as long as the signal is sparse or can be sparsely represented, the original signal can be reconstructed undistorted from the measurement of a linear combination far below Nyquist sampling frequency. The original signals of wireless sensor networks are sparse, as such, and CS theory is widely used in the reconstruction of sparse original signals in wireless sensor networks.

At present, the main reconstruction algorithms studied include greedy iterative algorithms [3], non-convex optimization algorithms [4], and convex optimization algorithms [5]. The most classical greedy iterative algorithm is the matching pursuit (MP) algorithm [6]. The algorithm uses residuals to reconstruct sparse signals. The algorithm is relatively simple, and the reconstruction rate is fast, but the sparsity of signals in a certain transformation domain is required, and the reconstruction accuracy is poor. It is suitable for cases with a large amount of data and low reconstruction accuracy requirements, but it is not suitable for fields with high reconstruction accuracy requirements. Gorodnitsky proposed a sparse signal reconstruction algorithm based on the wavelet transform [7]. Daubechies proposed a sparse reconstruction algorithm based on logic and iterative weighted least squares minimization [8]. Both algorithms belong to non-convex optimization algorithms, which can improve the reconstruction accuracy to a certain extent but whose improvement effect is limited. Daubechies et al. proposed convex optimization algorithms to reconstruct sparse signals in wireless sensor networks [9]. This method transforms the sparse signal recovery problem into a convex optimization problem and solves the minimum value of the objective function. The results obtained are globally optimal, and the reconstruction accuracy is good and applicable to the realm with high reconstruction accuracy. It requires fewer measurements, but the computational complexity is very high. A typical convex optimization algorithm is the basis pursuit (BP) algorithm [10]. The BP algorithm has high reconstruction accuracy but a low reconstruction rate. William et al. proposed a gradient-based sparse recovery method [11], which has high reconstruction accuracy and a fast first-order convergence rate.

Ma Duxiang proposed to apply Newton’s method to a sparse signal reconstruction algorithm [12]. Newton’s search direction is used to replace the steepest descent direction and obtain the second-order convergence rate, which improves the reconstruction rate of the sparse signal to a certain extent. Newton’s method requires the inverse of the Hessian matrix, which requires large computational quantities and can improve the reconstruction rate but is limited. The computational quantities are the complexity and time of the algorithm. The longer the algorithm runs, the greater the computational quantities. Chen Fenghua used the BFGS [13] algorithm to solve the problem of large computational quantities in wireless sensor networks. The BFGS algorithm replaces the inverse of the Hessian matrix with an approximate matrix H_k by iteration, which reduces the amount of computation. However, the BFGS algorithm needs to calculate and store the n × n matrix H_k. When dimension n is large, the reduced computation amount is limited. Therefore, the L-BFGS [14] quasi-Newton algorithm is proposed in this paper to solve the problem of sparse signal reconstruction in wireless sensors based on compressed sensing. The L-BFGS algorithm does not need to calculate and store H_k directly but only needs to store m (m<<n) vector pairs (s_k,u_k). This solves the shortcoming of the BFGS quasi-Newton algorithm, which must calculate and store the matrix H_k directly; the size of H_k is n × n. In Section 5, we prove the feasibility of using the L-BFGS quasi-Newton algorithm to solve the problem of sparse signal reconstruction in wireless sensors based on compressed sensing.

2. Signal Reconstruction Algorithm Based on Newton Method

In WSNs, it is known that sparse signals $\overline{x}\in R^n$, and the matrix $A\in R^{m\times n}$ (m<<n) [13]. $y\in R^m$ is the observation vector. They satisfy the following relation:

$$y=A\overline{x}.$$

(1)

How to reconstruct the original signal $\overline{x}$ from a linear system is the core problem of sparse signal reconstruction using compressed sensing in wireless sensor networks. Equation (1) is underdetermined and has infinite sets of solutions.

In the compressed sensing problem, if the original signal $\overline{x}$ is known to be sparse under a certain transformation, the Equation (1) can be transformed into an L₀ norm minimization problem, and the signal is reconstructed by solving the L₀ norm minimization problem:

$$\underset{x}{\min }{\Vert x\Vert }_0,s.t.Ax=y,$$

(2)

the L₀ norm here is the number of nonzero elements of the vector.

Research shows that sparse signals can be accurately reconstructed by solving the linear optimization of the L₀ norm minimization problem. However, the L₀ norm problem is NP-hard. In other words, the solution to the L₀ norm minimization problem needs to enumerate all the permutations and combinations of non-zero values in the original signal. Under certain conditions, the L₁ norm minimization problem is the optimal convex approximation of the L₀ norm minimization problem [15], and the solution to the L₁ norm minimization problem is simple. Therefore, solving the L₀ norm minimization problem is transformed into solving the L₁ norm minimization problem:

$$\underset{x}{\min }{\Vert x\Vert }_1,s.t.Ax=y.$$

(3)

The L₁ norm minimization problem is a convex optimization problem. There are many methods to solve convex optimization problems, and Newton’s method is one of them. Newton’s method uses the first-order matrix and second-order Hessian matrix to approximate the objective function quadratic, and the result is faster than other convex optimization algorithms.

In practice, it is difficult to directly solve the linear programming problem (3). Since matrix A is very large and complex to calculate. To simplify the calculation, problem (3) can be transformed into an L₁ regularized least squares problem [16].

$$\underset{x}{\min }\lambda {\Vert x\Vert }_1+\frac{1}{2}{\Vert y-Ax\Vert }_2^2,$$

(4)

where λ is a regularization parameter.

Since ∥x∥₁ is a nonsmooth convex function for x, the subgradient basic approach is not effective in solving the problem (4). The L₁ minimization problem (3) can be solved by solving a suitable smooth form of problem (4).

According to the literature [17], using the Nesterov smoothing technique, ∥x∥₁ is smoothed into the following smooth function:

$$f(x)={\displaystyle \sum _{i=1}^{n}H(x(i))},$$

where:

$$H(u)=\{\begin{array}{l}\frac{u^2}{2\tau }, \left|u\right|\le \tau ;\\ \left|u\right|-\frac{\tau }{2}, \left|u\right|>\tau , \end{array}$$

H(u) is the Huber penalty function, τ is a smooth parameter, see literature [18] for relevant research.

The smooth function f(x) is convex, the gradient ∇f (x) is Lipchitz continuous, and its components are:

$$\nabla f(x(i))=\{\begin{array}{l}\frac{x(i)}{\tau }, \left|x(i)\right|\le \tau \\ sign(x(i)), \left|x(i)\right|>\tau \end{array} (i=1,2,3,......,n),$$

which is:

$$sign(v)=\{\begin{array}{l}1, x>0; \\ 0, x=0;\\ -1, x<0.\end{array}$$

For ease of calculation, let $F(x)=\lambda {\Vert x\Vert }_1+\frac{1}{2}{\Vert y-Ax\Vert }_2^2$. Convert the L₁ regularized least squares problem (4) into an unconstrained smooth convex programming problem:

$$\min F(x)=\underset{x}{\min }\lambda {\Vert x\Vert }_1+\frac{1}{2}{\Vert y-Ax\Vert }_2^2,$$

(5)

where F(x) is differentiable when Newton’s method is adopted, the search direction of F(x) is:

$$d_k=-{\left[{\nabla }^{2}F(x)\right]}^{-1}\nabla F(x).$$

(6)

The gradient of F(x) is:

$$\nabla F(x)=\lambda \nabla f(x)+A^T(Ax-y).$$

∇F(x) is Lipchitz continuous, for the convenience of record, let:

$$s_k=x_{k+1}-x_k,$$

$$g_k=\nabla F(x_k),$$

$$u_k=\nabla F(x_{k+1})-\nabla F(x_k)=g_{k+1}-g_k.$$

x_k is the iteration point of step k, x_k+1 is the iteration point of step k + 1, s_k is the iteration difference of adjacent iteration points, g_k is the gradient of F(x), u_k is the gradient difference of F(x).

Then, the search direction of Newton’s method can be simplified as follows:

$$d_k=-{\left[{\nabla }^{2}F(x_k)\right]}^{-1}{g}_k.$$

When solving the problem (5), the iteration formula of Newton’s method is:

$$x_{k+1}=x_k+d_k.$$

When the Newton method is used to solve the sparse signal reconstruction problem in wireless sensor networks, its advantage is that it has a second-order convergence rate and that the reconstruction rate is higher than that of other convex optimization algorithms. The disadvantage of Newton’s method is that it needs the inverse of the second-order Hessian matrix and a large amount of computation, which will reduce the reconstruction rate to a certain extent. In addition, it cannot guarantee that the search direction is the descending direction of the objective function F(x) at x when ${\nabla }^{2}F(x_k)$ is not positive definite.

Based on the existing problems of the Newton method, this paper proposes the L-BFGS quasi-Newton method to solve the problem of sparse signal reconstruction in wireless sensor networks. In Section 5, it is proven whether the L-BFGS quasi-Newton method can solve the sparse reconstruction problem of wireless sensor networks.

3. Principles

The L-BFGS quasi-Newton method is an improvement of the BFGS quasi-Newton method. The L-BFGS quasi-newton method uses the information of the objective function value and the first derivative to construct a suitable H_k to approximate the inverse of the Hessian matrix without directly calculating and storing the matrix H_k. The complexity of the L-BFGS algorithm is lower than that of the BFGS algorithm, and the convergence speed of the Newton method is maintained. The constructed H_k is positive definite, which ensures that the search direction is the descending direction of the target function F(x) at x.

Before starting the L-BFGS algorithm, we first recall the famous BFGS method. An important problem in the BFGS quasi-Newton method is constructing a suitable matrix B_k, which makes B_k is an approximate matrix of the Hessian matrix. B_k needs to meet the following conditions:

(1) For all k, B_k is symmetric and positive definite, ensuring that the direction generated by the algorithm is the descending direction of the objective function F(x) at x_k;

(2) The updating rule of a matrix B_k is relatively simple.

In this paper, the search direction d_k is obtained by solving the following linear equation:

$$B_k{d}_k=-g_k.$$

The updating rule of the matrix B_k is:

$$B_{k+1}=B_k-\frac{B_k{s}_k{s}_k^T{B}_k}{s_k^T{B}_k{s}_k}+\frac{u_k{u}_k^T}{u_k^T{s}_k}.$$

(7)

When a suitable B_k has been constructed, H_k satisfies the condition $B_{k+1}=H_{k+1}^{-1}$. The Sherman-Morrison Woodbury [19] formula is used twice to obtain the updated formula of the matrix H_k is:

$$H_{k+1}=(I-\frac{s_k{u}_k^T}{u_k^T{s}_k})H_k(I-\frac{u_k{s}_k^T}{u_k^T{s}_k})+\frac{s_k{s}_k^T}{u_k^T{s}_k},$$

(8)

where H_k is the approximation of the inverse of the Hessian matrix and I is the identity matrix of order n, H_k should satisfy the following conditions:

(1)

H_k satisfies the Quasi-Newton equation:

$$B_{k+1}{s}_k=y_k \mathrm{or} H_{k+1}{y}_k=s_k;$$

(2)

H_k is a positive definite symmetric matrix;

(3)

The update from H_k to H_k+1 is a low-rank update.

The specific process of the BFGS algorithm is shown in the literature [13]. It is known that the curvature condition $u_k^T{s}_k>0$ can guarantee the positive definiteness of H_k+1 when H_k is positive definite. From Formula (8), an efficient recursive procedure is derived to compute the matrix-vector product H_k. For completeness, we describe the L-BFGS recursive procedure for H_k in Algorithm 1.

Algorithm 1: L-BFGS two-loop recursion

1. Input:$s_k=[s_{k-m},s_{k-m+1},\dots ,s_{k-1}]$$\mathrm{and} u_k=[u_{k-m},u_{k-m+1},\dots ,u_{k-1}]$; 2. $q\leftarrow g_k$ 3.  for $i=k-1:k-m$ do 6.  end 7. $r\leftarrow H_k^{(0)}q$ 8.  for $i=k-1:k-m$ do 11. end $r=-H_k{g}_k$ 12. Return the result

The two-loop recursive scheme can find the descent direction only through a simple calculation. Hence, it is cheap to generate the search direction by using Algorithm 1.

4. Algorithm

In the L-BFGS method, H_k no longer needs to be calculated and stored directly. Instead, the m latest vectors (s_k,u_k) saved in the memory are used to update the H_k, which only needs to store matrices of the size m × n, saving a lot of computation cost and improving the reconstruction rate. The specific step of the L-BFGS algorithm is Algorithm 2.

Algorithm 2: Limit memory BFGS Algorithm(L-BFGS)

1.Given: $\epsilon >0$$, k=0$$, {\sigma }_1\in (0,\frac{1}{2})$$, {\rho }_1\in (0,1)$$, t\in (0,1)$; 2. $\mathrm{Initialization}: x_0\in R^n$$; H_0=I$. 3.  while $\Vert g_k\Vert >\epsilon$ do 12. end

In the L-BFGS algorithm, the Wolfe line search is used to obtain the step size α_k. Wolfe line search belongs to a kind of inexact linear search. When using Wolfe line search to find the step size α_k, α_k is required to satisfy the following:

$$f(x_k+{\alpha }_k{d}_k)-f(x_k)\le {\rho }_1{\alpha }_k{g}_k^T{d}_k.$$

(9)

To make (9), flexible, we employ the non-monotone reduction condition on the:

$$g{(x_k+{\alpha }_k{d}_k)}^T{d}_k\ge {\rho }_2{g}_k^T{d}_k,$$

(10)

the parameterρ₁ and ρ₂ satisfies the conditions (0 < ρ₁ < ρ₂ < 1).

Finally, compared with the BFGS algorithm, the L-BFGS algorithm does not need to calculate and store H_k directly; it only needs to store matrices of the size m × d and calculate H_k by matrices of storage. The high reconstruction rate is improved by discarding some vectors and sacrificing a little reconstruction accuracy. Therefore, compared with the BFGS quasi-Newton method, the L-BFGS quasi-Newton method greatly reduces the computational complexity and makes the reconstruction rate of a sparse signal faster.

5. Verify the Feasibility of the L-BFGS Algorithm

According to Section 2, the sparse signal reconstruction problem of wireless sensor networks can be transformed into the L₁ norm minimization problem. When the solution is the optimal solution to the L₁ norm minimization problem, the sparse signal can be accurately reconstructed. In other words, when algorithm 2 meets global convergence, it is feasible.

First, we give some useful inequalities in the following lemma.

Lemma 1.

Let B_k be symmetric and positive definite, and B_k+1 is determined by the L-BFGS correction Equation (7), then the necessary and sufficient condition for B_k+1 symmetric and positive definite is $u_k^T{s}_k>0$.

Lemma 1 shows that, if the initial matrix B₀ is symmetric and positive definite and maintains $u_k^T{s}_k>0$ ($\forall k\ge 0$) during the iteration. Then, the matrix sequence { B_k+1 } generated by the L-BFGS correction formula is symmetric and positive definite, so that the equation $B_k{d}_k=-g_k$ has a unique solution d_k. It is easy to deduce that

$$d_k^T{B}_k{d}_k=-g_k^T{d}_k.$$

Since $d_k^T{B}_k{d}_k>0$, so $g_k^T{d}_k<0$. d_k is the descending direction of the target function F(x) at x_k.

Lemma 2.

If the Wolfe search criterion is adopted in the L-BFGS corrected quasi-Newton algorithm, there is $u_k^T{s}_k>0$.

Proof. 

Since $u_k^T{s}_k={(g_{k+1}-g_k)}^T{\alpha }_k{d}_k={\alpha }_k(g_{k+1}^T{d}_k-g_k^T{d}_k)$, according to step 5 of algorithm 2, we have

$$g_{k+1}^T{d}_k\ge {\rho }_2{g}_k^T{d}_k,$$

it is easy to deduce that

$$u_k^T{s}_k\ge {\alpha }_k({\rho }_2-1)g_k^T{d}_k.$$

Since ${\rho }_2<1$ and $g_k^T{d}_k<0$, so $u_k^T{s}_k>0$. B_k+1 is positively definite. The search direction generated by the algorithm is guaranteed to be the descending direction of the objective function F(x) at x_k, making the algorithm work normally.□

Lemma 3.

If the smooth function of the L₁ norm ∥x∥₁ obtained by the smoothing technique is:

$$f(x)={\displaystyle \sum _{i=1}^{n}H(x(i))},$$

where:

$$H(x(i))=\{\begin{array}{l}\frac{x^2(i)}{2\tau }, \left|x(i)\right|\le \tau ,\\ \left|x(i)\right|-\frac{\tau }{2}, \left|x(i)\right|>\tau ,\end{array}$$

then it can be proven that $f(x)\le {\Vert x\Vert }_1.$

Proof. 

when $\left|x(i)\right|\le \tau ,$$f(x)={\displaystyle \sum _{i=1}^n\frac{x^2(i)}{2\tau }}=\frac{1}{2\tau }{\displaystyle \sum _{i=1}^n{x}^2(i)}\le \frac{1}{2\tau }\tau {\displaystyle \sum _{i=1}^n\left|x(i)\right|=}\frac{1}{2}{\Vert x\Vert }_1\le {\Vert x\Vert }_1,$ when $\left|x(i)\right|>\tau ,$ $f(x)={\displaystyle \sum _{i=1}^n(\left|x(i)\right|-\frac{\tau }{2})}={\Vert x\Vert }_1-\frac{n\tau }{2}\le {\Vert x\Vert }_1,$ we have that: $f(x)\le {\Vert x\Vert }_1.$□

From Lemma 3 and the mechanism of Algorithm 2, we immediately obtain the following theorem.

Theorem 1.

Let {x_k} denote the sequence generated by L-BFGS quasi-Newton method iteration. When the smoothing parameter of ∥x∥₁ satisfies τ_k→0, then {x_k} is a bounded sequence. Let x* denote any limit point of {x_k}, then x* is the optimal solution to the L₁ norm minimization problem.

Prove the smooth parameter τ_k for the step k, make $x_k^{\ast }$ = arg $\underset{x}{\min }f\left(x\right)$ denotes the minimum point of the objective function F_k(x) at step k, and z denote any vector satisfying $Az=y$.

Because $x_k^{*}=\arg \underset{x}{\min }{F}_k(x),$ so $F_k(x_k^{*})\le F_k(z),$ also because $Az=y$, so:

$$F_k(z)=\lambda f_k(z)+\frac{1}{2}{\Vert Av-y\Vert }_2^2=\lambda f_k(z).$$

(11)

And from Lemma 3, $f_k(z)\le {\Vert z\Vert }_1,$ then:

$$F_k(x_k^{*})\le F_k(z)=\lambda f_k(z)\le \lambda {\Vert z\Vert }_1.$$

(12)

Since $F_k(x)=\lambda f_k(x)+\frac{1}{2}{\Vert Ax-y\Vert }_2^2,$ ${\Vert Ax-y\Vert }_2^2\ge 0,$ so:

$$F_k(x)\ge \lambda f_k(x).$$

(13)

In combination with Equations (11) and (12), the smoothness of $f_k(x)$ is:

$${\Vert x_k\Vert }_1\le f_{{\tau }_k}(x_k)+\frac{n{\tau }_k}{2}\le \frac{1}{\lambda }{F}_k(x_k)+\frac{n{\tau }_k}{2}\le \frac{1}{\lambda }\lambda {\Vert z\Vert }_1+\frac{n{\tau }_k}{2}={\Vert z\Vert }_1+\frac{n{\tau }_k}{2}.$$

In addition, when the smoothing parameter τ_k→0, {x_k} is a bounded sequence. On the other hand, it can also be proved that the limit point x* of the sequence {x_k} is feasible. The limit point x* is the KKT point of the L₁ norm minimization problem. Since ∥x∥₁ is convex and problem (3) is a convex programming problem, the KKT condition is sufficient for optimality, so x* is the optimal solution to the ∥x∥₁ norm minimization problem (3). It can be seen that the sparse signal of the wireless sensor network can be accurately reconstructed by the L-BFGS quasi-Newton method.

Corollary 1.

Let the L₁ norm minimization problem have a unique optimal solution, and let {x_k} represent the sequence generated by an iteration of the L-BFGS method. When k→∞ and τ_k→0, the x_k converges to x*, where x* = arg min{∥x ∥₁:Ax = y}.

6. L-BFGS Quasi-Newton Method Steps

The L-BFGS quasi-Newton method is developed from the BFGS quasi-Newton method. The basic idea of the BFGS quasi-Newton method is to use the identity matrix I to gradually approximate the H matrix, which avoids directly calculating the inverse of the Hessian matrix. However, H_k should be stored each time. H_k is very large, and the reconstruction rate of the algorithm is lost by direct calculation. According to Equation (8), each iteration of H_k is obtained by iterating curvature information (s_k,u_k). Since H_k cannot be stored easily, then store all the curvature information (s_k,u_k). This kind of storage saves memory space and improves the speed of the algorithm.

When the number of iterations is very large, all (s_k,u_k) cannot be saved. The reconstruction rate can be improved by discarding some original (s_k,u_k). Assuming that the number of storage vectors set is m. When the iteration is m + 1 times, (s₁,u₁) will be thrown away, and when the iteration is m + 2 times, (s₂,u₂) will be thrown away. By parity of reasoning, only the latest m-group (s_k,u_k) is retained. In this way, although the reconstruction accuracy is lost, the memory is saved, the algorithm complexity is reduced, and the reconstruction rate is improved. So the L-BFGS algorithm can be understood as another optimization of the BFGS algorithm.

When the L-BFGS quasi-Newton method is used to solve the sparse signal reconstruction problem in wireless sensor networks, the specific steps are as follows:

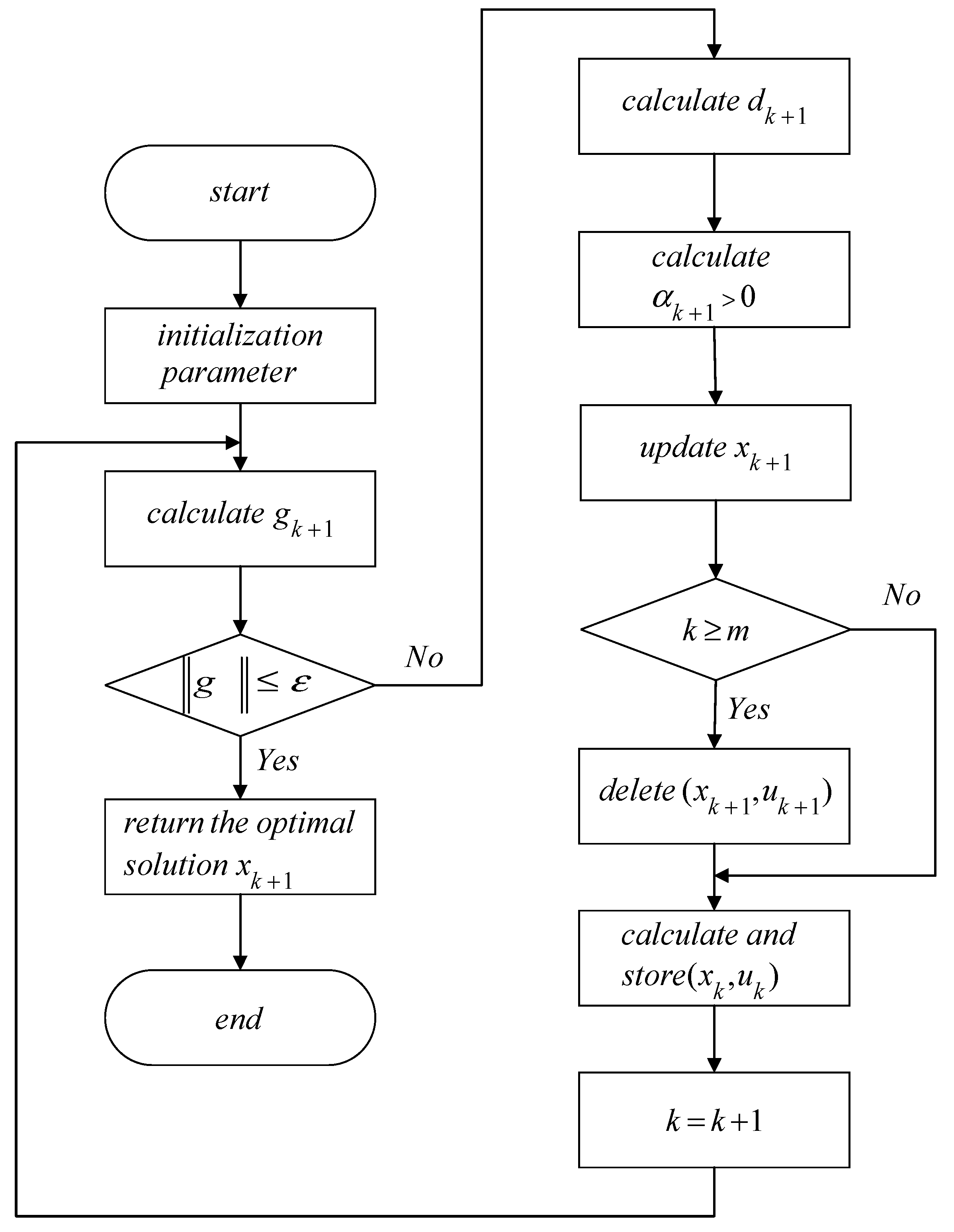
Step 1: First initialize the variable, select the initial point x₀, and define the operation error ε. The general value of ε is between 0 and 1, and the initial value of the H matrix is the identity matrix I of order n;

Step 2: Let k = 1 and calculate the gradient g_k at this time;

Step 3: Calculate g_k+1. If the norm of g_k+1 satisfies the operating error defined, namely $\Vert g_{k+1}\Vert \le \epsilon$, it indicates that the cut-off condition is met and the algorithm is terminated. The iteration point x_k+1 is the optimal solution. If the cut-off conditions are not met, it is necessary to go to step 4 and continue to solve the optimal solution;

Step 4: Calculate the search direction d_k and the step factor α_k, and update x_k+1; to ensure that the search direction is correct. There are many methods to calculate the step factor α_k. Here, the inexact Wolfe line search is used to solve the step factor α_k. The step size can be guaranteed to be larger than 0. In the correct search direction, the x_k+1 is closer and closer to the optimal solution;

Step 5: If k ≥ m, keep the latest curvature information (s_k,u_k), and delete (s_k-m,u_k-m). The L-BFGS quasi-Newton method will retain m bits of data. When it exceeds m bits, it will delete the curvature information before m bits to improve the calculation speed. This is also the difference between the BFGS quasi-Newton method;

Step 6: Let k = k + 1; transfer to step 3. Start iterating until the optimal solution is obtained and the algorithm stops.

Special remarks: In step 1, for the initial value x₀, the initial value x₀ of iteration should be selected near the root to ensure the convergence of the iterative process. The most common way is to choose the initial value by using Newton’s convergence theorem. In step 4, the correctness of the search direction d_k should be ensured. If the search direction is not the descending direction at x, the iterative point will deviate more and more from the optimal point, and the sparse signal cannot be accurately reconstructed. There are many ways to calculate the descending direction, d_k. In this paper, a two-loop recursive algorithm is adopted to find the search direction, which can ensure the accuracy of the search direction and the two-loop recursive algorithm is simple. In step 5, if k ≥ m is satisfied, calculate the new curvature information and discard the curvature information before m-bit

(s_k-m,u_k-m). By giving up small reconstruction accuracy in exchange for a faster reconstruction rate. If k ≥ m is not satisfied, directly calculate (s_k,u_k). In step 6, let k = k + 1 and start a new iteration; no initialization is required. The result of the previous iteration is its initial value, and the iteration continues until the optimal solution is obtained.

The flow chart of the L-BFGS quasi-Newton method is shown in Figure 1 as follows:

7. Experimental Simulation

To verify the effectiveness of the L-BFGS quasi-Newton method in wireless sensor networks for signal reconstruction, simulation experiments are carried out. The Gaussian matrix can satisfy the constraint isometry with high probability. In the experiment, the measurement matrix Φ∈R^M×N with Gaussian distribution is used as the observation matrix, and the Gaussian sparse signal x ∈ R^N with variable sparsity is used as the original signal. The value range of sparsity K is [1,70].

The simulation experiment in this paper takes the reconstruction accuracy and reconstruction time of each algorithm for the original signal as the main evaluation criteria, and the unit of time is a second (s). In the simulation experiment, each experiment is carried out 1000 times, and the average reconstruction accuracy and average reconstruction time of the 1000 experiments are taken as the final reconstruction accuracy and reconstruction time.

This paper mainly compares the reconstruction accuracy and reconstruction time of the BP algorithm, the NSHTP [20] algorithm, the BFGS algorithm, and the L-BFGS algorithm under conditions of sparsity. When the data changes, the difference in reconstruction accuracy is small. This paper mainly analyzes the reconstruction accuracy of two sets of data: n = 512, m = 256, and n = 256, m = 128. The reconstruction time is greatly affected by the data size. To better compare the reconstruction time of each algorithm, four groups of data are selected to compare and test: n = 128, m = 64; n = 256, m = 128; n = 512, m = 256; n = 1024, m = 512.

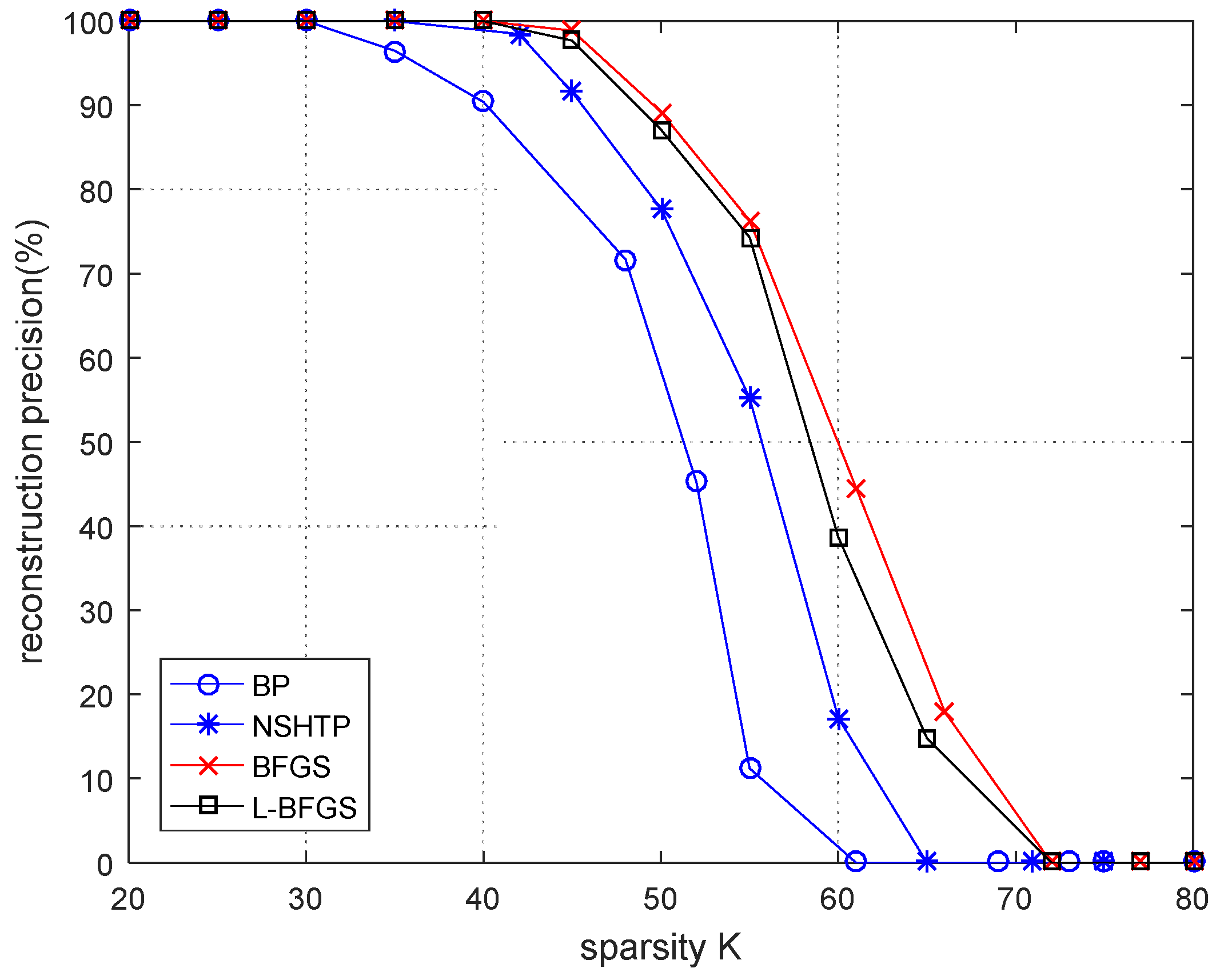
First, there are two simulation diagrams about the reconstruction accuracy. In Figure 2, n = 256 and m = 128. As can be seen from the figure, there is little difference in reconstruction accuracy between the four algorithms. The reconstruction rate of the four algorithms is high. The BP algorithm has the worst reconstruction accuracy. The reconstruction accuracy of the BP algorithm starts to decrease when K = 35. The BP algorithm cannot reconstruct the signal when K = 62. The BFGS algorithm has the best reconstruction accuracy, and the difference between the proposed algorithm and the BFGS algorithm is very small. Both algorithms begin to reduce the reconstruction accuracy when K = 40 and cannot reconstruct the signal when K = 72. In general, the reconstruction accuracy of the BFGS algorithm is slightly higher than that of the proposed algorithm, but the reconstruction accuracy of the proposed algorithm is higher than that of the NSHTP algorithm and the BP algorithm.

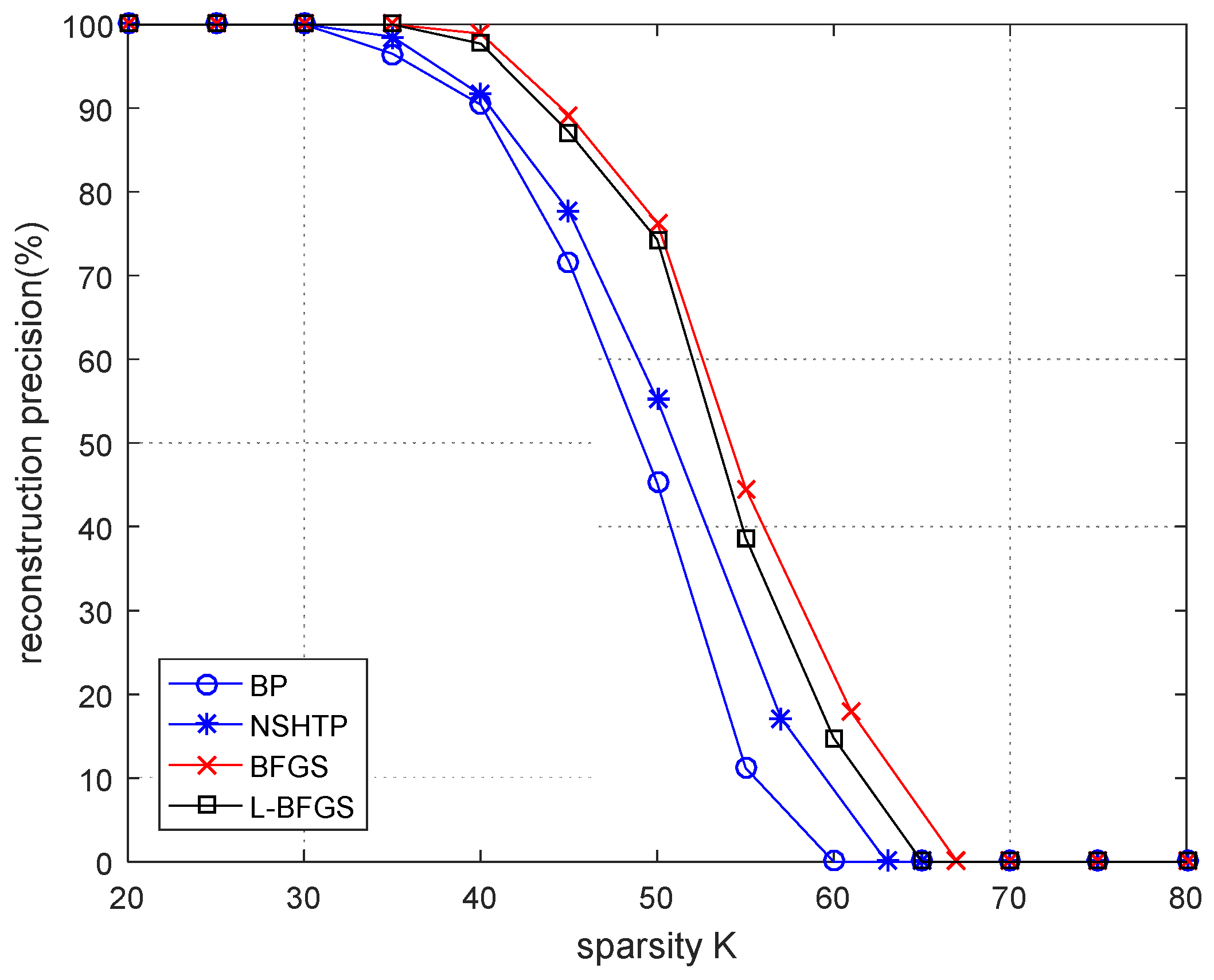
In Figure 3, n = 512 and m = 256. At this time, the reconstruction accuracy is slightly different for n = 256 and m = 128; however, the reconstruction accuracy of all algorithms has deteriorated. It shows that the larger n and m, the worse the reconstruction accuracy. The difference between the proposed algorithm and the BFGS algorithm is still very small and within an acceptable range.

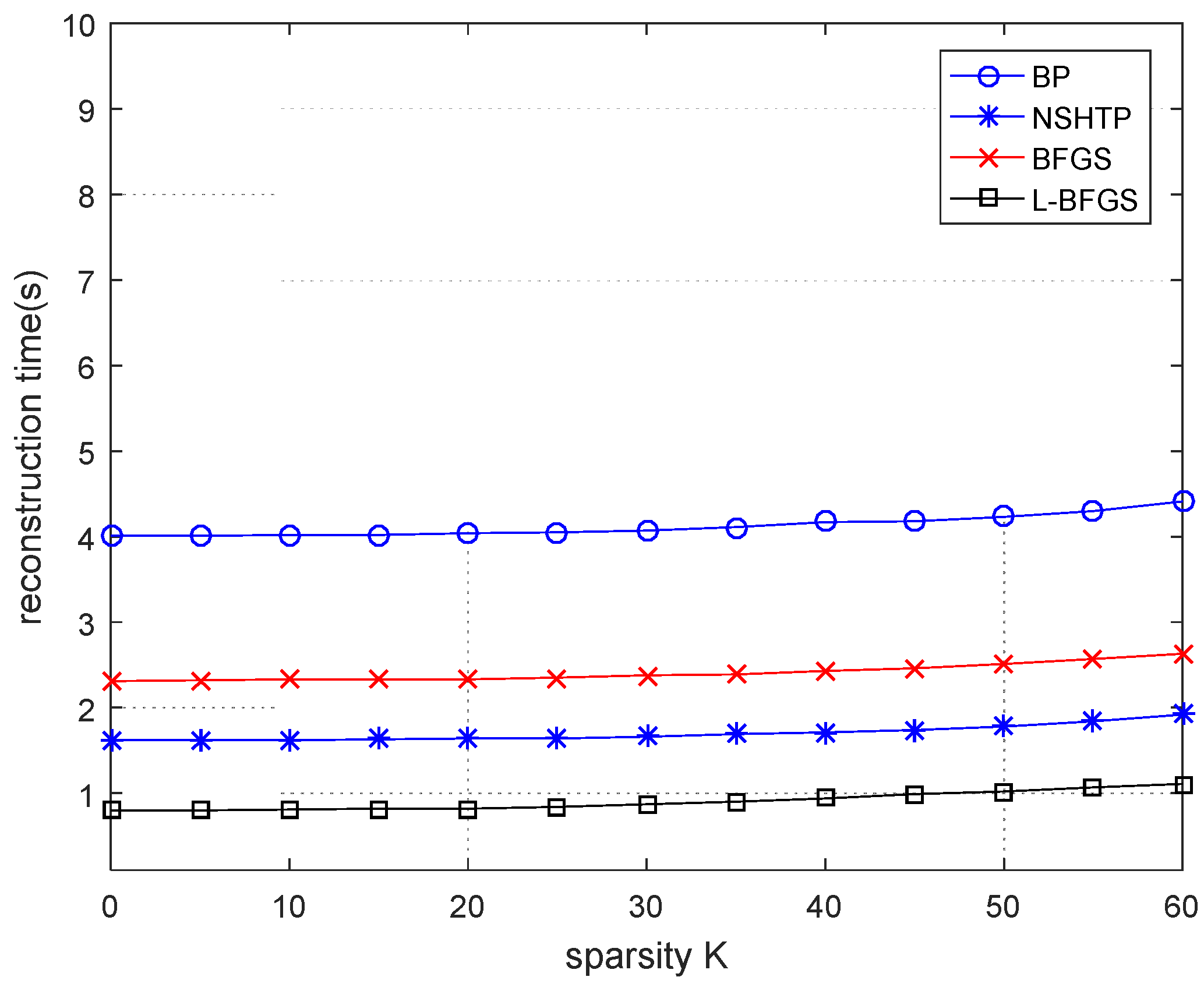
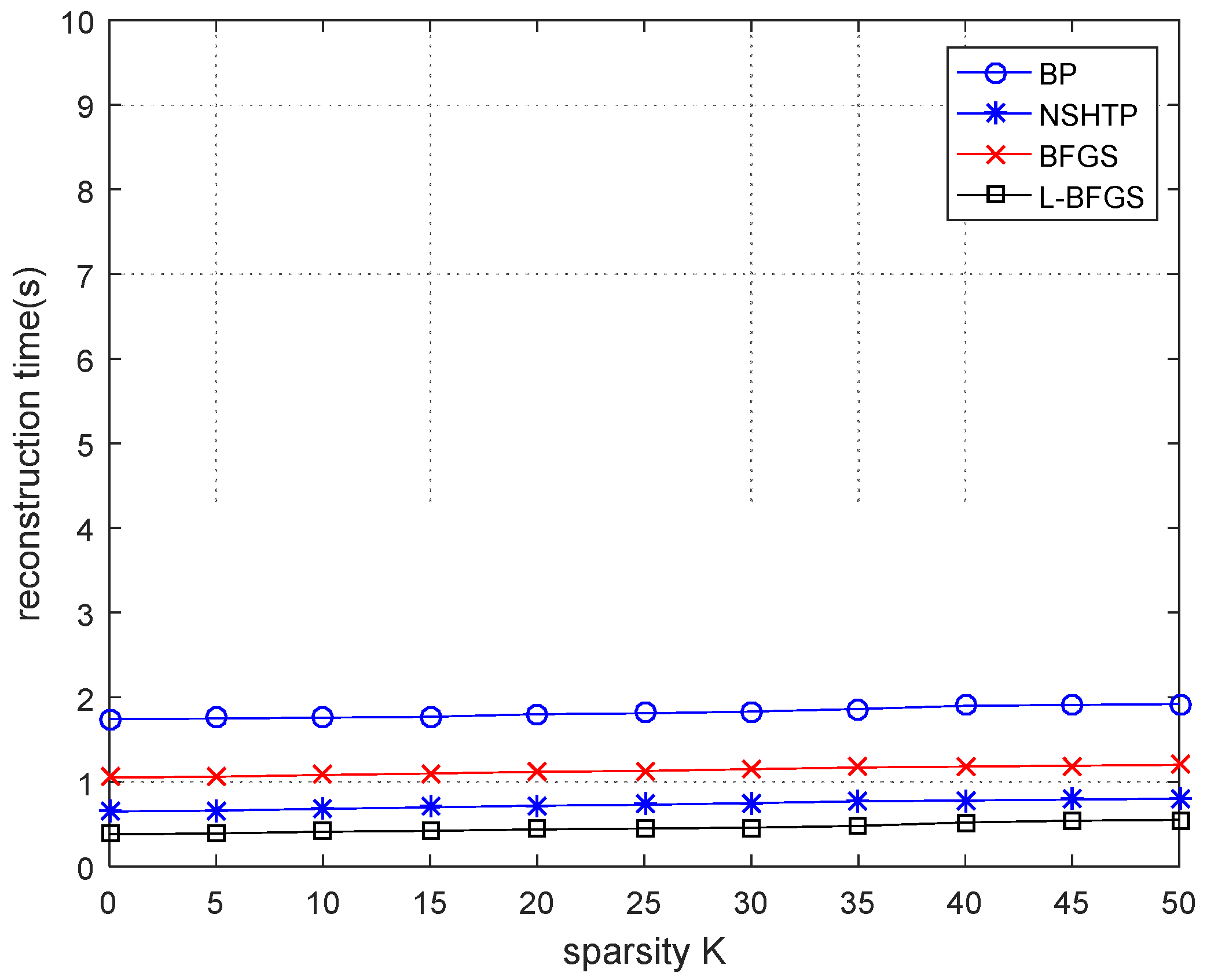
Secondly, there are four simulation diagrams about the reconstruction rate. In Figure 4, n = 128 and m = 64. It can be seen from Figure 4 that the reconstruction time of the BP algorithm is higher than the other three algorithms, which require the longest reconstruction time and the lowest reconstruction rate. The reconstruction time of the NSHTP algorithm and BFGS algorithm is between the BP algorithm and the proposed algorithm, and the proposed algorithm requires the shortest reconstruction time and the highest reconstruction rate. The reconstruction time of the BFGS algorithm is twice that of the proposed algorithm, and the reconstruction rate of the proposed algorithm is higher than that of the BFGS algorithm. As can be seen from the figure, when the data is short, the reconstruction rate of all algorithms is high, and the sparsity has little influence on the reconstruction time. There is no obvious mutation point when the sparsity increases in the reconstruction time.

In Figure 5, n = 256 and m = 128. The reconstruction time by the four algorithms is significantly higher than that when n = 128 and m = 64. It indicates that with the increase in data length, the time for signal reconstruction is longer and the reconstruction rate is lower. As can be seen from Figure 5, the proposed algorithm has the shortest reconstruction time and the fastest reconstruction rate. The reconstruction time of the BP algorithm is the longest, and the reconstruction rate is the worst. The reconstruction times of the NSHTP algorithm and the BFGS algorithm are between the BP algorithm and the proposed algorithm. In general, when the signal length increases, the reconstruction rate of all algorithms will be affected, but the reconstruction rate of the proposed algorithm is the fastest, which is significantly higher than the BFGS algorithm.

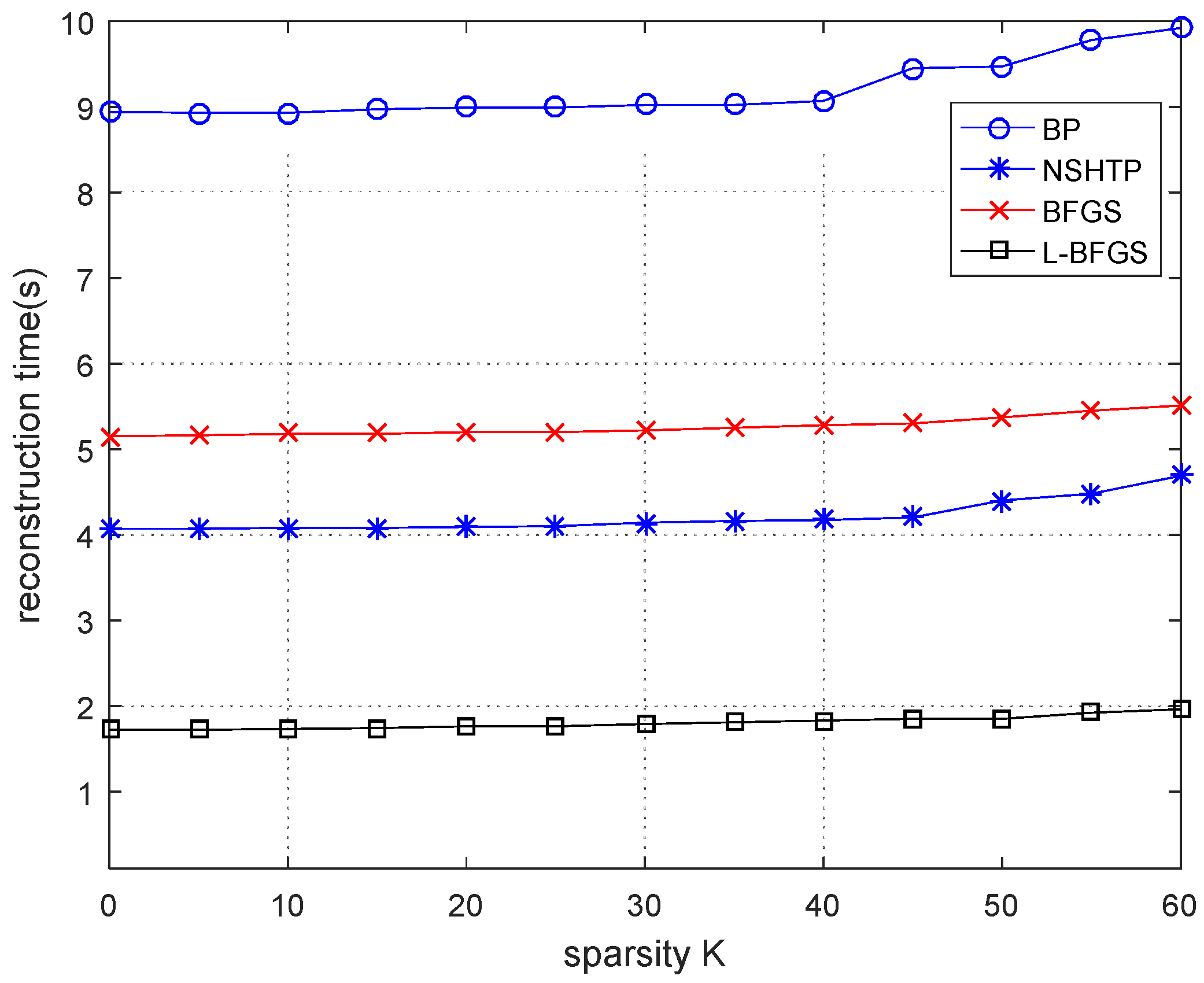
In Figure 6, n = 512 and m = 256. All algorithms require longer reconstruction times, which get longer as the length of the data increases. The proposed algorithm still has the shortest reconstruction time and the fastest reconstruction rate. The BP algorithm still has the worst reconstruction rate. When K = 40, the BP algorithm has a small mutation point, and when K = 45, the NSHTP algorithm also has a small mutation point. Both the proposed algorithm and the BFGS algorithm have no obvious mutation point. It indicates that when the data length increases, the sparsity has little influence on the BP algorithm and the NSHTP algorithm but no obvious influence on the proposed algorithm and the BFGS algorithm. In general, when n = 512 and m = 256, the proposed algorithm has the shortest reconstruction time and the fastest reconstruction rate among the four algorithms. It is less affected by sparsity, and the reconstruction rate is significantly higher than the BFGS algorithm.

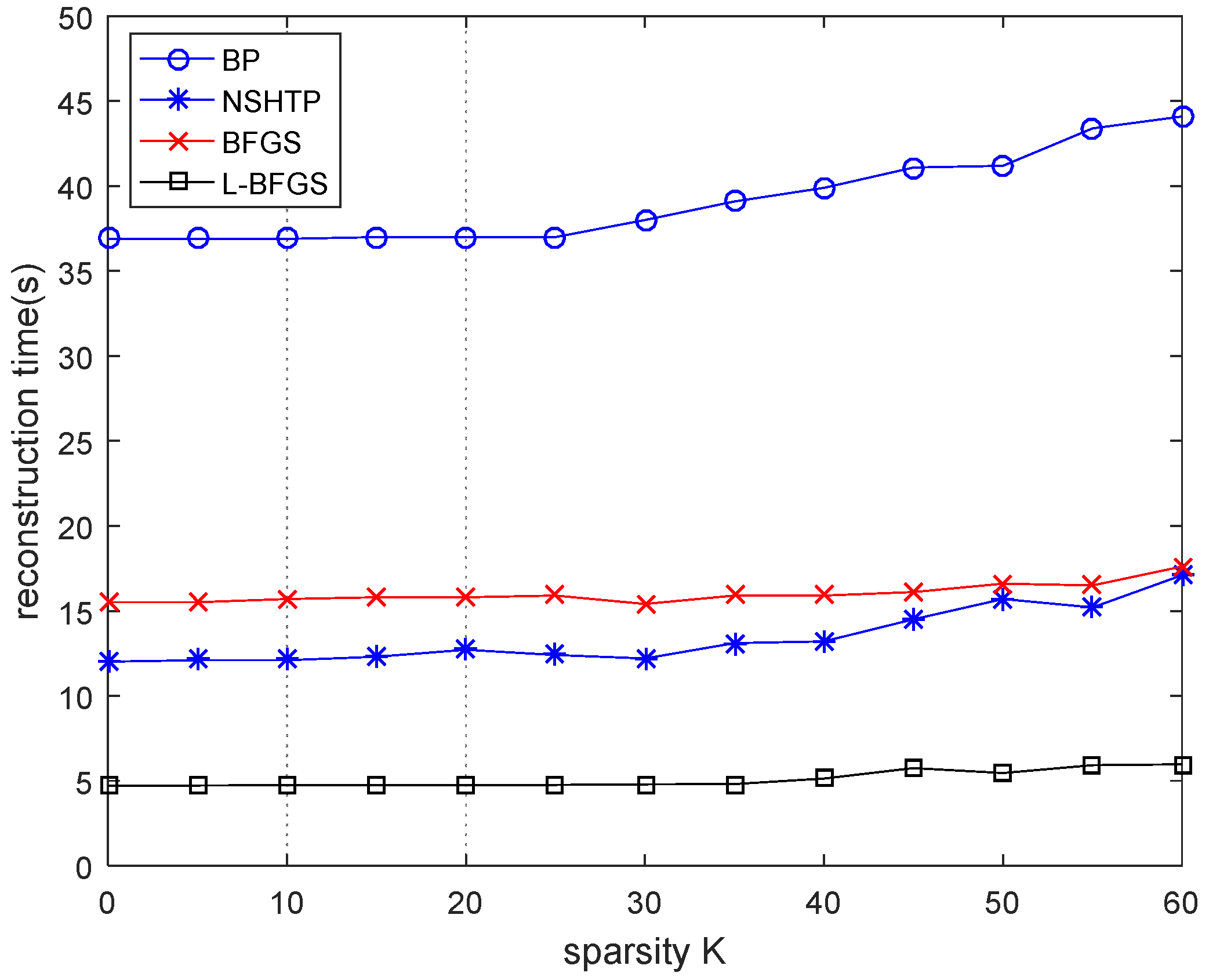
In Figure 7, n = 1024 and m = 512.The exact reconstruction time of all algorithms becomes longer, but the reconstruction time of the proposed algorithm is the shortest and the reconstruction rate is the fastest. The BP algorithm has the longest reconstruction time and the worst reconstruction rate. As shown in Figure 7, with the increase in sparsity, the BP algorithm has a mutation point when K = 30. When K = 35, the NSHTP algorithm has a mutation point, and the BFGS algorithm has a small mutation point. When K = 45, small mutation points appear in the proposed algorithm. It indicates that when n = 1024 and m = 512, sparsity has an impact on all algorithms. The BP algorithm and the NSHTP algorithm have a greater impact, and the proposed algorithm and the BFGS algorithm have a smaller impact. In general, the reconstruction rate of the proposed algorithm is the fastest and most stable, which is significantly better than the BFGS algorithm in the reconstruction rate.

Finally, by comparing n = 128, m = 64; n = 256, m = 128; n = 512, m = 256; n = 1024, m = 512, the reconstruction time of four groups of data was simulated. It can be found that the larger the length of data, the longer the time for signal reconstruction, and the worse the rate for signal reconstruction. When n = 512, m = 256, and K = 25, the signal reconstruction time of the BP algorithm is 9.11 s, the NSHTP algorithm is 4.23 s, the BFGS algorithm is 5.17 s, and the proposed algorithm is 1.93 s. When n = 1024, m = 512, and K = 25, the signal reconstruction time of the BP algorithm becomes 37.25 s, the NSHTP algorithm becomes 12.57 s, the BFGS algorithm becomes 15.93 s, and the proposed algorithm becomes 4.84 s. It can be seen that when the data length and matrix size are doubled, the reconstruction time of the BP algorithm is more than 4 times the growth of the data, the reconstruction times of the NSHTP algorithm and BFGS algorithm have been tripled, and the proposed algorithm becomes 2.5 times the growth of the data. It shows that when n and m grow, the reconstruction rate of the proposed algorithm is the most stable and fastest. Through the simulation of reconstruction accuracy and reconstruction rate, it can be seen that the L-BFGS algorithm is slightly worse than the BFGS algorithm in reconstruction accuracy, but the reconstruction rate is significantly higher than the BFGS algorithm. In general, the L-BFGS algorithm is superior to the BFGS algorithm and is more suitable for sparse signal reconstruction in wireless sensor networks.

8. Conclusions

Aiming at the problem of a low reconstruction rate when the Newton method is used to reconstruct sparse signals in wireless sensor networks, this paper proposes to use the L-BFGS quasi-Newton algorithm to improve the reconstruction rate. The L-BFGS does not need to store and calculate H_k directly; only two matrices of size m × n need to be stored. This algorithm, by discarding some vectors and sacrificing some reconstruction accuracy, greatly reduces the reconstruction time and improves the reconstruction rate compared with the BFGS algorithm. At the same time, the simulation experiment is carried out to compare the reconstruction accuracy and reconstruction time of the proposed algorithms, the BFGS algorithm, the NSHTP algorithm, and the BP algorithm. Experiments show that the reconstruction accuracy of the proposed algorithm is higher than that of the BP algorithm and the NSHTP algorithm but slightly lower than that of the BFGS algorithm. However, the reconstruction rate of the proposed algorithm is the fastest and most stable among the four algorithms, which is two times higher than the BFGS algorithm. Therefore, the proposed algorithm has a high reconstruction rate and certain advantages in terms of reconstruction accuracy. It is a better reconstruction algorithm than the BFGS algorithm.