Towards High-Performance Supersingular Isogeny Cryptographic Hardware Accelerator Design

Abstract

Cryptosystems based on supersingular isogeny are a novel tool in post-quantum cryptography. One compelling characteristic is their concise keys and ciphertexts. However, the performance of supersingular isogeny computation is currently worse than that of other schemes. This is primarily due to the following factors. Firstly, the underlying field is a quadratic extension of the finite field, resulting in higher computational complexity. Secondly, the strategy for large-degree isogeny evaluation is complex and dependent on the elementary arithmetic units employed. Thirdly, adapting the same hardware to different parameters is challenging. Considering the evolution of similar curve-based cryptosystems, we believe proper algorithm optimization and hardware acceleration will reduce its speed overhead. This paper describes a high-performance and flexible hardware architecture that accelerates isogeny computation. Specifically, we optimize the design by creating a dedicated quadratic Montgomery multiplier and an efficient scheduling strategy that are suitable for supersingular isogeny. The multiplier operates on ${\mathbb{F}}_{p^2}$ under projective coordinate formulas, and the scheduling is tailored to it. By exploiting additional parallelism through replicated multipliers and concurrent isogeny subroutines, our 65 nm SMIC technology cryptographic accelerator can generate ephemeral public keys in 2.40 ms for Alice and 2.79 ms for Bob with a 751-bit prime setting. Sharing the secret key costs another 2.04 ms and 2.35 ms, respectively.

1. Introduction

Currently, asymmetric cryptosystems are threatened by the development of large-scale quantum computers. Standard public key encryption algorithms, namely Rivest-Shamir-Adleman (RSA) and elliptic curve cryptography (ECC), are built on the underlying difficulty of factoring large integers and computing elliptic curve discrete logarithms. However, these mathematical problems would be vulnerable to a quantum machine running Shor’s algorithm [1].

To thwart this potential threat, the National Institute of Standards and Technology (NIST) has initiated a process to solicit, evaluate, and standardize one or more quantum-resistant public-key cryptographic algorithms [2]. Five renowned and universally accepted classes of primitives have been submitted and assessed, code-based cryptography, lattice-based cryptography, hash-based cryptography, multivariate cryptography, and isogeny-based cryptography. Among these candidates, there are various trade-offs regarding their underlying security assumptions, key sizes, and efficiency. Isogeny-based cryptography has the apparent advantage of a minor key length, which helps mitigate the transmission load and storage requirement. CSIDH is one such innovative scheme that has the smallest public-key size as a post-quantum key exchange or encapsulation scheme [3]. It has public keys of only 64 bytes at a conjectured AES-128 security level, matching NIST’s post-quantum security category I. Moreover, primitives for the lattice-based encryption scheme NTRU [4], the code-based encryption scheme McBits [5], and the ring-LWE-based signature scheme “New Hope” [6] have relatively large public and private keys. This drawback is especially obvious when compared with traditional public-key algorithms.

Isogeny-based cryptography relies on the difficulty of the isogeny-finding problem. An isogeny describes a morphism between elliptic curves that preserves the infinity point. Rather than computing with a secret scalar point multiplication, isogeny-based cryptography takes a secret walk on the isogeny graph to generate the public key or encrypt the message. The idea of using isogeny to build a cryptosystem was first proposed by Rostovsev, and Stolbunov [7] in 2006. This original isogeny scheme was later broken by a subexponential quantum algorithm discovered by Childs [8]. In 2011, Jao and De Feo proposed a key exchange protocol instead on isogenies between supersingular elliptic curves. This scheme is known as the supersingular isogeny Diffie–Hellman (SIDH) key exchange, The underlying supersingular isogeny problem is related to the claw problem, which is immune to quantum algorithms. However, the scheme also reveals auxiliary points in public keys, which exposes a potential vulnerability. In August 2022, Castryck and Decru proposed an efficient classical key recovery algorithm that exploits this vulnerability and allows for the attack of SIDH. The algorithm, which relies on the use of Richelot isogenies and abelian surfaces, employs a “glue-and-split” method to successfully break SIDH. In response to this attack, Moriya [9] and Fouotsa [10] proposed modifications to SIDH that would avoid the Castryck and Decru family of attacks. However, these modifications significantly degrade the performance and increase the key size of SIDH by at least an order of magnitude. Fortunately, there are still several isogeny-based cryptosystems, such as CGL [11], CSIDH [3], and SQIsign [12], which are not based on SIDH and, therefore, unaffected by the above-mentioned attacks. In addition, the supersingular isogeny problem has been used to create digital signatures [13,14] and undeniable signatures [15].

In this paper, we present a high-performance application-specific integrated circuit (ASIC) isogeny hardware accelerator. The main contributions of this paper are as follows.

• We provide a quadratic Montgomery multiplier operating on ${\mathbb{F}}_{p^2}$ operands on customized hardware which is suitable for supersingular isogeny. Our design architecture can be straightforwardly applied to different sizes of finite fields.
• We exploit the parallelism of processing units and isogeny subroutines to create an efficient scheduling strategy. It customizes the internal operation logics according to the feature of modular arithmetic units.
• We prototype our hardware accelerator based on 65 nm SMIC technology by integrating the computing units and the control logic. For the 751-bit prime setting, the design is 2.58 times faster than the state-of-the-art software design and 1.29 times faster than the prior field-programmable gate array (FPGA) implementation. The overall runtime drops to 6.77 ms and 6.10 ms for Alice and Bob in the key generation phase. and to 6.18 ms and 5.36 ms in the secret sharing phase.

The remainder of this paper is organized as follows. Section 2 provides an overview of supersingular isogeny and an abstract introduction to the SIDH protocol. Section 3 lists the parameter settings and the design specifications that we are working on and presents our quadratic Montgomery multiplier, which combines high-radix Montgomery multiplication and quadratic finite field arithmetic. The advantages and limitations of this design are also discussed. In Section 4, we introduce the hardware prototype of the isogeny accelerator and the scheduling methodology of primary isogeny subroutines. Section 5 presents the performance results of our implementation and a comparison with prior works. We also discuss potential improvements and show how our proposed design can help accelerate other isogeny-based cryptosystems. The main contributions are concluded in the final section.

2. Preliminaries

Before introducing our isogeny-based crypto-processor design, we present some prerequisite knowledge associated with elliptic curves and isogeny theory to help understand the basic computation. An abstract SIDH protocol is also described. For more details on the mathematical background and cryptography protocol, we recommend [16,17]. Fast software implementation of all subroutines involved in the key exchange scheme can be found in [18].

2.1. Elliptic Curves and Isogeny

Several classical ECC algorithms use a form of elliptic curves introduced by Montgomery in 1987 [19]. Such curves defined over a finite field ${\mathbb{F}}_q$ are described as

$$E_{(a.b)}/{\mathbb{F}}_q:b{y}^2=x^3+a{x}^2+x,$$

(1)

where $a,b\in {\mathbb{F}}_q$ and $b(a^2-4)\ne 0$. The Montgomery curves are the preferred choice because they allow very efficient x-only arithmetic. This will also feature in isogeny-based cryptography. All points $(x,y)$ satisfying the above equation together with the infinity point $\mathcal{O}$ compose an abelian group over point addition. Classical ECC relies on the difficulty of solving the elliptic curve discrete logarithm problem in this group. Specifically, it is hard to determine the scalar given any point P and its scalar multiplication $Q=kP=P+P+\cdots +P$. However, Shor’s algorithm [1] provides a sub-exponential method of recovering the scalar multiple on a feasible quantum machine. Fortunately, this is not the end of the story, as cryptographers have found that the supersingular elliptic curve group over isogeny is quantum-resistant, allowing isogeny-based cryptography to be constructed in such a way that ECC lives on.

Here, an isogeny is defined as a rational group morphism from an elliptic curve E to another elliptic curve $E^{\prime }$ that preserves its identity, written as

$$\varphi :E\to E^{\prime },\varphi \left(\mathcal{O}\right)={\mathcal{O}}^{\prime }.$$

(2)

Given any finite subgroup $\kappa$ of points on elliptic curve E, there is a unique isogeny $\varphi$ whose kernel is $\kappa$. Vélu has provided a method [20] of computing $\varphi :E\to E/\langle \kappa \rangle$. On the input of the coefficients of E and the points in $\kappa$, Vélu’s formula explicitly outputs the expression of the coefficients of $E^{\prime }$ and the morphism $\varphi$. The degree of isogeny is the number of elements in the kernel $\kappa$, equal to its degree as a rational morphism. Two curves E, $E^{\prime }$ are isogenous if an isogeny exists between them. The following theorem captures an interesting fact.

Theorem 1.

E and $E^{\prime }$ are isogenous if, and only if, they have a same number of points, #E = #E′.

Before elaborating on the SIDH protocol, two properties of elliptic curves should be explained. namely isomorphisms and j-invariants. Isomorphisms are actually a special case of an isogeny in which the kernel is $\left\{\mathcal{O}\right\}$, which are isogenies of degree 1. The j-invariant is a discriminant of an elliptic curve that determines the isomorphism class over ${\mathbb{F}}_q$. The j-invariant of a Montgomery curve is given by

$$j\left(E_{a,b}\right)=\frac{256{(a^2-3)}^3}{a^2-4}.$$

(3)

The relationship between the isomorphism class and the j-invariant can be stated as follows.

Theorem 2.

E, and $E^{\prime }$ are isomorphic if, and only if, they have the same j-invariant, $j\left(E\right)=j\left(E^{\prime }\right)$.

Isogenous curves have different j-invariants. Thus, an isogeny can be seen as a map from one isomorphism to another. The ostensible explanation of isogeny-based cryptography is that, Alice and Bob walk randomly around the isogeny graph, from one isomorphic class to another, one j-invariant to another, before eventually arriving at the same j-invariant as the shared secret. Based on this, the difficult mathematical problem is that, given the origin curve and the terminal curve, one cannot find the exact isogeny mapping between them in sub-exponential time. However, this problem is vulnerable when using the original curves [8]. Hence, cryptographers moved on to supersingular elliptic curves for which the isogeny problem is secure against classical and quantum cryptanalysis.

In algebraic geometry, supersingular elliptic curves are a certain class of elliptic curves over a field of characteristic $p>0$ with unusually large endomorphism rings of $\mathbb{Z}$-rank 4. Supersingular curves are defined over ${\mathbb{F}}_p$ or ${\mathbb{F}}_{p^2}$, and all can be represented in ${\mathbb{F}}_{p^2}$. The endomorphism ring is the ring composed of the set of endomorphisms of a given elliptic curve and the null map. Endomorphisms are a special case of isogenies for which the codomain is the same as the domain, written as

$$\varphi :E\to E,\left|ker\right(\varphi \left)\right|>1.$$

(4)

Eventually, we come to the specific case of isogenies on supersingular curves. Two theorems are crucial to understanding the isogeny graph, which is formed by isomorphism classes as vertices and l-isogenies as edges. Considering a specific l, this leads to a roughly regular graph $X(S_{p^2},l)$ in which almost all nodes have $l+1$ unique isogenies up to an isomorphism of degree l. Figure 1 shows an excerpt of the 2-isogeny graph over ${\mathbb{F}}_{{431}^2}$ [21]. In total, there are 37 j-invariants as nodes and 2 isogenies between them as edges.

Theorem 3.

Let $S_{p^2}$ be the set of supersingular j-invariants. Then $\#S_{p^2}=\lfloor \frac{p}{12}\rfloor +b$, $b\in \{0,1,2\}$.

Theorem 4.

For every prime $l\nmid p$, there exist $l+1$ isogenies of degree l originating from a supersingular base curve.

2.2. SIDH Key Exchange

Building on supersingular isogeny theory, Jao and Le Feo [16] proposed the SIDH key exchange scheme in 2011. The basic purpose of the Diffie–Hellman protocol is to enable two parties to agree on a shared secret securely through a public channel under a passive security model. SIDH works on elliptic curves in the same way as ECDH but replaces the underlying computation by handling large degree isogenies.

Initially, the involved parties agree on the public parameters. Alice and Bob publicly select a smooth isogeny prime in the form of Equation (5), where $l_A$ and $l_B$ are small primes, $e_A$ and $e_B$ are positive integers, and f is a small cofactor to make p prime.

$$p={l_A}^{e_A}·{l_B}^{e_B}·f\pm 1$$

(5)

A supersingular curve $E\left({\mathbb{F}}_{p^2}\right)$ is defined over this number. This elliptic curve group is the full $(p+1)$-torsion which is isomorphic to ${\mathbb{Z}}_{p\mp 1}\times {\mathbb{Z}}_{p\mp 1}$.

$$E\left({\mathbb{F}}_p^2\right)\cong {\mathbb{Z}}_{\left({l_A}^{e_A}{l_B}^{e_B}f\right)}\times {\mathbb{Z}}_{\left({l_A}^{e_A}{l_B}^{e_B}f\right)}$$

(6)

The cardinality of E is $\#E={\left({l_A}^{e_A}{l_B}^{e_B}f\right)}^2$. Next, Alice and Bob choose independent elliptic curve points so that the subgroups $E\left[{l_A}^{e_A}\right]$ and $E\left[{l_B}^{e_B}\right]$ can be generated as $E\left[{l_A}^{e_A}\right]=\langle P_A,P_B\rangle$ and $E\left[{l_B}^{e_B}\right]=\langle Q_A,Q_B\rangle$. We now have all the necessary presuppositions.

The first phase of the SIDH protocol is ephemeral key generation. Alice chooses two private keys $m_A,n_A\in \mathbb{Z}/{l_A}^{e_A}\mathbb{Z}$ with the condition that they are not both divisible by ${l_A}^{e_A}$. Analogously, Bob chooses $m_B,n_B\in \mathbb{Z}/{l_B}^{e_B}\mathbb{Z}$, where $m_B,n_B$ are not both divisible by ${l_B}^{e_B}$. The protocol then proceeds as follows.

• Alice computes the isogeny ${\varphi }_A:E\to E_A$ with the kernel $\langle R_A\rangle =\langle m_A{P}_A+n_A{Q}_A\rangle$. Alice then projects Bob’s basis points under the new curve $\{{\varphi }_A\left(P_B\right),{\varphi }_A\left(Q_B\right)\}\subset E_A$. Alice’s ephemeral public key is $\{E_A,{\varphi }_A\left(P_B\right),{\varphi }_A\left(Q_B\right)\}$.
• Bob computes the isogeny ${\varphi }_B:E\to E_B$ with the kernel $\langle R_B\rangle =\langle m_B{P}_B+n_B{Q}_B\rangle$. Bob then projects Alice’s basis points under the new curve $\{{\varphi }_B\left(P_A\right),{\varphi }_B\left(Q_A\right)\}\subset E_B$. Bob’s ephemeral public key is $\{E_B,{\varphi }_B\left(P_A\right),{\varphi }_B\left(Q_A\right)\}$.

For the second phase of the protocol, Alice and Bob compute the shared secret as follows once they have received the exchanged information from the other party. The second phase calculation is quite similar to that of the first phase, except that the basis points are no longer pushed through the isogeny.

• Alice computes her isogeny ${\varphi }_{AB}:E_B\to E_{AB}$ with the kernel $\langle {\varphi }_B\left(R_A\right)\rangle =\langle m_A{\varphi }_B\left(P_A\right)+n_A{\varphi }_B\left(Q_A\right)\rangle$.
• Bob computes his isogeny ${\varphi }_{BA}:E_A\to E_{BA}$ with the kernel $\langle {\varphi }_A\left(R_B\right)\rangle =\langle m_B{\varphi }_A\left(P_B\right)+n_B{\varphi }_A\left(Q_B\right)\rangle$.

The curves $E_{AB}$ and $E_{BA}$ reside in the same isomorphism class, so the j-invariant of these curves can be used as the shared secret. An abstract SIDH protocol is illustrated in Figure 2.

2.3. Large Degree Isogeny Decomposition

The main part of the SIDH protocol is computing the large degree isogeny given any specific kernel. The breakdown of all computations for the supersingular isogeny is shown in Figure 3, similar to a superset of the breakdown of point manipulation. The large degree isogeny is the core whereby the secret kernel is pushed to the public key and then to the shared secret. Thus, an efficient method of computing it is of the same importance as scalar point multiplication in ECC.

Given a finite subgroup $\langle R\rangle \subseteq E/{\mathbb{F}}_{p^2}\left[l^e\right]$ of order $l^e$, there is a unique isogeny ${\varphi }_R$ of degree $l^e$ with the kernel $\langle R\rangle$, that maps E to an isogenous curve $E/\langle R\rangle$. The direct calculation of a large degree isogeny is quite hard, but it can be decomposed into e isogenies of degree l, which then are computed in sequence using Vélu’s formulas. As proposed in [16], we can initialise $R_0:=R$ and $E_0:=E$ and then compute

$$\begin{array}{cc}\hfill E_{i+1}& =E_i/\langle l^{e-i-1}{R}_i\rangle ,\hfill \\ \hfill & {\varphi }_i:E_i\to E_{i+1},\hfill \\ \hfill & R_{i+1}={\varphi }_i\left(R_i\right).\hfill \end{array}$$

(7)

For each $i\in [0,e)$, the l-degree isogeny ${\varphi }_i$ is computed upon the kernel $\langle l^{e-i-1}{R}_i\rangle$ of order l, and then used to compute $R_{i+1}$. In each iteration, the point $R_i$ is an $l^{e-i}$-torsion point and so $l^{e-i-1}{R}_i$ has order l. Eventually, through each ${\varphi }_i$, the starting subgroup will be pushed to $\mathcal{O}$. Therefore, it is obvious that $\varphi ={\varphi }_R={\varphi }_{e-1}\circ \cdots \circ {\varphi }_0$ has degree $l^e$ with kernel $\langle R\rangle$.

There are two straightforward ways to compute $\varphi$ based on this decomposition, a multiplication-based strategy, and an isogeny-based method. The former iteratively computes $l^{e-i-1}{R}_i$ by scalar multiplication and ${\varphi }_i$ by Vélu’s formulas at each step. The latter method, however, only performs scalar multiplication once and stores every intermediate $Q_i=l^{i}R$, for $i\in [0,e)$. By iteratively computing ${\varphi }_i$ and ${\varphi }_i\left(Q_j\right),j<e-i$, it is possible to perform all of the l-degree isogenies, and, hence the composition $\varphi$. These two methods are illustrated as the two left graphs in Figure 4 in the form of a directed acyclic graph. Either scalar multiplications or isogeny evaluations of all nodes have to be processed, which makes these straightforward strategies inefficient. It should be noted that explicit expressions for isogeny evaluations are calculated through isogeny computations on leaf nodes on the left. Thus, points on the right side of the graph can only be obtained after the points on the left are processed. This also implies that we can concurrently execute isogeny evaluations in the same column but not point multiplications in the same row.

The optimal approach to schedule the scalar multiplications and isogeny evaluations in serial is first proposed in [16], which is the best permutation and combination of the above two methods. Such strategies are compared and visualized as two right graphs in Figure 4. We can traverse these graphs by storing the pivot points, rather than all intermediates, to obtain the final composition efficiently. The optimal strategy for a large degree isogeny evaluation may vary depending on the implementation, as the time required for certain operations can be different. Graphs (c) and (d) illustrate the impact of these differences. Graph (c) shows the case where isogeny evaluation takes an additional 20% time compared to point multiplication, while (d) shows the opposite case. Optimal strategies for parallel execution will be more complex due to the additional factors involved, including the number and delay of arithmetic units, data dependency, and the memory interface.

3. Quadratic Finite Field Arithmetic for Isogeny

3.1. Parameter Settings

We design our arithmetic unit to support four parameter settings predefined in the SIDH specification of NIST’s post-quantum cryptography round 2 and round 3 submissions [22], as listed in

Table 1. Public parameters specification.

Prime	Number of 4/3 Isogenies	Public Key Size
$p_{434}=2^{216}{3}^{137}-1$	108/137	330
$p_{503}=2^{250}{3}^{159}-1$	125/159	378
$p_{610}=2^{305}{3}^{192}-1$	152/192	462
$p_{751}=2^{372}{3}^{239}-1$	186/239	564

. Three of these primes have an even power for degree-2 isogeny, which facilitates the use of 4-isogeny. The primes $p_{503}$ and $p_{751}$ have been widely studied [23,24,25]. For the underlying curve, we start from the supersingular Montgomery curve $E_0/{\mathbb{F}}_{p^2}:y^2=x^3+6x^2+x$ by setting $a=6$ and $b=1$ without compromising security. Every curve in the isogeny class derived from this curve has ${(p+1)}^2$ points and is also supersingular. The starting curve $E_0$ is part of the public parameter of the SIDH key exchange protocol.

3.2. Quotient Pipeline

From the public parameter settings and the leveled breakdown of the supersingular isogeny protocol (Figure 3), it can be concluded that almost all fundamental arithmetic operations required to evaluate a supersingular isogeny work in ${\mathbb{F}}_{p^2}$. In Section 4, we will quantitatively analyze the operations in each phase of the protocol and demonstrate that modular multiplication is the most costly and frequently used building block. Thus, a dedicated and efficient quadratic field arithmetic unit will improve the hardware implementation.

Previous SIDH hardware designs [24,26,27] have mostly been applied to FPGAs. The typical ${\mathbb{F}}_{p^2}$ modular multiplier proposed in these works uses the native digital signal processors (DSPs) of reconfigurable hardware. The main part of the DSP slice is a high-performance $27\times 18$ multiplier. By wiring through the programmable connectivity, the DSP arrays or matrices consist of interleaved systolic Montgomery multipliers capable of processing large operands. This architecture is regarded as a modular multiplier with radix equivalent to the DSP bit-width, typically 16-bit. An appropriately higher radix will reduce the number of iterations needed in each modular multiplication, resulting in performance gains. FPGAs do not apply to native higher radix (e.g., 32-bit or 64-bit) because of their slice structure. Customized hardware, however, can implement such multipliers to enhance the computation speed.

When performing modular multiplication using the Montgomery method, it is essential to understand that the radix will significantly influence the architecture of the multiplier, even the part built on the arithmetic units. The original Montgomery multiplication indicates that a high radix decreases the number of iterations but increases the latency of every single iteration. Thus, there is no generic way to minimize the latency of complete modular multiplication. Specifically, the calculation of residue uses a carry-save adder (CSA) to compress the partial products, which may mitigate the accrued latency caused by a higher radix. The critical path of the CSA climbs slowly with respect to the bit-width of the operands. However, to obtain the result of the quotient, we must use a carry propagation adder (CPA), for which the computation time is highly dependent on the radix. To solve this problem, Holger [28] proposed a method to decouple the calculation of residue and quotient, which allows for concurrent execution of modular multiplication.

In addition to the influence of the selected radix, another possible improvement involves building a specific ${\mathbb{F}}_{p^2}$ modular multiplier instead of an ${\mathbb{F}}_p$ arithmetic unit. The traditional way to compute an extension field multiplication is to apply the Karatsuba–Ofman algorithm to the prime field multiplier. An ${\mathbb{F}}_{p^2}$ multiplication requires at least three ${\mathbb{F}}_p$ multiplications, with some pre- and post-additions. If operating using the schoolbook algorithm, the ${\mathbb{F}}_{p^2}$ multiplication will be resolved as Equation (8), where $A=a_0+a_{1}i$ and $B=b_0+b_{1}i$, $A,B\in {\mathbb{F}}_{p^2}$, $a_0,a_1,b_0,b_1\in {\mathbb{F}}_p$.

$$\begin{array}{cc}\hfill A·B=& (a_0+a_{1}i)·(b_0+b_{1}i)\hfill \\ \hfill =& (a_0{b}_0+(-a_1)b_1)+(a_0{b}_1+a_1{b}_0)i\hfill \end{array}$$

(8)

By defining an operator $\sigma (x_0,x_1,x_2,x_3)\triangleq x_0{x}_1+x_2{x}_3$, the ${\mathbb{F}}_{p^2}$ multiplication can be rewritten [29] as

$$A·B=\sigma (a_0,b_0,-a_1,b_1)+\sigma (a_0,b_1,a_1,b_0)i.$$

(9)

A dedicated $\sigma$ processing unit will help to build an ${\mathbb{F}}_{p^2}$ multiplier with similar latency to the ${\mathbb{F}}_p$ computation at a reasonable area cost. The design of the ${\mathbb{F}}_{p^2}$ modular multiplier will be discussed after its theoretical foundations are presented.

In the Montgomery multiplication, the following equation is the most costly iteration, where M is the modulus, r is the radix, and $M^{\prime }$ is the precomputed parameter satisfying $M^{\prime }=(-M^{-1})mod{2}^r$.

$$\left\{\begin{array}{cc}\hfill q_i=& (((S_i+b_{i}A)mod{2}^r)·M^{\prime })mod{2}^r\hfill \\ \hfill S_{i+1}=& (S_i+q_{i}M+b_{i}A)/2^r\hfill \end{array}\right.$$

(10)

To simplify the $q_i$ calculation, we first combine $M^{\prime }$ with M and rewrite as $\overline{M}=(M^{\prime }mod{2}^r)\times M$. Then $q_i$ can be defined as

$$q_i=(S_i+b_{i}A)mod{2}^r.$$

(11)

The residue calculation in each iteration can be expressed as

$$S_{i+1}=(S_i+q_i·\overline{M}+b_{i}A)/2^r.$$

(12)

Furthermore, by pre-scaling A by $2^r$ and adding one iteration to compensate for this extra factor, high-radix Montgomery multiplication can be performed in the following form.

$$\left\{\begin{array}{cc}\hfill q_i=& S_{i}mod{2}^r\hfill \\ \hfill S_{i+1}=& (S_i+q_i·\overline{M})/2^r+b_{i}A\hfill \end{array}\right.$$

(13)

Although the quotient determination only needs to reduce $mod{2}^r$ by right shifting, it is not trivial because $S_i$ exists in carry-save form. The ordinary form of $S_i$ has to be determined before it is used to calculate $q_i$. The data dependency between $S_i$ and $q_i$ limits the performance of the high-radix Montgomery multiplier. The quotient pipelining technique [28] delays the use of the quotient digit $q_{i-d}$ by d iterations, giving the carry ample time to propagate and ensuring there is sufficient time to determine a quotient at the cost of d extra iterations. The disadvantages of this method are the extra cycles required to merge $q_{-1},q_{-2},\cdots ,q_{-d}$ and the larger operand bit-width. The overhead will become more significant as the delay increases. In our situation, a delay of one cycle ($d=1$) is sufficient to remove the interference between the residue and the quotient calculation. By involving several precomputed parameters, the cost of the 1-stage quotient pipeline can be further mitigated.

The key point in decoupling the quotient and residue calculation is to remove the $q_i$ term from the $S_{i+1}$ expression, allowing $S_{i+1}$ and $q_i$ to be determined in parallel. By defining $\tilde{M}=(1+\overline{M})/2^r$, $S_{i+1}$ can then be represented as $S_{i+1}=S_i/2^r+q_i\tilde{M}+b_{i}A$. Furthermore, the core iteration of high-radix Montgomery multiplication becomes

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_{i+1}-q_i\tilde{M}& =S_i/2^r+b_{i}A\hfill \\ \hfill & =(S_i-q_{i-1}\tilde{M}+q_{i-1}\tilde{M})/2^r+b_{i}A,\hfill \\ \hfill S_{i+1}^{\prime }& =S_i^{\prime }/2^r+q_{i-1}\tilde{M}/2^r+b_{i}A\hfill \\ \hfill & =S_i^{\prime }/2^r+q_{i-1}\widetilde{M_1}+b_{i}A.\hfill \end{array}\end{array}$$

(14)

where $\widetilde{M_1}=(1+\overline{M_1})/2^{2r}$, $\overline{M_1}=(M_1^{\prime }mod{2}^{2r})\times M$, and $M_1^{\prime }=(-M^{-1})mod{2}^{2r}$ are pre-determined. The index 1 indicates that these pre-computed parameters work for a 1-stage quotient pipeline. The reason that specific factors have to be proposed for the delayed variant is that the correctness of the algorithm is built on $2^{2r}$ dividing $1+\overline{M_1}$. From Equation (14), we can tell that $S_{i+1}^{\prime }$ is now independent of $q_i$, which decouples the calculation in each iteration.

Furthermore, it is obvious that the $\sigma$ operator can be straightforwardly implemented with a minor modification to Equation (14). Setting up a sufficient digit range, the Montgomery algorithm can merge the post-addition with multiplication. The large integer addition can be processed along with the compression of partial products. Additionally, the $\sigma$ operator produces a similar effect as Karatsuba–Ofman multiplication. Karatsuba proposed a method for computing a complex multiplication, such as Equation (15), by saving a real number multiplication. Correspondingly, the $\sigma$ operator reduces the number of partial products in the $AB+CD$ computation by a quarter, which results in a lower area than two individual ${\mathbb{F}}_p$ multipliers. This design is highly suitable for supersingular isogeny calculation considering that these curves are defined over ${\mathbb{F}}_{p^2}$.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x\times y& =(x_0+x_{1}i)(y_0+y_{1}i)\hfill \\ \hfill & =(z_0-z_2)+z_{1}i\hfill \\ \hfill z_0& =x_0{y}_0\hfill \\ \hfill z_1& =(x_1+x_0)(y_1+y_0)-z_1-z_2\hfill \\ \hfill z_2& =x_1{y}_1\hfill \end{array}\end{array}$$

(15)

We obtain the final form of the high-radix Montgomery multiplication from Algorithm 1.

Algorithm 1 1-Stage High-Radix Montgomery Multiplication with Quotient Pipeline

Require:  A prime modulus $M>2$, a positive radix r, a positive integer n, such that $16M<2^{r(n-1)}$. Integer $R^{-1}$, where $\left(2^{rn}{R}^{-1}\right)modM=1$, and integers $\overline{M_1}=-M^{-1}mod{2}^{2r}\times M$, $\widetilde{M_1}=(\overline{M_1}+1)/2^{2r}$, $\overline{M}=-M^{-1}mod{2}^r\times M$, $\tilde{M}=(\overline{M}+1)/2^r$. Operands A, B, C, D where $0\le A,B,C,D<4·2^r·M$, $B={\sum }_{i=0}^{n-1}{b}_i{2}^{ri}$, $D={\sum }_{i=0}^{n-1}{d}_i{2}^{ri}$ Ensure:  Integer $S_{n+2}=(AB+CD)\times R^{-1}modM<4·2^r·M$ 1: $S_0=0$, $q_{-1}=0$ 2: for $i=0$ to n do 3:     $q_i=S_{i}mod{2}^r$ 4:     $S_{i+1}=S_i/2^r+q_{i-1}\widetilde{M_1}+b_{i}A+d_{i}C$ 5: end for 6: $S_{n+2}=S_{n+1}+q_n\tilde{M}$

Proof of Algorithm 1.

To verify the specific variant of Montgomery multiplication, we can simply accumulate each iteration.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 2^{r(i+1)}{S}_{i+1}& =-\sum _{j=0}^i{q}_j{2}^{rj}+\sum _{j=0}^{i-1}{q}_j{2}^{j+2}\widetilde{M_1}+\sum _{j=0}^i(b_{j}A+d_{j}C)2^{rj}·2^r\hfill \\ \hfill S_{n+1}& ={\displaystyle \frac{{\sum }_{j=0}^{n-1}{q}_j\overline{M_1}{2}^{rj}+(AB+CD)·2^r-q_n{2}^{rn}}{2^{r(n+1)}}}\hfill \\ \hfill S_{n+2}& =(AB+CD)2^{-rn}+{\displaystyle \frac{{\sum }_{j=0}^{n-1}{q}_j\overline{M_1}{2}^{rj}+q_n\overline{M}{2}^{rn}}{2^{r(n+1)}}}\hfill \\ \hfill & =(AB+CD)2^{-rn}modM\hfill \end{array}\end{array}$$

(16)

Considering that $\overline{M}<2^r·M$ and $\overline{M_1}<2^{2r}·M$, the last term of $S_{n+2}$ has an upper bound of $2·2^r·M$. Additionally, A, B, C, and D should individually have upper bounds of $\alpha ·2^r·M$. Therefore, the result satisfies $S_{n+2}<2{\alpha }^2·2^{2r}{M}^2{2}^{-rn}+2·2^r·M$. On the condition that $16M<2^{r(n-1)}$, the output and input share the same range $S_{n+2}<4·2^r·M$, which means the algorithm can be applied recursively.    □

3.3. Quadratic Finite Field Multiplier

From the perspective of circuit design, we can use a customized multiplier built with Booth encoding and a Wallace tree to implement the quadratic field modular multiplication unit (QMM). Without the limitation of the FPGA slice architecture, a larger elementary integer multiplier can be built to achieve a more efficient finite field arithmetic unit. The modified Booth-2 encoder reduces the number of partial products by half at little cost, which in turn allows us to process more bits with the same hardware resource. The Wallace tree is employed to accumulate partial products in carry-save form with a short critical path. These two techniques are usually combined to implement a dedicated large-size multiplier because of their regularity and efficiency.

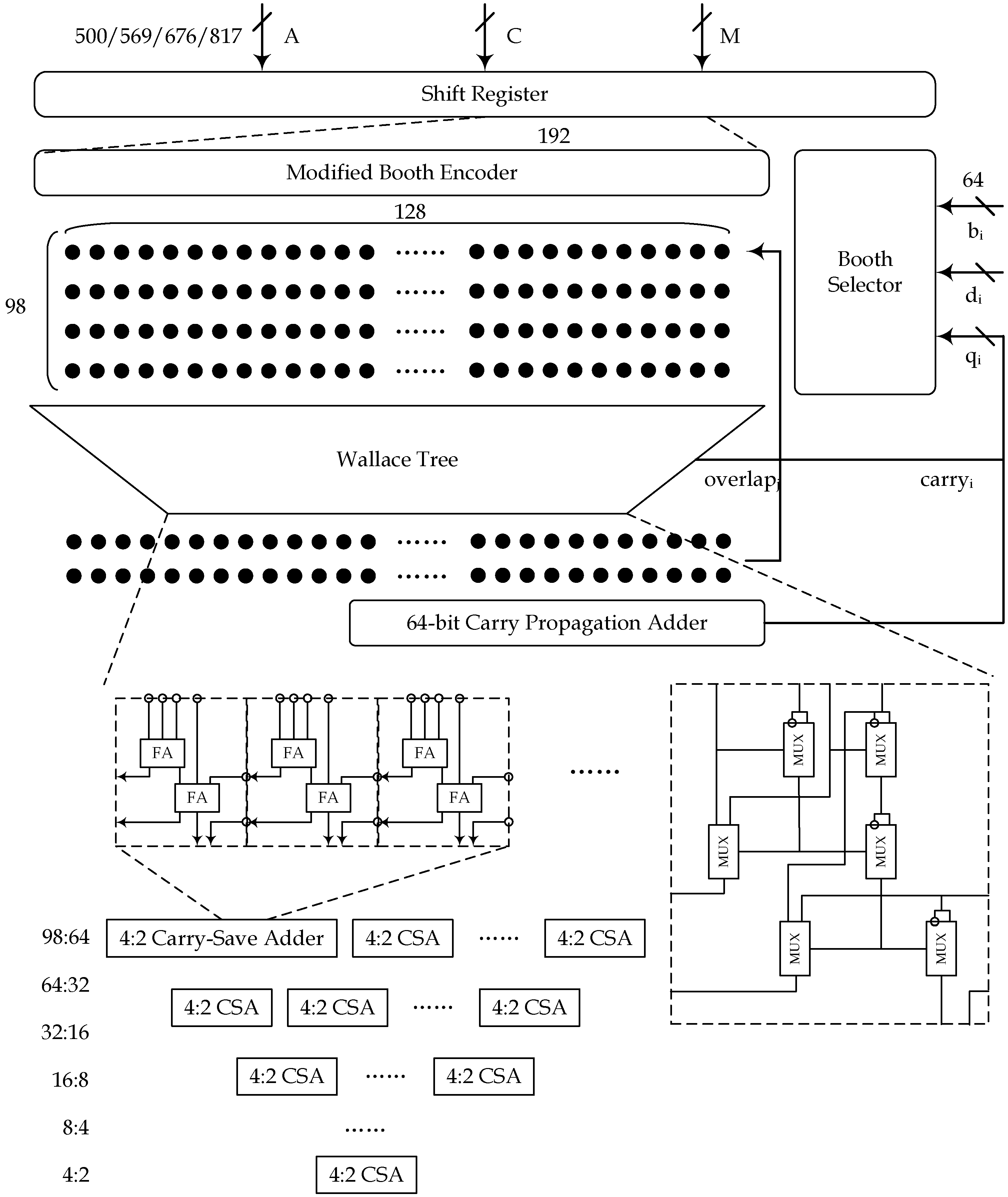
The architecture of the proposed QMM, shown in Figure 5, is equipped with a modified Booth-2 encoder, a Wallace tree, and a carry propagate adder (CPA). The multiplication dataflow is started by pushing the multiplicand into the shift register while padding its head and tail with sign bits and zeros. This register allows the Booth encoder to manipulate different segments of the multiplicand on each iteration, and is, therefore, suitable for diverse operand widths. Next, the Booth encoder takes a multiplicand segment from the ahead register and a multiplicator radix to produce the partial products of $b_{i}A$, $d_{i}C$, $q_i\tilde{M}$. A bundle of partial products is dropped into the Wallace tree and passes through a 6-layer 4:2 CSA. This yields the final result of $S_i$ in carry-save form. While the CPA combines $S_i$, the Wallace tree steps into the next iteration to process the next segment, which is the fundamental idea behind the quotient pipeline.

To work with operands of different bit widths, it is useful to develop a flexible multiplier architecture that can accommodate a range of input sizes. The radix of the multiplicators determines the number of partial products we need to compress in one cycle, and thus the critical delay of the multiplier. Additionally, the radix affects the size of the final addition which sums up the outputs from the Wallace tree. Theoretically, the 4:2 CSA tree has a latency of ∼$3·9·\lfloor {log}_2(\frac{3}{2}·\mathrm{radix})\rfloor$, whereas the CPA has a latency of $2·\mathrm{radix}$. To balance the performance of different parts and ensure a regular digit width, the multiplier uses a 64-bit radix. Afterward, the multiplicands expand to meet the requirement of the quotient pipeline. they are so large that an unnecessary connectivity delay will be introduced. Thus, the multiplicands are segmented and processed iteratively. According to the typical primes we are studying, the extended widths of the multiplicands are 570, 639, 746, and 887 bits, as listed in

Table 2. Quadratic multiplier unit parameters determination.

Parameters	${\mathit{p}}_{434}=2^{216}{3}^{137}-1$	${\mathit{p}}_{503}=2^{250}{3}^{159}-1$	${\mathit{p}}_{610}=2^{305}{3}^{192}-1$	${\mathit{p}}_{751}=2^{372}{3}^{239}-1$
Operand width	500	567	676	817
Partial product width	570	639	746	887
Multiplicand batch (v)	5	5	6	7
Multiplicator batch (w)	8	9	11	13
Total number of iterations	43	48	69	94
Radix	Booth encoder batch size		Number of partial products
64	128		96

. Considering the QMM utilization rate in each field and the circuit size of the processing unit, we would propose a multiplicand batch size of 128 bits for each iteration.

The workflow of QMM is summarised in Algorithm 2, which explains how the embedded iterations work. The total loop time depends on the size of the operands presented in Table 2. v and w indicate the batch number of the multiplicand and multiplicator, respectively, and the total number of loops can be calculated as $v·(w+2)+3$. The superscript $C,S$ indicates that $S_i$ is stored in a carry-save form which does not affect the correctness of the algorithm. Right before the quotient determination, the CPA is applied to $S_i$ to derive the original form. For each iteration, the Wallace tree compresses 98 integers into a single carry-save result. This can be efficiently implemented by cascading the six layers of 4:2 CSA. A schematic of the 1-bit CSA is given in Figure 5. Each pair of lines constitutes a carry-save encoding of input, output, or ‘double’ carry. The 4:2 structure has a more regular layout compared with 3:2 adders, which allows the use of binary tree structures. It can be seen as an adder taking two carry-save encoding numbers and producing the result in the same representation. To support the QMM and the subsequently introduced modular adder, the accelerator is equipped with 128-bit width memories for storing intermediate variables and caching larger operands. The specific design of the memory and access unit will be discussed in Section 4.

The dedicated design of the QMM offers several salient performance improvements over an individual field multiplier. The advantages depend to a certain extent on the specific ${\mathbb{F}}_{p^2}$ scenario and, therefore, have some limitations.

Algorithm 2 Quadratic field modular multiplier workflow

Require:  A prime modulus $M>2$, a positive radix r, a positive integer n such that $16M<2^{r(n-1)}$. Integer $R^{-1}$, where $\left(2^{rn}{R}^{-1}\right)modM=1$, and integers $\overline{M_1}=-M^{-1}mod{2}^{2r}\times M$, $\widetilde{M_1}=(\overline{M_1}+1)/2^{2r}$, $\overline{M}=-M^{-1}mod{2}^r\times M$, $\tilde{M}=(\overline{M}+1)/2^r$. Operands A, B, C, D where $0\le A,B,C,D<4·2^r·M$, $B={\sum }_{i=0}^{n-1}{b}_i{2}^{ri}$, $D={\sum }_{i=0}^{n-1}{d}_i{2}^{ri}$ Ensure:  Integer $(AB+CD)\times R^{-1}modM<4·2^r·M$ 1: $S_0=0$, $q_{-1}=0$, $carr{y}_{-1}=0$, $overla{p}_{-1}=0$ 2: for $i=0$ to w do 3:     $\{carr{y}_i,q_i\}=\mathtt{CPA}\left(S_{i,0}^{C,S}[r-1:0]\right)$      ▹ Quotient determination 4:     for $j=0$ to $v-1$ do 5:         $P{P}_j=\mathtt{BoothEncode}(A_j,b_i,C_j,d_i,{\widetilde{M_1}}_{,j},q_{i-1})$ 6:         if $j==0$ then 7:            $\{overla{p}_j,S_{i+1,j}^{C,S}\}=\mathtt{WallaceTree}(P{P}_j,\{S_{i,j+1}^{C,S}[r-1:0],S_{i,j}^{C,S}>>r\},overla{p}_{j-1},carr{y}_{i-1})$ 8:         else 9:            $\{overla{p}_j,S_{i+1,j}^{C,S}\}=\mathtt{WallaceTree}(P{P}_j,\{S_{i,j+1}^{C,S}[r-1:0],S_{i,j}^{C,S}>>r\},overla{p}_{j-1})$ 10:         end if 11:     end for 12:     $overla{p}_{-1}=overla{p}_{v-1}$ 13: end for 14: for $j=0$ to $v-1$ do 15:     $P{P}_j=\mathtt{BoothEncode}({\tilde{M}}_j,q_w)$        ▹ Last iteration 16:     if $j==0$ then 17:         $\{overla{p}_j,S_{w+2,j}^{C,S}\}=\mathtt{WallaceTree}(P{P}_j,\{S_{w+1,j+1}^{C,S}[r-1:0],S_{w+1,j}^{C,S}>>r\},overla{p}_{j-1},carr{y}_w)$ 18:     else 19:         $\{overla{p}_j,S_{w+2,j}^{C,S}\}=\mathtt{WallaceTree}(P{P}_j,\{S_{w+1,j+1}^{C,S}[r-1:0],S_{w+1,j}^{C,S}>>r\},overla{p}_{j-1})$ 20:     end if 21: end for 22: return $S_{w+2}^{C,S}=\left\{S_{w+2,j}^{C,S}\right\}$

• Performance and area. The $\sigma$ operator merges two ${\mathbb{F}}_p$ multiplications together, which saves a post-addition and reduces the number of partial products of $b_{i}A$ and $d_{i}C$ by a quarter. Although the QMM has to compress more partial products in each iteration, the critical path increases slightly because of the Wallace tree architecture. It takes two $\sigma$ operations in series or in parallel to complete an ${\mathbb{F}}_{p^2}$ multiplication, where one QMM has an area cost of 205k equivalent gates and a latency cost of 2.316 ns.
• Flexibility. Our design is flexible enough to support different operand sizes, including $p_{434}$, $p_{503}$, $p_{610}$, and $p_{751}$ with a high hardware utilization ratio. The architecture is intended for use with the parameters predefined in the SIDH protocol. Furthermore, the newly proposed primes in the round 3 submission of SIKE [22] are also supported by this circuit. The downside that the ASIC implementation is less scalable has been mitigated. Additionally, setting C and D to zero trivially transforms this quadratic modular multiplier into a normal multiplier.
• Regularity. Compared with the Karatsuba method, an additional advantage of deploying the QMM is its regularity, which benefits both scheduling and circuit layout. To parallelize the hundreds of field arithmetic calculations in the protocol, the sequencer needs to handle the data dependency and processing unit workload carefully. In the classical approach, a fully parallelized ${\mathbb{F}}_{p^2}$ occupies three basic modular multipliers simultaneously. If the number of modular multipliers is not a multiple of 3, it becomes less convenient to schedule the operations. From this point of view, QMM uses two $\sigma$ operations, which makes it easier to sequence different subroutines.

3.4. Quadratic Finite Field Adder

Modular addition and subtraction are similar to standard arithmetic operations, except that the results must be wrapped around to fit within the finite field. As subtraction can be implemented by a minor modification to an adder, we will focus on the design of modular addition first. We design a hierarchical carry-lookahead adder (HCLA) as the basic unit to process the modular addition. It consists of two layers, with the upper layer comprised of m ripple adders that process l-bit additions and the lower layer generating carry lookahead signals. The adder has a delay of $2{log}_2{r}_A+2l+1$, where $r_A=l·m$ is the bit-width of operands and l is the bit-width of each ripple adder. To match the critical path delay of QMM, $r_A$ is set to 256, and l is set to 16 in this work.

To avoid the additional time cost of modular reduction, two HCLA units are incorporated to work in parallel, with one only computing addition and the other computing addition with reduction. The final output is selected from two results based on their most significant bit. This architecture is suitable for large bit-width arithmetic due to the use of parallel carry generation and the modular design of units. Our proposed quadratic modular adder (QMA) employs four HCLAs to compute addition in extension finite field concurrently, and its schematic is shown in Figure 6. To support the four parameter settings defined in the SIKE specification, we use the elementary 256-bit HCLA to perform field additions of different sizes through iterative calculation. It takes two to four clock cycles to calculate an addition in a quadratic field.

3.5. Finite Field Inverse Unit

Several algorithms can be used to compute modular inverses. Fermat’s Little Theorem is an effective method in cases where modular exponentiation is highly optimized. However, this algorithm is unsuitable for fields with smooth characteristics $p={\prod }_i{l}_i^{e_i}-1$ used in large degree isogeny. This method requires roughly the same number of modular squares as the bit-width of the modulus and a certain number of modular multiplications. Even if the addition chain can accelerate the computation. The efficiency is still relatively low. The Euclidean extended algorithm and the Kaliski inversion can significantly reduce the complexity of modular inversion from $\mathcal{O}\left({log}^{3}n\right)$ to $\mathcal{O}\left({log}^{2}n\right)$. The drawback is their non-constant execution time, leading to side-channel leakage.

The Kaliski algorithm is designed specifically for the Montgomery modular arithmetic [30]. It takes an original field element as input and calculates its inverse in the Montgomery domain. Savas extends this algorithm to high-radix mode and proposes a new Montgomery modular inverse algorithm [31], which replaces the $k-n$ iterations in Phase II with up to three Montgomery multiplications. This algorithm is more suitable for our design. For example, computing the modular inverse in ${\mathbb{F}}_{p_{751}}$ using Fermat’s Little Theorem requires approximately 745 modular squares and 150 modular multiplications. By comparison, the new Montgomery inversion requires roughly 1066 iterations, with each iteration consisting of several additions and subtractions, as well as two to three additional modular multiplications.

Unlike the optimization employed for quadratic modular multiplication and addition, which require multiple operations in the base field for extension field arithmetic, modular inversion in ${\mathbb{F}}_{p^2}$ can be reduced to just one inversion in ${\mathbb{F}}_p$. Therefore, we design an inversion unit that operates solely in ${\mathbb{F}}_p$, as described in Algorithm 3. It utilizes the previously developed QMA and QMM components, obviating the need for a dedicated inversion unit. In particular, two QMAs perform two ${\mathbb{F}}_p$ subtractions and one ${\mathbb{F}}_p$ addition in parallel, thereby completing phase I of the Montgomery inversion. The final multiplications required in phase II can then be executed using the QMM.

Algorithm 3 New Montgomery modular inversion datapath

Require:  $A{2}^{rn}(modM)$, $rn$, $2^{2rn}(modM)$, and M Ensure:  $A^{-1}{2}^{rn}(modM)$ 1: $u=M$, $v=A{2}^{rn}(modM)$, $r=0$ and $s=1$     ▹ Phase I: AlmMonInv 2: while $v>0$ do 3:     if $u\left[0\right]=0$ then $u=u\gg 1$, $s=s\ll 1$ 4:     else if $v\left[0\right]=0$ then $v=v\gg 1$, $r=r\ll 1$ 5:     else 6:         $t_1=u-v$, $t_2=v-u$, $t_3=r+s$ 7:         if $t_{1,borrow}=\mathrm{False}$ then $u=t_1\gg 1$, $r=t_3$, $s=s\ll 1$ 8:         else $v=t_2\gg 1$, $s=t_3$, $r=r\ll 1$ 9:         end if 10:     end if 11:     $k=k+1$ 12: end while 13: $t_1=r-M$, $t_2=(M\ll 1)-r$ 14: if $t_{1,borrow}=\mathrm{True}$ then $t_1=t_2$ 15: end if 16: $t_2=rn-k$, $t_3=k+rn$             ▹ Phase II: correction 17: if $t_{2,borrow}=\mathrm{False}$ then 18:     $t_1=\mathtt{QMM}(t_1,2^{2rn})$ 19:     $k=t_3$ 20: end if 21: $t_1=\mathtt{QMM}(t_1,2^{2rn})$ 22: $A^{-1}{2}^{rn}(modM)=\mathtt{QMM}(t_1,2^{2rn-k})$

4. High-Level Architecture Design

We aim to build an efficient and scalable isogeny accelerator to support isogeny-based cryptography with different parameters based on the arithmetic unit mentioned above. At a high level, the isogeny accelerator has four components. The arithmetic logic unit, which includes several modular multipliers, modular adders, and a Keccek hash module, handles the intensive computation. The control unit manages the runtime, fetches instructions, and generates signals for the other components. The ROM stores the instruction sequence created by the scheduling script, and the RAM holds intermediates such as pivot point coordinates during computation. The datapath width is set to 256-bit, which meets the throughput requirements of the modular adder and multiplier. A true dual-port RAM is used as the cache, with a memory depth of 1024 and the ability to store 128 ${\mathbb{F}}_{p_{751}^2}$ operands to support pivot points storage.

The instruction sequence is generated by a scheduling strategy and each instruction has a bit-width of 32 bits. The first 12 bits comprise the opcode, which mainly specifies the arithmetic operation. Bits 12–21 and 22–31 represent the data addresses accessed by Port A and Port B, respectively. The first three bits in the opcode control memory load and store. Bits 3–5 instructs the modular adder to perform addition or subtraction with or without reduction. Bits 6–7 control the QMM to calculate either modular multiplication, modular squaring, or base field multiplication. The 8th bit is reserved for modular inversion, and bits 9–10 are the selection signal for the result multiplexer of the arithmetic unit. The 11th bit serves as a no-operation flag.

The scheduling strategy is structured into three hierarchical layers: extension field arithmetic, primary subroutine, and large-degree isogeny. Lower-level operations serve as abstractions to upper-level ones. Firstly, all operations in ${\mathbb{F}}_{p^2}$ are natively implemented as the arithmetic unit, eliminating the need for optimization like previous implementations. Secondly, primary subroutines are scheduled based on field arithmetic operations. Since modular multiplication takes approximately ten times longer than modular addition and subtraction, multiplication has a higher priority in the same time slot. The scheduling also takes the number of instantiated multiplication units into consideration. For example, in the case of 4_iso_eval, three QMMs can reduce the delay by one multiplication operation compared with two QMMs. The step-by-step workflow is shown in

Table 3. Comparison of a 4-isogeny evaluation with two and three quadratic modular multipliers.

Time Slots	QMA #1	QMA #2	QMM #1	QMM #2	QMM #3
1A	$t_0=X_Q+Z_Q$	$t_1=X_Q-Z_Q$			Idle
1M + 1A			$X_Q=t_0\times K_2$	$Z_Q=t_1\times K_3$
2M + 1A	$t_3=X_Q+Z_Q$	$Z_Q=X_Q-Z_Q$	$t_2=t_0\times t_1$
2M + 1S + 1A			$t_3=t_3^2$	$Z_Q=Z_Q^2$
3M + 1S + 1A			$t_2=t_2\times K_1$
3M + 1S + 2A	$X_Q=t_3+t_2$	$t_4=Z_Q-t_2$
4M + 1S + 2A			$X_Q^{\prime }=X_Q\times t_3$	$Z_Q^{\prime }=Z_Q\times t_4$
1A	$t_0=X_Q+Z_Q$	$t_1=X_Q-Z_Q$
1M + 1A			$X_Q=t_0\times K_2$	$Z_Q=t_1\times K_3$	$t_2=t_0\times t_1$
1M + 2A	$t_1=X_Q+Z_Q$	$Z_Q=X_Q-Z_Q$
2M + 2A			$t_2=t_2\times K_1$	$t_1=t_1^2$	$Z_Q=Z_Q^2$
2M + 3A	$X_Q=t_1+t_2$	$t_3=Z_Q-t_2$
3M + 3A			$X_Q^{\prime }=X_Q\times t_1$	$Z_Q^{\prime }=Z_Q\times t_3$

for these two scenarios. The required arithmetic operations of all subroutines after scheduling can be found in

Table 4. Summary of the primary subroutines. Define $(A_{24}^{+}:C_{24})=(A+2C:4C)$, $(A_{24}^{+}:A_{24}^{-})=(A+2C:A-2C)$, and $(a_{24}^{+}:1)=(A+2C:4C)$.

Subtoutine	Functions	Total Ops	Minimum Latency (Ops)
			2 QMMs	3 QMMs
2_iso_curve	$A_{24}^{+}=Z_{P_2}^2-X_{P_2}^2$	2S+A	S+A	-
	$C_{24}=Z_{P_2}^2$
2_iso_eval	$X_Q^{\prime }=2X_Q(X_{P_2}{X}_Q-Z_{P_2}{Z}_Q)$	4M+6A	2M+3A	-
	$Z_Q^{\prime }=2Z_Q(X_Q{Z}_{P_2}-X_{P_2}{Z}_Q)$
3_iso_curve	$A_{24}^{-}=(3X_{P_3}^2+2X_{P_3}{Z}_{P_3}-Z_{P_3}^2)(9X_{P_3}^2-6X_{P_3}{Z}_{P_3}+Z_{P_3}^2)$	2M+3S+13A	M+2S+7A	M+S+7A
	$A_{24}^{+}=(3X_{P_3}^2-2X_{P_3}{Z}_{P_3}-Z_{P_3}^2)(9X_{P_3}^2+6X_{P_3}{Z}_{P_3}+Z_{P_3}^2)$
	$K_1=X_{P_3}-Z_{P_3}$
	$K_2=X_{P_3}+Z_{P_3}$
3_iso_eval	$X_Q^{\prime }=X_Q·4{(X_{P_3}{X}_Q-Z_{P_3}{Z}_Q)}^2$	4M+2S+4A	2M+S+2A	-
	$Z_Q^{\prime }=Z_Q·4{(X_Q{Z}_{P_3}-X_{P_3}{Z}_Q)}^2$
4_iso_curve	$A_{24}^{+}=4X_{P_4}^4$	4S+5A	2S+A	-
	$C_{24}=4Z_{P_4}^4$
	$K_1=4Z_{P_4}^2$
	$K_2=X_{P_4}-Z_{P_4}$
	$K_3=X_{P_4}+Z_{P_4}$
4_iso_eval	$X_Q^{\prime }=(4{(X_Q{X}_{P_4}-Z_Q{Z}_{P_4})}^2+4Z_{P_4}^2(X_Q^2-Z_Q^2))·4{(X_Q{X}_{P_4}-Z_Q{Z}_{P_4})}^2$	6M+2S+6A	4M+S+2A	3M+3A
	$Z_Q^{\prime }=(4{(X_{P_4}{Z}_Q-X_Q{Z}_{P_4})}^2-4Z_{P_4}^2(X_Q^2-Z_Q^2))·4{(X_{P_4}{Z}_Q-X_Q{Z}_{P_4})}^2$
xDBL	$X_{\left[2\right]P}=C_{24}{(X_P^2-Z_P^2)}^2$	4M+2S+4A	2M+S+3A	-
	$Z_{\left[2\right]P}=(C_{24}{(X_P-Z_P)}^2+4A_{24}^{+}{X}_P{Z}_P)·4X_P{Z}_P$
xTPL	$X_{\left[3\right]P}={((X_P^4-6X_P^2{Z}_P^2-8X_P{Z}_P^3-3Z_P^4)A_{24}^{+}-(X_P^4-6X_P^2{Z}_P^2+8X_P{Z}_P^3-3Z_P^4)A_{24}^{-})}^2·2X_P$	7M+5S+10A	4M+3S+2A	3M+2S+3A
	$Z_{\left[3\right]P}={((3X_P^4+8X_P^3{Z}_P+6X_P^2{Z}_P^2-Z_P^4)A_{24}^{+}-(3X_P^4-8X_P^3{Z}_P+6X_P^2{Z}_P^2-Z_P^4)A_{24}^{-})}^2·2Z_P$
xDBLADD	$X_{\left[2\right]P}={(X_P^2-Z_P^2)}^2$	7M+4S+8A	4M+2S+2A	3M+S+3A
	$Z_{\left[2\right]P}=({(X_P-Z_P)}^2+4a_{24}^{+}{X}_P{Z}_P)·4X_P{Z}_P$
	$Z_{P+Q}=4{(X_Q{Z}_P-X_P{Z}_Q)}^2{X}_{Q-P}$
	$Z_{P+Q}=4{(X_P{X}_Q-Z_P{Z}_Q)}^2{Z}_{Q-P}$
j_inv	$j=\frac{256{(A^2-3C^2)}^3}{C^4(A^2-4C^2)}$	3M+4S+8A+I	2M+2S+4A+I	-
get_A	$a=\frac{{(1-x_P{x}_Q-x_P{x}_{Q-P}-x_Q{x}_{Q-P})}^2}{4x_P{x}_Q{x}_{Q-P}}-(x_P+x_Q+x_{Q-P})$	4M+S+7A+I	3M+6A+I	-

. Lastly, the large degree isogeny was computed by iteratively calculating the base isogeny operations. The optimal strategy for serial execution of subroutines is known, as described in Section 2.3. Due to the different relative weights of scalar multiplications and isogeny evaluations under various parameters, strategies were generated separately based on

Table 5. An overview of the latency associated with the primary subroutines (in clock cycles).

Subroutine	${\mathit{p}}_{434}$			${\mathit{p}}_{503}$			${\mathit{p}}_{610}$			${\mathit{p}}_{751}$
	1	2	3	1	2	3	1	2	3	1	2	3
2_iso_curve	101	54	54	113	61	61	155	82	82	207	109	109
2_iso_eval	230	115	115	262	131	131	346	173	173	458	229	229
3_iso_curve	326	190	143	377	219	167	482	282	209	633	371	273
3_iso_eval	310	155	155	348	174	174	474	237	237	632	316	316
4_iso_curve	223	101	101	253	113	113	337	155	155	447	207	207
4_iso_eval	418	249	162	470	278	183	638	383	246	850	512	327
xDBL	310	162	162	348	183	183	474	246	246	632	327	327
xTPL	634	343	256	714	382	287	966	529	392	1286	708	523
xDBLADD	573	296	209	644	330	235	875	456	319	1166	610	425
$\mathtt{j}\_\mathtt{inv}{}^{†}$	2215	2046	2046	3558	3366	3366	4389	4134	4134	6978	6640	6640
$\mathtt{get}\_\mathtt{A}{}^{†}$	2114	2013	2013	3445	3332	3332	4234	4079	4079	6771	6564	6564

^† The delay of Kaliski inversion may vary depending on different operands, the worst-case scenario is presented.

, which shows the number of clock cycles each subroutine needs. It shows that the latency of some subroutines, such as j_inv, increases more rapidly between parameters. This is because modular inversion requires more iterations.

5. Experimental Results and Discussion

We developed a hardware prototype for the isogeny accelerator under SMIC’s 65 nm technology, following the high-level design and arithmetic unit specification. The circuit was validated through post-synthesis simulation via the known answer test from the SIDH documentation. To evaluate the scalability of the isogeny accelerator, two implementations are created incorporating two and three modular multipliers, respectively. Programs for different parameters are executed on both designs, and the results indicate that the critical path delay remained stable in various scenarios. The longest latency of 1.912 ns was selected as the operating clock of the final design. The latency results for processing the SIDH protocol with predefined parameters can be found in

Table 6. Performance of the scalable isogeny accelerator under different parameter settings.

Function	${\mathit{p}}_{434}$		${\mathit{p}}_{503}$		${\mathit{p}}_{610}$		${\mathit{p}}_{751}$
	2	3	2	3	2	3	2	3
KeyGen	0.847	0.756	1.121	1.002	1.897	1.685	3.219	2.854
Encaps	1.432	1.209	1.898	1.609	3.233	2.708	5.415	4.530
Decaps	1.515	1.282	2.009	1.706	3.414	2.870	5.756	4.835
Encaps + Decaps	2.947	2.492	3.906	3.315	6.647	5.578	11.172	9.365

. The total delay is the sum of encapsulation and decapsulation. Key generation is not included as it can be performed offline.

The resource cost of our design and a comparison with other SIDH ${\mathbb{F}}_{p_{751}}$ implementations in the literature are shown in Table 7. Our implementation with three QMMs shows a delay that is almost equivalent to the previous most efficient implementation [32], completing encapsulation and decapsulation within 9.37 s at a clock frequency of 523 MHz. The comparison of the area is not straightforward, as other implementations utilized FPGA platforms such as Virtex-7 and Ultrascale+. In accordance with the metric presented in [27], we convert the resource utilization of the FPGA into slice equivalent cost and further transform it into equivalent gate counts at a rate of 19.2 ASIC gates per slice. The experimental results, including latency, normalized area, and AT product, are presented in Table 2. The AT product is calculated by multiplying latency with the equivalent gate cost.

Our isogeny accelerator shows an advantage in terms of delay, with an economical utilization of area. This is primarily attributed to the design of the specific ${\mathbb{F}}_{p^2}$ arithmetic unit, reducing the redundant computation commonly incurred when performing ${\mathbb{F}}_{p^2}$ operations using an ${\mathbb{F}}_p$ operator. On the other hand, it should be noted that due to the scalable design of our circuit, it is not as compact as the implementation targeting one parameter set. It is not feasible for all operands of different sizes to properly occupy the arithmetic unit, particularly when the radix is comparable with the size of operands.

5.1. Other Isogeny-Based Schemes

Despite the vulnerability of SIDH to Catryck and Decru family of attacks, there exist a number of isogeny-based cryptosystems, such as CGL, CSIDH, and SQIsign, which do not exploit auxiliary points and are thus unaffected by these particular attacks. For instance, Charles introduced a provable collision-resistant hash function derived from supersingular isogeny graphs [11]. These graphs, as proven by Pizer [33], are instances of Ramanujan graphs, which are expander graphs with excellent mixing properties. This allows the CGL hash function to offer a high level of collision resistance. Supersingular isogeny graphs utilized in CGL are similar to those used to evaluate a large-degree isogeny. A toy example of such a graph is shown in Figure 1. It is defined over a finite field and consists of vertices representing supersingular elliptic curves over that field, with edges representing isogenies between these curves.

The CGL hash function operates by walking around a supersingular isogeny graph based on the input without any backtracking. The final output is the compressed j-invariant of the terminal elliptic curve. In cases of 2-isogenies, a step in the walk involves finding and ordering the 2-torsion points of the current curve and then calculating the next elliptic curve from the selected 2-torsion. Our proposed isogeny accelerator can perform each step in 23,583 clock cycles, equating to approximately 41.25 $\mathsf{\mu }$s and yielding a 24.24 kbps throughput without optimization.

5.2. Side-Channel Considerations

Side-channel attacks (SCA) on implementations of cryptographic algorithms are also an important topic. Despite the theoretical security of the primitives, the software or hardware implementations may leak sensitive information through side channels, such as power consumption and electromagnetic radiation. For instance, various studies have investigated SCAs on key encapsulation mechanisms (KEMs). Refs. [34,35] have explored side-channel assisted plaintext-checking oracle attacks on KEMs. Ref. [36] presented a profiling SCA on an FPGA implementation of CRYSTALS-Kyber employing the sliced multi-bit error injection. Ref. [37] studied profiled SCA against Dilithium, targeting the first number theory transform stage and polynomial multiplication, and proposed countermeasures against such attacks. Ref. [38] mainly focused on the fault detection methods of Saber and Falcon. Ref. [39] discovered a vulnerability in KEM algorithms, where implementations using a Boolean conversion procedure similar to Saber’s may be susceptible to message recovery attacks, even in the case of higher-order masked implementation.

Table 7. Performance comparison with other implementations using the 751-bit prime setting.

Work	#Slices	#DSP	#BRAM	Frequency (MHz)	Latency ($\times {10}^6$ cc)	Latency (ms)	Equivalent Gates ${}^{‡}$ ($\times {10}^3$)	AT Product ($\times {10}^3$)
[22]	15,452 ${}^{†}$	512	43.5	296.9	4.54	15.3	1363	20,854
[40] *	8131	162	39.0	141.6	8.64	61.0	542	33,062
[27] **	15,384	512	43.5	163.1	4.53	27.8	1362	37,864
[41]	11,136	452	41.5	232.7	5.93	25.5	1161	29,606
[42]	15,246	456	54.0	182.3	3.32	18.2	1272	23,150
[32]	27,286	834	73.5	155.8	1.44	9.27	2266	21,005
Ours	-	-	-	523.0	4.90	9.365	1651	15,462
					5.84	11,172	1293	14,445

^† An Ultrascale+ CLB has two slices inside. * The work is a compact hardware/software co-design targeting speed/area trade-off. ** The implementation in this work is similar to that in SIDH specification, except for the execution platform. ^‡ SEC = 100 × BRAMs + 100 × DSPs + Slices [42], SEC = 19.2 equivalent gates.

Table 7. Performance comparison with other implementations using the 751-bit prime setting.

Work	#Slices	#DSP	#BRAM	Frequency (MHz)	Latency ($\times {10}^6$ cc)	Latency (ms)	Equivalent Gates ${}^{‡}$ ($\times {10}^3$)	AT Product ($\times {10}^3$)
[22]	15,452 ${}^{†}$	512	43.5	296.9	4.54	15.3	1363	20,854
[40] *	8131	162	39.0	141.6	8.64	61.0	542	33,062
[27] **	15,384	512	43.5	163.1	4.53	27.8	1362	37,864
[41]	11,136	452	41.5	232.7	5.93	25.5	1161	29,606
[42]	15,246	456	54.0	182.3	3.32	18.2	1272	23,150
[32]	27,286	834	73.5	155.8	1.44	9.27	2266	21,005
Ours	-	-	-	523.0	4.90	9.365	1651	15,462
					5.84	11,172	1293	14,445

^† An Ultrascale+ CLB has two slices inside. * The work is a compact hardware/software co-design targeting speed/area trade-off. ** The implementation in this work is similar to that in SIDH specification, except for the execution platform. ^‡ SEC = 100 × BRAMs + 100 × DSPs + Slices [42], SEC = 19.2 equivalent gates.

Compared to other cryptographic algorithms, curve-based schemes exhibit vulnerabilities at special points owing to the special characteristics of elliptic curves as a cyclic group. For instance, traditional ECC is susceptible to attacks, such as zero value, invalid curve, and invalid point. Randomized coordinates, point coherence checks, and curve integrity checks are commonly used to mitigate these attacks. In the context of isogeny-based cryptography, some attacks that target ECC, including refined power analysis, can also be utilized. In [43], Koziel employed three techniques to target SIDH. He analyzed the representation of zero in the context of quadratic extension fields and isogeny arithmetic and presented three distinct refined power analysis attacks on SIDH. The first and second attacks focused on the three-point Montgomery ladder, using partial-zero and zero-value attacks, respectively. The third attack suggested a method of exploiting zero-values in the context of isogenies to break the large-degree isogeny. The attacks proposed in this article raise further concerns about the security of using static-key in SIDH.

6. Conclusions

Isogeny-based cryptography has the apparent advantage of a minor key length, which helps mitigate the transmission load and storage requirement. It is meaningful to improve the efficiency of isogeny operations. We propose a scalable and high-performance isogeny accelerator that supports four parameter sets. The accelerator features a suite of specialized arithmetic units, including a ${\mathbb{F}}_{p^2}$ quotient pipelining multiplier, a ${\mathbb{F}}_{p^2}$ modular adder, and a ${\mathbb{F}}_p$ Kaliski inversion unit reutilizing these ${\mathbb{F}}_{p^2}$ blocks. The primary subroutines are scheduled specifically for these units. Customized instruction sequences are generated for different parameters individually to improve parallelism and performance while maintaining scalability. Our prototype 65 nm accelerator is capable of completing encapsulations in 4.53 ms and decapsulations in 4.84 ms under a 751-bit prime setting. This performance is comparable to the previous highest-performance FPGA implementation but with a more efficient area cost. The area time product is reduced by about a quarter compared with previous works. Additionally, we show that the proposed architecture can accelerate other isogeny applications such as the cryptographic hash function.