An Empirical Study of Segmented Linear Regression Search in LevelDB
Abstract
:1. Introduction
- We observe that there exist several real world datasets that have the linearity, providing an opportunity to apply machine learning algorithms for search;
- We design SLR search that integrates the linear regression and segmentation in a cooperative manner to mitigate the error margin caused by noisy data;
- We explore diverse design space for segmentation (equal-space and error-aware) and for last-mile search (linear, binary, and exponential);
- We implement SLR search in an actual key-value store and evaluate its effectiveness in terms of the lookup latency and number of comparisons.
2. Background
2.1. Learned Index
2.2. LevelDB
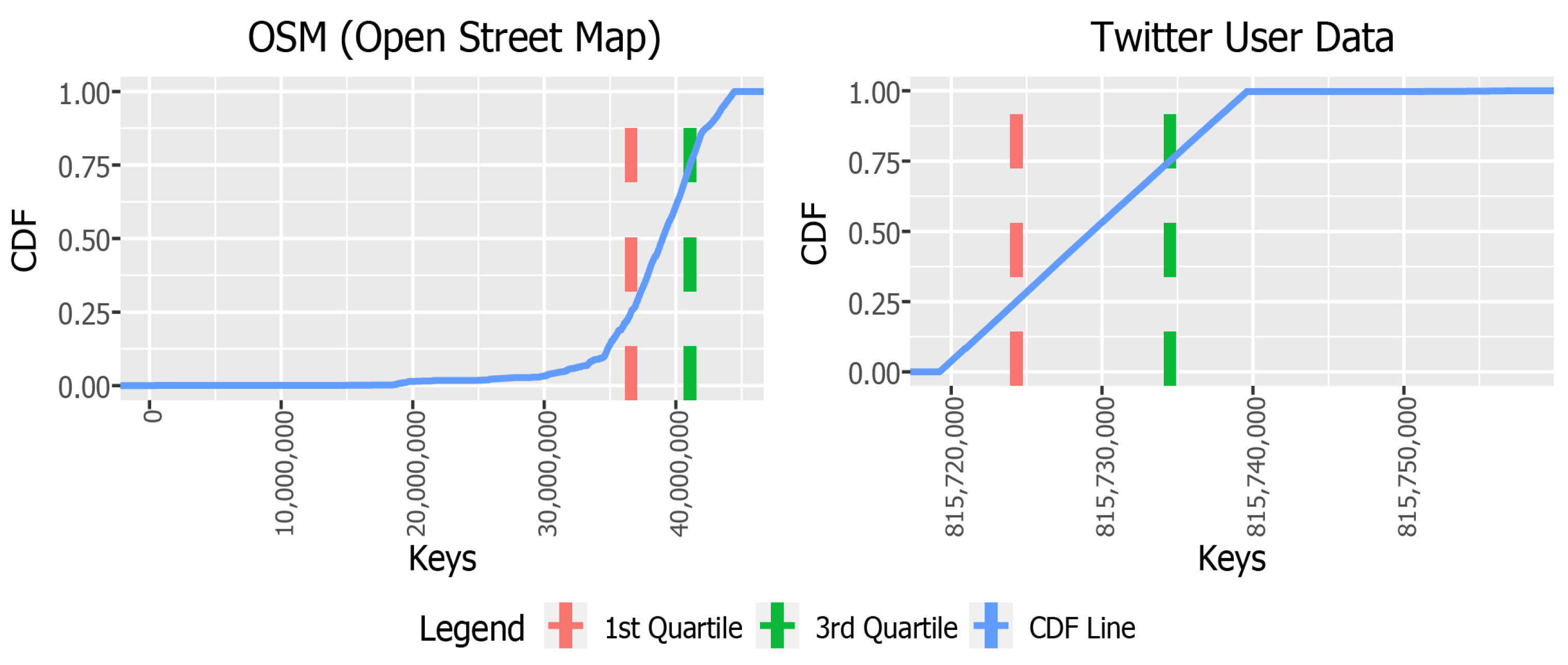
3. Observation
4. Design
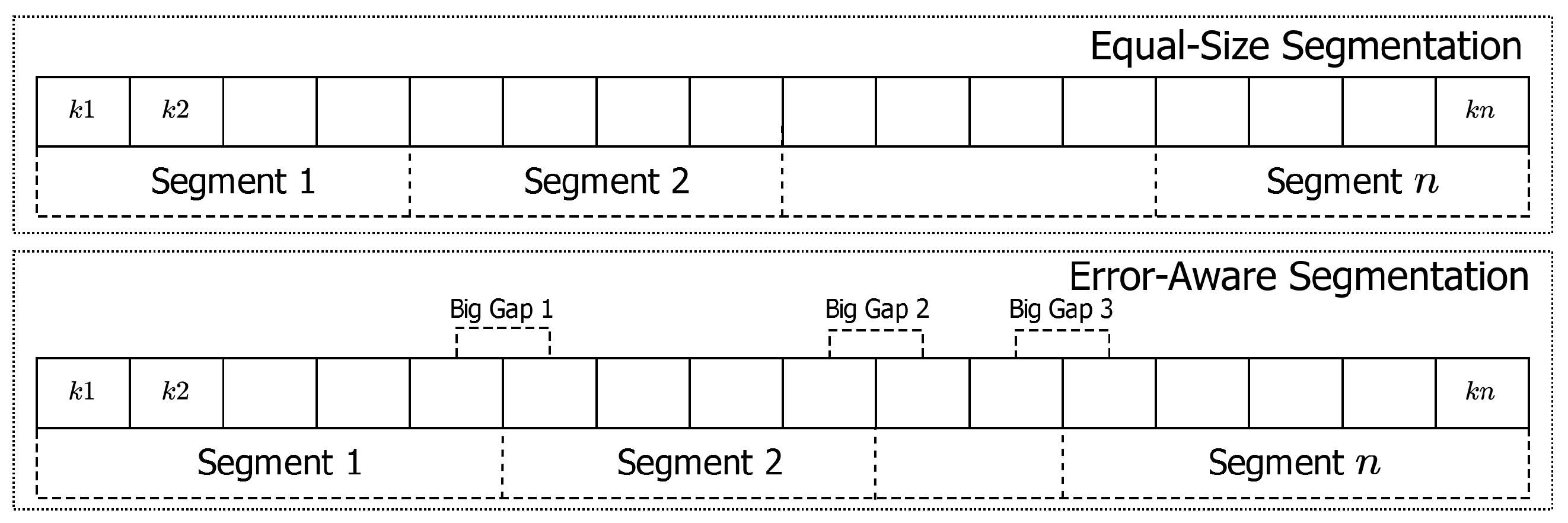
4.1. Segmentation
| Algorithm 1: Error-aware segmentation |
 |
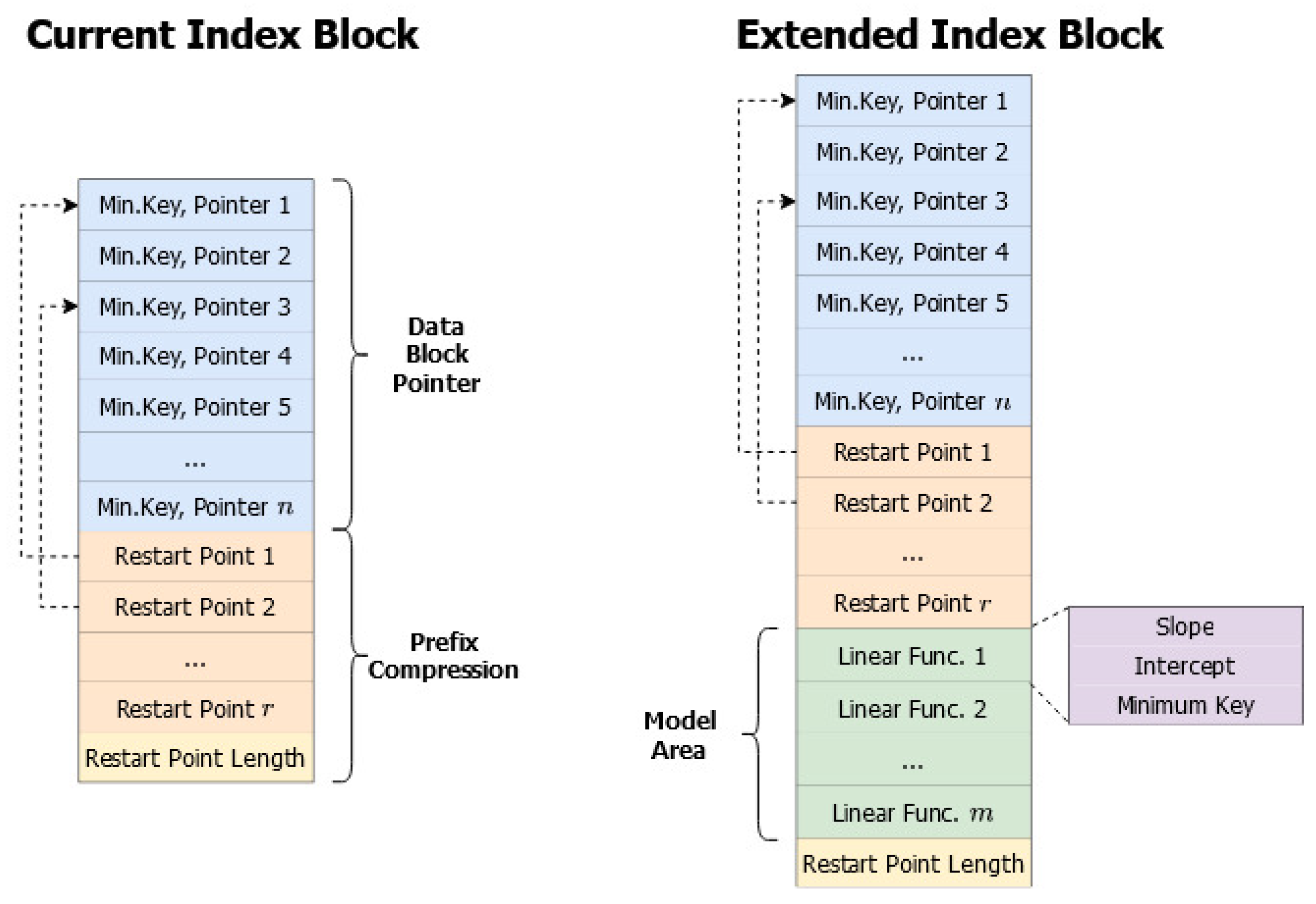
4.2. LevelDB Extension for SLR Search
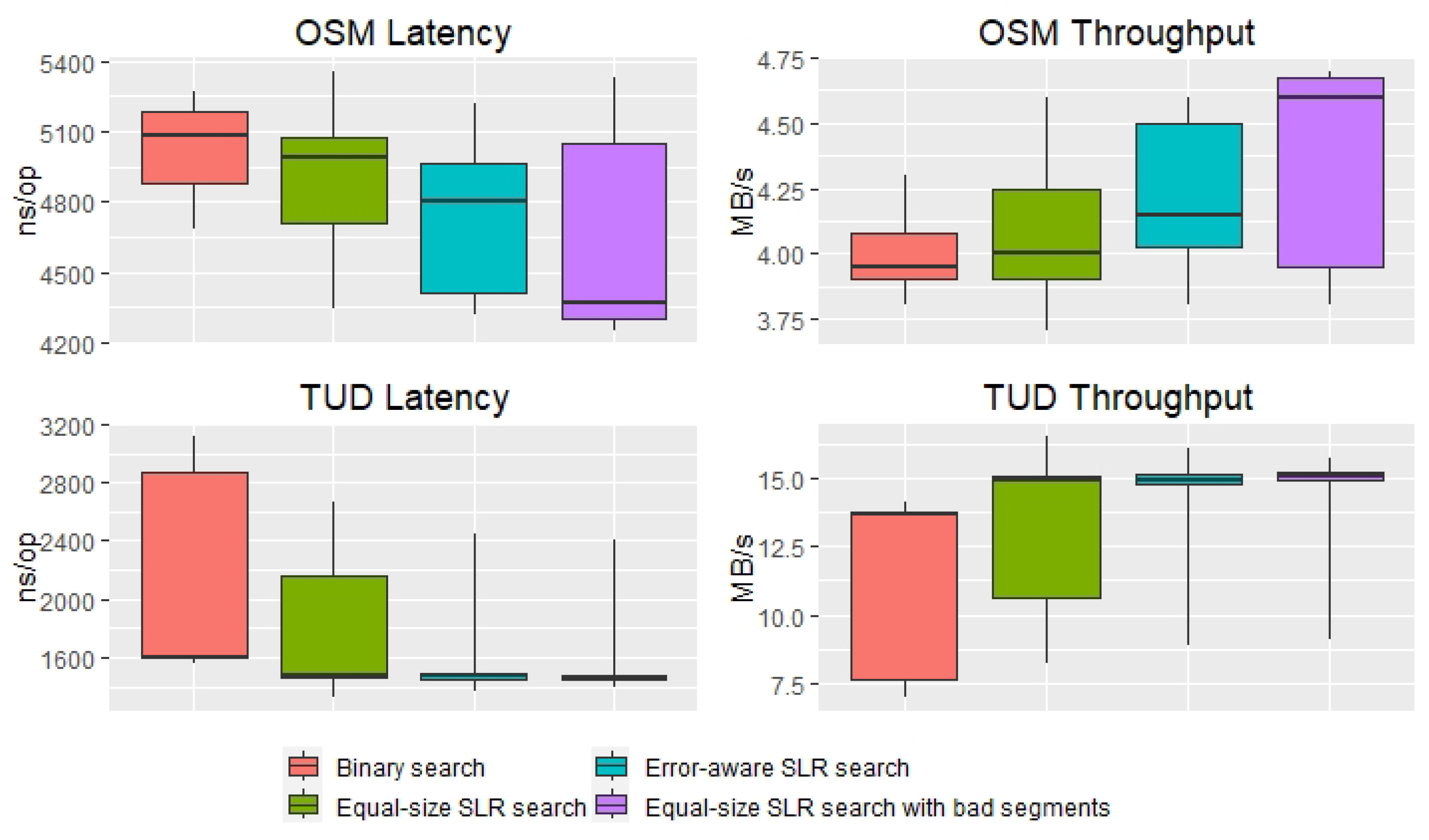
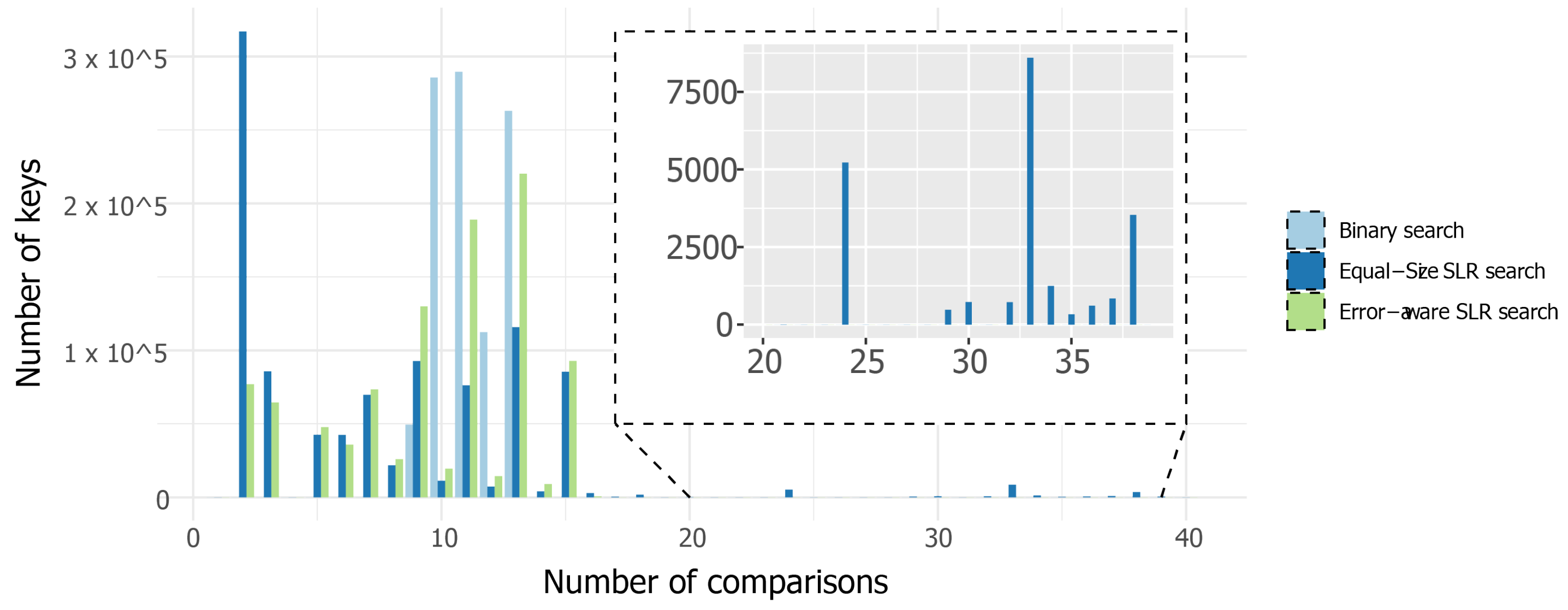
5. Evaluation
6. Related Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, S.; Kryczka, A.; Jin, Y.; Stumm, M. Evolution of Development Priorities in Key-value Stores Serving Large-scale Applications: The RocksDB Experience. In Proceedings of the 19th USENIX Conference on File and Storage Technologies (FAST’21), Online Conference, 23–25 February 2021. [Google Scholar]
- Chen, J.; Chen, L.; Wang, S.; Zhu, G.; Sun, Y.; Liu, H.; Li, F. HotRing: A Hotspot-Aware In-Memory Key-Value Store. In Proceedings of the 18th USENIX Conference on File and Storage Technologies (FAST’20), Santa Clara, CA, USA, 24–27 February 2020. [Google Scholar]
- Arpaci-Dusseau, R.H.; Arpaci-Dusseau, A.C. Operating Systems: Three Easy Pieces. Arpaci-Dusseau Books. Available online: https://pages.cs.wisc.edu/~remzi/OSTEP/ (accessed on 10 January 2023).
- Neal, I.; Zuo, G.; Shiple, E.; Khan, T.A.; Kwon, Y.; Peter, S.; Kasikci, B. Rethinking File Mapping for Persistent Memory. In Proceedings of the 19th USENIX Conference on File and Storage Technologies (FAST’21), Online Conference, 23–25 February 2021. [Google Scholar]
- Qiao, Y.; Chen, X.; Zheng, N.; Li, J.; Liu, Y.; Zhang, T. Closing the B+-tree vs. LSM-tree Write Amplification Gap on Modern Storage Hardware with Built-in Transparent Compression. In Proceedings of the 20th USENIX Conference on File and Storage Technologies (FAST’22), Online Conference, 22–24 February 2022. [Google Scholar]
- Wu, X.; Xu, Y.; Shao, Z.; Jiang, S. LSM-trie: An LSM-tree-based Ultra-Large Key-Value Store for Small Data Items. In Proceedings of the 2015 USENIX Annual Technical Conference (ATC’15), Santa Clara, CA, USA, 8–10 July 2015. [Google Scholar]
- Yu, G.; Song, Y.; Zhao, G.; Sun, W.; Han, D.; Qiao, B.; Wang, G.; Yuan, Y. Cracking In-Memory Database Index: A Case Study for Adaptive Radix Tree Index. In Proceedings of the 22nd International Conference on Extending Database Technology (EDBT), Edinburgh, UK, 30 March–2 April 2020. [Google Scholar]
- Wu, X.; Ni, F.; Jiang, S. Wormhole: A Fast Ordered Index for In-memory Data Management. In Proceedings of the Fourteenth EuroSys Conference 2019 (EuroSys’19), Dresden, Germany, 25–28 March 2019. [Google Scholar]
- Kraska, T.; Beutel, A.; Chi, E.H.; Dean, J.; Polyzotis, N. The Case for Learned Index Structures. In Proceedings of the 2018 International Conference on Management of Data (SIGMOD’18), Houston, TX, USA, 10–15 June 2018. [Google Scholar]
- Marcus, R.; Kipf, A.; Renen, A.; Stoian, M.; Misra, S.; Kemper, A.; Neumann, T.; Kraska, T. Benchmarking learned indexes. Proc. VLDB Endow. 2020, 14, 1. [Google Scholar] [CrossRef]
- Wongkham, C.; Lu, B.; Liu, C.; Zhong, Z.; Lo, E.; Wang, T. Are updatable learned indexes ready? Proc. VLDB Endow. 2022, 15, 11. [Google Scholar] [CrossRef]
- Fazal, N.; Mariescu-Istodor, R.; Fränti, P. Using Open Street Map for Content Creation in Location-Based Games. In Proceedings of the 29th Conference of Open Innovations Association (FRUCT’21), Tampere, Finland, 12–14 May 2021. [Google Scholar]
- Twitter User Data. Available online: https://data.world/data-society/twitter-user-data (accessed on 17 November 2022).
- LevelDB: A Fast Key-Value Storage Library Written at Google. Available online: https://github.com/google/leveldb (accessed on 17 November 2022).
- Lu, L.; Pillai, T.S.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. WiscKey: Separating Keys from Values in SSD-conscious Storage. In Proceedings of the 14th USENIX Conference on File and Storage Technologies (FAST’16), Santa Clara, CA, USA, 22–25 February 2016. [Google Scholar]
- Kaiyrakhmet, D.; Lee, S.; Nam, B.; Noh, S.H.; Choi, Y. SLM-DB: Single-Level Key-Value Store with Persistent Memory. In Proceedings of the 17th USENIX Conference on File and Storage Technologies (FAST’19), Boston, MA, USA, 22–25 February 2019. [Google Scholar]
- Products Related to LevelDB. Available online: https://discovery.hgdata.com/product/leveldb (accessed on 17 November 2022).
- Ferragina, P.; Vinciguerra, G. The PGM-index: A fully-dynamic compressed learned index with provable worst-case bounds. Proc. VLDB Endow. 2020, 13, 8. [Google Scholar] [CrossRef]
- Kipf, A.; Marcus, R.; Renen, A.; Stoian, M.; Kemper, A.; Kraska, T.; Neumann, T. RadixSpline: A single-pass learned index. In Proceedings of the third International Workshop on Exploiting Artificial Intelligence Techniques for Data Management (aiDM’20), Portland, OR, USA, 19 June 2020. [Google Scholar]
- Galakatos, A.; Markovitch, M.; Binnig, C.; Fonseca, R.; Kraska, T. FITing-Tree: A Data-aware Index Structure. In Proceedings of the 2019 International Conference on Management of Data (SIGMOD’19), Amsterdam, The Netherlands, 30 June–5 July 2019. [Google Scholar]
- Elhemali, M.; Gallagher, N.; Gordon, N.; Idziorek, J.; Krog, R.; Lazier, C.; Mo, E.; Mritunjai, A.; Perianayagam, S.; Rath, T.; et al. Amazon DynamoDB: A Scalable, Predictably Performant, and Fully Managed NoSQL Database Service. In Proceedings of the 2022 USENIX Annual Technical Conference (ATC’22), Carlsbad, CA, USA, 11–13 July 2022. [Google Scholar]
- Raju, P.; Kadekodi, R.; Chidambaram, V.; Abraham, I. PebblesDB: Building Key-Value Stores using Fragmented Log-Structured Merge Trees. In Proceedings of the 26th Symposium on Operating Systems Principles (SOSP’17), Shanghai, China, 28–31 October 2017. [Google Scholar]
- Balmau, O.; Dinu, F.; Zwaenepoel, W.; Gupta, K.; Chandhiramoorthi, R.; Didona, D. SILK: Preventing Latency Spikes in Log-Structured Merge Key-Value Stores. In Proceedings of the 2019 USENIX Annual Technical Conference (ATC’19), Renton, WA, USA, 10–12 July 2019. [Google Scholar]
- Im, J.; Bae, J.; Chung, C.; Arvind; Lee, S. PinK: High-speed In-storage Key-value Store with Bounded Tails. In Proceedings of the 2020 USENIX Annual Technical Conference (ATC’20), Online Conference, 15–17 July 2020. [Google Scholar]
- Dai, Y.; Xu, Y.; Ganesan, A.; Alagappan, R.; Kroth, B.; Arpaci-Dusseau, A.C.; Arpaci-Dusseau, R.H. From WiscKey to Bourbon: A Learned Index for Log-Structured Merge Trees. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation (OSDI’20), Online Conference, 4–6 November 2021. [Google Scholar]
- Lu, K.; Zhao, N.; Wan, J.; Fei, C.; Zhao, W.; Deng, T. TridentKV: A Read-Optimized LSM-Tree Based KV Store via Adaptive Indexing and Space-Efficient Partitioning. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 8. [Google Scholar] [CrossRef]
- Setiawan, N.F.; Rubinstein, B.I.P.; Borovica-Gajic, R. Function Interpolation for Learned Index Structures. In Proceedings of the 31st Australasian Database Conference (ADC’20), Melbourne, Australia, 3–7 February 2020. [Google Scholar]
- Uftrace. Available online: https://github.com/namhyung/uftrace (accessed on 17 November 2022).
- Ding, J.; Minhas, U.F.; Yu, J.; Wang, C.; Do, J.; Li, Y.; Zhang, H.; Chandramouli, B.; Gehrke, J.; Kossmann, D.; et al. Alex: An updatable adaptive learned index. In Proceedings of the 2020 International Conference on Management of Data (SIGMOD ’20), Portland, OR, USA, 14–19 June 2020. [Google Scholar]
- Wu, J.; Zhang, Y.; Chen, S.; Wang, J.; Chen, Y.; Xing, C. Updatable learned index with precise positions. Proc. VLDB Endow. 2021, 14, 8. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, C.; Wang, Z.; Chen, H. SIndex: A Scalable Learned Index for String Keys. In Proceedings of the 11th ACM SIGOPS Asia-Pacific Workshop on Systems (APSys ’20), Tsukuba, Japan, 24–25 August 2020. [Google Scholar]
- Abu-Libdeh, H.; Altınbüken, D.; Beutel, A.; Chi, E.; Doshi, L.; Kraska, T.; Li, X.; Ly, A.; Olston, C. Learned Indexes for a Google-scale Disk-based Database. In Proceedings of the Workshop on ML for Systems at NeurIPS 2020, Vancouver, BC, Canada, 12 December 2020. [Google Scholar]






| Keys | Locations |
|---|---|
| 77,880 | 3 |
| 77,881 | 4 |
| 77,883 | 5 |
| 77,885 | 6 |
| 77,886 | 7 |
| 77,887 | 8 |
| 77,888 | 9 |
| 77,889 | 10 |
| 77,890 | 11 |
| 77,892 | 12 |
| 77,893 | 13 |
| 77,894 | 14 |
| 77,895 | 15 |
| 77,897 | 16 |
| 77,898 | 17 |
| 77,899 | 18 |
| Keys | Locations |
|---|---|
| 78,101 | 82 |
| 78,102 | 83 |
| 78,103 | 84 |
| 78,104 | 85 |
| 78,105 | 86 |
| 78,109 | 87 |
| 78,110 | 88 |
| 78,197 | 89 |
| 78,198 | 90 |
| 78,204 | 91 |
| 78,215 | 92 |
| 219,850 | 93 |
| 219,851 | 94 |
| 219,966 | 95 |
| 219,968 | 96 |
| 219,969 | 97 |
| CPU | Intel(R) Core(TM) i7-10700K CPU @ 3.80 GHz |
| Memory | 16,384 MB |
| Storage | 150 GB NVMe SSD |
| OS | Debian 11 (Bullseye) |
| Key-value store | LevelDB version 1.23 |
| Workloads | OSM (Open Street Map), TUD (Twitter User Data) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramadhan, A.R.; Choi, M.-g.; Chung, Y.; Choi, J. An Empirical Study of Segmented Linear Regression Search in LevelDB. Electronics 2023, 12, 1018. https://doi.org/10.3390/electronics12041018
Ramadhan AR, Choi M-g, Chung Y, Choi J. An Empirical Study of Segmented Linear Regression Search in LevelDB. Electronics. 2023; 12(4):1018. https://doi.org/10.3390/electronics12041018
Chicago/Turabian StyleRamadhan, Agung Rahmat, Min-guk Choi, Yoojin Chung, and Jongmoo Choi. 2023. "An Empirical Study of Segmented Linear Regression Search in LevelDB" Electronics 12, no. 4: 1018. https://doi.org/10.3390/electronics12041018
APA StyleRamadhan, A. R., Choi, M.-g., Chung, Y., & Choi, J. (2023). An Empirical Study of Segmented Linear Regression Search in LevelDB. Electronics, 12(4), 1018. https://doi.org/10.3390/electronics12041018











