A Magnetic Field Containment Method for an IPT System with Multiple Transmitting Coils Based on Reflective Properties
Abstract
:1. Introduction
2. Reflective Segmentation Basic
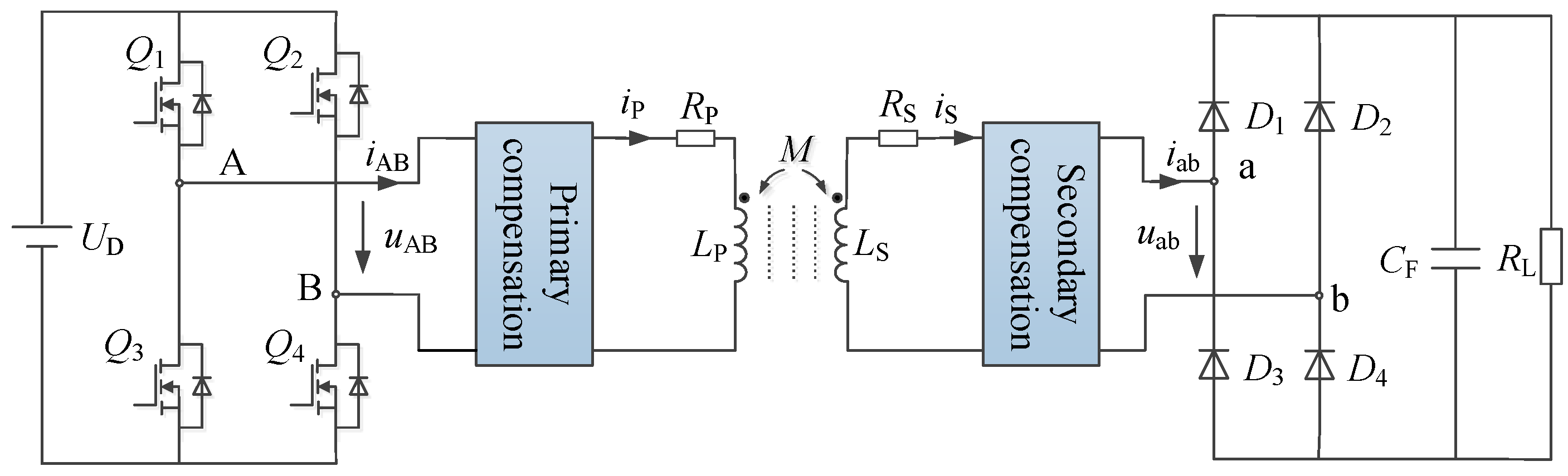
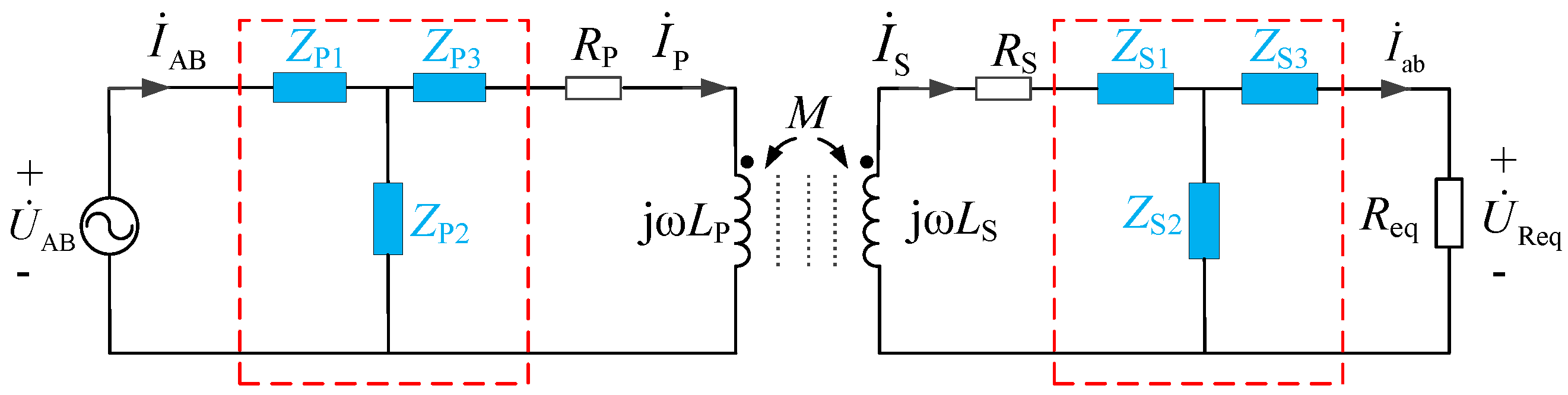
2.1. Equivalent Circuit of the IPT System with Unified Passive Compensation Network
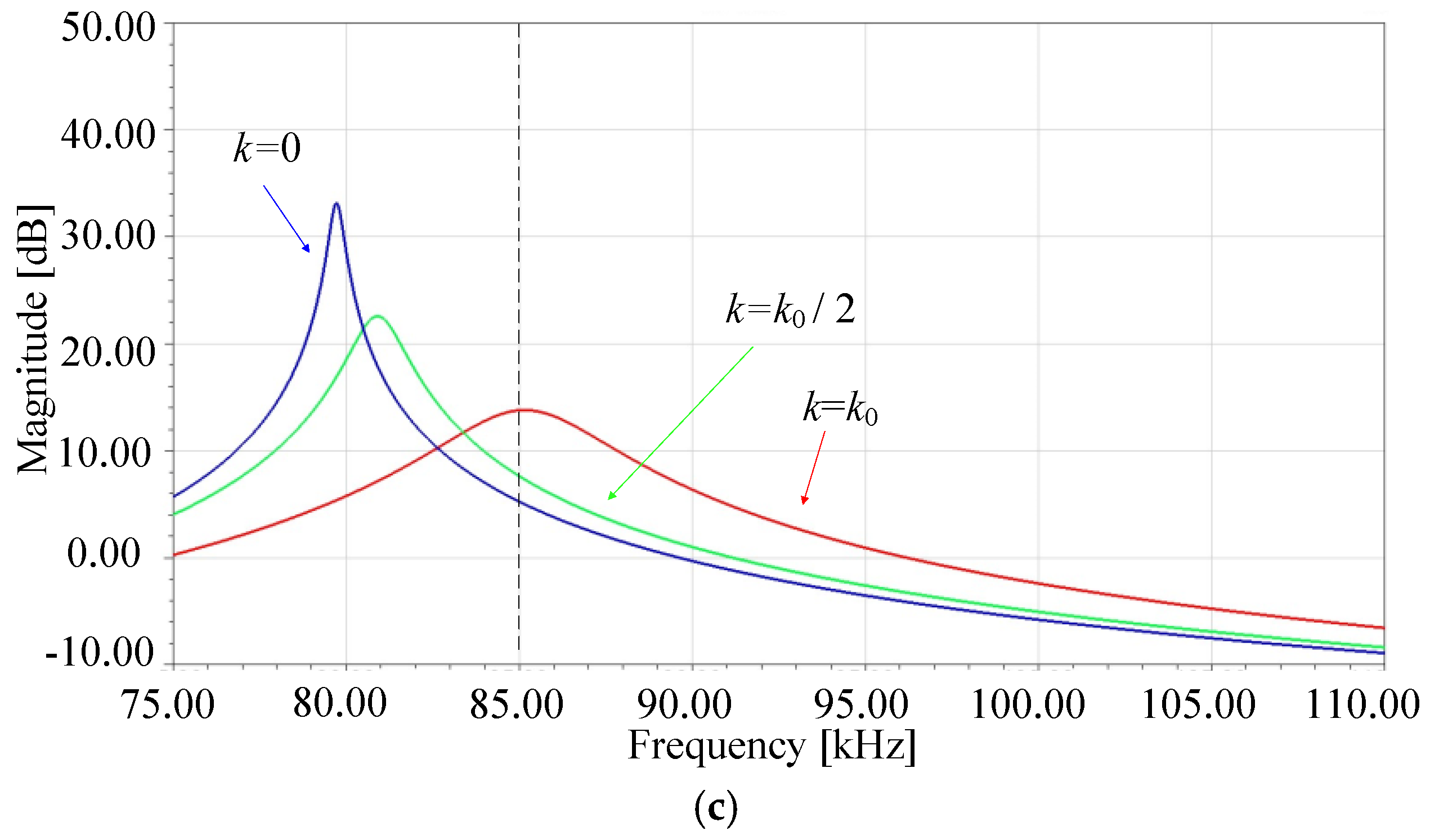
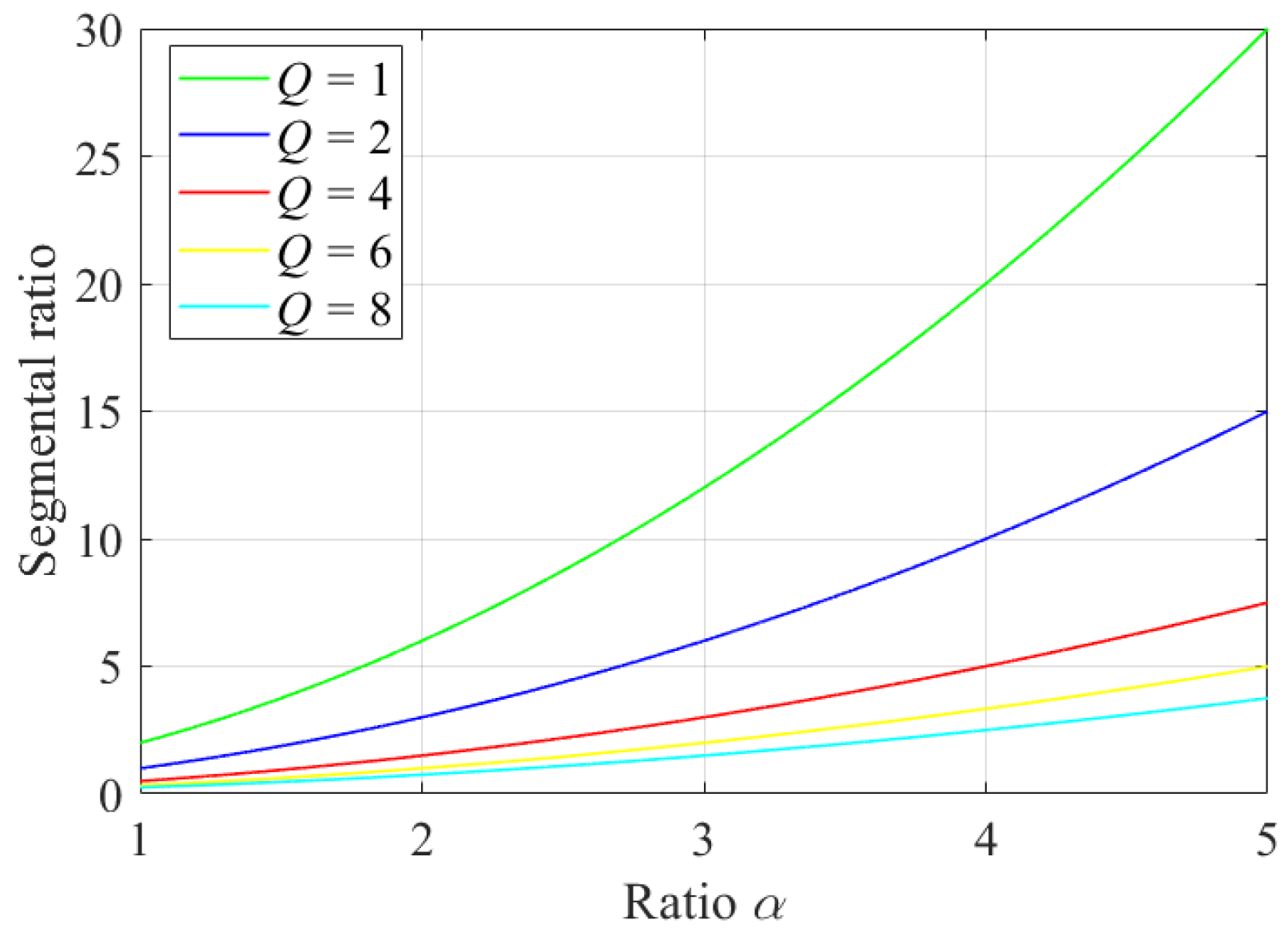
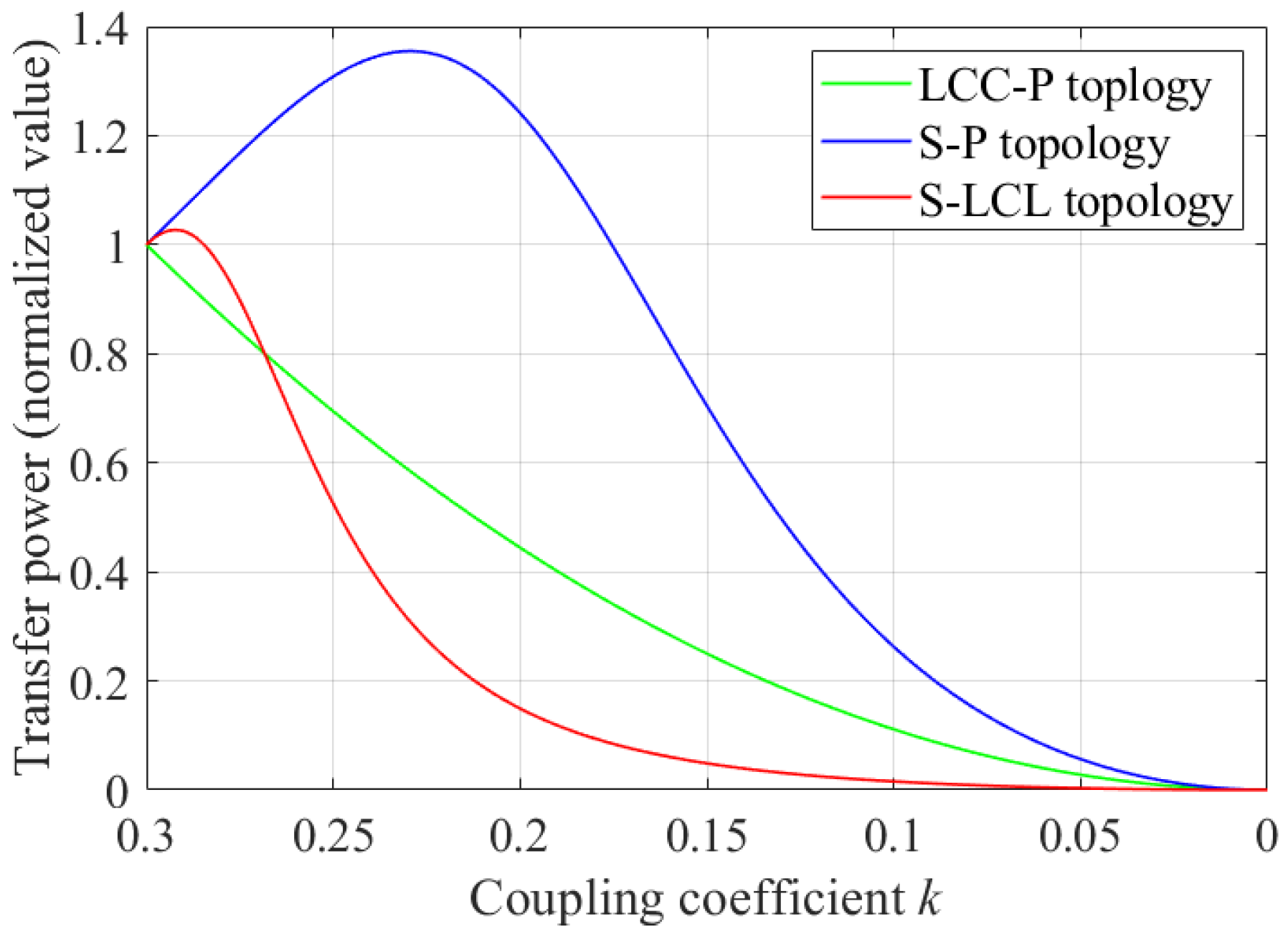
2.2. Reflective Properties and Performance Figures
3. Proposed Topology and Operation
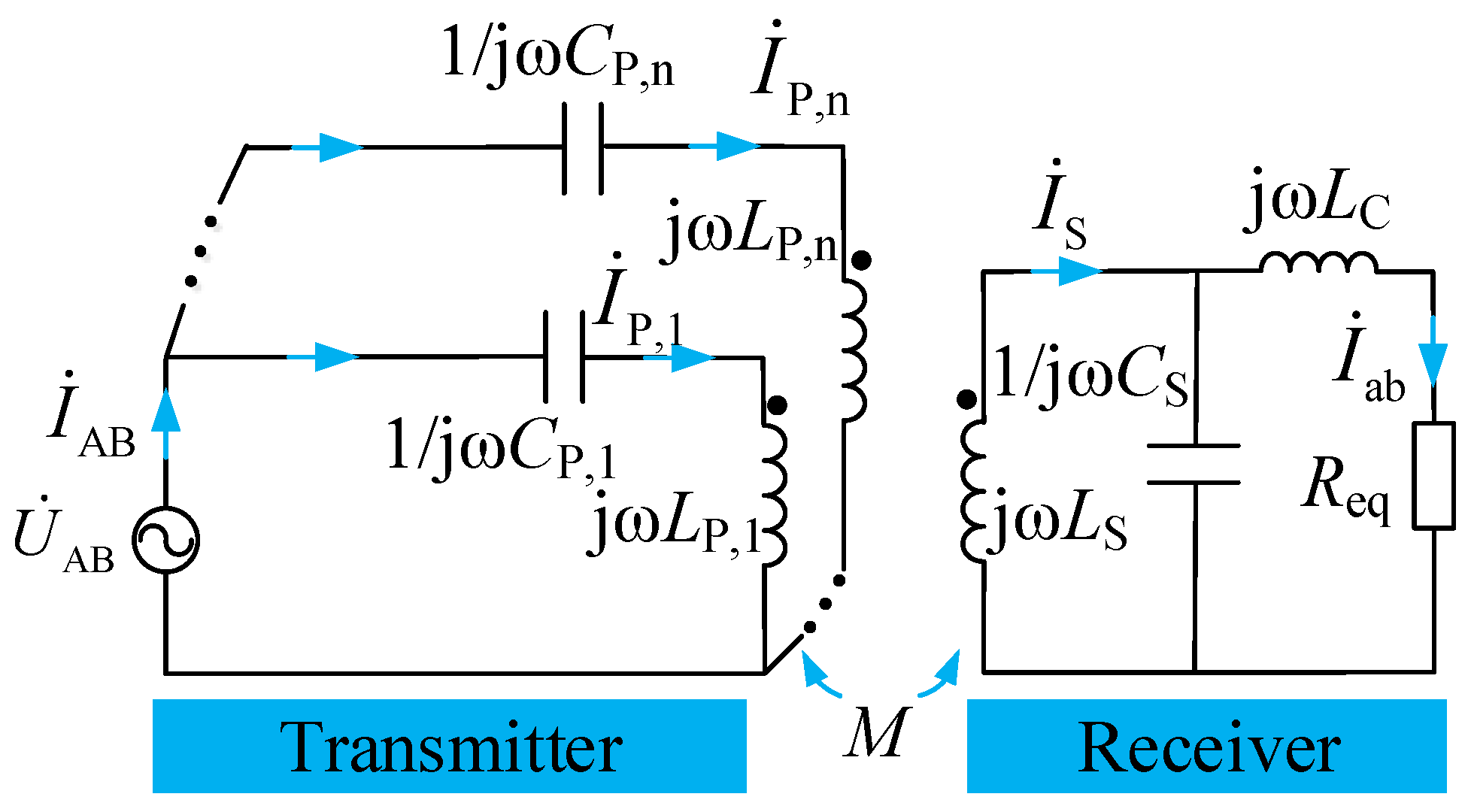
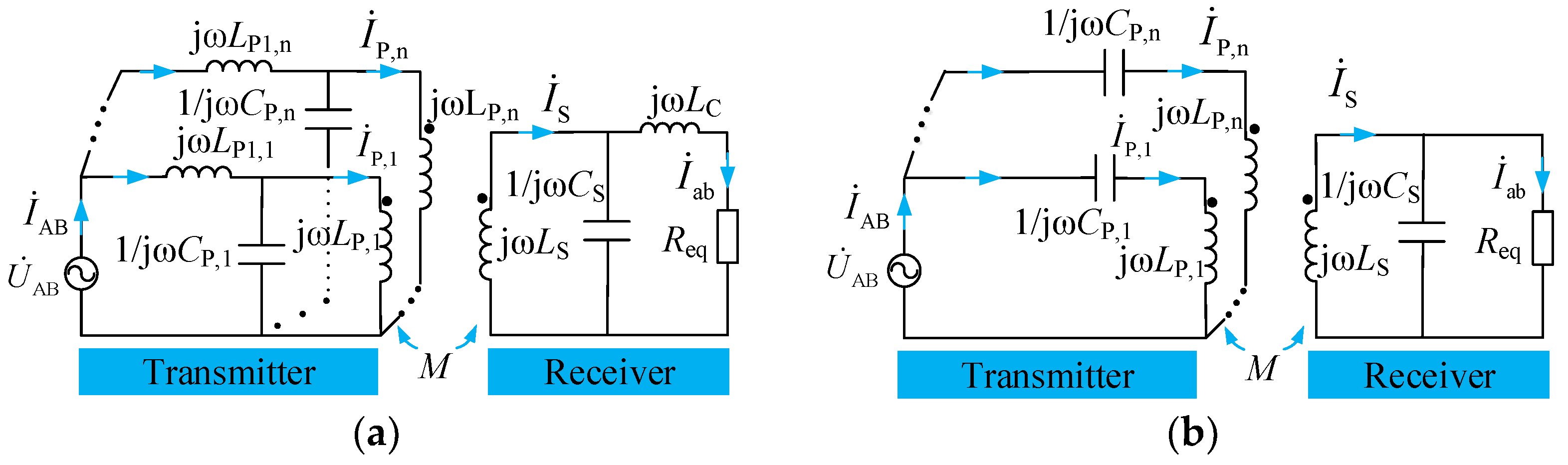
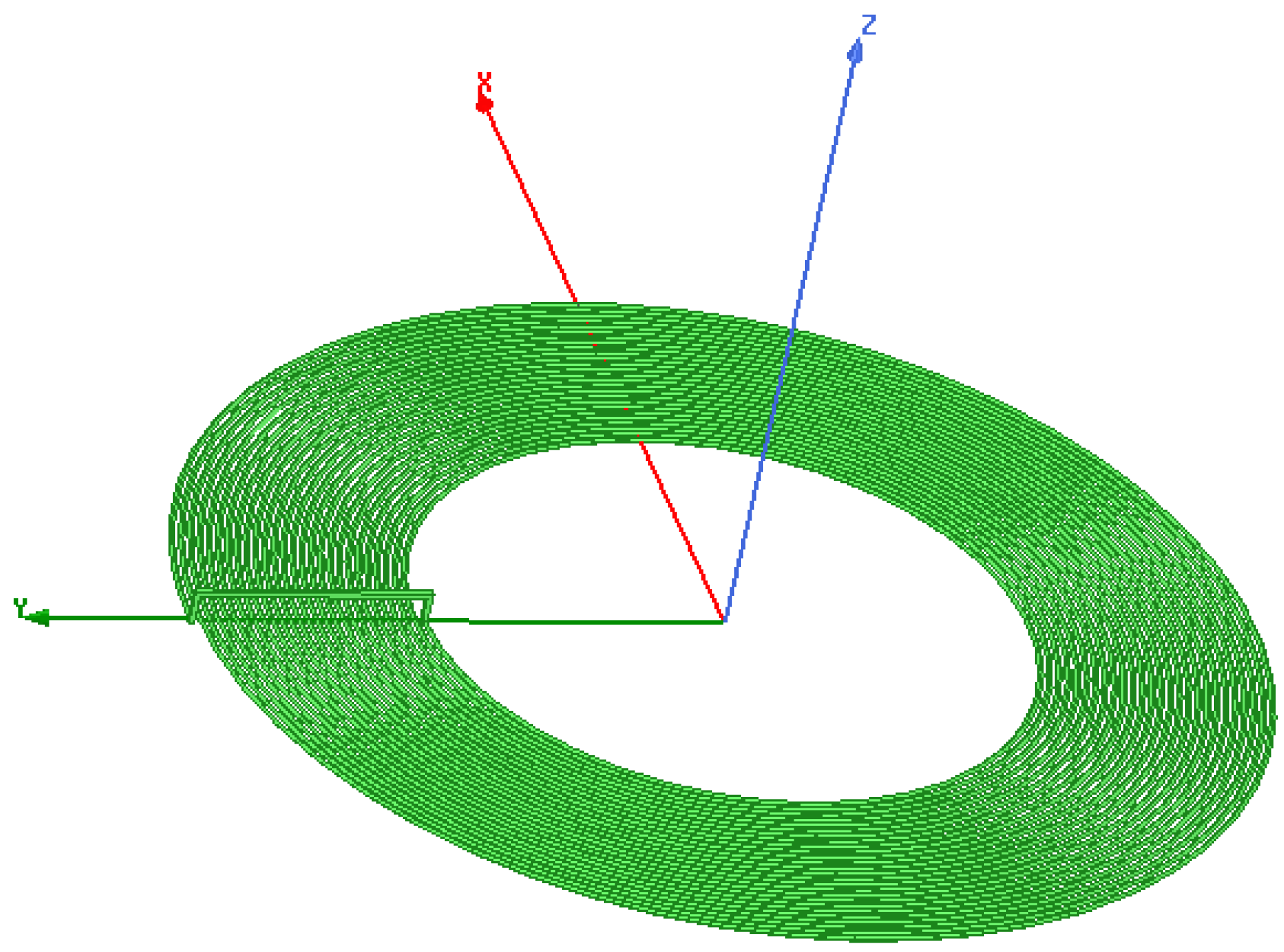
3.1. Receiver Design
3.2. Transmitter Design
4. System Design and Analysis
4.1. Transmitter Design
4.2. Power Transfer and Efficiency Considerations
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Okasili, I.; Elkhateb, A.; Littler, T. A review of wireless power transfer systems for electric vehicle battery charging with a focus on inductive coupling. Electronics 2022, 11, 1355. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Zhu, C.; Chan, C.C. A study on the safety analysis of an inductive power transfer system for kitchen appliances. Energies 2022, 15, 5218. [Google Scholar] [CrossRef]
- Jayalath, S.; Khan, A. Design, challenges, and trends of inductive power transfer couplers for electric vehicles: A review. IEEE Trans. Emerg. Sel. Topics Power Electron. 2021, 9, 6196–6218. [Google Scholar] [CrossRef]
- An, H.; Yuan, J.; Li, J.; Cao, L. Design and analysis of omnidirectional receiver with multi-coil for wireless power transmission. Electronics 2022, 11, 3103. [Google Scholar] [CrossRef]
- Huang, M.; Lu, Y.; Martins, R.P. A Reconfigurable bidirectional wireless power transceiver for battery-to-battery wireless charging. IEEE Trans. Power Electron. 2019, 34, 7745–7753. [Google Scholar] [CrossRef]
- Kim, D.; Kim, S.; Kim, S.; Moon, J.; Cho, I.; Ahn, D. Coupling extraction and maximum efficiency tracking for multiple concurrent transmitters in dynamic wireless charging. IEEE Trans. Power Electron. 2020, 35, 7853–7862. [Google Scholar] [CrossRef]
- Kim, D.H.; Ahn, D. Maximum efficiency point tracking for multiple-transmitter wireless power transfer. IEEE Trans. Power Electron. 2020, 35, 11391–11400. [Google Scholar] [CrossRef]
- Al Mahmud, S.A.; Panhwar, I.; Jayathurathnage, P. Large-area free-positioning wireless power transfer to movable receivers. IEEE Trans. Ind. Electron. 2022, 69, 12807–12816. [Google Scholar] [CrossRef]
- Liu, W.; Chau, K.; Lee, C.; Jiang, C.; Han, W.; Lam, W.H. Multi-frequency multi-power one- to-many wireless power transfer system. IEEE Trans. Magn. 2019, 55, 8001609. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, B.; Rong, C.; Shu, X.; Wei, Z. A Multi receiver wireless power transfer system using self-oscillating source composed of zero-voltage switching full-bridge inverter. IEEE Trans. Ind. Electron. 2022, 69, 2885–2895. [Google Scholar] [CrossRef]
- Chen, L.; Nagendra, G.; Boys, J.; Covic, G.A. Double-coupled systems for IPT roadway applications. IEEE Trans. Emerg. Sel. Topics Power Electron. 2015, 3, 37–49. [Google Scholar] [CrossRef]
- Nagendra, G.R.; Covic, G.; Boys, J.T. Sizing of inductive power pads for dynamic charging of EVs on IPT highways. IEEE Trans. Transp. Electrif. 2017, 3, 405–417. [Google Scholar] [CrossRef]
- Ahn, D.; Hong, S. Effect of Coupling between multiple transmitters or multiple receivers on wireless power transfer. IEEE Trans. Ind. Electron. 2013, 60, 2602–2613. [Google Scholar] [CrossRef]
- Mai, R.; Luo, Y.; Yang, B.; Song, Y.; Liu, S.; He, Z. Decoupling circuit for automated guided vehicles IPT charging systems with dual receivers. IEEE Trans. Power Electron. 2020, 35, 6652–6657. [Google Scholar] [CrossRef]
- Lee, K.; Pantic, Z.; Lukic, S.M. Reflective field containment in dynamic inductive power transfer systems. IEEE Trans. Power Electron. 2014, 29, 4592–4602. [Google Scholar] [CrossRef]
- Dayerizadeh, A.; Feng, H.; Lukic, S.M. Dynamic wireless charging: Reflective field containment using saturable inductors. IEEE Trans. Ind. Appl. 2020, 56, 1784–1792. [Google Scholar] [CrossRef]
- Dashora, H.K.; Bertoluzzo, M.; Buja, G. Reflective properties for different pick-up circuit topologies in a distributed IPT track. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 69–75. [Google Scholar]
- Dashora, H.K.; Giacomuzzi, S.; Bertoluzzo, M.; Buja, G. Performance analysis of segmentation-reflective DWC systems with capacitor-based compensation networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florance, Italy, 23–26 October 2016; pp. 4535–4540. [Google Scholar]
- Jeong, S.Y.; Park, J.; Hong, G.; Rim, C.T. Autotuning control system by variation of self-inductance for dynamic wireless ev charging with small air gap. IEEE Trans. Power Electron. 2019, 34, 5165–5174. [Google Scholar] [CrossRef]
- Luo, Y.; Song, Y.; Yang, H.; Mai, R. Research on reflective properties in the IPT system with dual secondary loops. IEEE Trans. Ind. Appl. 2022, 58, 1126–1135. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Y.; Chen, K.; Zhao, Z.; Yuan, L. A comparative study of load characteristics of resonance types in wireless transmission systems. In Proceedings of the 2016 Asia-Pacific International Symposium on EMC (APEMC), Shenzhen, China, 18–21 May 2016; pp. 203–206. [Google Scholar]
- Cai, C.; Wang, J.; Fang, Z.; Zhang, P.; Hu, M.; Zhang, J.; Li, L.; Lin, Z. Design and optimization of load-independent magnetic resonant wireless charging system for electric vehicles. IEEE Access 2018, 6, 17264–17274. [Google Scholar] [CrossRef]
- Meng, X.; Qiu, D.; Lin, M.; Tang, S.; Zhang, B. Output voltage identification based on transmitting side information for implantable wireless power transfer system. IEEE Access 2019, 7, 2938–2946. [Google Scholar] [CrossRef]






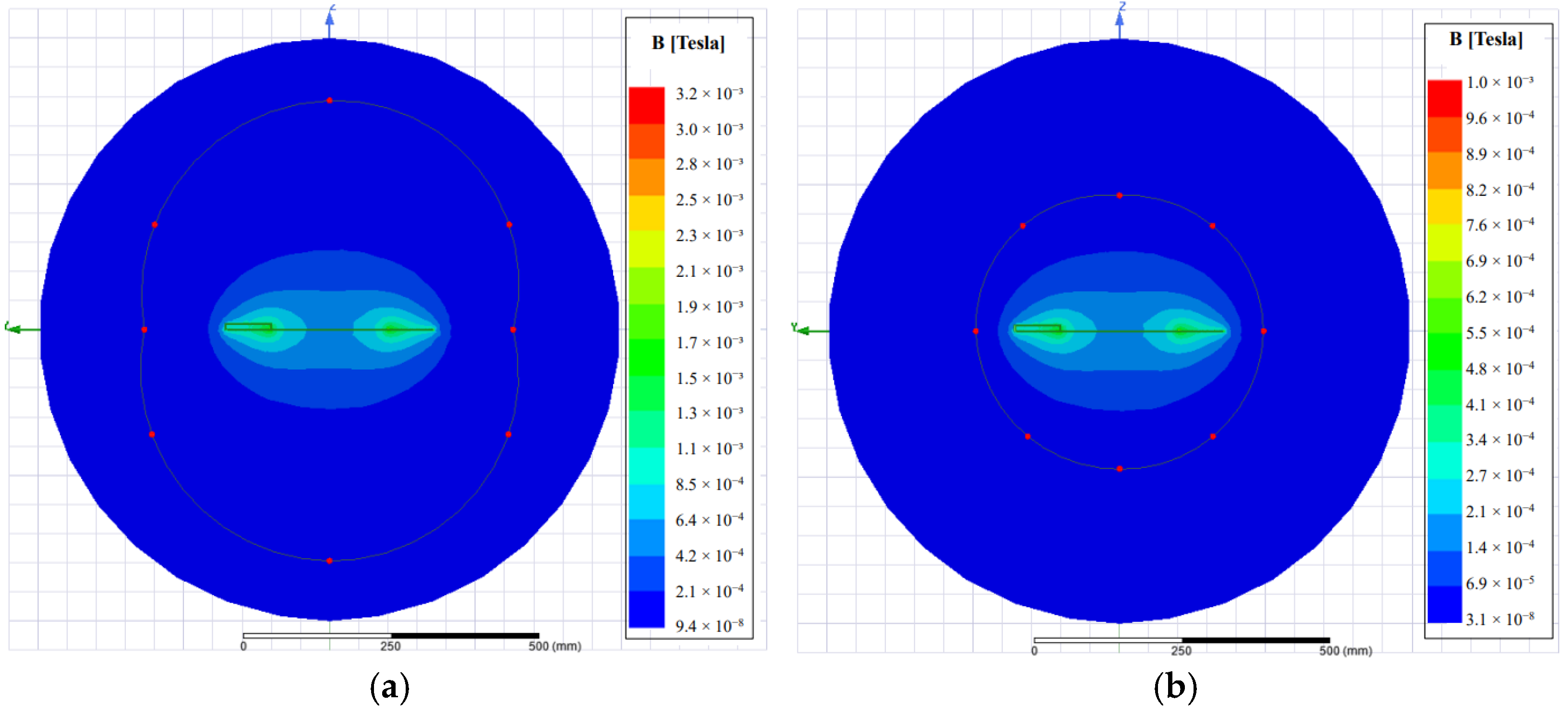
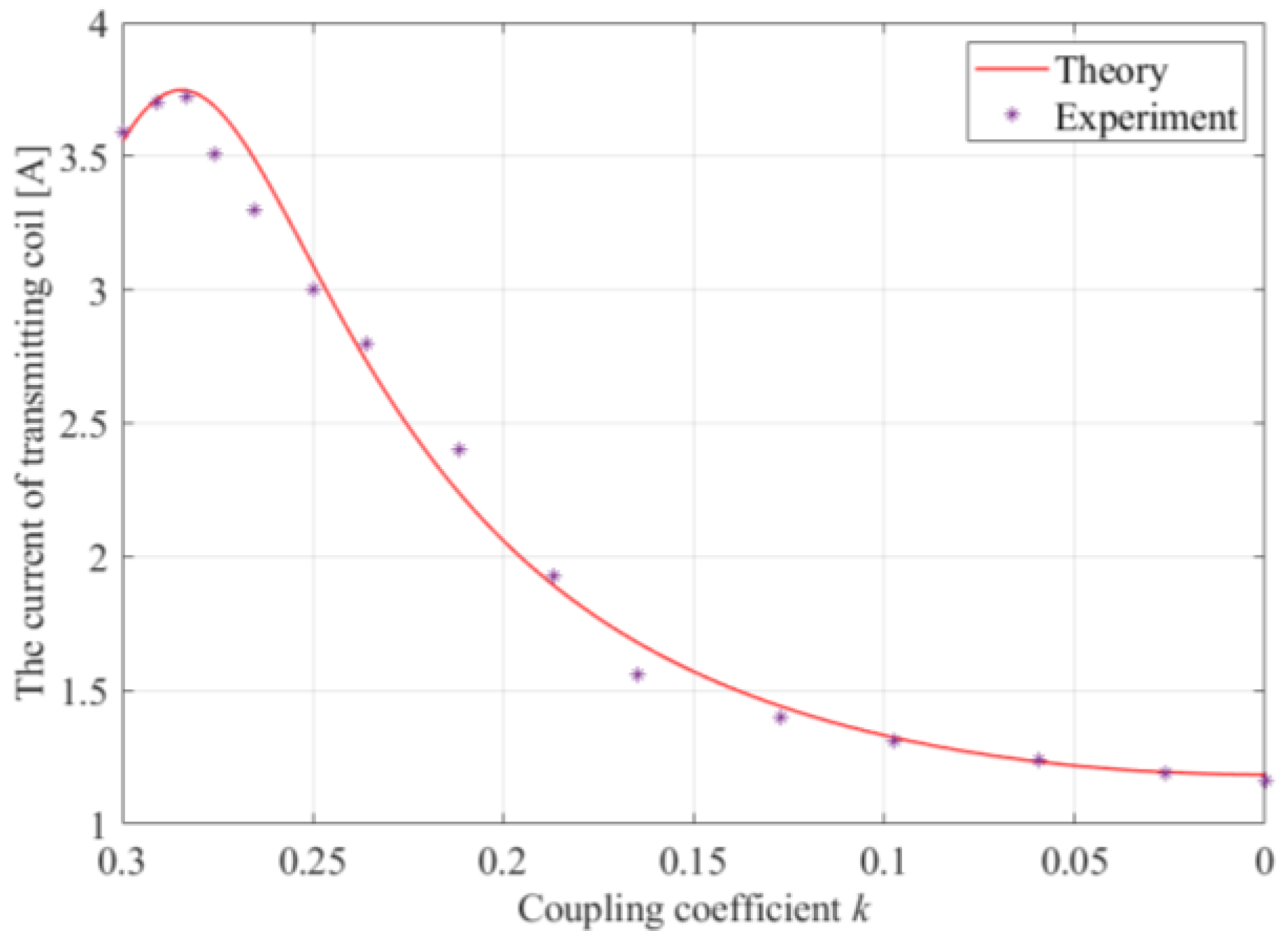
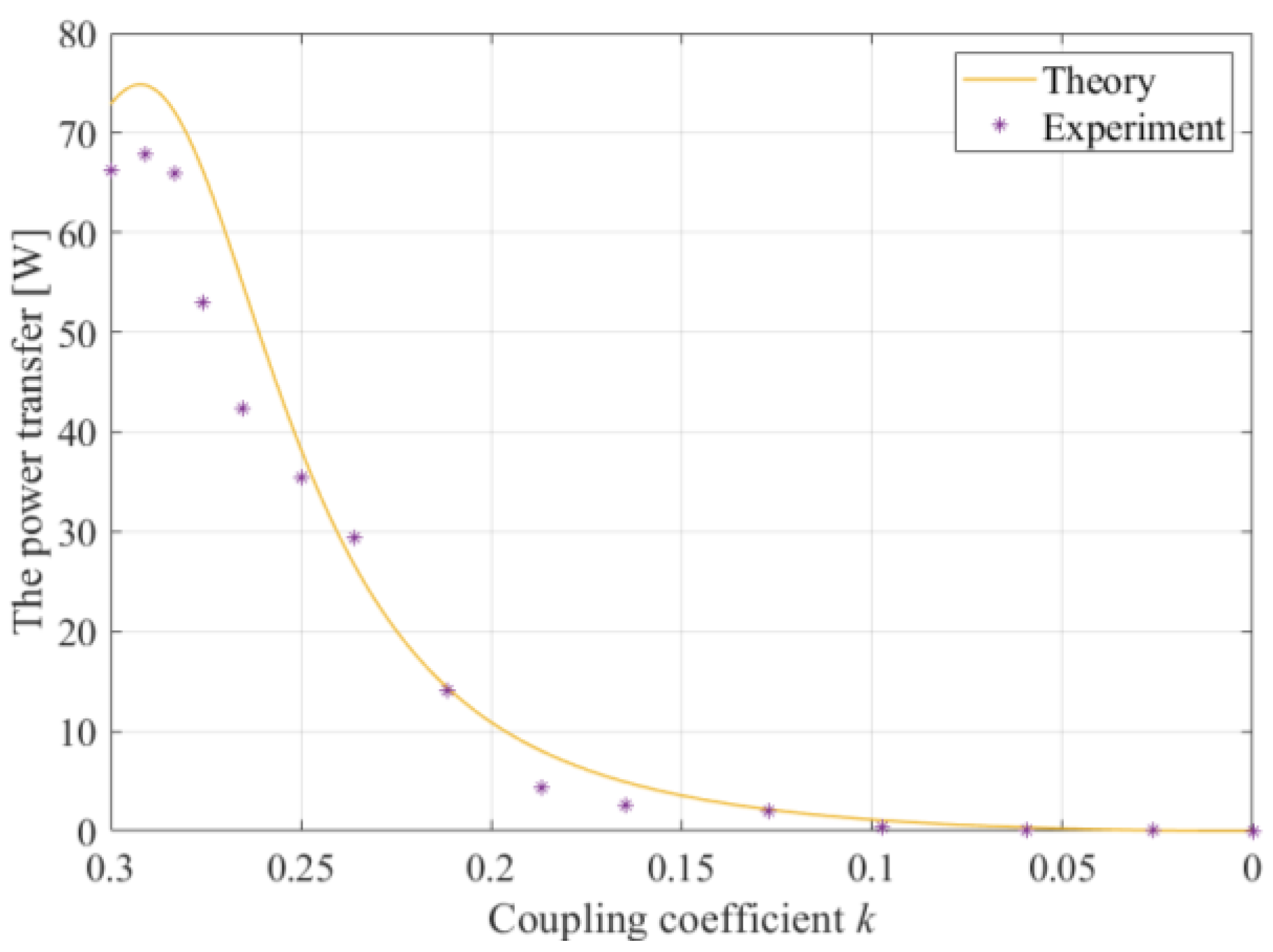
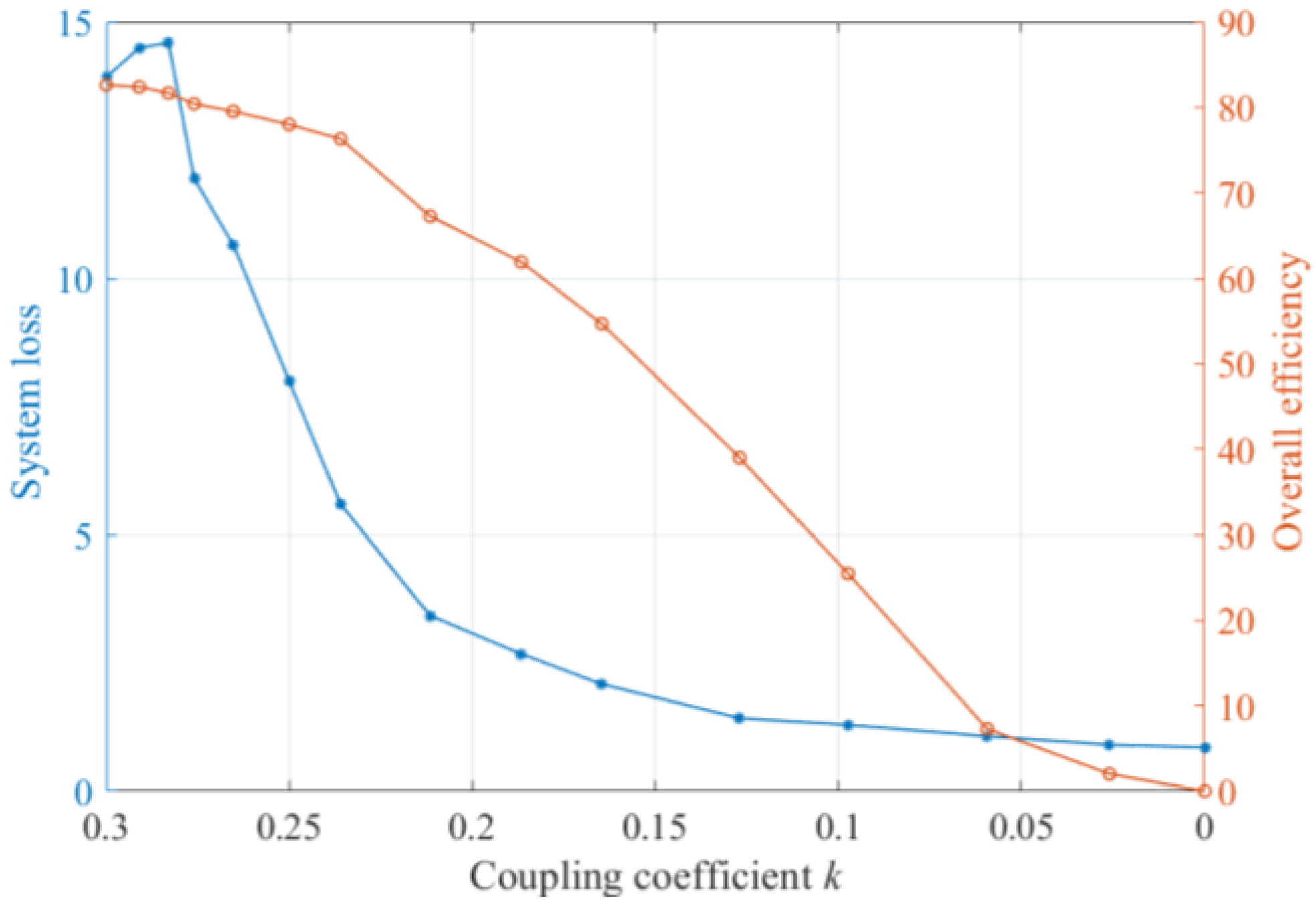
| Parameters | LCC−P Topology | S−P Topology | S−LCL Topology |
|---|---|---|---|
| UD | 50 V | 22.5 V | 22.5 V |
| LP1 | 72 μH | −−− | −−− |
| CP1 | 48.71 nF | 14.27 nF | 14.76 nF |
| CP2 | 17.71 nF | −−− | −−− |
| CS | 12.99 nF | 12.99 nF | 51.95 F |
| LC | −−− | −−− | 90 H |
| Req | 200 Ω | 200 Ω | 36 Ω |
| Parameters | α = 2, Q = 2 | α = 3, Q = 2 | α = 3, Q = 4 |
|---|---|---|---|
| CP | 15.02 nF | 14.76 nF | 14.76 nF |
| CS | 38.96 nF | 51.95 nF | 51.95 nF |
| LC | 135 H | 90 H | 90 H |
| Req | 72 Ω | 72 Ω | 36 Ω |
| IP,k0 | 3.10 A | 6.69 A | 3.45 A |
| IP,un | 1.01 A | 1.12 A | 1.12 A |
| SR | 3.07 | 5.97 | 3.08 |
| Pin | 68.4 W | 135.6 W | 80.2 W |
| Pout | 57.9 W | 101.8 W | 66.2 W |
| Ploss | 10.2 W | 33.8 W | 13.9 W |
| η | 84.6% | 75.1% | 82.6% |
| Pidle−loss | 0.69 W | 0.85 W | 0.85 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yang, J.; Fan, J.; Wang, B.; Li, D. A Magnetic Field Containment Method for an IPT System with Multiple Transmitting Coils Based on Reflective Properties. Electronics 2023, 12, 653. https://doi.org/10.3390/electronics12030653
Yang X, Yang J, Fan J, Wang B, Li D. A Magnetic Field Containment Method for an IPT System with Multiple Transmitting Coils Based on Reflective Properties. Electronics. 2023; 12(3):653. https://doi.org/10.3390/electronics12030653
Chicago/Turabian StyleYang, Xu, Junfeng Yang, Jing Fan, Bao Wang, and Dingzhen Li. 2023. "A Magnetic Field Containment Method for an IPT System with Multiple Transmitting Coils Based on Reflective Properties" Electronics 12, no. 3: 653. https://doi.org/10.3390/electronics12030653
APA StyleYang, X., Yang, J., Fan, J., Wang, B., & Li, D. (2023). A Magnetic Field Containment Method for an IPT System with Multiple Transmitting Coils Based on Reflective Properties. Electronics, 12(3), 653. https://doi.org/10.3390/electronics12030653







