Few-Shot Classification Based on the Edge-Weight Single-Step Memory-Constraint Network
Abstract
:1. Introduction
2. Related Work
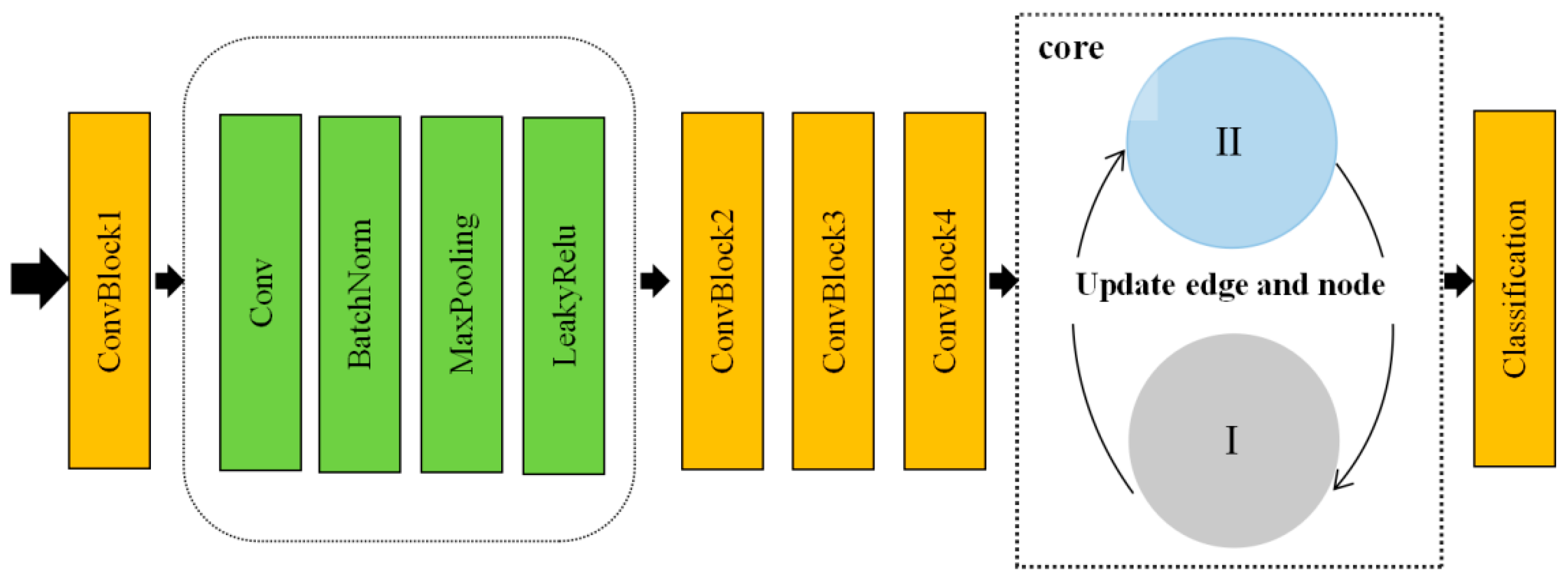
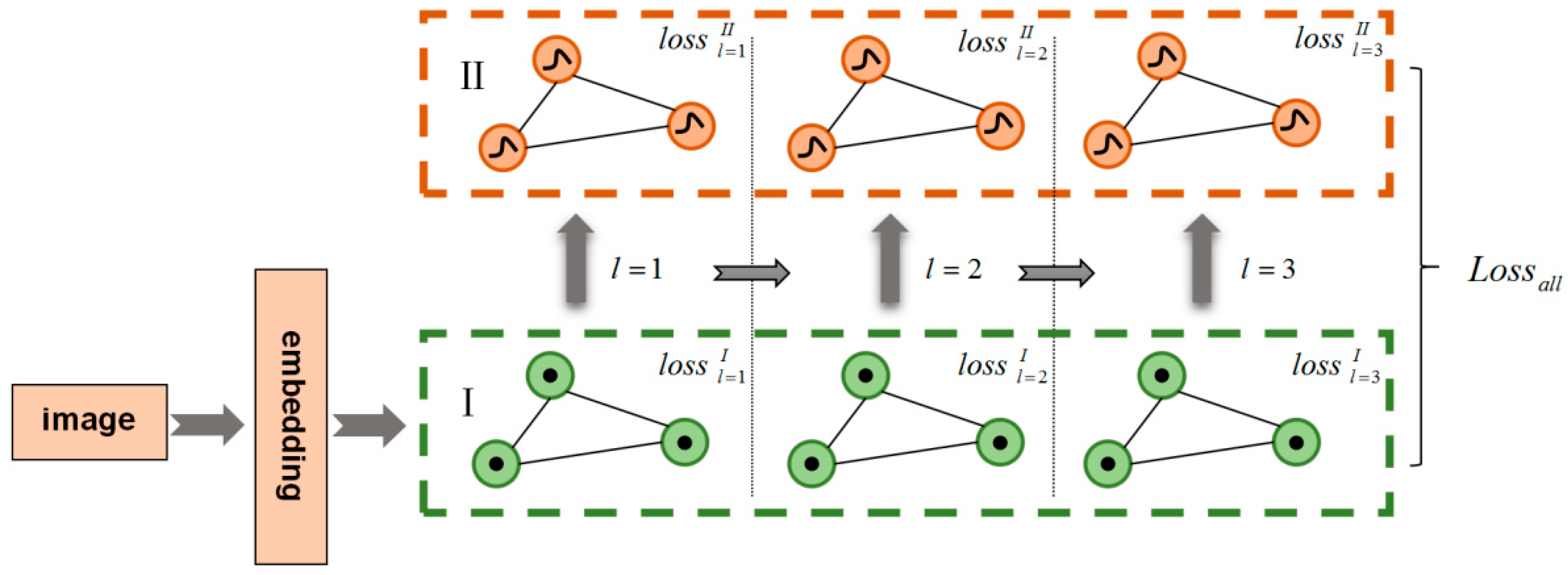
3. Edge-Weight Single-Step Memory-Constraint Network (ESMC)
3.1. N-Way K-Shot Mode
3.2. Graph Neural Network
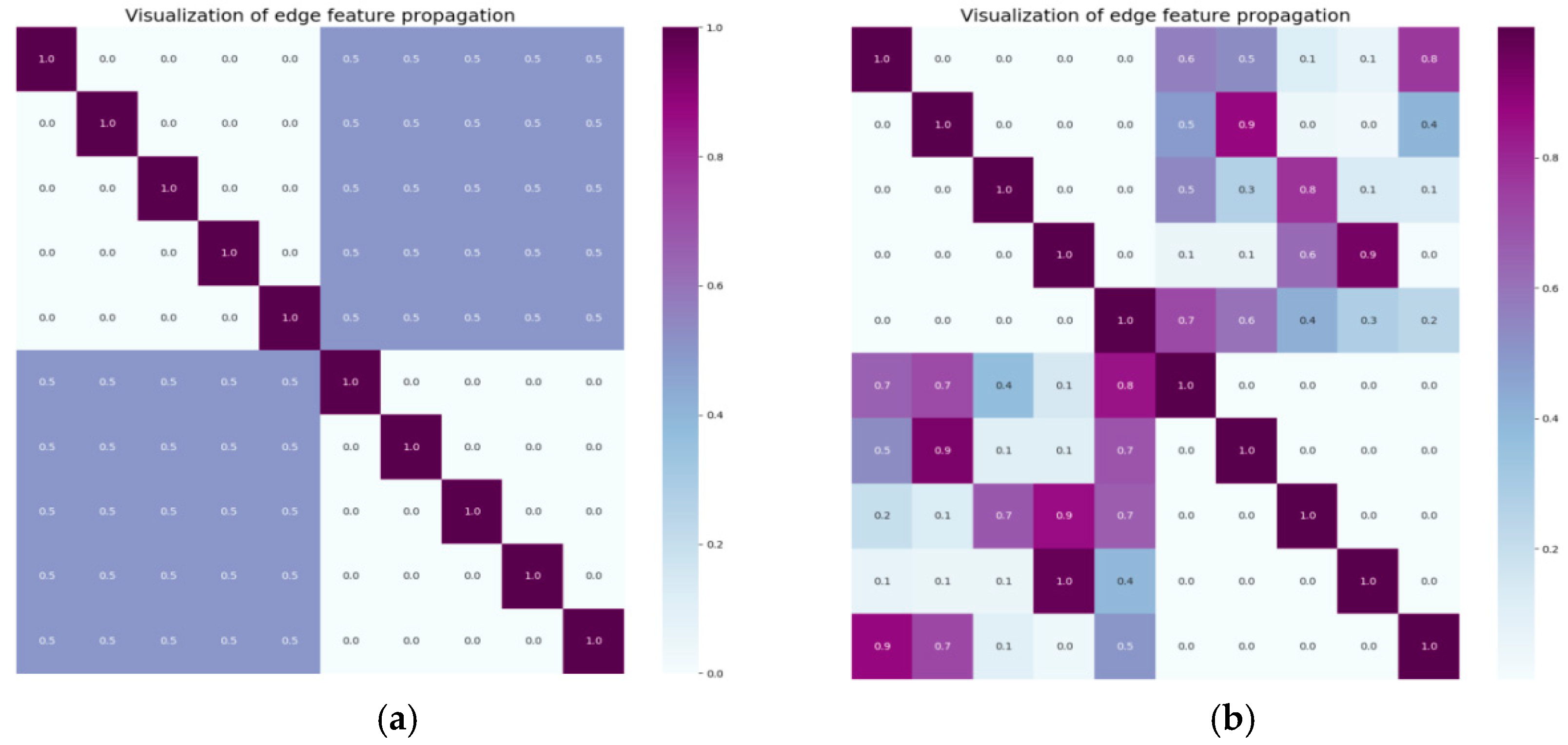
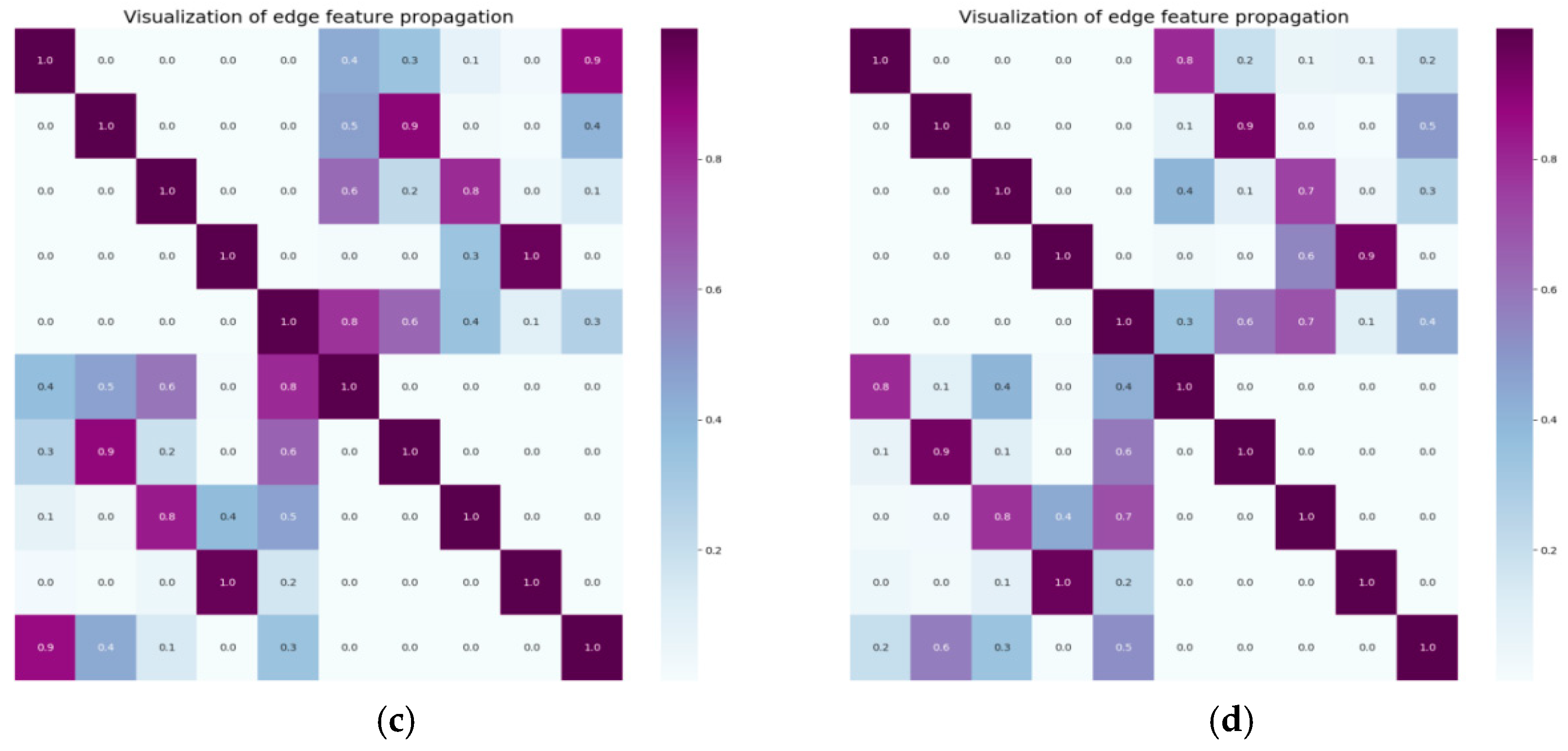
3.2.1. Edge Initialization and Update of the Graph Structure in Zone I
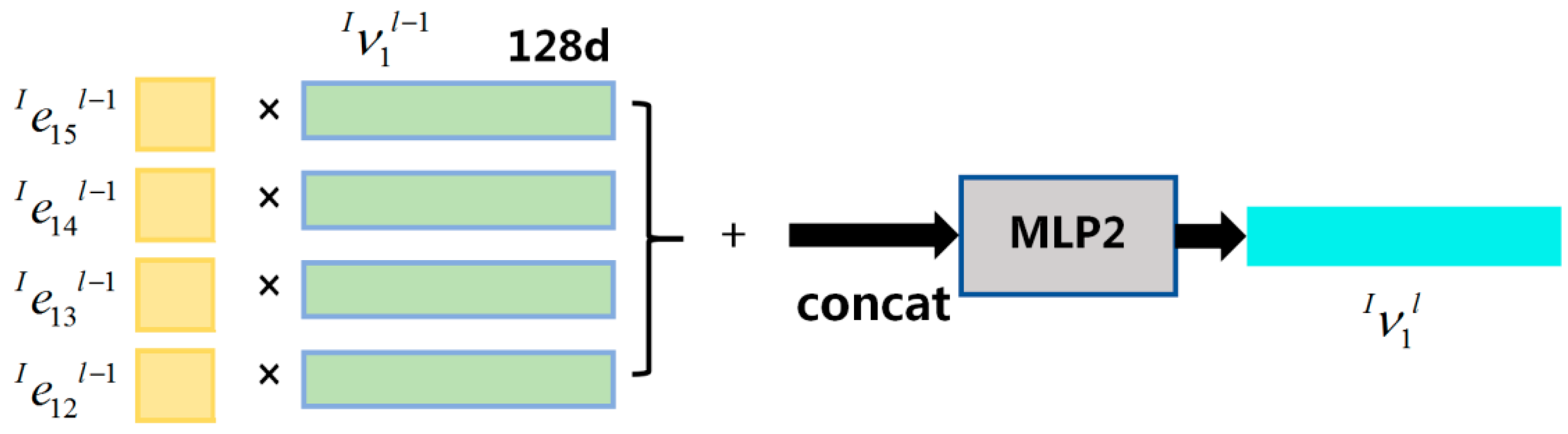
3.2.2. Node Initialization and Update of the Graph Structure in Zone I
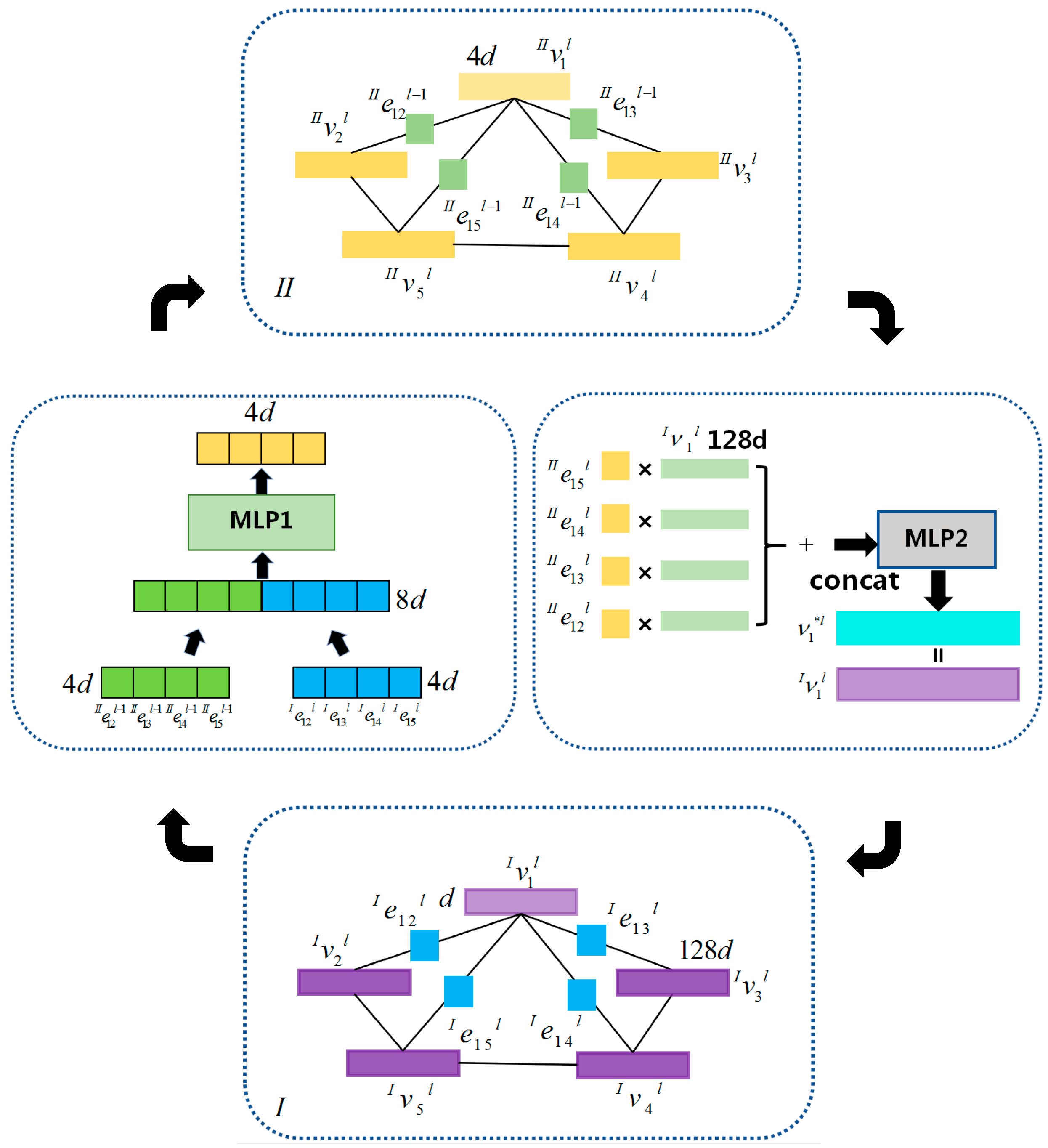
3.2.3. Edge Initialization of the Edge Weights Structure in Zone II
3.2.4. Node Update of the Edge-Weight Implicit Distribution Graph Structure in Zone II
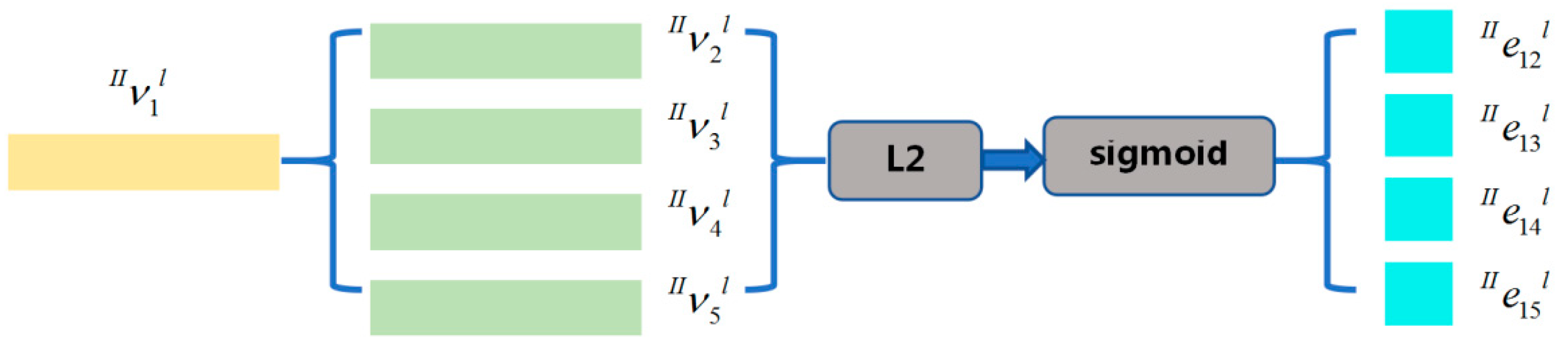
3.2.5. Edge Update of the Edge-Weight Implied Distribution Graph Structure Zone II
3.2.6. Feature Fusion Update of Zone II and Zone I
3.2.7. Loss Function
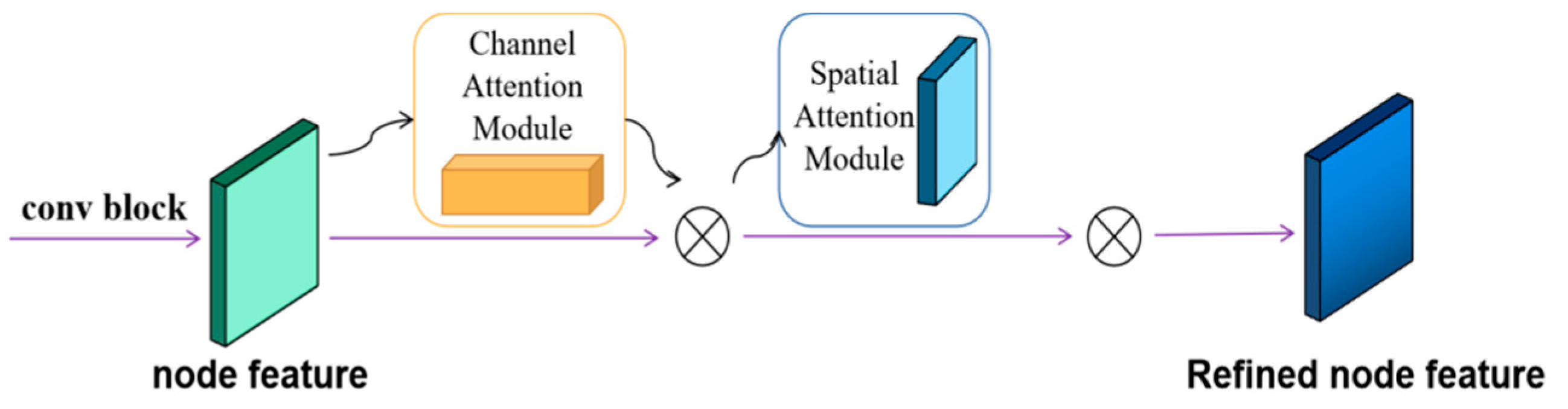
3.3. Feature Extraction of the Initialized Nodes Based on Attention
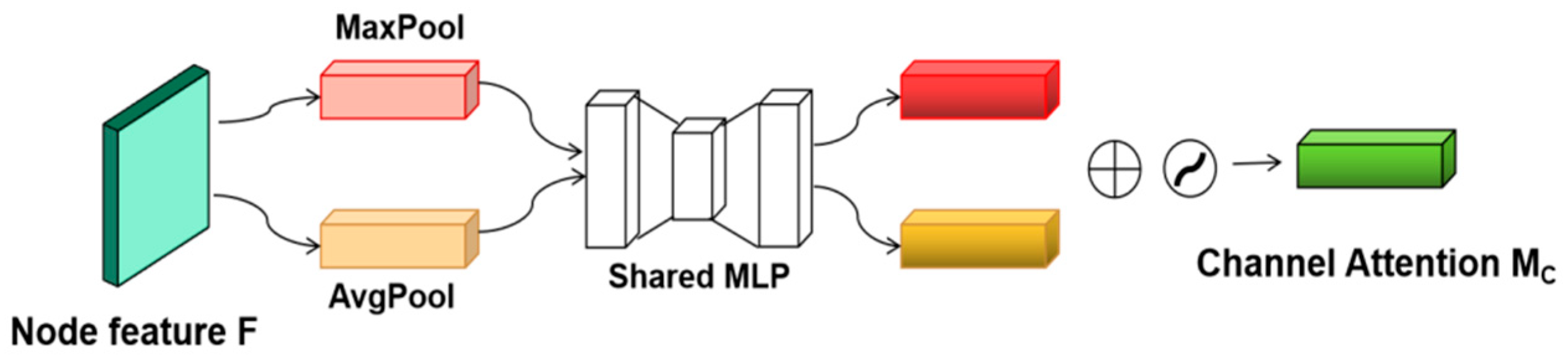
3.3.1. Initialized Node-Feature Extraction Based on Channel Attention
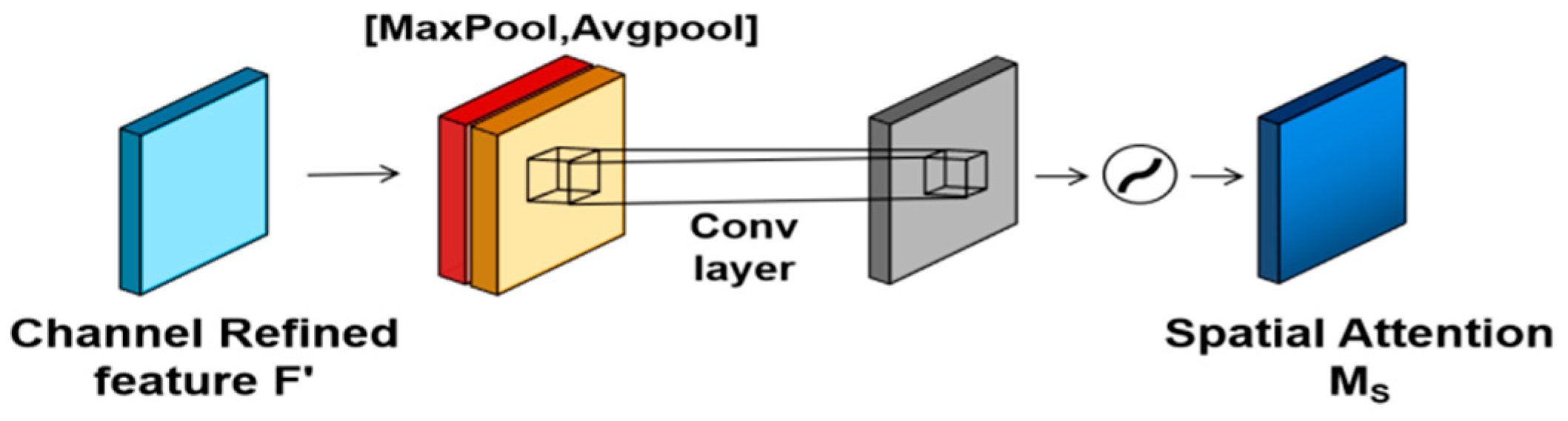
3.3.2. Initialized Node-Feature Extraction Based on Spatial Attention
4. Experimental Results and Analysis
4.1. Parameters Setting
4.2. Experimental Results
4.2.1. Impact of ESMC on Classification Performance
4.2.2. Impact of Initialization Feature Updates on Classification Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, S.; Zeng, X.; Wu, S.; Yu, Z.; Azzam, M.; Wong, H.S. Behavior Regularized Prototypical Networks for Semi-Supervised Few-Shot Image Classification. Pattern Recognit. 2021, 112, 107765. [Google Scholar] [CrossRef]
- Guo, J. Prototype Calibration with Feature Generation for Few-Shot Remote Sensing Image Scene Classification. Remote Sens. 2021, 13, 2728. [Google Scholar]
- Singh P, Mazumder P. Dual class representation learning for few-shot image classification. Knowl.-Based Syst. 2022, 238, 107840. [CrossRef]
- Han, H.; Huang, Y.; Wang, Z. Collaborative Self-Supervised Transductive Few-Shot Learning for Remote Sensing Scene Classification. Electronics 2023, 12, 3846. [Google Scholar] [CrossRef]
- Song, H.; Deng, B.; Pound, M.; Zcan, E.; Triguero, I. A fusion spatial attention approach for few-shot learning. Inf. Fusion 2022, 81, 187–202. [Google Scholar] [CrossRef]
- Jing, Z.; Li, P.; Wu, B.; Yuan, S.; Chen, Y. An Adaptive Focal Loss Function Based on Transfer Learning for Few-Shot Radar Signal Intra-Pulse Modulation Classification. Remote Sens. 2022, 14, 1950. [Google Scholar] [CrossRef]
- Rostami, M.; Kolouri, S.; Eaton, E.; Kim, K. Deep Transfer Learning for Few-Shot SAR Image Classification. Remote Sens. 2019, 11, 1374. [Google Scholar] [CrossRef]
- Xing, L.; Shao, S.; Liu, W.; Han, A.; Pan, X.; Liu, B.D. Learning task-specific discriminative embeddings for few-shot image classification. Neurocomputing 2022, 488, 1–13. [Google Scholar] [CrossRef]
- Liang, M.; Huang, S.; Pan, S.; Gong, M.; Liu, W. Learning multi-level weight-centric features for few-shot learning. Pattern Recognit. 2022, 128, 108662. [Google Scholar] [CrossRef]
- Li, X.; Yu, L.; Fu, C.W.; Fang, M.; Heng, P.A. Revisiting Metric Learning for Few-Shot Image Classification. Neurocomputing 2020, 406, 49–58. [Google Scholar] [CrossRef]
- Zhu, W.; Li, W.; Liao, H.; Luo, J. Temperature network for few-shot learning with distribution-aware large-margin metric. Pattern Recognit. 2021, 112, 107797. [Google Scholar] [CrossRef]
- Lee, T.; Yoo, S. Augmenting Few-Shot Learning With Supervised Contrastive Learning. IEEE Access 2021, 9, 61466–61474. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, X.; Yuan, L.; Feng, J. Few-shot adaptive faster r-cnn. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7173–7182. [Google Scholar]
- Kim, J.; Kim, T.; Kim, S.; Yoo, C.D. Edge-labeling graph neural network for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11–20. [Google Scholar]
- Wertheimer, D.; Hariharan, B. Few-shot learning with localization in realistic settings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6558–6567. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? arXiv 2014, arXiv:1411.1792. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3630–3638. [Google Scholar]
- Xia, M.; Yuan, G.; Yang, L.; Xia, K.; Ren, Y.; Shi, Z.; Zhou, H. Few-Shot Hyperspectral Image Classification Based on Convolutional Residuals and SAM Siamese Networks. Electronics 2023, 12, 3415. [Google Scholar] [CrossRef]
- Dvornik, N.; Schmid, C.; Mairal, J. Diversity with cooperation: Ensemble methods for few-shot classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3723–3731. [Google Scholar]
- Gidaris, S.; Komodakis, N. Generating classification weights with gnn denoising autoencoders for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 21–30. [Google Scholar]
- Alfassy, A.; Karlinsky, L.; Aides, A.; Shtok, J.; Harary, S.; Feris, R.; Giryes, R. Laso: Label-set operations networks for multi-label few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6548–6557. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.; Hospedales, T. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1199–1208. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 2030–2096. [Google Scholar]
- Sun, Q.; Liu, Y.; Chua, T.; Schiele, B. Meta-transfer learning for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 403–412. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Kim, J.W.; Kim, S.Y.; Sohn, K.-A. Dataset Bias Prediction for Few-Shot Image Classification. Electronics 2023, 12, 2470. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Zhang, Y.; Jiang, Y.G.; Xue, X.; Sigal, L. Semantic feature augmentation in few-shot learning. arXiv 2018, arXiv:1804.05298. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical networks for few-shot learning. arXiv 2017, arXiv:1703.05175. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Wang, Y.X.; Ma, L.; Liu, W.; Hebert, M. Image deformation meta-networks for one-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8680–8689. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Lifchitz, Y.; Avrithis, Y.; Picard, S.; Bursuc, A. Dense classification and implanting for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9258–9267. [Google Scholar]
- Elsken, T.; Staffler, B.; Metzen, J.H.; Hutter, F. Meta-learning of neural architectures for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12365–12375. [Google Scholar]
- Chu, W.H.; Li, Y.J.; Chang, J.C.; Wang, Y.C.F. Spot and learn: A maximum-entropy patch sampler for few-shot image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6251–6260. [Google Scholar]
- Liu, Y.; Lee, J.; Park, M.; Kim, S.; Yang, E.; Hwang, S.J.; Yang, Y. Learning to propagate labels: Transductive propagation network for few-shot learning. arXiv 2018, arXiv:1805.10002. [Google Scholar]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7260–7268. [Google Scholar]
- Bertinetto, L.; Henriques, J.F.; Torr, P.H.S.; Vedaldi, A. Meta-learning with differentiable closed-form solvers. arXiv 2018, arXiv:1805.08136. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Gidaris, S.; Komodakis, N. Dynamic few-shot visual learning without forgetting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4367–4375. [Google Scholar]
- Garcia, V.; Bruna, J. Few-shot learning with graph neural networks. arXiv 2017, arXiv:1711.04043. [Google Scholar]
- Rusu, A.A.; Rao, D.; Sygnowski, J.; Vinyals, O.; Pascanu, R.; Osindero, S.; Hadsell, R. Meta-learning with latent embedding optimization. arXiv 2018, arXiv:1807.05960. [Google Scholar]
- Li, A.; Luo, T.; Xiang, T.; Huang, W.; Wang, L. Few-shot learning with global class representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9715–9724. [Google Scholar]
- Yang, L.; Li, L.; Zhang, Z.; Zhou, X.; Zhou, E.; Liu, Y. Dpgn: Distribution propagation graph network for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13390–13399. [Google Scholar]
- Yoon, S.W.; Seo, J.; Moon, J. Tapnet: Neural network augmented with task-adaptive projection for few-shot learning. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 7115–7123. [Google Scholar]
- Qiao, S.; Liu, C.; Shen, W.; Yuille, A.L. Few-shot image recognition by predicting parameters from activations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7229–7238. [Google Scholar]
- Zhang, H.; Zhang, J.; Koniusz, P. Few-shot learning via saliency-guided hallucination of samples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2770–2779. [Google Scholar]
- Yu, Y.; Liu, G.; Odobez, J.M. Improving few-shot user-specific gaze adaptation via gaze redirection synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11937–11946. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Chen, W.Y.; Liu, Y.C.; Kira, Z.; Wang, Y.C.F.; Huang, J.B. A closer look at few-shot classification. arXiv 2019, arXiv:1904.04232. [Google Scholar]



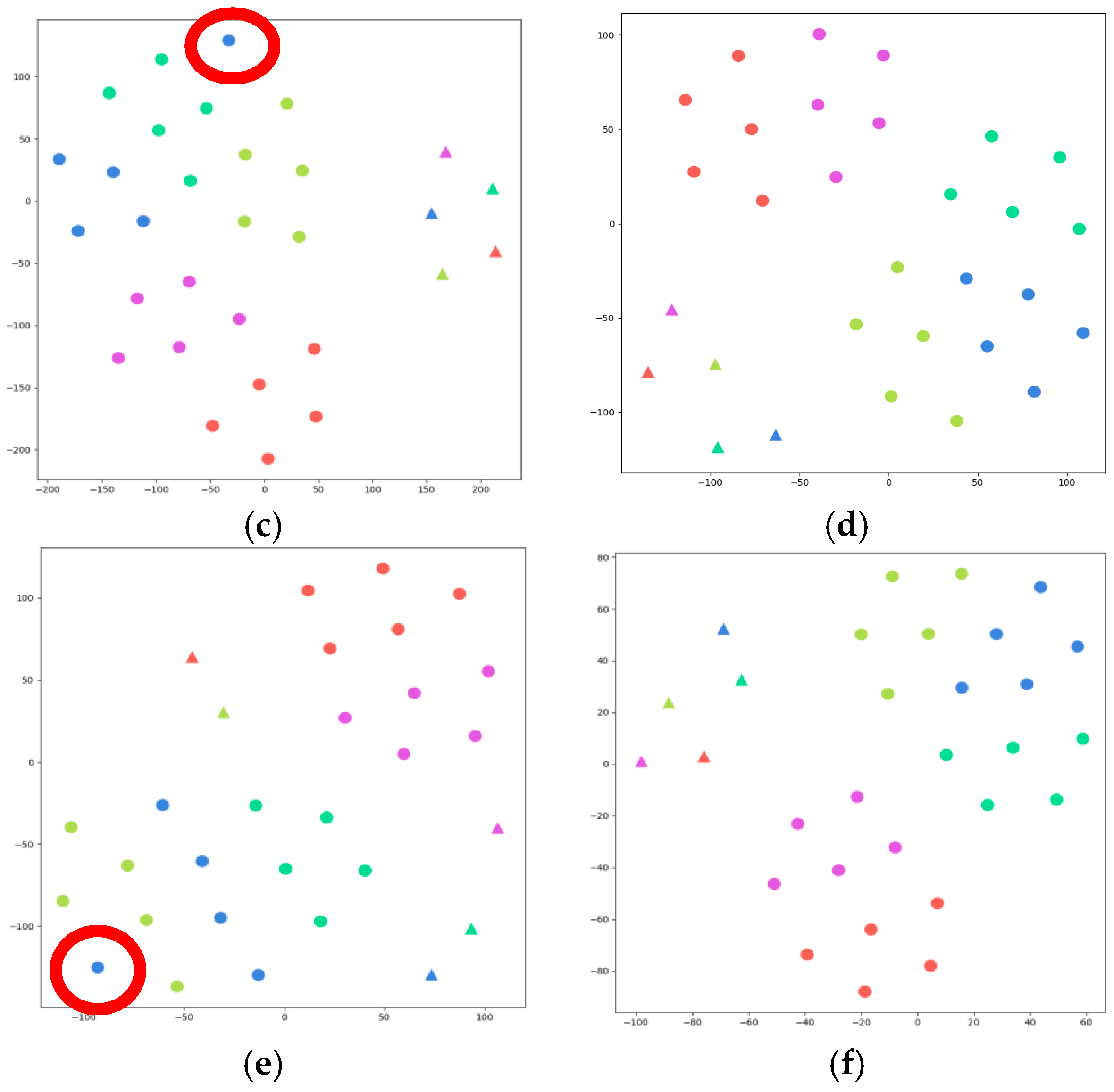
 “ represents the samples of query set, and “
“ represents the samples of query set, and “ ” represents the samples of suppport set. Different colors represent different categories. The samples in the red circle are the samples that were shifted during clustering.
” represents the samples of suppport set. Different colors represent different categories. The samples in the red circle are the samples that were shifted during clustering.
 “ represents the samples of query set, and “
“ represents the samples of query set, and “ ” represents the samples of suppport set. Different colors represent different categories. The samples in the red circle are the samples that were shifted during clustering.
” represents the samples of suppport set. Different colors represent different categories. The samples in the red circle are the samples that were shifted during clustering.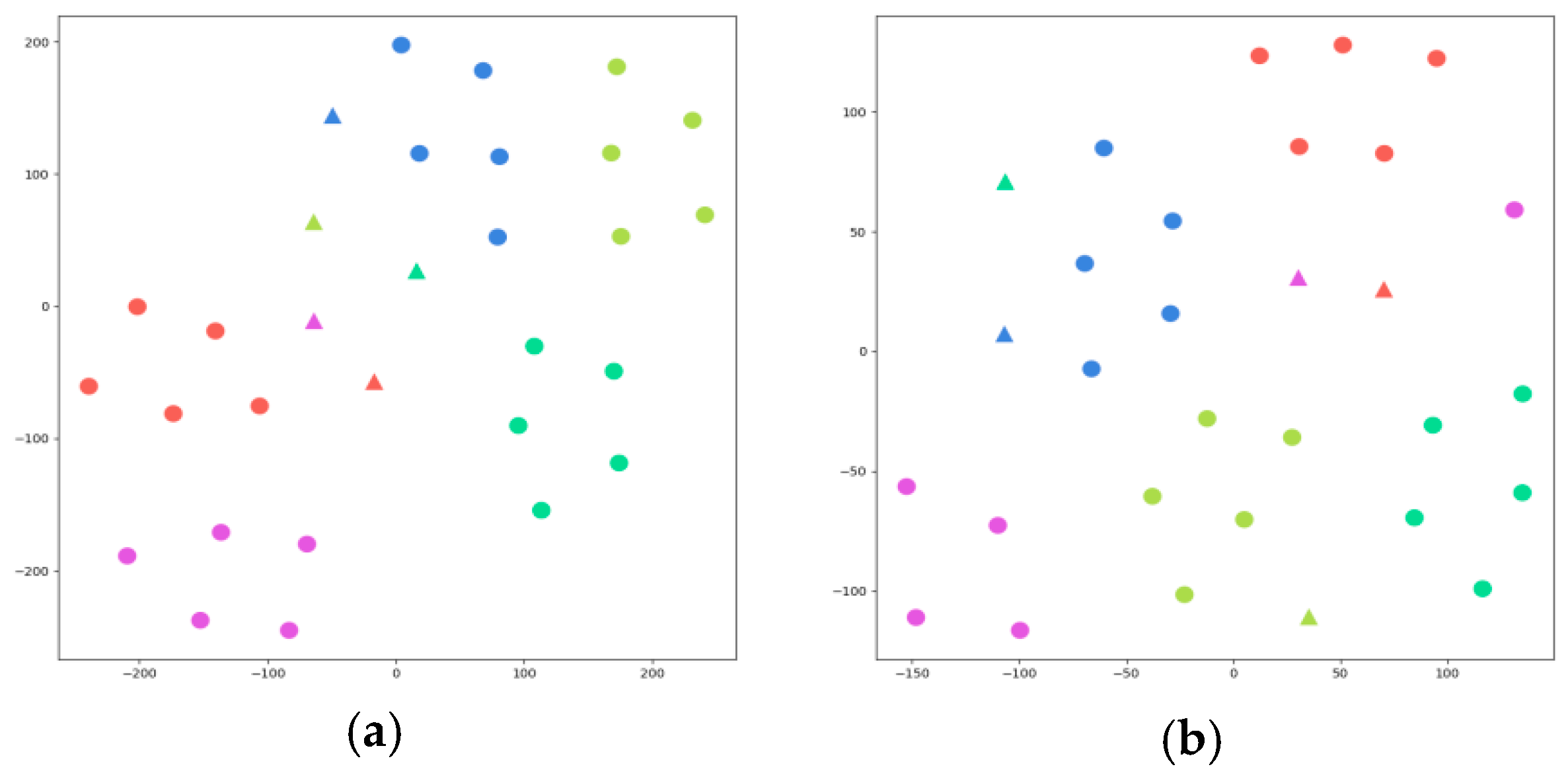

| Method | Backbone | 5 Way-1 Shot (%) | 5 Way-5 Shot (%) |
|---|---|---|---|
| MatchingNet | ConvNet | 43.56 ± 0.84 | 55.31 ± 0.73 |
| ProtoNet | ConvNet | 49.42 ± 0.86 | 68.20 ± 0.54 |
| RelationNet | ConvNet | 50.44 ± 0.82 | 65.32 ± 0.70 |
| R2D2 | ConvNet | 51.20 ± 0.78 | 68.20 ± 0.61 |
| MAML | ConvNet | 48.70 ± 1.84 | 63.11 ± 0.92 |
| Dynamic | ConvNet | 56.20 ± 0.86 | 71.94 ± 0.62 |
| GNN | ConvNet | 50.33 ± 0.36 | 66.41 ± 0.63 |
| TPN | ConvNet | 55.51 ± 0.93 | 69.86 ± 0.78 |
| Global | ConvNet | 53.21 ± 0.89 | 72.34 ± 0.74 |
| wDAE | WRN | 61.07 ± 0.15 | 76.75 ± 0.11 |
| CloserLook | Resnet18 | 51.75 ± 0.83 | 74.59 ± 0.64 |
| Meta-Transfer | ResNet12 | 61.20 ± 1.8 | 75.53 ± 0.80 |
| EGNN | ConvNet | 59.14 ± 0.71 | 76.37 ± 0.60 |
| ESMC(ours) | ConvNet | 65.97 ± 0.69 | 77.46 ± 0.44 |
| Model | EGNN | ESMC | |
|---|---|---|---|
| Method Mean Acc | |||
| No attention module is added | 59.14% | 65.97% | |
| ① | 59.34% | 62.83% | |
| ② | 57.50% | 66.12% | |
| ③ | 56.62% | 56.40% | |
| ④ | 59.68% | 67.31% | |
| Model | EGNN | ESMC | |
|---|---|---|---|
| Method Mean Acc | |||
| No attention module is added | 76.37% | 77.46% | |
| ① | 76.89% | 74.08% | |
| ② | 75.28% | 74.93% | |
| ③ | 75.35% | 74.89% | |
| ④ | 77.52% | 77.66% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhu, H.; Bi, Y.; Wu, Z.; Liu, Y.; Du, S. Few-Shot Classification Based on the Edge-Weight Single-Step Memory-Constraint Network. Electronics 2023, 12, 4956. https://doi.org/10.3390/electronics12244956
Shi J, Zhu H, Bi Y, Wu Z, Liu Y, Du S. Few-Shot Classification Based on the Edge-Weight Single-Step Memory-Constraint Network. Electronics. 2023; 12(24):4956. https://doi.org/10.3390/electronics12244956
Chicago/Turabian StyleShi, Jing, Hong Zhu, Yuandong Bi, Zhong Wu, Yuanyuan Liu, and Sen Du. 2023. "Few-Shot Classification Based on the Edge-Weight Single-Step Memory-Constraint Network" Electronics 12, no. 24: 4956. https://doi.org/10.3390/electronics12244956
APA StyleShi, J., Zhu, H., Bi, Y., Wu, Z., Liu, Y., & Du, S. (2023). Few-Shot Classification Based on the Edge-Weight Single-Step Memory-Constraint Network. Electronics, 12(24), 4956. https://doi.org/10.3390/electronics12244956






