A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
- The study and modeling of classic PID and optimal FPID controllers in relation to the PLIM that drives variable systems is presented in this study.
- To accomplish the working conditions, an FPID controller is suggested to maintain the speed of PRIM at the present settings.
- The simulation results of a direct trust control approach to PLIM control are explained.
- To compare the functioning of an FPID controller with a typical PID controller, operational indicators are offered, including steady state error (SSE), oscillation index (OI), overall steady state value (OSSV), and rise time index (RTI).
- These indices are used to calculate the controller rise time and motor linear speed.
1.3. Paper Organization
2. PLIM Dynamic Model with End Effects
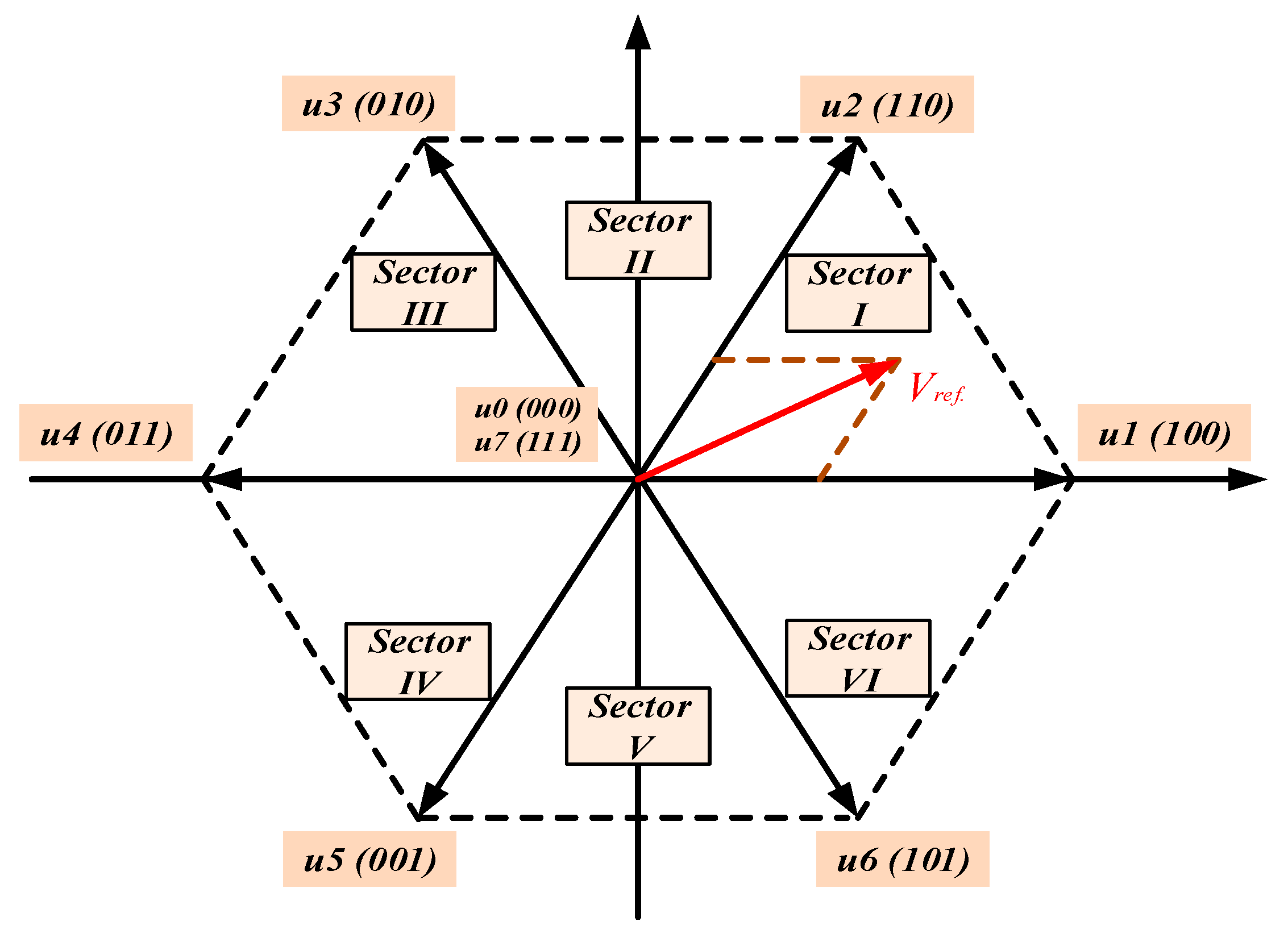
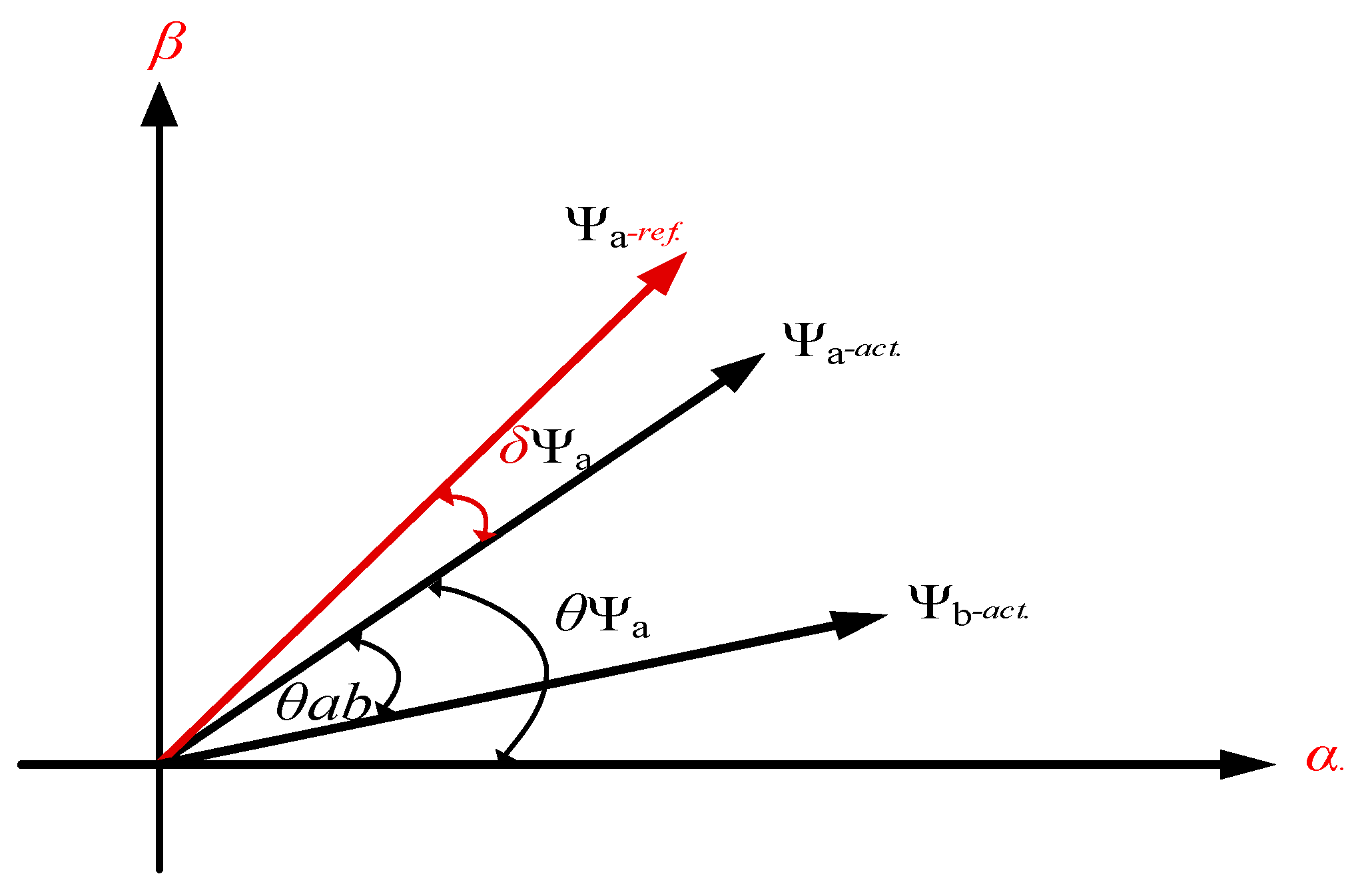
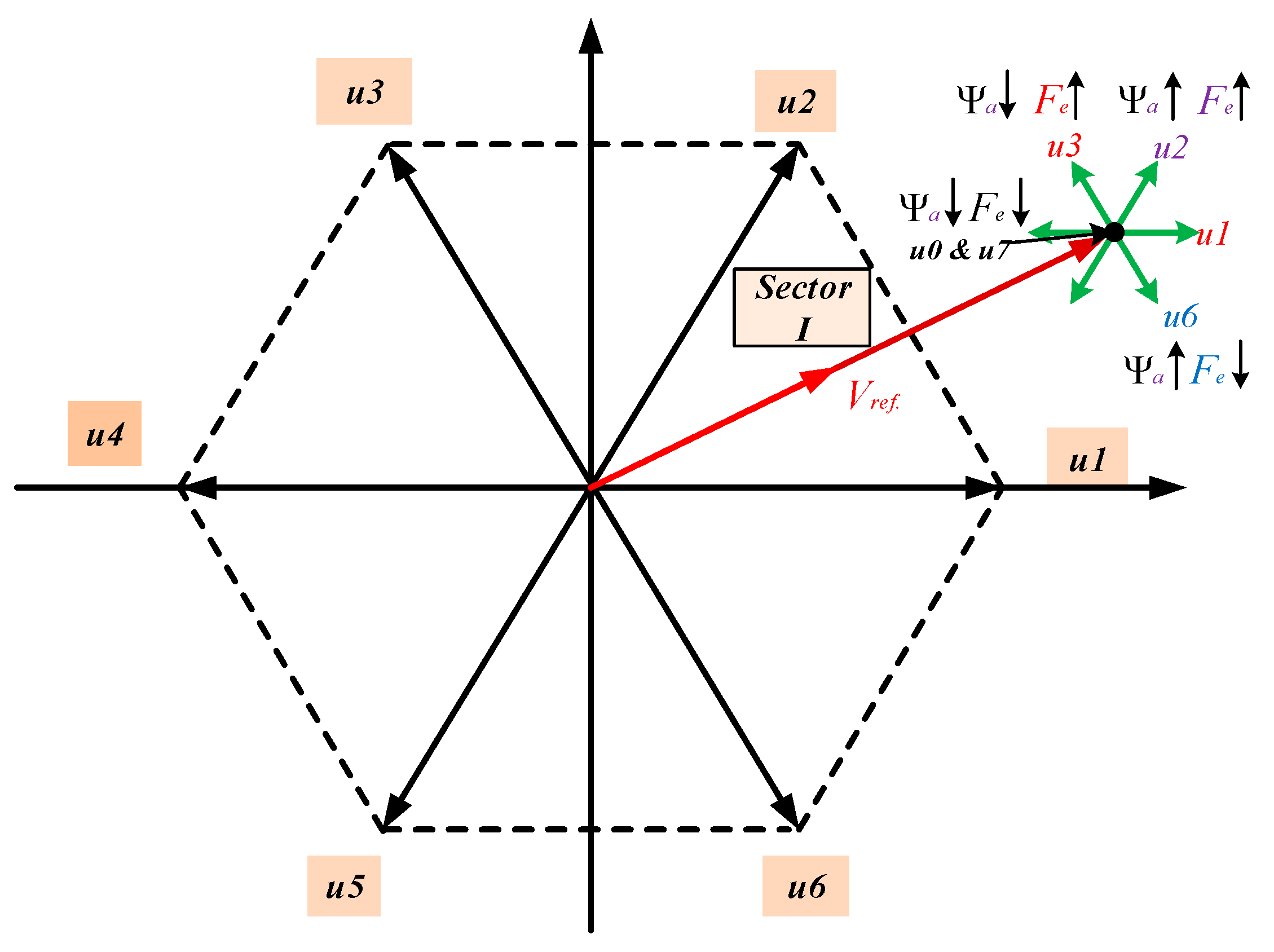
3. Direct Thrust Control of PLIM by Space-Vector Modulation
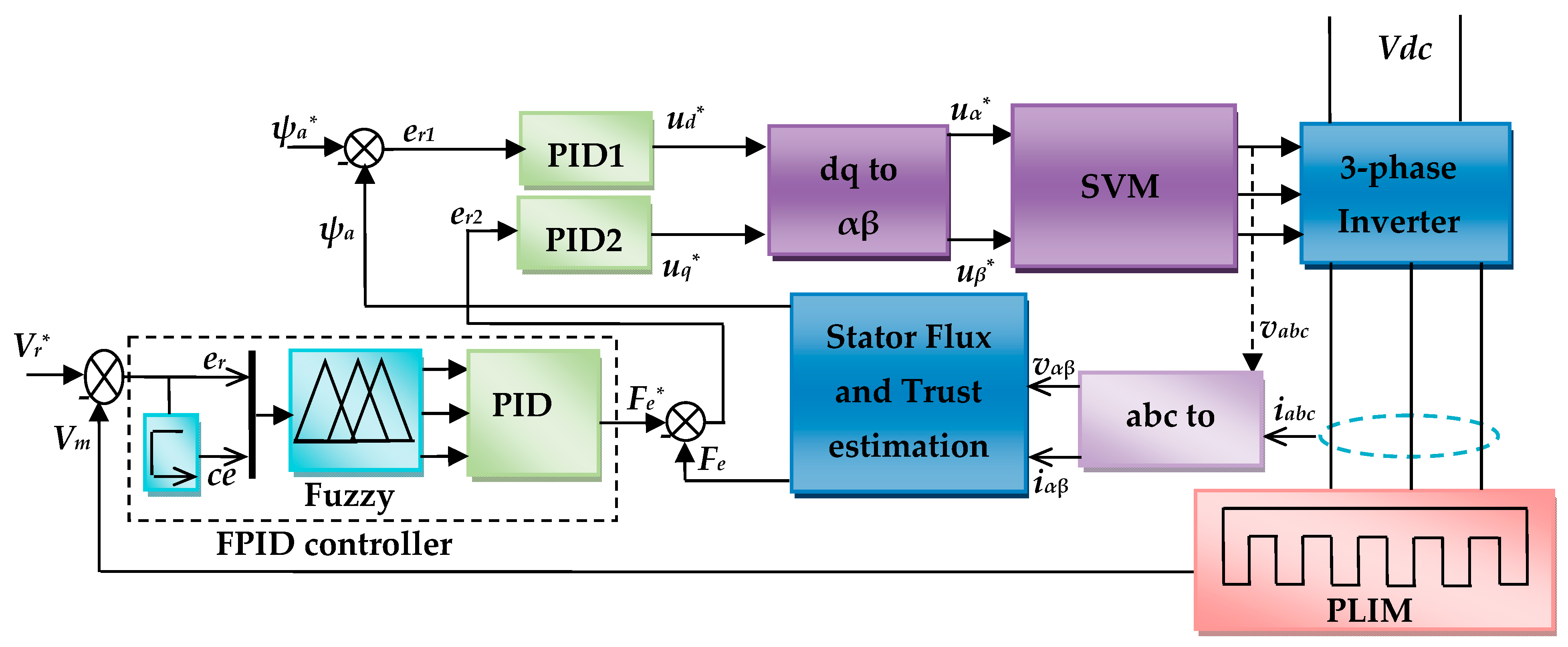
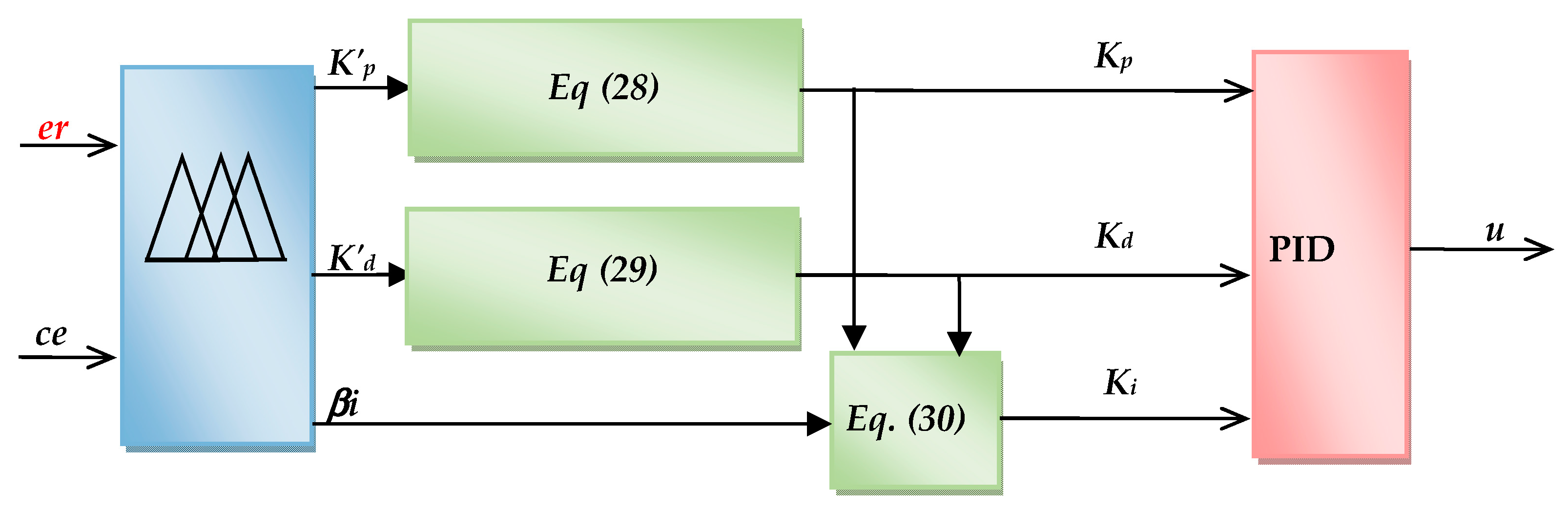
4. The Suggested Design Process for the PLIM Fuzzy Controller
4.1. Fuzzy-Based Control Strategy with Vector Control
4.2. Design of Closed-Loop Control Systems
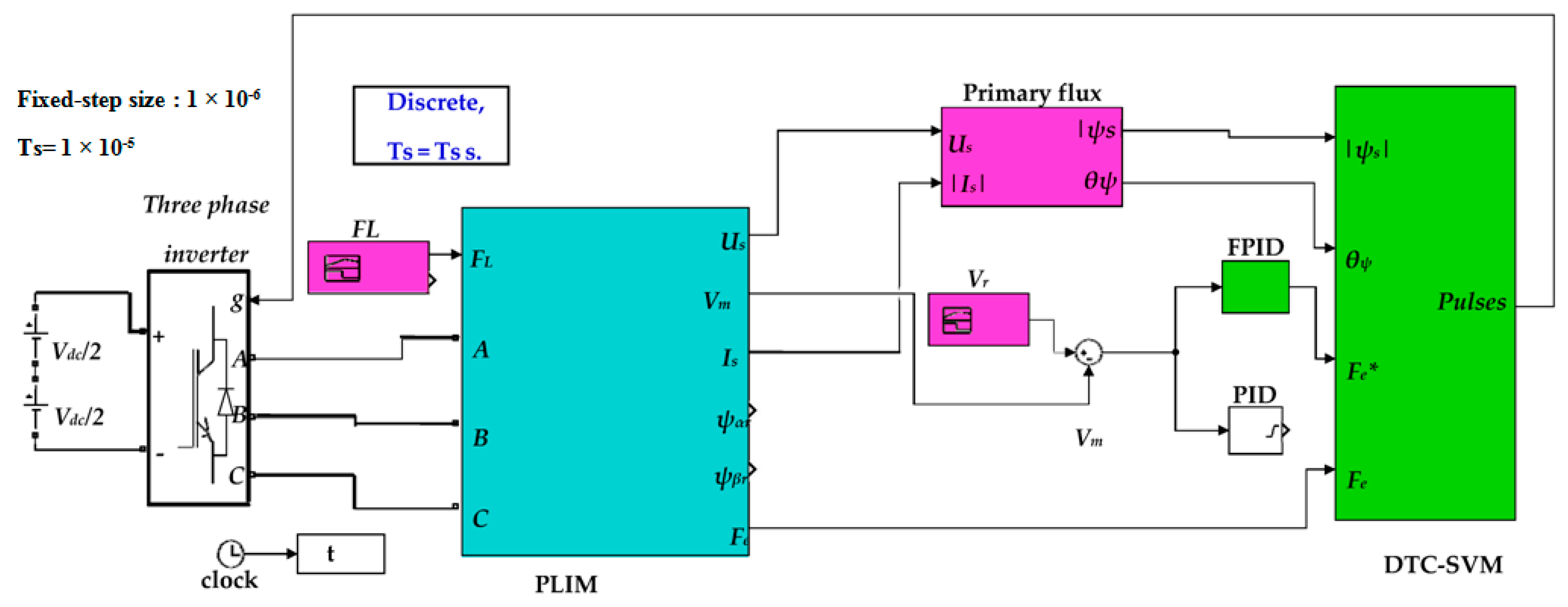
5. Applications
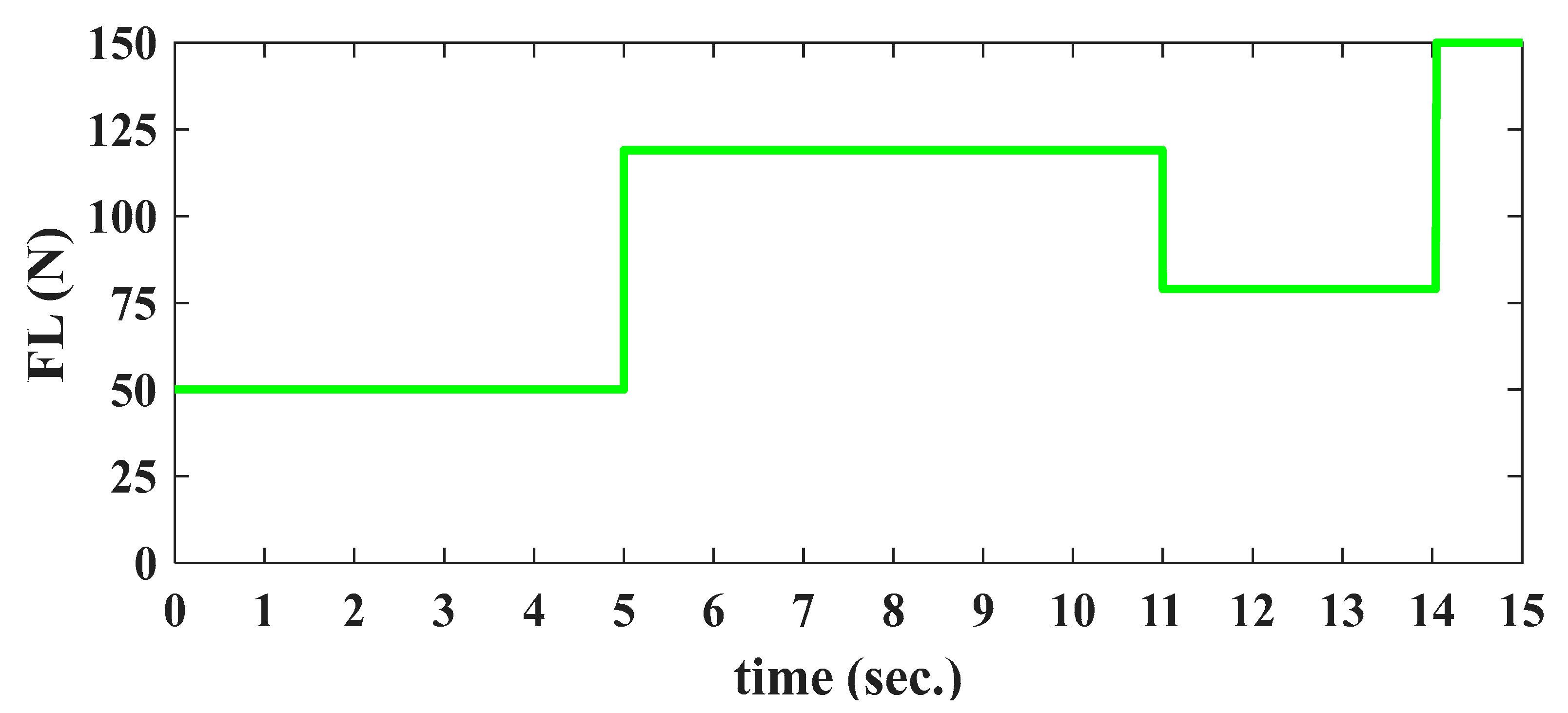
5.1. Simulated Cases
5.2. Proposed Evaluation Indices
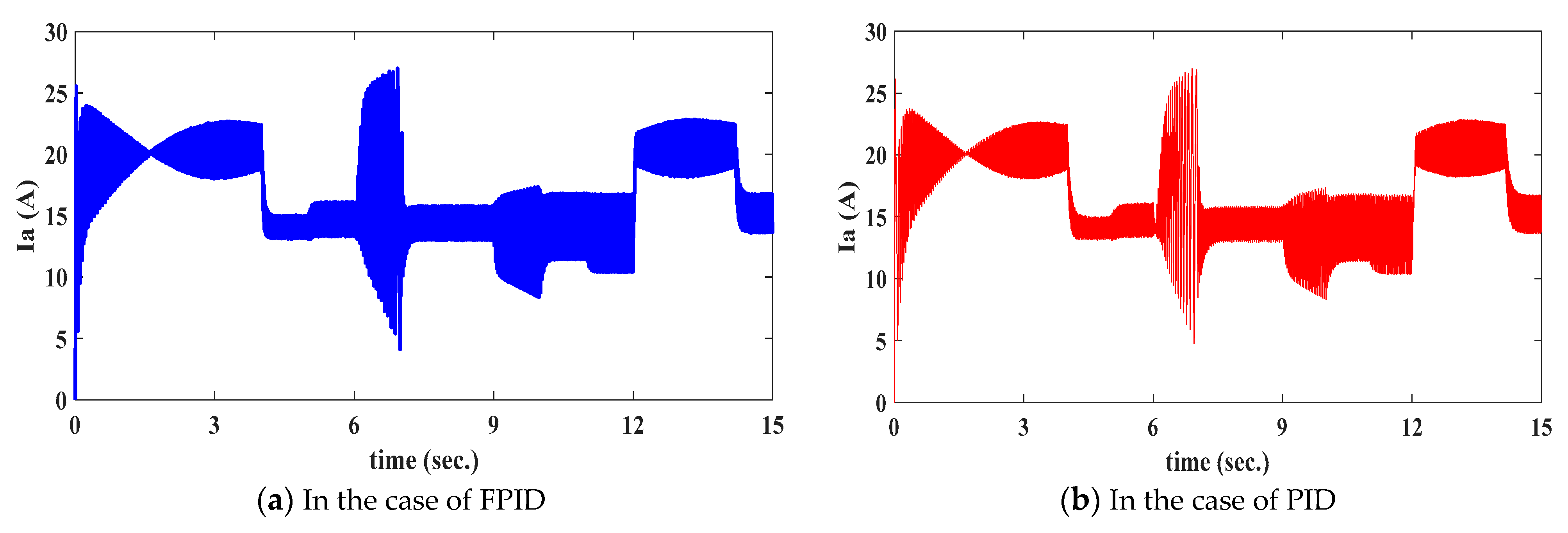
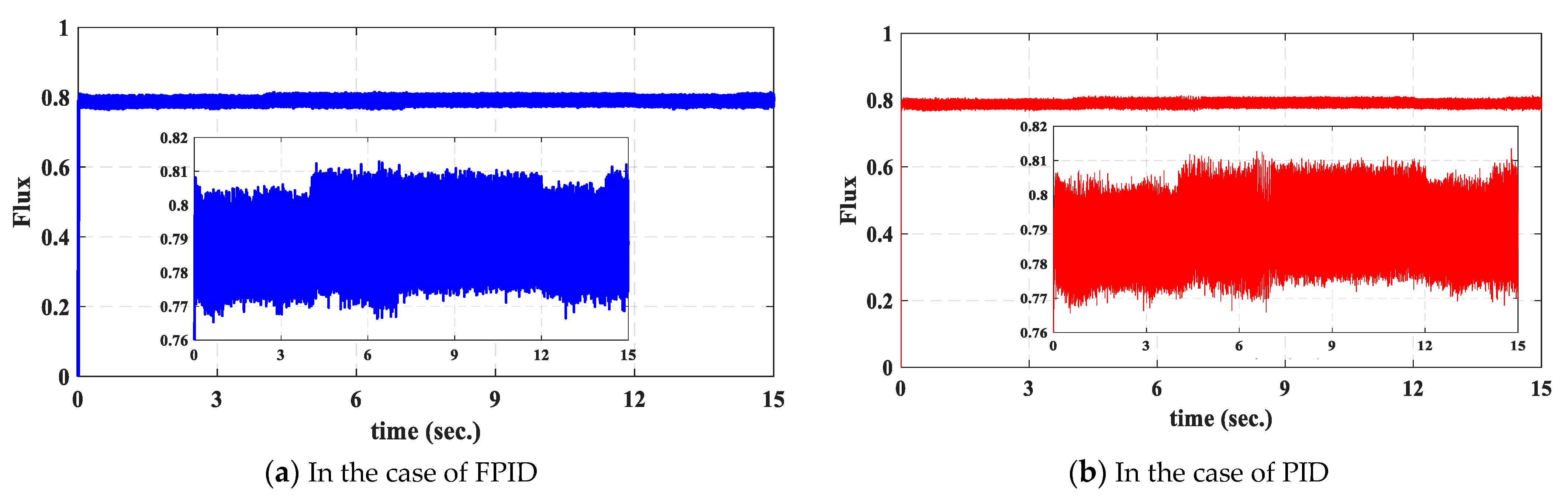
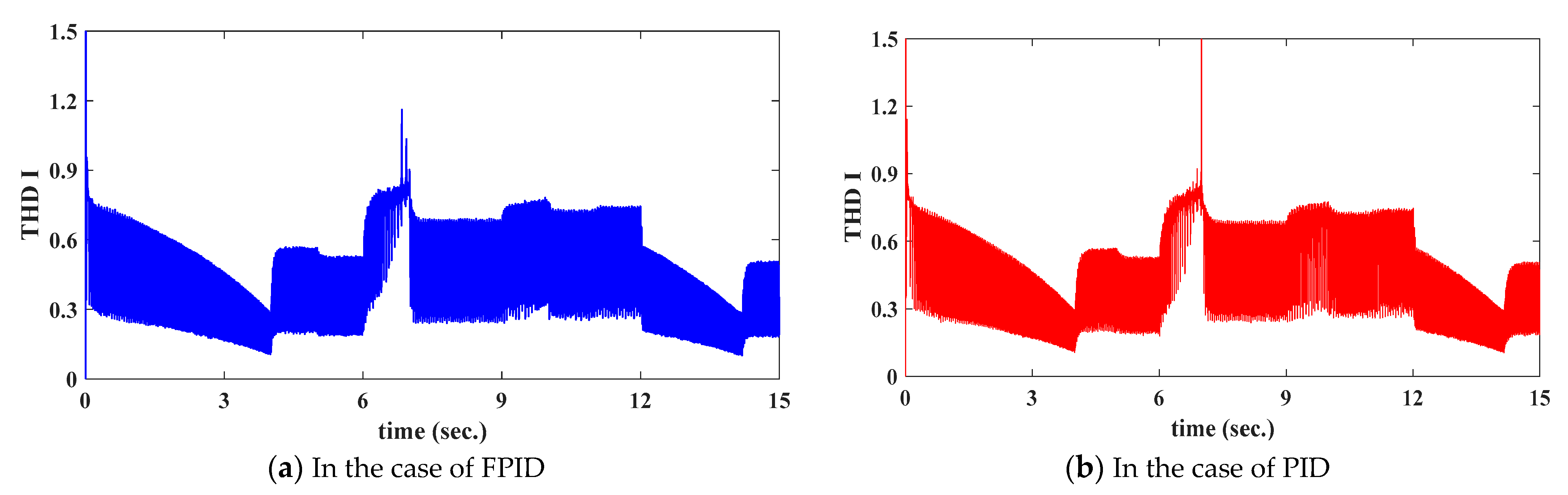
5.3. Results of Simulation Model
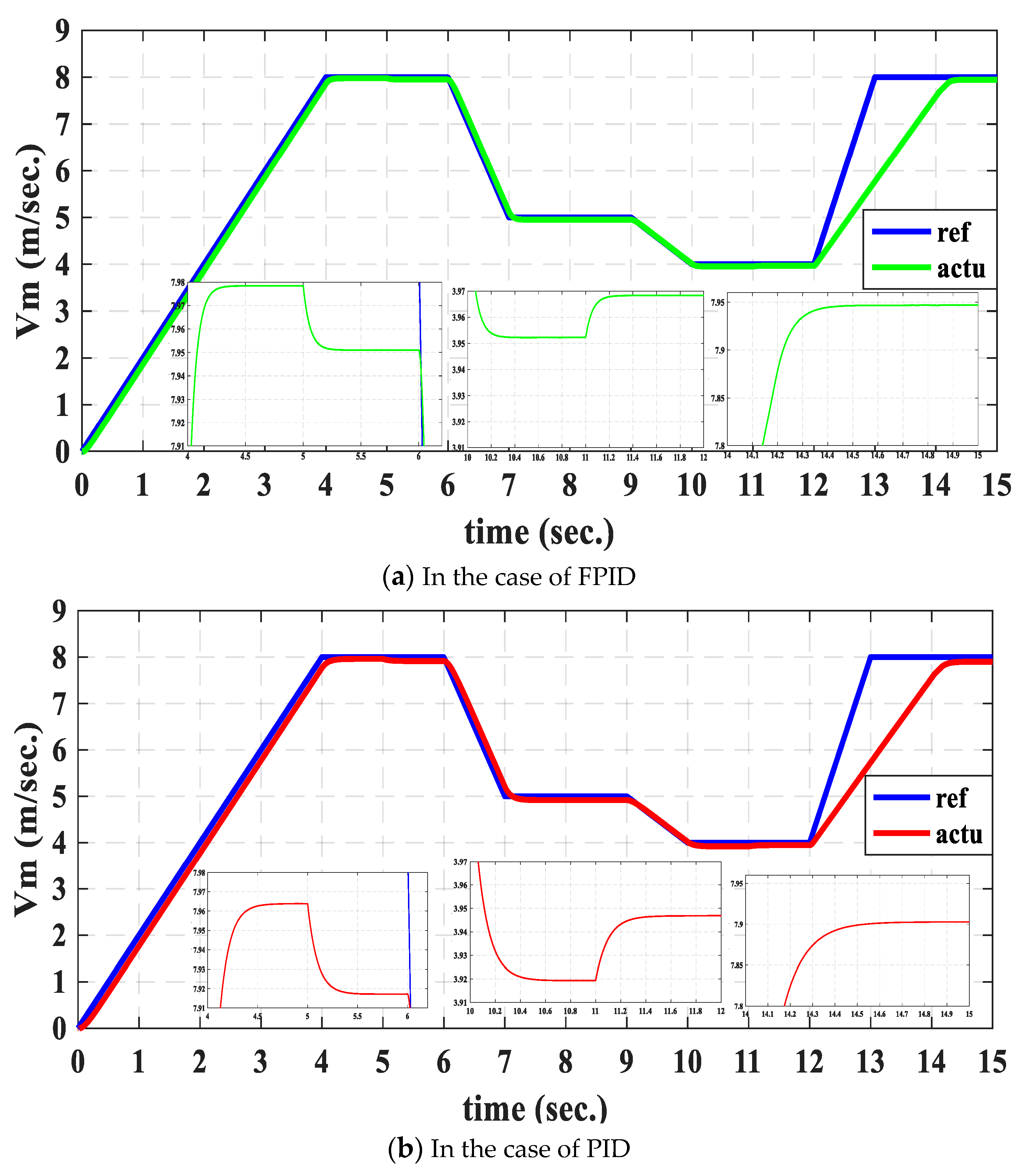
- For periods 2–4, using an FPID controller reduces speed oscillation and the resulting linear speed error.
- When compared to the suggested FPID controller, the RTI for modes 1–4 is lowered by 4.35%, 3.85%, 2.35%, and 1.35%, respectively.
- With a 38.9% reduction rate in the first period, the SSE for the speed signals decreased from 0.036 m/s to 0.022 m/s. When compared to a standard PID controller, the FPID controller’s rise time is lowered by 4.35%.
- Compared to the suggested FPID controller, the OI for modes 1–4 is lowered from 30 × 10−5 m/s to 7 × 10−5 m/s in the second period.
6. Conclusions
- A mathematical model is provided to examine and study the equivalent circuit diagram for both the PLIM and DTC-SVPWM inverters.
- A closed-loop linear motor speed control system based on fuzzy logic is provided for both high and low speed levels. The suggested FPID controller improves overall performance at over/under shoot speed, speed error, and rise time for low/high-speed working circumstances.
- For the cycle of operation, the suggested controller FPID is evaluated for different speeds of operation under different loading conditions.
- Four operational indices—individual steady state error, total steady state error, individual oscillation index, and total oscillation index—are used to evaluate the proposed fuzzy PID controller. The quality of the FPID compared to the PID for modes 1–4 is demonstrated by the reduction in RTI values by 4.35%, 3.85%, 2.35%, and 1.35%, respectively. With a decrease rate of 38.9% in the first period, the SSE of the velocity signals decreased from 0.036 m/s to 0.022 m/s. When comparing the rise time using the FPID compared to the PID controller, it was noted that it was reduced by 4.35%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Full name |
| PLIM | Poly phase linear induction machine |
| FPID | Fuzzy PID controller |
| DTC | Direct thrust control |
| PRIM | Poly-phase rotary induction machines |
| DTC-SVM | DTC with space-vector modulation |
| PID | Proportional–integral–derivative |
| RTI | Rise time index |
| OSSV | Overall steady state value |
| SSE | Steady state error |
| OI | Oscillation index |
| FOC | Field-oriented control |
References
- Wang, Y.; Liu, X.; Lu, W.; Wen, T.; Yu, F.; Wu, Q. Longitudinal Dynamic End Effect of Single-Sided Linear Induction Motor for Medium–Low Speed Maglev. J. Electr. Eng. Technol. 2021, 16, 2109–2117. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; Zaky, A.A.; Ali, M.M. Performance study of linear induction motor fed from perovskite solar cells based on GAMPPT. In Proceedings of the 202223rd International Middle East Power Systems Conference(MEPCON), Cairo, Egypt, 13–15 December 2022; pp. 1–7. [Google Scholar]
- Elmorshedy, M.F.; Xu, W.; Liu, Y. Speed Control of Linear Induction Motor with Thrust and Stator Flux Ripple Reduction. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 1789–1794. [Google Scholar]
- Xu, W.; Sun, G.; Wen, G.; Wu, Z.; Chu, P.K. Equivalent Circuit Derivation and Performance Analysis of a Single-Sided Linear Induction Motor Based on the Winding Function Theory. IEEE Trans. Veh. Technol. 2012, 61, 1515–1525. [Google Scholar] [CrossRef]
- Hung, C.-Y.; Liu, P.; Lian, K.-Y. Fuzzy Virtual Reference Model Sensorless Tracking Control for Linear Induction Motors. IEEE Trans. Cybern. 2013, 43, 970–981. [Google Scholar] [CrossRef] [PubMed]
- Rizk-Allah, R.M.; Abdelwanis, M.I.; El-Sehiemy, R.A.; Abd-Elrazek, A.S. An interior search algorithm based on chaotic and crossover strategies for parameter extraction of poly phase induction machines. Neural Comput. Appl. 2022, 35, 6647–6664. [Google Scholar] [CrossRef]
- Abdelwanis, M.I. Linear Induction Motor Parameter Estimation Based on Gray Wolves Optimization Algorithm. In Proceedings of the 2022 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022; pp. 1–6. [Google Scholar]
- Elmorshedy, M.F.; Almakhles, D.J.; El-Sousy, F.F. Modified primary flux linkage for enhancing the linear induction motor performance based on sliding mode control and model predictive flux control. IEEE Access 2003, 11, 26184–26198. [Google Scholar] [CrossRef]
- Zheng, Y.; Cao, Z.; Wang, S.; Man, Z.; Chuei, R. Extreme learning machine-based field-oriented feedback linearization speed control of permanent magnetic synchronous motors. Neural Comput. Appl. 2022, 34, 5267–5282. [Google Scholar] [CrossRef]
- Boucheta, A.; Bousserhane, I.K.; Hazzab, A.; Sicard, P.; Fellah, M.K. Speed Control of Linear Induction Motor using SlidingMode Controller Considering the End Effects. J. Electr. Eng. Technol. 2012, 7, 34–45. [Google Scholar] [CrossRef]
- Zou, J.; Xu, W.; Yu, X.; Liu, Y.; Ye, C. Multistep Model Predictive Control with Current and Voltage Constraints for Linear Induction Machine Based Urban Transportation. IEEE Trans. Veh. Technol. 2017, 66, 10817–10829. [Google Scholar] [CrossRef]
- Ali, M.M.; Xu, W.; Elmorshedy, M.F.; Liu, Y.; Dong, M. An Improved Finite-Set Model Predictive Current Control with Nonlinear Speed Regulator for Linear Induction Machine based on Linear Metro. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5141–5147. [Google Scholar]
- Abdelfatah, N.; Brahim, G. A Novel Lithium Ion Battery Autonomous Strategy Improvement Based on SVM-DTC for Urban Electric Vehicle under Several Speeds Tests. Majlesi J. Electr. Eng. 2011, 5, 40–45. [Google Scholar]
- Karuppannan, A.; Muthusamy, M. Wavelet neural learning-based type-2 fuzzy PID controller for speed regulation in BLDC motor. Neural Comput. Appl. 2021, 33, 13481–13503. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, R.; Zhou, S.; Liu, Z. Design and Analysis of a Drive System for a Series Manipulator Based on Orthogonal-Fuzzy PID Control. Electronics 2019, 8, 1051. [Google Scholar] [CrossRef]
- Xu, W.; Ali, M.M.; Elmorshedy, M.F.; Allam, S.M.; Mu, C. One Improved Sliding Mode DTC for Linear Induction Machines Based on Linear Metro. IEEE Trans. Power Electron. 2021, 36, 4560–4571. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, J.G.; Zhang, Y.; Li, Y.; Wang, Y.; Guo, Y. An improved equivalent circuit model of a single-sided linear induction motor. IEEE Trans. Veh. Technol. 2010, 59, 2277–2289. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Durairaj, S.; Padmavathi, S. A Performance Improvement of the Fuzzy Controller-Based Multi- Level Inverter-Fed Three-Phase Induction Motor with Enhanced Time and Speed of Response. J. Electr. Eng. Technol. 2021, 16, 1131–1141. [Google Scholar] [CrossRef]
- Du, L.; Lu, X.; Yu, M.; Dong, B.; Li, Y. Experimental Investigation on Fuzzy PID Control of Dual Axis Turntable Servo System. Procedia Comput. Sci. 2018, 131, 531–540. [Google Scholar] [CrossRef]
- Mohan, V.; Chhabra, H.; Rani, A.; Singh, V. An expert 2 DOF fractional order fuzzy PID controller for nonlinear systems. Neural Comput. Appl. 2019, 31, 4253–4270. [Google Scholar] [CrossRef]
- Nithilasaravanan, K.; Thakwani, N.; Mishra, P.; Kumar, V.; Rana, K.P.S. Efficient control of integrated power system using self-tuned fractional-order fuzzy PID controller. Neural Comput. Appl. 2019, 31, 4137–4155. [Google Scholar] [CrossRef]
- Kudinov, Y.I.; Kolesnikov, V.A.; Pashchenko, F.F.; Pashchenko, A.F.; Papic, L. Optimization of Fuzzy PID Controller’s Parameters. Procedia Comput. Sci. 2017, 103, 618–622. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Q.; Zhang, R. Improved fuzzy PID controller design using predictive functional control structure. ISA Trans. 2017, 71, 354–363. [Google Scholar] [CrossRef]
- Verma, O.P.; Manik, G.; Jain, V.K. Simulation and control of a complex nonlinear dynamic behavior of multi-stage evaporator using PID and Fuzzy-PID controllers. J. Comput. Sci. 2018, 25, 238–251. [Google Scholar] [CrossRef]
- Ustun, S.; Demirtas, M. Optimal tuning of PI coefficients by using fuzzy-genetic for V/f controlled induction motor. Expert Syst. Appl. 2008, 34, 2714–2720. [Google Scholar] [CrossRef]
- Ranjbar, N.A.; Kholerdi, H.A. Chaotification and fuzzy PI control of three-phase induction machine using synchronization approach. Chaos Solitons Fractals 2016, 91, 443–451. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Zhang, G.; Sheng, X. Fuzzy Auto-adjust PID Controller Design of Brushless DC Motor. Phys. Procedia 2012, 33, 1533–1539. [Google Scholar] [CrossRef][Green Version]
- Fathy, A.; Kassem, A.M.; Abdelaziz, A.Y. Optimal design of fuzzy PID controller for deregulated LFC of multi-area power system via mine blast algorithm. Neural Comput. Appl. 2020, 32, 4531–4551. [Google Scholar] [CrossRef]
- Kumar, J.; Kumar, V.; Rana, K.P.S. Fractional-order self-tuned fuzzy PID controller for three-link robotic manipulator system. Neural Comput. Appl. 2020, 32, 7235–7257. [Google Scholar] [CrossRef]
- deAlmeida, J.F.M.; Valdenebro, L.R.; Bin, E. Fuzzy logic based maximum torque control for asingle-phase induction motor. In Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society (Cat. No. 99CH37029), SanJose, CA, USA, 29 November–3 December 1999; Volume 2, pp. 619–624. [Google Scholar]
- Ozkop, E.; Akpinar, A.S.; Okumus, H.I. Direct torque control for Linear Induction Motor. In Proceedings of the 12th International Middle-East Power System Conference, Aswan, Egypt, 12–15 March 2008; pp. 373–376. [Google Scholar]
- Wang, D. Sensorless Fuzzy Variable Speed Control with Torque Optimization for the Improvements of Single Phase Capacitor-RunInduction Motors. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010; pp. 325–328. [Google Scholar]
- Bouhoune, K.; Yazid, K.; Boucherit, M.S. Hybrid neural-fuzzy control of the single-phase induction machine. In Proceedings of the 2011 International Conference on Communications, Computing and Control Applications (CCCA), Hammamet, Tunisia, 3–5 March 2011; pp. 1–5. [Google Scholar]
- Chen, D.; Fang, Z.; Li, S. A Novel BSO Algorithm for Three-Layer Neural Network Optimization Applied to UAV Edge Control. Neural Process. Lett. 2023, 55, 1–20. [Google Scholar] [CrossRef]
- Nanda, A.B.; Bhattacharya, T.K. High performance vector control of single phase induction motor drives based on rotorMEMF. In Proceedings of the 2011 International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 1–5. [Google Scholar]
- Chhabra, H.; Mohan, V.; Rani, A.; Singh, V. Robust nonlinear fractional order fuzzy PD plus fuzzy I controller applied to robotic manipulator. Neural Comput. Appl. 2020, 32, 2055–2079. [Google Scholar] [CrossRef]
- Bhandari, K.S.; Cho, G.H. A resource Oriented Route Selection Framework Using Contextual Information Based on Fuzzy Logic. Electronics 2019, 8, 1023. [Google Scholar] [CrossRef]
- Lin, F.-J.; Wai, R.-J. Hybrid control using recurrent fuzzy neural network for linear induction motor servo drive. IEEE Trans. Fuzzy Syst. 2001, 9, 102–115. [Google Scholar] [CrossRef]
- Elmorshedy, M.F.; Xu, W.; Ali, M.M.; Liu, Y.; Allam, S.M. High Performance Speed Sensorless Finite-Set Predictive Thrust Control of a Linear Induction Motor based on MRAS and Fuzzy Logic Controller. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 3039–3044. [Google Scholar]
- Xu, W.; Zhu, J.G.; Zhang, Y.; Li, Z.; Li, Y.; Wang, Y.; Guo, Y.; Li, Y. Equivalent Circuits for Single-Sided Linear Induction Motors. IEEE Trans. Ind. Appl. 2010, 46, 2410–2423. [Google Scholar] [CrossRef]
- Yu, H.; Fahimi, B. A Direct Control Scheme to Achieve Maximum Acceleration in Linear Induction Motors. In Proceedings of the IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 977–982. [Google Scholar] [CrossRef]
- Wogi, L.; Ayana, T.; Morawiec, M.; Jąderko, A. A Comparative Study of Fuzzy SMC with Adaptive Fuzzy PID for Sensorless Speed Control of Six-Phase Induction Motor. Energies 2022, 15, 8183. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, H.; Mu, Y.; Yao, F.; Zhang, X. A novel fuzzy PID velocity control of linear elevator driven by the permanent magnet linear synchronous motor. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 1539–1542. [Google Scholar]
- Tao, Y.; Zheng, J.; Lin, Y.; Wang, T.; Xiong, H.; He, G.; Xu, D. Fuzzy PID control method of deburring industrial robots. J. Intell. Fuzzy Syst. 2015, 29, 2447–2455. [Google Scholar] [CrossRef]
- Yun, J.; Sun, Y.; Li, C.; Jiang, D.; Tao, B.; Li, G.; Liu, Y.; Chen, B.; Tong, X.; Xu, M. Self-adjusting force/bit blending control based on quantitative factor-scale factor fuzzy-PID bit control. Alex. Eng. J. 2022, 61, 4389–4397. [Google Scholar] [CrossRef]
- Barakat, M. Optimal design of fuzzy-PID controller for automatic generation control of multi-source interconnected power system. Neural Comput. Appl. 2022, 34, 18859–18880. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; El-Sehiemy, R.A.; Hamida, M.A. Parameter estimation of permanent magnet synchronous machines using particle swarm optimization algorithm. Rev. Roum. Sci. Techn.-Électrotechn. Énerg. 2022, 67, 377–382. [Google Scholar]

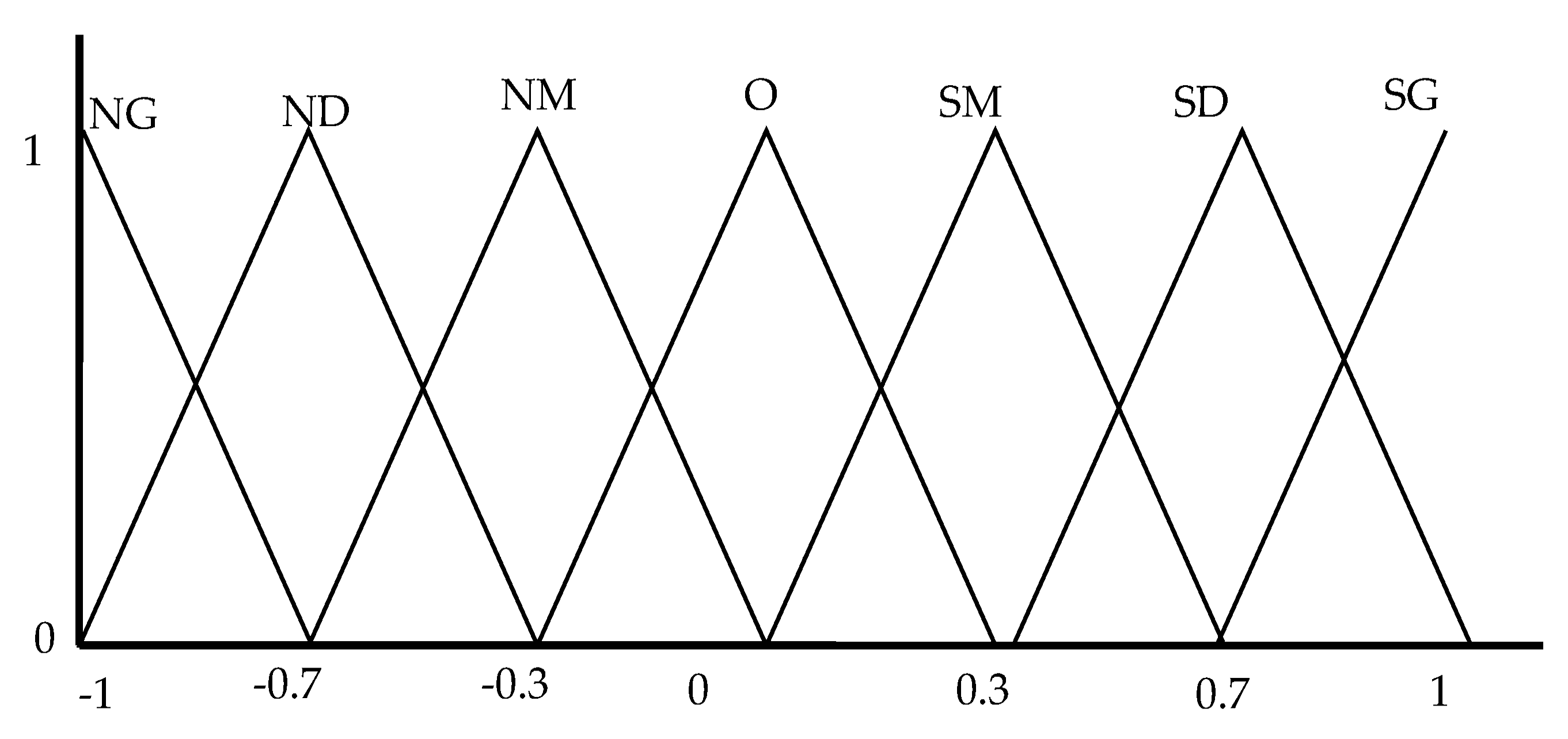
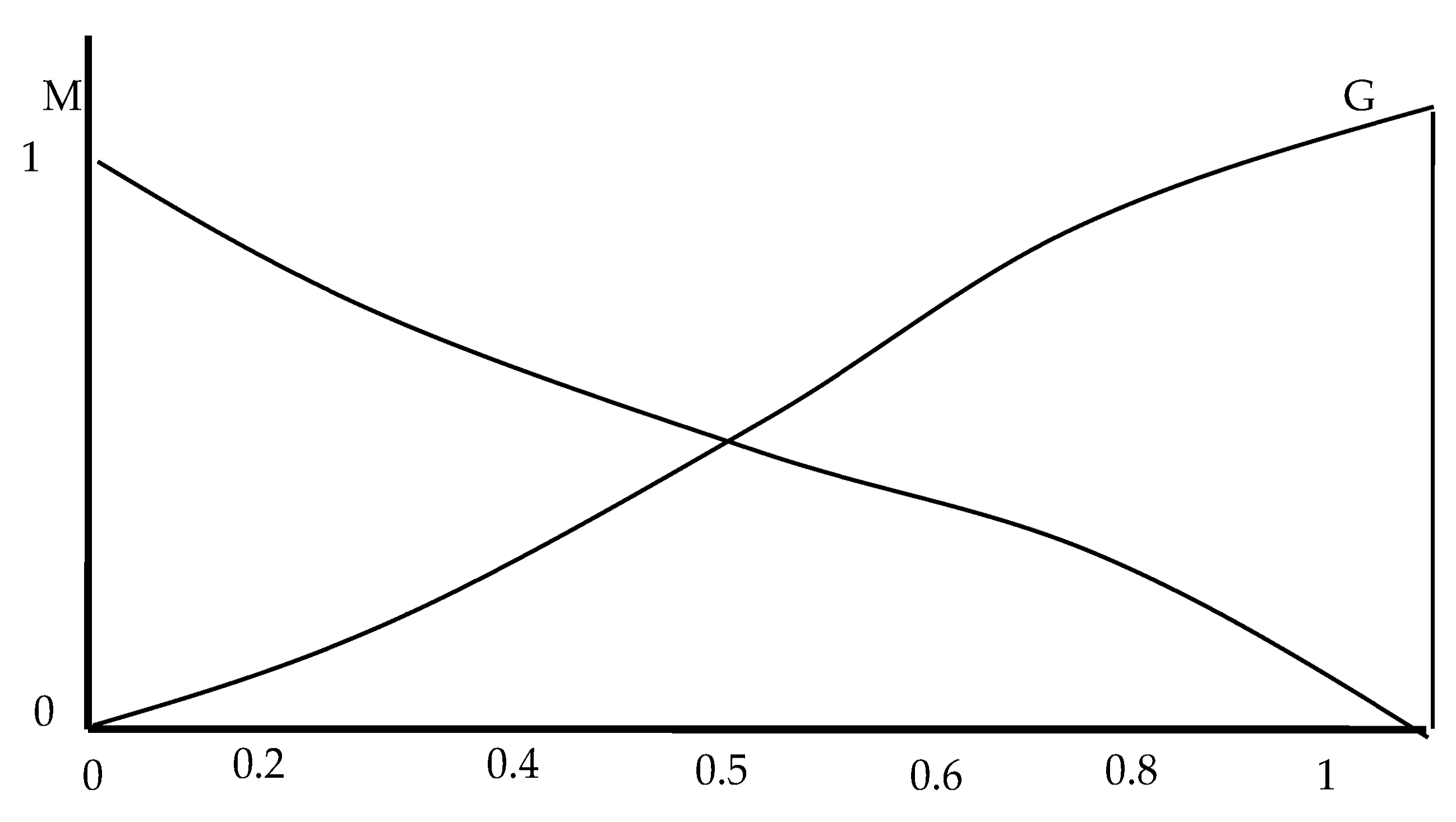
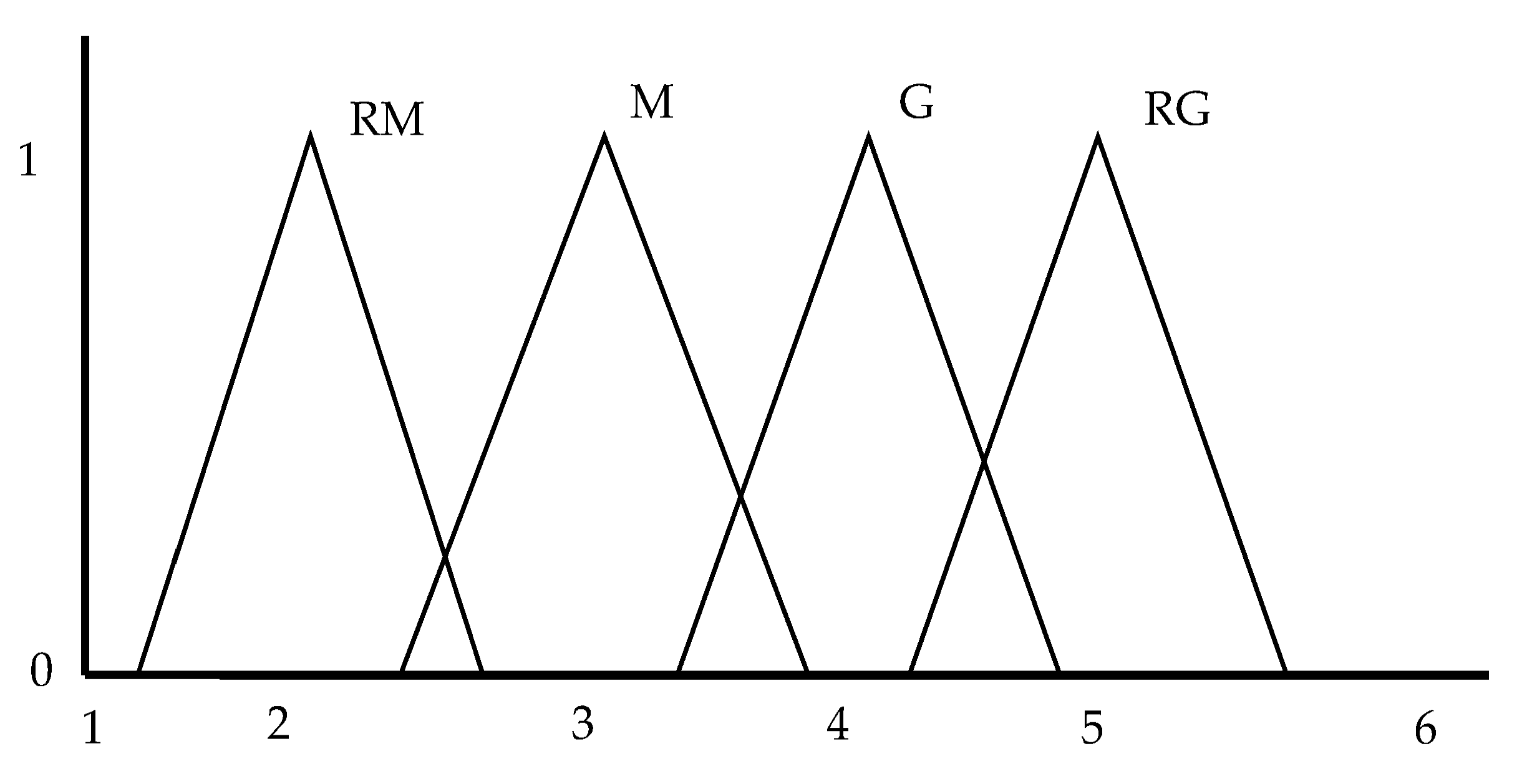



| er | ce | kp | kd | βi | er | ce | Kp | kd | βi |
|---|---|---|---|---|---|---|---|---|---|
| NG, SG | NG | G | M | RM | NM, SM | NG | M | G | G |
| ND | G | M | RM | ND | M | G | M | ||
| NM | G | M | RM | NM | G | G | M | ||
| O | G | M | RM | O | G | M | RM | ||
| SM | G | M | RM | SM | G | G | M | ||
| SD | G | M | RM | SD | M | G | M | ||
| SG | G | M | RM | SG | M | G | G | ||
| ND, SD | NG | M | G | M | O | NG | M | G | RG |
| ND | G | G | M | ND | M | G | G | ||
| NM | G | M | RM | NM | M | G | M | ||
| O | G | M | RM | O | G | G | M | ||
| SM | G | M | RM | SM | M | G | M | ||
| SD | G | G | M | SD | M | G | G | ||
| SG | G | G | M | SG | M | G | RG |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Input voltage, UN | 180 V | kp | 2114.5 |
| Motor current, IN | 22 A | ki | 3.59 |
| motor speed, vN | 11 m/s | kd | 0.0 |
| Resistance of Primary, Ra | 1 Ω | kp1 | 3000 |
| Resistance of Secondary, Rb | 2.4 Ω | ki1 | 50 |
| Secondary leakage inductance, Llb | 0.0043 H | kd1 | 0.0 |
| leakage inductance of Primary, Lla | 0.0114 H | kp2 | 1000 |
| Primary Pole pitch, τ | 0.1485 m | ki2 | 5 |
| Length of Primary, ls | 1.3087 m | kd2 | 0.0 |
| Motor power, PN | 3 kW | Sample time Ts | 1 × 10−5 s |
| Thrust force, FN | 280 N | ψa* | 0.8 |
| Period | Index | PID | FPID | ||
|---|---|---|---|---|---|
| 1 | RTI sec | 4.6 | 5.5 | 4.4 | 5.38 |
| OSSV m/s | 7.964 | 7.917 | 7.978 | 7.951 | |
| OI m/s | 6 × 10−5 | 12 × 10−5 | 4 × 10−5 | 8 × 10−5 | |
| SSE m/s | 0.036 | 0.083 | 0.022 | 0.049 | |
| 2 | RTI sec | 7.8 | 7.5 | ||
| OSSV m/s | 4.918 | 4.952 | |||
| OI m/s | 30 × 10−5 | 7 × 10−5 | |||
| SSE m/s | 0.082 | 0.048 | |||
| 3 | RTI sec | 10.65 | 11.6 | 10.4 | 11.4 |
| OSSV m/s | 3.9193 | 3.9468 | 3.9523 | 3.9683 | |
| OI m/s | 14 × 10−5 | 11 × 10−5 | 12 × 10−5 | 10 × 10−5 | |
| SSE m/s | 0.0807 | 0.0532 | 0.0477 | 0.0317 | |
| 4 | RTI sec | 14.8 | 14.6 | ||
| OSSV m/s | 7.9027 | 7.9468 | |||
| OI m/s | 15 × 10−5 | 9 × 10−5 | |||
| SSE m/s | 0.0973 | 0.0532 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelwanis, M.I.; El-Sousy, F.F.M.; Ali, M.M. A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor. Electronics 2023, 12, 4955. https://doi.org/10.3390/electronics12244955
Abdelwanis MI, El-Sousy FFM, Ali MM. A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor. Electronics. 2023; 12(24):4955. https://doi.org/10.3390/electronics12244955
Chicago/Turabian StyleAbdelwanis, Mohamed I., Fayez F. M. El-Sousy, and Mosaad M. Ali. 2023. "A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor" Electronics 12, no. 24: 4955. https://doi.org/10.3390/electronics12244955
APA StyleAbdelwanis, M. I., El-Sousy, F. F. M., & Ali, M. M. (2023). A Fuzzy-Based Proportional–Integral–Derivative with Space-Vector Control and Direct Thrust Control for a Linear Induction Motor. Electronics, 12(24), 4955. https://doi.org/10.3390/electronics12244955








