Abstract
Stratospheric drones operating in extreme environments are very important for predicting reliability and are high-efficiency, high-performance, and lightweight power units. Multilevel inverters are suitable for application as power conversion units for stratospheric drones. A guideline is needed to evaluate whether it is suitable for practical application from a reliability perspective among various multilevel topologies. Existing reliability prediction models cannot reflect the operating characteristics of multilevel inverters. In this paper, we analyze the driving characteristics of each topology from the perspective of half-bride, which is the basic configuration of multilevel inverters, and we propose a fault tree analysis (FTA) design with three operating modes. The proposed method has the advantage of being able to easily analyze the failure rate by expanding to single-phase and three-phase and to analyze the failure rate according to changes in modulation index (MI) and power factor (PF). The failure rates of the proposed method and the part count method are analyzed using MIL-HDBK-217F. We also analyze the impact of different various operating characteristics on the failure rate. From a reliability perspective, we provide a variety of guidelines for selecting a multilevel topology that fits the operation conditions.
1. Introduction
The stratospheric drone has recently been studied for weather observation, communication relay role, surveillance, and reconnaissance at an altitude of 18 to 20 km. The stratospheric drones use solar energy and energy storage to maintain altitude for long stays. To maintain the target altitude for a long period in the stratosphere, high efficiency and high performance of the power unit are required, and it is very important to improve and predict reliability for mission performance in extreme environments [1,2,3].
The pulse width modulation (PWM) method, which is widely applied to motor drives and power conversion, has the advantage of simultaneously controlling the magnitude and frequency of the output voltage and is relatively easy to implement. Owing to the switching operation, the output waveform of the inverter includes various harmonic components in addition to the fundamental harmonic components. Harmonics can cause various disturbances to other peripherals due to electromagnetic inductance, motor noise and torque pulsation, and current leakage due to common mode voltage. Therefore, harmonics cause the reliability and efficiency of the entire system to deteriorate. Therefore, it is necessary to minimize the harmonic component caused by PWM switching [4,5].
A common method is to configure a filter at the inverter output, but the larger the filter, the worse the control response characteristics and the larger the overall size and weight. For stratospheric drones that need to be reliable and lightweight, it may be effective to apply multilevel inverters to suppress harmonic components [6,7]. Therefore, it is important to select reliable circuit topologies for long-term flight and mission performance in the stratosphere.
To improve reliability, a risk analysis of the operating environment of major parts such as semiconductor switching elements and capacitors is important. Among the indicators of reliability, the failure rate is defined as the number of failures per unit of time for an individual part. Mean time between failure (MTBF), an indicator of average life, is a reciprocal expression of the failure rate [8,9]. The most common method for predicting lifespan is accelerated life testing. This is not based on the failure rate of the part unit, but rather a method of predicting the lifespan of the actual operating environment by testing the completed system in a harsh environment. However, it requires a large number of samples for accurate lifetime prediction and is not suitable for the topology selection stage [10,11,12]. Other reliability prediction models include Markov models, binomial distributions, and part count models.
The Markov model is useful for quantifying the failure rate for systems with frequent failures, but it is impossible to evaluate when the failure rate of the devices varies depending on the time of use. In addition, there is the problem that the size of the state space increases exponentially with the number of parts [13,14,15,16]. The binomial distribution model is a reliability analysis method based on probability distribution and evaluates reliability by probabilistically analyzing system failures using the DeMoivre equation [17,18]. The part count model is a method of prediction by assuming that the subsystem has a serial structure and that the failure rate of individual parts is constant. A simple prediction method is useful in the initial design stage, but the condition that the failure rate of the unit part is constant can make a big difference from the actual failure rate [19,20,21]. These reliability models can interpret the reliability of the inverter itself but cannot consider the operating characteristics. To find the optimal circuit topology, a more accurate lifetime prediction and failure risk analysis that reflects the driving and operating conditions in detail is needed. To compensate for this problem, we would like to apply a fault tree technique that can analyze failures by reflecting the type of components, connection status, and operating characteristics of the multi-level inverter. The fault tree analysis may reflect the operation characteristics of the analysis target by logically using the relationship between the causes of system failure to create a fault tree and calculating the probability of system failure. Therefore, logical and probabilistic quantitative results can be derived [22,23,24,25,26,27,28].
In this paper, we analyze the behavioral characteristics of three types of multilevel half-bridge topologies and propose three modes of fault-tree for each topology. Based on MIL-STD-217F, we present and calculate the criteria for selecting part failure rates for major parts. The failure rates of the proposed FTA and part count fault analysis (PCA) using the part count method are compared for each topology. We analyze the impact of changes in temperature, MI, and PF on failure rates and provide a variety of guidelines to select the appropriate topology for stratospheric drones from a reliability perspective.
2. Fault Tree Design Based on the Operating Characteristics of Multilevel Inverter
The main failure factors of multilevel inverters are voltage unbalance and short circuits on the DC link, overvoltage on the AC output side, overcurrent, voltage imbalance, etc. Semiconductor switching devices that repeat ON/OFF at high switching frequencies and capacitors that repeat charging and discharging accordingly are major parts and weak reliability devices. In addition, failures may occur due to electronic components such as a control board and a communication board. In this paper, we analyze the operation characteristics based on the half-bridge, which is a basic module in the inverter, and we design a fault tree that logically shows the relationship with the failure causes. Through this, the failure probability is analyzed for each circuit topology of the multilevel inverter, and the lifetime is predicted.
2.1. Analyze the Mode of Operation for Each Topology
It analyzes the operation of three topologies commonly used in multilevel inverters: Diode Clamped Circuit (DCC), Flying Capacitor Circuit (FCC), and T-Type Neutral Clamped circuit (TNPC). To reflect the failure conditions according to the operating conditions in the fault tree design, it is classified into four types according to the polarity of the output voltage and current and analyzed.
2.1.1. Analysis of DCC Topology Operation
DCC requires a clamping diode to obtain the m-level phase voltage and initially has the advantage that the entire DC link voltage can be charged using a single power source. In addition, switching operation and control techniques are simpler than other multilevel inverters. However, as the number of levels increases, the number of serial connections of diodes increases, making it difficult to keep the voltage of each capacitor uniform and making it difficult to modularize each bridge. The number of switching required to make the m-level is (m−1), the number of capacitors of the direct current link is (m−1), and the number of clamping diodes is (m−1) × (m−2) [29,30,31,32]. Figure 1 shows the operation mode of the DCC. It is classified according to the direction of the output voltage and the output current and analyzes the switching pattern and current flow when forming a 1-level voltage and in zero-level freewheeling mode.
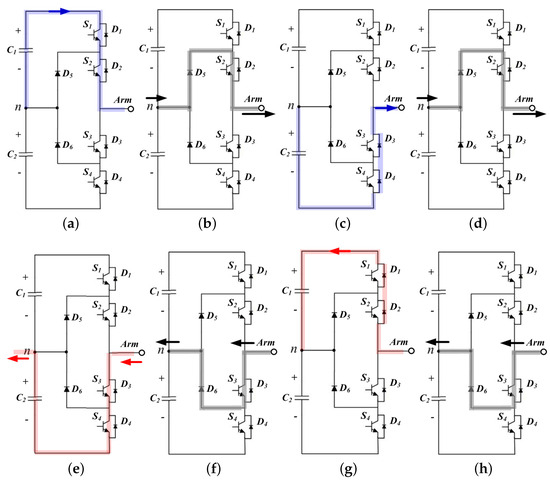
Figure 1.
The operation mode of DCC, (a) +1 level at , , (b) zero-level at , , (c) −1 level at , , (d) zero-level at , , (e) −1 level at , , (f) zero-level at , , (g) +1 level at , , (h) zero-level at , .
Figure 1 shows the current flow and switching state by dividing the operation into eight types depending on the output voltage, output current polarity, and level formation to analyze the operation of the DCC topology. The switching operation and power flow according to the eight operating states from Figure 1a–h are summarized in Table 1.

Table 1.
Analysis of DCC operating modes.
When the level is formed, if the output voltage and current polarity are the same, power flows from the DC link to the output terminal and the capacitor goes into discharge mode. Conversely, if the output voltage and current polarity are different, power flows from the output terminal to the DC link, and the capacitor goes into charging mode. At zero level, current flows due to the clamping action of the diode connected to the neutral point, and the output terminal and capacitor are separated.
2.1.2. Analysis of FCC Topology Operation
The FCC is similar in structure to the DCC but uses a capacitor instead of a clamping diode to create the zero-level, allowing for a more modular structure. In addition, by using a capacitor, the internal voltage level can obtain a margin, enabling a stable power supply. However, as the number of levels increases, the control becomes more complicated, switching losses increase, and a large number of capacitors are required. The number of switching required to make the m-level is 2 (m−1), the number of capacitors of the direct current link is (m−1), and the number of flying capacitors is (m−1) (m−2)/2 [33,34,35]. Figure 2 shows the operation mode of the FCC topology, which is analyzed by dividing it into voltage and the current directions, zero-level, and 1-level.
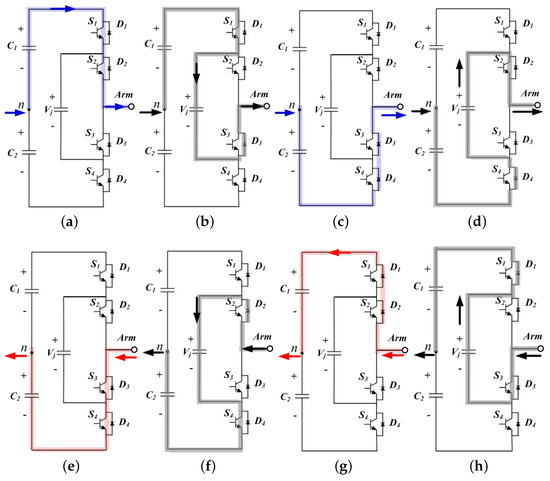
Figure 2.
The operation mode of FCC, (a) +1 level at , , (b) zero-level at , , (c) −1 level at , , (d) zero-level at , , (e) −1 level at , , (f) zero-level at , , (g) +1 level at , , (h) zero-level at , .
Figure 2 shows the current flow and switching state by dividing the operation into eight depending on the output voltage, output current polarity, and level formation to analyze the operation of the FCC topology. The switching operation and power flow according to the eight operating states from Figure 2a–h are summarized in Table 2. When the level is formed, the charge/discharge state of the dc link capacitor and the power flow are the same as in DCC, and the flying capacitor is separated from the output stage. When at zero level, zero level is created by the flying capacitor. If the polarity of the output voltage and current are the same, it is discharged, and in the opposite case, it is charged.

Table 2.
Analysis of FCC operating modes.
2.1.3. Analysis of TNPC Topology Operation
The TNPC is a variant of DCC and consists of four switching elements per leg, which can reduce two diodes. Compared to DCC or FCC, it has the advantage of having fewer series switching devices for one-level output, and even compared to a two-level topology, the voltage applied to the switching devices is halved, which reduces switching losses. However, when implementing more than 5-levels, it is difficult to increase it in a modular form compared to other multi-level inverters, and switching patterns and control are difficult [36,37,38,39,40].
Figure 3 shows the current flow and switching state by dividing the operation into eight types depending on the output voltage, output current polarity, and level formation to analyze the operation of the FCC topology. The switching operation and power flow according to the eight operating states from Figure 3a–h are summarized in Table 3. When the level is formed, the capacitor charging/discharging operation and power flow according to the polarity of the output voltage and current are the same as the DCC. When the level is zero, the output terminal and the capacitor are separated by the operation of S2 and S3 and the clamping operation of D2 and D3 at the neutral point.
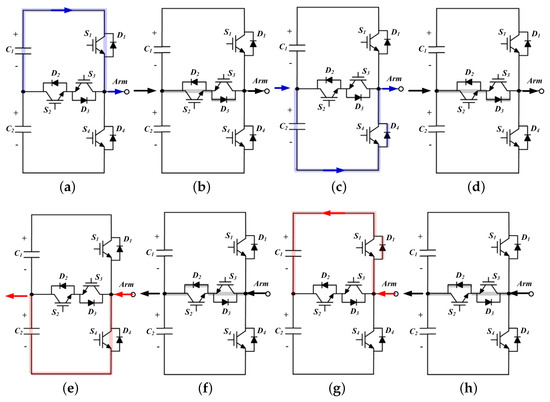
Figure 3.
The operation mode of TNPC, (a) +1 level at , , (b) zero-level at , , (c) −1 level at , , (d) zero-level at , , (e) −1 level at , , (f) zero-level at , , (g) +1 level at , , (h) zero-level at , .

Table 3.
Analysis of TNPC operating modes.
2.2. Design a Fault Tree for Each Topology
In this chapter, we design a fault tree that considers the risks that reflect the operating characteristics of the half-bridge for each topology. FTA is a fault tree design method that logically analyzes the relationship between the causes of power converter failures and obtains the probability of a failure of the system. This allows you to derive probabilistic and quantitative results to respond to risks in your system.
Looking at the operation status of each topology analyzed in Section 2.1, the output voltage is repeated at +1 level and zero-level based on one cycle of the output voltage, and the DC link capacitor is charged or discharged depending on the arm current direction. In the other half cycle, the power voltage is repeated at −1 level and zero-level, and the charging and discharging of the DC link capacitor is determined according to the direction of the current. It can be found that the operations of the switching device, diode, and capacitor are complementary operations according to the polarity of the output voltage. Therefore, the design of the fault tree is divided into three categories: “1 level capacitor charging failure”, “1 level capacitor discharging failure”, and “zero level failure”, and each lower level event is designed. For each mode, the failure analysis focuses on the parts connected to the closed circuit where the current is conducted and does not account for conditions where two or more parts fail simultaneously.
2.2.1. DCC Fault Tree Design
Figure 4 shows the fault tree considering the operating characteristics when in 1-level capacitor charging mode. Each sub-step is defined based on 1-level voltage formation and capacitor charging. The [Level formation fault] is designed as an OR-gate combination of [Diode switching failure] and [IGBT S3 switching failure]. The [Diode switching failure] event is independent of the IGBT S1 and S2 control failures, the current path is opened in the event of a D1 or D2 failure and no output voltage level is formed. The [IGBT S3 switching failure] event means that the output voltage will be at 0 level when IGBT S3 fails to switch off. Causes related to IGBT switching-off failure are caused by IGBT self-failure, switching signal failure in the controller, and short circuits between the IGBT collector–emitter. The [Capacitor charging function fault] event is caused by the loss of the capacitor charging function, drift, or damage to the enclosure.
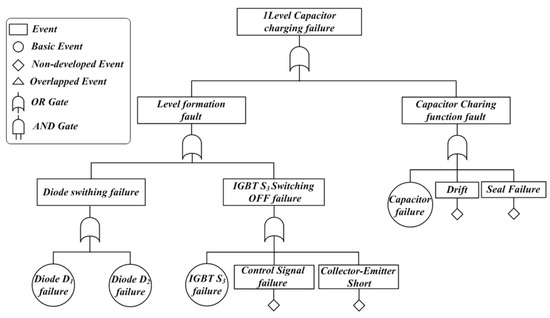
Figure 4.
Fault-tree of 1-Level capacitor charging faulure at DCC.
Figure 5 shows the fault tree considering the operation characteristics when in 1-level capacitor discharging mode. Each sub-step is defined based on 1-level voltage formation and capacitor discharge. The [Level formation failure] event is designed as an OR-gate combination of the [IGBT S1 switching ON failure] event and the [IGBT S2 switching ON failure] event, and when IGBT S1 or S2 ON fails, the current path is open and the output voltage level is not formed. Causes related to IGBT switching ON failure are caused by IGBT self-failure, switching signal error in the controller, short circuit between gate-emitter, and open between collector-emitter. The [Capacitor discharging function fault] is designed as an OR-gate combination of the [Capacitor discharging failure] event and the [IGBT S3 switching ON failure] event. The [Capacitor discharge failure] event may cause level formation to fail due to capacitor failure. The [IGBT S3 switching ON failure] event can cause C1 to be short-circuited through S1, S2, S3, and D6 when IGBT S3 is turned OFF, resulting in device failure and level failure.
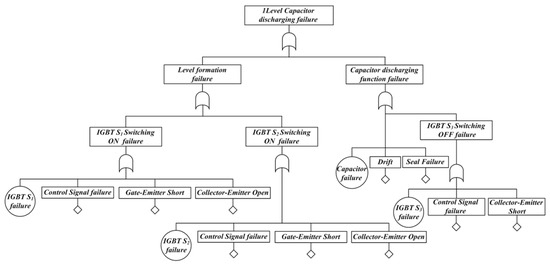
Figure 5.
Fault tree of 1-Level capacitor discharging failure at DCC.
Figure 6 shows the fault tree considering the operation characteristics when in zero-level mode. Each sub-step is defined based on level voltage formation and capacitor function failure. The [Level formation failure] is designed as an OR-gate combination of [D5 failure] event, [IGBT S2 switching ON failure] event, and [IGBT S1 switching OFF failure] event. In case of D5 failure or IGBT S2 ON failure, the current path is opened to make the zero level. In case of IGBT S1 OFF failure, current is delivered to the output stage through C1 to form 1 level. The [capacitor function failure] event can cause C2 to be short-circuited through D5, S2, S3, and S4 when IGBT S4 OFF fails, resulting in device failure and level failure.
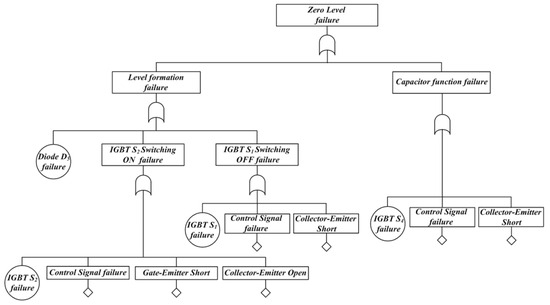
Figure 6.
Fault tree of zero-level failure at DCC.
2.2.2. FCC Fault Tree Design
Figure 7 shows a fault tree considering the operation characteristics when in 1-level capacitor charging mode. Each sub-step is defined based on 1-level voltage formation and flying capacitor and capacitor charging. The [Level formation fault] event is independent of the IGBT S1 and S2 control failure, and the output voltage level is not formed because the current path is open when D1 or D2 fails. The [capacitor function failure] event is designed as an OR-gate combination of IGBT S3 and S4 switching OFF failure. When IGBT S3 OFF fails, is short-circuited through S2 and S3, causing device failure and level failure. When IGBT S4 OFF fails, voltage is applied to , causing failure and level failure. The [CAPACITOR DISCHARGE FAILURE] event may cause the level formation to fail due to capacitor failure.
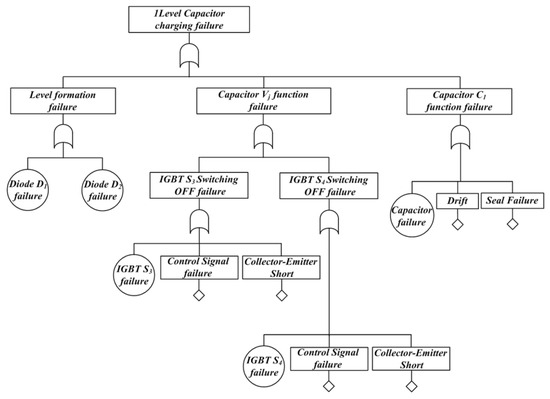
Figure 7.
Fault tree of 1-Level capacitor charging failure at FCC.
Figure 8 shows the fault tree considering the operation characteristics when in 1-level capacitor discharging mode. Each sub-step is defined based on 1-level voltage formation and flying capacitor and capacitor discharging. The [Level formation fault] event occurs when IGBT S1 or S2 ON fails, the current path is open and the output voltage level is not formed. The [capacitor function failure] event is designed as an OR-gate combination of IGBT S3 and S4 switching OFF failure and has the same failure cause as the flying capacitor event in Figure 7. The [Capacitor discharge failure] event is a capacitor failure that can cause level formation to fail.
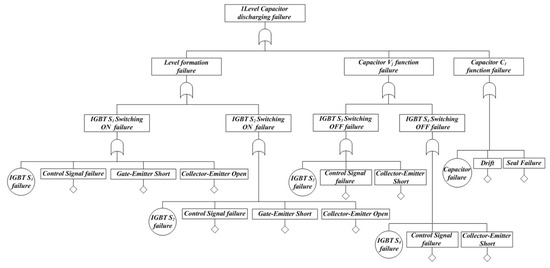
Figure 8.
Fault tree of 1-Level capacitor discharging failure at FCC.
Figure 9 shows the fault tree considering the operation characteristics when in zero-level mode. Each sub-step is defined based on 1-level voltage formation, flying capacitor, and capacitor discharge. The [Level formation fault] event is designed as an OR-gate combination of the [D3 failure] event, the [IGBT S1 switching ON failure] event, and the [IGBT S2 switching OFF failure] event. In case of D3 failure or IGBT S1 ON failure, the current path to create the zero level is opened and the zero leveler is not formed. In the case of IGBT S2 OFF failure, the current is delivered to the output stage through C1, so the zero level is not formed. In case of IGBT S1 or S2 ON failure, the current path is open and no output voltage level is formed. The [capacitor function failure] event is designed as an OR-gate combination of IGBT S3 and S4 switching OFF failure and has the same failure cause as the flying capacitor event in Figure 7. The [capacitor discharge failure] event is a capacitor failure that can cause the level formation to fail. In the [capacitor function failure] event, voltage is applied to when S4 OFF fails, causing failure and level failure. And when fails, level formation may fail. The [capacitor C1 function failure] event can cause the same level of formation failure when C1 fails.
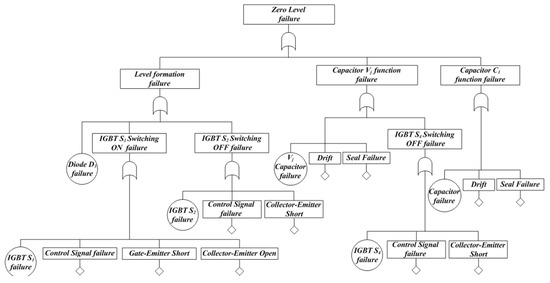
Figure 9.
Fault tree of zero-level failure at FCC.
2.2.3. TNPC Fault Tree Design
Figure 10 shows the fault tree considering the operation characteristics when in level 1 capacitor charging mode. Each sub-step is defined based on 1-level voltage formation and capacitor charging. The [Level formation fault] event is designed as an OR-gate combination of the [D1 failure] event and the [IGBT S3 switching OFF failure] event. In case of D1 failure, regardless of IGBT S1 control failure, the current path is open and the output voltage level is not formed. In the case of IGBT S3 OFF failure, the current is conducted to S3 and D2, resulting in a zero level. The [capacitor function failure] event occurs when IGBT S4 switching OFF fails, and a short circuit occurs with C1 and C2 through S1 and S2, resulting in component failure and level failure. If the C1 capacitor itself fails, the level formation may fail.
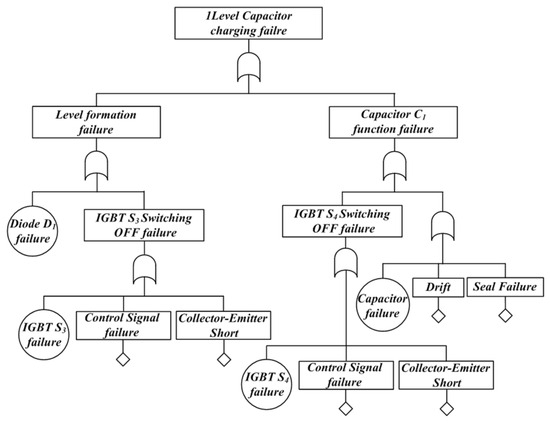
Figure 10.
Fault tree of 1-Level capacitor charging failure at TNPC.
Figure 11 shows a fault tree considering the operation characteristics when in 1-level capacitor discharging mode. Each sub-step is defined based on 1-level voltage formation and capacitor discharge. The [Level formation fault] event is designed as an OR-gate combination of the [IGBT S1 switching ON failure] event and the [IGBT S3 switching OFF failure] event. In case of IGBT S1 ON failure, the current path is open and the output voltage level is not formed. When IGBT S3 OFF fails, current is conducted to S3 and D2, causing C1 to be short-circuited, resulting in part failure and level failure. The [capacitor function failure] event has the same failure cause as the C1 capacitor event in Figure 10.
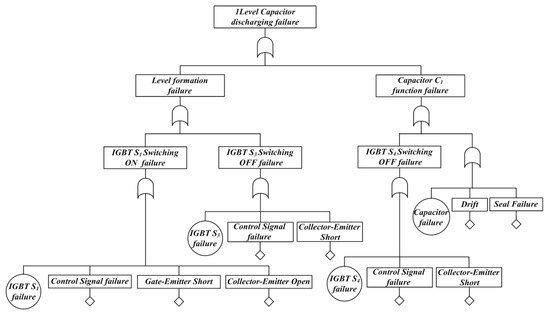
Figure 11.
Fault tree of 1-Level capacitor discharging failure at TNPC.
Figure 12 shows the fault tree considering the operation characteristics in zero-level mode. Each sub-step is defined based on the 1-level voltage formation and capacitor function. The [Level formation fault] event is designed as an OR-gate combination of the [D1 failure] event, the [IGBT S2 switching ON failure] event, and the [IGBT S1 switching OFF failure] event. In the case of IGBT S1 OFF failure, the current is delivered to the output terminal through C1 so that zero-level is not formed. In the case of IGBT S2 ON failure or D3 failure, the current path is open and no output voltage level is formed. The [capacitor function failure] event occurs when IGBT S4 OFF fails and C2 is short-circuited through S2, D3, and S4, causing device failure and level failure.
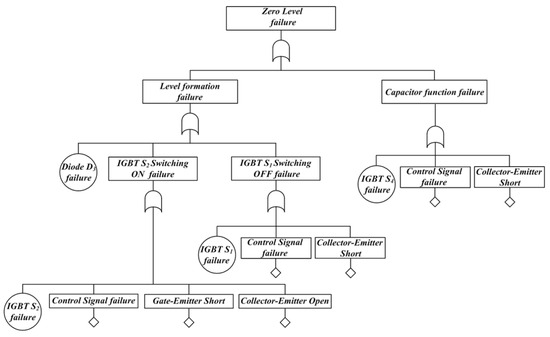
Figure 12.
Fault tree of zero-level failure at TNPC.
2.3. Part Failure Rate Based on MIL-HDBK-217F
To calculate the failure rate of the failure tree for each topology by reflecting the failure rate in the basic event of the failure tree, it is necessary to calculate the part failure rate for the main parts, IGBT, diode, and capacitor [41,42]. The stratospheric 3-phase multilevel inverter has a rated power of 3000 W and an IGBT rating of 250 V, 55 A. The diode is an IGBT internal body diode, and the zero-level diode of the DCC is rated at 250 V, 40 A. The capacitor specifications reflected in the design have a capacity of 680 μF and an insulation withstand voltage of 250 V. Regarding temperature, the junction temperature of the switching device and the ambient temperature of the capacitor vary depending on the loss and heat dissipation structure. Since many factors other than temperature must be reflected in the failure rate, we would like to analyze trends while setting the temperature as the same for each topology. The junction temperature of the switching element is analyzed in the range of 25 °C to 180 °C, and the ambient temperature of the capacitor is interpreted in the range of −40 °C to 115 °C.
2.3.1. IGBT Failure Rate
MIL-HDBK-217F does not provide failure rates for IGBT components. Since an IGBT is internally composed of a bipolar junction transistor (BJT) and a metal-oxide-semiconductor field-effect transistor (MOSFET) in series, the combination of the two can be used to estimate the IGBT component failure rate [43,44]. The BJT component failure rate is shown in Equation (1).
Here, the basic failure rate of BJT is 0.00074, the application factor is 0.7 because it is a switching type, the quality factor is 2.4, which is the standard value for military and aviation applications, and the environment factor is 9.0, which is the value of under the condition that it operates in an environment with large changes in ambient temperature. Temperature factor is defined by Equation (2), and represents the junction temperature.
Since the power rating factor, has a rated power of 0.1 W or more, Equation (3) is applied and represents the rated power.
The voltage stress factor is defined by Equation (4), where is the collector-emitter rated voltage at base open and is the voltage applied to the device.
The MOSFET component failure rate is given by Equation (5).
Here, the basic failure rate of MOSFET is 0.012, the application factor is selected as 10 because the rated power is more than 250 W, and the quality factor and environment factor are the same as BJT. Temperature factor is defined by Equation (6), and represents the junction temperature.
Since the IGBT is composed of a BJT and a MOSFET in series, if either of them fails, the failure of the IGBT occurs. Therefore, the failure rate of the IGBT is defined as follows through the OR-gate operation of the two devices.
2.3.2. Capacitor Failure Rate
The capacitor is analyzed as a metalized film capacitor sealed in a durable metal case, and the failure rate equation is as follows.
The default failure rate for metalized film capacitors is 0.00037 and the series resistance factor is 1.0. The quality factor is 1.5, which is the reference value for military and aviation applications, and the environment factor is 20 of . Temperature factor is defined by Equation (9), where T is the capacitor ambient temperature.
The capacitance factor is defined by Equation (10), where C is the capacitance value of the capacitor.
The voltage stress factor is defined by Equation (11), where is the rated voltage of the capacitor and is the operating voltage applied to the capacitor.
2.3.3. Diode Failure Rate
The component failure rate of a diode is given by Equation (12).
The diode’s basic failure rate is 0.025, the contact construction factor is 1 for metallurgically bonded, the quality factor is 2.4 for military and aviation applications, and the environment factor is 9 for . Temperature factor is defined by Equation (13), where represents the junction temperature.
The electrical stress factor is equal to Equation (14), where is the voltage applied to the diode and is the reverse voltage across the diode.
Table 4 shows the change in failure rate of IGBTs, capacitors, and diodes as a function of temperature. The temperature was analyzed by dividing the junction temperature of the switching device and the ambient temperature of the capacitor, and the values in parentheses in the table indicate the ambient temperature of the capacitor. IGBT Junction: When the temperature is 125 °C, the failure rate is 0.133 [Failures/ h], and a mean time to failure of 74,986 h and a lifetime of 8.56 years can be expected. If the operating temperature is maintained at 25 °C, the failure rate is significantly reduced to 0.0263 [Failures/ h], resulting in a mean time to failure of 380,319 h and a life expectancy of 43.42 years. In the case of capacitors, the failure rate is relatively good compared to IGBTs at 0.001063 [Failures/ h] under harsh conditions with a temperature of 85 °C and decreases to 0.000131 [Failures/ h] if the ambient temperature is maintained at −40 °C. As for the diode, there is some difference between the diode used in the DCC and the IGBT body diode, and it can be seen that the failure rate is lower than the IGBT and the capacitor under the same temperature condition.

Table 4.
The failure rate of IGBT, diode, and capacitor.
3. Reliability Analysis Based on Operating Characteristics
3.1. Analysis of Failure Rate of Multi-Level Inverter Using Fault-Tree
In this chapter, we analyze the failure rate by reflecting the part failure rate in the failure tree designed for each topology. A failure tree designed with three modes for half a cycle has the same failure rate because the modes are applied repeatedly, and in the next half cycle, all the elements have the complementary operation. Therefore, it should reflect the rate at which the three modes are applied during one cycle. MI determines the ratio of the 1-level capacitor charge/discharge mode to the zero-level mode, and PF determines the ratio of the 1-level capacitor charge mode and the 1-level capacitor discharge mode.
When applying space vector PWM(SVPWM), the maximum output phase voltage is 57.7% of the DC link voltage. Generally, MI is selected between 0.8 and 0.95 based on the rated power, considering the output power margin. The 1-level voltage formation interval and the zero-level voltage formation interval are determined using the average value of the output phase voltage and the DC link voltage according to the MI. When MI is applied to 0.85, the maximum output phase voltage is 49% of the DC link voltage, and when the average value of the output phase voltage is applied, the 1-level voltage formation interval is about 62.4% and the zero-level voltage formation interval is 37.6% in one cycle. If the inverter PF is assumed to be 98% when the motor is running, the capacitor discharge mode is 93.6% of one cycle, and the capacitor charge mode is 6.4% of one cycle during the 1-level voltage formation interval. In this way, the rate at which three fault tree events are applied during a half cycle is defined as Equation (15).
Here, , , and represent the rate at which the three fault tree events are applied in a half cycle. is the rate of [1-level discharging failure] events, is the rate of [1-level charging failure] events, and is the rate of [zero-level failure] events. Table 5 shows the number of major parts whose operation characteristics are reflected for each of the three fault tree events by the fault tree design for each topology described in Section 2.2. The failure rate for each fault tree event is calculated by OR combining the number of major components for each mode defined in Table 5.

Table 5.
Main part number of each topology for FTA design.
Using the ratio of the three fault tree events according to Equation (15) and the failure rate for each fault tree event, the half-cycle average failure rate is defined as Equation (16).
Here, means the weighted average failure rate during the half-bridge half cycle.
x represents three topologies, represents the failure rate of the [1-level discharging failure] event, represents the failure rate of the [1-level charging failure] event, and represents the failure rate of [zero-level failure].
The half-bridge one-cycle failure rate () defined in Equation (17) can be obtained by connecting with an OR-gate combination. In the same way, using , the failure rates for the single-phase () and three-phase () multilevel inverters defined in Equations (18) and (19) can be obtained on an FTA basis.
3.2. Comparison of DCC, FCC, TNPC, and MMC
3.2.1. Comparison of Failure Rates based on PCA and FTA
PCA does not consider the operation characteristics of multilevel inverters but simply calculates the failure rate by OR combining the type and number of parts. The failure rates based on PCA and the proposed FTA are compared for three topologies. Table 6 shows the types and number of components for the three topologies.

Table 6.
Part type and Number by topology.
Figure 13 shows the failure rates of PCA and FTA methods for the half-bridge as a function of temperature. Figure 13a shows the failure rate calculated by the PCA method using Table 2, and Figure 13b shows the failure rate calculated by the FTA method using Equations (15)–(17) when MI is 0.85 and PF is 0.98. The results show that the failure rate of DCC > FCC > TNPC is higher in the PCA method, but the failure rate of FCC > TNPC > DCC is higher in the FTA method. When comparing the average failure rate, FCC increased the failure rate by about 18.8% compared to PCA, and TNPC increased the failure rate by about 7.7% in the FTA method. DCC decreased by about 0.9%, and the difference in failure rate between DCC and TNPC was about 0.5% in the FTA method.
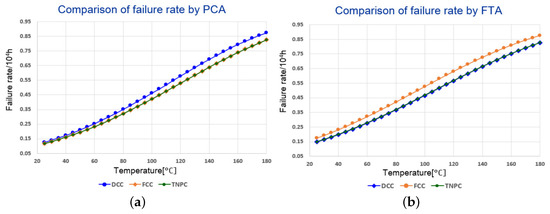
Figure 13.
Comparison of failure rate at half-bridge, (a) failure rate by PCA (b) failure rate by FTA.
Figure 14 shows the comparative analysis of each topology for a three-phase multilevel inverter using Equation (19) when MI is 0.85 and PF is 0.98 based on FTA. Compared to the half-bridge, the failure rate increases overall and the expected lifetime is 862 days for DCC, 761 days for FCC, and 855 days for TNPC at 40 °C. The different results for PCA and FTA can be seen as a reflection of the risks associated with the drive characteristics.
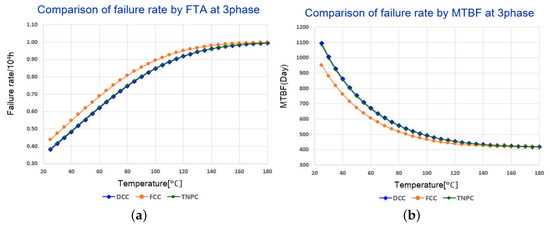
Figure 14.
Failure rate and MTBF at 3phase by FTA, (a) failure rate (b) MTBF(Day).
3.2.2. Comparison of Failure Rate Based on Modulation Ratio and Power Factor
In this chapter, we use the advantages of the proposed FTA method to see how the failure rate is affected when the MI value is varied and when the PF value is varied.
Figure 15 shows the results of the failure rate when MI and PF are varied at 80 °C conditions. Figure 15a shows the change in the failure rate of the half-bridge when MI is varied from 0.7 to 0.95 at 0.98 PF. A larger MI means a larger proportion of the 1-level voltage formation interval is applied, and the failure rate of DCC and TNPC decreased by 1.83% and 1.58%, respectively, when MI was changed from 0.7 to 0.95, while FCC increased by 2.7%. Figure 15b shows the change in the failure rate of the half-bridge when PF is varied from 0.9 to 1.0 when MI is 0.83. It means that the higher the PF, the greater the proportion of the 1-level discharge interval is applied, and DCC, FCC, and TNPC increased by 3.54%, 2.7%, and 1.69%, respectively, when PF changed from 0.9 to 1.0.
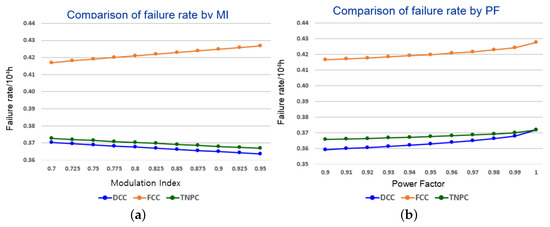
Figure 15.
Comparison of failure rate by MI & PF (a) failure rate BY MI (b) failure rate by PF.
Figure 16 shows the change in half-bridge failure rate values when MI changes from 0.76 to 1.0 and PF changes from 0.88 to 1.0 under 80 °C condition. Figure 16a is the failure rate value of FCC, which shows that the failure rate is proportional to PF and MI, and the minimum failure rate is 0.4127 [Failures/ h] and the maximum failure rate is 0.4345 [Failures/ h]. In terms of life expectancy, it is reduced by about 5% from 1010 days to 956 days. Figure 16b shows the result values for the TNPC, where failure rates and PF are proportional and MI is inversely proportional. The minimum failure rate is 0.6309 [Failures/ h] and the maximum failure rate is 0.3707 [Failures/ h], which is a decrease of about 3.5% from 1154 days to 1115 days in terms of expected lifetime.
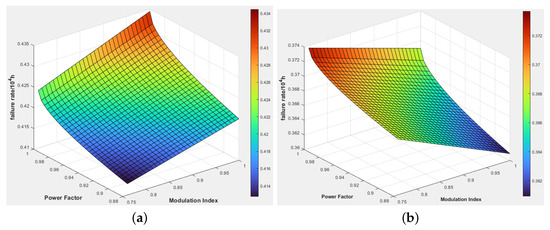
Figure 16.
Failure rate according to MI and PF changes (a) failure rate in FCC (b) failure rate in TNPC.
4. Conclusions
This paper analyzes the failure rate from a reliability perspective for the multilevel inverter topology applicable to stratospheric drones. For each topology, we analyze the operation characteristics of the half-bridge and classify them into three operation modes, and the FTA is designed. The three FTAs for each half-bridge are easy to apply to single-phase and three-phase and have the advantage of being able to analyze reliability according to changes in MI and PF that cannot be confirmed in the PCA. The comparison of failure rates by topology between PCA and FTA shows that the values and rankings of the failure rates are different. Since PCA only considers the type, number, and failure dependence of simple components, it cannot reflect the operation characteristics of inverters by topology.
Using the proposed three FTAs for each half-bride, the failure rate and lifetime of a three-phase multilevel inverter were predicted. The effect of the variation between MI value and PF value on the failure rate was analyzed, respectively, and the failure rate was affected when the three indicators of temperature, MI, and PF changed together. In addition to the FTA-based failure rate analysis that considers conventional voltage and current stresses and voltage margins, the proposed method designs the FTA to reflect PF and MI variations. It provides various guidelines for selecting the topology of multilevel inverters from the reliability point of view. The three topologies show high failure rate in order of FCC > TNPC > DCC. In terms of reliability, DCC is the best, but when compared to TNPC, the average failure rate of 3phase is about 0.34% lower. The difference between DCC and TNPC in terms of failure rate shows a slight difference, but TNPC is better than DCC in terms of efficiency [45,46]. Among the three topologies compared in this paper, TNPC can be considered the most suitable topology for stratospheric drones.
Author Contributions
Conceptualization, J.-H.L. and J.-H.P.; methodology, S.-K.L.; software, J.-H.L. and J.-H.P.; validation, H.-S.J. and H.-M.P.; formal analysis, J.-H.L. and S.-K.L.; investigation, H.-S.J. and H.-M.P.; data curation, J.-H.P. and S.-K.L.; writing—original draft preparation, J.-H.L. and S.-K.L.; writing—review and editing, J.-H.L. and J.-H.P.; Funding acquisition, H.-S.J.; Project administration, H.-S.J. and J.-H.P. All authors have read and agreed to the published version of the manuscript.
Funding
This researchwas supported by the Stratospheric Drone Technology Development Program through the National Research Foundation of Korea (NRF) and the Stratospheric Drone Technology Development Center funded by the Ministry of Science and ICT, the Republic of Korea (Grant No. 2022M3C1C7090617).
Data Availability Statement
The data presented in this study are available in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mateja, K.; Skarka, W.; Drygała, A. Efficiency Decreases in a Laminated Solar Cell Developed for a UAV. Materials 2022, 15, 8774. [Google Scholar] [CrossRef]
- Arum, S.C.; Grace, D.; Mitchell, P.D.; Zakaria, M.D.; Morozs, N. Energy management of solar-powered aircraft-based high altitude platform for wireless communications. Electronics 2020, 9, 179. [Google Scholar] [CrossRef]
- Pham, K.L.; Leuchter, J.; Bystricky, R.; Andrle, M.; Pham, N.N.; Pham, V.T. The study of electrical energy power supply system for UAVs based on the energy storage technology. Aerospace 2022, 9, 500. [Google Scholar] [CrossRef]
- Pupadubsin, R.; Mecrow, B.C.; Widmer, J.D.; Steven, A. Smooth voltage pwm for vibration and acoustic noise reduction in switched reluctance machines. IEEE Trans. Energy Convers. 2020, 36, 1578–1588. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Zhang, W.; Zou, J. Hybrid RPWM technique based on modified SVPWM to reduce the PWM acoustic noise. IEEE Trans. Power Electron. 2018, 34, 5667–5674. [Google Scholar] [CrossRef]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An overview of small unmanned aerial vehicles for air quality measurements: Present applications and future prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Q.; Li, K.; Valtchev, S.; Li, S.; Yin, L. A survey of electromagnetic influence on UAVs from an EHV power converter stations and possible countermeasures. Electronics 2021, 10, 701. [Google Scholar] [CrossRef]
- Afsharnia, F. Failure rate analysis. In Failure Analysis and Prevention; IntechOpen: London, UK, 2017. [Google Scholar]
- Krasich, M. How to estimate and use MTTF/MTBF would the real MTBF please stand up? In Proceedings of the 2009 Annual Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; IEEE: New York, NY, USA, 2009; pp. 353–359. [Google Scholar]
- Zhou, W.; Wang, M.; Wu, Q.; Xi, L.; Xiao, K.; Bhat, K.P.; Chen, C. Accelerated life testing method of metallized film capacitors for inverter applications. IEEE Trans. Transp. Electrif. 2020, 7, 37–49. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, M.; Zhou, W.; Lu, X.; Xiao, K.; Bhat, K.P.; Chen, C. Traction inverter highly accelerated life testing with high-temperature stress. IEEE Trans. Transp. Electrif. 2020, 7, 304–316. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Shen, Y.; Chub, A.; Liivik, E.; Vinnikov, D.; Wang, H.; Blaabjerg, F. Design for accelerated testing of DC-link capacitors in photovoltaic inverters based on mission profiles. IEEE Trans. Ind. Appl. 2020, 57, 741–753. [Google Scholar] [CrossRef]
- Dhople, S.V.; Davoudi, A.; Chapman, P.L.; Domínguez-García, A.D. Integrating photovoltaic inverter reliability into energy yield estimation with Markov models. In Proceedings of the 2010 IEEE 12th Workshop on Control and Modeling for Power Electronics (COMPEL), Boulder, CO, USA, 28–30 June 2010; IEEE: New York, NY, USA, 2010; pp. 1–5. [Google Scholar]
- Cristaldi, L.; Khalil, M.; Soulatintork, P. A root cause analysis and a risk evaluation of PV balance of system failures. Acta Imeko 2017, 6, 113–120. [Google Scholar] [CrossRef]
- Theristis, M.; Papazoglou, I.A. Markovian reliability analysis of standalone photovoltaic systems incorporating repairs. IEEE J. Photovolt. 2013, 4, 414–422. [Google Scholar] [CrossRef]
- Song, Y.; Wang, B. Survey on reliability of power electronic systems. IEEE Trans. Power Electron. 2012, 28, 591–604. [Google Scholar] [CrossRef]
- Wylie, J.; Merlin, M.C.; Green, T.C. Analysis of the effects from constant random and wear-out failures of sub-modules within a modular multi-level converter with varying maintenance periods. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; IEEE: New York, NY, USA, 2017; p. P1. [Google Scholar]
- Bakouch, H.S.; Ristić, M.M.; Asgharzadeh, A.; Esmaily, L.; Al-Zahrani, B.M. An exponentiated exponential binomial distribution with application. Stat. Probab. Lett. 2012, 82, 1067–1081. [Google Scholar] [CrossRef]
- Choudhary, K.; Sidharthan, P. Reliability prediction of Electronic Power Conditioner (EPC) using MIL-HDBK-217 based parts count method. In Proceedings of the 2015 International Conference on Computer, Communication and Control (IC4), Indore, India, 10–12 September 2015; IEEE: New York, NY, USA, 2015; pp. 1–4. [Google Scholar]
- Krishnachaitanya, D.; Chitra, A. Quantitative analysis of asymmetric multilevel inverters with reduced device count from reliability and cost function perspective—A review. IEEE Trans. Power Electron. 2021, 36, 11068–11086. [Google Scholar] [CrossRef]
- Frey, D.; Palladino, J.; Sullivan, J.; Atherton, M. Part count and design of robust systems. Syst. Eng. 2007, 10, 203–221. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault tree analysis: A survey of the state-of-the-art in modeling, analysis and tools. Comput. Sci. Rev. 2015, 15, 29–62. [Google Scholar] [CrossRef]
- Shalev, D.M.; Tiran, J. Condition-based fault tree analysis (CBFTA): A new method for improved fault tree analysis (FTA), reliability and safety calculations. Reliab. Eng. Syst. Saf. 2007, 92, 1231–1241. [Google Scholar] [CrossRef]
- Kang, F.S.; Song, S.G. Life-cycle expectation using fault-tree analysis for improved hybrid submodule in HVDC system. Electronics 2021, 10, 133. [Google Scholar] [CrossRef]
- Kabir, S. An overview of fault tree analysis and its application in model based dependability analysis. Expert Syst. Appl. 2017, 77, 114–135. [Google Scholar] [CrossRef]
- Spertino, F.; Amato, A.; Casali, G.; Ciocia, A.; Malgaroli, G. Reliability analysis and repair activity for the components of 350 kW inverters in a large scale grid-connected photovoltaic system. Electronics 2021, 10, 564. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Bartolini, A.; Del Rio, C.; Guidi, G.; Patrizi, G. Reliability analysis of wireless sensor network for smart farming applications. Sensors 2021, 21, 7683. [Google Scholar] [CrossRef] [PubMed]
- Yeo, S.C.; Kang, F.S. Fault-tree based failure-rate analysis for boost converter and interleaved boost converter. J. Electr. Eng. Technol. 2019, 14, 2375–2387. [Google Scholar] [CrossRef]
- Khairnar, D.D.; Deshmukh, V. Performance Analysis of Diode Clamped 3 Level MOSFET Based Inverter. Int. Electr. Eng. J. (IEEJ) 2014, 5, 1484–1489. [Google Scholar]
- Ahmadi, S.; Poure, P.; Saadate, S.; Khaburi, D.A. Fault tolerance analysis of five-level neutral-point-clamped inverters under clamping diode open-circuit failure. Electronics 2022, 11, 1461. [Google Scholar] [CrossRef]
- Barros, L.A.; Martins, A.P.; Pinto, J.G. A comprehensive review on modular multilevel converters, submodule topologies, and modulation techniques. Energies 2022, 15, 1078. [Google Scholar] [CrossRef]
- Alepuz, S.; Busquets-Monge, S.; Nicolás-Apruzzese, J.; Filbà-Martínez, À.; Bordonau, J.; Yuan, X.; Kouro, S. A survey on capacitor voltage control in neutral-point-clamped multilevel converters. Electronics 2022, 11, 527. [Google Scholar] [CrossRef]
- Taul, M.G.; Pallo, N.; Stillwell, A.; Pilawa-Podgurski, R.C. Theoretical analysis and experimental validation of flying-capacitor multilevel converters under short-circuit fault conditions. IEEE Trans. Power Electron. 2021, 36, 12292–12308. [Google Scholar] [CrossRef]
- Shukla, A.; Ghosh, A.; Joshi, A. Flying-capacitor-based chopper circuit for dc capacitor voltage balancing in diode-clamped multilevel inverter. IEEE Trans. Ind. Electron. 2009, 57, 2249–2261. [Google Scholar] [CrossRef]
- Salem, M.; Richelli, A.; Yahya, K.; Hamidi, M.N.; Ang, T.Z.; Alhamrouni, I. A comprehensive review on multilevel inverters for grid-tied system applications. Energies 2022, 15, 6315. [Google Scholar] [CrossRef]
- Zygmanowski, M. Detailed Power Loss Analysis of T-Type Neutral Point Clamped Converter for Reactive Power Compensation. Electronics 2022, 11, 2129. [Google Scholar] [CrossRef]
- Zhang, Z.; Anthon, A.; Andersen, M.A. Comprehensive loss evaluation of neutral-point-clamped (NPC) and T-Type three-level inverters based on a circuit level decoupling modulation. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; IEEE: New York, NY, USA, 2014; pp. 82–87. [Google Scholar]
- Bahrami, A.; Narimani, M. A new five-level T-type nested neutral point clamped (T-NNPC) converter. IEEE Trans. Power Electron. 2019, 34, 10534–10545. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, S.; Din, Z.; Hu, X. Hybrid multilevel converters: Topologies, evolutions and verifications. Energies 2019, 12, 615. [Google Scholar] [CrossRef]
- Rojas, C.A.; Kouro, S.; Inzunza, R.; Mitsugi, Y.; Alcaide, A.M. Harmonic Impedance Model of Multiple Utility-Interactive Multilevel Photovoltaic Inverters. Energies 2022, 15, 9462. [Google Scholar] [CrossRef]
- Mou, H.; Hu, W.; Sun, Y.; Zhao, G. A comparison and case studies of electronic product reliability prediction methods based on handbooks. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Emeishan, China, 15–18 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 112–115. [Google Scholar]
- Jones, J.; Hayes, J. A comparison of electronic-reliability prediction models. IEEE Trans. Reliab. 1999, 48, 127–134. [Google Scholar] [CrossRef]
- Valentine, N.; Das, D.; Pecht, M.; Pecht, M. Failure mechanisms of insulated gate bipolar transistors (IGBTs). In Proceedings of the NREL Photovoltaic Reliability Workshop, Center for Advanced Life Cycle Engineering (CALCE), Golden, CO, USA, 24–27 February 2015; University of Maryland: College Park, MD, USA, 2015. [Google Scholar]
- Pokorni, S. Reliability prediction of electronic equipment: Problems and experience. In Proceedings of the 7th International Scientific Conference on Defensive Technologies OTEH, Belgrade, Serbia, 6–7 October 2016; pp. 6–7. [Google Scholar]
- Lee, K.; Shin, H.; Choi, J. Comparative analysis of power losses for 3-Level NPC and T-type inverter modules. In Proceedings of the 2015 IEEE International Telecommunications Energy Conference (INTELEC), Osaka, Japan, 18–22 October 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Tehrani, K.A.; Rasoanarivo, I.; Sargos, F.M. Power loss calculation in two different multilevel inverter models (2DM2). Electr. Power Syst. Res. 2011, 81, 297–307. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).