A Multi-Terminal Control Method for AC Grids Based on a Hybrid High-Voltage Direct Current with Cascaded MMC Converters

Abstract

The hybrid high-voltage direct current (HVDC) transmission system with cascaded MMC converters has become a promising alternative for possessing the technical merits of both line-commuted converter (LCC) and voltage source converter (VSC), resulting in favorable characteristics and potential control of good prospect. This paper pays heightened attention to the feasible power and DC voltage control modes of a hybrid HVDC system; characteristics of master–slave control show higher flexibility than the LCC-VSC HVDC system, which demonstrates that the exceptional potential can serve to stability support the AC power grids. To optimize the control effect, besides damping level to attenuate power oscillations, the robustness suitable for various faults is also considered to obtain a multi-objective control problem. A detailed solution is proceeding using the TLS-ESPRIT identification algorithm and H₂/H_∞ hybrid robust control theory. This motivates multi-terminal controllers in the LCC rectifier and MMC inverters, which immensely improve the stability of both sending and receiving girds at the same time. According to the parameters of the actual hybrid HVDC project, the simulation model is established in PSCAD v4.6.2 software, and proposed control methods have been verified to satisfy damping objectives and perform well in multiple operating scenarios.

1. Introduction

The distribution of energy in China and the trend of power reform have determined that DC transmission has become an essential direction for power grid construction [1]. In recent years, the State Grid of China and China Southern Power Grid Corporation have successively planned and constructed multiple DC lines [2,3]. However, the conventional direct current (LCC-HVDC) has a higher risk of commutation failure (CF); at the same time, the flexible direct current (VSC-HVDC) also has shortcomings, such as smaller capacity and higher cost. Therefore, combining conventional LCC converters with flexible VSC converters for hybrid DC transmission has become the development direction of DC transmission in China [4]. The ±800 kV ultra-high voltage hybrid DC transmission project from Baihetan to Jiangsu (BTH-JS) is expected to be put into operation in 2023.

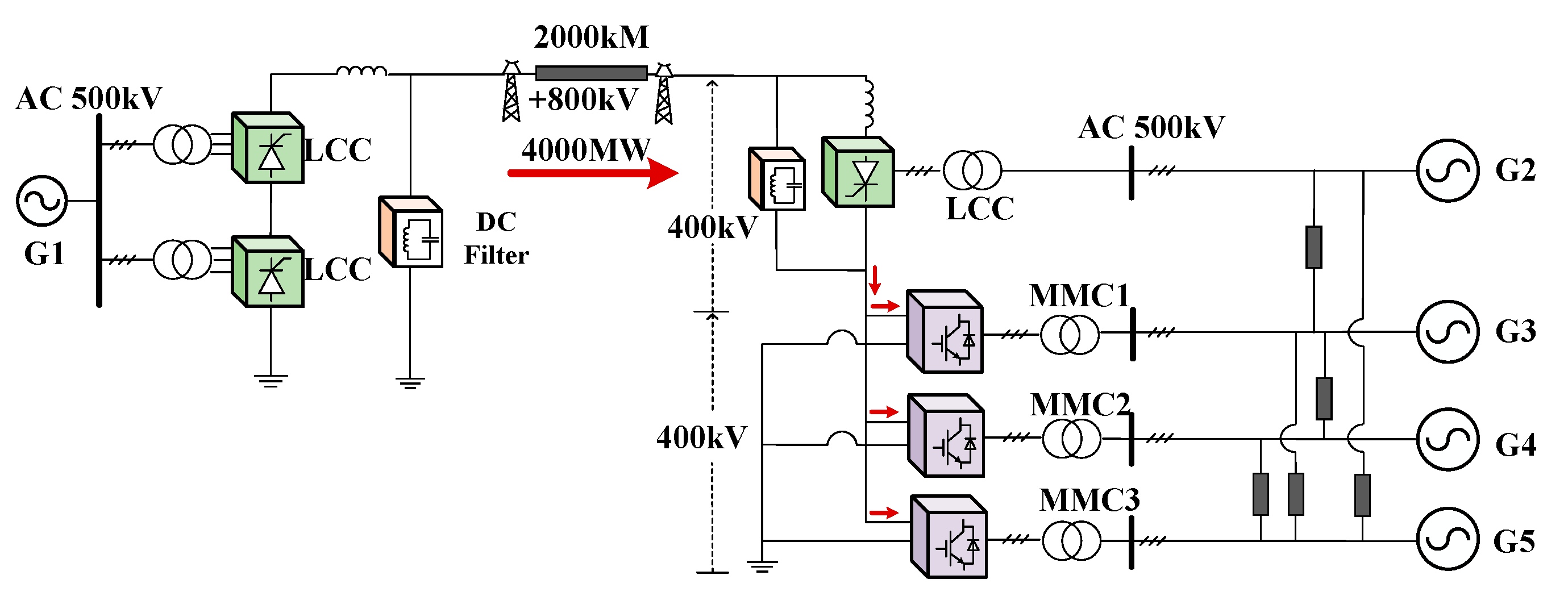
The rectifier of the BTH-JS hybrid HVDC system employs LCC. As for the inverters, they introduce innovative LCC cascaded with multiple MMCs, making the world’s first hybrid cascaded DC transmission system a real project. The ultra-high-voltage hybrid cascaded DC system fully utilizes the advantages of the MMC converter and LCC converter. On the one hand, the MMCs can stabilize the receiving end voltage of AC grids, reducing the probability of LCC CF. On the other hand, multiple MMCs are configured in parallel to increase the acceptable capacity of the system. Notably, the unique topology of LCC and MMC parallel groups enables the receiving end to have the conditions for decentralized access to the AC power grid, which can form a multi-point form that meets the electricity demand of multiple load centers. Whether in the early construction or later operation, it can significantly improve the flexibility and reliability of the system.

Recent research concerning hybrid DC transmission primarily focuses on topology structure and control methods. Reference [5] proposes a hybrid DC topology structure using LCC for rectification measurement and a VSC inverter, which reduces system cost and power loss, as well as avoids CF, which is suitable for unidirectional power transmission. Reference [6] proposes an electro-mechanical transient modeling and power flow calculation method for LCC-MMC, laying the foundation for subsequent research on the transient stability of multi-terminal hybrid DC transmission. Due to the LCC commutation components, it is not possible to achieve power flow reversal. Reference [7] proposes a hybrid bipolar high-voltage DC system in which the positive electrode uses LCC and the negative electrode uses VSC. The coordinated control method decreases the risk of CF, stabilizes AC voltage, and enhances system robustness. However, VSC and LCC at the same end limit the current of LCC and cannot maximize its effectiveness. Reference [8] proposes a doubly fed HVDC structure in that the LCC inverter is linked with the VSC rectifier on the same bus and analyzes the impact of VSC on the power control characteristics of LCC. Reference [9] analyzes the influence of LCC on the strength of VSC systems based on the aforementioned topological structure. Reference [10] proposes a hybrid three-terminal DC transmission system topology, where the LCC rectifier and dual MMC inverter are connected in parallel to form a more flexible and larger capacity DC transmission method, providing a theoretical basis for the application of the Wudongde DC project. Reference [11] proposes a topology structure of LCC rectifier and LCC connected in series with MMC inverters. The different topologies and control methods of the system’s receiving end are analyzed and compared, indicating that decentralized access of the receiving MMCs can effectively isolate fault points, providing a reference for constructing the BTH-JS DC project.

As for the control methods, reference [11] analyzes the different receiver topologies and control methods of hybrid cascaded systems, laying the foundation for the next step of research. It is also possible to adjust the power command value through the imbalance of MMC current when the receiving system malfunctions, suppressing the imbalance current and DC overcurrent between MMC and reducing the impact on flexible and direct equipment [12]. Reference [13] proposes a hybrid DC transmission system based on LCC-HVDC at both ends, where two down-side parallel MMCs are on the inverter side, and proposes a fault recovery strategy. However, this control strategy only focuses on DC faults and does not analyze faults either on the rectifier side or the AC system. A hybrid multi-drop DC transmission system proposes a dynamic power-adjustment strategy based on master–slave mode is investigated in [14], which can maintain voltage stability during system faults and prevent the large-scale transfer of power at the receiving end, leading to overvoltage and overcurrent problems at the receiving end. Reference [15] designs a control strategy and equipment parameters for a hybrid cascaded DC transmission receiving end MMC centralized topology, thereby verifying the feasibility of its strategy on a dynamic simulation experimental platform, providing technical support for the actual BTH-JS DC project. The damping control VSC-HVDC is proposed and separated active and reactive controls are implemented in [16], which provides a solution for AC power control. Reference [17] presents a control method to suppress the CF of hybrid cascaded receiver LCCs. The main idea is to adjust the reactive power output of the MMC during faults, thereby raising the AC voltage, increasing the commutation angle, and avoiding CF. However, this strategy is only aimed at one case of centralized MMC topology and cannot improve the fault voltage of decentralized MMC topology. Reference [18] analyzes the applicability of five different control strategies for line faults and finds that when the MMC group is controlled by fixed DC voltage, the best effect is achieved in suppressing faults. However, it loses flexibility and controllability, making it challenging to adopt this control method in practical engineering projects. Moreover, droop control is widely applied in DC systems owing to the power balance ability, especially with multi-DC converters [19], which means it can also be applied in the BTH-JS HVDC system.

It is noticeable that the implementations of the BTH-JS hybrid HVDC system generally focus on its own operation characteristics, as the operation modes of such hybrid DC systems are complex. However, few studies take advantage of cascaded hybrid HVDC to suppress power oscillations. As the BTH-JS hybrid HVDC system has several converters in constant active and constant current control modes, its oscillation control ability is evident. To make use of such ability of the cascaded hybrid DC system, this study proposes an additional damping control strategy for a distinctive BTH-JS HVDC system. The novelties of this paper can be concluded as follows.

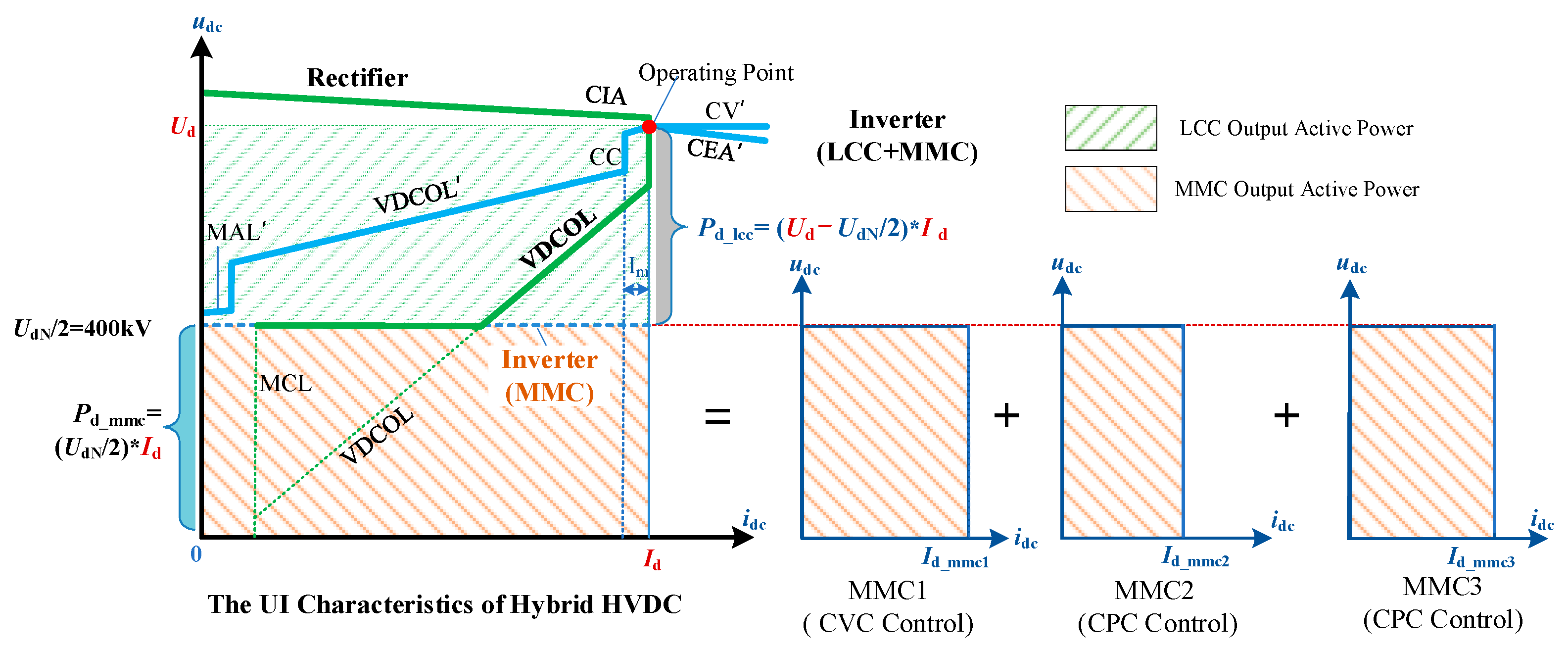
(1) Feasible control modes and respective control characteristics of hybrid HVDC are clarified. The inverters are regarded as conventional LCC cascaded with multi-infeed MMC inverters whereby a master–slave control is designed to control active power and DC voltage of MMCs. The mathematical model of the compositive hybrid HVDC system is presented, and UI curves are investigated subsequently;

(2) As a promising alternative, a multi-terminal control strategy serving AC grids’ stability improvement is proposed. Motivated by the attractively flexible and controllable characteristics, multi-objective damping controllers are designed in both sending LCC rectifier and receiving MMC inverter, which complies with damping enhancement paired with robustness assurance using the H₂/H_∞ control theory and LMI solution procedure;

(3) The electromagnetic simulation model of hybrid cascaded on the basis of the actual operation project is established on PSCAD/EMTDC v4.6.2 software. Simulations under different operation conditions are conducted, and the results verify the effectiveness of robust damping control methods in this study and guarantee desirable 20% damping and robust performance.

The organization of this paper is as follows. Section 2 introduces the system configuration and master–slave control characteristics of the hybrid cascaded HVDC system. Section 3 designs the multi-terminal control strategy to suppress the AC power disturbances. Section 4 validates the control effect of the proposed control method using simulations based on engineering parameters. Section 5 presents relevant conclusions in the final.

2. The Control Characteristics of Hybrid Cascaded HVDC

Compared to the conventional LCC-MMC hybrid HVDC, the inverters of hybrid HVDC in this study are expanded into an original structure in that the LCC inverter is cascaded with multiple MMC inverters. Consequently, the control method of inverter DC voltage and power of such a hybrid HVDC system is more complicated. Thus, the primary control mode and control characteristics are discussed in this section.

2.1. HVDC System Configuration

In the BHT-JS hybrid HVDC system which is presented in Figure 1, the rectifier is an LCC converter, and the inverters include one LCC inverter at a high-voltage terminal and three MMC inverters at a low-voltage terminal. In this study, the MMCs apply all half-bridge inverters. The nominal transmission active power is 4000 MW under ±800 kV nominal voltage. As for the inverters, the nominal voltage of both LCC inverter and MMC inverters is 400 kV. Moreover, the high voltage terminal LCC inverter and low voltage terminal cascaded three MMC converters carry about 2000 MW, respectively. In other words, each MMC inverter transmits about 667 MW of active power to various ending AC grids, which are interconnected with different impedances. Such a structure makes it more flexible to control and to improve the stability of the AC system.

2.2. Control Modes

2.2.1. LCC Converters

The control modes of the hybrid HVDC system are necessary to be discussed. The conventional control modes are applicable for both the LCC rectifier and inverter, which is presented in Figure 2. The abbreviations are interpreted in

Table 1. The abbreviations of control modes for LCC converters.

Control Modes	Descriptions
CIA	Constant Ignition Angle Control
CC	Constant DC Current Control
VDCOL	Voltage-Dependent Current Order Limit Control
MCL	Minimum DC Current Limit Control
CVC	Constant DC Voltage Control
CEA	Constant Extinction Angle Control
MAL	Minimum Alpha Angle Control

.

The aim is to obtain constant DC current I_d and DC voltage U_d of LCC converters. The LCC rectifier concludes classical CIA, CC, VDCOL, and MCL control. The LCC inverter applies CEA (CV), CC, as well as MAL. Based on the control mode of LCC, the red operating point is certain to be the red point in Figure 2.

2.2.2. MMC Converters

Differing from the hybrid LCC-VSC HVDC system, the inverters in this study consist of the LCC inverter series with cascaded MMC inverters. The control method of three MMC inverters is a significant part. Since each MMC inverter may consider constant DC voltage control (CVC) or constant DC active power control (CPC), there are many alternatives for MMC control, such as all CVC control and master–slave control. Specifically, in the master–slave control, MMC1 is usually considered to control the DC voltage of the DC bus, and MMC2 and MMC3 inverters apply the CPC control mode. The control diagram is drawn in Figure 3. The input signals of control are active power P_s and the reference P_ref of MMC, then the outer loop PI controller with K_p and K_i and the limiter with a threshold of i_dlim would output the reference of the d-qxis DC active current i_dref.

Meanwhile, droop control is also a possible choice for the advantage of no need for communication. In this paper, the practical need for precise DC voltage and DC power control should be taken into account. Thus, in the three control modes above, master–slave control is more rational. As for reactive power, all MMC inverters apply constant AC voltage control.

2.2.3. The Mathematical Model

According to the separated and coordinated control modes analysis of LCC converters and MMC converters above, the power characteristics and mathematical model of the hybrid HVDC system can be deduced. Noting that the DC power control of the LCC rectifier is the same as the steady state equations, the critical part of the model is the power and voltage characteristics of inverters.

For the upper LCC inverter, from the control mode in Figure 2, the mathematical relationship can be established as follows.

$$u_{\mathrm{d}\_\mathrm{lcc}}=\frac{U_{\mathrm{dN}}}{2}$$

(1)

$$u_{\mathrm{dc}\_\mathrm{lcc}}=k_{\mathrm{CEA}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{CEA}}$$

(2)

$$u_{\mathrm{dc}\_\mathrm{lcc}}=k_{\mathrm{VDCOL}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{VDCOL}}$$

(3)

$$u_{\mathrm{dc}\_\mathrm{lcc}}=k_{\mathrm{MAL}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{MAL}}$$

(4)

$$P_{\mathrm{d}\_\mathrm{lcc}}=(U_{\mathrm{d}}-u_{\mathrm{d}\_\mathrm{lcc}})\times I_{\mathrm{d}}$$

(5)

where U_dN is the nominal DC voltage (800 kV) of hybrid HVDC, U_d and U_{d_lcc} are the real DC voltage of hybrid HVDC and upper LCC inverter, respectively. I_d is the real DC current, $k_{\mathrm{VDCOL}}^{\prime }$ and $k_{\mathrm{MAL}}^{\prime }$ are the slopes of the corresponding control segment, and the subscripts represent each control mode of the LCC converter, respectively. $U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{CEA}}$, $U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{VDCOL}}$ and $U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{MAL}}$ are DC voltage of each line segment under different control modes cross the u_dc-axis. P_{d_lcc} is the DC transmission power of the LCC inverter. Significantly, the superscript ′ in this section denotes that the control coefficients of the LCC inverter in a hybrid HVDC system are half of the conventional two-terminal LCC HVDC system. This is because the DC voltage of the LCC inverter (400 kV) is half of the rectifier (800 kV).

Moreover, the DC voltage and power characteristics of MMC inverters are described as

$$u_{\mathrm{d}\_\mathrm{mmc}}=\frac{U_{\mathrm{dN}}}{2}$$

(6)

$$P_{\mathrm{d}\_\mathrm{mmc}}=u_{\mathrm{d}\_\mathrm{mmc}}\times I_{\mathrm{d}\_\mathrm{mmc}}$$

(7)

where u_{d_mmc}, P_{d_mmc}, and I_{d_mmc} are the DC voltage, the DC active power, and the DC current of each MMC inverter, respectively.

Combining (1) to (7), the overall mathematical model of the hybrid HVDC system is concluded.

$$u_{\mathrm{dc}}=u_{\mathrm{dc}\_\mathrm{lcc}}+u_{\mathrm{dc}\_\mathrm{mmc}}=U_{\mathrm{dN}}$$

(8)

$$u_{\mathrm{dc}}=u_{\mathrm{dc}\_\mathrm{lcc}}+u_{\mathrm{dc}\_\mathrm{lcc}}=k_{\mathrm{CEA}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{CEA}}+\frac{U_{\mathrm{dN}}}{2}$$

(9)

$$u_{\mathrm{dc}}=u_{\mathrm{dc}\_\mathrm{lcc}}+u_{\mathrm{dc}\_\mathrm{mmc}}=k_{\mathrm{VDCOL}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{VDCOL}}+\frac{U_{\mathrm{dN}}}{2}$$

(10)

$$u_{\mathrm{dc}}=u_{\mathrm{dc}\_\mathrm{lcc}}+u_{\mathrm{dc}\_\mathrm{mmc}}=k_{\mathrm{MAL}}^{\prime }{i}_{\mathrm{dc}}+U_{\mathrm{dc}\_\mathrm{lcc}}^{\mathrm{MAL}}+\frac{U_{\mathrm{dN}}}{2}$$

(11)

$$P_{\mathrm{d}}=P_{\mathrm{d}\_\mathrm{lcc}}+P_{\mathrm{d}\_\mathrm{mmc}1}+P_{\mathrm{d}\_\mathrm{mmc}2}+P_{\mathrm{d}\_\mathrm{mmc}3}$$

(12)

Based on the mathematical equations above, the complete UI characteristics can be depicted in Figure 4. Compared with the control curves of LCC in Figure 2, the superscript ′ means the DC voltage and DC capacity of the LCC inverter are half of the LCC rectifier.

3. The Multi-Terminal Coordinated Control Method for AC Grids Based on Hybrid HVDC

It is proved that the power of the hybrid HVDC can be controlled more flexibly, so it can be applied to power oscillation control for AC grids at sending and receiving ends and enhance system stability. The coordinated control method is proposed in this Section.

3.1. Identification of Controlled AC-DC System

The operation analysis in Section 2 presents a clear additional control advantage from the implementation point of view. In other words, viable damping controllers in both rectifiers and inverters can be designed. Thus, the control theory and specific solution procedure for the two terminal damping controller designs are disclosed in this part.

Before improving the stability of the AC-DC system, it is essential to acquire system state equations. For a single-machine system, the differential equation has a lower order and can be directly solved. However, for large-scale power grids, the state equations may reach several thousand orders, which can bring dimensionality disaster to calculations. The speed of the solution cannot be guaranteed, and it cannot satisfy real-time calculation expectations and monitoring of the power grid. Therefore, it is very important to identify the oscillation signals and reduce the order of the controlled AC-DC system. Based on the measured input/output responses, we can obtain the corresponding lower-order transfer function to design the desirable controller. This paper applies the TLS-ESPRIT identification method, which stands out among the other methods because of its robust and accurate estimation of the model. Compared to other algorithms, such as the Prony algorithm, the TLS-ESPRIT algorithm has more minor computational complexity and stronger anti-interference ability.

The TLS-ESPRIT algorithm is practicable for parameter estimation of oscillation attenuation sinusoidal signals. The key step is to form autocorrelation and cross-correlation matrices by sampling data to gain the rotation factor. Then, it is combined with TLS to calculate both amplitude and phase. The detailed identification progress of the TLS-ESPRIT algorithm is elucidated as follows.

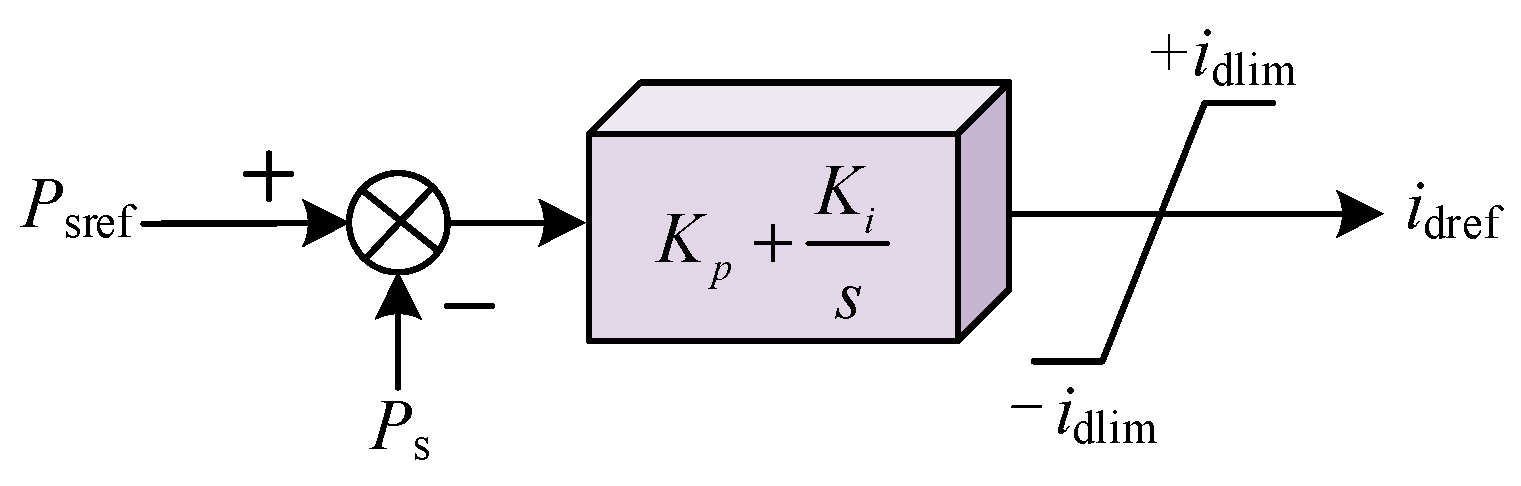
Firstly, the multi-terminal control objects are selected as hybrid DC rectifiers, as well as inverters in CPC mode on the inverter side. Secondly, for LCC rectifiers, the input is selected as the DC current, the input is defined as the DC power for MMC inverters, and the rotor speed signal of the AC generator is chosen as the output for control. Finally, the transfer function can be calculated using the TLS-ESPRIT identification method, where small perturbations need to be excited at the input side to measure output results. As a result, the theoretical state space model G(s) of the controlled system can be established as

$$\begin{array}{l}\dot{x}=A_{d}x+b_{d}u\\ y=c_{d}x\end{array}$$

(13)

where x represents the state matrix, u denotes the control matrix, y is the output matrix, A_d indicates the characteristics matrix, b_d and c_d represent the coefficient matrix of control signals, and c_d expresses the output matrix. Moreover, the dimension of A_d varies with the system parameters.

3.2. Controller Design

Further designing additional controllers based on the G(s) obtained from system model identification, the H₂/H_∞ hybrid robust control theory is considered to be a satisfying alternative to ensure the effectiveness of the controller under different operating conditions. Specifically, the H₂ index optimization means good system performance and anti-interference ability, while the H_∞ index optimization yields good robustness and stability. Combining the two aspect fields, the H₂/H_∞ hybrid control problem. This problem involves designing a multi-objective additional HVDC damping controller on a multi-terminal hybrid HVDC transmission system through the regional pole placement method. 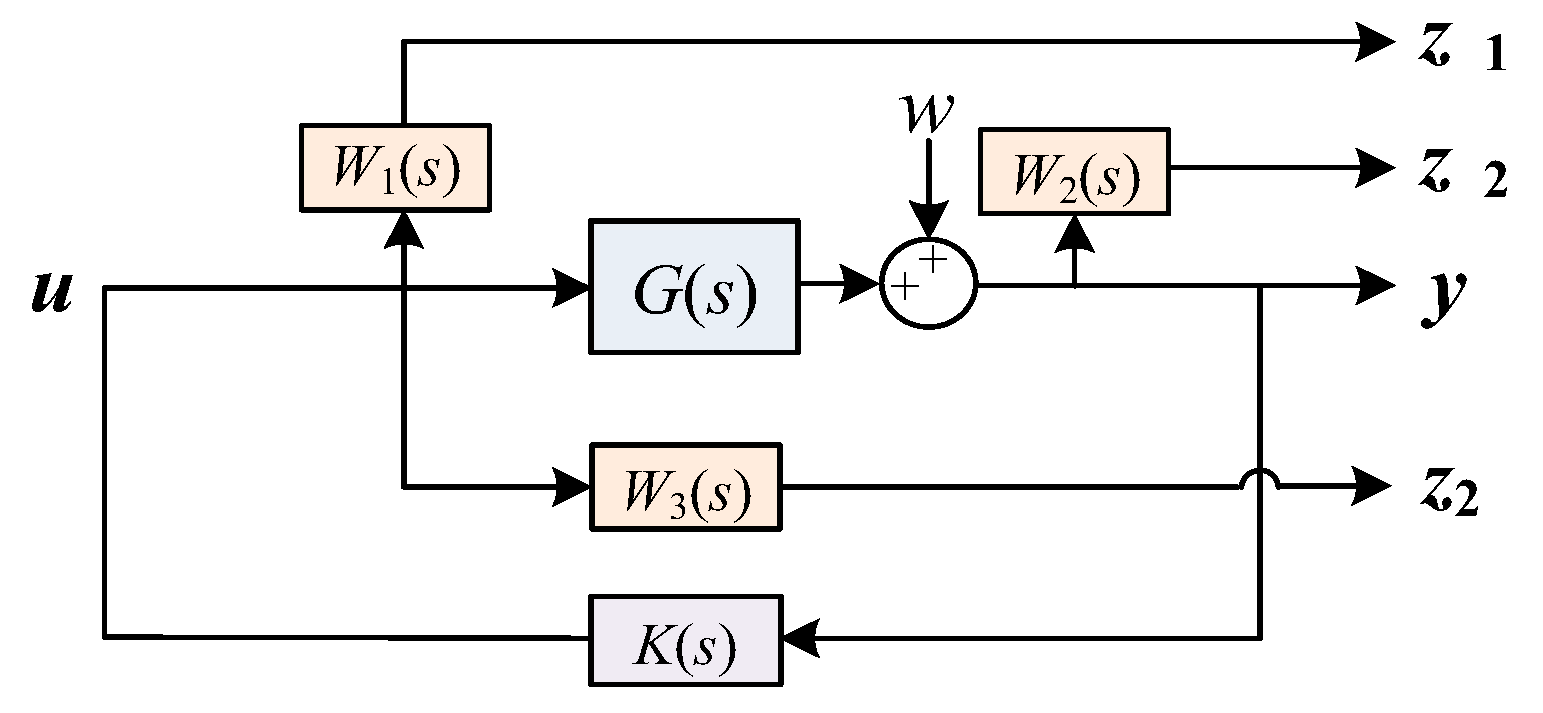In this sense, the H₂/H_∞ hybrid robust control has an outstanding advantage in ensuring both control effectiveness and robustness of the control process over other control methods, such as PI control. In other words, it can improve the stability of AC systems under various conditions. The proposed multi-objective control diagram is drawn in Figure 5.

When there occurs unknown external disturbance w for controlled system G(s), W(s) indicates the weight function to evaluate the control performances, the input signals of which are selected from different links of the controlled system; noting that K(s) is the desired controller to be designed and z_∞1 and z_∞2 are the loops to measure H_∞ performance, which can be defined as ${\mathit{z}}_{\infty }={\left[\begin{array}{cc}{\mathit{z}}_{\infty 1}& {\mathit{z}}_{\infty 2}\end{array}\right]}^T$ and the transfer function is $T_{wz\infty }(s)$, while the loop z₂ is for H₂ performance monitoring, which is defined as $T_{wz2}(s)$.

Before configuring with K(s), the state space equations can be denoted as

$$\left\{\begin{array}{l}\stackrel{.}{\mathit{x}}=\mathit{A}\mathit{x}+{\mathit{B}}_1\mathit{w}+{\mathit{B}}_2\mathit{u}\\ {\mathit{z}}_{\infty }={\mathit{C}}_1\mathit{x}+{\mathit{D}}_{11}\mathit{w}+{\mathit{D}}_{12}\mathit{u}\\ {\mathit{z}}_2={\mathit{C}}_2\mathit{x}+{\mathit{D}}_{22}\mathit{u}\\ \mathit{y}={\mathit{C}}_3\mathit{x}+{\mathit{D}}_{31}\mathit{w}+{\mathit{D}}_{32}\mathit{u}\end{array}\right.$$

(14)

Further, the state equations of anticipated K(s) can be described as

$$\left\{\begin{array}{l}{\stackrel{.}{\mathit{x}}}_{\mathit{k}}={\mathit{A}}_{\mathit{k}}{\mathit{x}}_{\mathit{k}}+{\mathit{B}}_{\mathit{k}}\mathit{y}\\ \mathit{u}={\mathit{C}}_{\mathit{k}}{\mathit{x}}_{\mathit{k}}\end{array}\right.$$

(15)

where x_k are the state variables, A_k, B_k, and C_k are the matrixes to be solved.

Thus, once the K(s) is obtained, the closed-loop system can be constructed as

$$\left\{\begin{array}{l}\stackrel{.}{\widehat{\mathit{x}}}=\widehat{\mathit{A}}\widehat{\mathit{x}}+\widehat{\mathit{B}}\mathit{w}\\ {\mathit{z}}_{\infty }={\widehat{\mathit{C}}}_1\widehat{\mathit{x}}+{\widehat{\mathit{D}}}_1\mathit{w}\\ {\mathit{z}}_2={\widehat{\mathit{C}}}_{\mathit{2}}\widehat{\mathit{x}}+{\widehat{\mathit{D}}}_2\mathit{w}\end{array}\right.$$

(16)

where

$$\left[\begin{array}{cc}\widehat{\mathit{A}}& \widehat{\mathit{B}}\\ {\widehat{\mathit{C}}}_1& {\widehat{\mathit{D}}}_1\\ {\widehat{\mathit{C}}}_2& {\widehat{\mathit{D}}}_2\end{array}\right]=\left[\begin{array}{ccc}\mathit{A}& {\mathit{B}}_2{\mathit{C}}_k& {\mathit{B}}_1\\ {\mathit{B}}_{\mathit{k}}{\mathit{C}}_3& {\mathit{A}}_{\mathit{k}}+{\mathit{B}}_{\mathit{k}}{\mathit{D}}_{32}{\mathit{C}}_{\mathit{k}}& {\mathit{B}}_{\mathit{k}}{\mathit{D}}_{31}\\ {\mathit{C}}_1& {\mathit{D}}_{12}{\mathit{C}}_{\mathit{k}}& {\mathit{D}}_{11}\\ {\mathit{C}}_2& {\mathit{D}}_{22}{\mathit{C}}_{\mathit{k}}& 0\end{array}\right]$$

and $\widehat{\mathit{x}}={[\begin{array}{cc}\mathit{x}& {\mathit{x}}_k\end{array}]}^{\mathrm{T}}$.

To achieve the multi-control objectives, the following three goals are decomposed: expected H₂ Performance, H_∞ Performance, and damping characteristics.

(1)

H₂ Performance

The H₂ norm reflects the control effort performance, the H₂ optimal control problem can be mathematically formulated as minimizing the H₂ norm defined as $T_{wz2}(s)$ with constraint η

$$\left|\right|T_{wz2}(s)|{|}_2<\eta$$

(17)

where η is the given a positive real number to obtain control effort performance. The controlled system would satisfy (17) if and only if a symmetric matrix X₂ satisfies

$$\left[\begin{array}{cc}{\widehat{\mathit{A}}}^{\mathit{T}}{\mathit{X}}_2+{\mathit{X}}_2\widehat{\mathit{A}}& {\mathit{X}}_2\widehat{\mathit{B}}\\ {\widehat{\mathit{B}}}^{\mathit{T}}{\mathit{X}}_2& -\mathit{I}\end{array}\right]<0$$

(18)

$$\left[\begin{array}{cc}{\mathit{X}}_2& {\widehat{\mathit{C}}}_2^T\\ {\widehat{\mathit{C}}}_2& \mathit{Q}\end{array}\right]>0$$

(19)

$$\mathrm{Trace}(\mathit{Q})<{\eta }^2$$

(20)

(2)

H_∞ Performance

At the same time, for a certain positive γ as the upper bound, to compromise with the uncertainty from w, the H_∞ of $T_{wz\infty }(s)$ should be constrained as

$$\left|\right|T_{wz\infty }(s)|{|}_{\infty }<\gamma$$

(21)

The inequality above would be satisfied if and only if a symmetric matrix X₁ satisfies

$$\left[\begin{array}{ccc}{\widehat{\mathit{A}}}^{\mathit{T}}{\mathit{X}}_1+{\mathit{X}}_1\widehat{\mathit{A}}& {\mathit{X}}_1\widehat{\mathit{B}}& {\widehat{\mathit{C}}}_1{}^{\mathit{T}}\\ {\widehat{B}}^{\mathit{T}}{\mathit{X}}_1& -\gamma \mathit{I}& {\widehat{\mathit{D}}}_1{}^{\mathit{T}}\\ {\widehat{\mathit{C}}}_1& {\widehat{\mathit{D}}}_1& -\gamma \mathit{I}\end{array}\right]<0$$

(22)

(3)

LMI Solution Procedure

The damping characteristic is the core of the designed controller to enhance the stability of AC grids. In other words, defining left-half D as the desirable damping zone in Figure 6, D is also called a linear matrix inequality (LMI) region. The damping effectiveness is guaranteed to be equivalent to all the poles of the G(s) within D.

To obtain the objectives of the robust controller, the linear matrix inequality (LMI) method is applied in this paper; the details are as follows. Defining matrixes $\mathit{L}\in R^{m\times m}$, $\mathit{M}\in R^{m\times m}$ and $D=\{s\in C:\mathit{L}+s\mathit{M}+s^{\ast }{\mathit{M}}^{\mathrm{T}}<0\}$, the symbol * indicates conjugation. If a symmetric matrix X₃ and the poles of $\widehat{\mathit{A}}$ satisfies

$$\left[\begin{array}{cc}\sin \theta (\widehat{\mathit{A}}{\mathit{X}}_3+{\mathit{X}}_3{\widehat{\mathit{A}}}^{\mathrm{T}})& \cos \theta (\widehat{\mathit{A}}{\mathit{X}}_3-{\mathit{X}}_3{\widehat{\mathit{A}}}^{\mathrm{T}})\\ \cos \theta ({\mathit{X}}_3{\widehat{\mathit{A}}}^{\mathrm{T}}-\widehat{\mathit{A}}{\mathit{X}}_3)& \sin \theta (\widehat{\mathit{A}}{\mathit{X}}_3+{\mathit{X}}_3{\widehat{\mathit{A}}}^{\mathrm{T}})\end{array}\right]<0$$

(23)

Then, the poles of the controlled system are constrained in D, and the damping ratios are desirable.

(4)

Multi-Objectives Solution

Further consider above matrix constraint conditions above, letting ${\mathit{X}}_1={\mathit{X}}_2={\mathit{X}}_3=\mathit{X}$, the designed K(s) can be obtained by

$$\underset{K(s)}{\min }\left\{{\lambda }_1\right||T_{wz\infty }(s)|{|}_{\infty }+{\lambda }_2\left|\right|T_{wz2}(s)\left|{|}_2\right\}$$

(24)

where λ₁ and λ₂ are the weights of robustness and control effect, respectively. For simplicity, both λ₁ and λ₂ can be set as 0.5 in this paper.

Hence, the mixed objective controller with perfect damping ratio as well as pregnant control effectiveness and robustness to perturbation can be feasible.

3.3. Multi-Terminal Controller for AC Grids

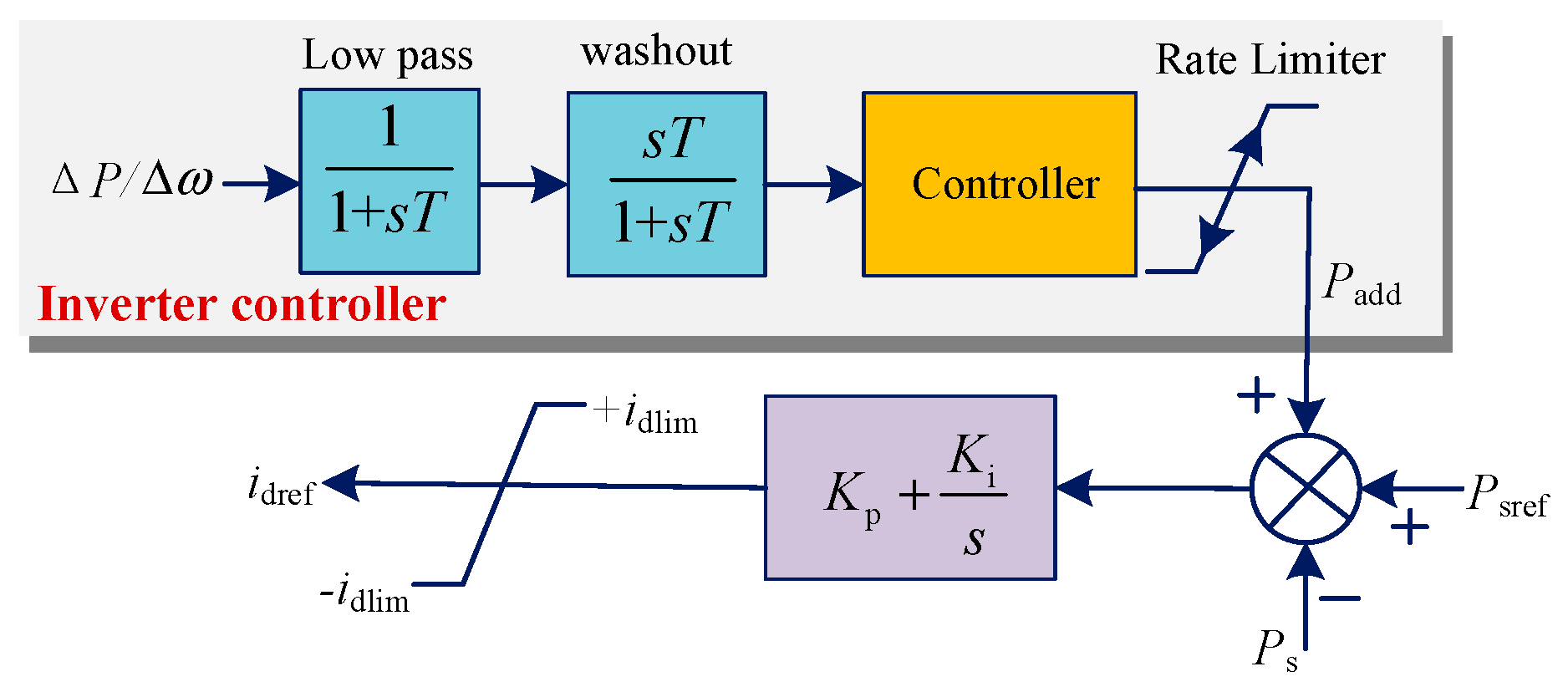
Based on the H₂/H_∞ robust control above, the supplementary controllers of both the rectifier LCC converter and the MMC3 inverter with CPC control can be designed, respectively, which are illustrated in Figure 7 and Figure 8.

4. Simulations and Verification

The hybrid HVDC system with cascaded MMCs simulation model based on a practical project is established according to Figure 1. Furthermore, the control effectiveness is simulated in this section.

4.1. The Controller Design

The aforementioned model identification is conducted by simulations in PSCAD/EMTDC. The parameters according to the actual project are given in

Table 2. The simulation parameters.

Parameters	Value	Parameters		Value	Parameters		Value
Pdc (MW)	4000	G1	PG1 (MW)	4100	G2	PG2 (MW)	1920
Pdc_lcc (MW)	3000		TJ1 (s)	6.5		TJ1 (s)	6
Pdc_mmc (MW)	667 × 3		Xd (p.u.)	1.8		Xd (p.u.)	1.5
Udc (kV)	800	G3	PG3 (MW)	530	G4/G5	PG4 (MW)	650
Udc_lcc (kV)	400		TJ1 (s)	6		TJ1 (s)	5.5
Udc_mmc (kV)	400		Xd (p.u.)	1.1		Xd (p.u.)	1.6

.

4.1.1. Identification of Controlled AC-DC System

Based on TLS-ESPRIT identification theory, the two controlled AC grids at multi-terminals can be written as G₁(s) and G₄(s), where

$$\left\{\begin{array}{c}{y}_1(s)=G_1(s)u_1(s)\\ y_4(s)=G_4(s)u_4(s)\end{array}\right.$$

(25)

Specifically, the G(s) can be identified based on the perturbation to u(s). In this study, the aim is to support AC grid stability via DC power adjustment; the generators’ output power, grid frequency, or rotor speed can be the input u. On the other hand, the DC powers of both the LCC rectifier at the sending side and MMC inverters at the inverter side are defined as the output y. To find out the ideal u, the dominant mode ratio (DMR) index is much more suitable to determine. The DMR index is formulated to measure the control effect.

$$DMR=\frac{\left|c{\varphi }_i\right|}{{\displaystyle \sum _{k=1}^n\left|c{\varphi }_k\right|\left|z_k(0)\right|}}$$

(26)

where $\left|c{\varphi }_k\right|$ and $\left|c{\varphi }_i\right|$ represent the observability of output to k_th oscillation mode and dominant mode, respectively. $\left|z_k(0)\right|$ is amplitude.

Based on the index in (26), the input signals of the LCC rectifier are compromised with the rotor speeds of G1 in sending the AC grid. The G4 in the receiving AC system is confirmed as input u of MMC inverters.

Simultaneously, the transfer functions G₁(s) and G₄(s) are obtained, respectively.

$$G_1(s)=\frac{-4.508\times {10}^{-7}{s}^4- 8.281\times {10}^{-5}{s}^3+0.009316s^2+8.287\times {10}^{-5}s}{s^4+12.26s^3+30.34s^2+236.7s+28.31}$$

(27)

$$G_4(s)=\frac{-4.395\times {10}^{-6}{s}^4-1.552\times {10}^{-5}{s}^3+0.01099s^2+0.0001569s}{s^4+11.48s^3+33.05s^2+262.7s+34.5}$$

(28)

Though the transfer function is proceeding by order-reducing progress, it is enough to acquire the significant oscillation features for controlling.

4.1.2. Controller Design

In Figure 5, the weight functions are important to be determined, and their orders should be as low as possible. In general, W₁(s) and W^₂(s) are both filters. Moreover, W₃(s) is usually regarded as a small constant. Then, they can be referred to

$$W_1(s)=\frac{5s}{s+100}$$

(29)

$$W_2(s)=\frac{100}{s+100}$$

(30)

$$W_3(s)=1$$

(31)

The design procedure can be achieved using a robust toolbox in MATLAB v2021b software. As mentioned above, the λ₁ = λ₂ = 0.5, and the damping level of ideal LMI is set to be ξ > 20%. The hinfmix function is of high efficiency to serve to design K(s).

$$\left\{\begin{array}{c}{K}_1(s)=\frac{-1207s^3-7001s^2-2.288\times 10^{4}s+7.543\times 10^4}{s^4+13.74s^3+135s^2+549.4s+1494}\\ K_4(s)=\frac{1.309s^3+91.13s^2+2140s+1.418 \times 10^4}{s^4+125.3s^3+2689s^2+1.555\times 10^{4}s+5.748\times 10^4}\end{array}\right.$$

(32)

where

$$\left\{\begin{array}{c}{u}_1(s)=K_1(s)y_1(s)\\ u_4(s)=K_4(s)y_4(s)\end{array}\right.$$

(33)

Figure 9 presents the pole locations of G₁(s), where the blue poles and red ones denote the controlled system with and without mixed robust controllers. It indicates that the proposed damping control yields the dominant poles with a stronger damping ratio.

4.2. The Simulations of Controllers

For the sake of effectiveness verification of implemented multi-terminal control, three fault circumstances considering the degree and sequence of disturbance are simulated as follows.

• Scenario 1: under small disturbances at both terminals;
• Scenario 2: under simultaneous large disturbances at both terminals;
• Scenario 3: under successive large disturbances at both terminals.

(1)

Scenario 1

In scenario 1, the small disturbances of 5% load shedding occur at the sending and ending AC system at 6 s, simultaneously, which are at the converter substation outlet lines. In steady-state operation, the hybrid HVDC transmits 4000 MW to the Jiangsu Power Grid. The rotor speed ω₁ and ω₄ of the sending and ending AC system, as well as the active power of LCC inverters, are given in Figure 10, Figure 11, Figure 12 and Figure 13.

The results of small disturbances show that the load fluctuations cause oscillations in generator rotor speed and active power. If the transmission power of the hybrid HVDC remains constant as normal operation, the power oscillation of the AC system at both terminals lasts for a long time, and the sending oscillation has not even subsided at 20 s in Figure 10. With designed multi-terminal robust controllers, both the sending LCC rectifier and the ending MMC inverter with CPC adjust their DC power based on changes in the rotor angle. This means the hybrid HVDC has the ability to participate in stability improvement by tuning the active power in Figure 12 and Figure 13; this is beneficial to compensate for unbalanced power. The damping of both sending and ending systems is strengthened because the results present ω₁ and ω₄ restored to a steady state at about 15 s and 9 s, respectively. Thus, the small-signal stabilities of both terminals are enhanced; in other words, the control effectiveness is verified.

(2)

Scenario 2

In scenario 2, single-phase grounding faults occur at the sending and ending AC bus at 6 s and last for 0.01 s simultaneously. The consequential results are given in Figure 14, Figure 15, Figure 16 and Figure 17.

It is evident that although the low-frequency oscillation is worse than small disturbance, the proposed multi-terminal robust controllers are also effective under simultaneous large disturbance. By the function of power modulation and damping control, the damping level of sending and ending systems has been increased by 37% and 62%, respectively. The oscillation is declined in a shorter duration with the robust control. Hence, the robustness of the proposed controller under different disturbances has proved to be effective.

(3)

Scenario 3

To further prove the control characteristics of multi-terminal control, the successive large disturbances are simulated in scenario 3. A single-phase grounding fault is simulated at the sending AC side at 6 s and the ending AC side at 8 s, respectively. The duration is 0.01 s. Moreover, a classical PI controller is configured there for comparisons. The control effect is expressed in Figure 18, Figure 19, Figure 20 and Figure 21.

It is evident that even when AC systems are faced with the risk of successive large disturbances, the designed controllers and parameters are feasible to effectively suppress system power oscillations. On the one hand, the proposed damping controller performs better than the PI controller on both sending and receiving AC faults, as shown in Figure 18 and Figure 19. On the other hand, the controllers decrease the rotor speed fluctuation and power fluctuation significantly from Figure 19 and Figure 20, which means the proposed controller not only improves the system damping but also enhances the transient stability of the system.

In conclusion, based on the simulations of the three fault scenarios above, the effectiveness and strong robustness of multi-terminal control have been verified. The multi-terminal control makes use of both the LCC rectifier and MMC inverters to promote the stability of AC grids tremendously.

5. Conclusions

The hybrid HVDC system with cascaded MMCs is applied in practical long-distance transmission projects. This study investigates both essential master–slave control characteristics and implements multi-terminal coordinated damping control to make use of its fast adjustment capacity. The main conclusions are obtained.

(1) The inverters of a hybrid cascaded HVDC transmission system can be seen as an LCC inverter in series with multi-infeed MMCs, possessing a larger transmission capacity than LCC-VSC HVDC. The characteristics of the hybrid HVDC are analyzed, and it finds that the master–slave control mode of MMCs leads to stable DC voltage and precise power control, which is more suitable for actual project operation;

(2) The power controllability of a hybrid cascaded HVDC system is more flexible, which yields an alternative for stability support for sending and receiving AC grids. We proposed a multi-terminal coordinated control method. The controllers on both the LCC rectifier and MMC inverters are designed by TLS-ESPRIT identification, H₂/H_∞mixed robust theory, and LMI solution procedure and both damping enhancement and robustness are guaranteed;

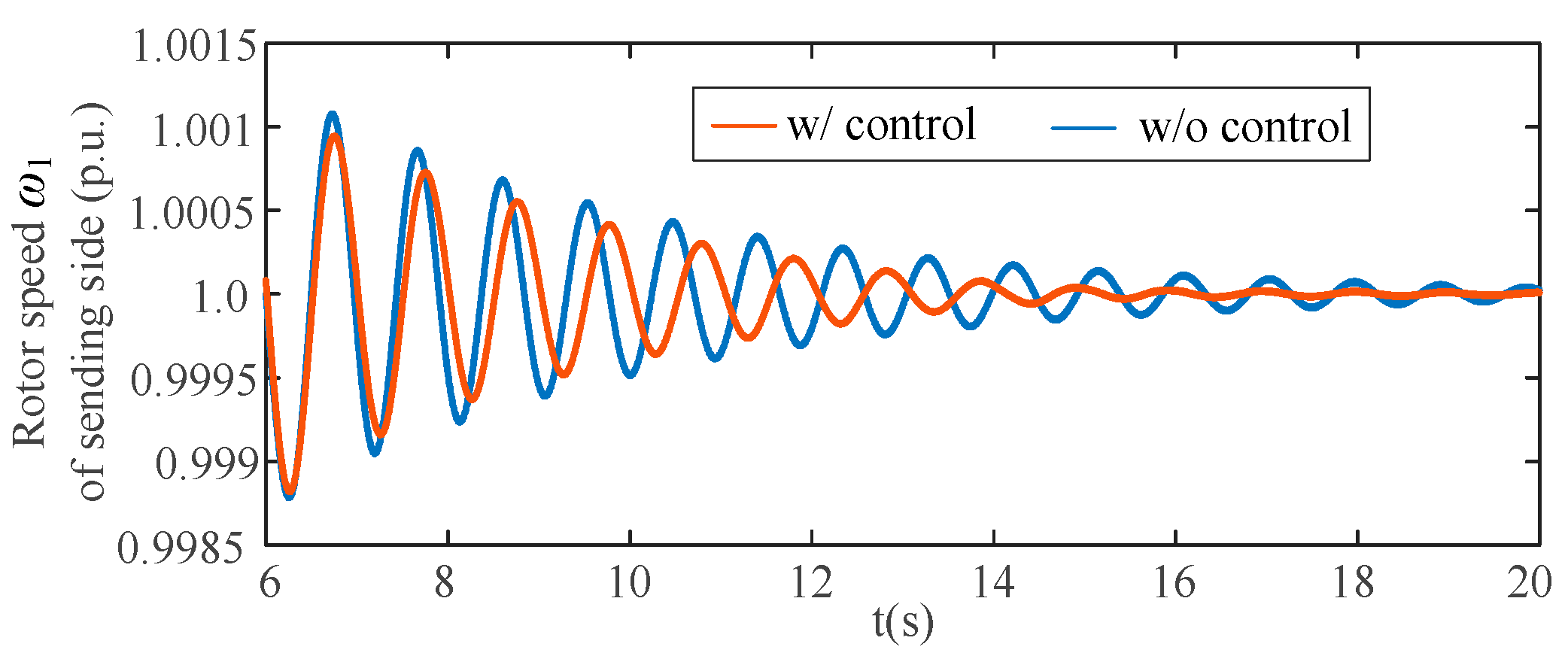
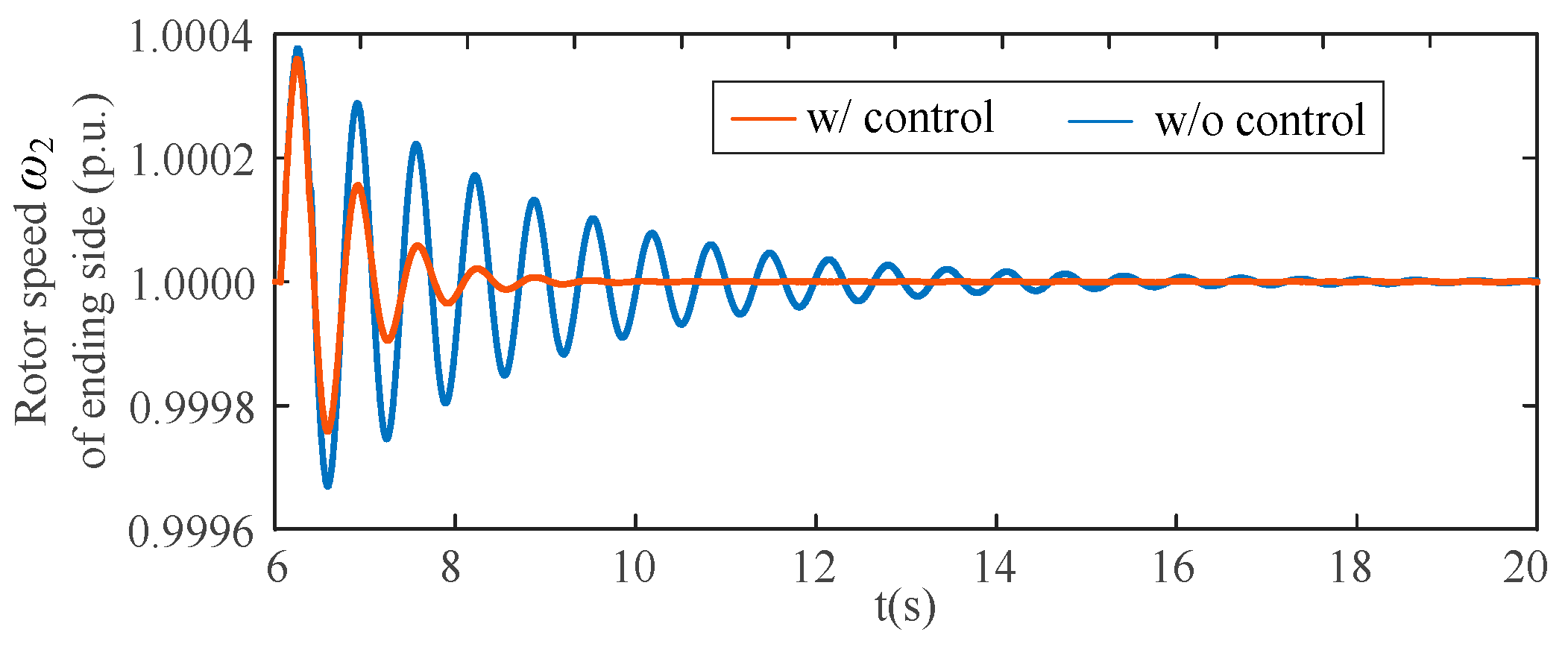
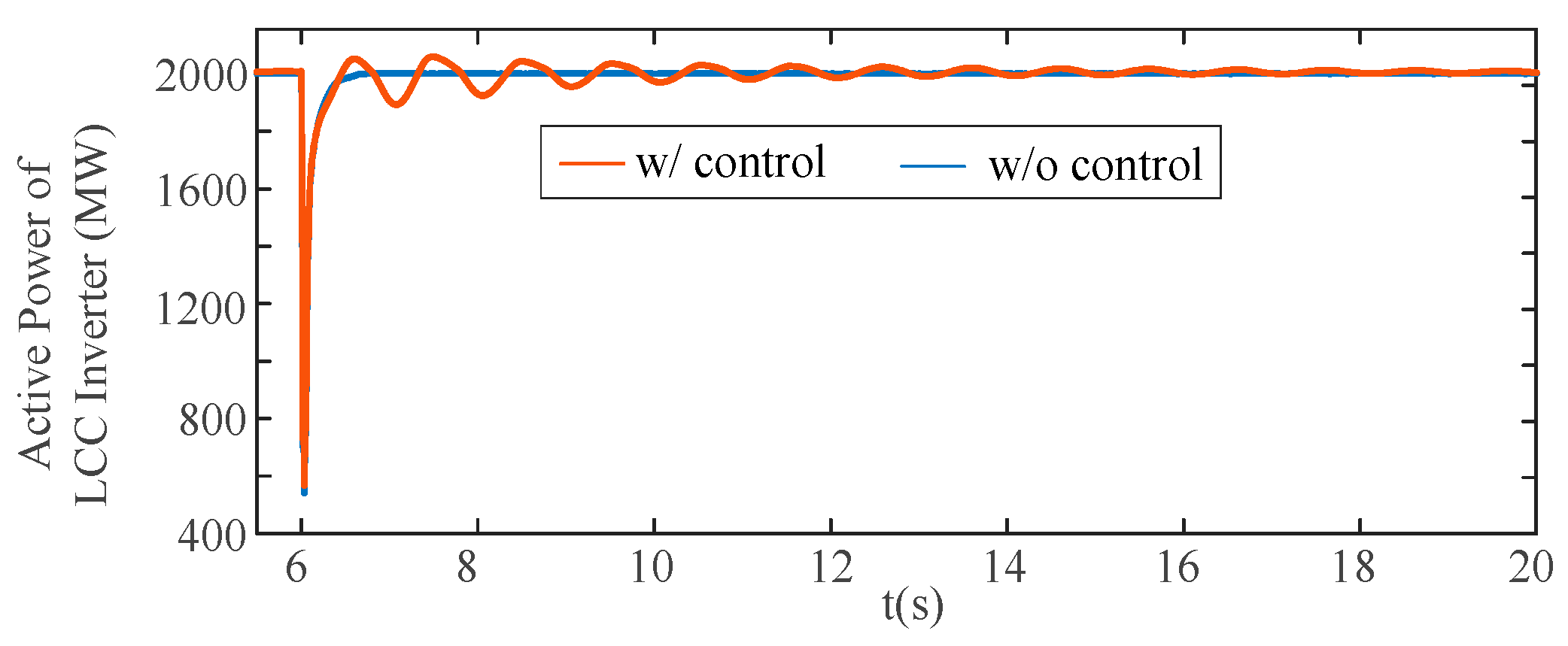
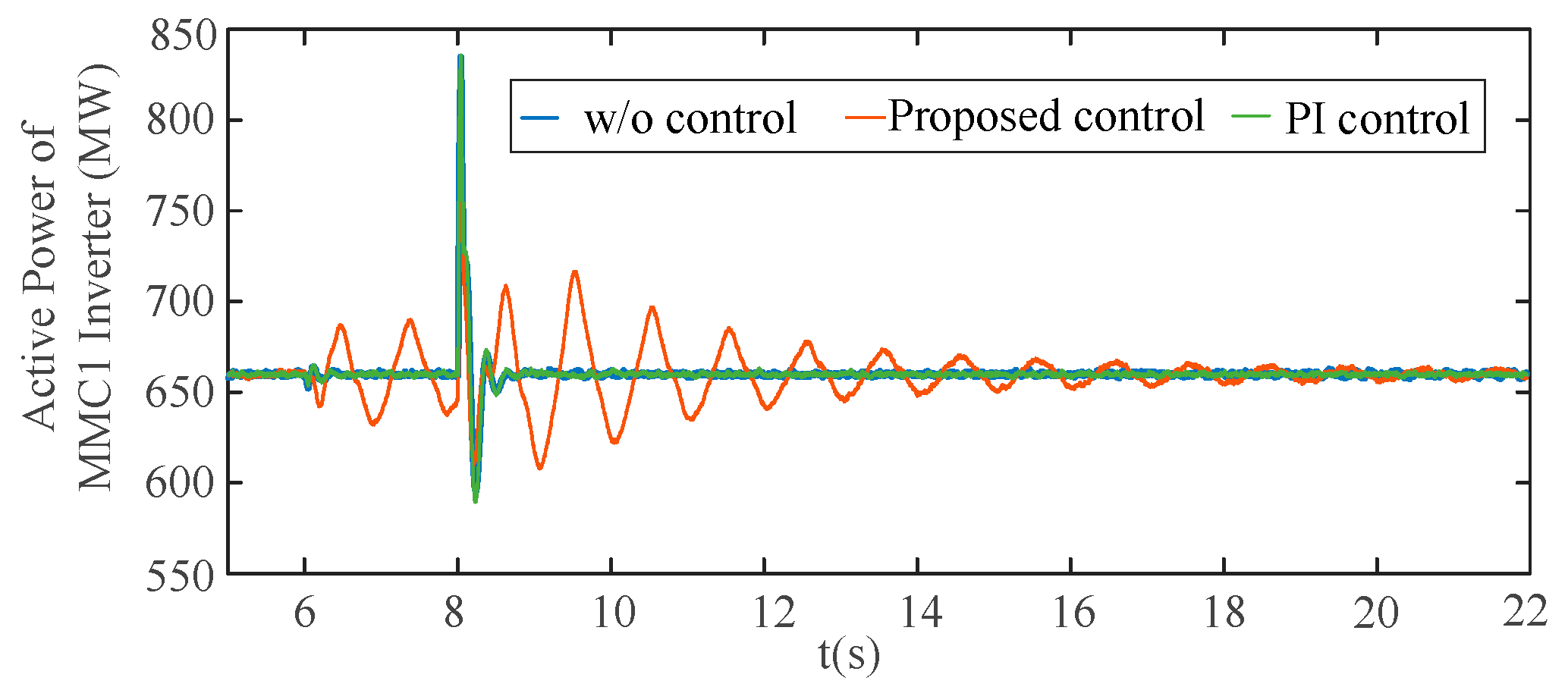
(3) Simulation results based on actual engineering parameters show satisfactory damping performance, and the proposed coordinated robust control is robust to various disturbances at both AC grids;

(4) In future studies, the integration of renewable energy and coordinated control with multiple DC lines can be further considered.