Learing Sampling and Reconstruction Using Bregman Iteration for CS-MRI
Abstract
:1. Introduction
Related Work
2. Proposed Method
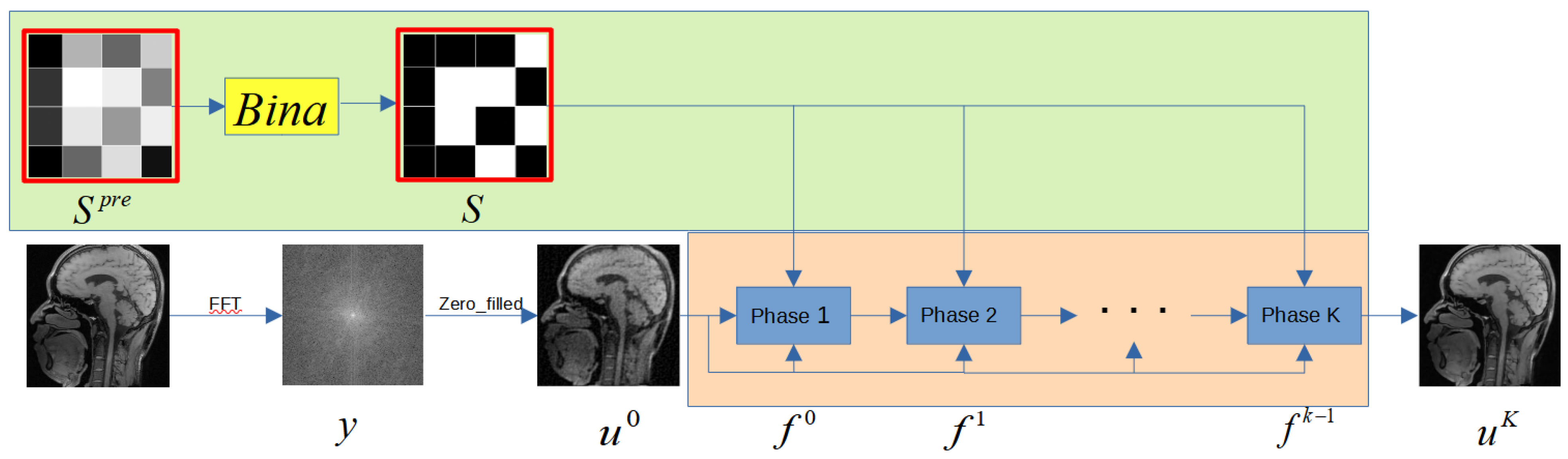
2.1. Problem Formulation
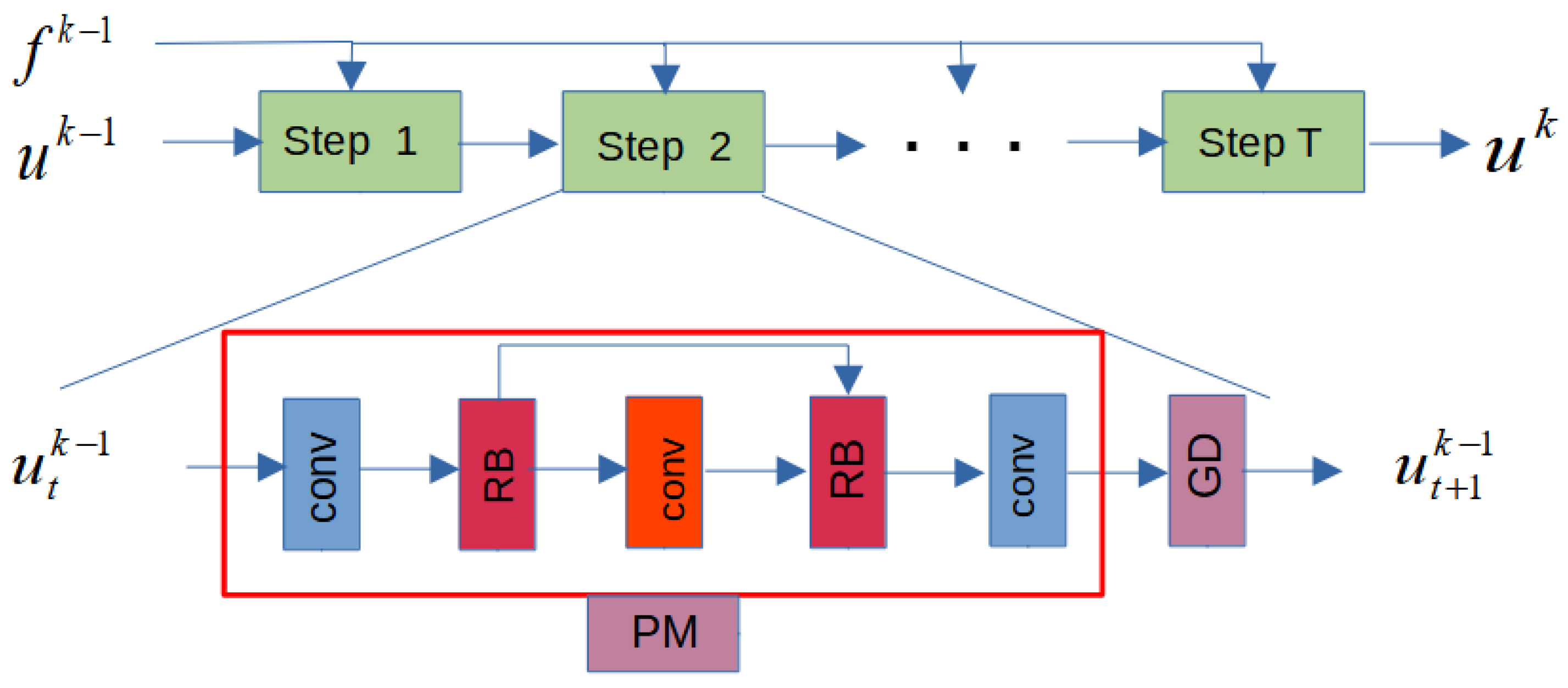
2.2. Reconstruction Subnet
2.3. Sampling Subnet
2.4. Initialization and Parameters
3. Experiment
3.1. Comparison with Classical Masking under Multiple Reconstruction Methods
3.2. Comparison with State-of-the-Art Methods
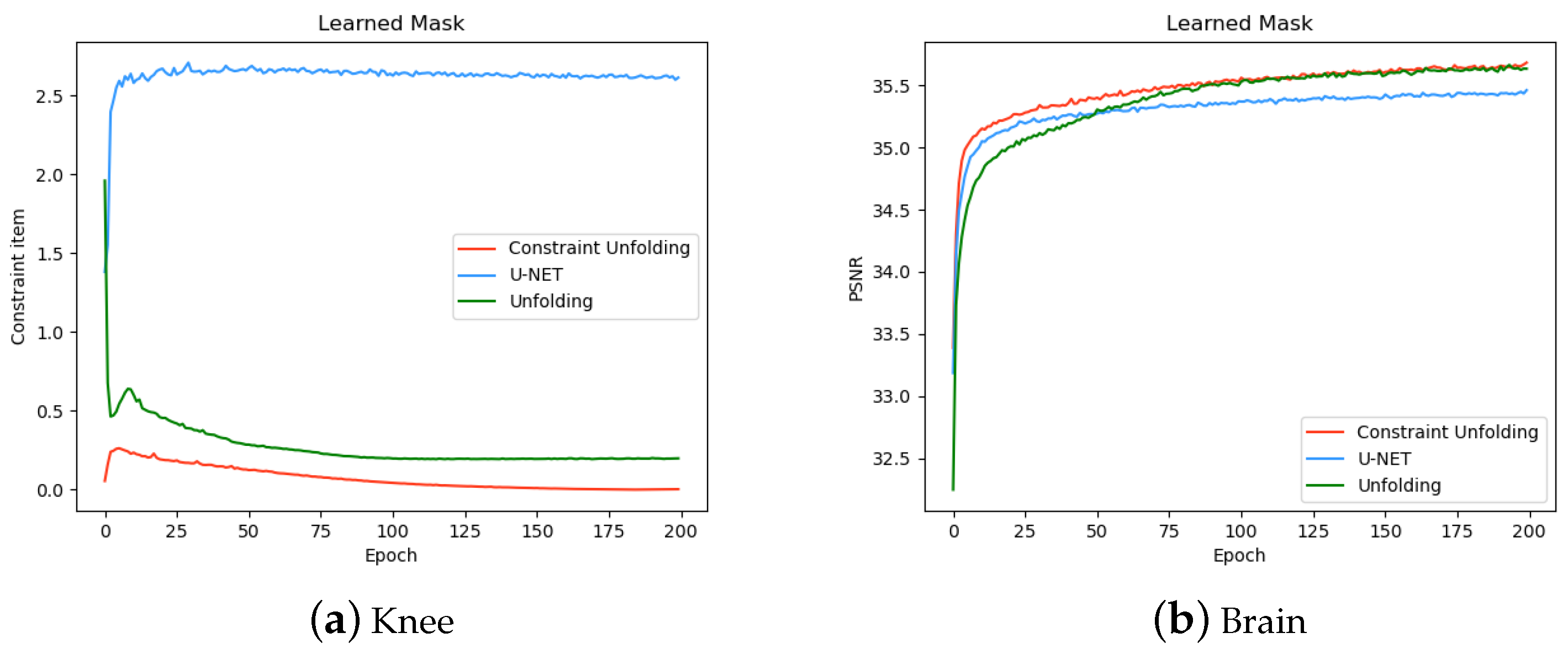
3.3. Effect of Data Constraints
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Haldar, J.P.; Hernando, D.; Liang, Z.-P. Compressed-Sensing MRI With Random Encoding. IEEE Trans. Med Imaging 2010, 30, 893–903. [Google Scholar] [CrossRef]
- Gamper, U.; Boesiger, P.; K ó zerke, S. Compressed sensing in dynamic MRI. Magn. Reson. Med. 2008, 59, 365–373. [Google Scholar] [CrossRef]
- Letourneau, M.; Sharp, J.W.; Wang, Z.; Arce, G.R. Variable density compressed image sampling. IEee Trans. Image Process. 2009, 19, 264–270. [Google Scholar]
- Yiasemis, G.; Zhang, C.; Sánchez, C.I.; Fuller, C.D.; Teuwen, J. Deep MRI reconstruction with radial subsampling. Med. Imaging 2022 Phys. Med. Imaging 2022. [Google Scholar] [CrossRef]
- Lustig, M.; Pauly, J.M. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010, 64, 457–471. [Google Scholar] [CrossRef]
- Ehrhardt, M.; Betcke, M.M. Multi-Contrast MRI Reconstruction with Structure-Guided Total Variation. Siam J. Imaging Sci. 2016, 9, 1084–1106. [Google Scholar] [CrossRef]
- Block, K.T.; Uecker, M.; Frahm, J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn. Reson. Med. 2007, 57, 1086–1098. [Google Scholar] [CrossRef]
- Trzasko, J.; Manduca, A. Highly Undersampled Magnetic Resonance Image Reconstruction via Homotopic l0-Minimization. IEEE Trans. Med. Imaging 2009, 28, 106–121. [Google Scholar] [CrossRef]
- Qu, X.; Guo, D.; Ning, B.; Hou, Y.; Lin, Y.; Cai, S.; Chen, Z. Undersampled MRI reconstruction with patch-based directional wavelets. Magn. Reson. Imaging 2012, 30, 964–977. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.; Yin, W. A fast alternating direction method for TVL1-L2 signal reconstruction from partial fourier data. IEEE J. Sel. Top. Signal Process. 2010, 4, 288–297. [Google Scholar] [CrossRef]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An Iterative Regularization Method for Total Variation-Based Image Restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Zhang, K.; Gool, L.V.; Timofte, R. Deep Unfolding Network for Image Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhang, J.; Ghanem, B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Qin, C.; Schlemper, J.; Caballero, J.; Price, A.N.; Hajnal, J.V.; Rueckert, D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med Imaging 2018, 38, 280–290. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. “U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Martinez, B.; Yang, J.; Bulat, A.; Tzimiropoulos, G. Training binary neural networks with real-to-binary convolutions. arXiv 2019, arXiv:2003.11535. [Google Scholar]
- Matthieu, C.; Itay, H.; Daniel, S.; Ran, E.; Yoshua, B. Bi-narized Neural Networks: Training Deep Neural Networks with Weights and ActivationsConstrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Xie, J.; Zhang, J.; Zhang, Y.; Ji, X. PUERT: Probabilistic Under-Sampling and Explicable Reconstruction Network for CS-MRI. IEEE J. Sel. Top. Signal Process. 2022, 16, 737–749. [Google Scholar] [CrossRef]
- Benning, M.; Gladden, L.; Holland, D.; Schönlieb, C.-B.; Valkonen, T. Phase reconstruction from velocity-encoded MRI measurements—A survey of sparsity-promoting variational approaches. J. Magn. Reson. 2014, 238, 26–43. [Google Scholar] [CrossRef]
- Zhao, N.; Wei, Q.; Basarab, A.; Dobigeon, N.; Kouamé, D.; Tourneret, J.-Y. Fast Single Image Super-Resolution Using a New Analytical Solution for l2 − l2 Problems. IEEE Trans. Image Process. 2016, 25, 3683–3697. [Google Scholar] [CrossRef]
- Nikam, R.D.; Lee, J.; Choi, W.; Kim, D.; Hwang, H. On-Chip Integrated Atomically Thin 2D Material Heater as a Training Accelerator for an Electrochemical Random-Access Memory Synapse for Neuromorphic Computing Application. ACS Nano 2022, 16, 12214–12225. [Google Scholar] [CrossRef]
- Nikam, R.D.; Kwak, M.; Hwang, H. All-Solid-State Oxygen Ion Electrochemical Random-Access Memory for Neuromorphic Computing. Adv. Electron. Mater. 2021, 7, 2100142. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Jacob, M. J-MoDL: Joint Model-Based Deep Learning for Optimized Sampling and Reconstruction. IEEE J. Sel. Top. Signal Process. 2020, 14, 1151–1162. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Su, Z.; Ying, L.; Peng, X.; Zhu, S.; Liang, F.; Feng, D.; Liang, D. Accelerating magnetic resonance imaging via deep learning. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. Deep ADMM-Net for compressive sensing MRI. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Yang, G.; Yu, S.; Dong, H.; Slabaugh, G.; Dragotti, P.L.; Ye, X.; Liu, F.; Arridge, S.; Keegan, J.; Guo, Y.; et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1310–1321. [Google Scholar] [CrossRef]
- Jun, Y.; Shin, H.; Eo, T.; Hwang, D. Joint Deep Model-based MR Image and Coil Sensitivity Reconstruction Network (Joint-ICNet) for Fast MRI. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Eksioglu, E.M. Decoupled Algorithm for MRI Reconstruction Using Nonlocal Block Matching Model: BM3D-MRI. J. Math. Imaging Vis. 2016, 56, 430–440. [Google Scholar] [CrossRef]
- Chen, S.; Luo, C.; Deng, B.; Qin, Y.; Wang, H.; Zhuang, Z. BM3D vector approximate message passing for radar coded-aperture imaging. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Fall (PIERS—FALL), Singapore, 19–22 November 2017. [Google Scholar]
- Bahadir, C.D.; Wang, A.Q.; Dalca, A.V.; Sabuncu, M.R. Deep-Learning-Based Optimization of the Under-Sampling Pattern in MRI. IEEE Trans. Comput. Imaging 2020, 6, 1139–1152. [Google Scholar] [CrossRef]
- Lee, D.H.; Hong, C.P.; Lee, M.W.; Kim, H.J.; Jung, J.H.; Shin, W.H.; Kang, J.; Kang, S.; Han, B.S. Sparse sampling MR image reconstruction using bregman iteration: A feasibility study at low tesla MRI system. In Proceedings of the 2011 IEEE Nuclear Science Symposium Conference Record, Valencia, Spain, 23–29 October 2011. [Google Scholar]
- Zibetti, M.V.W.; Herman, G.T.; Regatte, R.R. Fast data-driven learning of parallel MRI sampling patterns for large scale problems. Sci. Rep. 2021, 11, 19312. [Google Scholar] [CrossRef]
- Choi, J.; Kim, H. Implementation of time-efficient adaptive sampling function design for improved undersampled MRI reconstruction. J. Magn. Reson. 2016, 273, 47–55. [Google Scholar] [CrossRef]
- Gözcü, B.; Mahabadi, R.K.; Li, Y.H.; Ilıcak, E.; Cukur, T.; Scarlett, J.; Cevher, V. Learning-based compressive MRI. IEEE Trans. Med. Imaging 2018, 37, 1394–1406. [Google Scholar]
- Sherry, F.; Benning, M.; De los Reyes, J.C.; Graves, M.J.; Maierhofer, G.; Williams, G.; Schönlieb, C.; Ehrhardt, M.J. Learning the sampling pattern for MRI. IEEE Trans. Med. Imaging 2020, 39, 4310–4321. [Google Scholar] [CrossRef]
- Simons, T.; Lee, D.-J. A Review of Binarized Neural Networks. Electronics 2019, 8, 661. [Google Scholar] [CrossRef]
- Alizadeh, M.; Fernández-Marqués, J.; Lane, N.D.; Gal, Y. An empirical study of binary neural networks optimisation. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Lin, X.; Zhao, C.; Pan, W. Towards accurate binary convolutional neural network. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zbontar, J.; Knoll, F.; Sriram, A.; Murrell, T.; Huang, Z.; Muckley, M.J.; Defazio, A.; Stern, R.; Johnson, P.; Bruno, M.; et al. FastMRI: An open dataset and benchmarks for accelerated MRI. arXiv 2018, arXiv:1811.08839. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]







| Brain | |||||
|---|---|---|---|---|---|
| Method | VD-2D | Random | Radial | LOUPE | Proposed |
| BM3D-MRI | 32.12 | 32.98 | 31.84 | 34.62 | 34.84 |
| U-Net | 32.41 | 32.91 | 31.21 | 34.78 | 35.34 |
| OUR | 32.49 | 32.37 | 31.77 | 34.66 | 35.62 |
| Dataset | Method | Mask | CS Ratio | ||
|---|---|---|---|---|---|
| 5% | 10% | 20% | |||
| Brain | Zero _ Filled | Radial | 25.31/0.5824 | 27.02/0.6085 | 29.12/0.6717 |
| U-Net | 32.13/0.8433 | 35.21/0.8874 | 38.35/0.9328 | ||
| Admm-Net | 31.48/0.8371 | 34.92/0.9052 | 37.72/0.9343 | ||
| Ista-Net | 31.72/0.8453 | 34.66/0.8692 | 37.49/0.9404 | ||
| LOUPE | 1d | 32.17/0.8233 | 35.49/0.9140 | 36.62/0.9136 | |
| 2d | 35.66/0.9121 | 38.16/0.9259 | 39.21/0.9473 | ||
| PUERT | 1d | 32.33/0.8677 | 35.82/0.9142 | 37.17/0.9227 | |
| 2d | 35.48/0.9027 | 38.23/0.9410 | 39.74/0.9590 | ||
| Proposed | 1d | 32.14/0.8414 | 35.61/0.9167 | 37.22/0.9214 | |
| 2d | 36.12/0.9245 | 38.56/0.9345 | 39.41/0.9526 | ||
| Knee | Zero _ Filled | Radial | 24.93/0.5930 | 27.56/0.6227 | 28.71/0.6564 |
| U-Net | 29.17/0.6618 | 32.54/0.6866 | 35.66/0.7930 | ||
| Admm-Net | 29.05/0.6927 | 32.06/0.7280 | 35.24/0.8057 | ||
| Ista-Net | 29.41/0.6714 | 31.97/0.7043 | 35.08/0.7794 | ||
| LOUPE | 1d | 30.37/0.6991 | 31.93/0.7178 | 33.85/0.7428 | |
| 2d | 31.46/0.7316 | 34.14/0.7671 | 36.41/0.8590 | ||
| PUERT | 1d | 30.71/0.6824 | 32.57/0.7143 | 34.23/0.7411 | |
| 2d | 31.76/0.7230 | 34.02/0.7573 | 36.24/0.8568 | ||
| Proposed | 1d | 30.47/0.6726 | 33.61/0.7268 | 34.28/0.7467 | |
| 2d | 32.57/0.7557 | 34.41/0.7829 | 36.36/0.8624 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, T.; Feng, X. Learing Sampling and Reconstruction Using Bregman Iteration for CS-MRI. Electronics 2023, 12, 4657. https://doi.org/10.3390/electronics12224657
Fei T, Feng X. Learing Sampling and Reconstruction Using Bregman Iteration for CS-MRI. Electronics. 2023; 12(22):4657. https://doi.org/10.3390/electronics12224657
Chicago/Turabian StyleFei, Tiancheng, and Xiangchu Feng. 2023. "Learing Sampling and Reconstruction Using Bregman Iteration for CS-MRI" Electronics 12, no. 22: 4657. https://doi.org/10.3390/electronics12224657
APA StyleFei, T., & Feng, X. (2023). Learing Sampling and Reconstruction Using Bregman Iteration for CS-MRI. Electronics, 12(22), 4657. https://doi.org/10.3390/electronics12224657






