Human Body as a Signal Transmission Medium for Body-Coupled Communication: Galvanic-Mode Models
Abstract
:1. Introduction
- Present two electrical circuit models of a BCC system: one adapted from existing work (Model #1) and another that is simpler but similarly accurate (Model #2);
- Provide closed-form expressions of the transfer function in both circuit models;
- Apply linear regression and random forest regression methods to construct and evaluate multiple predictive models.
2. Related Work
3. Electrical Circuit Models
3.1. Problem Formulation
- Makes the system more energy-efficient and alleviates any health-related concerns by minimizing the electric current that enters the human body;
- Reduces the sophistication required from the detector on the Rx side, as higher amplitude signals are easier to register and decode without errors.
- Provide circuit models (Figure 1 and Figure 4) of the communication system that include the human body and the BCC equipment;
- Simplify and divide the models into parts to make it tractable to express the AFR with closed-form algebraic equations;
- Find nominal values of the components in the models using experimental AFR data as the ground truth.
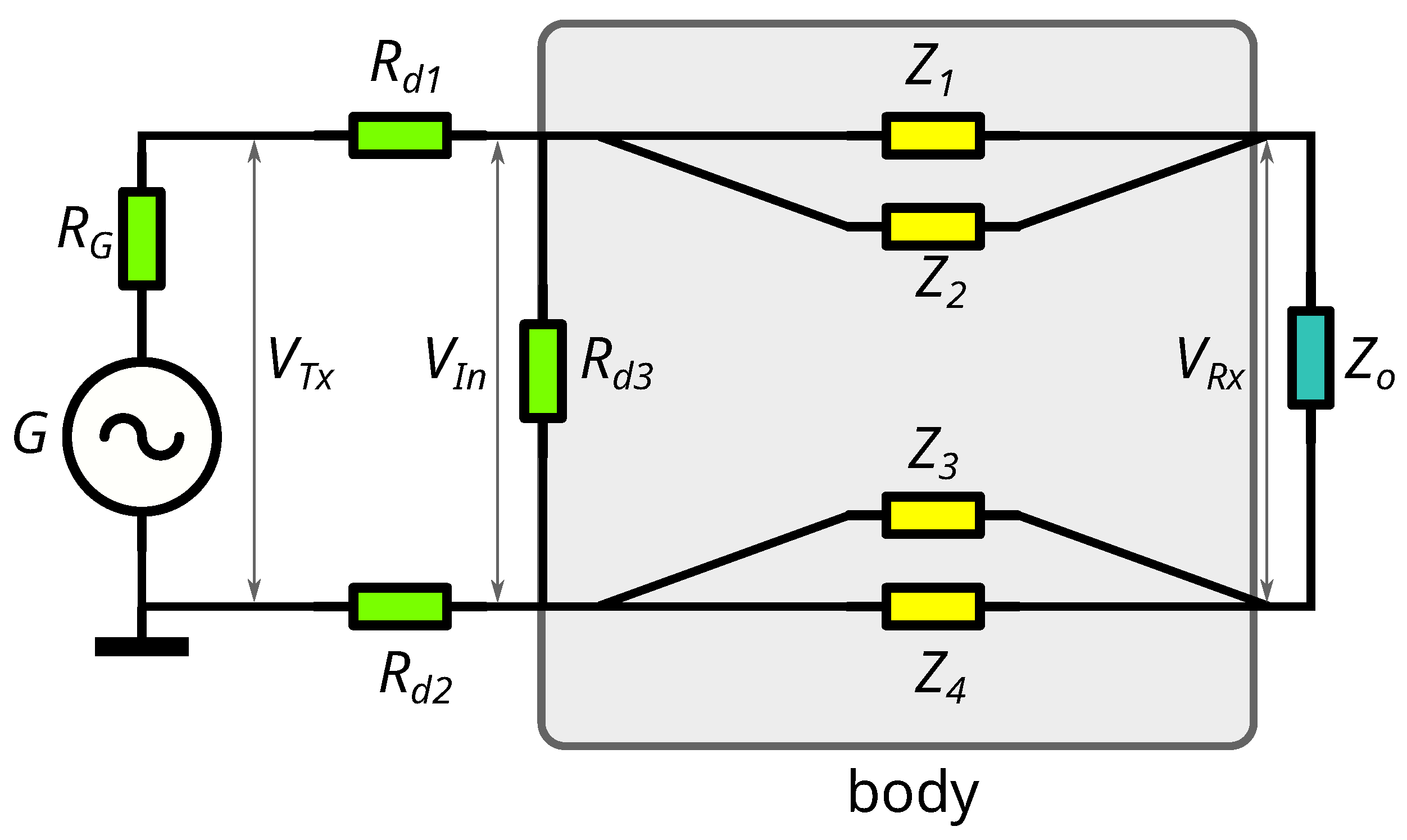
3.2. Circuit Model #1
- G and — signal generator and its internal resistance;
- — resistances related to electrode and skin contacts;
- — the entry impedance of the signal detector;
- — impedances between the receiver and transmitter electrodes.
3.3. Circuit Model #2
3.4. Instantiation of the Models
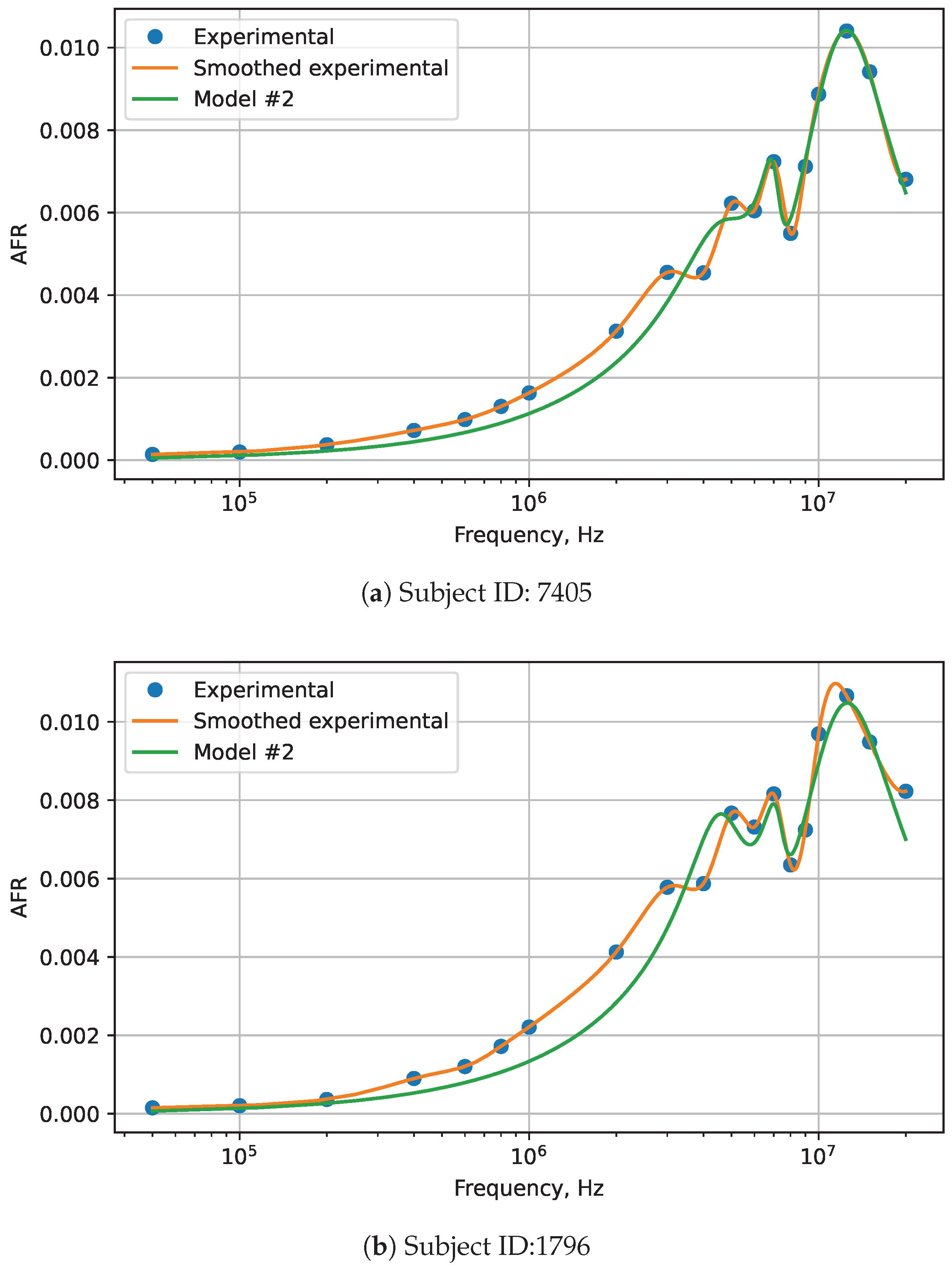
3.5. Model #1 Instantiation
3.6. Model #2 Instantiation
4. Predictive Models
4.1. Problem Formulation
- Create a single model that takes the frequency as one of the input data features.
- Create a custom-fitted model for each of the measured frequencies.
4.2. Model Description
- Linear regression models;
- Random forest (RF) regression models.
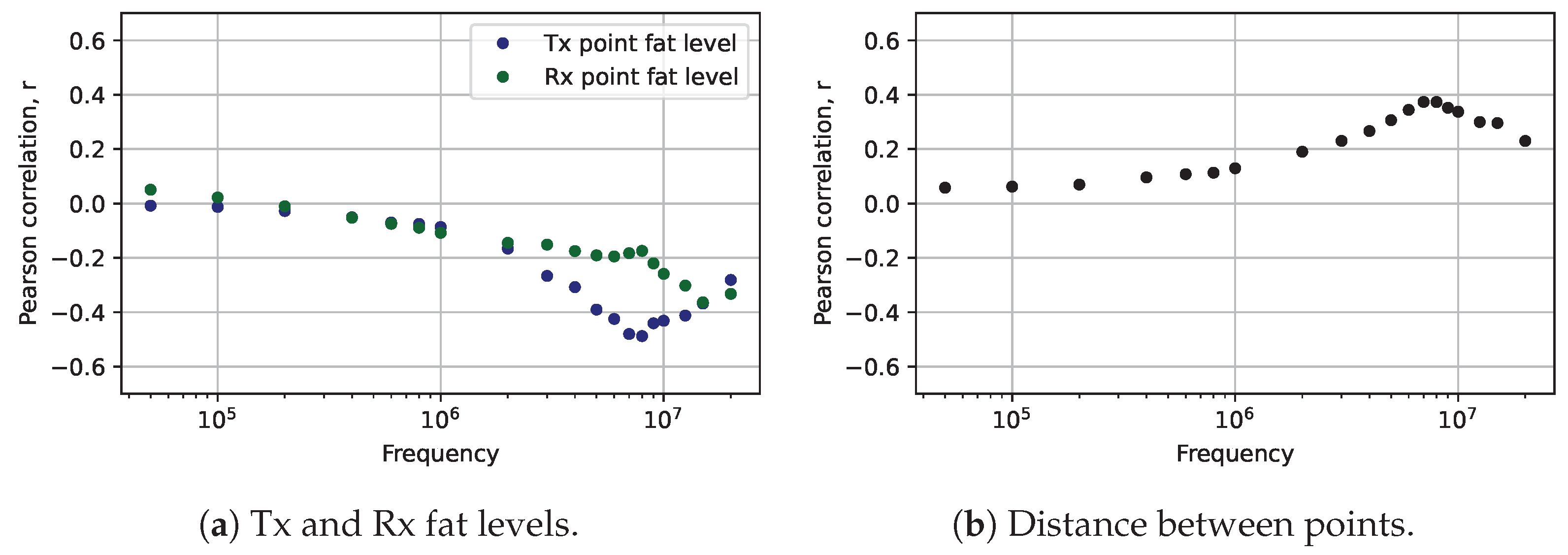
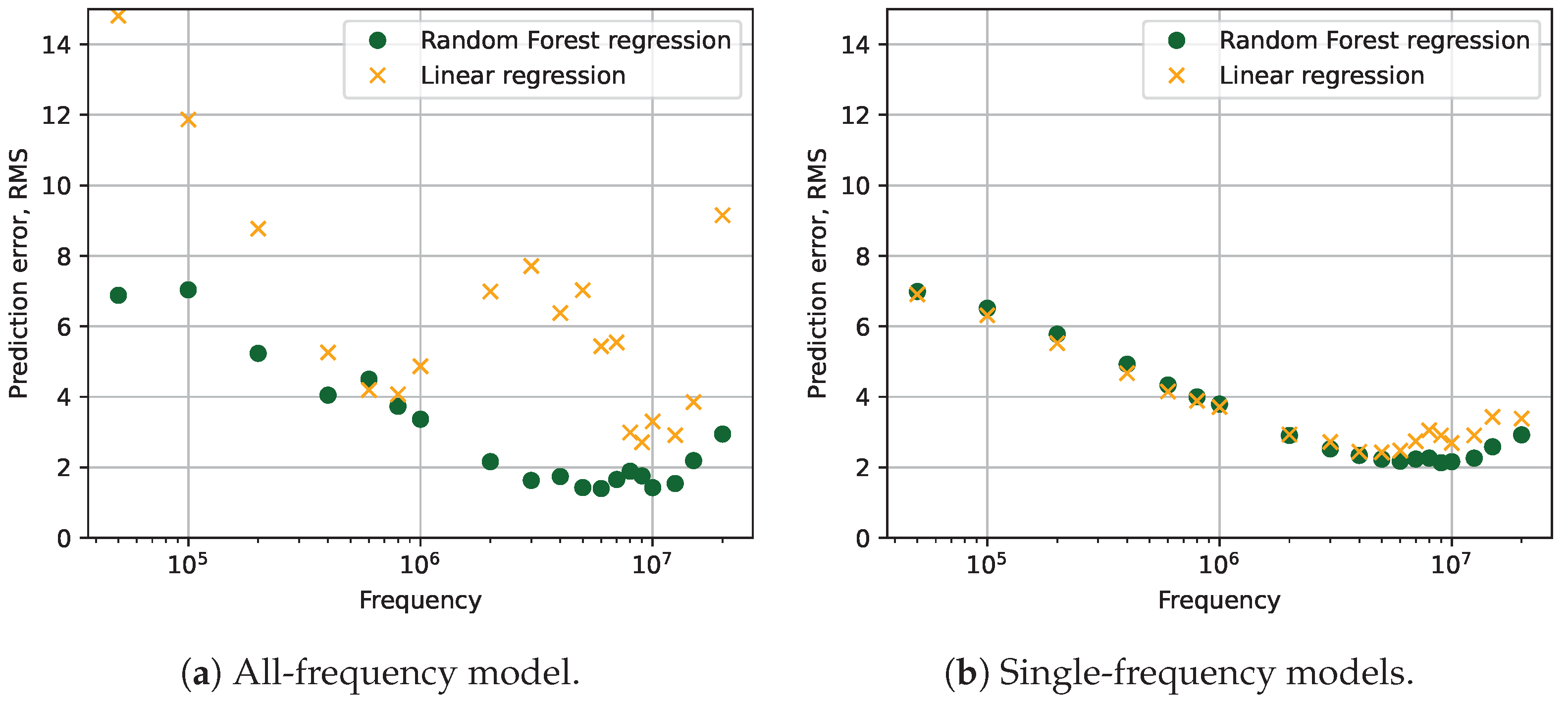
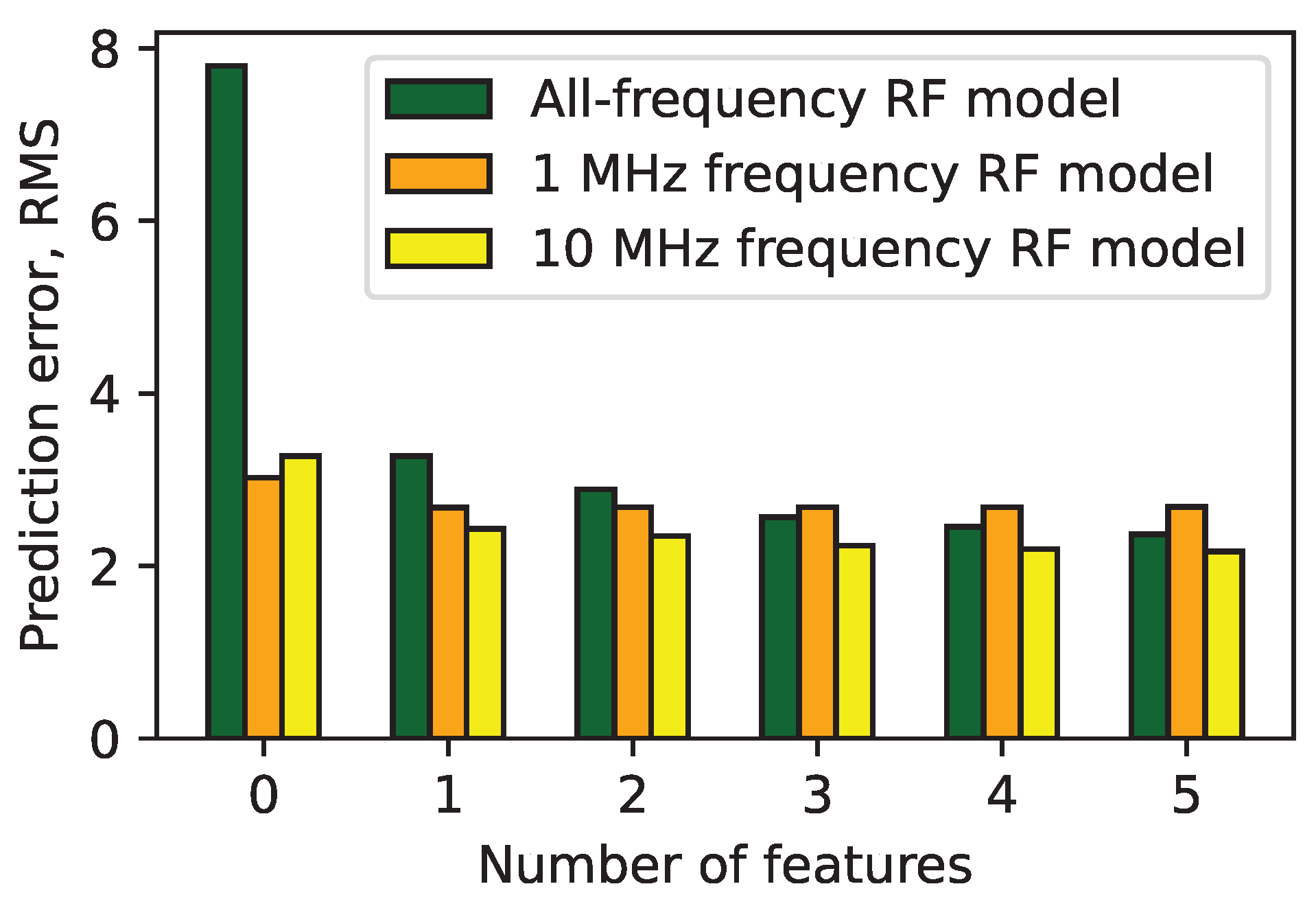
4.3. Model Evaluation
- The linear regression model, with frequency as the input data, has larger errors as it fails to capture the complex, nonlinear relationship between the input variables and the signal loss.
- For the other models, the prediction error is the highest at the lower frequencies; this decreases up to 10 MHz, reaching or going below 2 dB RMSE, and then starts increasing again.
- If the frequency is fixed, linear regression shows a similar performance to RF.
- RF shows even better results if the frequency is passed as a feature, likely due to the larger training dataset size.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maity, S.; Das, D.; Sen, S. Wearable health monitoring using capacitive voltage-mode human body communication. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Republic of Korea, 11–15 July 2017; pp. 1–4. [Google Scholar]
- Ormanis, J.; Medvedevs, V.; Aristovs, V.; Abolins, V.; Sevcenko, A.; Elsts, A. Dataset on the Human Body as a Signal Propagation Medium. 2023. Available online: https://zenodo.org/records/8214497 (accessed on 4 November 2023). [CrossRef]
- Ormanis, J.; Medvedevs, V.; Sevcenko, A.; Aristov, V.; Abolins, V.; Elsts, A. Dataset on the Human Body as a Signal Propagation Medium for Body Coupled Communication. Submitt. Data Brief 2023. [Google Scholar]
- Medvedevs, V.; Elsts, A. Simulating the Physical Layer of Body-Coupled Communication Protocols. In Proceedings of the International Workshop on Embedded Digital Intelligence (IWoEDI’2023), Riga, Latvia, 20–22 June 2023. [Google Scholar]
- Aristovs, V.; Elsts, A. Model of the Human Body as Signal Transmission Medium for Body-Coupled Communication. In Proceedings of the International Workshop on Embedded Digital Intelligence (IWoEDI’2023), Riga, Latvia, 20–22 June 2023. [Google Scholar]
- Wegmueller, M.S.; Oberle, M.; Felber, N.; Kuster, N.; Fichtner, W. Signal transmission by galvanic coupling through the human body. IEEE Trans. Instrum. Meas. 2009, 59, 963–969. [Google Scholar] [CrossRef]
- Zhao, J.F.; Chen, X.M.; Liang, B.D.; Chen, Q.X. A review on human body communication: Signal propagation model, communication performance, and experimental issues. Wirel. Commun. Mob. Comput. 2017, 2017, 5842310. [Google Scholar] [CrossRef]
- Sen, S.; Maity, S.; Das, D. The body is the network: To safeguard sensitive data, turn flesh and tissue into a secure wireless channel. IEEE Spectr. 2020, 57, 44–49. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless body area networks: A survey. IEEE Commun. Surv. Tutorials 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Tang, T.; Yan, L.; Park, J.H.; Wu, H.; Zhang, L.; Li, J.; Dong, Y.; Lee, B.H.Y.; Yoo, J. An active concentric electrode for concurrent EEG recording and body-coupled communication (BCC) data transmission. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1253–1262. [Google Scholar] [CrossRef]
- Maity, S.; Chatterjee, B.; Chang, G.; Sen, S. BodyWire: A 6.3-pJ/b 30-Mb/s- 30-dB SIR-tolerant broadband interference-robust human body communication transceiver using time domain interference rejection. IEEE J. Solid-State Circuits 2019, 54, 2892–2906. [Google Scholar] [CrossRef]
- Lucev, Ž.; Krois, I.; Cifrek, M. A capacitive intrabody communication channel from 100 kHz to 100 MHz. IEEE Trans. Instrum. Meas. 2012, 61, 3280–3289. [Google Scholar] [CrossRef]
- Song, Y.; Hao, Q.; Zhang, K. Review of the modeling, simulation and implement of intra-body communication. Def. Technol. 2013, 9, 10–17. [Google Scholar] [CrossRef]
- Maity, S.; He, M.; Nath, M.; Das, D.; Chatterjee, B.; Sen, S. Bio-physical modeling, characterization, and optimization of electro-quasistatic human body communication. IEEE Trans. Biomed. Eng. 2018, 66, 1791–1802. [Google Scholar] [CrossRef]
- Modak, N.; Nath, M.; Chatterjee, B.; Maity, S.; Sen, S. Bio-physical modeling of galvanic human body communication in electro-quasistatic regime. IEEE Trans. Biomed. Eng. 2022, 69, 3717–3727. [Google Scholar] [CrossRef]
- Park, J.; Garudadri, H.; Mercier, P.P. Channel modeling of miniaturized battery-powered capacitive human body communication systems. IEEE Trans. Biomed. Eng. 2016, 64, 452–462. [Google Scholar]
- Ito, K.; Hotta, Y. Signal path loss simulation of human arm for galvanic coupling intra-body communication. J. Adv. Simul. Sci. Eng. 2016, 3, 29–46. [Google Scholar] [CrossRef]
- Wen, E.; Sievenpiper, D.F.; Mercier, P.P. Channel characterization of magnetic human body communication. IEEE Trans. Biomed. Eng. 2021, 69, 569–579. [Google Scholar] [CrossRef] [PubMed]
- Asan, N.B.; Hassan, E.; Perez, M.D.; Shah, S.R.M.; Velander, J.; Blokhuis, T.J.; Voigt, T.; Augustine, R. Assessment of blood vessel effect on fat-intrabody communication using numerical and ex-vivo models at 2.45 GHz. IEEE Access 2019, 7, 89886–89900. [Google Scholar] [CrossRef]
- Demir, A.F.; Ankarali, Z.; Liu, Y.; Abbasi, Q.H.; Qaraqe, K.; Serpedin, E.; Arslan, H.; Gitlin, R.D. In vivo wireless channel modeling. arXiv 2019, arXiv:1902.08199. [Google Scholar]
- Jiang, W.; Bos, T.; Dehaene, W.; Verhelst, M.; D’hooge, J. Modelling of channels for intra-corporal ultrasound communication. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Callejón, M.A.; Reina-Tosina, J.; Naranjo-Hernandez, D.; Roa, L.M. Measurement issues in galvanic intrabody communication: Influence of experimental setup. IEEE Trans. Biomed. Eng. 2015, 62, 2724–2732. [Google Scholar] [CrossRef]
- Maity, S.; Mojabe, K.; Sen, S. Characterization of human body forward path loss and variability effects in voltage-mode hbc. IEEE Microw. Wirel. Components Lett. 2018, 28, 266–268. [Google Scholar] [CrossRef]
- Störchle, P.; Müller, W.; Sengeis, M.; Lackner, S.; Holasek, S.; Fürhapter-Rieger, A. Measurement of mean subcutaneous fat thickness: Eight standardised ultrasound sites compared to 216 randomly selected sites. Sci. Rep. 2018, 8, 16268. [Google Scholar] [CrossRef]
- Metshein, M. Wearable Solutions for Monitoring Cardiorespiratory Activity. Ph.D. Thesis, Tallinn University of Technology, Tallinn, Estonia, 2018. [Google Scholar]


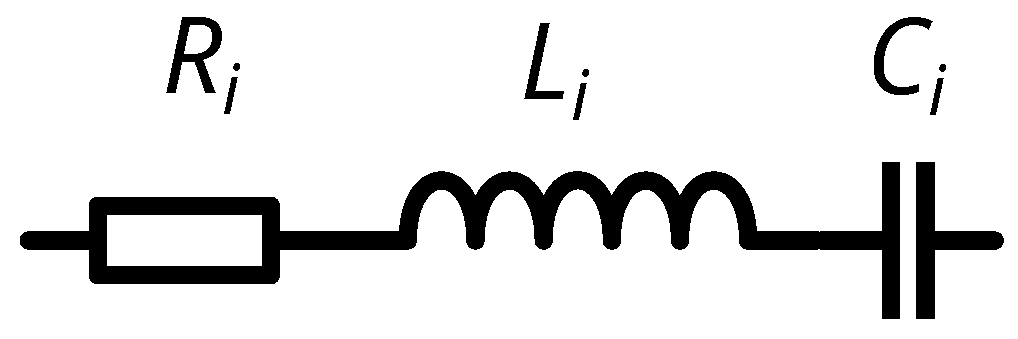

| Name | Units |
|---|---|
| Signal variables | |
| Frequency | Hz |
| Measurement point variables | |
| Distance between points | relative units |
| Tx point fat level | relative units |
| Rx point fat level | relative units |
| Human body variables | |
| Height | cm |
| Weight | kg |
| BMI | kg/m |
| Body fat | % |
| Male | Boolean |
| Age group | years |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aristov, V.; Elsts, A. Human Body as a Signal Transmission Medium for Body-Coupled Communication: Galvanic-Mode Models. Electronics 2023, 12, 4550. https://doi.org/10.3390/electronics12214550
Aristov V, Elsts A. Human Body as a Signal Transmission Medium for Body-Coupled Communication: Galvanic-Mode Models. Electronics. 2023; 12(21):4550. https://doi.org/10.3390/electronics12214550
Chicago/Turabian StyleAristov, Vladimir, and Atis Elsts. 2023. "Human Body as a Signal Transmission Medium for Body-Coupled Communication: Galvanic-Mode Models" Electronics 12, no. 21: 4550. https://doi.org/10.3390/electronics12214550
APA StyleAristov, V., & Elsts, A. (2023). Human Body as a Signal Transmission Medium for Body-Coupled Communication: Galvanic-Mode Models. Electronics, 12(21), 4550. https://doi.org/10.3390/electronics12214550











