Energy Efficient Power Allocation in Massive MIMO Based on Parameterized Deep DQN

Abstract

Machine learning offers advanced tools for efficient management of radio resources in modern wireless networks. In this study, we leverage a multi-agent deep reinforcement learning (DRL) approach, specifically the Parameterized Deep Q-Network (DQN), to address the challenging problem of power allocation and user association in massive multiple-input multiple-output (M-MIMO) communication networks. Our approach tackles a multi-objective optimization problem aiming to maximize network utility while meeting stringent quality of service requirements in M-MIMO networks. To address the non-convex and nonlinear nature of this problem, we introduce a novel multi-agent DQN framework. This framework defines a large action space, state space, and reward functions, enabling us to learn a near-optimal policy. Simulation results demonstrate the superiority of our Parameterized Deep DQN (PD-DQN) approach when compared to traditional DQN and RL methods. Specifically, we show that our approach outperforms traditional DQN methods in terms of convergence speed and final performance. Additionally, our approach shows 72.2% and 108.5% improvement over DQN methods and the RL method, respectively, in handling large-scale multi-agent problems in M-MIMO networks.

1. Introduction

With the increasing demand for mobile communications and Internet of Things technologies, wireless networks are facing increased data traffic and resource management issues owing to the rapid growth of wireless applications. Fifth-generation cellular networks have gained considerable attention for achieving spectrum efficiency and storage capacity. Massive multiple-input multiple-output (M-MIMO) networks are reliable options to overcome data storage and capacity issues to satisfy diverse user requirements. The main concept in M-MIMO technology is to equip the base stations (BSs) with a large number (i.e., 100 or more) of wireless antennas to simultaneously serve numerous users, enabling significant improvement in spectrum efficiency [1,2].

The presence of a huge number of antennas in M-MIMO, data multiplexing, and management would make MIMO transceiver optimization more challenging compared to single-antenna networks. The multi-objective nature of M-MIMO transceivers has resulted in various optimization strategies being performed in the past, including user association [3], power allocation [4], and user scheduling [5]. A joint user association and resource allocation problem was investigated in [6,7,8]. Given the non-convex multiple objective function in the M-MIMO problem, achieving the Pareto optimal solution set in a multi-objective environment becomes more challenging. Recently, proposed methods to solve multi-objective problems include approaches based on linear programming [9], game-theory [10], and Markov approximation [11,12]. Success of these methods requires complete knowledge of the system, which is rarely available.

Thus, emerging machine learning (ML) is an efficient tool to solve such complex multi-objective problems. In this ML field, Reinforcement Learning (RL) is the most appropriate branch to solve a non-convex problem. In RL-based optimization methods, three major elements (i.e., agents, reward, and action) of the proposed solution enable the self-learning abilities from the environment.

The Q-learning algorithm is one of the widely used RL methods because it requires minimal computation. It can be expressed using single equations and does not need to know the state transition probability. The RL agents maximize the long-term rewards over the current optimal reward function [13,14] using a Q-learning algorithm [14,15,16]. The agents are free to change their actions independently in a single-agent RL method, leading to a fluctuation in the overall action space, as well as action and rewards of the different agents in the process [16]. Q-learning methods have been used for power and resource allocation in heterogeneous and cellular networks [17]. However, it may be considerably difficult to handle such large state and action spaces in M-MIMO systems using Q-learning methods. To handle these issues of RL methods, deep reinforcement learning (DRL) methods are coupled with deep learning and RL to enhance the performance of RL for large-scale scenario problems. Nowadays, DRL methods [18] are promising to handle these complicated objective functions. DRL methods have already been applied to several tasks, such as resource allocation, fog radio access networks, dynamic channels, access, and mobile computing [19,20,21].

In DRL, the deep Q-network (DQN) method is mostly employed to train the agents to achieve an optimal scheme from a large state and action space. In [22], Rahimi et al. gave an algorithm of DQN, which was based on deep neural networks and has been previously used in the literature. Zhao et al. used the DRL method for the efficient management of user association and resource allocation for maximizing the network utility and maintaining the quality of service (QoS) requirements [23]. In [24,25,26,27], the authors proposed a DQN algorithm to allocate power using a multi-agent DRL method. Recent advancements in DRL, particularly techniques like Deep Q-Networks (DQNs), have opened up new avenues for addressing resource allocation challenges in wireless networks. However, when it comes to applying DQNs to solve the combined problem of power allocation and user association, a critical step involves converting the continuous action space for power allocation into a discrete action space. This quantization process can potentially result in suboptimal power allocation decisions, limiting overall performance. Additionally, the complexity of a DQN grows significantly as the dimensions of the action space increase. This exponential complexity can lead to high power consumption and slow convergence rates, which are highly undesirable in practical applications. The motivation for our research stems from the evolving landscape of wireless communication networks, particularly resource allocation in massive MIMO systems. As the demand for high-speed, reliable, and energy-efficient wireless transmission increases, optimizing resource allocation becomes dominant. This challenge becomes even more noticeable when dealing with complex circumstances that involve both discrete and continuous decision-making. EE has appeared as a critical metric in modern wireless networks, as it directly effects sustainability and operational costs. Achieving high EE while ensuring seamless user association and power allocation is a complicated problem that necessitates advanced solutions. Our motivation, therefore, lies in addressing this pressing need for more efficient and sustainable wireless networks. We are driven by the potential to make a substantial impact on the way resources are managed, energy is conserved, and user satisfaction is enhanced. By introducing the PD-DQN algorithm and applying it to the joint user association and power allocation problem, we aim to contribute valuable insights and practical solutions to the field of wireless communication.

We are motivated by the vision of network operators and engineers with a versatile tool that can adapt to the workings of hybrid action spaces, ultimately leading to more high-performing wireless networks. To address these challenges, our paper introduces the use of Parameterized Deep Q-Network (PD-DQN) techniques, which deal with parameterized state spaces. However, it falls short in terms of estimation capabilities and tends to produce suboptimal policies due to its tendency to overestimate Q-values [28]. Our approach outperforms traditional DQN and RL methods with significant improvements in convergence speed and final performance. In [29], authors concentrate on hybrid beamforming in integrated satellite–terrestrial networks. Their research lies in achieving both secrecy and energy efficiency through carefully designed beamforming strategies. In this work [30], authors focus on the security aspects of resource allocation within cognitive satellite–terrestrial networks. They delve into the design of secure transmission techniques through strategic power and resource allocation. In [31], authors present a comprehensive examination of the issue of malicious reflector-assisted beamforming in IoT networks. Their primary focus is on devising power allocation strategies to counteract the impact of destructive beamforming. In [32], authors explore the advantages of incorporating reconfigurable intelligent surfaces (RISs) and their role in power allocation and system performance. PD-DQN is well suited for solving problems involving hybrid action spaces, making it a more efficient choice for the joint power allocation and user association problem, which uses discrete and continuous action space [28]. This hybrid approach is designed to address the challenges posed by a mixed discrete–continuous action space.

In this study, we introduced a novel approach with a PD-DQN algorithm [28]. The main contributions of this paper are as follows:

• Our work presents an advanced approach to the user association and power allocation problem, with the overarching objective of maximizing EE in the context of a massive MIMO network. By aiming for EE as the primary goal, we address a critical aspect of modern wireless communication networks, highlighting the practical relevance of our research.
• To effectively address power allocation challenges, we have carefully considered the design of the action space, the state space, and the reward function. Our approach leverages the model-free Deep Q-Network (DQN) framework and, notably, the PD-DQN framework, which empowers us to update policies within the hybrid discrete–continuous action space. This innovation is pivotal in enabling adaptive decision-making within complex real-world scenarios, underscoring the practicality of our methodology.
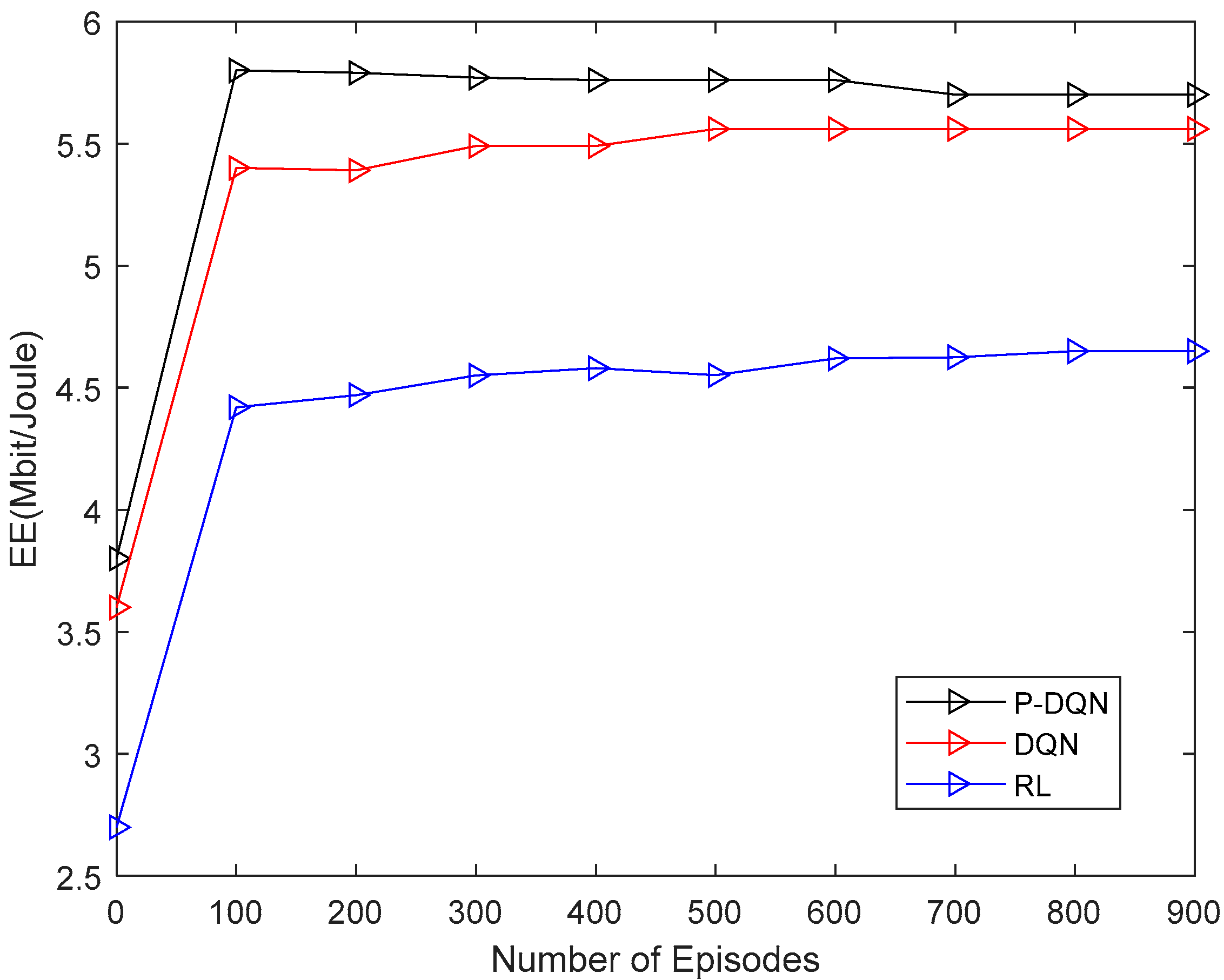
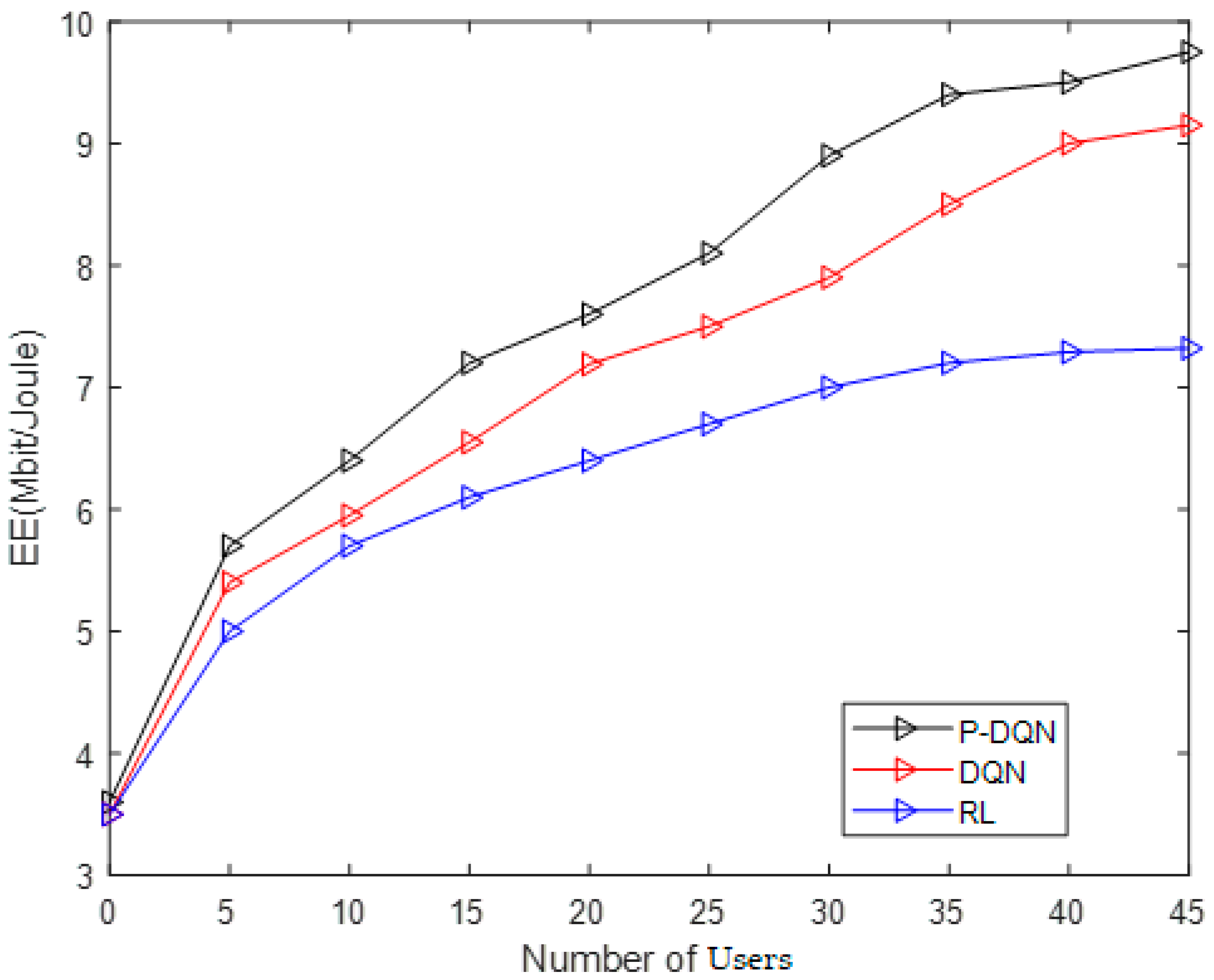
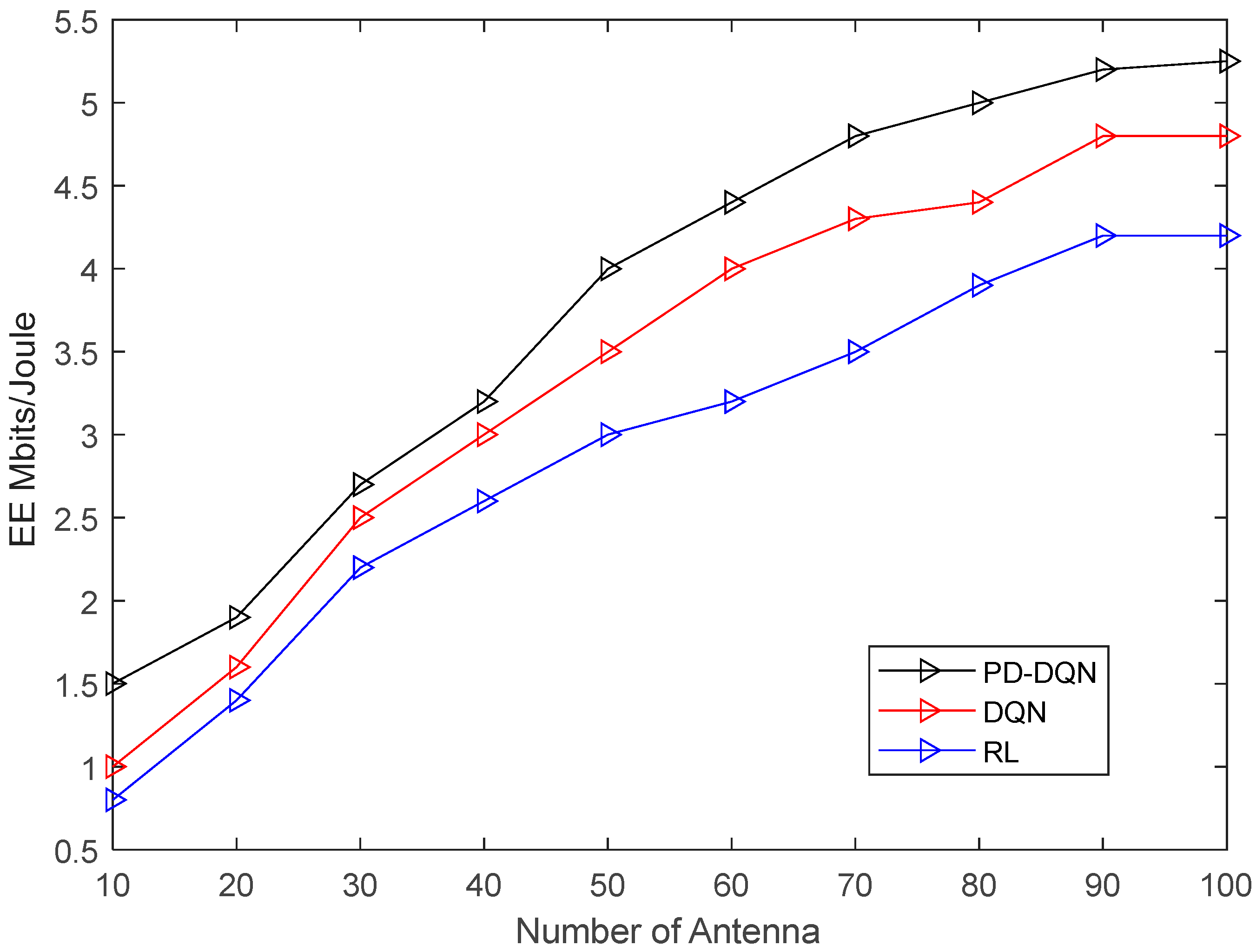
• The simulation results show that the proposed user association and power allocation method based on PD-DQN performs better than DRL and RL methods.

2. System Model

In this study, we considered a single-cell massive MIMO network, which consists of N remote radio heads (RRHs) and single antenna users. Here, RRHs are connected to a baseband unit via backhaul connections. Each RRH is equipped with $M_{max}$ antennas. There are U single-antenna users served by N RRHs together operating in the same time frequency domain. It is assumed that $M_{max}$ > U. In this network, we associate each user with a single RRH [7]. The set of users is denoted by U. Figure 1 shows the network architecture based on a DRL. These approaches utilize a credit assignment system to reward parameters based on their recent impact on the search process. They also employ an operator selection mechanism to determine which parameters to use, guided by the assigned credits.

It is assumed that the channel between the uth users and the nth RRH is given by

$${\mathbf{h}}_{n,u}=\sqrt{{\beta }_{n,u} {\mathrm{g}}_{n,u}}$$

(1)

where ${\beta }_{n,u}$ signifies the large-scale fading coefficient, and ${\mathrm{g}}_{n,u}$signifies the small-scale fading coefficient. ${\mathrm{g}}_{n,u}$ is also known as Rayleigh fading, and the elements are independent and identically distributed (i.i.d) random variables having zero mean and unit variance [8].

The received signal of the uth user on the nth RRH can be given by [7]

$$Y_{n,u}=\sqrt{{\mathit{p}}_{\mathit{u}}{\mathbf{h}}_{n,u}{\mathbf{w}}_{n,u}}{s}_{n,u}+\mathsf{\sum }_{\mathit{j}=\mathbf{1},\mathit{j}\ne \mathit{u}}^{\mathit{U}}\sqrt{{\mathit{p}}_{\mathit{j}}{\mathbf{h}}_{n,u}}{{\mathbf{w}}_{n,u}s}_{\mathit{n},\mathit{j}}+{\mathbf{z}}_{n,u}$$

(2)

where ${\mathit{p}}_u$ is power transmitted through the uth user; $s_{\mathit{n},\mathit{u}}$ is the $N_r\times 1$ data symbol of the uth user on the nth RRH; ${\mathbf{w}}_{n,u}$ is the $N_t\times N_r$ beamforming vector of the uth user on the nth RRH, which is given by ${\mathbf{w}}_{\mathit{n},u}=\raisebox{1ex}{${\mathbf{h}}_{n,u}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{\mathbb{E}\left\{{‖{\widehat{\mathbf{h}}}_{n,u}‖}^2\right\}}$}\right.$; and ${\mathbf{h}}_{n,u}$ is the channel matrix of the uth user on the nth RRH. ${\mathbf{z}}_{n,u}$ is the noise vector of independent and identically distributed (i.i.d.) additive complex Gaussian noise having zero mean and variance of $\sigma$. Without loss of generality, we set

$$E\left[s_{m,u^{s}m,u}^H\right] =\mathrm{I}, E\left[s_{m,u^{s}m,j}^H\right] =0, (k\ne \mathrm{j}), E\left[s_{m,u^{\mathbf{n}}m,u}^H\right]=0$$

Power Consumption

We considered the downlink phase for power consumption. The overall $P_c$ is expressed as the sum of the transmit power and fixed power consumption of the RRHs and base units denoted as $P_{\mathit{F}\mathit{I}\mathit{X}}$ and the power consumed by the components of the active antennas [5]. The total $P_c$ can then be given by

$$P_c=P_{Fix}+P_a\sum _{n=1}^N{M}_n+\sum _{n=1}^N\sum _{u=1}^U\frac{1}{\nu }{P}_{n,u}$$

(3)

where $P_a$ denotes power assumed for active antenna, and $\nu$ denotes power amplifier efficiency, $\mathit{\nu }\in \left(\mathrm{0,1}\right).$

3. Problem Formulation

According to the system model, the ergodic achievable rate of the uth user is given by [10]

$${\mathit{R}}_{\mathit{n},\mathit{u}}={\mathbf{log}}_{\mathbf{2}}\left(\mathbf{1}+{\mathsf{\Gamma }}_{\mathit{u},\mathit{n}}\right)$$

(4)

where ${\mathsf{\Gamma }}_{\mathit{u},\mathit{n}}$ is signal-to-interference-plus-noise ratio of the uth and nth RRH and is given by

$$R_{n,u}=\frac{M_n{p}_n{\Gamma }_{n,u}}{{\sum }_{j=1}^N{\sum }_{q=1}^U{p}_{j,q}{\beta }_{j,u}+{\sigma }^2}$$

(5)

To deal with the above problem, the association between the uth users and nth RRH is given by

$${\mathit{x}}_{\mathit{n},\mathit{u}}=\left\{\begin{array}{l}1,\mathit{u}\in {\mathit{L}}_{\mathit{l}}\\ 0,\mathit{u}\in \frac{\mathit{U}}{{\mathit{L}}_{\mathit{l}}}l=1,...L\end{array}\right.$$

(6)

The system energy efficiency (EE) can be expressed as

$$\underset{\mathrm{X},\mathrm{P}}{\mathrm{m}\mathrm{a}\mathrm{x}} \eta =\frac{{\sum }_{\mathit{u}=\mathbf{1}}^{\mathit{U}}{\mathit{R}}_{\mathit{u}}}{{\mathit{P}}_{\mathit{F}\mathit{I}\mathit{X}}+{\mathit{p}}_{\mathit{a}}{\sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\mathit{M}}_{\mathit{n}}+{\sum }_{\mathit{n}=\mathbf{1}}^{\mathit{N}}{\sum }_{\mathit{u}=\mathbf{1}}^{\mathit{U}}\frac{\mathbf{1}}{\mathit{v}}{\mathit{p}}_{\mathit{n},\mathit{u}}}$$

(7)

The optimization problem maximizing the system EE can be formulated as

$$\begin{array}{l}\mathrm{P}1: \underset{X,P}{\mathrm{m}\mathrm{a}\mathrm{x} }\mathit{\eta }=\frac{{\sum }_{\mathit{u}=\mathbf{1}}^{\mathit{U}}{\mathit{R}}_{\mathit{u}}(\mathit{X},\mathit{P})}{{\mathit{P}}_{\mathit{c}}\left(\mathit{X},\mathit{P}\right)}, \mathrm{s}.\mathrm{t} \mathrm{C}1: 0<P_{u,m}\le P_u^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ \mathrm{C}2: a_{u,m}\in \left\{\mathrm{0,1}\right\}\\ \mathrm{C}3: \sum _m{a}_{u,m}=1\\ \mathrm{C}4: R_u\ge R_{\min }\end{array}$$

(8)

In the above problem, C1 indicates that the transmitted power consumption is smaller than the transmit power limit of each RRH. Constraints C2 and C3 indicate that one user can only be associated with one RRH. C4 maintains the QoS requirement of each user and signifies the lower limit of the required transmit rate of users. Problem (8) is NP-hard and is usually difficult to find a feasible solution for [22]. Therefore, a multi-agent DRL approach was used to solve this problem, as described in the next section.

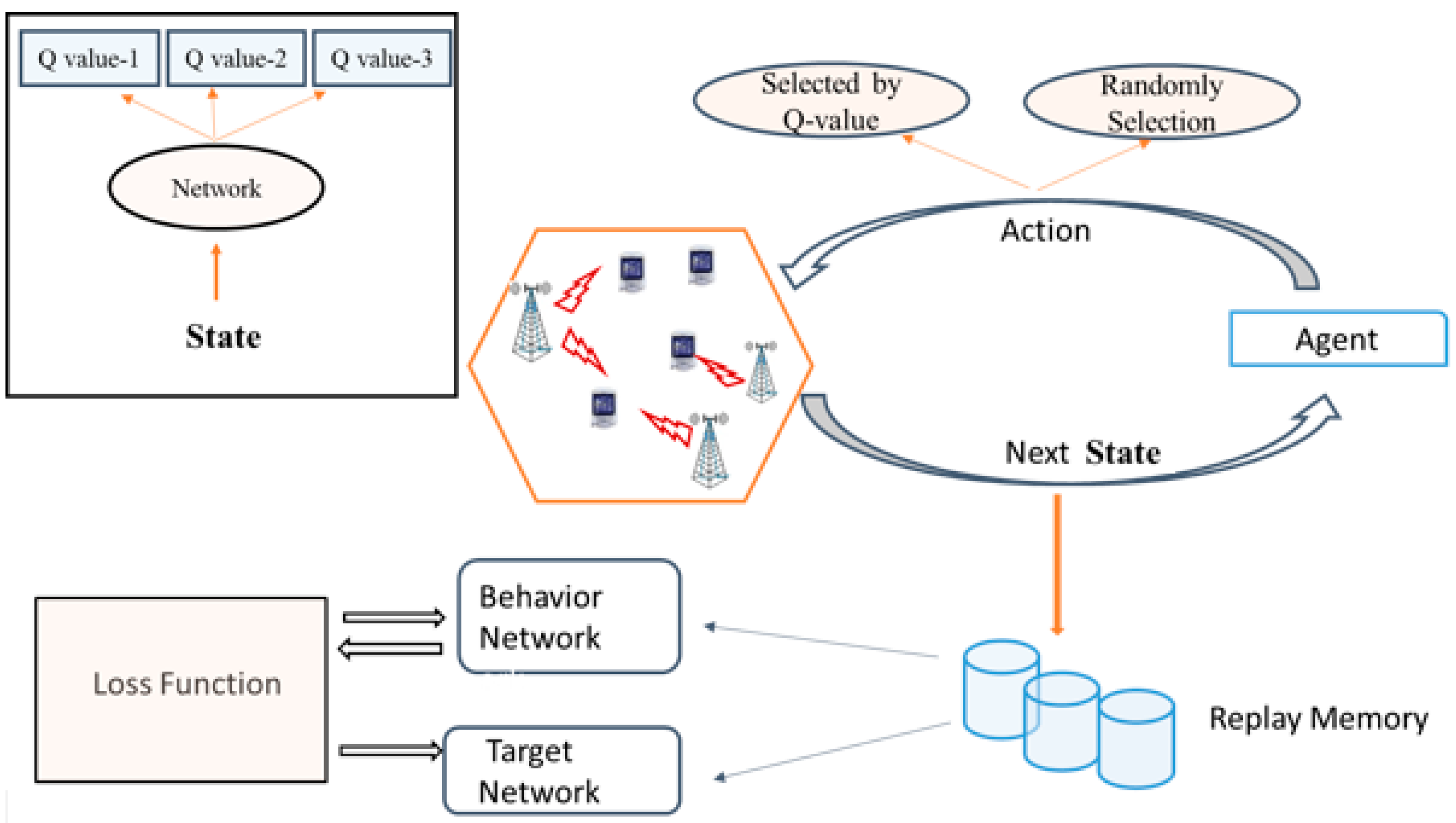
4. Multi-Agent DRL Optimization Scheme

The problem P1 is a non-convex problem where user association as well as power allocation approaches are involved. To solve this tractable problem, a multi-agent DQN-based RL technique was applied. The major component of the RL approach is based on the Markov decision-making process (MDP), which is a new proposed reward function, prior to the application of the multi-agent DQN approach.

4.1. Overview of RL Method

In this section, we present the overview of RL. In RL, the aim is to find optimal policy. The problem P1 is converted into a MDP (s, a, r, $P_{s{s}^{new}}$) similar to the existing work [26,27], where s, a, and r represent the set of state, set of action, and reward functions, respectively. $P_{s{s}^{new}}$ is the transition probability from state s to $s^{new}$ with reward r. In the DRL, these state variables are defined as follows:

State space: In problem P1, the users as agents select the BSs for communication at time t. The network consists of U agents. The state space can be expressed as

$$s\left(t\right)=\left\{s_1\left(t\right),s_2\left(t\right),...s_u\left(t\right),...,s_U\left(t\right)\right\}$$

(9)

Action space: At time t, the action of the agent is to control the transmit power level between the user association and BS. The action space consisting of each user can be defined as

$$a\left(t\right)=\left\{a_1\left(t\right),a_2\left(t\right),..a{s}_u\left(t\right),...,a_U\left(t\right)\right\}$$

(10)

Reward function: The energy efficiency of all users can be expressed as a system reward function

$$r(t)=\sum _u^U{r}_u\left(t\right)=\sum _{u=1}^U{\eta }_u\left(t\right)$$

(11)

where is $r\left(t\right)$ the reward function, which is maximized to achieve the optimal policy with interaction with the outer environment.

Therefore, within the RL framework, the problem P1 can be transformed into problem P2, as follows:

$$\mathrm{P}1: \underset{\mathrm{X},\mathrm{P},\mathrm{M}}{\max }{\mathit{r}}_{\mathit{n}}$$

(12)

where X represents the user association matrix, and P denotes the power allocation vector. The agent identifies its state s(t) at time t and follows a policy $\mathit{\pi }$ to perform an action a(t), that is, $a\left(t\right)=\pi \left(s\right(t\left)\right)$. Following this, the users communicate with the BSs, and the reward function becomes $r\left(t\right)=r\left(t|s=s(t),a=a(t)\right).$ Therefore, the future cumulative discounted reward at time t can be given by

$$\mathit{R}(\mathit{t})=\sum _{\mathit{\tau }=\mathit{t}}^{\mathit{T}}{\mathit{\gamma }}^{\mathit{\tau }-\mathit{t}}\mathit{r}\left(\mathit{\tau }\right)$$

(13)

where $\mathit{\gamma }$ ∈ [0, 1] denotes the discount factor for the upcoming rewards. To solve the P2, a value function for policy ${\pi }_u$ is defined as

$$V_u^{{\pi }_u}={\rm E}\left[\sum _{\tau =t}^T{\gamma }^{\tau -t}{r}_u(\tau )|s_u^{\tau },a_u(\tau )\right]$$

(14)

where E[·] denotes the expectation operator. Using the Markov property, the value function is defined as

$$V_u^{{\pi }_u}=r(s_u^{\tau },{\pi }_u)+\gamma \sum _{s^{new}\in S}{P}_{s{s}^{new}}({\pi }_u)V_u^{{\pi }_u}(s_u^{{\tau }^{new}})$$

(15)

The Q-function when performing action $a_u\left(\tau \right)$ in state $s_u^{\tau }$ with policy ${\pi }_u$ can be expressed as in [24], that is,

$$Q_{\pi }\left(s^{\tau },a\left(\tau \right)\right)={\rm E}\left[R\left(\tau \right)|s^{\tau },a(\tau )\right]$$

(16)

The optimal Q-value function satisfies the Bellman equation [33,34] derived as

$$Q_{{\pi }^{*}}\left(s^{\tau },a(\tau )\right)=r\left(s^{\tau },a(\tau )\right)+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}a\left(\tau \right)V^{\pi *}(s^{{\tau }^{\prime }})$$

(17)

Accordingly, the Bellman optimality Equation (17) [24], $V_u^{{\pi }_u^{*}}\left(s_u^{{\tau }^{new}}\right)$ can be obtained as

$$V_u^{{\pi }_u^{*}}(s_u^{{\tau }^{new}})=\underset{{a^{\prime }}_u}{max}{Q}_{{\pi }_u^{*}}\left(s_u^{{\tau }^{new}},a_u^{{\tau }^{new}}\left(\tau \right)\right)$$

(18)

Adding Equations (17) and (18), we get

$$Q_{{\pi }^{*}}\left(s^{\tau },a\left(\tau \right)\right)=r\left(s^{\tau },a\left(\tau \right)\right)+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}a\left(\tau \right)\underset{{a^{\prime }}_u}{max}{Q}_{{\pi }_u^{*}}\left(s_u^{{\tau }^{new}},a_u^{{\tau }^{new}}\left(\tau \right)\right)$$

(19)

The update of the Q-value function is given by [14] as

$$Q_{{\pi }^{*}}\left(s^{\tau },a\left(\tau \right)\right)=(1-\alpha )Q_{\pi }\left(s^{\tau },a\left(\tau \right)\right)+\alpha \left[r\left(s^{\tau },a\left(\tau \right)\right)\right]+\gamma \underset{a^{\prime }}{max}{Q}_{{\pi }^{\prime }}\left(s^{\tau },a^{\prime }\left({\tau }^{\prime }\right)\right)$$

(20)

where $\mathit{\alpha }$ is learning rate scaled between 0 and 1 and updating speed of $Q_{{\pi }_u}\left(s_u^{\tau },a_u\left(\tau \right)\right)$. The RL algorithm shows good performance if size of states is small. In case of high dimensional state space, classical RL approaches fail to perform. Some states are not sampled because of the high dimensional state space, and they require several restrictions. First, the convergence rate might become slow, and storage of the lookup table becomes impractical. Thus, the use of the DRL method was explored to solve the problem with the large space.

4.2. Multi-Agent DQN Frameworks

In contrast to the classical Q-learning approach, the author in [23] proposed the DQN method, which was basically a DRL method. This DQN method relies on two components, e.g., replay memory and target network. The agent stores transitions $\left(s_u^{\tau },a_u\left(\tau \right),r_u\left(\tau \right),s_u^{{\tau }^{new}}\right)$in a replay memory D. Then, it extracts this transition from memory D by using random sampling to compute the Q-value function. The agent uses the memory D in a part of mini-batch to train the Q-network, and then a gradient descent method is applied to update the weight parameter $\mathit{\theta }$ of the behavior network:

$${\pi }_u=\underset{\mathit{a}\mathbf{\prime }}{\max Q_{{\pi }_u}^{*}\left(s_u^{\tau },a_u^{new}\left(\tau \right)\right)}$$

(21)

In the DQN method, the types of networks are included; that is, DQN sets the ${\mathit{\theta }}_{\mathrm{target}}$ target networks. The learning model calculates the target value ${\mathit{y}}_{\mathit{j}}$ with a weight parameter ${\mathit{\theta }}_{\mathrm{target}}$ for a certain time t, which can mitigate the volatility of the learning scheme. During the learning process, after several iterations of H the weight parameter θ is synchronized with the target network, $\theta \to {\theta }_{\mathrm{target}}$. The agent utilizes a greedy random policy, which means that the agent randomly selects an action $a_u\left(\tau \right)$ parameter $\theta$ for the behavior network. Consequently, $\mathit{a}\left(\mathit{\tau }\right)$ value and $\theta$ are updated iteratively using the minimum loss function [35]:

$$L\left(\theta \right)=\sum \left[y_j-Q_{{\pi }_u}(s_u,a_u;\theta )\right],$$

(22)

where ${\mathit{y}}_j=r_j+\gamma \underset{a_u^{new}\left(j\right)}{max}{Q}_{{\pi }_u}(s_u^{j^{new}},a_u^{new}(j);{\theta }_{\mathrm{target}})$.

The proposed DQN algorithm for user association and power allocation is shown in Algorithm 1.

Algorithm 1: DQN Based for User Association and Power Allocation Algorithm
1.	Initialize Q(s, a) = 0; learning rate α, target network and replay memory D.
2.	Set the weight, discount factor
3.	for each training episode do
4.	Initialize state s
5.	Choose a random number
6.	$\mathrm{if} \mathit{x}<\mathit{\epsilon }$ then
7.	Choose action randomly;
8.	else
9.	Select action ${\mathit{a}}_{\mathit{u}}(\mathit{\tau })=\underset{{\mathit{a}}^{\mathit{n}\mathit{e}\mathit{w}}}{\mathit{m}\mathit{a}\mathit{x}}\left({\mathit{s}}_{\mathit{u}}^{\mathit{\tau }},{\mathit{a}}_{\mathit{u}}^{\mathit{n}\mathit{e}\mathit{w}}(\mathit{\tau });\mathit{\theta }\right)$
10.	end if
11.	Execute action ${\mathit{a}}_{\mathit{u}}\left(\mathit{\tau }\right)$ and next state ${\mathit{s}}_{\mathit{u}}^{{\mathit{\tau }}^{\mathit{n}\mathit{e}\mathit{w}}}$
12.	Calculate energy efficiency using Equation (13).
13.	Store transition ${\mathit{s}}_{\mathit{u}}^{\mathit{\tau }},{\mathit{a}}_{\mathit{u}}\left(\mathit{\tau }\right),{\mathit{r}}_{\mathit{u}}\left(\mathit{\tau }\right),{\mathit{s}}_{\mathit{u}}^{{\mathit{\tau }}^{\mathit{n}\mathit{e}\mathit{w}}}$ in D
14.	If the replay memory is full then
15.	Random sampling a mini-batch from D
16.	Perform gradient descent on ${{\mathit{y}}_{\mathit{j}}-{\mathit{Q}}_{{\mathit{\pi }}_{\mathit{u}}}({\mathit{s}}_{\mathit{u}},{\mathit{a}}_{\mathit{u}};\mathit{\theta })}^2$$\mathrm{w}.\mathrm{r}.\mathrm{t}. \mathrm{parameter} \mathit{\theta }$
17	end if
18	Update target network
19	End for

4.3. Parameterized Deep Q-Network Algorithm

The combined user association and power allocation procedure in a hybrid action space can be solved via parameterization, but it still has generalization problems. In order to solve this problem, we used the epsilon greedy exploration method, which enables the DQN to explore a wide variety of states and actions and improves generalization. In a hybrid action space, the Q-value is recast as $Q(s,a)=Q(a,\beta ,\chi )$ where $\beta$ denotes a discrete action, and $\mathit{\chi }$ denotes a continuous action. The reward is defined as parameterized double DQN with replay buffer EE. Whether UE is associated with BS or not, the user association will only have the two discrete values $\beta$ = 0 and 1. On the other hand, $\mathit{\chi }$ is a matrix that represents various levels of power distribution. The PD-DQN for the user association and power allocation algorithm is presented in Algorithm 2.

Algorithm 2: PD-DQN for User Association and Power Allocation Algorithm
1.	Initialize primary and target Deep Q-Networks (DQN) with random weights.
2.	Set up a Mini-batch and a Replay Buffer for experience storage.
3.	For each episode:
Generate an initial state (s_i) by selecting a random action.
4.	Inside each episode loop:
	While the episode is ongoing:
	Choose an action based on an epsilon-greedy policy.
	If a random number is less than epsilon:
	Select a discrete action from a predefined set $(\mathit{\beta }$).
	Otherwise:
	Estimate Q-values for discrete actions using the primary Q-network and choose the highest.
	If a random number is less than epsilon:
	Choose a continuous action from a predefined set $(\mathit{\chi }$).
	Otherwise:
	Estimate Q-values for continuous actions using the primary Q-network and choose the highest.
	Execute the selected action in the environment following an epsilon-greedy policy.
5.	After each episode loop, sample a minibatch of experiences from the replay buffer.
6.	For each experience in the minibatch:
	Calculate the target Q-value using the target network.
	If the episode is ongoing, compute the target Q-value for the next state.
	If the episode is complete, compute the target Q-value with the reward.
	Calculate the predicted Q-value for the current state.
	Determine the difference between predicted and target Q-values and update the primary Q-network accordingly.
	Update the current state, target network weights.
7.	Update the environment with user associations and power allocations.
8.	Repeat the process for the next episode if needed.
9.	End

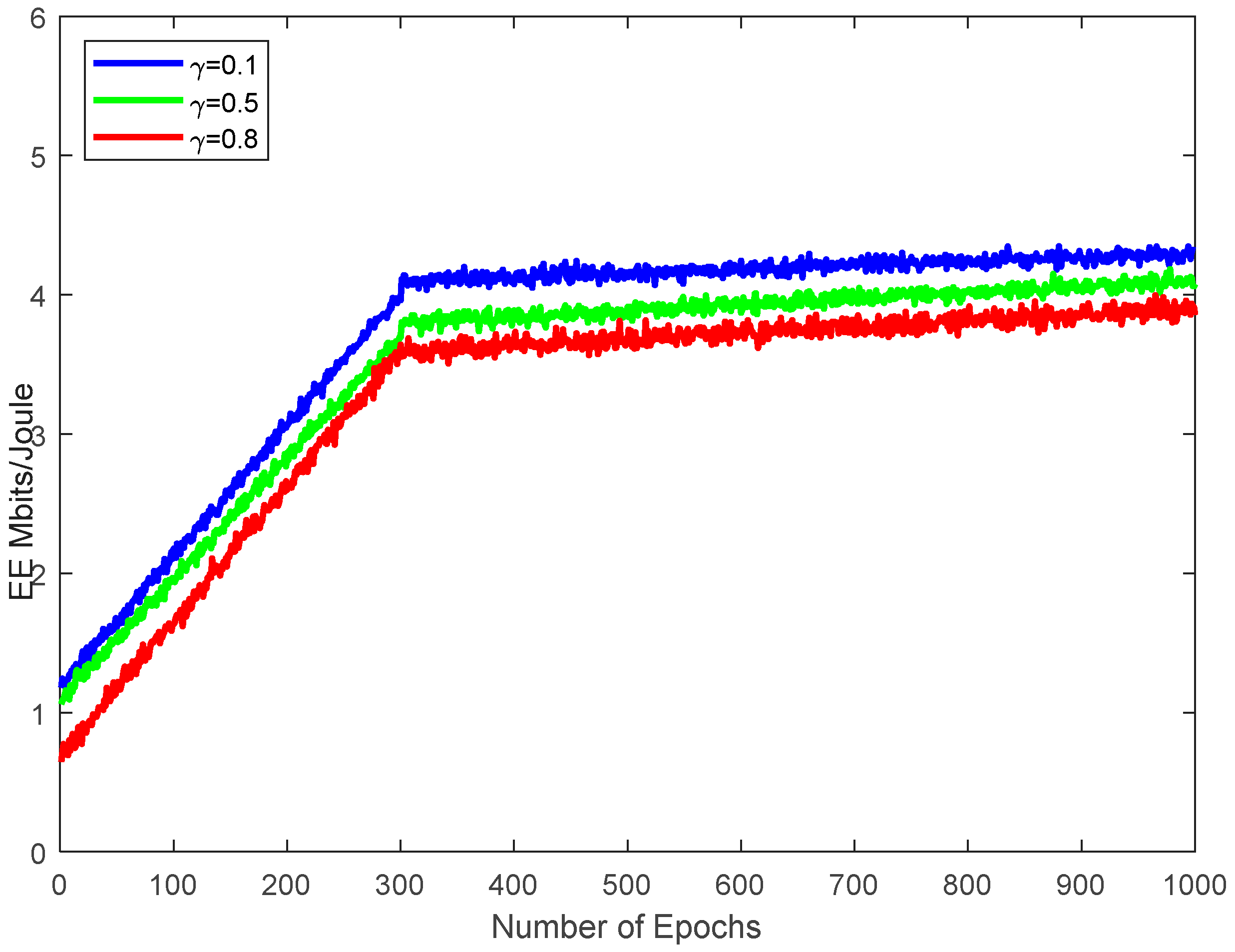
5. Simulation Results

In this section, the results of the simulation using the DRL algorithms are presented. We consider a distributed M-MIMO with three RRHs equipped with 300 antennas in the cell with diameter of 2000 m. We consider K = 20 randomly distributed users within the cell. The PC of each RRH is set to 10,000 mW.

The power consumed by the component of active antennas is 200 mW, and the power amplifier efficiency, ν, is 0.25. We assume a transmission bandwidth of 10 MHz [7]. The other parameters are given in

Table 1. Simulation parameters.

Parameter	Values
Standard deviation	8 dB
Path loss model PL	PL = −140.6−35log10(d)
Episodes	500
Steps T	500
Discount rate γ	0.9
Mini-batch size b	8
Learning rate	0.01
Replay memory size D	5000

. We consider the Hata-COST231 propagation model [8]. The large-scale-fading β in Equation (1) is borrowed from the literature [8] and is given by $10{\mathit{log}}_{10}\left({\beta }_{n,u}\right)=P{L}_{n,u}+\Omega$ where PL is path loss, and $\mathsf{\Omega }$ represents standard deviation. Here, d_n,u is the distance between uth users and the nth RRH.

Figure 2 shows the energy efficiency of the proposed DRL algorithm and RL algorithm. Figure 2 demonstrates two observations that indicate that the EE achieved by the DRL method outperforms the RL methods. As the number of episodes increases up to 50, the system EE increases and tends to converge after 250 episodes for both schemes. Additionally, the learning speed of the Q-learning method is lower than that of the multi-agent DQN algorithm. For the Q-learning method, there is a slight improvement in the system EE at episode 120, whereas in the DRL approach, the system EE tends to be stable at episode 257. The EE is unstable at the beginning as seen in the DRL scheme, and the stability increases as the episodes increase, and thereafter increases slowly. This is because the agent selects actions in a random manner and stores the transition information in D.

Figure 3 shows the EE versus the number of users fixed at M = 20. From the figure we can see that, the EE generally first increases with K from 5 to 45 and then decreases flatten. This is due to the fact that when scheduling more users, more RRHs are activated to serve users creating more interference noise. Furthermore, proposed DRL algorithm performs superior to QL.

Figure 4 compares the EE performance at different discounted factors, γ = {0.1, 0.5, and 0.8}. It can be observed that a lower discount factor results in higher EE through different discount factors. Figure 4 illustrates that the PD-DQN method optimizes the user association and power allocation. Moreover, when the number of epochs increases, the EE performance of each user is better at a different discount factor.

From the Figure 5, we can observe that PDQN consistently outperforms both DQN and RL in terms of energy efficiency. The EE values achieved by PDQN show a steady increase, starting from 1.5 and reaching 5.25, indicating significant improvement. DQN and RL also exhibit improvements, but their EE values remain below that of PDQN. In terms of percentage improvement, PDQN surpasses DQN by an average of around 35%, while PDQN outperforms RL by approximately 40%. Additionally, DQN exhibits a slight advantage over RL, with an average improvement of about 5%.

6. Conclusions

In this paper, we have studied the user association and power allocation problem in a massive MIMO based on a PD-DQN framework. The numerical results indicate that the PD-DQN approach performs better than the DQN and classical Q-learning schemes. The main motivation of this paper is to study the resource allocation scheme in M-MIMO. In addition, for the simulation results in this study, we considered the DQN approach to tackle the problem of user association and power allocation in M-MIMO. The aforementioned optimization problem was formulated to maximize the EE in the downlink network, and the convergence of the multi-agent DRL (DQN) algorithm was studied. Furthermore, convergence analyses confirmed that the proposed methods perform better in terms of EE than the RL method. Establishing the upper bound is important to set a benchmark for the achievable EE. In our study, this upper bound signifies the theoretical maximum EE that can be achieved in the given massive MIMO resource allocation problem under ideal conditions. Our study has showcased the potential of our PD-DQN framework to enhance energy efficiency in massive MIMO systems. The inclusion of the upper bound in our evaluation has not only validated the effectiveness of our approach but has also shed light on areas for further improvement. The convergence rate indicates that the proposed algorithm excels in terms of energy efficiency. Furthermore, additional simulation outcomes demonstrate superior energy efficiency across varying user counts, number of antennas, and diverse learning rates. The enhancement of the proposed PD-DQN on average may reach 72.2% and 108.5% over the traditional DQN and RL methods, respectively.