Decentralized Controller Design for Large-Scale Uncertain Discrete-Time Systems with Non-Block-Diagonal Output Matrix

Abstract

This research paper addresses the challenge of designing a decentralized controller for a discrete-time uncertain polytopic system with a linear large-scale (LSS) structure. Specifically, we investigate this problem in cases where the subsystem’s output matrix lacks a decentralized structure. Firstly, the proposed novel procedure of a decentralized controller design transforms the LSS model to have a fully decentralized structure (both input and output matrices are block-diagonal). Then, the robust stability boundary parameter is calculated for the open-loop system. This stability boundary parameter is considered in robust decentralized controller design where an appropriate controller design method is used. The entire process of designing a robust decentralized controller takes place at the subsystem level, and the influence of interaction is considered through the robust stability boundary parameter. Lastly, we present an example of a five-order system comprising two subsystems to show the effectiveness of the new method.

1. Introduction

Having obtained its maturity during recent decades, decentralized and robust control ([1,2,3,4,5,6] and others mentioned in this article) still belong to the topical issues of control theory and practice. The concept of a large-scale system highlights the fundamental feature of a complex system for which centralized control is challenging or unfeasible due to its sheer size and complexity. This is the reason why such systems are divided into independent subsystems for the purposes of control design, and subsequently controlled in a decentralized way using an algorithm with information constraints. Decentralized control consists of several independent controllers, each of which controls only the local output using the local input of a corresponding subsystem. Since the 1970s, a large number of suitable methods for a decentralized controller design have been developed in the time domain, the frequency domain, and also using the approach of Variable System Structure (switch systems approach).

In the time domain, the main results can be characterized as follows: methods based on the aggregation matrix approach [7] and methods based on the Linear Matrix Inequality–Bilinear Matrix Inequality (LMI-BMI) approach, where interesting results have been obtained in the design of decentralized robust controllers [8]. The latter contributed significantly to the advancement of the theory concerning the design of robust and decentralized controllers, in [9,10,11,12] and others. The approach for designing adaptive decentralized controllers with both state and output feedback was introduced in [13,14].

The main results, i.e., methods developed in the frequency domain, can be summarized as follows: sequential design, independent design [15], and the methods using an equivalent subsystem approach [16]. The design of decentralized controllers in the field of Variable-Structure Systems (VSS) was introduced in [17], where a decentralized VSS control law for a robot manipulator was presented. Later, a diagonal-dominant approach to the design of a decentralized controller for complex systems was proposed.

In [16], a presentation of decentralized control techniques for linear systems is provided for the frequency domain. Additionally, an exceptional overview of decentralized controller design procedures for continuous- and discrete-time systems can be encountered in [18] and the book in [19].

The new decentralized controller design approach presented in this paper represents the integration of two methodologies from our earlier works [20,21], specifically tailored for discrete-time systems in the time domain. Focused on discrete-time systems, the new method offers a counterpart for continuous-time control [21], where specifics of discrete-time system controller design are considered. Discrete-time systems prevail in real-world applications, such as digital control and sampled data systems. Discrete-time models more accurately capture the practical implementation of controllers in modern technology, allowing for direct integration with digital hardware and offering inherent benefits in terms of computational efficiency and ease of implementation.

This paper introduces a novel approach to designing a robust decentralized controller for linear uncertain discrete-time systems whose structure is not decentralized: while an input matrix is decentralized, an output matrix does not have a decentralized structure. The method presented in this manuscript is executed in three sequential steps as outlined below:

During the first step, the state-space system with an output matrix with a general structure is transformed to a large-scale uncertain descriptor system, with a fully decentralized structure.

The second step includes the determination of whether the open-loop uncertain descriptor system is stable and the stability degree is calculated. The overall system stability degree sets the required properties of the corresponding closed-loop descriptor subsystems such as their stability, robustness, and dynamic properties, which guarantees the analogical qualities of the entire closed-loop descriptor system. The stability of the entire descriptor system implies the stability of the original large-scale system.

In the third step, parameters of the descriptor decentralized controller are calculated at the subsystem level, to guarantee the required dynamic properties of the subsystems obtained in the second step.

The findings presented in this paper introduce a novel approach to the design of decentralized controllers, which involves the design of decentralized controllers for both stable and unstable complex systems.

The structure of this paper is as follows: In Section 2, we present preliminary results and formulate the problem. Section 3 introduces the transformation of a non-decentralized structure of output subsystem matrices to a decentralized one and the calculation of the robust stability boundary of a corresponding complex descriptor system. Section 4 provides complex descriptor system and subsystem models for a proportional–integral (PI) or proportional–integral–derivative (PID) controller. Section 5 demonstrates the efficacy of the proposed method through an example of a fifth-order model with two subsystems. Section 6 summarizes the benefits of the proposed approach.

2. Preliminaries and Problem Formulation

In this section, the studied problem is introduced and a description of a considered system and basic stability conditions are presented.

2.1. System Description

Consider a large-scale uncertain linear discrete-time invariant system that is described as follows:

$$x(t+1)=\overline{A}\left(\xi \right)x\left(t\right)+\overline{B}\left(\xi \right)u\left(t\right),y\left(t\right)=\overline{C}x\left(t\right),$$

(1)

where $x\left(t\right)\in R^n$ is a state vector, $u\left(t\right)\in R^m$ a control input vector, $y\left(t\right)\in R^l$ a controlled output vector. The matrices

$$(\overline{A}\left(\xi \right),\overline{B}\left(\xi \right))=\sum _{i=1}^N({\overline{A}}_i,{\overline{B}}_i){\xi }_i$$

(2)

belong to a polytopic uncertainty domain with N-vertices and uncertainties belonging to the set

$${\Omega }_{\xi }=\{{\xi }_i\ge 0,i=1,2,\dots ,N,\sum _{i=1}^N{\xi }_i=1\}.$$

(3)

Matrices ${\overline{A}}_i,{\overline{B}}_i$, and $\overline{C}$ have constant entries. We assume that system (1) consists of M subsystems, the j-th subsystem has ${\overline{n}}_j$ states, $m_j$ inputs, and $l_j$ outputs, and matrices ${\overline{B}}_i,i=1,2,\dots ,N$ have a decentralized structure [7].

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\overline{A}}_i=\left[\begin{array}{ccc}{\overline{A}}_{i11}& \cdots & {\overline{A}}_{i1M}\\ {\overline{A}}_{i21}& \cdots & {\overline{A}}_{i2M}\\ ⋮& \ddots & ⋮\\ {\overline{A}}_{iM1}& \cdots & {\overline{A}}_{iMM}\end{array}\right]\in R^{n\times n},\hfill \\ \hfill & {\overline{B}}_i=blockdiag[{\overline{B}}_{i1}\dots {\overline{B}}_{iM}]\in R^{n\times m},\hfill \\ \hfill & \overline{C}=\left[\begin{array}{c}{\overline{C}}_1\\ \dots \\ {\overline{C}}_M\end{array}\right]\in R^{l\times n}\hfill \end{array}\end{array}$$

(4)

where ${\overline{A}}_{ijk}\in R^{{\overline{n}}_j\times {\overline{n}}_k}$, ${\overline{B}}_{ij}\in R^{{\overline{n}}_j\times m_j}$, ${\overline{C}}_j\in R^{l_j\times n}$, ${\sum }_{j=1}^M{\overline{n}}_j=n$, ${\sum }_{j=1}^M{m}_j=m$, ${\sum }_{j=1}^M{l}_j=l$.

A general form of the output matrix $\overline{C}$ is considered, without assuming its decentralized structure. Let us additionally presume that the complex system (1) is observable and controllable under the decentralized control structure [22].

System (1) can be formally partitioned into subsystems through various formal decomposition methods. In this manuscript, the segmentation of the aforementioned matrices into submatrices is indicative of the intrinsic characteristics of the system, as discussed by [7].

2.2. Stability Conditions

System (1) is said to be asymptotically stable if $\overline{A}\left(\xi \right)$ is Schur-stable for all ${\xi }_i,i=1,2,\dots ,N$, that is, all eigenvalues of $\overline{A}\left(\xi \right)$ lie in the unit circle.

Next, Lemma 1 directly follows from the well-known Lyapunov stability theory and Lyapunov matrix inequality for Schur-stable matrices.

Lemma 1.

The summation of two discrete-time matrices, denoted as $G+H\in R^{n\times n}$, exhibits Schur stability if and only if there exists a positive definite Lyapunov matrix $P>0$ satisfying the condition that

$${(G+H)}^{T}P(G+H)-P<0$$

(5)

holds.

Proof. 

Inequality (5) is a standard condition for matrix Schur stability written for the matrix $L=G+H$. □

Let us consider an LSS with subsystems and interactions which can vary within the specified limits as described in the next definition.

Definition 1.

Consider the matrix $F_s={\left\{f_{ij}\right\}}_{M\times M}$ as the structured perturbation matrix for system (1), where

• $f_{ij}=1$, when an interaction exists between subsystems i and j;
• $f_{ij}=0$, when no interaction exists between subsystems i and j.

To address varying levels of interaction between the subsystems, we consider setting the value of $f_{ij}\in <0,1>$.

Definition 2

([7]). A complex system (1) is connective-stable if and only if it is asymptotically stable for all possible entries $f_{ij}$ of the matrix $F_s\left(e_{ij}\right)$.

3. Main Steps for a Decentralized Stabilization Controller Design

This paper primarily addresses the task of devising a decentralized control

$$u\left(t\right)=K_{dec}y\left(t\right),K_{dec}=blockdiag[K_{dec1},K_{dec2},\dots ,K_{decM}],$$

(6)

or, in other words, to find a block-diagonal control gain matrix $K_{dec}$ of dimensions corresponding to dimensions of ${\overline{B}}_i$, such that the corresponding closed-loop system is connectively stable with the defined stability degree. The main aim is to develop a decentralized controller design procedure at a subsystem level.

In this section, basic steps are studied, which are used in a proposed decentralized control design in the next section. These steps can be summarized as follows.

• Transformation of the system to the form with an output block-diagonal matrix.
• Robust stability conditions for a descriptor system.
• Robust stability conditions of a large-scale system under decentralized control.
• Subsystem model augmentation for PID controllers designed at the subsystem level.

The presented material is based on our previous results from [20,21].

3.1. Transformation of the Output Matrix to a Block-Diagonal Form

In a recent work of two of authors [21], the transformation of a continuous-time system is proposed based on the augmentation of a system to a descriptor one with a block-diagonal output matrix. In this subsection, we present the discrete-time counterpart for the previous result.

The system can be decomposed into individual subsystems and their interconnections. We can split matrix ${\overline{A}}_i,i=1,2,\dots N$ from (2) and (4) to a diagonal and non-diagonal part, $\overline{A}{d}_i$ and $\overline{A}{m}_i$, respectively, where $\overline{A}{d}_i=blockdiag[{\overline{A}}_{i11},{\overline{A}}_{i22},\dots ,{\overline{A}}_{iMM}]$ corresponds to subsystems and $\overline{A}{m}_i$ to their interconnections.

Then, the following plant model is obtained for the i-th vertex of the uncertainty domain

$$x(t+1)=(\overline{A}{d}_i+\overline{A}{m}_i)x\left(t\right)+{\overline{B}}_{i}u\left(t\right),y\left(t\right)=\overline{C}x\left(t\right)$$

(7)

$i=1,2,\dots ,N.$

Recall that the j-th subsystem has ${\overline{n}}_j$ states, $m_j$ inputs, and $l_j$ outputs. The corresponding expression for the output matrix $\overline{C}$ is as follows:

$$y\left(t\right)=\left[\begin{array}{c}{\overline{C}}_1\\ \dots \\ {\overline{C}}_M\end{array}\right]x\left(t\right)=\left[\begin{array}{cccc}{\overline{C}}_{11}& {\overline{C}}_{12}& \dots & {\overline{C}}_{1M}\\ \dots \\ {\overline{C}}_{j1}& {\overline{C}}_{j2}& \dots & {\overline{C}}_{jM}\\ \dots \\ {\overline{C}}_{M1}& {\overline{C}}_{M2}& \dots & {\overline{C}}_{MM}\end{array}\right]x\left(t\right),j=1,2,\dots ,M,$$

$${\overline{C}}_j\in R^{l_j\times n},{\overline{C}}_{jk}\in R^{l_j\times {\overline{n}}_k},k=1,2,\dots ,M.$$

In order to transform the system to the form with a decentralized block-diagonal structure of the output matrix, the following new state variable for the overall system is defined:

$$x_d{\left(t\right)}^T=\left[\begin{array}{ccccccc}{x}_1{\left(t\right)}^T& y_1{\left(t\right)}^T& x_2{\left(t\right)}^T& y_2{\left(t\right)}^T& \dots & x_M{\left(t\right)}^T& y_M{\left(t\right)}^T\end{array}\right]$$

where $x_j\left(t\right)\in R^{{\overline{n}}_j}$ are the state variables and $y_j\left(t\right)\in R^{l_j}$ are the output variables of the j-th subsystem. In this way, we can describe the large-scale linear uncertain system (1) alternatively as a uncertain descriptor system having decentralized structure, with block-diagonal input and output matrices B and C

$$E{x}_d(t+1)=A\left(\xi \right)x_d\left(t\right)+B\left(\xi \right)u_d\left(t\right),y_d\left(t\right)=C{x}_d\left(t\right),$$

(8)

where the descriptor system matrices are $(A\left(\xi \right),B\left(\xi \right))={\sum }_{i=1}^N(A_i,B_i){\xi }_i$,

$$A_i=\left[\begin{array}{ccc}{A}_{i11}& \dots & A_{i1M}\\ \dots & \dots & \dots \\ A_{iM1}& \dots & A_{iMM}\end{array}\right]$$

$$A_{ijj}=\left[\begin{array}{cc}{\overline{A}}_{ijj}& 0_{jj}\\ {\overline{C}}_{jj}& -I_{n_j}\end{array}\right]$$

$$A_{ijk}=\left[\begin{array}{cc}{\overline{A}}_{ijk}& 0_{jk}\\ {\overline{C}}_{jk}& 0\end{array}\right]$$

and $j,k=1,2\dots M$, $n_j={\overline{n}}_j+l_j, A_{ijj}\in R^{n_j\times n_j}=A{d}_{ij}$, $A_{ijk}\in R^{n_j\times n_k}$, $0_{jk}\in R^{n_j\times l_k}$ is a zero matrix, $I_{n_j}\in R^{n_j\times n_j}$ is identity matrix.

The input matrix is then

$$B_i=blockdiag\left[\begin{array}{ccc}{B}_{i1}& \dots & B_{iM}\end{array}\right]$$

$$B_{ij}=\left[\begin{array}{c}{\overline{B}}_{ij}\\ 0\end{array}\right]$$

and the output matrix C has now a decentralized structure

$$C=blockdiag\left[\begin{array}{cccc}\left[0_{n_1}{I}_{l_1}\right];& \left[0_{n_2}{I}_{l_2}\right];& \dots ;& \left[0_{n_M}{I}_{l_M}\right]\end{array}\right]$$

where $0_{n_j}\in R^{l_j\times n_j}$ is a zero matrix, $j=1,2,\dots ,M$.

The corresponding descriptor matrix in (8) is

$$E=blockdiag\left[\begin{array}{cccc}\left[\begin{array}{c}{I}_{n_1}\\ 0_1\end{array}\right],& \left[\begin{array}{c}{I}_{n_2}\\ 0_2\end{array}\right],& \left[\begin{array}{c}\dots \end{array}\right],& \left[\begin{array}{c}{I}_{n_M}\\ 0_M\end{array}\right]\end{array}\right]$$

where $0_j\in R^{l_j\times n_j}$ is a zero matrix, $E\in R^{n\times n},n={\sum }_{j=1}^M{n}_j,rank\left(E\right)<n$.

The above model (8) describes the uncertain polytopic descriptor system in the decentralized structure. In this way, the challenge of designing a decentralized controller for an uncertain system (1) with a general (non-diagonal) output matrix is transformed to a decentralized control design problem for a descriptor system with a block-diagonal output matrix.

Suppose the complex system (1) is both controllable and observable in the centralized sense, and there are no unstable fixed modes [22]. The current challenge lies in formulating a decentralized controller for the j-th subsystem, $j=1,2,\dots ,M$. The objective is to ensure that this decentralized controller not only maintains the closed-loop stability, robustness, and performance of each individual subsystem but also preserves the overall stability of the complex descriptor system, while meeting the designer’s specified performance criteria. Then, the obtained decentralized controller ensure the stability of the original uncertain large-scale system (1). For example, the controller can take the form of a proportional–integral (PI), proportional–integral–derivative (PID), or any other suitable type.

Below, we will consider a control algorithm for a decentralized PID controller in the following form:

$$u_j\left(t\right)=k{p}_j{C}_j{x}_j\left(t\right)+k{i}_j{C}_j\sum _{t=t_0}^{\infty }{x}_j\left(t\right)+k{d}_j{C}_j\Delta x{\left(t\right)}_j,$$

(9)

where

$$\Delta x_j\left(t\right)=x_j\left(t\right)-x_j(t-1),j=1,2,\dots ,M.$$

3.2. Robust Stability of Uncertain Descriptor System

Let us recall recent results of descriptor system regularity and stability [23,24,25,26,27], which will be used in our further development

Definition 3

([28]). The linear descriptor system

$$Ex(t+1)=Ax\left(t\right),x\left(t_0\right)=x_0$$

(10)

is said to be regular if there exist s such that $det(sE-A)\ne 0$.

Definition 4

([28]). A linear discrete descriptor system is said to be stable if (10) is regular and all of its finite poles are in the unit circle and asymptotically stable if all finite eigenvalues of pencil $(zE-A)$ are inside the unit circle.

Lemma 2

([28]). Linear discrete descriptor system (10) is regular, causal, and asymptotically stable if and only if there exists a generalized Lyapunov function $V\left(Ex\left(t\right)\right)=x{\left(t\right)}^T{E}^{T}PEx\left(t\right)$ satisfying

$$\Delta V\left(Ex\right(t\left)\right)=V\left(E\right(x(t+1))-V(Ex\left(t\right))<0$$

(11)

when $Ex\left(t\right)\ne 0.$

Robust controller design for an uncertain discrete-time descriptor system (8) is based on Lemma 2, and follows the approach used for a robust controller design and discrete descriptor system, which is summarized in the following theorem.

Theorem 1.

Linear discrete-time descriptor polytopic system (8) is regular, causal, and asymptotically stable if and only if:

Case a. For the case without uncertainty ($i=1$ in (8)), there exists a positive definite Lyapunov matrix $P>0$ such that the following inequality holds:

$$A^{T}PA-E^{T}PE\le 0.$$

(12)

Case b. For the uncertain system with polytopic uncertainty ($i=1,\dots ,N$ in (8)), there exist auxiliary matrices $N_1,N_2\in R^{n\times n}$ and positive definite matrices $P_i$ such that the following inequalities hold for $i=1,2,\dots ,N$:

$$\left[\begin{array}{cc}{N}_1{A}_i+A_i^T{N}_1^T-E^T{P}_{i}E& -N_1+A_i^T{N}_2^T\\ -N_1^T+N_2{A}_i& -N_2-N_2^T+P_i\end{array}\right]\le 0.$$

(13)

Proof. 

Case A. Equation (12) directly follows from (11) after substituting for $E\left(x\right(t+1)$ from (8).

Case B. Consider the following Lyapunov function for the uncertain system: $V\left(Ex\left(t\right)\right)=x{\left(t\right)}^T{E}^{T}P\left(\xi \right)Ex\left(t\right)$. Substitute from (8) and (11) for $A\left(\xi \right)$ and $P\left(\xi \right)$ the following $A\left(\xi \right)={\sum }_{i=1}^N{A}_i{\xi }_i,P\left(\xi \right)={\sum }_{i=1}^N{P}_i{\xi }_i$ and introduce two auxiliary matrices $N_1,N_2\in R^{n\times n}$ such that for the i-th vertex of uncertainty polytope

$$\mathrm{He}\left({[Ex(t+1)-A_{i}x\left(t\right)]}^T[-N_1^{T}x\left(t\right)-N_2^{T}Ex(t+1)]\right)=0$$

(14)

where $i=1,2,\dots ,N$ and $\mathrm{He}\left(X\right)$ denotes $X+X^T$.

Introducing denotation $v^T=\left[x{\left(t\right)}^T{\left(Ex(t+1)\right)}^T\right]$, stability condition (12) can be rewritten as

$$\Delta V\left(Ex\left(t\right)\right)=v^T\left[\begin{array}{cc}-E_i^T{P}_{i}E& 0\\ 0& P_i\end{array}\right]v.$$

(15)

Summing up (14) written in the matrix form using vector v and (15), inequality (13) is obtained for the first difference of Lyapunov function (11), which proves the necessary and sufficient robust stability conditions for the polytopic discrete uncertain descriptor system. □

3.3. Robust Stability of Large-Scale System with Decentralized Control

This subsection states the robust stability boundary according to our recent results. Consider the descriptor system (8) and split the system matrix $A_i$ analogously as in (7) $A_i=A{d}_i+A{m}_i$ where $A{d}_i=blockdiag\left[\begin{array}{ccc}{A}_{i11},& \dots ,& A_{iMM}\end{array}\right]$. To study the stability of a descriptor system considering its decentralized structure, let us introduce an unknown positive coefficient $\alpha >0$ and modified system matrix $A_i=\alpha A{d}_i+A{m}_i$. The next step is to find a maximal value of $\alpha >0$ so that (12) or (13) hold, that is appropriate to the considered case. According to the obtained value of $\alpha$, it is possible to assess the stability of the overall system, which can be summarized as follows:

• If the obtained $\alpha \ge 1$, the uncertain descriptor complex system is impulse-free and asymptotically stable.
• If the obtained $\alpha <1$, the uncertain complex system is not stable.

The closed-loop stability condition for discrete-time descriptor complex systems can be obtained from the following inequality, where a decentralized control $u_d\left(t\right)=K_{dec}{y}_d\left(t\right)=K_{decx}{x}_d\left(t\right)$ is considered:

$${(A{d}_i+B_i{K}_{decx})}^T(A{d}_i+B_i{K}_{decx})\le \left({\alpha }^{2}A{d}_i^{T}A{d}_i\right).$$

Inequality (13) falls within the category of Bilinear Matrix Inequalities (BMI). When dealing with complex systems of higher order, both the elimination lemma and the linearization approach can be employed to derive a computationally manageable Linear Matrix Inequality (LMI) representation of (13), as described in our earlier work.

According to the review paper on decentralized control [18], complex systems can be split into two large groups: with strong or weak interactions. In this research, we classify complex systems into stable and unstable categories. The parameter $\alpha$ obtained through our analysis holds crucial significance in the formulation of resilient decentralized controller designs. A robust stability boundary condition for complex systems can be set with respect to subsystem eigenvalues ${\lambda }_{ik}=eig\left(A{d}_i\right),k=1,2,\dots ,n;i=1,2,\dots ,N$ as follows:

$$S_c=\alpha \underset{i}{min}\underset{k}{max}\left|{\lambda }_{ik}\right|,k=1,2,\dots ,n.$$

(16)

The achieved result determines a sufficient condition for the size of the radius of the circle, which determines the limit of robust stability for the complex system. If all the eigenvalues of the closed-loop subsystems with a decentralized controller are placed inside the determined circle, the complex system will be robustly stable. The result indicates the possibility of designing decentralized controllers for individual subsystems, irrespective of the presence of intersubsystem interaction links.

Remark 1.

If the positive coefficient $S_c$ is known, the degree of stability ${\alpha }_d$ for all subsystems $j=1,2,\dots ,M$ is given as

$${\alpha }_d=1-S_c^2.$$

The following condition must be satisfied for a stable complex discrete-time descriptor system:

$$\Delta V_j\left(x\right)\le -{\alpha }_d{V}_j\left(x\right)j=1,2,\dots ,M$$

where $V_j\left(x\right),j=1,2,\dots ,M$ represents the Lyapunov function for the closed-loop j-th subsystem.

3.4. PID Controller as a Static Output Feedback

For the design of a robust PID controller (9) for uncertain decentralized discrete descriptor systems, we recall the procedure of transforming the PID(PI) controller design problem to a static output feedback problem [12]. The new state variables are introduced as follows: $z\left(t\right)={\left[z_1{\left(t\right)}^T{z}_2{\left(t\right)}^T\right]}^T$, where $z_1\left(t\right)={\sum }_{i=0}^{t-2}y\left(i\right),z_2\left(t\right)={\sum }_{i=0}^{t-1}y\left(i\right)$ and then $z_2\left(t\right)-z_1\left(t\right)=y(t-1)$. On the base of the new state variables $y_n\left(t\right)={\left[y{\left(t\right)}^T{z}_1{\left(t\right)}^T{z}_2{\left(t\right)}^T\right]}^T$, the modified static output feedback PID algorithm is given as follows:

$$u\left(t\right)=[kp+ki+kdkdki-kd]y_n\left(t\right)=K{y}_n\left(t\right).$$

(17)

Discrete-time descriptor system matrices are augmented by also considering states $z_1\left(t\right),z_2\left(t\right)$ to include PID controller dynamics

$$A_n\left(\xi \right)=\left[\begin{array}{ccc}A\left(\xi \right)& 0& 0\\ 0& 0& I\\ C& 0& I\end{array}\right];C_n=\left[\begin{array}{ccc}C& 0& 0\\ 0& I& 0\\ 0& 0& I\end{array}\right]$$

(18)

and the input matrix

$$B_n{\left(\xi \right)}^T={\left[B\left(\xi \right)00\right]}^T.$$

For PI controller one, $k_d=0$ is set and the variable $z_1\left(t\right)$ is omitted. The PI control algorithm is then in the form

$$u\left(t\right)=[kp+kiki]y_n\left(t\right)$$

and dynamic model (18) reduces to

$$A_n\left(\xi \right)=\left[\begin{array}{cc}A\left(\xi \right)& 0\\ C& I\end{array}\right];C_n=\left[\begin{array}{cc}C& 0\\ 0& I\end{array}\right];B_n{\left(\xi \right)}^T={\left[B\left(\xi \right)0\right]}^T.$$

In the following text, we assume that without a change in denotation, the discrete-time descriptor system matrices comply with robust PID or PI controller design.

4. Robust Decentralized Controller Design

The decentralized controller design procedure for a discrete-time large-scale system is presented in this section. Controller design is realized at the subsystem level where an overall system parameter $\alpha$ and robust stability boundary $S_c$ (see (16)) are considered to guarantee the robust stability of descriptor system (8). In order to design a (robust) PID decentralized controller, the method of the regional pole placement approach gives promising results [10]. The formulation of the corresponding stability condition for a descriptor system is presented in the next subsection.

4.1. Regional Pole Placement Approach to Descriptor Systems

Following [10], the $D_R$ region in a complex domain is defined as

$$D_R=\{z\in C:R_{11}+R_{12}z+R_{12}^T{z}^{\ast }+R_{22}z{z}^{\ast }<0\}$$

(19)

where $R_{11}=R_{11}^T\in R^{d\times d}$, $R_{12}\in R^{d\times d}$, and $R_{22}=R_{22}^T\in R^{d\times d}$; we consider $R_{22}\ge 0$. A matrix A is considered to exhibit $D_R$ stability when all of its eigenvalues are situated within the designated $D_R$ region. The condition of $D_R$ stability for a matrix A is equivalent to the existence of a positive definite matrix P that satisfies the following inequality:

$$R_{11}\otimes P+R_{12}\otimes PA+R_{12}^T\otimes A^T{P}^T+R_{22}\otimes A^{T}PA<0$$

(20)

where ⊗ denotes the Kronecker product. For a discrete-time system $x(t+1)=Ax\left(t\right)$, a necessary and sufficient $D_R$ stability condition can be formulated in matrix form for a positive definite matrix P such that

$$\Delta V_e=v^T\left[\begin{array}{cc}{R}_{11}\otimes P& R_{12}\otimes P\\ \ast & R_{22}\otimes P\end{array}\right]v\le 0$$

(21)

where $v^T=\left[(1_d\otimes x{\left(t\right)}^T)(1_d\otimes x{(t+1)}^T)\right]$, $1_d$ denotes a column vector of d ones and ∗ denotes the conjugate transpose of the symmetrically placed submatrix. Following [10] and using (15) and (21), the $D_R$ robust stability condition for closed-loop descriptor system (8) with a system matrix $Ad{c}_i=A{d}_i+B_i\ast K_{dec}$ can be formulated in the matrix form as

$$\Delta V_d=v_d^T\left[\begin{array}{cc}{R}_{11}\otimes (-E^T\ast P\left(\xi \right)\ast E)& R_{12}\otimes P\left(\xi \right)\\ \ast & R_{22}\otimes P\left(\xi \right)\end{array}\right]v_d\le 0.$$

(22)

For a disk region with the center in origin and radius r, we have $R_{11}=-1,R_{12}=0,R_{22}=\frac{1}{r^2},d=1$ and $D_R$ robust stability is reduced to

$$\Delta V_{exd}=v_d^T\left[\begin{array}{cc}{R}_{11}\otimes (-E^T\ast P_i\ast E)& 0\\ 0& R_{22}\otimes P_i\end{array}\right]v_d\le 0.$$

(23)

Robust stability condition (23) for a descriptor system will be used in the decentralized controller design.

4.2. Robust Decentralized Control for Descriptor Systems

The design of a robust decentralized controller is based on the closed-loop robust stability condition. This condition is derived in a matrix form by analogy to the continuous-time result presented in our recent paper [21]. A disk $D_R$ region with radius $r=S_c$, where $S_c$ is given by (16), is considered for individual subsystems to achieve stability of the overall system. To obtain the closed-loop robust stability condition, $D_R$ stability condition (23) is considered for a descriptor system (8) with augmented matrices (23). Descriptor system model (8) and decentralized control law (6) are considered for individual subsystems and uncertainty domain vertices as constraints, and auxiliary matrices $N_3,N_4,N_5,N_6$ of corresponding dimensions are included analogically to $N_1,N_2$ in (14), resulting in system constraints (24) and (25). All conditions are formulated and solved on a subsystem level (index j denotes the j-th subsystem; subsystem matrices corresponding to the i-th uncertainty domain vertex are $A_{ij}$ and $B_{ij}$; subsystem controller parameters are in a matrix $K_{d}ecj$).

$$\mathrm{He}\left({[E_j{x}_j(t+1)-A_{ij}x\left(t\right)-B_{ij}u\left(t\right)]}^T[-N_2^{T}E{x}_j(t+1)-N_1^T{x}_j\left(t\right)-N_3^T{u}_j\left(t\right)]\right)=0,$$

(24)

$$\mathrm{He}\left({[-K_{decj}^T{x}_j\left(t\right)+u_j\left(t\right)]}^T[N_4^T{x}_j\left(t\right)+N_5^T{E}_j{x}_j(t+1)+N_6^T{u}_j\left(t\right)]\right)=0.$$

(25)

Vector $v\left(t\right)$ from (15) is further extended to $v_{uj}^T=\left[x_j{\left(t\right)}^T{\left(E_j{x}_j(t+1)\right)}^T{u}_j\left(t\right)\right]$, and formulas (24) and (25) are rewritten in a matrix form and add up to (23) so that the final robust stability condition is achieved as

$$v_{uj}^T{W}_j{v}_{uj}\le 0$$

(26)

where a symmetric matrix $W_j=\left(w_{ik}\right)$ and for $i=1,\dots ,N$

$$\begin{array}{cc}\hfill w_{11}& =\mathrm{He}(N_1{A}_{ij}-N_4{K}_{decj})+R_{11}\otimes \left(E_j^T{P}_{ij}{E}_j\right)\hfill \\ \hfill w_{12}& =-N_1+A_{ij}^T{N}_2^T-K_{decj}^T{N}_5^T\hfill \\ \hfill w_{13}& =N_1{B}_{ij}+N_4-K_{decj}^T{N}_6^T+A_{ij}^T{N}_3^T\hfill \\ \hfill w_{22}& =-N_2-N_2^T+R_{22}\otimes P_{ij}\hfill \\ \hfill w_{23}& =N_2{B}_{ij}-N_3^T+N_5\hfill \\ \hfill w_{33}& =\mathrm{He}(N_3{B}_{ij}+N_6).\hfill \end{array}$$

The decentralized controller design for system (1) with an already decentralized input matrix (4) can be summed up as follows:

• Transform a system into the fully decentralized form using an auxiliary descriptor system (8).
• Calculate the robust stability boundary $S_c$ as in (16).
• For a PID controller, use the augmented subsystem description according to (17) and (18).
• Solve BMI matrix inequality (26) for each subsystem considering the $D_R$ region complying with the value of $S_c$ (disc region with radius $S_c$).

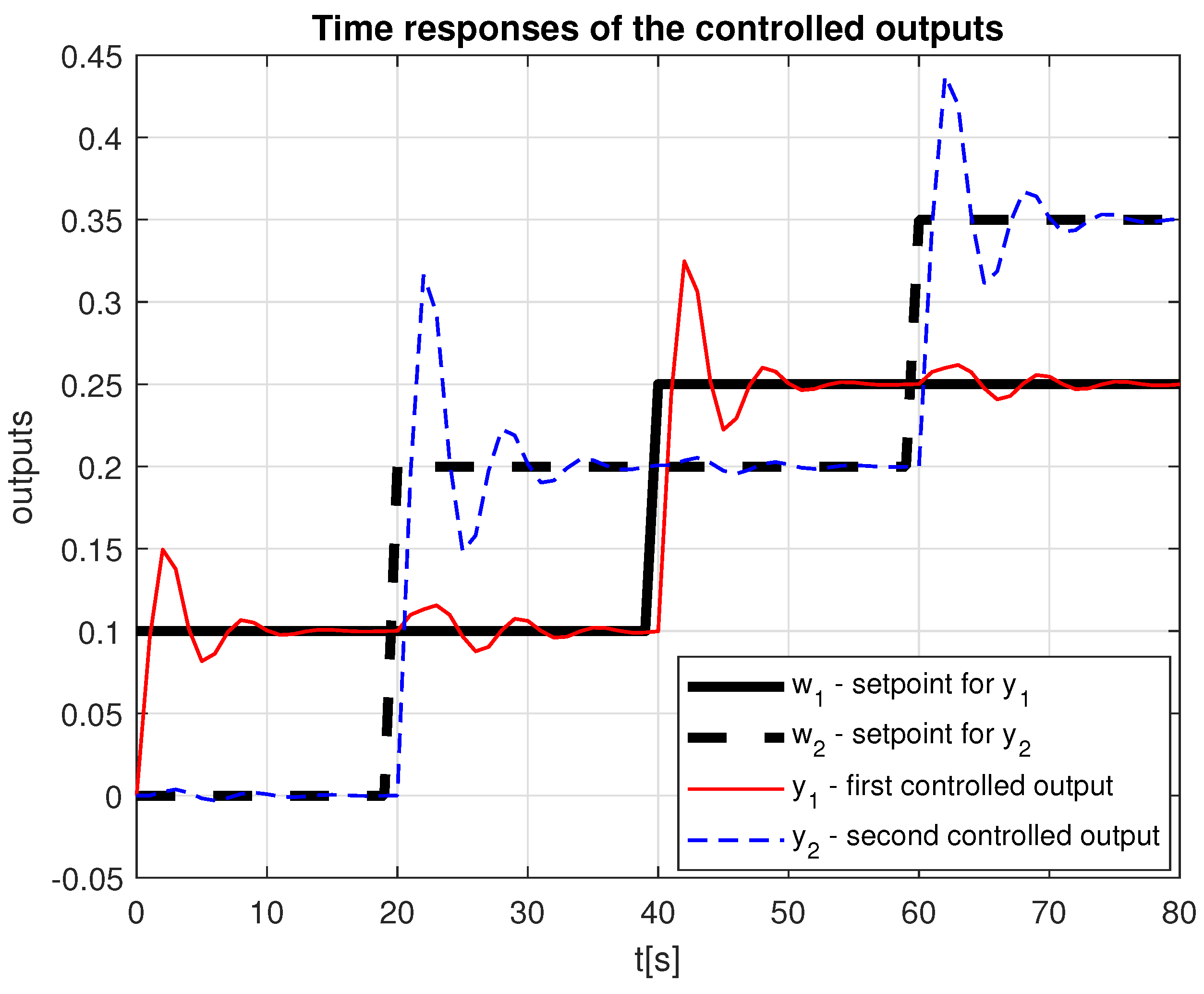
5. Example

The next example illustrates the detailed procedure for designing a decentralized control for the complex linear discrete-time system. We consider a fifth-order system with two subsystems, second and third order, respectively. The aim is to design a PID decentralized controller for the mentioned system. The structure of the example is typical of some practical applications, e.g., control of the active power of a turbo unit and control of the terminal voltage of a synchronous generator. Here, the models used for the decentralized controller are simplified. We consider two cases: Case A—only the nominal system is considered; Case B—an uncertain system is considered, where uncertainties are in the interactions.

The nominal system parameters are as follows:

first subsystem, $j=1$

$${\overline{A}}_{11}=\left[\begin{array}{cc}0.517& 0.7\\ 0.1& 0.23\end{array}\right]{\overline{B}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right]$$

$${\overline{C}}_1=\left[100.050.060.078\right];$$

second subsystem, $j=2$

$${\overline{A}}_{22}=\left[\begin{array}{ccc}0.59& 0.37& 0.28\\ 0.0143& 0.04& 0.1\\ 0.3& 0.41& 0.12\end{array}\right]{\overline{B}}_2=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$$

$${\overline{C}}_2=\left[00.110.050.01\right];$$

interactions

$$\overline{A}m=\left[\begin{array}{ccccc}0& 0& 0.02& 0.07& 0.3\\ 0& 0& 0.09& 0.05& 0.1\\ 0.027& 0.04& 0& 0& 0\\ 0.012& 0.05& 0& 0& 0\\ 0.07& 0.04& 0& 0& 0\end{array}\right].$$

It is assumed that the interaction matrix is stable; in our case all eigenvalues of $Am$ lay within <$-0.16,0.0459$>. In the first step, described in Section 3.1, the system is transformed into the descriptor form with a block-diagonal output matrix. The descriptor state vector is chosen as $[x_1,x_2,y_1,x_3,x_4,x_5,y_2]$ and the corresponding descriptor systems (8) is obtained in the form

$$A_1=\left[\begin{array}{ccccccc}0.517& 0.7& 0& 0.02& 0.07& 0.03& 0\\ 0.1& 0.23& 0& 0.09& 0.05& 0.1& 0\\ 1& 0& -1& 0.05& 0.06& 0.07& 0\\ 0.027& 0.04& 0& 0.59& 0.37& 0.2& 0\\ 0.12& 0.05& 0& 0.0143& 0.04& 0.1& 0\\ 0.07& 0.04& 0& 0.3& 0.41& 0.12& 0\\ 0& 0.1& 0& 1& 0.05& 0.01& -1\end{array}\right]$$

$C_1=\left[001\right]$ and $C_2=\left[0001\right]$, $C=blockdiag[C_1,C_2]$, the descriptor matrix is $E=diag\{1,1,0,1,1,1,0\}$.

Checking the stability condition $A_i=\alpha A{d}_i+A{m}_i$ (Section 3.3), and maximizing $\alpha$, one obtains $\alpha =1.16$ with stability radius to complex descriptor system $S_c=0.8922$. The value of $\alpha$ implies that the complex system is stable, near to the stability boundary.

Case A

(interactions $\overline{A}m$)

Utilizing the regional pole placement approach for a circle centered in origin with a radius corresponding to $S_c$, the obtained PID controller parameters are as follows:

first subsystem

$k{p}_1=0.9544,k{i}_1=0.9541,k{d}_1=-5.8218e-005;$

second subsystem

$k{p}_2=0.9744,k{i}_2=0.9740,k{d}_2=-6.3422e-005.$

The designed decentralized controller is checked for the overall system by computing closed-loop system eigenvalues and using simulations. The corresponding subsystem eigenvalues are as follows:

first subsystem closed-loop eigenvalues

$-0.9643,0.4015\pm 0.1254i,-0.0001$;

second subsystem closed-loop eigenvalues

$-0.9256,0.4194\pm 0.1761i,-0.1114,-0.0001$.

Note that each subsystem has two extra eigenvalues since PID controller dynamics are included.

The eigenvalues characterizing the behavior of the entire closed-loop complex system are:

$-0.9437\pm 0.068i,0.4647\pm 0.1976i,0.4057,0.2864,-0.0937,-0.0001,-0.0001$.

Note that the complex system with the designed decentralized controller is asymptotically stable.

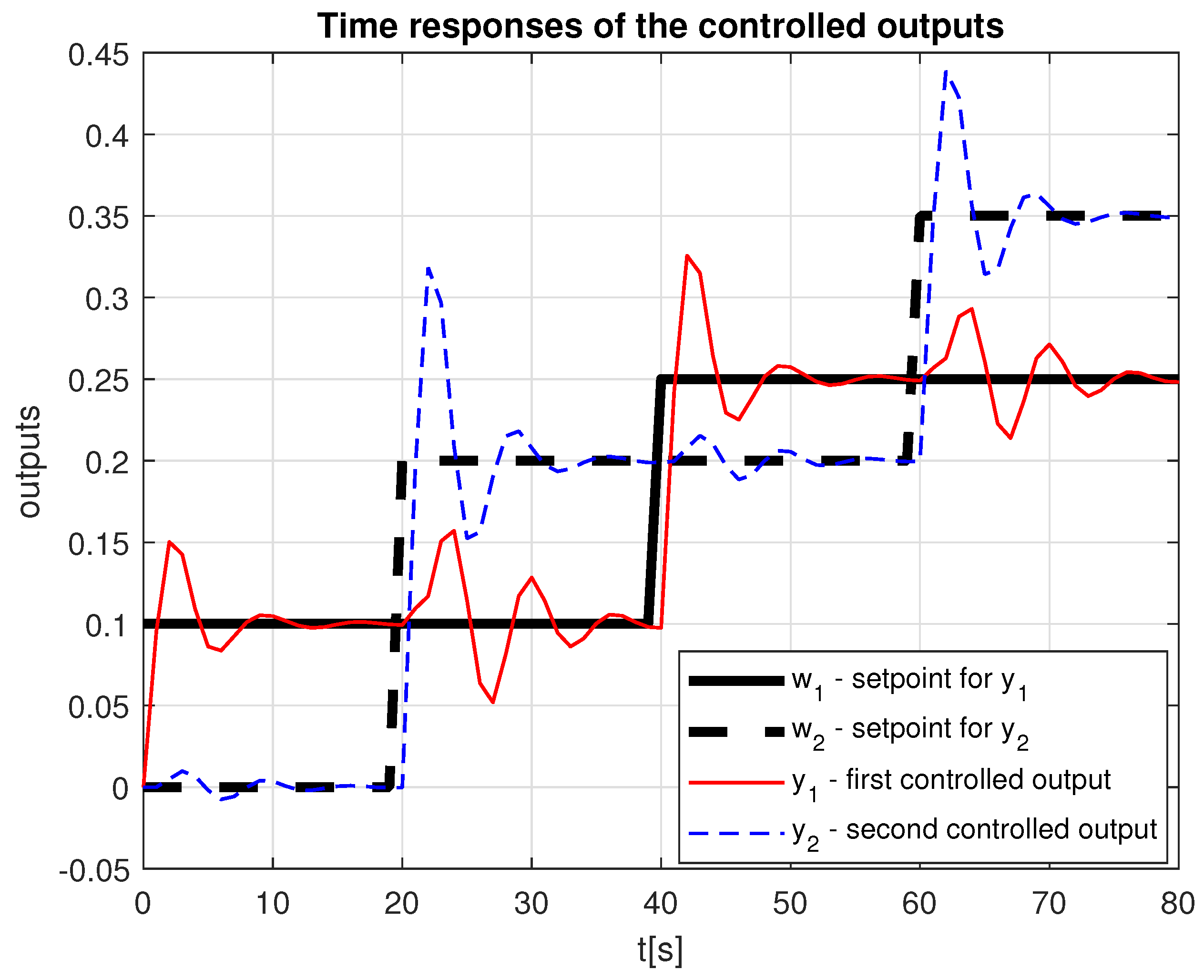
Case B

(uncertain interactions $\overline{A}m$ to $3\overline{A}m$)

In this scenario, we consider the design of a robust PID controller for the previously discussed complex system, taking into account uncertainties in the interactions within the subsystems. Therefore, we consider polytopic uncertainty with two vertices, where for $i=1$ the interaction matrix $A{m}_1$ is the same as for Case A, and for the second vertex (second working point), $i=2$, the interaction matrix is equal to $A{m}_2=3A{m}_1$. For these different values of interactions, we design a decentralized PID controller such that the closed-loop complex system will be stable over the uncertainty domain. Increasing the interactions, the corresponding complex system is unstable, $\alpha =0.7$. A regional pole placement approach gives the results, which are very close to those in Case A. Therefore, we check the same decentralized controller as in Case A for the case with interactions $3A{m}_1$. The closed-loop eigenvalues of the complex system in the second vertex are

$-0.9873\pm 0.0853i,0.613\pm 0.2944i,0.5258,-0.0684\pm 0.1142i,-0.0001,-0.0001$.

The complex system for Case B is asymptotically stable.

The dynamic response of the closed-loop system for Case A is depicted in Figure 1 (${\xi }_1={\xi }_2=0.5$). The impact of interactions is evident from the simulation results, particularly on the output $y_2$ at times of 20 and 60 s and with smaller interactions at times of 0 and 40 s. The dynamic response of the closed-loop system for Case B, characterized by increased interactions, is illustrated in Figure 2 (${\xi }_1={\xi }_2=0.5$). This simulation demonstrates higher levels of interactions and the stability of the closed-loop system. The simulation results substantiate the precision of the numerical computations and affirm the soundness of the proposed control method.

6. Conclusions

This paper addresses a key challenge in decentralized control of linear discrete-time complex systems. Concerning a decentralized control design, a decentralized (block-diagonal) structure of the input and output matrices is typically assumed. However, many real-world plants do not meet this requirement.

In this paper, we introduce a novel approach that transforms the model of a complex plant when the output matrix does not possess a decentralized structure. This transformation converts the plant’s model into a descriptor complex uncertain matrix, ensuring that both the input and output matrices become block-diagonal. Subsequently, we apply a recently developed decentralized control design method [20] to design a decentralized controller at the subsystem level for the transformed decentralized system.

Our method focuses on the relationship between subsystems and the interaction matrix, prioritizing stability considerations over strong or weak interactions between subsystems. The outcomes achieved in the presented paper are the following:

1.

A novel transformation method for discrete-time dynamic systems is proposed, enabling the transformation of a linear state-space system into an uncertain descriptor system with a decentralized structure of input and output matrices appropriate for a decentralized controller design.

2.

Derivation of conditions for determining the stability boundaries of complex descriptor systems and their use in subsystem controller design [20].

3.

Validation of the proposed discrete-time system transformation method using the recently developed decentralized control design approach.

4.

Modification of the regional pole placement method to accommodate descriptor systems.

5.

Demonstration of the effectiveness of the proposed decentralized control design procedure through a practical example.

It is important to highlight that the robust decentralized controller design process is executed at the subsystem level, with due consideration to the interactions introduced through design parameters, while the interactions between subsystems are not explicitly considered in this process.