Adaptive Spectrum Anti-Jamming in UAV-Enabled Air-to-Ground Networks: A Bimatrix Stackelberg Game Approach
Abstract
:1. Introduction
1.1. Related Work
1.2. Motivations and Contributions
2. System Model and Problem Formulation
2.1. System Model
2.2. Communication Model
3. Bimatrix Stackelberg Game
3.1. Game Model
3.2. Optimization Objectives
3.3. Optimal Mixed Strategy for UAV
3.4. Algorithm Design and Analysis
| Algorithm 1 Algorithm for solving mixed strategies. |
|
| Algorithm 2 Algorithm for solving standardized linear programming problem. |
|
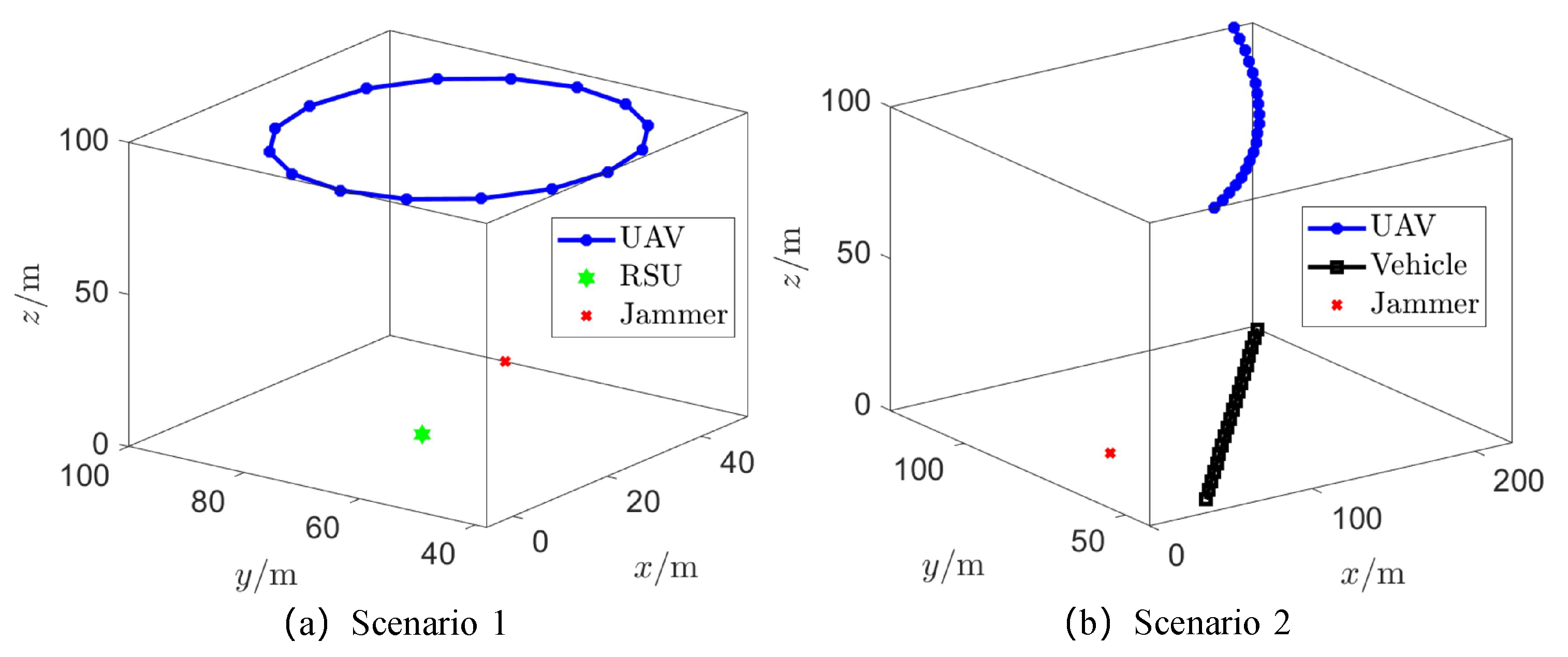
4. Simulation Results and Discussions
4.1. Simulation Parameters
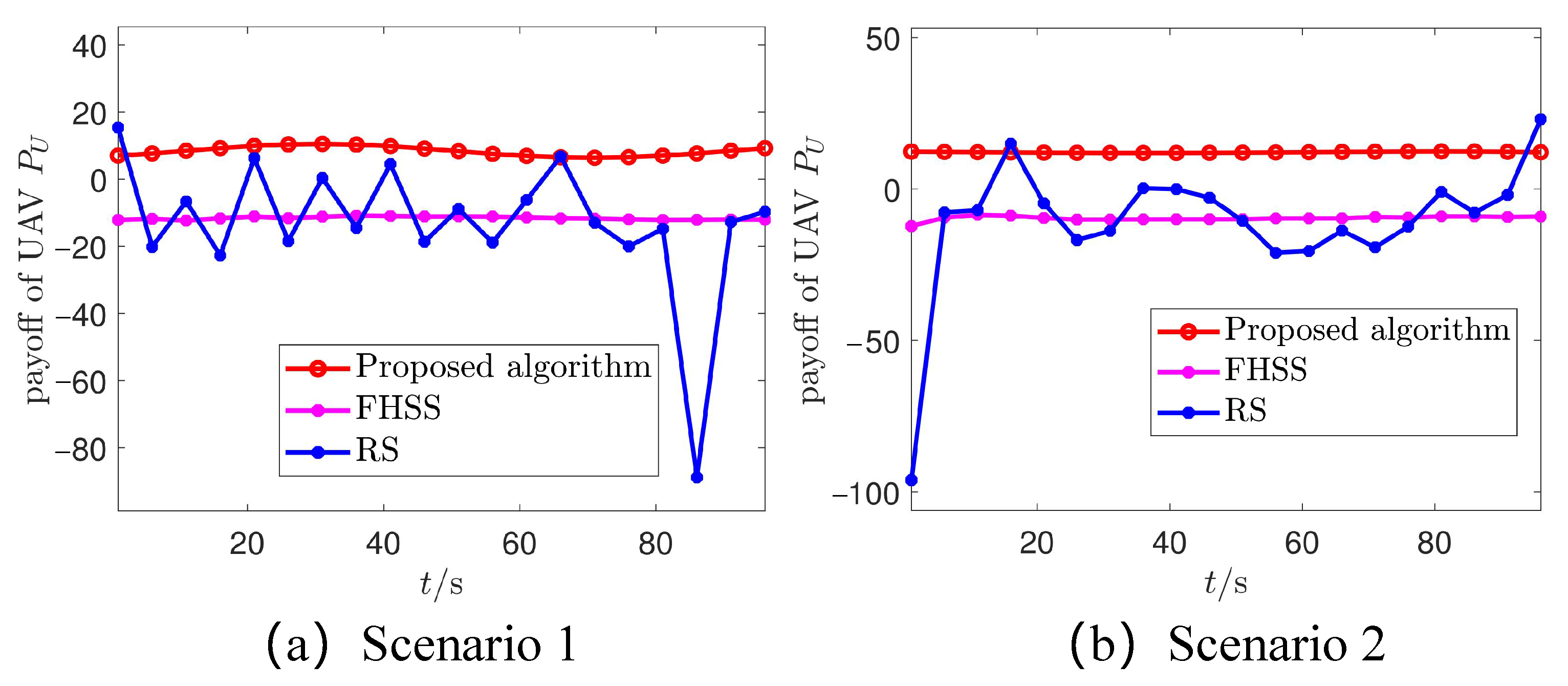
4.2. Performance Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wang, F.; Fan, G.; Liu, Y.; Zhang, Y. A Fast Estimation Algorithm for Parameters of Multiple Frequency-Hopping Signals Based on Compressed Spectrum Sensing and Maximum Likelihood. Electronics 2023, 12, 1808. [Google Scholar] [CrossRef]
- Liu, X.; Guan, M.; Zhang, X.; Ding, H. Spectrum Sensing Optimization in an UAV-Based Cognitive Radio. IEEE Access 2018, 6, 44002–44009. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, X. A High-efficiency Collaborative Spectrum Sensing with Gated Recurrent Unit for Multi-UAV Network. In Proceedings of the 31st International Telecommunication Networks and Applications Conference (ITNAC), University of New South Wales, Sydney, Australia, 24–16 November 2021; pp. 180–187. [Google Scholar]
- Abdel-Rahman, M.J.; Krunz, M. Game-theoretic quorum-based frequency hopping for anti-jamming rendezvous in DSA networks. In Proceedings of the 2014 IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN), McLean, VA, USA, 1–4 April 2014; pp. 248–258. [Google Scholar] [CrossRef]
- Si, P.; Yu, F.R.; Yang, R.; Zhang, Y. Dynamic Spectrum Management for Heterogeneous UAV Networks with Navigation Data Assistance. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015; pp. 1078–1083. [Google Scholar]
- Jia, L.; Xu, Y.; Sun, Y.; Feng, S.; Yu, L.; Anpalagan, A. A Game-Theoretic Learning Approach for Anti-Jamming Dynamic Spectrum Access in Dense Wireless Networks. IEEE Trans. Veh. Technol. 2019, 68, 1646–1656. [Google Scholar] [CrossRef]
- Lee, C.; Jang, G.; Dao, N.N.; Lakew, D.S.; Lee, C.; Cho, S. Competitive Game Theoretic Clustering-Based Multiple UAV-Assisted NB-IoT Systems. Electronics 2021, 10, 356. [Google Scholar] [CrossRef]
- Charlesworth, P.B. A Non-cooperative Game to Coordinate the Coverage of two Communications UAVs. In Proceedings of the IEEE Military Communications Conference, BAE Syst, San Diego, CA, USA, 18–20 November 2013; pp. 668–673. [Google Scholar]
- Chen, X.C.; Chen, Y.J. A Machine Learning Based Attack in UAV Communication Networks. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Chang, Z.; Guo, W.; Guo, X.; Ristaniemi, T. Machine Learning-based Resource Allocation for Multi-UAV Communications System. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC WORKSHOPS), Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Du, F.; Li, J.; Lin, Y.; Wang, Z.; Qian, Y. Mean-Field Multi-Agent Reinforcement Learning for Adaptive Anti-Jamming Channel Selection in UAV Communications. In Proceedings of the 14th IEEE International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 1–3 November 2022; pp. 910–915. [Google Scholar]
- Gao, Y.; Xiao, Y.; Wu, M.; Xiao, M.; Shao, J. Game Theory-Based Anti-Jamming Strategies for Frequency Hopping Wireless Communications. IEEE Trans. Wirel. Commun. 2018, 17, 5314–5326. [Google Scholar] [CrossRef]
- Du, J.; Tian, W.; Ji, X.; Du, M.; Liu, G.; Dai, Y.; Han, Z. Strategic UAV-Assisted Game Model for Detection in Covert Communication. IEEE Trans. Veh. Technol. 2023, 72, 7426–7438. [Google Scholar] [CrossRef]
- Jose, S.T.; Kulkarni, A.A. Shannon Meets von Neumann: A Minimax Theorem for Channel Coding in the Presence of a Jammer. IEEE Trans. Inf. Theory 2020, 66, 2842–2859. [Google Scholar] [CrossRef]
- Yu, J.; Li, Q. Optimal Deployment in Moving Target Defense against Coordinated Cyber-Physical Attacks via Game Theory. Electronics 2023, 12, 2484. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, B.; Liu, K.J.R.; Clancy, T.C. Anti-Jamming Games in Multi-Channel Cognitive Radio Networks. IEEE J. Sel. Areas Commun. 2012, 30, 4–15. [Google Scholar] [CrossRef]
- Ruan, L.; Wang, J.; Chen, J.; Xu, Y.; Yang, Y.; Jiang, H.; Zhang, Y.; Xu, Y. Energy-Efficient Multi-UAV Coverage Deployment in UAV Networks: A Game-Theoretic Framework. China Commun. 2018, 15, 194–209. [Google Scholar] [CrossRef]
- Li, H.; Han, Z. Blind Dogfight in Spectrum: Combating Primary User Emulation Attacks in Cognitive Radio Systems with Unknown Channel Statistics. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Lei, Z.; Yang, P.; Zheng, L. Detection and Frequency Estimation of Frequency Hopping Spread Spectrum Signals Based on Channelized Modulated Wideband Converters. Electronics 2018, 7, 170. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, G.; Chen, J.; Zhang, X.; Jia, L.; Kong, L. Interference-Aware Cooperative Anti-Jamming Distributed Channel Selection in UAV Communication Networks. Appl. Sci. 2018, 8, 1911. [Google Scholar] [CrossRef]
- Jia, L.; Yao, F.; Sun, Y.; Niu, Y.; Zhu, Y. Bayesian Stackelberg Game for Antijamming Transmission with Incomplete Information. IEEE Commun. Lett. 2016, 20, 1991–1994. [Google Scholar] [CrossRef]
- Garnaev, A.; Petropulu, A.; Trappe, W.; Poor, H.V. A Multi-Jammer Power Control Game. IEEE Commun. Lett. 2021, 25, 3031–3035. [Google Scholar] [CrossRef]
- Feng, Z.; Ren, G.; Chen, J.; Zhang, X.; Luo, Y.; Wang, M.; Xu, Y. Power Control in Relay-Assisted Anti-Jamming Systems: A Bayesian Three-Layer Stackelberg Game Approach. IEEE Access 2019, 7, 14623–14636. [Google Scholar] [CrossRef]
- Qi, N.; Wang, W.; Zhou, F.; Jia, L.; Wu, Q.; Jin, S.; Xiao, M. Two Birds with One Stone: Simultaneous Jamming and Eavesdropping with the Bayesian-Stackelberg Game. IEEE Trans. Commun. 2021, 69, 8013–8027. [Google Scholar] [CrossRef]
- Su, Z.; Wu, Q.; Qi, N.; Jia, L.; Du, Z. Biased Stackelberg game-based UAV relay anti-jamming communications: Exploiting trajectory optimization and transmission mode selection. IET Commun. 2022, 16, 2467–2478. [Google Scholar] [CrossRef]
- Xie, L.; Su, Z.; Chen, N.; Xu, Q.; Fan, Y.; Benslimane, A. A Game Theory Based Scheme for Secure and Cooperative UAV Communication. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Han, C.; Huo, L.; Tong, X.; Wang, H.; Liu, X. Spatial Anti-Jamming Scheme for Internet of Satellites Based on the Deep Reinforcement Learning and Stackelberg Game. IEEE Trans. Veh. Technol. 2020, 69, 5331–5342. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, G.; Chen, J.; Jia, L.; Xu, Y. Anti-jamming transmission in UAV communication networks: A Stackelberg game approach. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017. [Google Scholar] [CrossRef]
- Xu, J.; Wang, K.; Zhang, X.; Liu, P.; Kong, D.; Zhou, H. Anti-jamming strategy based on game theory in single-channel UAV communication network. In Proceedings of the 2021 Sixth International Conference on Fog and Mobile Edge Computing (FMEC), Gandia, Spain, 6–9 December 2021; pp. 63–69. [Google Scholar]
- Liao, C.; Xu, K.; Zhu, H.; Xia, X.; Su, Q.; Sha, N. Secure transmission in satellite-UAV integrated system against eavesdropping and jamming: A two-level stackelberg game model. China Commun. 2022, 19, 53–66. [Google Scholar] [CrossRef]
- Zhu, X.; Huang, Y.; Wang, S.; Wu, Q.; Ge, X.; Liu, Y.; Gao, Z. Dynamic Spectrum Anti-Jamming with Reinforcement Learning Based on Value Function Approximation. IEEE Wirel. Commun. Lett. 2023, 12, 386–390. [Google Scholar] [CrossRef]
- Zou, M.; Chen, J.; Luo, J.; Hu, Z.; Chen, S. Equilibrium Approximating and Online Learning for Anti-Jamming Game of Satellite Communication Power Allocation. Electronics 2022, 11, 3526. [Google Scholar] [CrossRef]
- Hashesh, A.O.; Hashima, S.; Zaki, R.M.; Fouda, M.M.; Hatano, K.; Eldien, A.S.T. AI-Enabled UAV Communications: Challenges and Future Directions. IEEE Access 2022, 10, 92048–92066. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Xu, Y.; Liu, X.; Wang, X.; Li, W.; Anpalagan, A. Dynamic Spectrum Anti-Jamming in Broadband Communications: A Hierarchical Deep Reinforcement Learning Approach. IEEE Wirel. Commun. Lett. 2020, 9, 1616–1619. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, H.; Li, X.; Zhang, B.; Peng, J. Reinforcement Learning-Based Anti-Jamming in Networked UAV Radar Systems. Appl. Sci. 2019, 9, 5173. [Google Scholar] [CrossRef]
- Von Neumann, J. Zur Theorie der Gesellschaftsspiele. Math. Ann. 1928, 100, 295–320. [Google Scholar] [CrossRef]
- Vajda, S. Games and Decisions. By R. Duncan Luce and Howard Raiffa. Pp. xi, 509. 70s. 1957. (J Wiley & Sons). Math. Gaz. 1959, 43, 152–153. [Google Scholar]




| Parameters | Notation | Value |
|---|---|---|
| UAV sensing start frequency | ||
| Total bandwidth | B | |
| Sub-bands’ number | M | 25 |
| UAV’s transmission power | ||
| UAV’s transmission cost | ||
| Jammer’s transmission cost | ||
| Roll-off factor | ||
| Channel gain at the one-meter distance | ; | |
| Path loss exponent | 3 | |
| Gaussian white noise PSD | ||
| Parameter in the standard linear programming | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Xu, Z.; Zhou, J.; Tian, D.; Duan, X.; Qu, K.; Zhao, D. Adaptive Spectrum Anti-Jamming in UAV-Enabled Air-to-Ground Networks: A Bimatrix Stackelberg Game Approach. Electronics 2023, 12, 4344. https://doi.org/10.3390/electronics12204344
Cheng L, Xu Z, Zhou J, Tian D, Duan X, Qu K, Zhao D. Adaptive Spectrum Anti-Jamming in UAV-Enabled Air-to-Ground Networks: A Bimatrix Stackelberg Game Approach. Electronics. 2023; 12(20):4344. https://doi.org/10.3390/electronics12204344
Chicago/Turabian StyleCheng, Longbo, Zixuan Xu, Jianshan Zhou, Daxin Tian, Xuting Duan, Kaige Qu, and Dezong Zhao. 2023. "Adaptive Spectrum Anti-Jamming in UAV-Enabled Air-to-Ground Networks: A Bimatrix Stackelberg Game Approach" Electronics 12, no. 20: 4344. https://doi.org/10.3390/electronics12204344
APA StyleCheng, L., Xu, Z., Zhou, J., Tian, D., Duan, X., Qu, K., & Zhao, D. (2023). Adaptive Spectrum Anti-Jamming in UAV-Enabled Air-to-Ground Networks: A Bimatrix Stackelberg Game Approach. Electronics, 12(20), 4344. https://doi.org/10.3390/electronics12204344








