Accuracy Analysis of Visual Odometer for Unmanned Rollers in Tunnels
Abstract
:1. Introduction
2. Related Work
3. Feature-Based Visual Odometer System
- Image pre-processing: Image distortion removal and calibration.
- Feature extraction: Corners, edges, and patches in each frame are chosen as the feature points.
- Feature description: The appearance of the neighboring region is described, producing descriptors.
- Feature matching: Each descriptor is matched with all descriptors in the adjacent image frame using brute-force matching. The one with the shortest distance is chosen as the matching point. Mismatches are then eliminated through random sample consensus (RANSAC).
- Motion estimation: The pose updates between adjacent frames are computed using the filtered, matched features.
- Pose tracking: The camera pose from the previous frame is combined with the pose update to calculate the current frame’s pose, which gives the actual pose of the roller, representing the compaction trajectory.
3.1. Feature Detection and Description
- Constructing a scale space and the Hessian matrix: The H matrix is a square matrix composed of the second-order partial derivatives of a multivariate function, providing local curvature information of the function at a given point. The Hessian matrix of a pixel in the image is shown as in (1):
- Since the feature points need to be scale-independent, Gaussian filtering is required before building the Hessian matrix [28], as shown in (2):
- 2.
- Key points detection: Key points are detected by finding extreme points in the scale space and image plane. SURF uses the determinant and trace of the Hessian matrix to determine whether it is a key point and performs non-maximum suppression to retain a unique and stable key point.
- 3.
- Principal direction allocation of feature points: For each detected key point, its main direction is calculated so that the feature has rotational invariance. SURF uses the direction of the Haar wavelet response to estimate the principal direction.
- 4.
- Generating feature point descriptors: Taking the feature points as the center, the image is divided into 4 × 4 sub-blocks along the principal direction, and each sub-block statistically contains four values of Haar wavelet features, forming a 64-dimensional vector as a feature descriptor.
3.2. Feature Matching
3.3. Pose Estimation
3.4. Evaluation Indicators
4. Result & Discussion
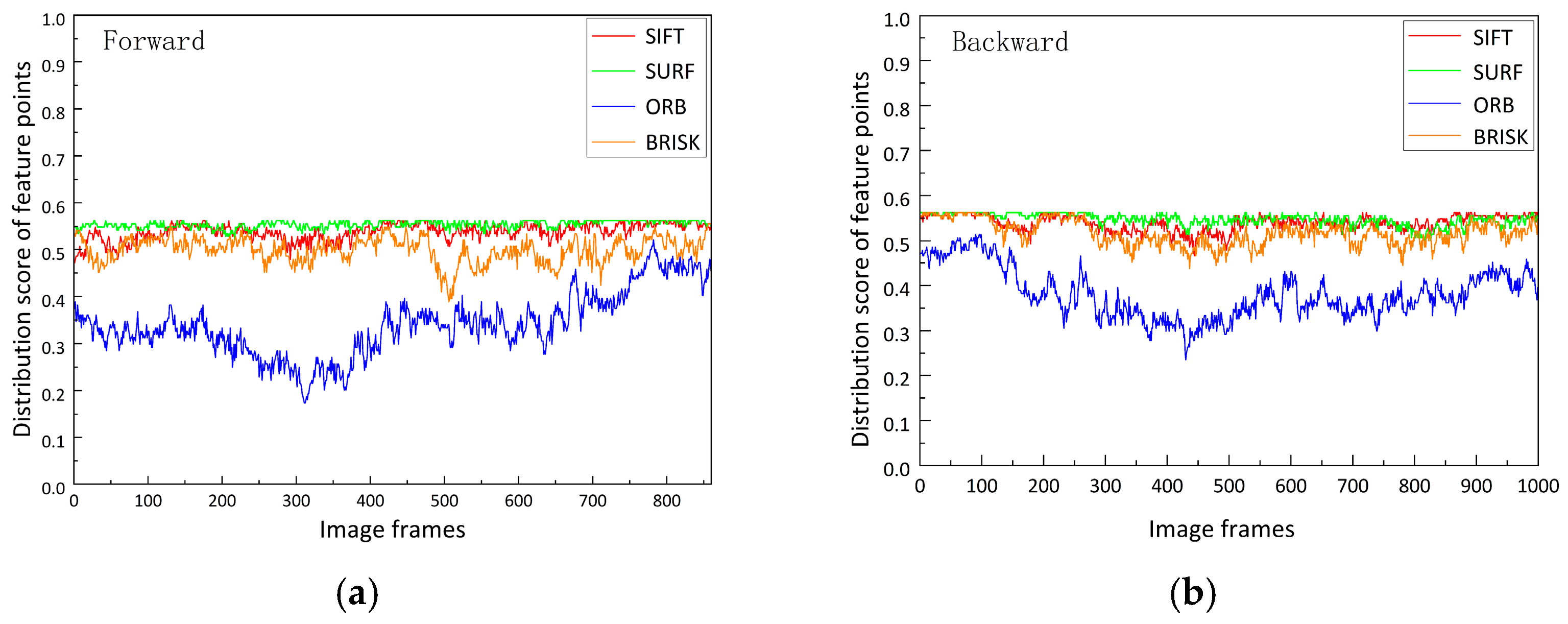
4.1. Feature Extraction
4.2. Feature Matching
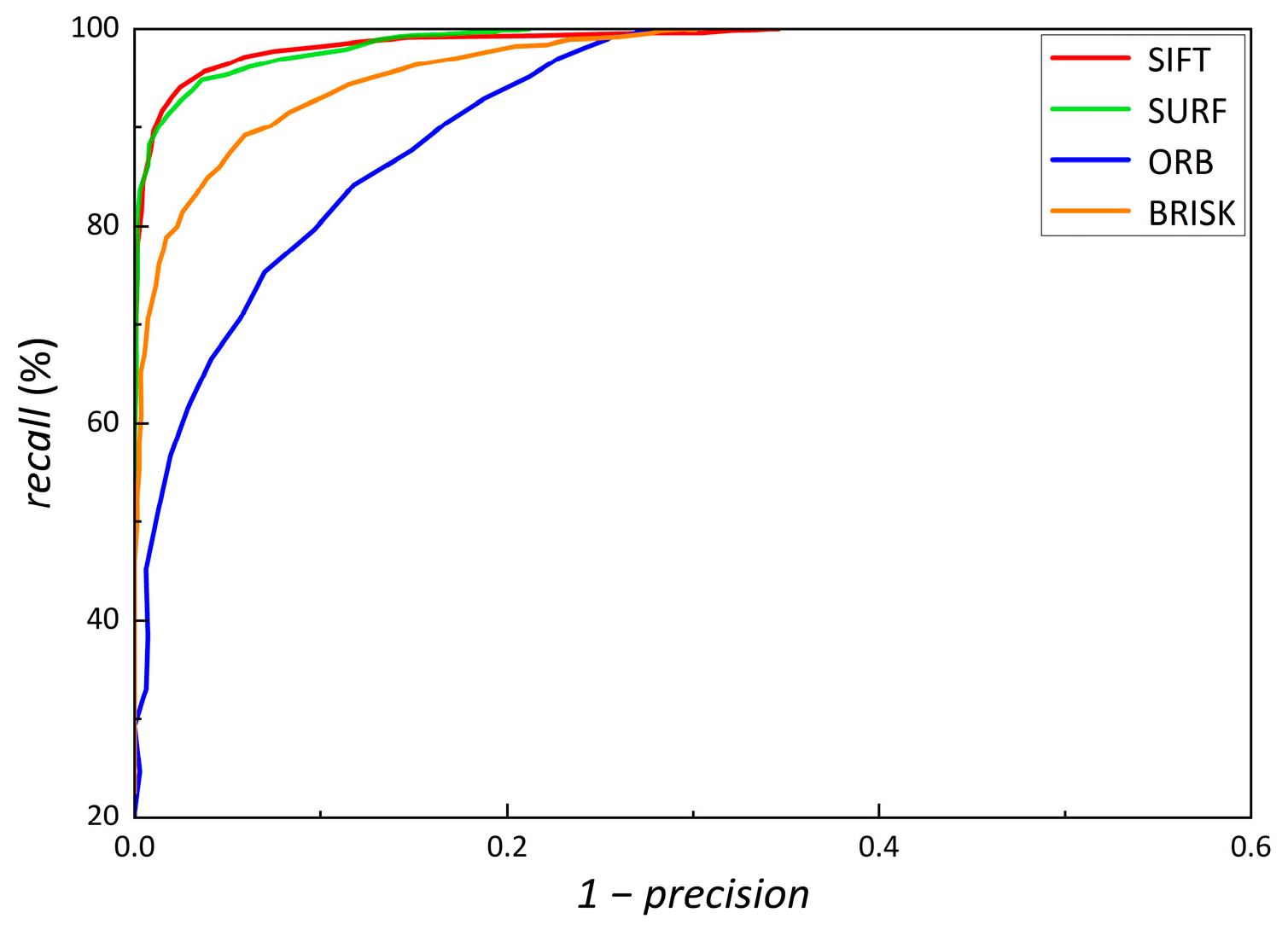
4.3. Precision and Recall
4.4. Real-Time Performance
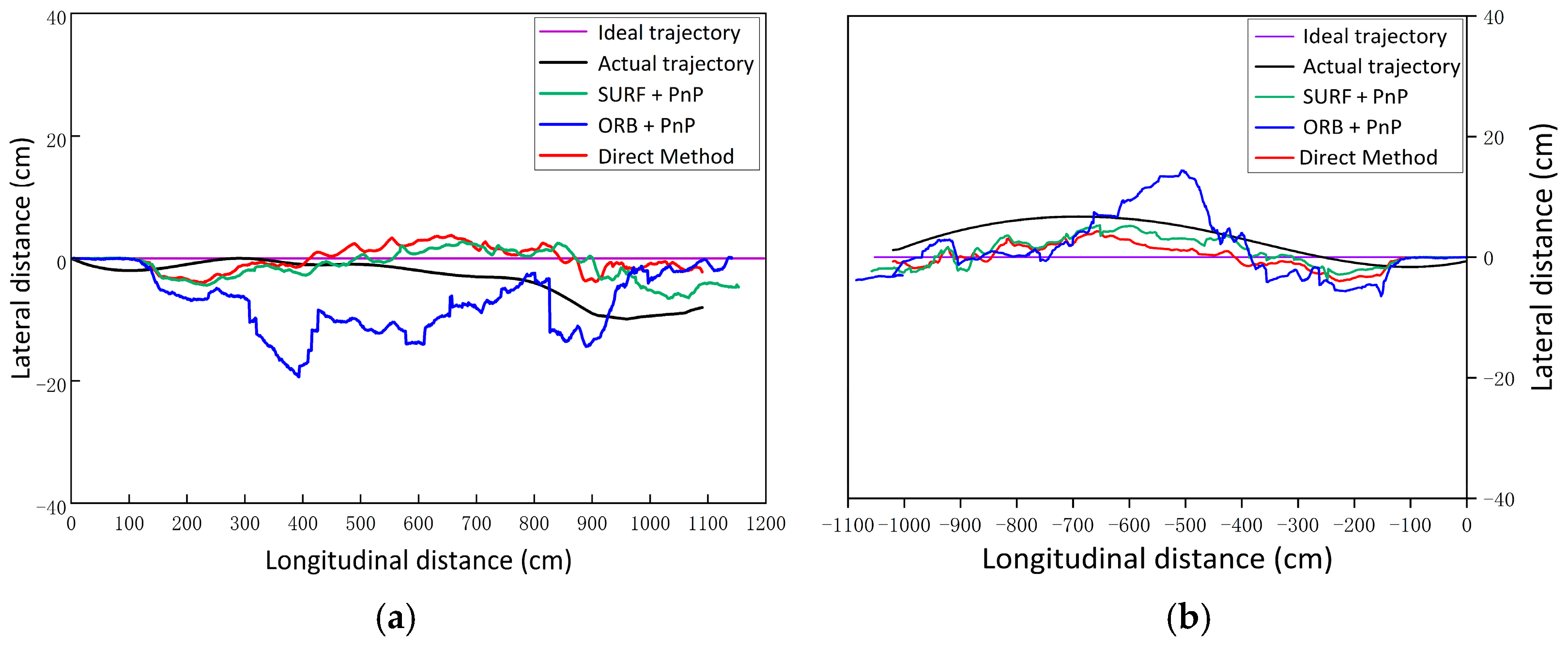
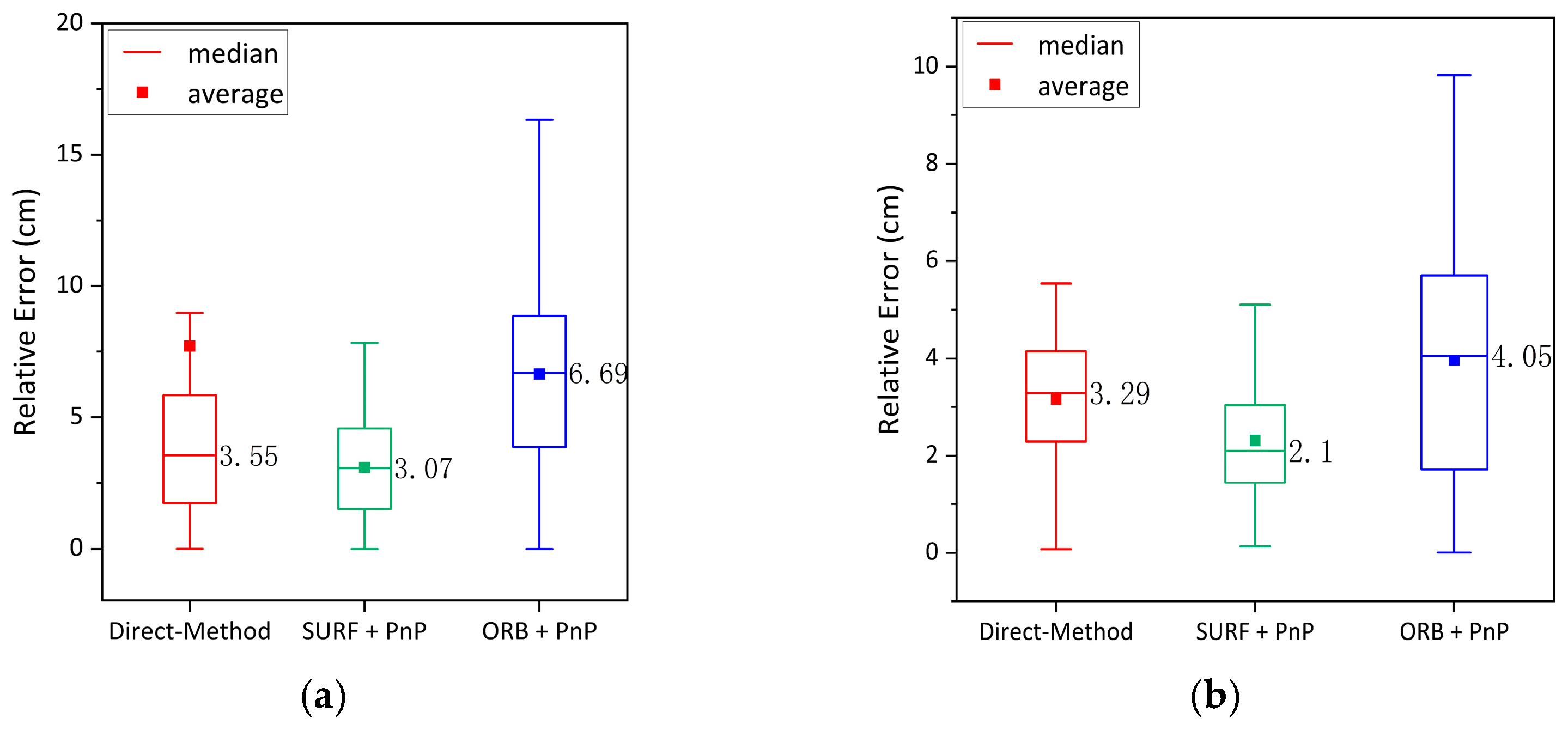
4.5. Pose Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BRIEF | Binary robust independent elementary features |
| BRISK | Binary robust invariant scalable key-points |
| CenSurE | Center surround extremas |
| DSO | Direct sparse odometry |
| DTAM | Dense tracking and mapping |
| FAST | Features from accelerated segment test |
| FLANN | Fast library for approximate nearest neighbors |
| FN | False negative |
| FP | False positive |
| FREAK | Fast retina key point |
| GNSS | Global navigation satellite system |
| GPU | Graphic processing unit |
| LSD-SLAM | Large-scale direct monocular SLAM |
| NASA | National Aeronautics and Space Administration |
| ORB | Oriented FAST and rotated BRIEF |
| ORB-SLAM2 | Oriented FAST and rotated BRIEF simultaneous localization and mapping 2 |
| PnP | perspective-n-point |
| RANSAC | Random sample consensus |
| RGB-D | RGB-depth |
| RTK | Real-time kinematic |
| SURF | Speed-up robust features |
| SIFT | Scale-invariant feature transform |
| SVO | Semi-direct visual odometry |
| TP | True positive |
| TN | True negative |
| V-SLAM | Visual simultaneous localization and mapping |
| VO | Visual odometry |
References
- Zhang, Q.; An, Z.; Liu, T.; Zhang, Z.; Huangfu, Z.; Li, Q.; Yang, Q.; Liu, J. Intelligent rolling compaction system for earth-rock dams. Autom. Constr. 2020, 116, 103246. [Google Scholar] [CrossRef]
- Shi, M.; Wang, J.; Li, Q.; Cui, B.; Guan, S.; Zeng, T. Accelerated Earth-Rockfill Dam Compaction by Collaborative Operation of Unmanned Roller Fleet. J. Constr. Eng. Manag. 2022, 148, 04022046. [Google Scholar] [CrossRef]
- Fang, X.; Bian, Y.; Yang, M.; Liu, G. Development of a path following control model for an unmanned vibratory roller in vibration compaction. Adv. Mech. Eng. 2018, 10, 1687814018773660. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, T.; Zhang, Z.; Huangfu, Z.; Li, Q.; An, Z. Unmanned rolling compaction system for rockfill materials. Autom. Constr. 2019, 100, 103–117. [Google Scholar] [CrossRef]
- Yang, M.; Bian, Y.; Liu, G.; Zhang, H. Path Tracking Control of an Articulated Road Roller with Sideslip Compensation. IEEE Access 2020, 8, 127981–127992. [Google Scholar] [CrossRef]
- Tak, S.; Buchholz, B.; Punnett, L.; Moir, S.; Paquet, V.; Fulmer, S.; Marucci-Wellman, H.; Wegman, D. Physical ergonomic hazards in highway tunnel construction: Overview from the Construction Occupational Health Program. Appl. Ergon. 2011, 42, 665–671. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Hu, Y.; Jia, F.; Wang, X. Intelligent compaction quality evaluation based on multi-domain analysis and artificial neural network. Constr. Build. Mater. 2022, 341, 127583. [Google Scholar] [CrossRef]
- Lu, T.; Liu, Y.; Yang, Y.; Wang, H.; Zhang, X. A Monocular Visual Localization Algorithm for Large-Scale Indoor Environments through Matching a Prior Semantic Map. Electronics 2022, 11, 3396. [Google Scholar] [CrossRef]
- Xuexi, Z.; Guokun, L.; Genping, F.; Dongliang, X.; Shiliu, L. SLAM Algorithm Analysis of Mobile Robot Based on Lidar. In Proceedings of the 2019 Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 4739–4745. [Google Scholar] [CrossRef]
- Xia, X.; Bhatt, N.P.; Khajepour, A.; Hashemi, E. Integrated Inertial-LiDAR-Based Map Matching Localization for Varying Environments. IEEE Trans. Intell. Veh. 2023, 1, 1–12. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Cheng, Y.; Maimone, M.; Matthies, L. Visual odometry on the Mars exploration rovers. In Proceedings of the 2005 IEEE Inter-national Conference on Systems, Man and Cybernetics, Waikoloa, HI, USA, 10–12 October 2005; pp. 903–910. [Google Scholar]
- Nistér, D.; Naroditsky, O.; Bergen, J. Visual odometry. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; p. I-I. [Google Scholar]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the 13th European Con-ference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the 2015 IEEE/RSJ Interna-tional Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar]
- Caruso, D.; Engel, J.; Cremers, D. Large-scale direct SLAM for omnidirectional cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 141–148. [Google Scholar]
- Engel, J.; Sturm, J.; Cremers, D. Semi-dense visual odometry for a monocular camera. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1449–1456. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Lin, M.; Yang, C.; Li, D.; Zhou, G. Intelligent Filter-Based SLAM for Mobile Robots with Improved Localization Performance. IEEE Access 2019, 7, 113284–113297. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Zhang, T.; Liu, C.; Li, J.; Pang, M.; Wang, M. A New Visual Inertial Simultaneous Localization and Mapping (SLAM) Algorithm Based on Point and Line Features. Drones 2022, 6, 23. [Google Scholar] [CrossRef]
- He, M.; Zhu, C.; Huang, Q.; Ren, B.; Liu, J. A review of monocular visual odometry. Vis. Comput. 2019, 36, 1053–1065. [Google Scholar] [CrossRef]
- Wu, D.; Wang, M.; Li, Q.; Xu, W.; Zhang, T.; Ma, Z. Visual Odometry with Point and Line Features Based on Underground Tunnel Environment. IEEE Access 2023, 11, 24003–24015. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, M.; Garg, A. Improved object recognition results using SIFT and ORB feature detector. Multimed. Tools Appl. 2019, 78, 34157–34171. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Jakubovic, A.; Velagic, J. Image Feature Matching and Object Detection Using Brute-Force Matchers. In Proceedings of the 2018 International Symposium ELMAR, Zadar, Croatia, 16–19 September 2018; pp. 83–86. [Google Scholar] [CrossRef]
- Guo, G.; Dai, Z.; Dai, Y. Robust stereo visual odometry: A comparison of random sample consensus algorithms based on three major hypothesis generators. J. Navig. 2022, 75, 1298–1309. [Google Scholar] [CrossRef]
- Eudes, A.; Lhuillier, M.; Naudet-Collette, S.; Dhome, M. Fast Odometry Integration in Local Bundle Adjustment-Based Visual SLAM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 290–293. [Google Scholar]





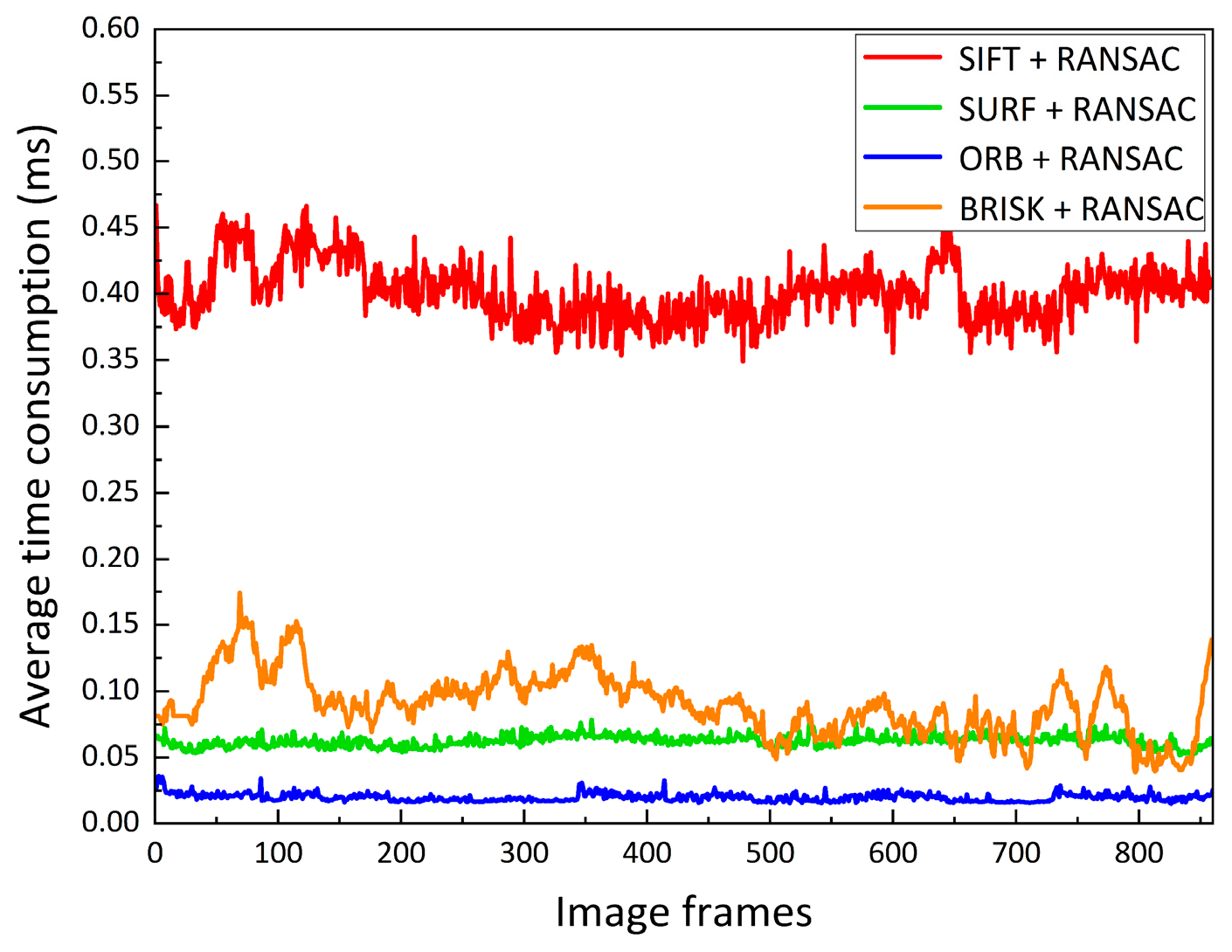
| Algorithm | Feature Extraction (ms) | Feature Description (ms) | Feature Matching (ms) | Average Total Time Consumption (ms) |
|---|---|---|---|---|
| SIFT | 0.2259 | 0.1942 | 0.0184 | 0.4386 |
| SURF | 0.0316 | 0.0205 | 0.0125 | 0.0646 |
| ORB | 0.0198 | 0.0093 | 0.0015 | 0.026 |
| BRISK | 0.0427 | 0.0275 | 0.0392 | 0.1094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Wang, X.; Hu, Y.; Tan, P. Accuracy Analysis of Visual Odometer for Unmanned Rollers in Tunnels. Electronics 2023, 12, 4202. https://doi.org/10.3390/electronics12204202
Huang H, Wang X, Hu Y, Tan P. Accuracy Analysis of Visual Odometer for Unmanned Rollers in Tunnels. Electronics. 2023; 12(20):4202. https://doi.org/10.3390/electronics12204202
Chicago/Turabian StyleHuang, Hao, Xuebin Wang, Yongbiao Hu, and Peng Tan. 2023. "Accuracy Analysis of Visual Odometer for Unmanned Rollers in Tunnels" Electronics 12, no. 20: 4202. https://doi.org/10.3390/electronics12204202
APA StyleHuang, H., Wang, X., Hu, Y., & Tan, P. (2023). Accuracy Analysis of Visual Odometer for Unmanned Rollers in Tunnels. Electronics, 12(20), 4202. https://doi.org/10.3390/electronics12204202






