Examination of a Method for Estimating Solid Fraction at Flow Cessation from Flow Velocity of Mushy Formation Molten Alloys

Abstract

The purpose of this study was to experimentally estimate the solid fraction at which the cessation of the flow of a molten Al–7%Si–0.3%Mg alloy and Cu–8%Sn alloy occurs in casting. The flow cessation mechanism of two alloys is known as the “mushy” formation type, which means that the flow ceases when the solid fraction at the molten metal tip reaches a certain critical value. Therefore, the flow velocity at the molten metal tip is assumed to decrease gradually. Thus, a new method for calculating the solid fraction at flow cessation based on computer simulations was examined using experimental measurements of the flow velocity and flow length. The result of the experiment shows the experimental flow length is consistent with the simulation results, the calculated solid fraction at flow cessation. The flow velocity gradually decreased from the initial stage, but there was a region where the velocity was almost constant after the initial stage. The molten metal temperature became lower from the root side to the tip side, and the solid fraction at the time of flow cessation was calculated from the measurement results, for the Al–7%Si–0.3%Mg alloy it was 0.35–0.4 near the tip, and for the Cu–8%Sn alloy it was 0.25. Computer simulations were performed by tuning the heat transfer coefficient so that the flow length and flow velocity would match the experimental results. Computer simulations were performed by tuning the heat transfer coefficients so that the flow length and flow velocity would match the experimental results and could simulate the changes in flow velocity obtained from the experiments. The solid fraction at the tip of the molten metal was almost the same as the experimental results. These results show that it is possible to estimate the solid fraction at the flow cessation from the flow velocity at the tip.

1. Introduction

In order to produce high-quality castings, the molten metal must be filled without cold shut. For this reason, various studies have been conducted on the fluidity factors of molten metal.

M. Nikawa et al. developed an experimental setup for measuring the temperature of a mushy alloy melt during flow and used it to perform high-precision temperature measurements. By measurement, the maximum solid fraction was found to be slightly away from the melt front towards the gate, about $0.3$. Through the fluidity experiments of Al–7%Si–0.3%Mg alloys, it was found that the flow stop mechanism is a mixture of tip metal skin formation and mushy formation type that hinders the flow of molten metal [1].

Y. Iwata et al. developed a highly sensitive thermal sensor with a low response time to study the solidification behavior of molten metal during mold filling, which can correctly measure the temperature of the flowing molten metal. They found that the types of surface defects in castings vary with the way the aluminum alloy solidifies. The occurrence of surface wrinkling can be predicted by the thickness of the solidified layer of molten metal on the surface of the cavity [2].

A. Sugiyama et al., by direct observation of mold filling and comparing with simulations, found that the computer simulation results, although generally consistent with the observations, were difficult to model well for flow separation on curved surfaces, detailed wavy free surfaces, and similar flow changes in pouring [3].

Meanwhile, H. Nakae et al. investigated the effect of wettability between molten metal and mold material on fluidity using a glass and Teflon thin tube/water solution system. The flow rate in the water/glass tube system was higher than that of the water/Teflon tube one, namely due to the contact angles and surface tension. The influence of the work of adhesion is considerably weaker than that of external pressure [4].

To estimate the solidus fraction when the flow ceases, the temperature change usually is measured [5]. However, the temperature of the molten aluminum alloy during flowing drops sharply, making accurate measurement difficult. Therefore, in this study, a method of estimating the solid fraction at the cessation of the flow of a mushy solidified alloy that shows a “mushy” formation morphology from the change in flow velocity during molten metal flow was investigated. In the experiments on the Al–7%Si–0.3%Mg alloy, this was performed by pouring molten metal into a mold equipped with observation windows with a horizontal flow channel and photographing the flowing molten metal tip with a digital camera. In addition, a thermocouple was installed in the flow channel to measure the temperature change in the molten metal in the flow. In addition, using copper alloys with the same solidification type, comparative verification experiments were carried out under the spiral cavity of the sand mold. In the Cu–8%Sn alloy fluidity experiment, a sand mold with a spiral cavity was used for the experiment, and the molten metal flow length was measured under the same observation method. Simultaneously, computer simulations were performed to analyze the flow and solidification of the casting material considering the temperature dependence of the physical properties. The flow velocity and flow length of the castings were calculated experimentally, and a new method for calculating the solid fraction at flow cessation based on computer simulation was examined.

2. Calculation Method

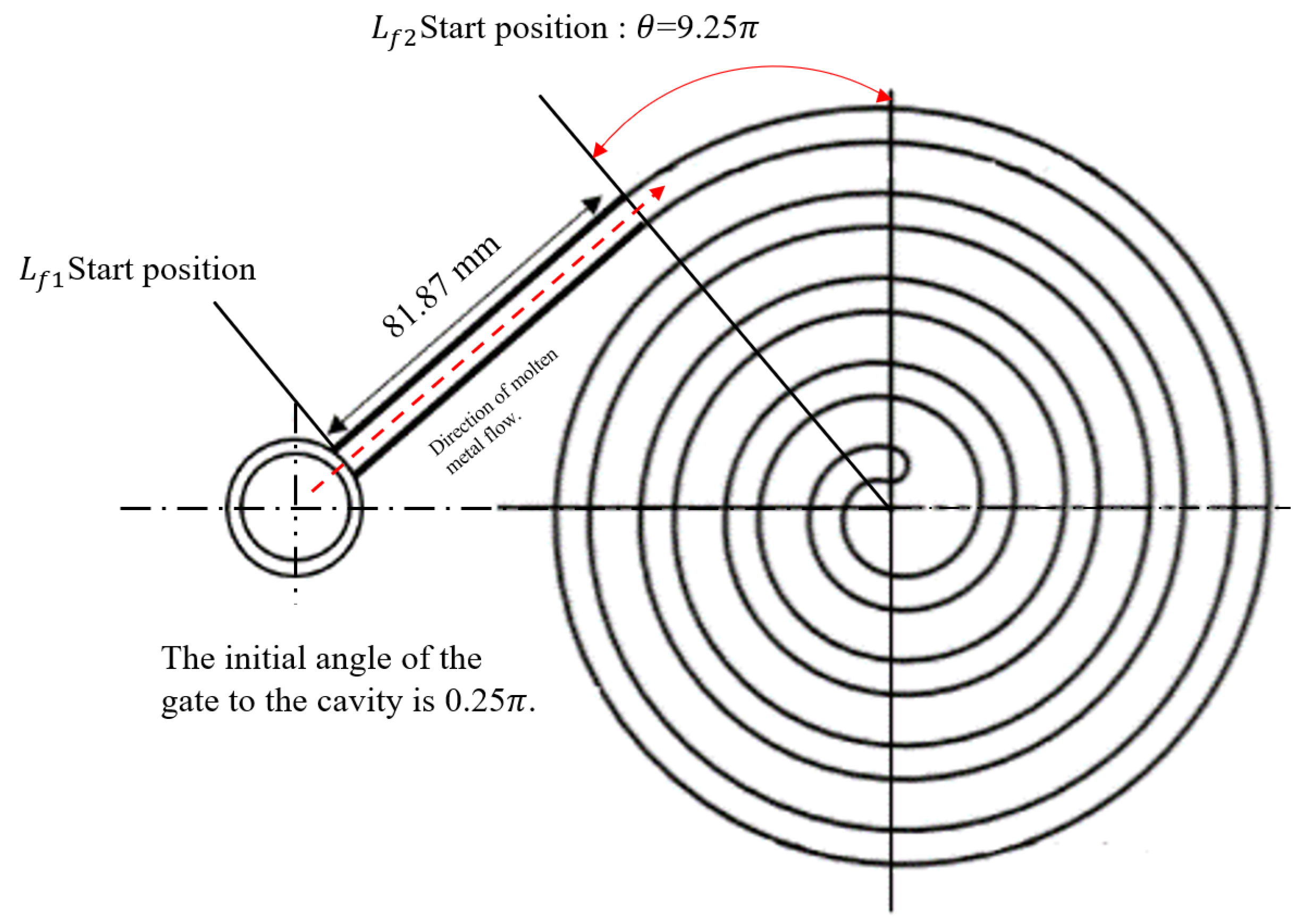
2.1. Calculation Method of Flow Length in Spiral Cavity

The flow length is obtained from the sum of the straight part and the spiral part. Let the length of the straight part be $L_{f2}$ and the length of the spiral part be $L_{f1}$, as shown in Figure 1.

Figure 1. Schematic diagram of spiral cavity.

$L_{f1}$ is 81.87 mm, and $L_{f2}$ is an algebraic spiral, so the length of the curve can be obtained by integration. The Archimedes’ spiral is a spiral with equal intervals and is represented by Equation (1) as an equation in polar coordinates to the experiment results of K. Miura et al. [6]. The distance of each arm of such a spiral is always equal to 2$\pi$a.

$$r=a\theta ,$$

(1)

In Equation (1), the unit of a is Archimedes’ helix coefficient 3 (mm/°). $\theta$: declination (°). The molten metal initial inflow angle is 45°, which is 0.25 $\pi$. Among them, a is a constant; if expressed as a parameter, it is Equation (2).

$$\left\{\begin{array}{c}x=acos\theta \hfill \\ y=asin\theta ,\hfill \end{array}\right.$$

(2)

Moreover, if the curve length $\left\{\begin{array}{c}x=f\left(t\right)(t_1\le t\le t_2)\hfill \\ y=g\left(t\right)(t_1\le t\le t_2)\hfill \end{array}\right.$ is $L_{f2}$, it is expressed by Equation (3).

$$L_{f2}={\int }_{t_1}^{t_2}\sqrt{{(\mathrm{dx}/\mathrm{dt})}^2+{(\mathrm{dy}/\mathrm{dt})}^2}dt,$$

(3)

Substituting Equation (2) into Equation (3) gives Equation (4). Based on Equation (4), the distance that the molten metal flows during the time difference can be calculated, and the flow rate can be calculated from this.

$$L_{f2}=a{\int }_{t_1}^{t_2}\sqrt{(1+{\theta }^2)}d\theta ,$$

(4)

Now, the function of the sand spiral is given by r = $3\theta$$(2\pi \le \theta \le 9.24\pi )$, considering the flow of molten metal from the periphery; so, when the molten metal tip is $\theta =\mathsf{\Theta }$, $L_{f2}$ is given by Equation (5) below.

$$L_{f2}=3{\int }_{\mathsf{\Theta }}^{9.24\pi }\sqrt{(1+{\theta }^2)}d\theta ,$$

(5)

Ultimately, the flow length $L_f$ is expressed by Equation (6).

$$\left\{\begin{array}{c}{L}_f=L_{f1}(0\le L_f\le 81.87)\hfill \\ L_f=(L_{f1}+L_{f2})=81.87+3{\int }_{\theta }^{9.24\pi }\sqrt{(1+{\theta }^2)}d\theta (81.87\le L_f\le L_{max}),\hfill \end{array}\right.$$

(6)

2.2. Proposed Method for Estimating the Solid Fraction at the Flow Cessation

The Flemings equation, shown in Equation (7), has been proposed as a method for estimating the flow length of castings of alloys exhibiting a mushy formation morphology [7].

$$L_f=\frac{\rho wS[c(T_c-T_L)+f_{sc}{H}_f]}{h(T_L-T_0)C},$$

(7)

where $L_f$ is the flow length (mm), $\rho$ is the density (kg/m³), c is the specific heat (J/kg·K), $T_c$ is the melt temperature, $T_L$ is the liquid temperature of the alloy, $f_{sc}$ is the solid fraction at flow cessation, $H_f$ is the latent heat of solidification (J/kg), w is the flow velocity (m/s), S is the surface area of the flow channel (m²), h is the heat transfer coefficient (kW/m²·K), $T_0$ is the mold temperature, and C is the peripheral length of the flow channel (m). For the parameters in Equation (7), the values that are difficult to obtain experimentally are $f_{sc}$ and h. Transforming Equation (7) and expressing $f_{sc}$ as a function of h yields Equation (8).

$$f_{sc}=\frac{h{L}_{f}C(T_L-T_o)}{\rho H_{f}wS}-\frac{c(T_c-T_L)}{H_f}$$

(8)

This means that it is possible to estimate $f_{sc}$ by determining h. In this study, the flow length and change in flow velocity during casting were obtained by casting experiments. Second, h was determined to simulate the changes in the obtained flow velocity by computer simulation. Based on this result, $f_{sc}$ was estimated from Equation (8).

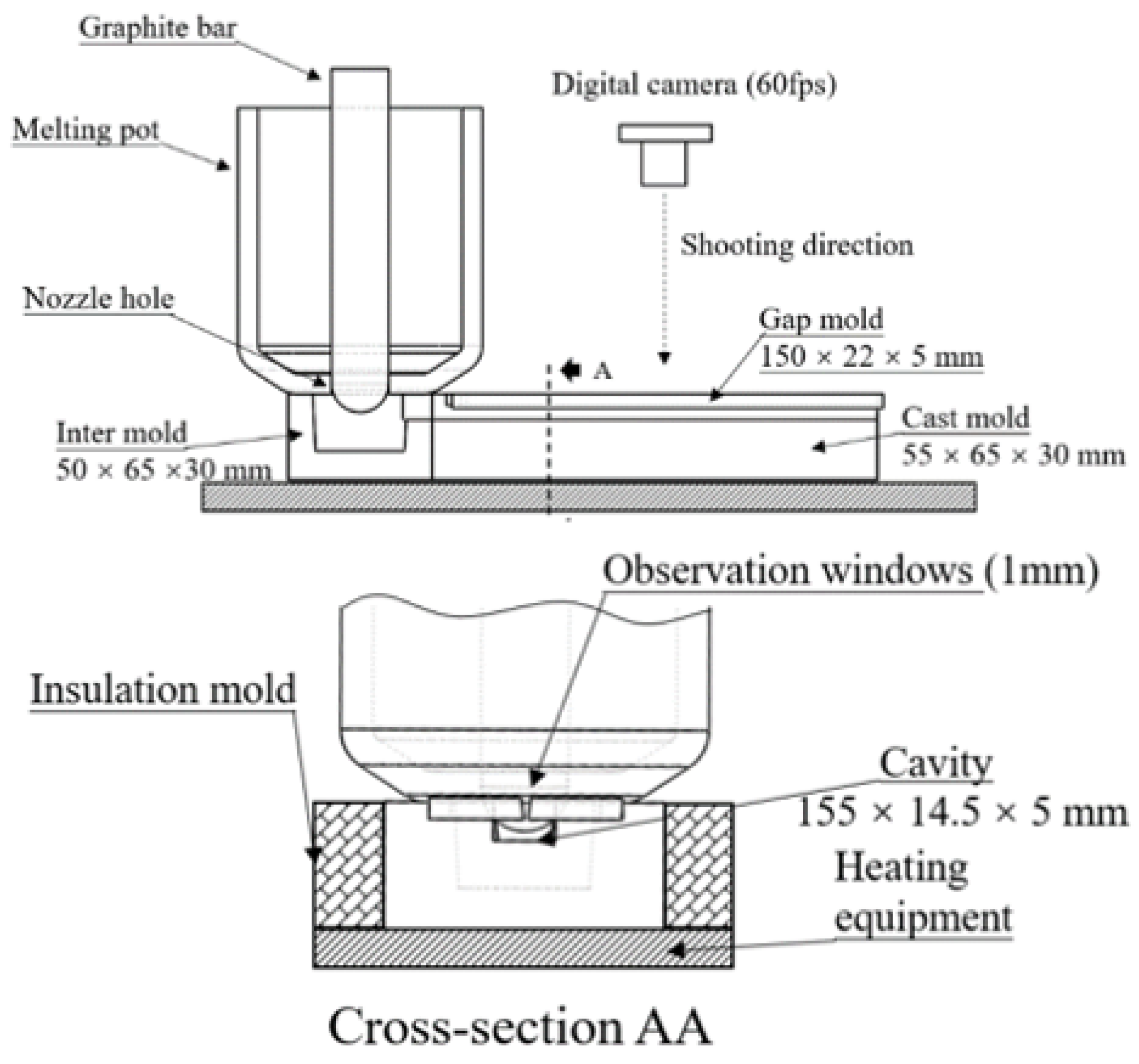
3. Experimental Method

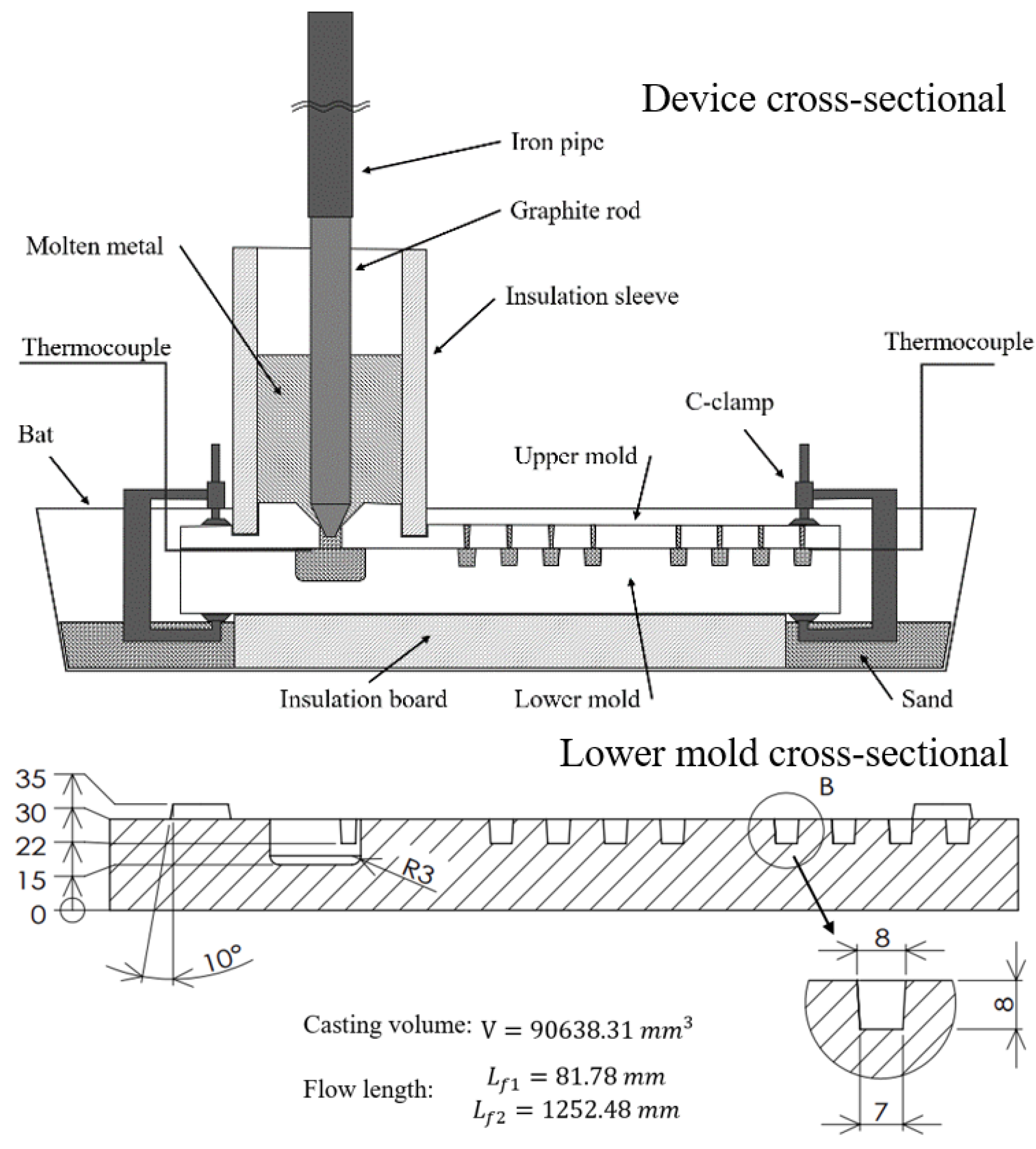
3.1. Linear Cavity Aluminum Alloy Experiment

The mold used in this experiment is shown in Figure 2. All experiments were divided into four groups, and the changes in the tip molten metal velocity and flow length under different casting conditions were examined. The casting conditions were mold temperatures of 100 and 200 °C and molten metal temperatures of 620 and 650 °C. Gravity casting was performed using a JIS-S50C steel mold with a cavity length of 155 mm and width of 22 mm. A gap of 1 mm was provided at the upper mold, and the molten metal flowing through the gap was directly observed using a digital camera. The flow velocity of the molten metal was calculated by differentiating the moving distance of the molten metal tip, which was captured at 60 fps using a digital camera through the observation window. A graphite melting pot at 300 °C with a hole at the bottom was used for pouring. Molten Al–7%Si–0.3%Mg alloy at 650 °C was poured into the melting pot, and the hole was closed using a graphite rod at 300 °C. The molten metal was poured into the mold by pulling out the graphite rod when the temperature dropped to 650 and 620 °C in the melting pot. The mold temperature was set to 100 and 200 °C.

Figure 2. Schematic diagram of experimental device (front and section view).

K-type thermocouples were placed on the center line of the cavity at intervals of 10 mm, and the temperature of the molten metal was measured until the flow ceased. When the flow ceased, the solid fraction was calculated experimentally from the area fraction of the $\alpha$-Al phase. Casting was performed under the same conditions as in the fluidity experiments, and the growth of the solid phase was stopped by rapid cooling of the molten metal from the front of the mold with water. Subsequently, microstructural observation were performed, primary crystals with three or more secondary dendrite arms were extracted, and the solid fraction at the time of flow cessation was obtained experimentally by calculating the area ratio of primary crystals in the observation field by image analysis [8].

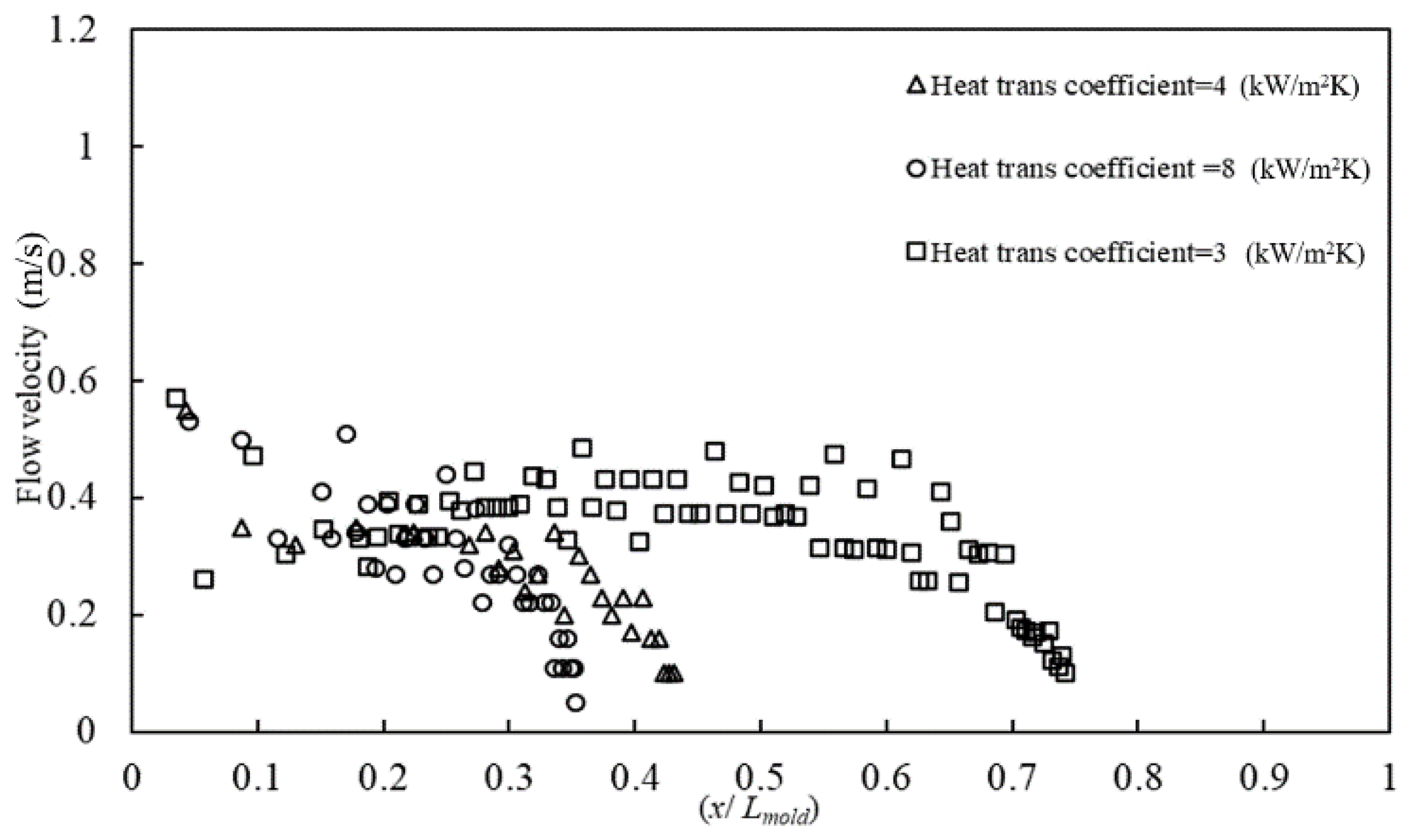
3.2. Computer Simulation of the Linear Cavity

In the computer simulation, ADSTEFAN v.2019 was used to perform the flow and solidification analyses. To ensure the accuracy of the simulation, the mesh size was divided into 0.5 mm, and there were 10 meshes in the vertical direction in the cavity. The physical properties of the Al–Si–Mg alloy were calculated using JMatPro v.9.0, based on the Chemical composition shown in Table 1.

Table 1. Chemical composition of Al–Si–Mg Alloy (%).

Si	Mn	Mg	Fe	Ti	Cu	Zn	Cr
7.0	0.40	0.35	0.25	0.16	0.10	0.07	0.01

The solid fraction at the tip of the molten metal when the flow ceased was estimated by tuning the h between the molten metal and the mold so that the flow velocity and flow length calculated by the simulation matched the values obtained experimentally. Figure 3 and Figure 4 show the specific heat and thermal conductivity of the Al–7%Si–0.3%Mg alloy molten metal calculated using JMatPro v.9.0. These values agree with the research results of Nikawa et al., who conducted actual casting experiments. Referring to the calculation results used in the study of Al–7%Si–0.3%Mg alloys by M. Adachi et al., the results of specific heat and thermal conductivity calculated this time are correct [9].

Figure 3. Specific heat–temperature relationship diagram of Al–Si–Mg alloy.

Figure 4. Thermal conductivity–temperature relationship diagram of Al–Si–Mg alloy.

Table 2 lists the conditions used in the simulation, and the input parameters are from the experimental data. The initial temperatures of the molten metal and the mold were 620 and 100 °C, respectively, which were the experimental conditions for one set of experiments. The simulation was divided into three groups. Under the same initial temperatures of the mold and molten metal, the h between the mold and molten metal was adjusted to 3.0, 4.0, and 8.0 kW/m²K, respectively, and the analysis was performed.

Table 2. Casting simulation input data of Al–7%Si–0.3%Mg alloy.

Simulation Parameters	Input Parameters
Mesh size (mm)	0.5
Initial temperatures molten metal (°C)	620
Initial temperatures cast mold (°C)	100
Ambient temperature (°C)	22
Liquidus temperature (°C)	615
Solidus temperature (°C)	540
Initial flow velocity distribution of gate (m/s)	0.53
	3.0
Heat transfer coefficient (kW/m2·K)	4.0
	8.0

Figure 3 and Figure 4 show that the physical properties of the Al–Si–Mg alloy vary significantly in the range of 610–540 °C. It was difficult to incorporate this directly into Equation (8) for the calculation. Therefore, in this experiment, the solid fraction at the flow cessation of the tip molten metal was calculated from the start of flow to solidification by averaging the physical property values in the range of 610–540 °C. The data used to calculate the solid fraction at flow cessation are shown in Table 3.

Table 3. Physical property data of Al–7%Si–0.3%Mg alloy(For calculation).

Physical Property	Input Data
Latent heat of solidification (J/kg)	$3.893\times {10}^5$
Denticity (kg/m3	$2.596\times {10}^3$
Specific heat (J/kg·K)	$1.100\times {10}^3$
Flow length (m)	Experimental value
Flow velocity (m/s)	Experimental value
Peripheral length of the flow channel (m)	Measured value
Surface area of the flow channel (m2)	Measured value
Heat transfer coefficient (kW/m2·K)	Simulation value

Here, the selection of the tip flow velocity and the displacement value was calculated using the “calculation result” or “measurement result” (data measured through the observation window in the experiment) of the mesh at the center line of the cavity horizontal plane as the simulation result.

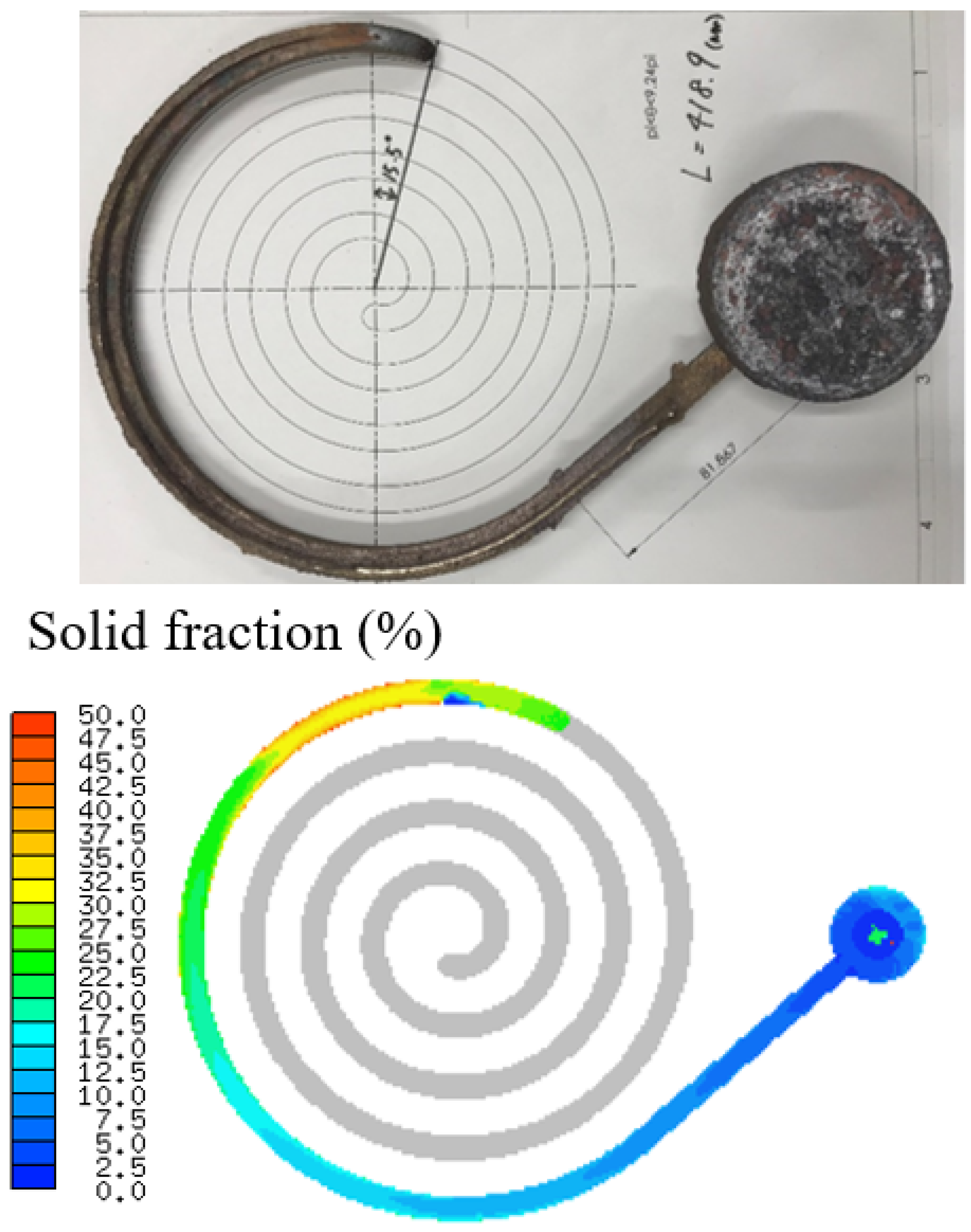
3.3. Spiral Cavity Copper Alloy Experiment

The cross-sectional view of the experimental device and the dimensions of the lower mold and cavity under the experiment shown in Figure 5. The spout of the sand mold with a spiral cavity was stopped by a stopper, and the molten metal was accumulated in the sleeve up to a height of 65mm from the upper surface of the upper mold. The metal material used in the experiments was a paste-solidified Cu-8%Sn alloy, which solidified in the same way as the Al–7%Si–0.3%Mg alloy.When the temperature of the molten metal dropped to 1100 °C, the stopper was removed and the molten metal was filled. The upper mold has a groove with a 1mm observation windows for direct observation of molten metal flow, and the outer periphery of the pouring hole is a groove for fitting a sleeve. On the other hand, in the lower mold, the cavity, which is the flow part, consists of a straight part and a spiral part. Three mandrel vices were used to fix the upper and lower dies. The dimensions of the sleeve are 65 mm inner diameter, 90 mm outer diameter, and 120 mm height. A core with a diameter of 10 mm, which matches the shape of the sprue, was used as the stopper.

Figure 5. Schematic diagram of spiral flow test (cross-section).

The molten metal tip flow stopped solid fraction of the Cu–8%Sn alloy, calculated using computer simulations. When the tip of the molten metal in the computer simulation reaches the same flow length as the experiment, the solid fraction of the tip is calculated. In addition, in order to determine the accuracy of the calculated values, we refer to the results of other research papers for the same alloy in our discussion.

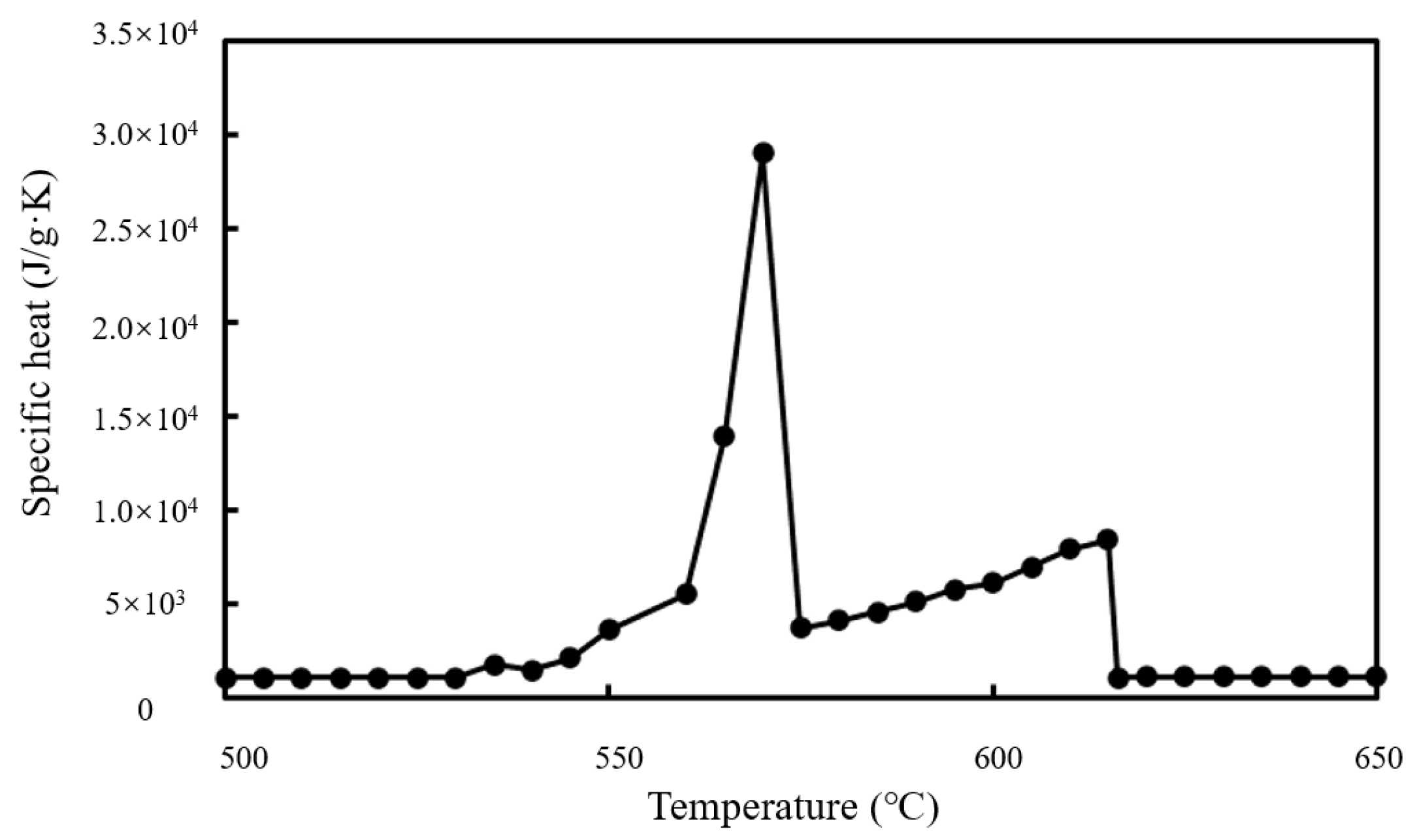
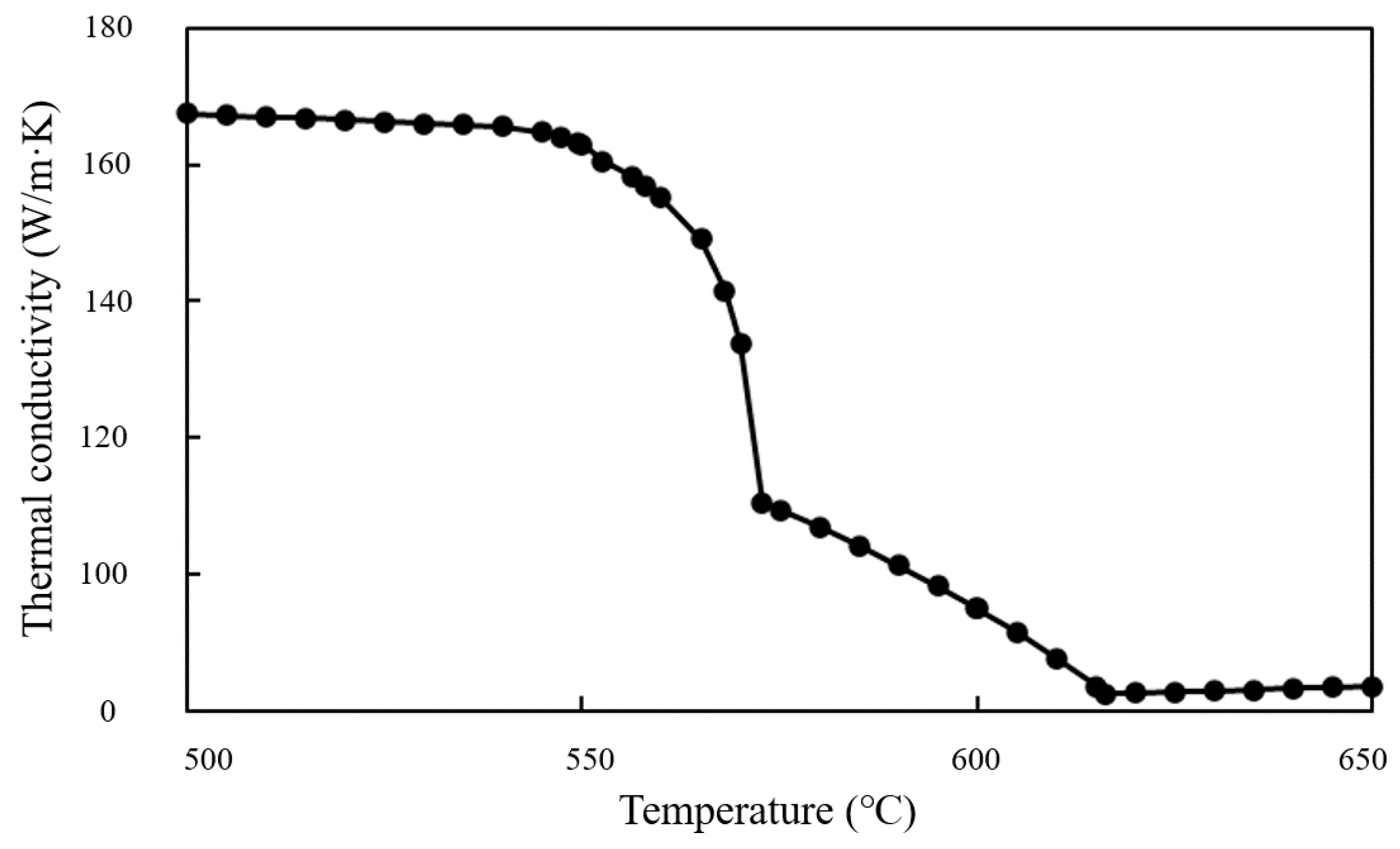
3.4. Computer Simulation of the Spiral Cavity

The computer simulation uses the same calculation method as the linear cavity experiment. Among them, the chemical composition of Cu–8%Sn alloys is shown in Table 4, and the calculated physical properties are shown in Table 5. The calculation conditions of the simulation are shown in Table 6. [10]

Table 4. Chemical compositions of Cu–8%Sn alloy(%).

Sn	Pb	Zn
8.0	6.0	4.0

Table 5. Physical property data of Cu–8%Sn alloy (for calculation).

Physical Property	Input Data
Latent heat of solidification (J/kg)	$2.05\times {10}^5$
Denticity (kg/m3)	$8.83\times {10}^3$
Specific heat (J/kg·K)	$0.38\times {10}^3$
Flow length (m)	Experimental value
Flow velocity (m/s)	Experimental value
Peripheral length of the flow channel (m)	Measured value
Surface area of the flow channel (m2)	Measured value
Heat transfer coefficient (kW/m2·K)	Simulation value

Table 6. Casting simulation input data of Cu–Sn alloy.

Simulation Parameters	Input Parameters
Mesh size (mm)	0.5
Initial temperatures molten metal (°C)	1080
Initial temperatures sand mold (°C)	23
Liquidus temperature (°C)	1010
Solidus temperature (°C)	855

4. Results and Discussion

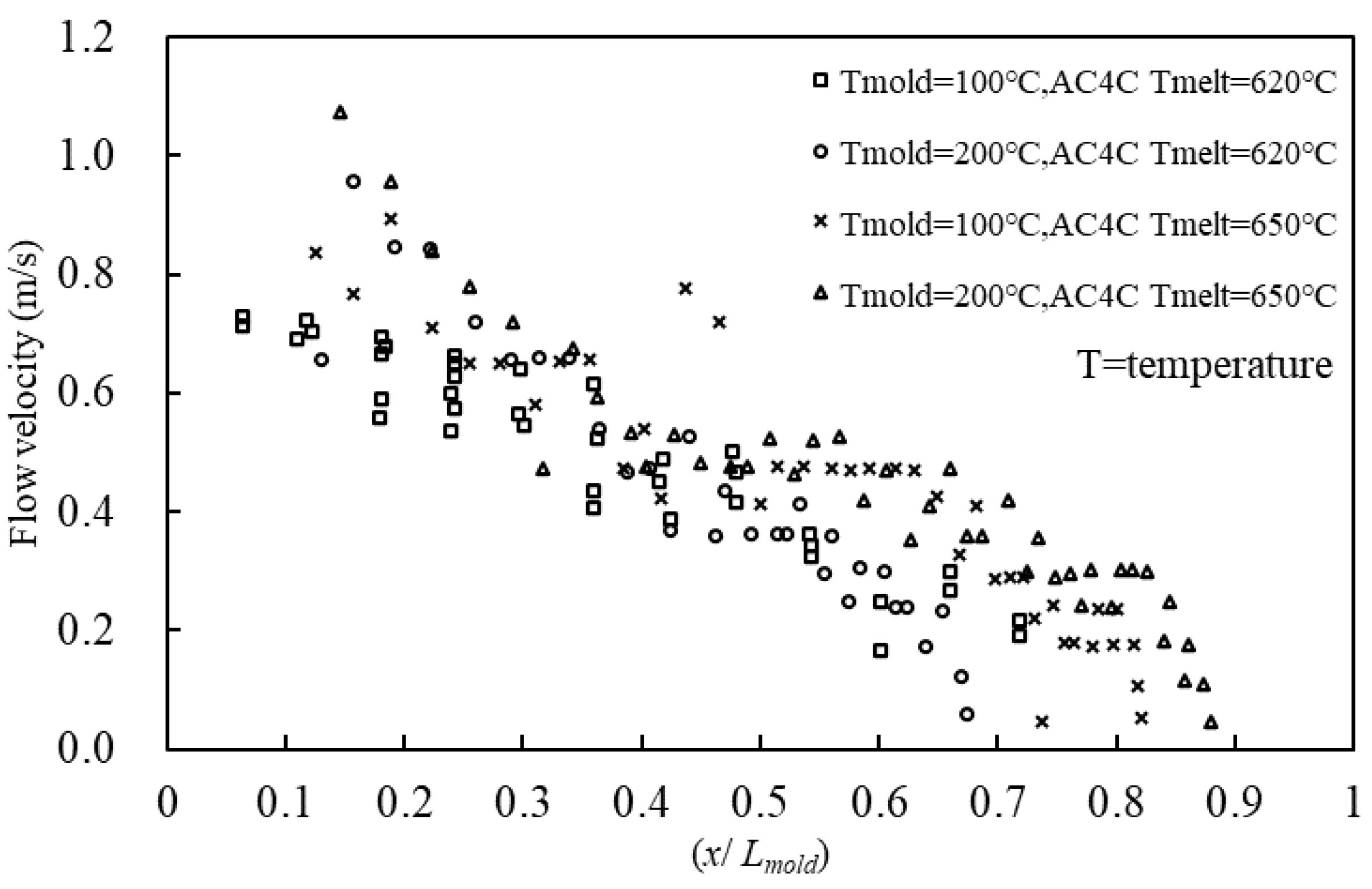
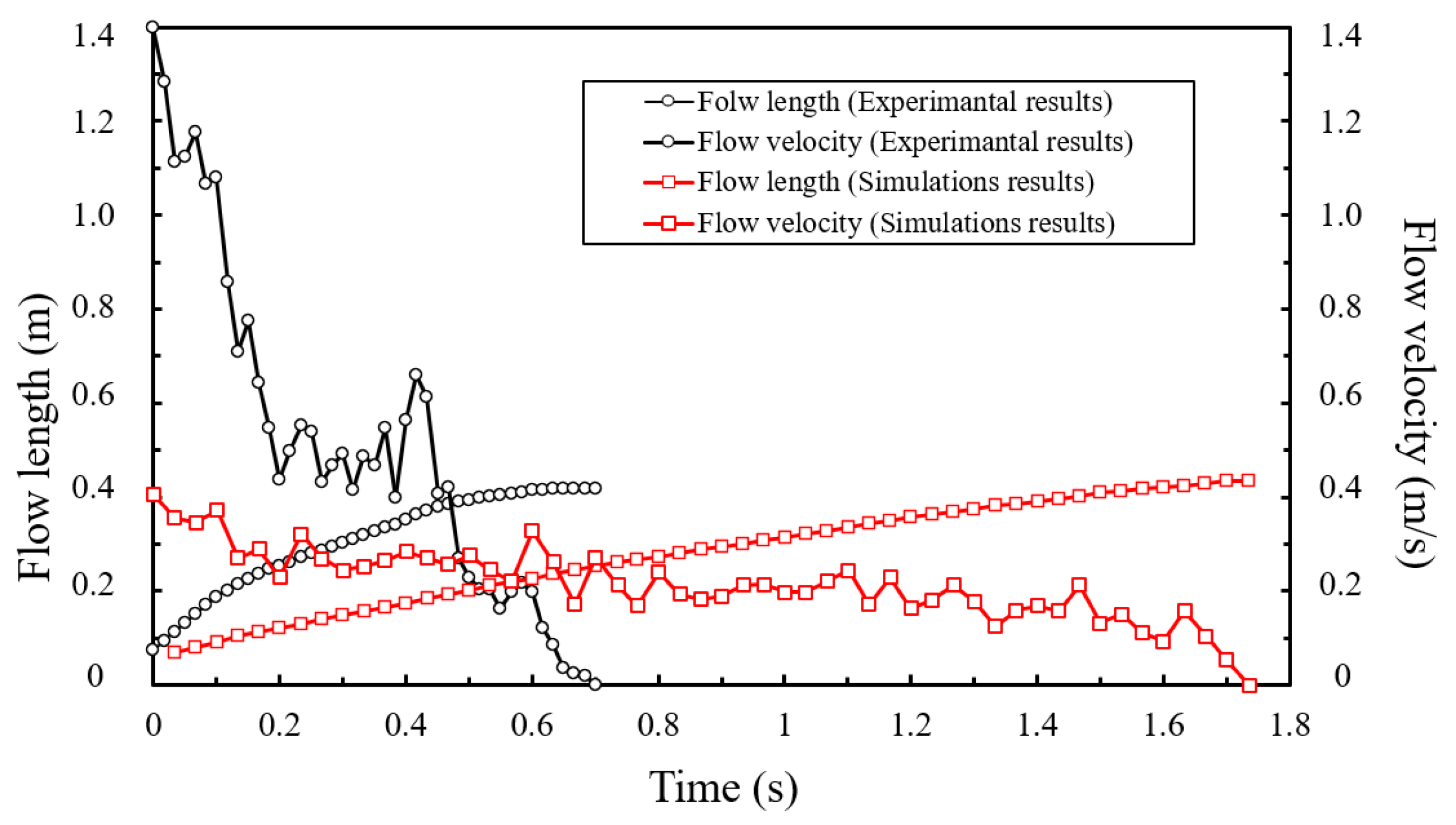
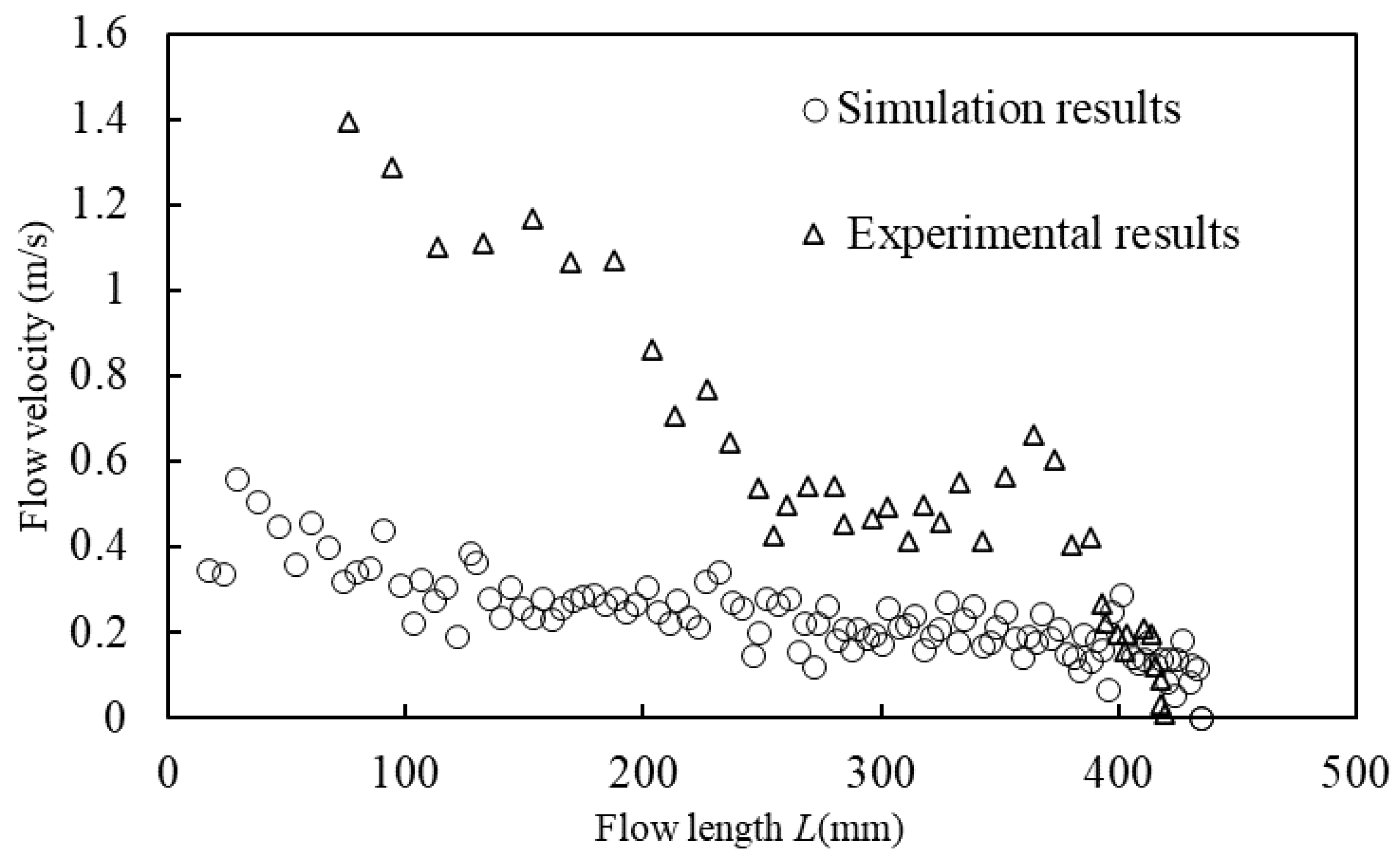
4.1. Linear Cavity Aluminum Alloy Experiment Results

Figure 6 shows the change in velocity at the molten metal tip during flow. The horizontal axis $(x/L_f)$ in the figure indicates the ratio of the measured position $\left(x\right)$ to the obtained maximum flow length $(x/L_f)$. The velocity of the flowing molten metal decreased rapidly during the initial stage of the flow. Subsequently, the decrease in flow velocity was small in the region of $x/L_f$ = $0.3-0.5$; then, the velocity decreased rapidly, and the flow ceased. The flow velocity reduction in each experiment was almost the same for different molds and initial temperatures of the molten metal. When the mold temperature was 100 °C, the flow length of the molten aluminum alloy at the initial temperature 650 °C was longer than 620 °C, and the flow velocity decreased relatively smoothly. This comparison provided the same results, even when the mold temperature was 200 °C. When the initial mold and molten metal temperature was relatively high, the heat transfer between the molten metal in the flow and the mold was slow; thus, the solidification rate was also slow. This relationship also affected the tendency of the molten metal tip to decrease in flow velocity [11].

Figure 6. Relationship between the flow velocity and melt tip flow length, as shown by experimental results (Al–Si–Mg).

Figure 7 shows a cross-sectional view of the simulation results. The change in the flow of the molten metal at the tip was almost the same as the experimental result. It started to decrease sharply because the molten metal was filled in the cavity, the heat transfer took to the mold, and there was a gentle section similar to the experimental result in the middle. It decreased rapidly again. Finally, it solidified and then stopped flowing. This area was influenced by the initial conditions of the experiment. When the mold temperature and molten metal temperature were low, the time was shorter and vice versa. This was because the initial temperature of the mold and molten metal affected the solidification rate. This phenomenon was directly reflected in the change in the velocity of the molten metal.

Figure 7. Cross-sectional diagram of simulation results.

At the same time, when observing the change in the solid fraction of the molten metal, the solidification rate on the surface of the molten metal was faster than the solidification rate inside, because the filling of the internal molten metal was not affected by the heat transfer caused by the subsequent filling of the molten metal that continued to flow. The simulation results indicate that the w of the molten metal at the tip decreased as the filling continued. This was because the solid fraction inside the advanced molten metal increased, which affected the flow. The w in the middle part continued to increase until the tip movement stopped.

Figure 8 shows the simulation results of the w at the tip of the molten metal when the h was varied. For all the h, there is a region where the decrease in w becomes small.

Figure 8. Relationship between the flow velocity and molten metal flow length of simulation results (Al–Si–Mg).

Table 7 shows the simulation results for the $L_f$. The $L_{fcal}/L_f$ shows the ratio of the simulation result $L_{fcal}$ to the experimental result $L_f$. The flow length decreased with an increase in the h.

Table 7. Comparison of experimental and simulation data.

Heat Transfer Coefficient	${\mathit{L}}_{\mathit{fcal}}/{\mathit{L}}_{\mathit{f}}$
3 kW/m2K	1.04
4 kW/m2K	0.61
8 kW/m2K	0.50

From these results, the h in this experiment was estimated to be h = 3 kW/m²K. The results of all calculations by Equation (8) are shown in Table 8 below. Among them, the calculated h values are lower when the molten metal temperature is 650 °C and the mold temperature is 100 °C. This is due to the fact that the flow rate, as well as the $L_f$, in the experiment are similar to the w at a mold temperature of 620 °C, thus causing the difference in the calculated results. However, its calculation falls within the range of 0.3–0.45 flow stop solid fraction for the Al–7%Si–0.3%Mg alloy, so this calculation is considered correct. Since the other data agreed with the expected values and the difference was small, it was possible to conclude that the average value of the solid fraction at the flow cessation of the Al–7%Si–0.3%Mg alloy used in this experiment is 0.37. This value is almost the same as the values in other research [12], which shows the validity of the proposed method.

Table 8. Calculation result of the solid fraction at the flow cessation.

Initial Cast Mold Temp (°C)	Initial Molten Metal Temp	Calculation Result
	620	0.35
100	650	0.30
	620	0.40
200	650	0.36

4.2. Spiral Cavity Copper Alloy Experiment Results

The experimental and simulation results of the $L_f$ measurement and w calculation of the Cu–8%Sn alloy are shown in Figure 9. The position shown by the simulation results is the center position of the casting longitudinal section, 26 mm from the bottom surface. Since the mesh size is 0.5mm, it is in the position of 52 mesh above the bottom surface. Since the longitudinal section of the cavity is a square (8 mm × 8 mm), the cross-sectional area of each position is the same. Because the $L_f$ of the experimental results is much smaller than the maximum flow length, the results are directly discussed using the measured results $L_f$. Figure 10 shows the calculated w and $L_f$ of the molten metal tip in this experiment and simulation results. Converting the data in the figure to $L_f$ versus w gives the results shown in Figure 11. It can be seen that the w at the tip continues to decrease as the $L_f$ of the molten metal increases. That is, the flow length increase in the experimental results decreases as the molten metal tip casting solidifies, while the simulated results remain stable. This is due to the relatively stable variation of the w in the simulation results, while the experimental w distribution has large fluctuations. At this time, the $L_f$ of the Cu–8%Sn alloy when the molten metal flow stops is 418.9 mm. In the computer simulation, by adjusting the h between the sand mold and the copper alloy, the $L_f$ of the simulation results is the same as the experimental results. When the h = 1.68 kW/m²K, the w calculation results are smoother than the experimental results, the w changes are more constant, and the simulation results can be considered correct under the same flow length.

Figure 9. Spiral cavity copper alloy experiment results and simulation results.

Figure 10. Calculation of flow velocity and flow length in experimental as well as simulation results (Cu–Sn).

Figure 11. Relationship between flow length and flow velocity (Cu–Sn).

The flow-stopped solid fraction of the tip of the molten copper alloy is calculated by the Equation (8) to obtain $f_{sc}$ = 0.23; this is similar to the solid fraction of the molten metal tip of the computer simulation results. According to related research, the flow limit solid fraction of Cu–8%Sn was estimated to be 0.2–0.4, and the h = 1.62 kW/m²K between the sand mold and Cu–8%Sn alloy, so this result can be considered correct [13]. It can be considered that it is a reasonable value when compared with the research report which estimated it [14]. The w distribution was calculated by measuring the $L_f$ of molten metal in the actual experiment by conducting flow experiments and corresponding computer simulations using the Al–7%Si–0.3%Mg alloy and Cu–Sn alloy. In addition, the calculation of the h between the molten metal and the mold was carried out through computer simulation, and finally, the value of the solid fraction of the flow stopped at the tip was calculated. This calculation method for mushy-type formation solid fraction alloys was confirmed to be valid and accurate under different conditions of cavity geometry and alloy type.

5. Conclusions

The following conclusions were drawn from the results of this research:

• A method was proposed to estimate the solid fraction at flow cessation in Al–7%Si–0.3%Mg alloys with a mushy formation morphology from the flow velocity at the tip of the molten metal.
• The resulting solid fraction was similar to the values reported in other studies, and it was verified in the fluidity experiment of the Cu–8%Sn alloy with the same solidification mode, demonstrating the effectiveness of this method.
• This method was examined only for mushy-type solidified metals. Its effectiveness has not been proved with other solidification-type metals. Additional research is planned.