The 5G-FR1 Signals: Beams of the Phased Antennas Array and Time-Recurrence of Emissions with Consequences on Human Exposure
Abstract
1. Introduction
2. Materials and Methods
2.1. Computational Dosimetric Study
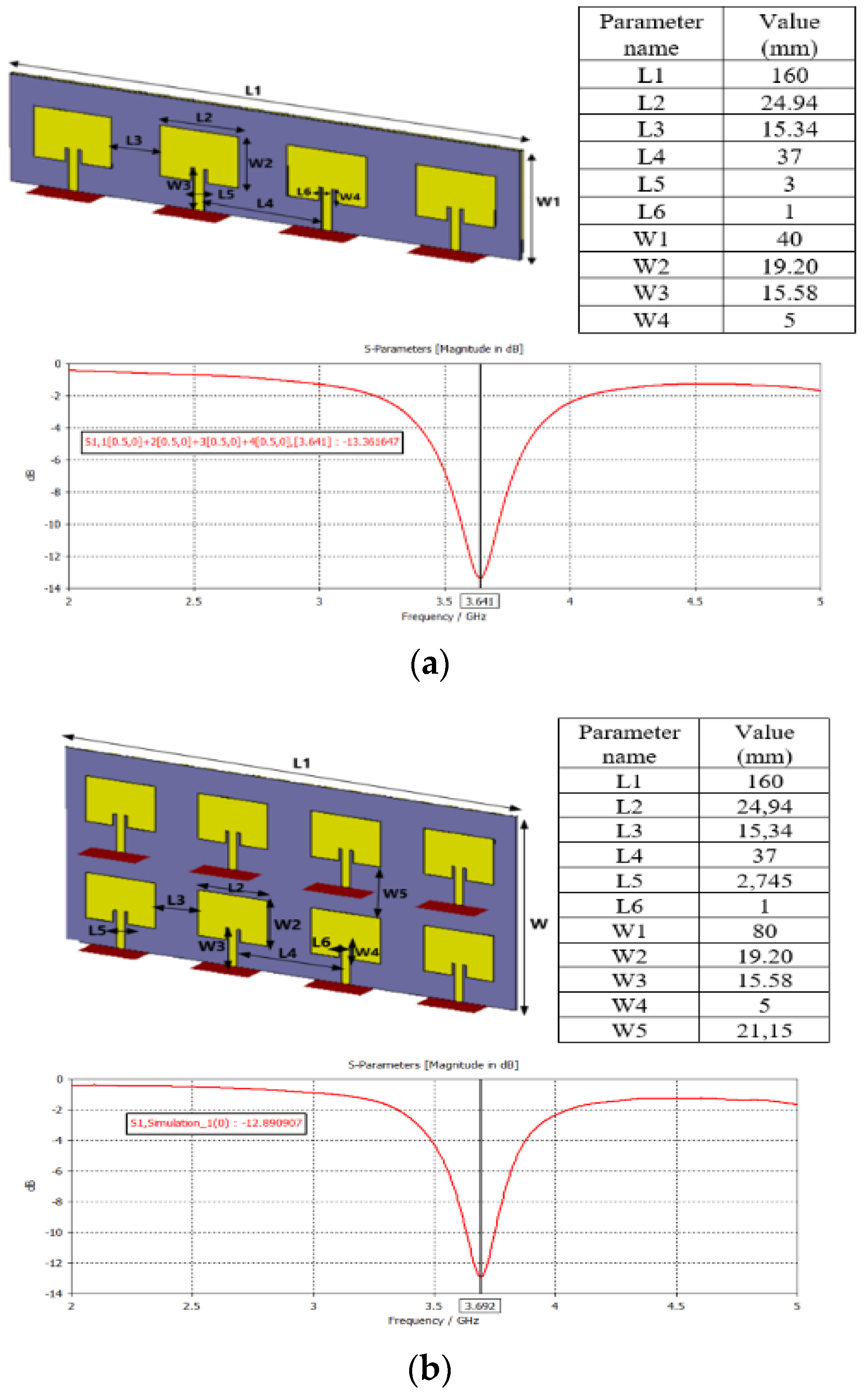
2.1.1. Antenna Models
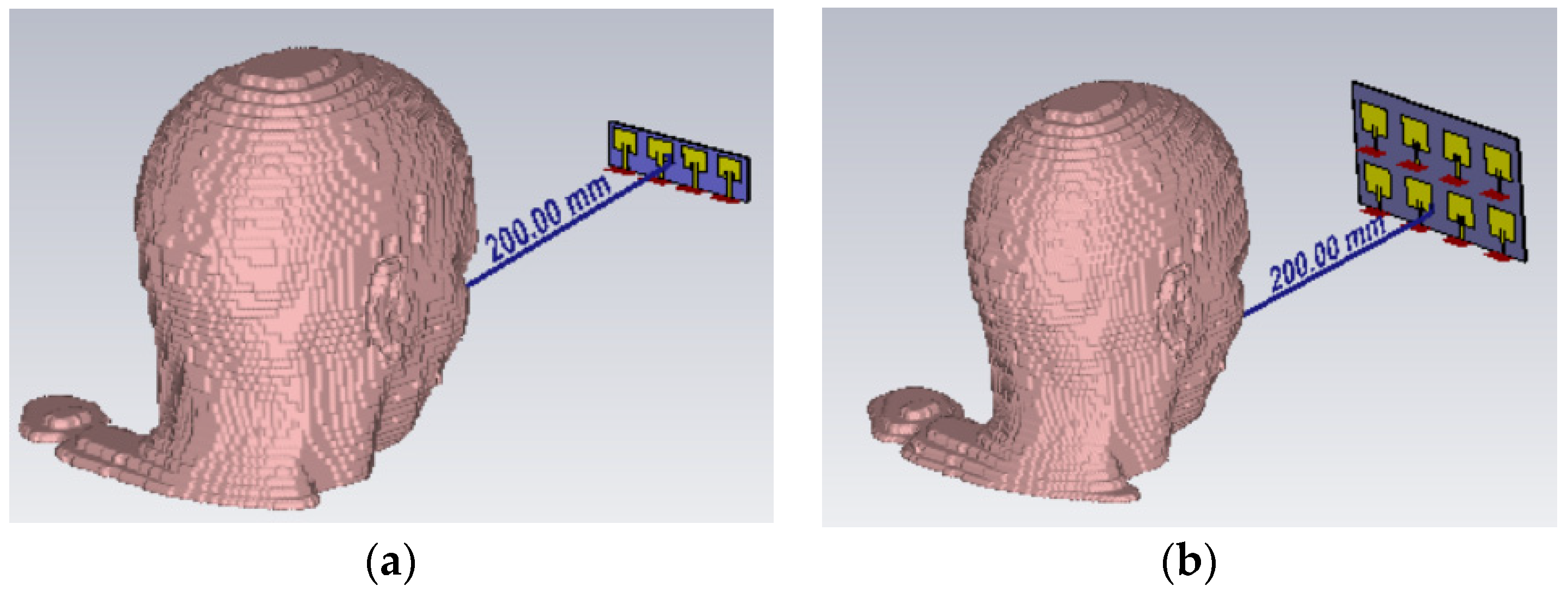
2.1.2. Exposure and Dosimetric Assessment
2.2. Experimental Setup and Procedure for the Emitted Field Real-Variability Measurement
3. Results and Discussion
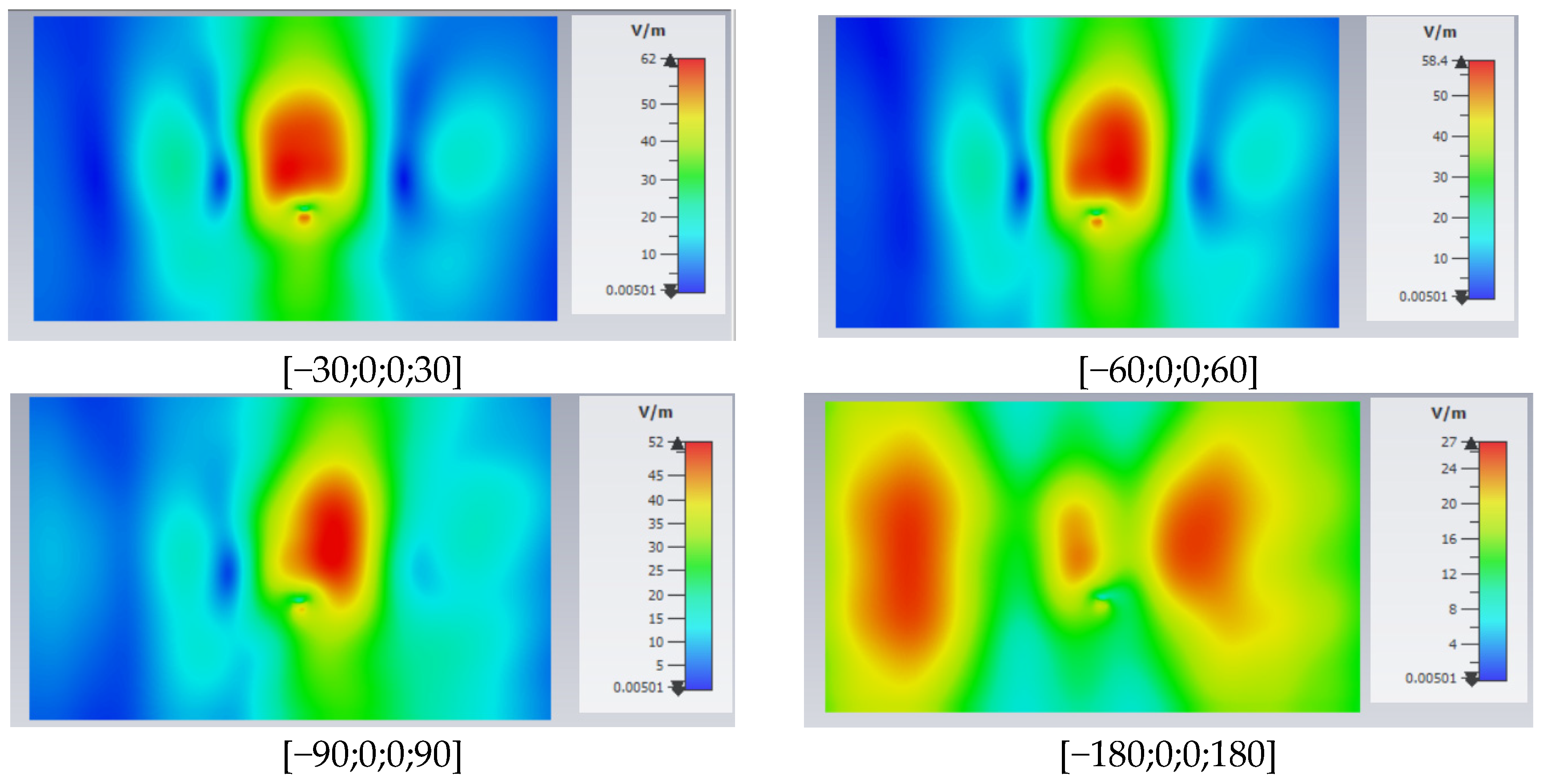
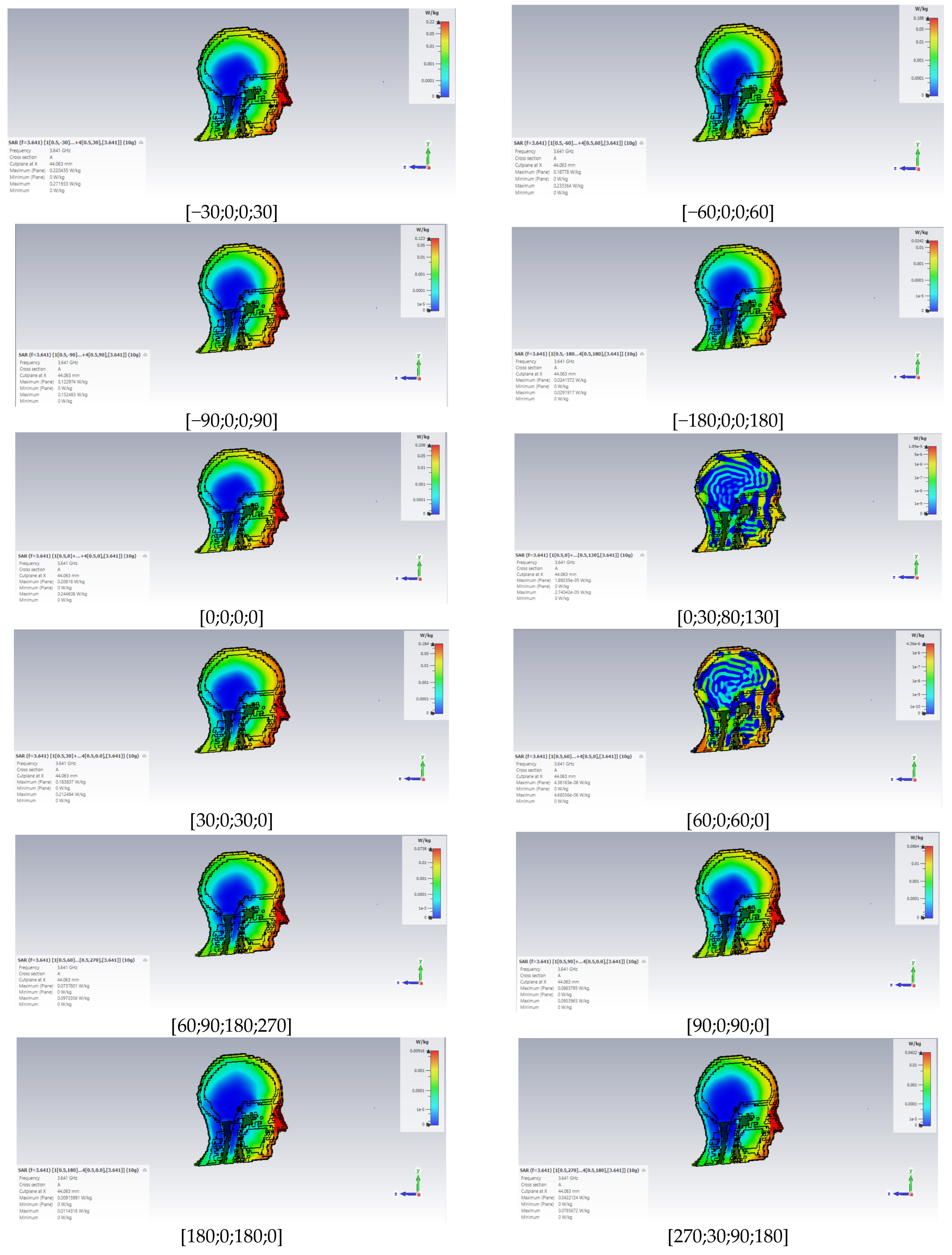
3.1. Numerical Results of the Dosimetric Study Related to Beam Steering
3.1.1. Numerical Analysis for 1×4 Linear Patch Antenna Array
3.1.2. Numerical Analysis for Planar 2×4 Patch Antenna Array
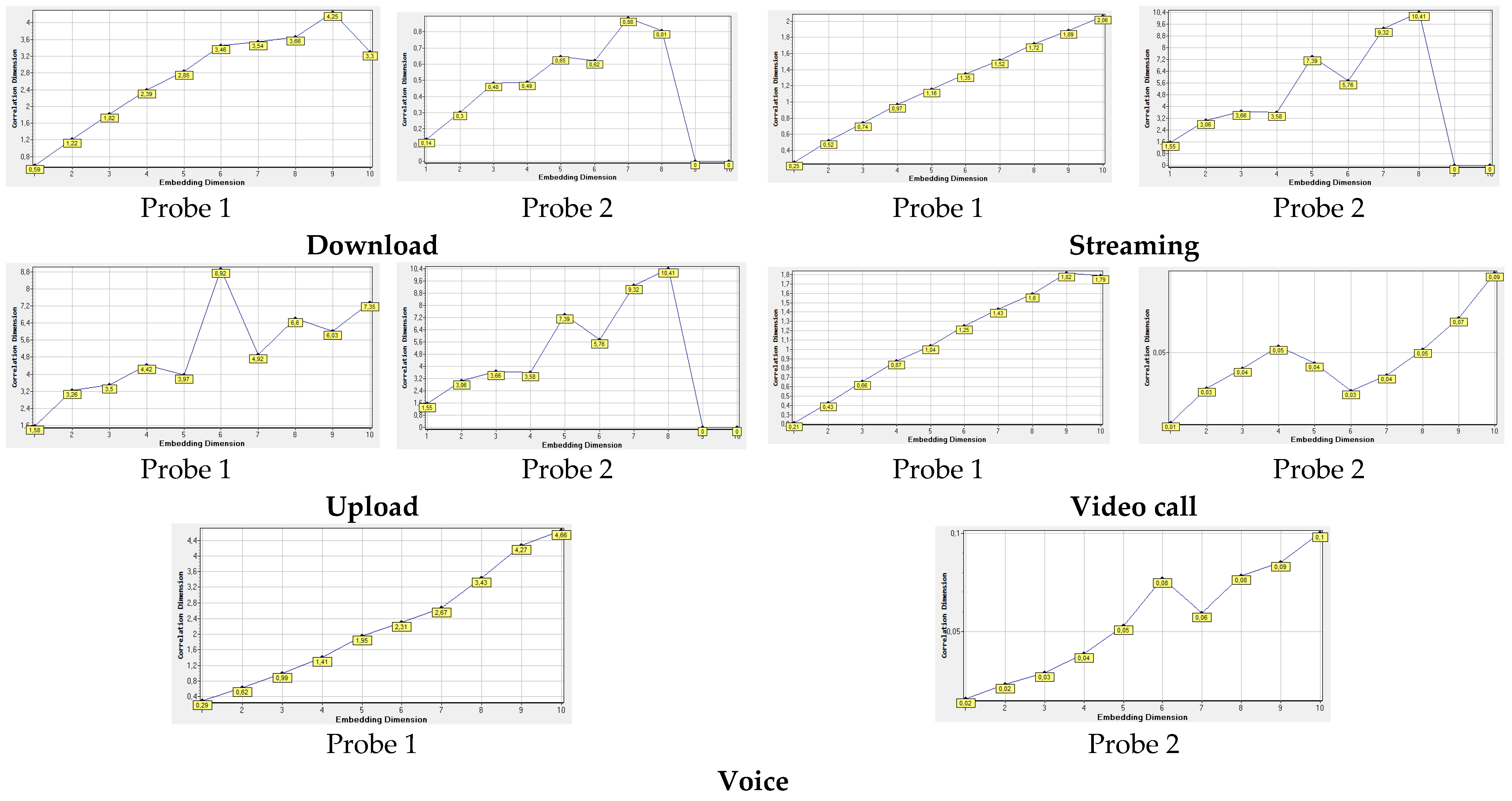
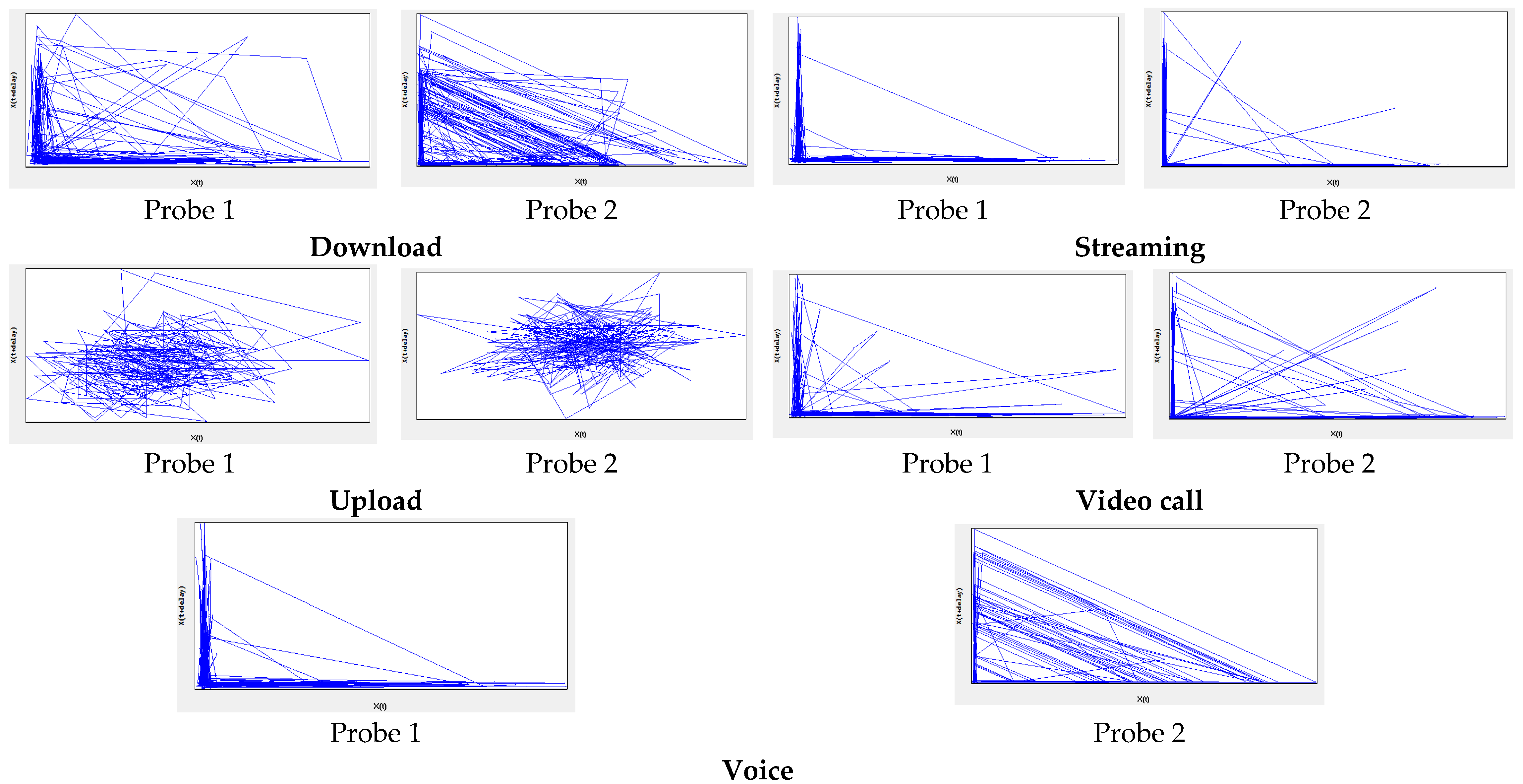
3.2. Experimental Results of Recurrent Exposure Dynamics for Mobile-Phone Emission Situations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morelli, M.S.; Gallucci, S.; Siervo, B.; Hartwig, V. Numerical Analysis of Electromagnetic Field Exposure from 5G Mobile Communications at 28 GHZ in Adults and Children Users for Real-World Exposure Scenarios. Int. J. Environ. Res. Public Health 2021, 18, 1073. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.D.; Zhao, S. Internet of things: A survey. Ind. Inf. Integr. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE JSAC 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- TS 38-101.1: NR; User Equipment (UE) Radio Transmission and Reception. Part 1: Range 1 Standalone, (17.2.0 ed.); 3GPP: Sophia Antipolis, France, 2021.
- Morgando, A.; Huq, K.M.S.; Rodriguez, J.; Mumtaz, S. A survey of 5G technologies: Regulatory, standardization and industrial perspectives. Digit. Com. Net. 2018, 4, 87–97. [Google Scholar] [CrossRef]
- The European Commission. Commission Implementing Decision (EU) 2019/784 of May 2019 on harmonisation of the 24.25–27.5 GHz frequency band for terrestrial systems capable of providing wireless broadband electronic communications services in the Union. Off. J. E.U. 2019. Available online: https://eur-lex.europa.eu/eli/dec_impl/2019/784/oj/ (accessed on 15 November 2022).
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for Next Generation Wireless Systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Ojaroudi Parchin, N.; Jahanbakhsh Basherlou, H.; Abd-Alhameed, R.A. Design of Multi-Mode Antenna Array for Use in Next-Generation Mobile Handsets. Sensors 2020, 20, 2447. [Google Scholar] [CrossRef] [PubMed]
- Betta, G.; Capriglione, D.; Cerro, G.; Miele, G.; Migliore, M.D.; Šuka, D. Experimental analysis of 5G pilot signals’ variability in urban scenarios. In Proceedings of the IEEE International Symposium on Measurements & Networking (M&N), Padua, Italy, 18–20 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- El Gholb, Y.; El Amrani EL Idrissi, N. Mimo Implementation. In Proceedings of the IEE WITS, Fez, Morocco, 3–4 April 2019; pp. 1–9. [Google Scholar] [CrossRef]
- Betta, G.; Capriglione, D.; Cerro, G.; Miele, G.; Migliore, M.D.; Šuka, D. 5G DSS communications: Pilot signals’ variability analysis from measurments on the field. In Proceedings of the IEE I2MTC, Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Betta, G.; Capriglione, D.; Cerro, G.; Miele, G.; D’Amata, M.S.; Šuka, D.; Pejović, P.; Simic-Pejović, M. On the Measurement of Human Exposure to Cellular Network. IEEE Instrum. Meas. Mag. 2020, 23, 5–13. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Turco, S.; Bianchi, G.; Melazzi, N.B. “Cellular Network Densification Increases Radio-Frequency Pollution”: True or False? IEEE Trans. Wireless Commun. 2022, 21, 2608–2622. [Google Scholar] [CrossRef]
- ITU-T, The Impact of RF-EMF Exposure Limits Stricter than the ICNIRP or IEE Guidelines on 4G and 5G Mobile Network Deployment, Series K, Suppleant 14. 2018. Available online: https://www.itu.int/rec/T-REC-K.Sup14-201909-I/en (accessed on 12 November 2022).
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for Limiting Exposure to Time-Varying Electric, Magnetic and Electromagnetic Fields (100 KHz–300 GHz). Health Phys. 2020, 118, 483–524. [Google Scholar] [CrossRef] [PubMed]
- IEEE Std C95.1-2019; IEEE Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic, and Electromagnetic Fields, 0 Hz to 300 GHz. The Institute of Electrical and Electronics Enguneers, Inc.: New York, NY, USA, 2019; pp. 1–312.
- Federal Communications Commission. Radio Frequency Radiation Exposure Limits, Code of Federal Regulation Title 47, Part 1.1310; Federal Communications Commission: Washington, DC, USA, 2017.
- Kojima, M.; Hanazawa, M.; Yamashiro, Y.; Sasaki, H.; Watanabe, S.; Taki, M.; Suzuki, Y.; Hirata, A.; Kamimura, Y.; Sasaki, K. ACUTE OCULAR INJURIES CAUSED BY 60-GHZ MILLIMETER-WAVE EXPOSURE. Health Phys. 2009, 97, 212–218. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Cacciapuoti, A.S.; Martino, G.D.; Fiore, M.; Montesano, M.; Trucchi, D.; Melazzi, N.B. Planning 5G Networks Under EMF Constraints: State of the Art and Vision. IEEE Access 2018, 6, 51021–51037. [Google Scholar] [CrossRef]
- Gultekin, D.H.; Siegel, P.H. Absorption of 5G Radiation in Brain Tissue as a Function of Frequency, Power and Time. IEEE Access 2020, 8, 115593–115612. [Google Scholar] [CrossRef]
- Ciorap, R.; Ciorap, M.; David, V.; Andritoi, D.; Corciova, C. Analysis of brain activity in the case of magnetic field exposure. Environ. Eng. Manag. J. 2013, 12, 1223–1230. [Google Scholar] [CrossRef]
- Bonato, M.; Dossi, L.; Chiaramello, E.; Fiocchi, S.; Tognola, G.; Parazzini, M. Stochastic Dosimetry Assessment of the Human RF-EMF Exposure to 3D Beamforming Antennas in Indoor 5G Networks. Appl. Sci. 2021, 11, 1751. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Rossetti, S.; Saida, S.; Bartoletti, S.; Blefari-Melazzi, N. “Pencil Beamforming Increases Human Exposure to ElectroMagnetic Fields”: True or False? IEEE Access 2021, 9, 25158–25171. [Google Scholar] [CrossRef]
- Šuka, D.S.; Simić-Pejović, M.I.; Pejović, P.V. An overview of EMF exposure assessment metrics. In Proceedings of the 19th International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 18–20 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Lodovisi, C.; Bartoletti, S.; Elzanaty, A.; Alouini, M.-S. Dominance of Smartphone Exposure in 5G Mobile Networks. arXiv 2022, arXiv:2211.01077, submitted. [Google Scholar] [CrossRef]
- Lopes, M.A.; Zhang, J.; Krzemiński, D.; Hamandi, K.; Chen, Q.; Livi, L.; Masuda, N. Recurrence quantification analysis of dynamic brain networks. Eur. J. Neurosci. 2021, 53, 1040–1059. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Guo, R.; Wang, Y.; Yan, J.; Yan, H. Reccurence quantification analysis on pulse morphologicalchanges in patients with coronaty heart disease. J. Tradit. Chin. Med. 2012, 32, 571–577. [Google Scholar] [CrossRef]
- Melillo, P.; Bracale, M.; Pecchia, L. Nonlinear Heart Rate Variability Features for Real-Life Stress Detection. Case Study: Students under Stress Due to University Examination. BioMed Eng. OnLine 2011, 10, 96. [Google Scholar] [CrossRef]
- Miclaus, S.; Deaconescu, D.B.; Buda, A.M.; Vatamanu, D. The temporal imprint of mobile phone emission level when running various applications in 4G versus 5G networks. In Proceedings of the ISETC, Timisoara, Romania, 10–11 November 2022. in press. [Google Scholar]
- Rashid, M.; Hossain, S. Antenna solution for millimeter wave mobile communication (MWMC): 5G. Int. J. Sci. Res. Eng. Technol. 2014, 3, 1157–1161. [Google Scholar]
- CST MICROWAVE STUDIO®. CST STUDIO SUITE®. Available online: http://www.cst.com/ (accessed on 5 August 2022).
- Darimireddy, N.K.; Ramana Reddy, R.; Mastan Vali, S. Analysis of effect of concavity in linear and planar microstrip patch antenna arrays. Microelectron. Electromagn. Telecommun. 2019, 521, 811–819. [Google Scholar] [CrossRef]
- Jain, K.; Gupta, K. Different Substrates Use in Microstrip Patch Antenna-A Survey. IJSR 2012, 3, 2. [Google Scholar]
- Tissue Dielectric Properties of Body Tissues. Available online: http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.php (accessed on 10 September 2022).
- Weiland, T. Finite Integration Method and Discrete Electromagnetism. In Computational Electromagnetics; Monk, P., Carstensen, C., Funken, S., Hackbusch, W., Hoppe, R.H.W., Eds.; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2003; Volume 28. [Google Scholar] [CrossRef]
- Bodwin, G.T.; Chung, H.S.; Repond, J. Implementation of Maxwell’s Equations in the Reconstruction of the Magnetic Field in the G−2 Storage Ring. J. Inst. 2019, 14, P07002. [Google Scholar] [CrossRef]
- Miclaus, S.; Deaconescu, D.-B.; Vatamanu, D.; Buda, A.M.; Sarbu, A.; Pindaru, B. Peculiarities of the Radiated Field in the Vicinity of a Mobile Terminal Connected to 4G versus 5G Networks during Various Applications Usage. Electreng 2022, 6, 161–177. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warick 1980; Rand, D., Young, L.S., Eds.; Lecture Notes in Mathematics; Springer: Coventry, UK, 1980; Volume 898. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A Gen. Phys. 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Webber, C.L.; Zbilut, J.P. Recurrence quantifications: Feature extractions from recurrence plots. Int. J. Bifurc. Chaos 2007, 17, 3467–3475. [Google Scholar] [CrossRef]
- Fabretti, A.; Ausloos, M. Recurrence plot and recurrence quantification analysis techniques for detecting a critical regime. Int. J. Mod. Phys. 2005, 16, 671–706. [Google Scholar] [CrossRef]
- Nayak, S.K.; Bit, A.; Dey, A.; Mohapatra, B.; Pal, K. A Review on the Nonlinear Dynamical System Analysis of Electrocardiogram Signal. J. Healthc. Eng. 2018, 2018, 6920420. [Google Scholar] [CrossRef]
- Wu, T.; Rappaport, T.S.; Collins, C.M. Safe for Generations to Come. IEEE Microw. Mag. 2015, 16, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Shikhantsov, S.; Thielens, A.; Vermeeren, G.; Tanghe, E.; Demeester, P.; Martens, L.; Torfs, G.; Joseph, W. Hybrid ray-tracing/FDTD method for human exposure evaluation of a massive MIMO technology in an industrial indoor environment. IEEE Access 2019, 7, 21020–21031. [Google Scholar] [CrossRef]


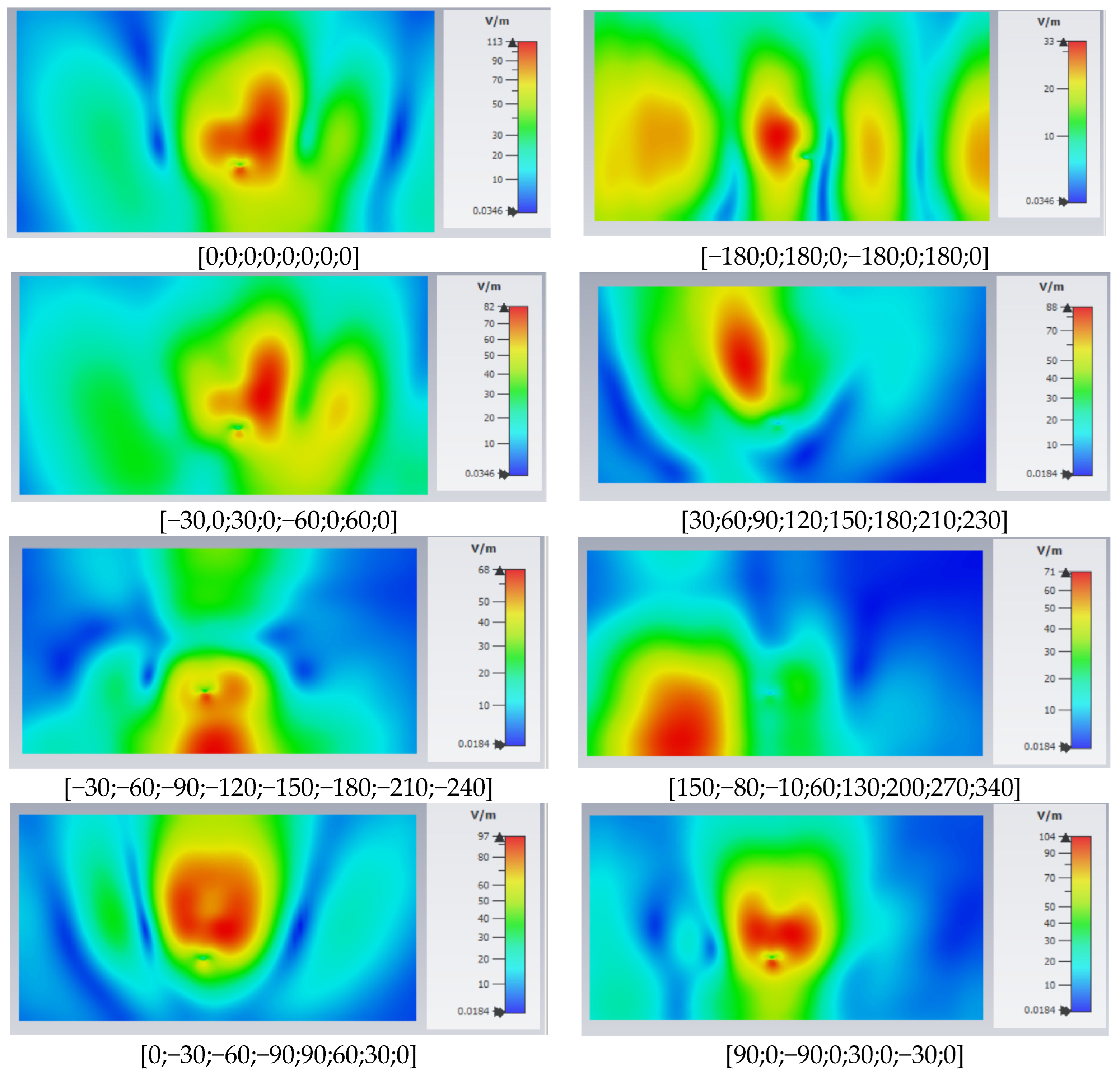
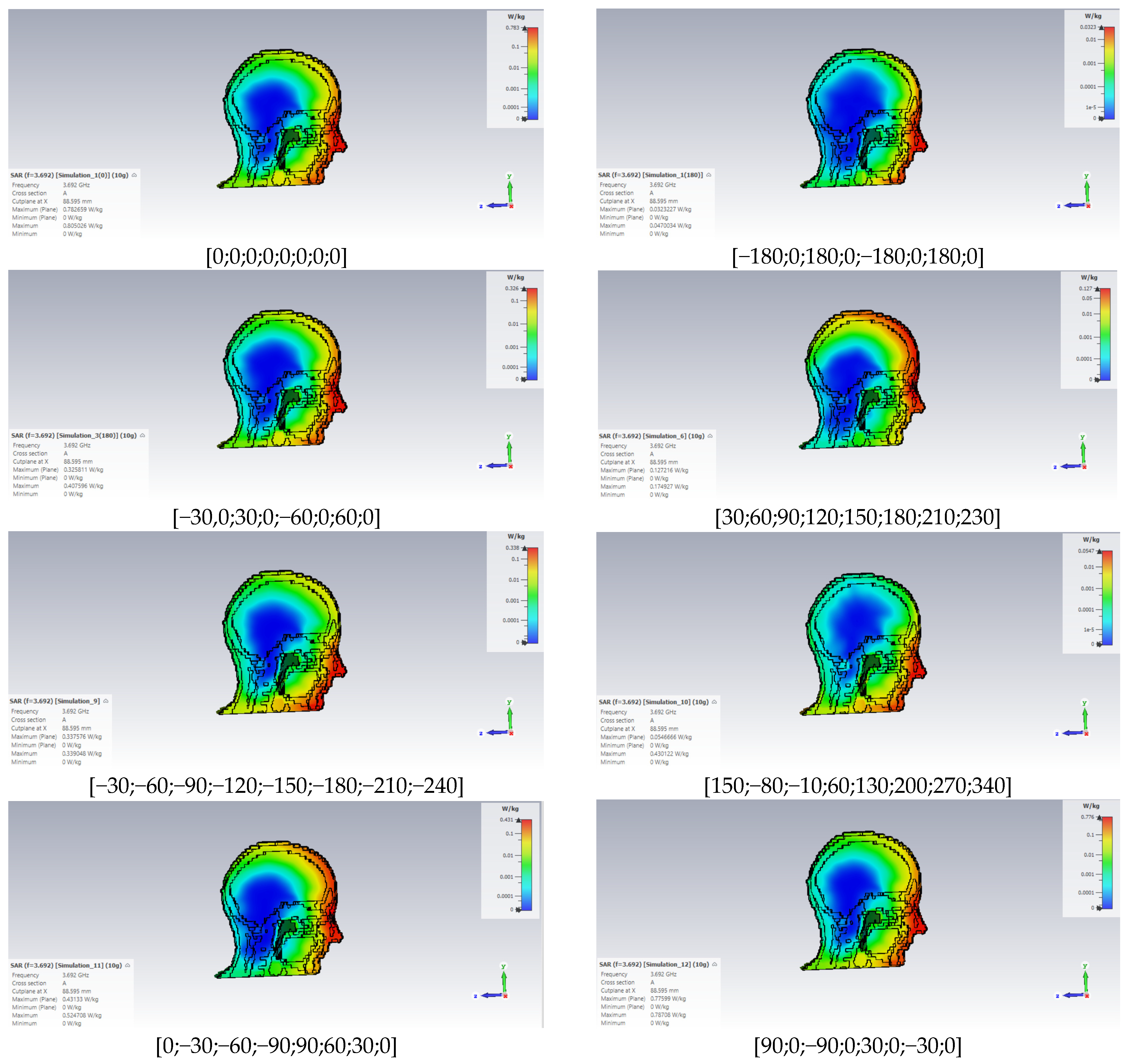
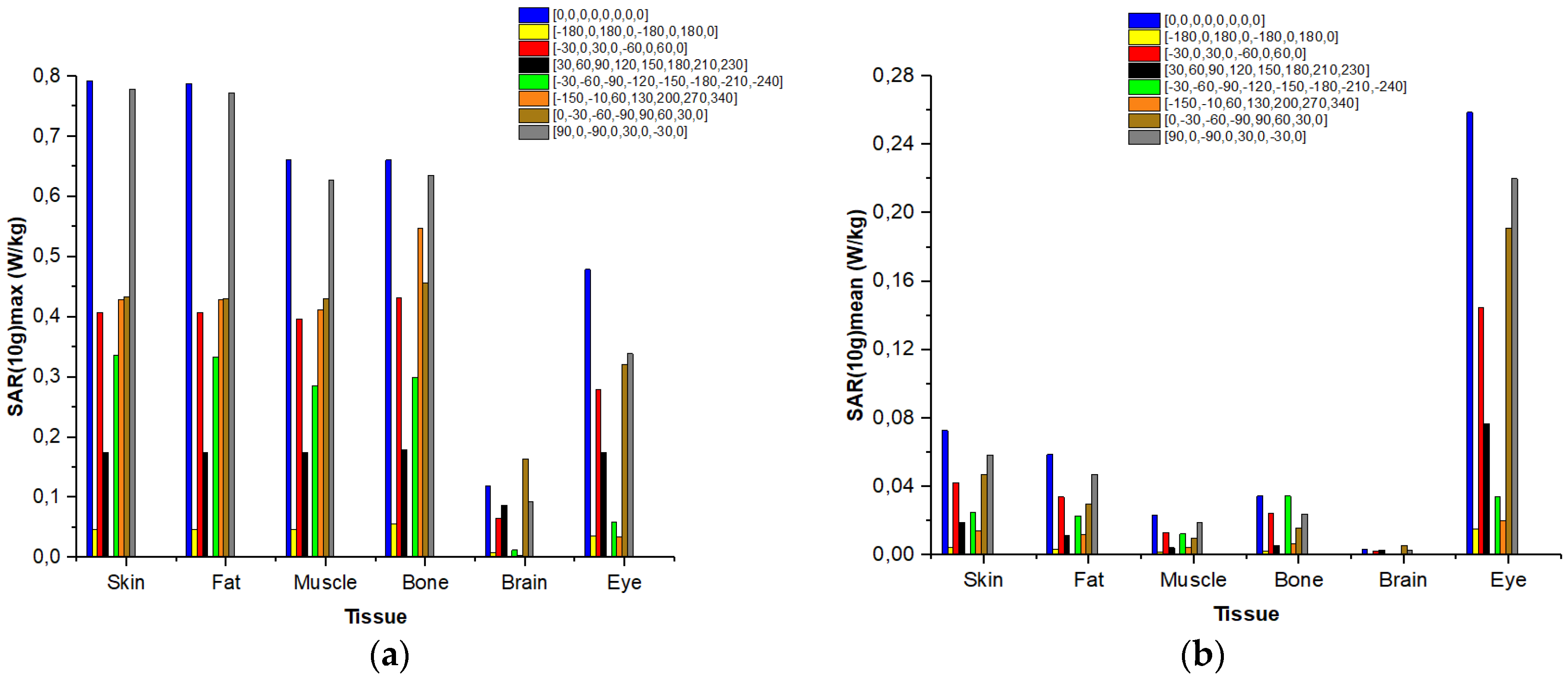

| Phase of the Elements (Degrees) | Antenna Maximum Gain (dBi) | Total Efficiency (dB) |
|---|---|---|
| [−30;0;0;30] | 6.86 | −3.84 |
| [−60;0;0;60] | 6.61 | −4.14 |
| [−90;0;0;90] | 6.27 | −4.19 |
| [−180;0;0;180] | 5.14 | −3.99 |
| [0;0;0;0] | 6.81 | −3.84 |
| [0;30;80;130] | 6.95 | −3.95 |
| [30;0;30;0] | 6.5 | −4.00 |
| [60;0;60;0] | 5.67 | −4.26 |
| [60;90;180;270] | 6.91 | −3.82 |
| [90;0;90;0] | 4.43 | −4.78 |
| [180;0;180;0] | 2.74 | −6.19 |
| [270;30;90;180] | 6.5 | −3.90 |
| Phase of the Elements (Degrees) | Antenna Maximum Gain (dBi) | Total Efficiency (dB) |
|---|---|---|
| [0;0;0;0;0;0;0;0] | 6.76 | −4.81 |
| [−180;0;180;0;−180;0;180;0] | 4.8 | −6.03 |
| [−30,0;30;0;−60;0;60;0] | 6.12 | −4.31 |
| [30;60;90;120;150;180;210;230] | 9.13 | −3.41 |
| [−30;−60;−90;−120;−150;−180;−210;−240] | 10.07 | −3.04 |
| [150;−80;−10;60;130;200;270;340] | 10.03 | −3.31 |
| [0;−30;−60;−90;90;60;30;0] | 8.16 | −4.27 |
| [90;0;−90;0;30;0;−30;0] | 6.24 | −4.97 |
| RQA Variables | Download | Upload | Streaming | Video Call | Voice Call | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Probe 1 | Probe 2 | Probe 1 | Probe 2 | Probe 1 | Probe 2 | Probe 1 | Probe 2 | Probe 1 | Probe 2 | |
| Determinism (DET) | 0 | 0 | −1 | −1 | 0 | 0 | 0 | 0 | 0 | 1.31 |
| Reccurence rate (RR) | 0 | 0 | 0 | 0 | 0.1 | 7.45 | 0.6 | 9.19 | 0.1 | 30.6 |
| Laminarity (LAM) | −1 | −1 | −1 | −1 | 0 | 0 | 0 | 0 | 0 | 8.7 |
| Trapping time (TT) | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 11 |
| Entropy (ENTR) | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 0 |
| Trend | 0 | 0 | 0 | 0 | 3.27 | −32.6 | 2.5 | −9.2 | 3.3 | −136 |
| Longest diagonal line (Lmax) | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deaconescu, D.B.; Miclaus, S. The 5G-FR1 Signals: Beams of the Phased Antennas Array and Time-Recurrence of Emissions with Consequences on Human Exposure. Electronics 2023, 12, 297. https://doi.org/10.3390/electronics12020297
Deaconescu DB, Miclaus S. The 5G-FR1 Signals: Beams of the Phased Antennas Array and Time-Recurrence of Emissions with Consequences on Human Exposure. Electronics. 2023; 12(2):297. https://doi.org/10.3390/electronics12020297
Chicago/Turabian StyleDeaconescu, Delia Bianca, and Simona Miclaus. 2023. "The 5G-FR1 Signals: Beams of the Phased Antennas Array and Time-Recurrence of Emissions with Consequences on Human Exposure" Electronics 12, no. 2: 297. https://doi.org/10.3390/electronics12020297
APA StyleDeaconescu, D. B., & Miclaus, S. (2023). The 5G-FR1 Signals: Beams of the Phased Antennas Array and Time-Recurrence of Emissions with Consequences on Human Exposure. Electronics, 12(2), 297. https://doi.org/10.3390/electronics12020297









