2.1. Human Body Models
The study of the interaction between electromagnetic waves and the body requires the determination of the power density in the tissue area. This parameter is typically calculated with computer simulations using a numerical model of the human body. The recommended method, in this case, is the finite-difference time-domain (FDTD) method [
13]. The research described in this article was carried out using the Remcom XFdtd program [
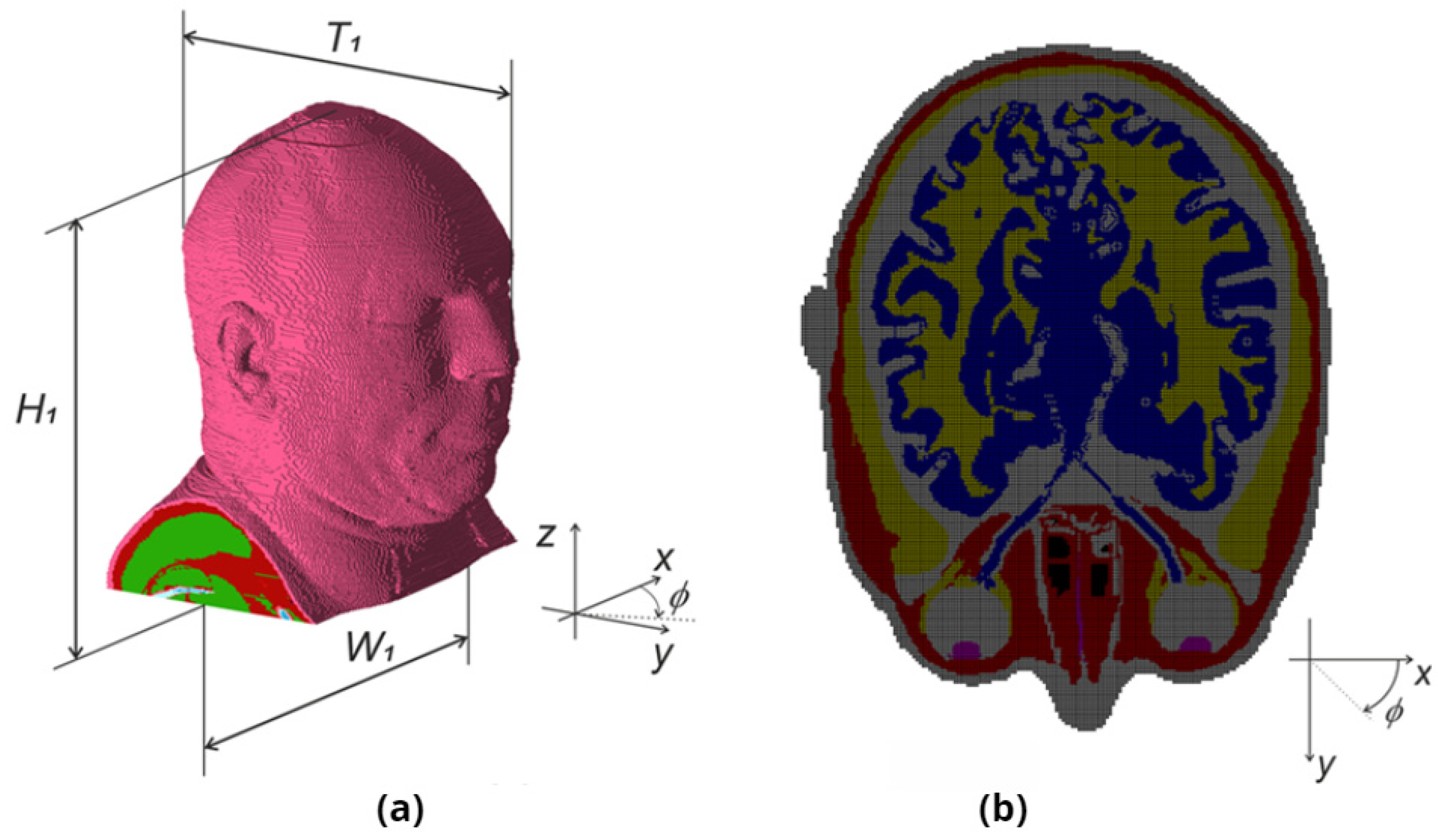
14], which implements the FDTD method. It provides access to a heterogeneous human head model that consists of 24 tissues and is divided into unit cells (voxels) with a size of 1 mm. The model and its horizontal cross-section in the eye plane are presented in
Figure 2. The dimensions of the model (referring to
Figure 2) were the following:
W1 = 484 mm,
T1 = 277 mm, and
H1 = 300 mm. Computer simulation of the body’s exposure to EM waves of a 3.5 GHz frequency, with the use of this model, requires 1.5 GB of computer memory. Moreover, it is quite time-consuming and takes about 6 min on a computer equipped with a graphics card with a GPU computing unit having 16 GB of memory. Such a long simulation time can be a limitation in the design process of a shielding structure, which requires many iterations. As it was planned to use an optimization algorithm in this research, we aimed to reduce the time required for the simulation that utilized the head model.
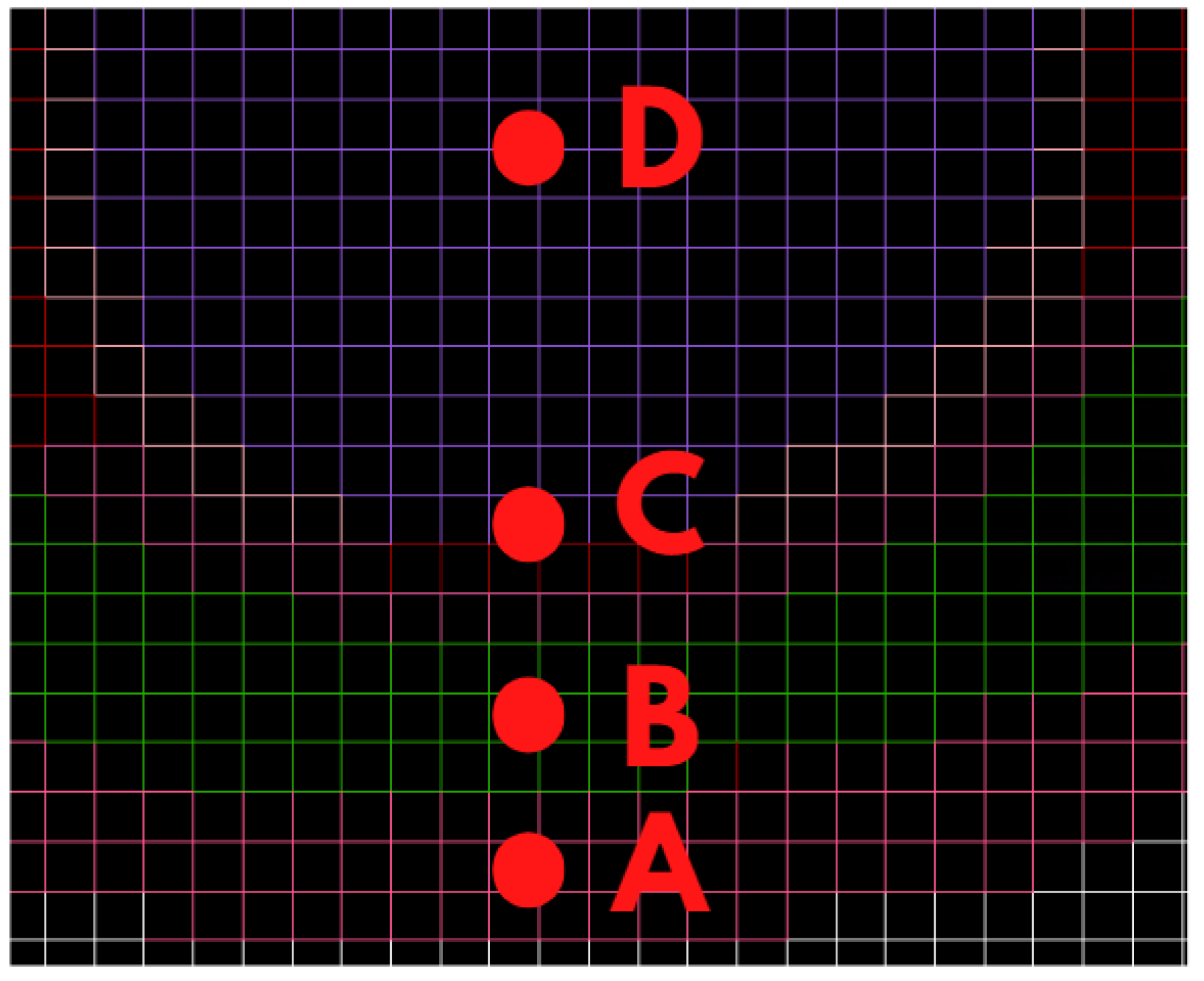
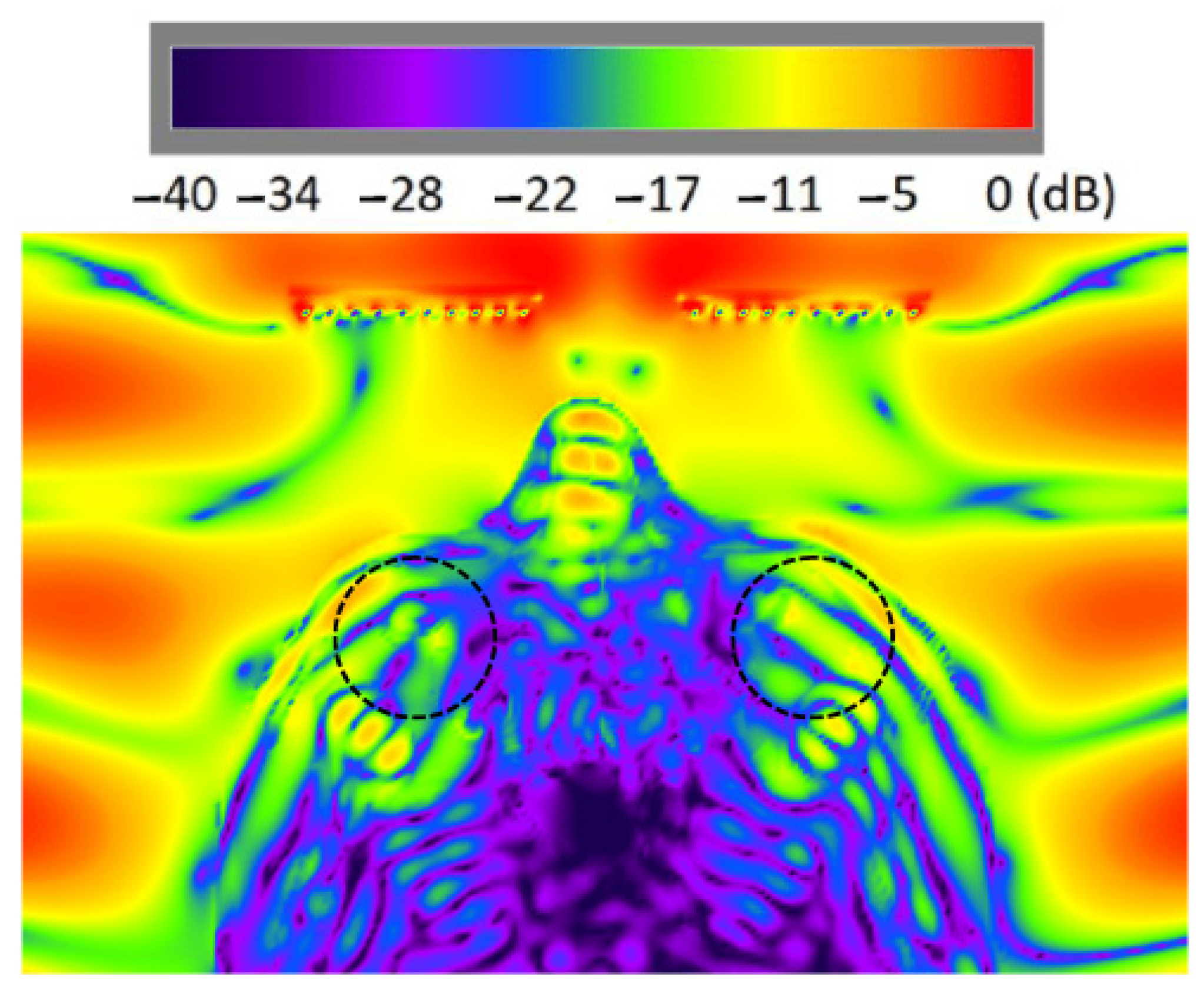
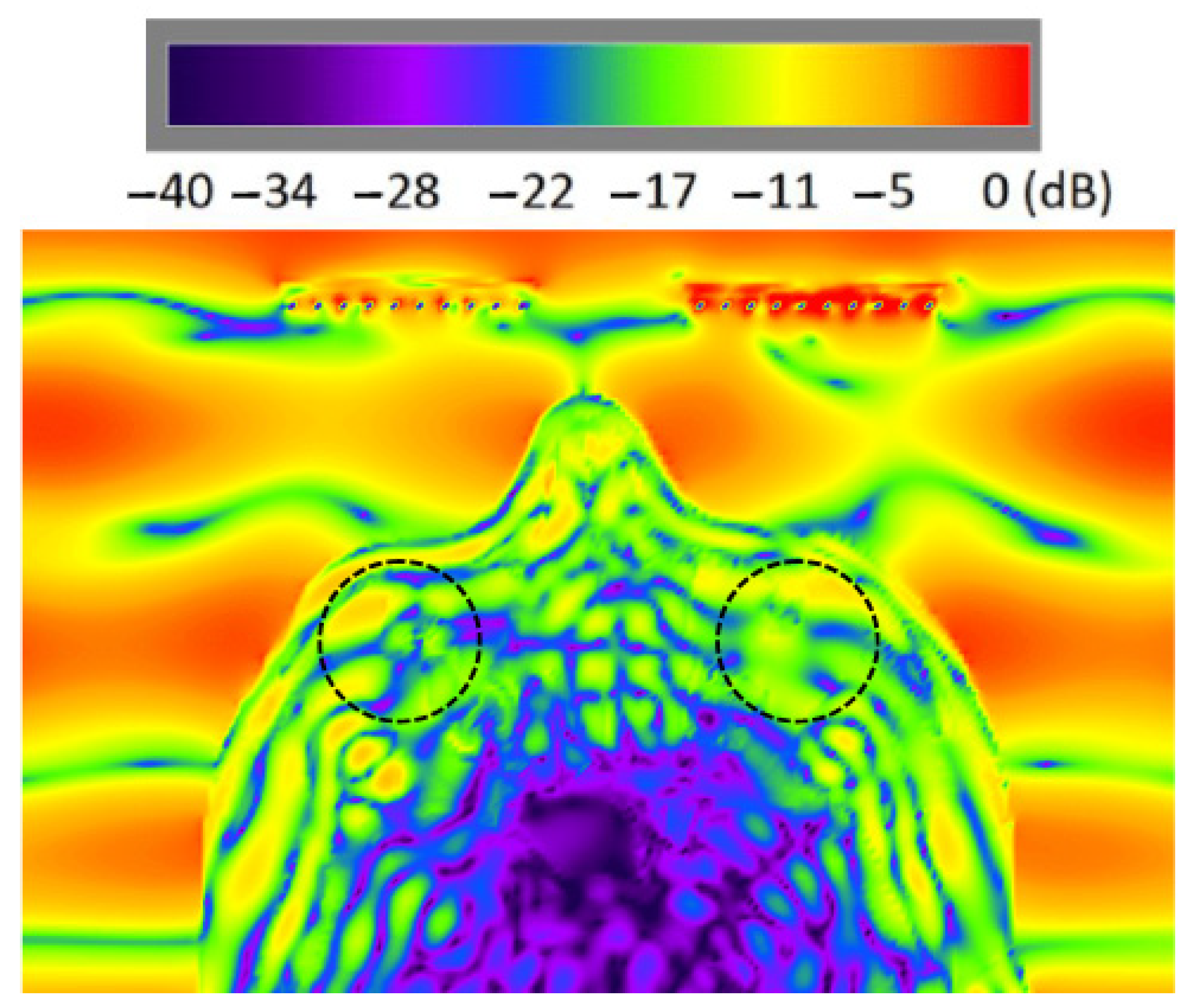
As the eye region is our main interest in this paper, we used 4 test points located inside the eyeball to obtain the values of power density. At each point, we simulated the absolute value of the Poynting vector. The placement of test points is presented in
Figure 3 in which it is shown that the test points are located in the following regions of eye tissues: eyelid (A), muscle (B), lens (C), and eye vitreous (D).
The values of the Poynting vector in the test points were verified and compared for different angles of incidence of the electromagnetic wave, relevant to the face.
Table 1 presents the values of the Poynting vector computed for the source of the electromagnetic wave directed towards the face for different values of the angle
ϕ (defined in
Figure 2). The direction of
ϕ = 90° refers to the case of the EM wave coming from the front. Other cases were studied to cover the EM wave coming from a side direction with an angle of
ϕ = 67.5°, as well as at 45°. Based on the analysis of the data presented in
Table 1, it can be concluded that the highest power density occurs in the eye region in the case where the energy source is located in front of the face. For this reason, in further studies of eye shields, it was assumed that the head would be exposed to a wave propagating from the
ϕ = 90° direction.
Therefore, in order to study this phenomenon, it is necessary to develop a model that mainly maps the eyeballs. Due to the fact that the heterogeneous model of the whole head contains many voxels that also mimic the posterior part of the head and the top part of the shoulders, we investigated how limiting the volume of this model to only the facial region would affect the simulation results.
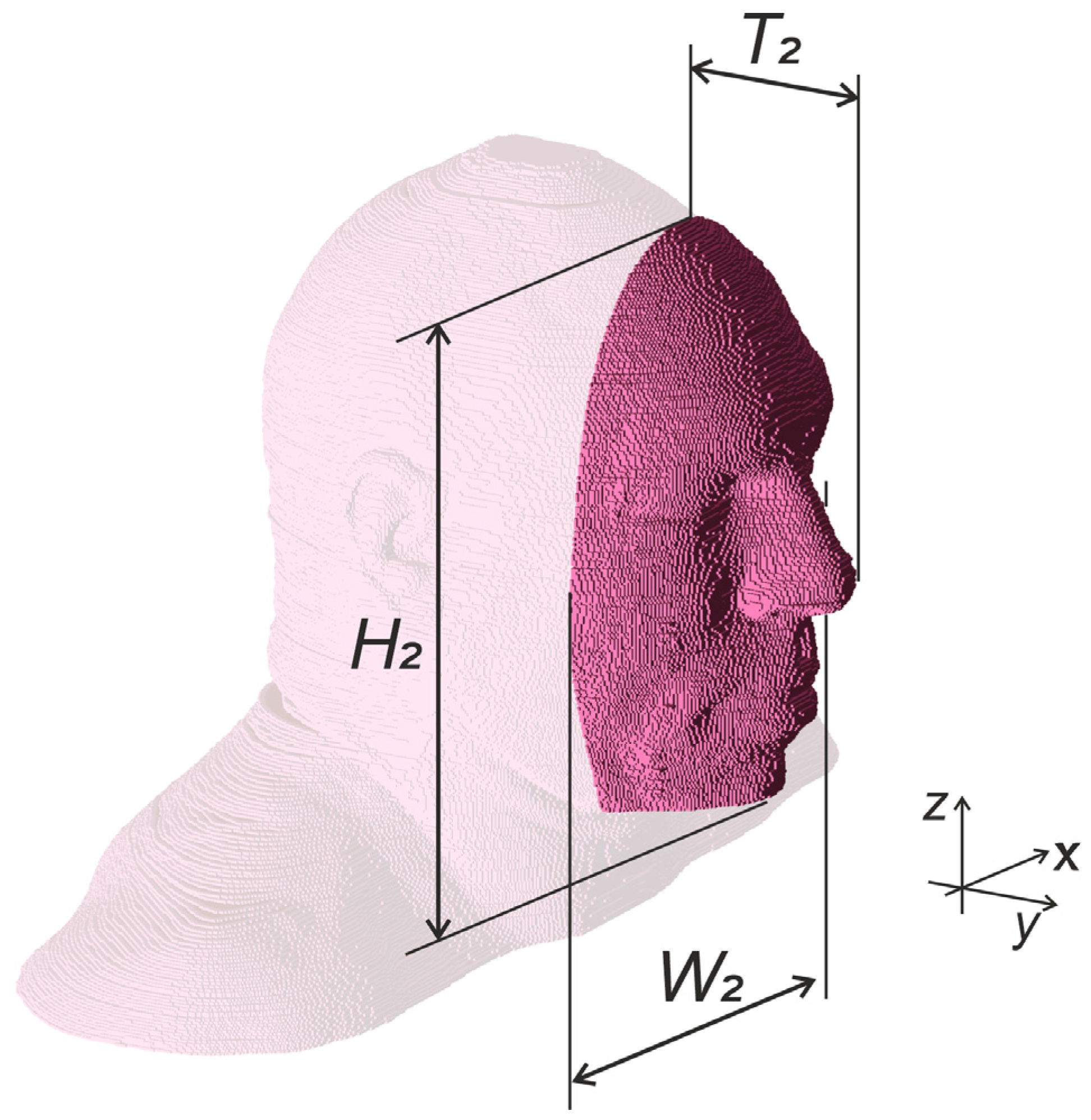
Figure 4 shows a heterogeneous model of the head fragment, which was made by cutting out a part of the Hershey NMR heterogeneous model (
Figure 2), available in the XFdtd program. The cutout fragment had the following dimensions:
W2 = 147 mm,
T2 = 70 mm, and
H2 = 204 mm. While it preserves the shape of the face and the tissues properties, it was used to investigate whether limiting the size of the heterogenous model without changing its electric properties can result in faster simulations with acceptable accuracy in reference to the full model. To investigate this, a numerical experiment was performed in which the human head was exposed to an EM wave of linear vertical polarity and 3.5 GHz frequency. The wave was propagating from the
ϕ = 90° direction, and the amplitude of the electric field component was equal to 87 V/m.
Table 2 presents a comparison of the Poynting vector module (
S) obtained for the 4 points located in the layers of the eye for the reference model (heterogeneous, full size) and the cutout model, respectively.
The above data prove that the geometric reduction of the heterogeneous model results in a high discrepancy between the values of the Poynting vector module obtained between the full-size reference model and the reduced model. The whole head reference model contained 40.2 million voxels and covered an area of 484 × 300 × 277 mm3. The cutout model was limited to an area of 147 × 204 × 70 and thus contained only 2.1 million voxels. It allowed for the reduction of the simulation time by 40%. Unfortunately, however, the results of the simulation of power density in the eyeball area obtained with the use of the whole head model differed by even 30 times from the results obtained with the cutout model.
2.2. Optimal Synthesis of the Simplified Model of the Face
The next stage of the research was devoted to the development of a simplified model of the face and eyes, which would consist of a smaller number of voxels compared with the whole head model; at the same time, it would allow us to obtain similar values of power density. For this purpose, the model shown in
Figure 5 was developed. The face is represented by a fragment of an ellipsoid, and the eyes are represented by spheres and concentric surfaces. The dimensions of the model were selected for the best representation of the eye area in relation to the heterogeneous model. This model had the dimensions of
W3 = 147 mm,
T3 = 70 mm, and
H3 = 204 mm, and it contained only 2.1 million voxels of 1 mm size.
The selection of the material parameters for the simplified model was carried out with the use of the Remcom XFdtd software and EStra automatic optimization algorithm [
15,
16]. This new model requires solving for the optimal design problem. Generally, optimal shape design problems might be classified according to five types, as follows:
Searching for the best shape of an object among an admissible set of shapes;
Searching for the best location of an object, given its shape;
Searching for the material property values, given the shape and location of an object;
Searching for the part of the boundary that is not accessible to the physical measurement, given the remaining part of the boundary;
Free boundary problems.
In this study, we used the same algorithm of numerical optimization for subsequently solving type 3 and type 2 problems, respectively.
An algorithm based on a single-objective (1 + 1)-evolution strategy (EStra) inspired by Darwinian evolution was used [
15,
16]. The algorithm was implemented in such a way that a new design vector
x =
m +
du (offspring) was accepted if and only if
x dominates the current design vector
m (parent), i.e.,
f(
x) <
f(
m), subject to the problem constraints. This means that the offspring was only accepted if it simultaneously improved the objective function and fulfilled constraints. In turn,
d was the standard deviation vector associated with
m, while
was a normally distributed perturbation. Vector
d was initialized as
do, and the value of its elements was proportional to the feasible range of the corresponding design variable. Vector
d, which drives the search, was updated according to the prescribed rate of success in improving the objective function; that is where the self-adaptation of the strategy parameter comes in.
d itself undergoes a modification, which is ruled by a randomized process. In fact, given the correction rate
, considering the
kth iteration,
(or
) is set to force a larger (or smaller) standard deviation of Gaussian distribution associated with
x in the next iteration, respectively. In other words, the solution vector x and the standard deviation vector
d are both subject to random mutation. In a basic, cost-effective (1 + 1) implementation, the operator of selection allows for the best individual out of parent
m and offspring
x to survive to the next generation. In other words, an offspring individual is selected to survive if and only if it is better, or at least non-worse, than the parent individual against objectives and constraints. This way, given an initial point, there is a non-zero probability that the optimization trajectory eventually leads to a point close to the optimal solution point. The algorithm converges when the ratio of the largest value of
d vector elements to the corresponding element of the initial standard deviation vector
do is smaller than a prescribed search tolerance.
The basic computational cost
c of the EStra algorithm can be a priori estimated as
where
c0 is the hardware-dependent time necessary to run a single solution of the direct problem associated with the optimization problem,
ni is the number of convergence iterations for a prescribed search accuracy,
np is the number of evolving solutions (in our case,
np = 1), and
nc is the number of constraints.
The most important parameters that influence the performance of the EStra algorithm are p and q; in a sense, they are the ‘tuning knobs’ ruling the algorithm performance. In particular, p is the prescribed probability of a successful iteration: an iteration is considered to be successful if the values of the objective function improve, and the ratio of the number of successful iterations to the current number of iterations is the actual probability; in turn, q is the rate of correction of the standard deviation
Remarkably, the algorithm is derivative-free, and this is a great advantage for solving non-convex optimization problems.
In summary, the evolutionary algorithm starts from a guess solution, which can be either user-supplied or randomly generated, and iteratively originates a search trajectory driven by the concept of a non-dominated solution, eventually converging to a quasi-optimal solution.
As far as the case study is concerned, the unknowns in the identification process were εk—electrical permittivity of the kth model layer, σk—electrical conductivity of the kth model layer, and k = 1, 3; layers refer to the region of skin, muscle, and eye sclera, respectively. The results of this identification process are non-physical, meaning that there is such material in the human body that results from the identification process. As we are designing the equivalent model, the materials are made to model the interaction of EM waves in a similar way to the human body, but only for the simulation of power density in the region of the eyes.
The target function
f1 that was minimized was the largest difference between the data obtained from the reference model (heterogeneous model of the whole head) and the simplified model. The Poynting vector modules obtained at 4 test points located in areas of different eye tissues (see
Figure 3) were compared.
where:
The problem reads: starting from the initial guess, find the design parameters (
εk,
σk) that minimize (1) subject to suitable constraints, for instance 1 <
εk < 100, 1 <
σk < 100. In
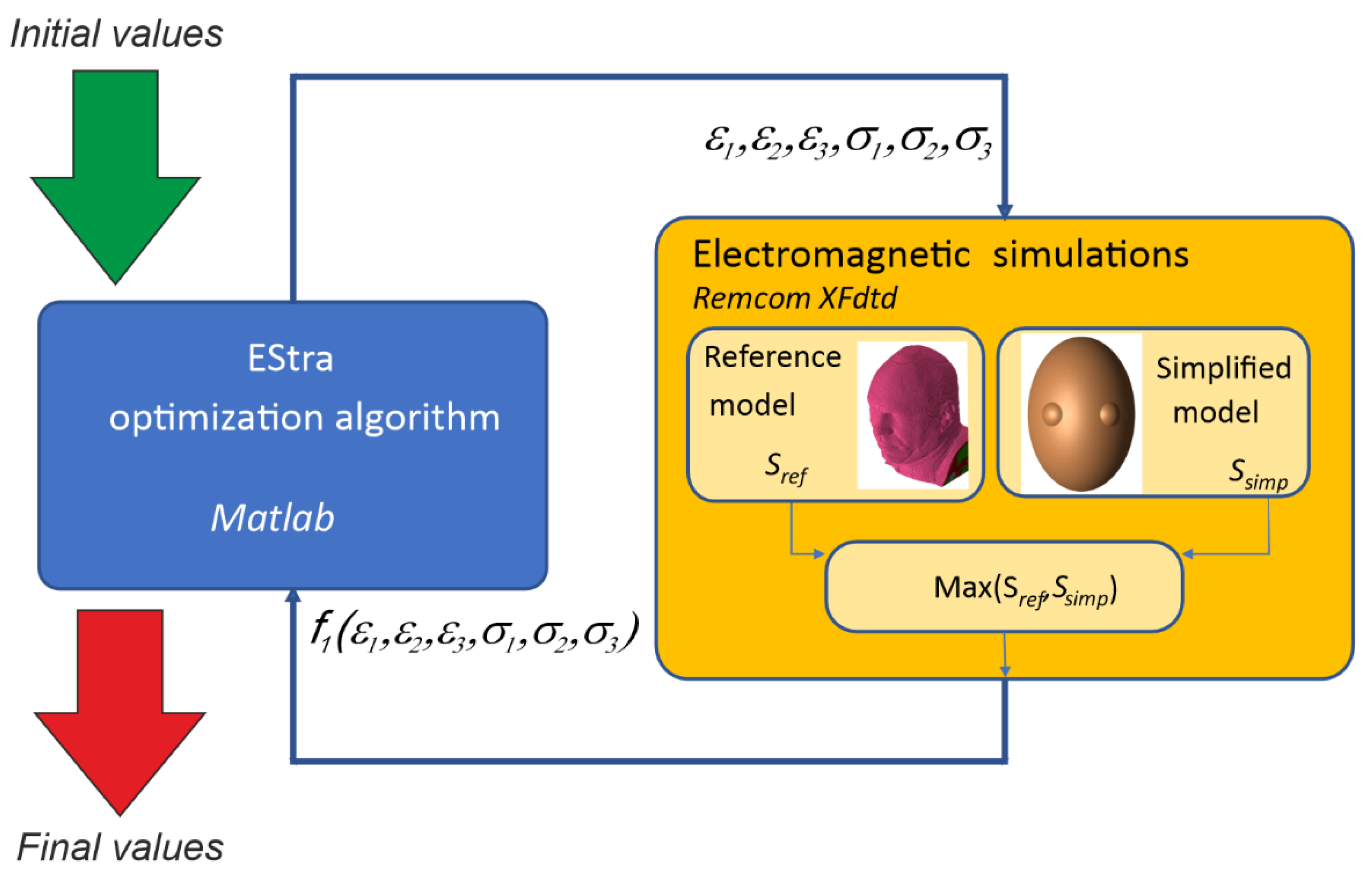
Figure 6, the procedure of the identification of the head model parameters is presented. The optimization algorithm was implemented in a Matlab environment, while the evaluation of the objective function was performed with the XFdtd program.
The values of the material parameters identified in the optimization process are presented in
Table 3. For the purpose of model assessment, the values of the power density obtained for the reference model and simplified model are presented in
Table 4. The initial values were identical to the parameters of the actual head tissues (skin, muscle, and eye sclera). The initial value of the objective function
f1 was 5.64, and the final value obtained as a result of 47 iterations was 1.58. It is the value of the maximum difference between the power density obtained with the reference and the simplified model, and this discrepancy is acceptable for the purpose of a shielding structure design. Due to the limited size of the simplified model, it uses only 2.1 million voxels, thanks to which the calculation time was reduced by about 50% in relation to the whole head model. The simplified model developed in this way was used in further research to design the shielding structure.
2.3. Shielding Structure Optimal Design
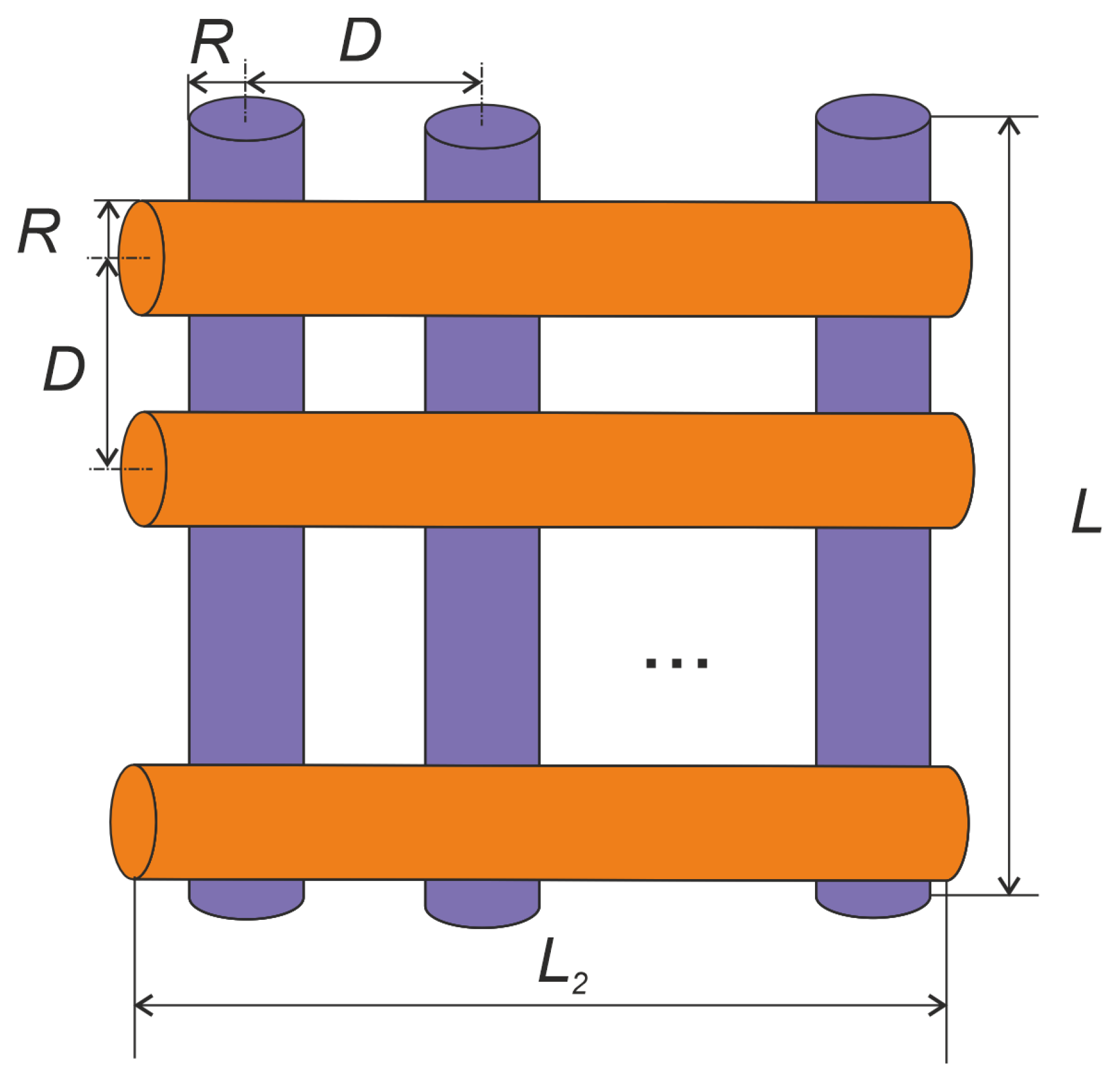
The developed shielding structure was designed to limit the power density in the eye region when the body is exposed to a wave of 3.5 GHz frequency for both linear vertical and linear horizontal polarization. In order to not restrict visibility, such a cover cannot be made of a solid conductive material. Accordingly, a system of thin rectilinear wires was used [
17], the conductivity and length of which were selected to partially absorb the wave energy. Such elements can be made in the form of sputtered tracks on transparent plastic, which will minimize the reduction of the user’s visibility. The structure of the screen is shown in
Figure 7. The distance between the shield and the eye was fixed in our research; it results from our assumption that the shield will be incorporated into the protective glasses. In such a case, the distance between the glass lens and the eye is fixed and defined by the back vertex distance. The latter is the distance between the front face of the cornea/corneal vertex and the back side of the glass lens. Normally, this parameter varies from 13 mm to approximately 16 mm according to standard ophthalmology practice.
In this study, we investigated how the conductivity of the elements and their length influence the performance of a shielding structure without assuming the technology of the structure fabrication. For simplicity, we assumed that the wires are cylindrical in shape, as their exact cross-sectional shape does not affect the effectiveness of the design. Accordingly, the structure consists of 20 vertical and 20 horizontal wires that were placed 32 mm from the eye. The radius of the conductors is
R = 0.5 mm, and the distance between them is
D = 4 mm. The design variables (
L,
L2,
σ), where
σ is the conductivity of the material, were synthesized using the EStra automatic optimization algorithm and Remcom XFdtd program. The objective function
f2 minimized in the optimization process was the maximum value of the power density in the eye area, similarly obtained to the previous case for 4 points inside the eye.
where:
SEz—Vector values in the eye area for vertical polarization (W/m2)
SEx—Poynting vector values in the eye area for horizontal polarization (W/m2)
L—Length of vertical wire in the shielding structure (mm)
L2—Length of horizontal wire in the shielding structure (mm)
σ—Conductivity of the material (S/m)
The problem reads: starting from the initial guess, find the design parameters (
L,
L2,
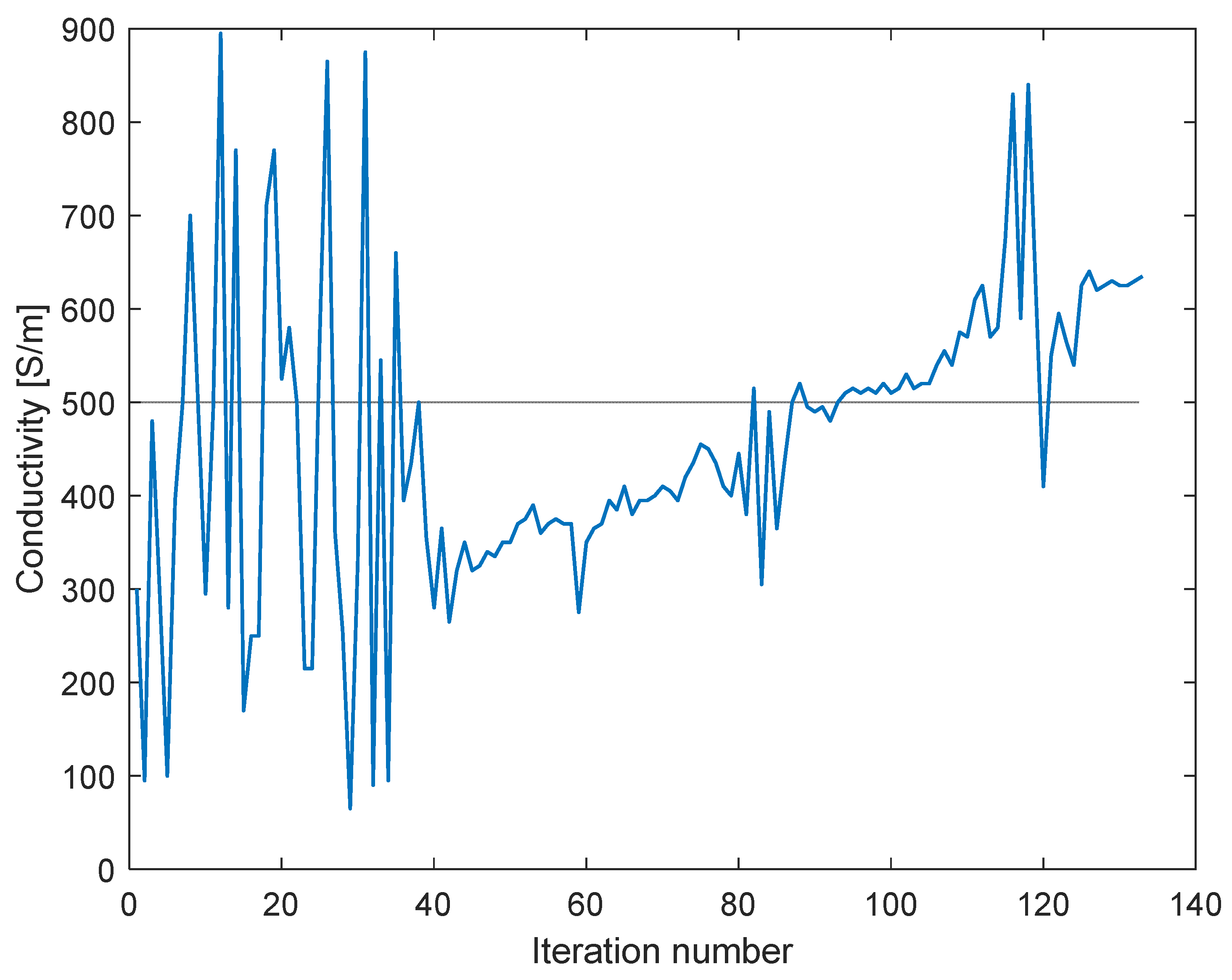
σ) minimizing (2) subject to suitable constraints. The geometrical constraints were resulting from the location of the structure in the proximity of the face. The length of vertical elements could change from 10 mm to 70 mm; in the case of horizontal elements, the length could change from 10 mm to 50 mm. The material conductivity could change from 1 S/m to 900 S/m.
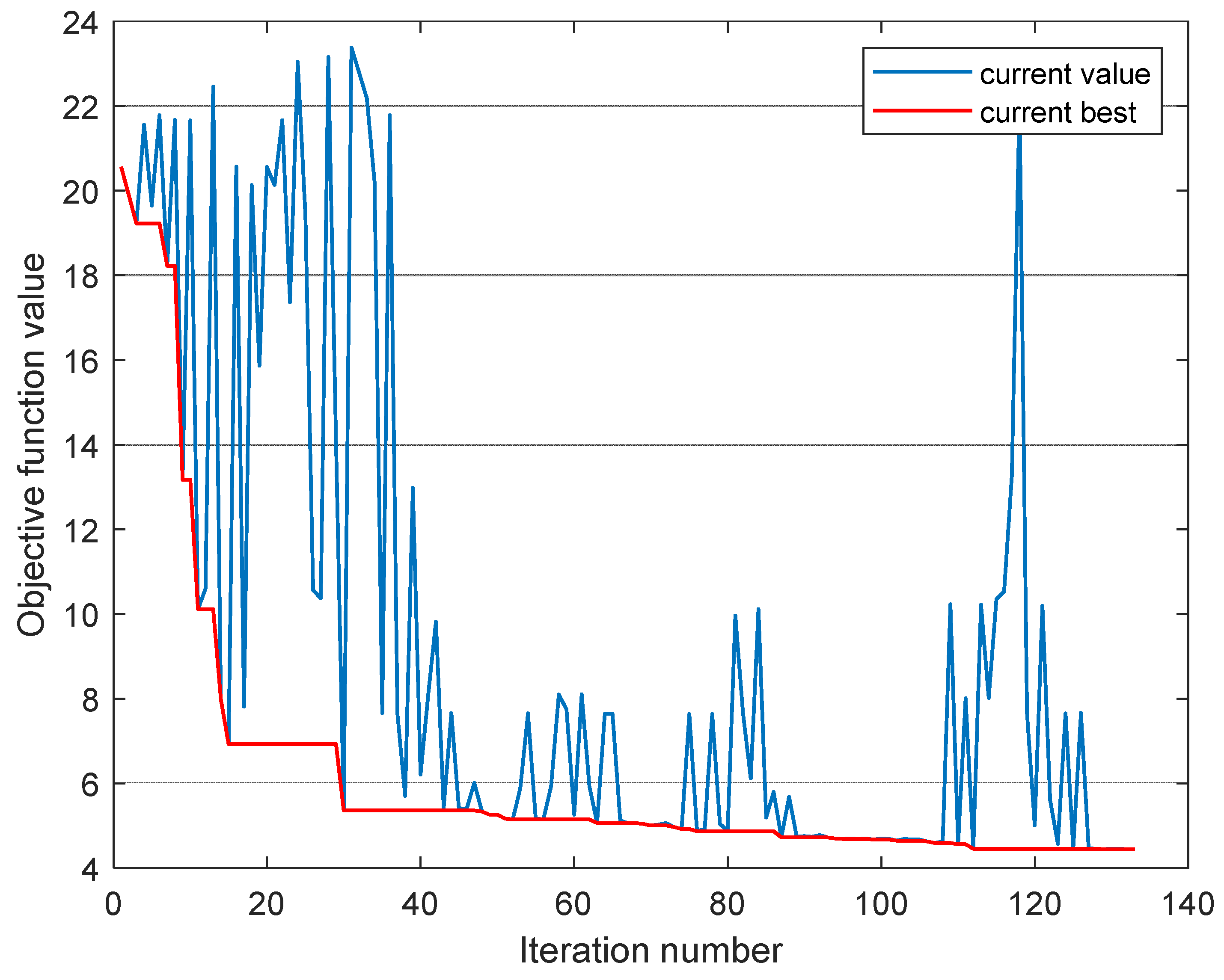
Figure 8 presents the procedure of the shield design. Again, the optimization algorithm was implemented in a Matlab environment, while the evaluation of the objective function relied on the XFdtd program. At each iteration, two simulations of the shielding structure were performed, located in front of a simplified model of the face. One field analysis was run for the vertical polarization of EM waves, and another one for the horizontal polarization. In both cases, the frequency was equal to 3.5 GHz, and the amplitude of the electric field component was equal to 87 V/m. The greatest overall value of the Poynting vector was sent to the EStra algorithm as the updated value of the objective function.