Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model
Abstract
:1. Introduction
- (1)
- In this paper, the intersection and union MPC algorithms under the semi-honest model are studied, and then the possible malicious attacks in the algorithms are analyzed.
- (2)
- (3)
- Through the efficiency analysis, the algorithm remains efficient, and the real/ideal model paradigm [26] is used to prove the security of the algorithm under the malicious model.
2. Preliminary Knowledge
2.1. MPC Security Definition
2.2. Lifted-ElGamal Cryptosystem
2.3. Lifted-ElGamal Threshold Cryptosystem
2.4. Ciphertext Re-Randomization
2.5. Discrete Logarithms Equality
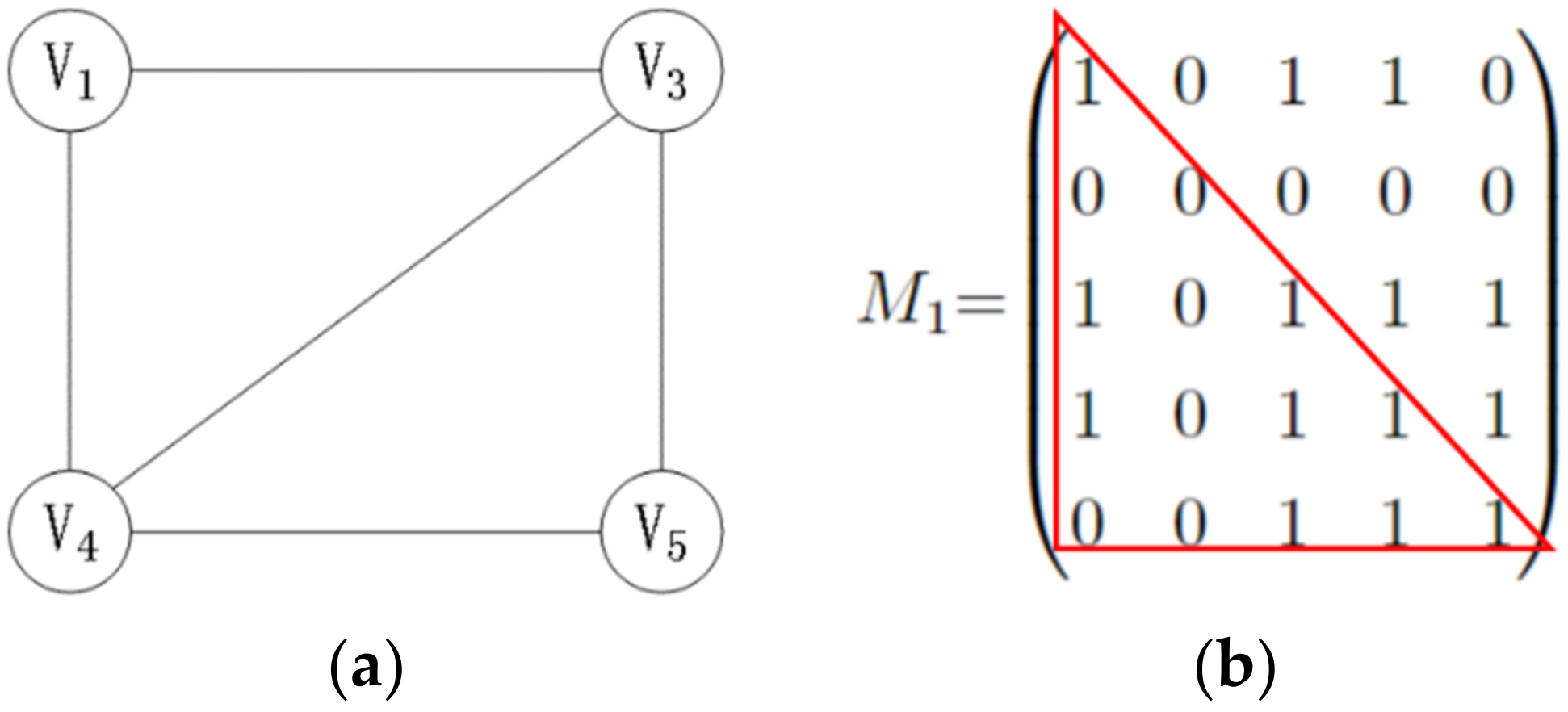
2.6. 0–1 Coding Rule
3. The MPC Algorithm of Graphs’ Intersection and Union under the Semi-Honest Model
| Algorithm 1.Graphs’ intersection MPC algorithm under the semi-honest model. |
| Input: Participants respectively own graphs . Output: Intersection of . Start: (1) All participants jointly select a large prime and a generator ; each participant selects as their private key and publishes ; all participants jointly generate the public key of the Lifted-ElGamal threshold cryptosystem . (2) converts graph into storage matrix according to 0–1 coding rule, and takes diagonal and lower triangular elements to form vector . After encryption, it is marked as , and sent to . (3) Participant overwrites the element in with the value is 0 in . Then, the unmodified element is re-randomized and assigned to , before being sent to . (4) Participant overwrites the element in with the value of 0 in . The unmodified element is re-randomized and assigned to and then published. (5) All participants jointly decrypt , restore the storage matrix of the intersection of graphs according to , and restore to the intersection matrix of graphs according to the 0–1 coding rule. The algorithm ends. |
4. The MPC Algorithm of Graphs’ Intersection and Union under the Malicious Model
4.1. Ideas and Solution
- (1)
- In step (3), retains the correct result and sends the wrong result.
- (2)
- In step (4), publishes an incorrect result.
- (3)
- When all participants jointly decrypt, the participant provides wrong decryption information, which leads to a decryption error.
4.2. Correctness Analysis
- (1)
- Steps (1) and (2) of Algorithm 2 are mainly to re-encode the elements in the graph according to the coding rule, before encrypting and publishing them after coding. Because each participant is encrypted after coding, the participants’ data cannot decrypt the data of other participants; therefore, the algorithm is correct.
- (2)
- In step (3), all participants compute the product of each column, and each participant computes the product of all column elements to avoid unfairness.
- (3)
- In step (4), the participant judges whether the decrypted data provided by the other participant is correct through the zero-knowledge proof. Here, the method of proving the equality of discrete logarithms is used to prove . If they are all correct, the algorithm continues to be executed, and the intersection can be restored according to the results.
- (4)
- Step (5) uses the additive homomorphism of the Lifted-ElGamal threshold cryptosystem, i.e., , to decrypt, and the intersection elements are judged according to the decrypted value.
- (5)
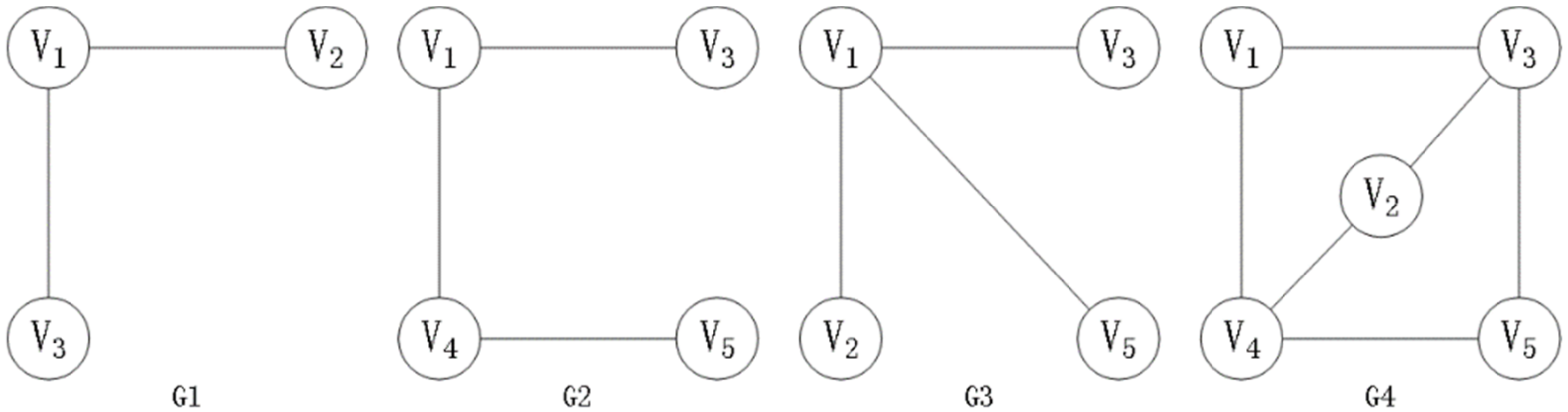
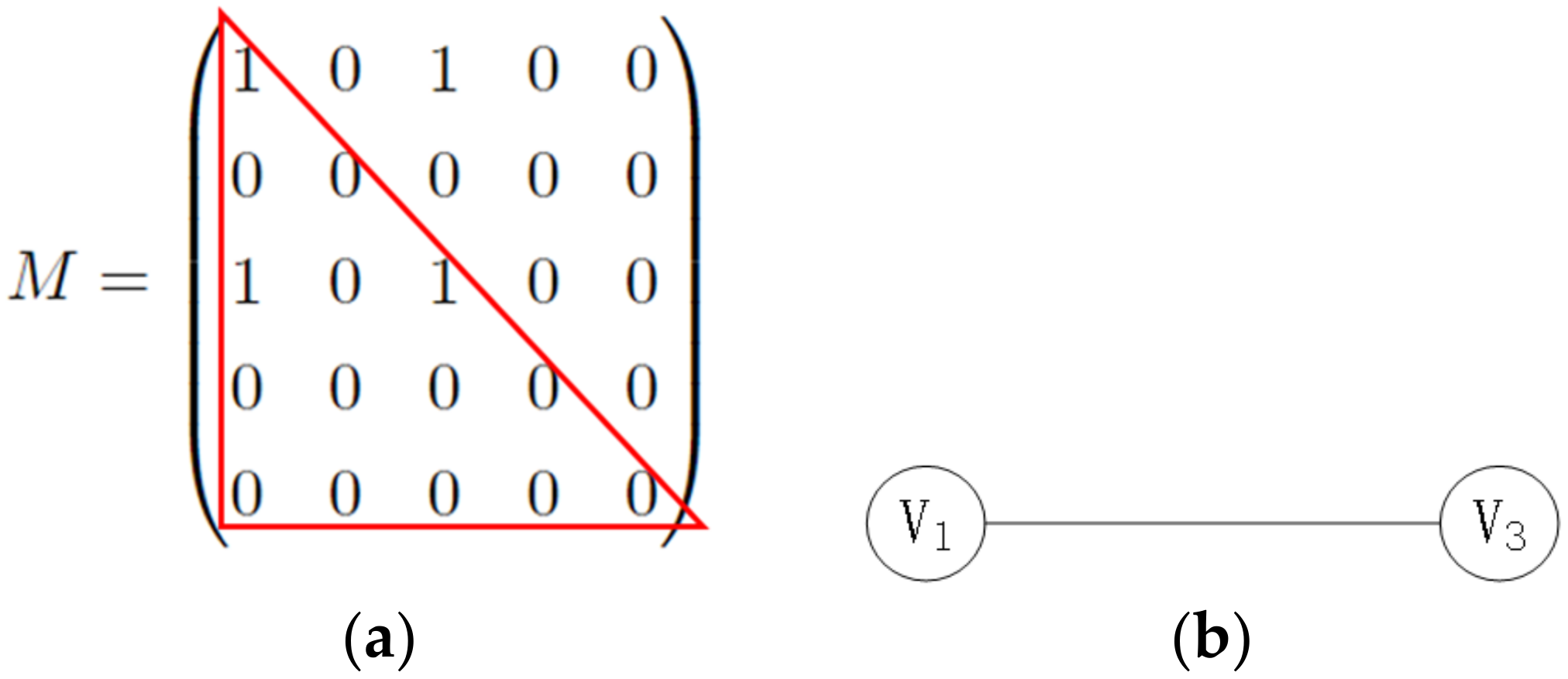
- Example: suppose vertex set , ; participants respectively have as shown in Figure 2 to compute the intersection of the graph.
| Algorithm 2. The MPC algorithm of graphs’ intersection under the malicious model. |
| Input: Participant respectively own graphs . Output: Intersection of . Preparation stage: The plaintext space of the Lifted-ElGamal threshold cryptosystem is ; is used to form an addition group. There is no difference between positive and negative in this group; however, if and , there must be . In this case, is the addition inverse of . When encoding , the vertices and edges existing in the additive inverse of are set. All participants jointly select a large prime and a generator , and each participant selects as their private key and publishes ; all participants jointly generate the public key of the Lifted-ElGamal threshold cryptosystem with additive homomorphism . Start: (1) sets the existing vertices and edges as the additive inverse of , and the nonexistent vertices and edges as the random number . re-encode according to the 0–1 coding rule, and take the diagonal and lower triangular elements to form the vector . (2) Vector of participant is encrypted and recorded as , and is made public. (3) All participants compute the component product of each column separately. Let . (4) All participants jointly decrypt; assuming decryption of , participant first computes and publishes , and then uses the zero-knowledge proof to prove to other participants that the decrypted data provided by themselves are correct, i.e., . If the verification fails, this indicates that there is deception, and the algorithm is terminated. If the verification is passed, decryption continues. (5) All participants decrypt and get . If = 1, it exists in the intersection; if , it does not exist. According to the decrypted data and 0–1 coding rule, the intersection of the graph is restored. The algorithm ends. |
4.3. Security Proof
4.4. The MPC Algorithm of Graphs’ Union under the Malicious Model
| Algorithm 3.The MPC algorithm of graphs’ union under the malicious model. |
| Input: Participants respectively own graphs . Output: Union of . Preparation stage: All participants jointly select a large prime and a generator , and each participant selects a as their private key and publishes ; all participants jointly generate the public key of the Lifted-ElGamal threshold cryptosystem with additive homomorphism . Start: (1) is encoded according to the 0–1 coding rule, and the diagonal and lower triangular elements are taken to form the vector . (2) Participant vector is encrypted and recorded as , and is made public. (3) All participants compute the component product of each column separately. Let . (4) All participants jointly decrypt; assuming decryption of , participant first computes and publishes , and then use the zero-knowledge proof to prove to other participants that the decrypted data provided by themselves are correct, i.e., . If the verification fails, it indicates that there is deception, and the algorithm is terminated. If the verification is passed, decryption continues. (5) All participants decrypt and get . If 1, it exists in the intersection; if , it does not exist. According to the decrypted data and coding rule, the intersection of the graph is restored. The algorithm ends. |
5. Efficiency Analysis
5.1. Computational Complexity and Communication Complexity
5.2. Experimental Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Goldwasser, S. Multi party computations: Past and present. In Proceedings of the Sixteenth Annual ACM Symposium on Principles of Distributed Computing, Santa Barbara, CA, USA, 21–24 August 1997; pp. 1–6. [Google Scholar]
- Cramer, R.; Damgård, I.B. Secure Multi-Party Computation. Ph.D. Thesis, Cambridge University Press, Cambridge, UK, 2015. [Google Scholar]
- Akram, A.; Giannakou, A.; Akella, V.; Lowe-Power, J.; Peisert, S. Performance analysis of scientific computing workloads on general purpose tees. In Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Portland, OR, USA, 17–21 May 2021; pp. 1066–1076. [Google Scholar]
- Fagin, R.; Naor, M.; Winkler, P. Comparing information without leaking it. Commun. ACM 1996, 39, 77–85. [Google Scholar] [CrossRef]
- Yao, Y.; Xiong, N.; Park, J.H.; Ma, L.; Liu, J. Privacy-preserving max/min query in two-tiered wireless sensor networks. Comput. Math. Appl. 2013, 65, 1318–1325. [Google Scholar] [CrossRef]
- Wang, J.; Wu, L.; Zeadally, S.; Khan, M.K.; He, D. Privacy-preserving data aggregation against malicious data mining attack for iot-enabled smart grid. ACM Trans. Sens. Netw. 2021, 17, 1–25. [Google Scholar] [CrossRef]
- Li, S.; Mu, N.; Le, J.; Liao, X. Privacy preserving frequent itemset mining:Maximizing data utility based on database reconstruction. Comput. Secur. 2019, 84, 17–34. [Google Scholar] [CrossRef]
- Veeraragavan, N.R.; Nygård, J.F. Decansec: A decentralized architecture for secure statistical computations on distributed health registry data. In Proceedings of the 16th International Conference on Availability, Reliability and Security, Vienna, Austria, 17–20 August 2021; pp. 1–9. [Google Scholar]
- Wang, Z.; Pang, X.; Chen, Y.; Shao, H.; Wang, Q.; Wu, L.; Chen, H.; Qi, H. Privacy-preserving crowd-sourced statistical data publishing with an untrusted server. IEEE Trans. Mob. Comput. 2018, 18, 1356–1367. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Srivastava, G.; Gupta, G.P.; Tripathi, R.; Gadekallu, T.R.; Xiong, N.N. PPSF: A privacy-preserving and secure framework using blockchain-based machine-learning for IoT-driven smart cities. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2326–2341. [Google Scholar] [CrossRef]
- Kikuchi, H.; Eto, K.; Waki, K.; Mori, T. Vulnerability of privacy visor used to disrupt unauthorized face recognition. In Proceedings of the 2021 IEEE Conference on Dependable and Secure Computing (DSC), Aizuwakamatsu, Japan, 30 January–2 February 2021; pp. 1–7. [Google Scholar]
- Chen, Z.; Li, S.; Chen, L.; Huang, Q.; Zhang, W. Fully privacy-preserving determination of point-range relationship. Sci. Sin. Inf. 2018, 48, 187–204. [Google Scholar] [CrossRef]
- Fu, A.; Zhang, X.; Xiong, N.; Gao, Y.; Wang, H.; Zhang, J. VFL: A verifiable federated learning with privacy-preserving for big data in industrial IoT. IEEE Trans. Ind. Inform. 2020, 18, 3316–3326. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, L.; Pei, S.; Yu, Z.; Chen, Y.; Liu, X.; Du, J.; Xiong, N. KNN-BLOCK DBSCAN: Fast clustering for large-scale data. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3939–3953. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Zhang, R.; Luo, D.; Xu, G.; Chen, X. Securely Computing the Manhattan Distance under the Malicious Model and Its Applications. Appl. Sci. 2022, 12, 11705. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, S.; Zhao, M.; Chen, Z.; Gao, C.-Z.; Li, H.; Tan, Y.-A. Secure multi-party computation: Theory, practice and applications. Inf. Sci. 2019, 476, 357–372. [Google Scholar] [CrossRef]
- Wei, Q.; Li, S.; Wang, W.; Yang, Y. Privacy-preserving computational geometry. Int. J. Netw. Secur. 2019, 21, 1071–1080. [Google Scholar]
- Xu, J.; Wang, A.; Wu, J.; Wang, C.; Wang, R.; Zhou, F. Spcss: Social network based privacy-preserving criminal suspects sensing. IEEE Trans. Comput. Soc. Syst. 2020, 7, 261–274. [Google Scholar] [CrossRef]
- Xia, F.; Hao, R.; Li, J.; Xiong, N.; Yang, L.T.; Zhang, Y. Adaptive GTS allocation in IEEE 802.15. 4 for real-time wireless sensor networks. J. Syst. Archit. 2013, 59, 1231–1242. [Google Scholar] [CrossRef]
- Akavia, A.; Moran, T. Topology-hiding computation beyond logarithmic diameter. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Paris, France, 30 April–4 May 2017; pp. 609–637. [Google Scholar]
- Frikken, K.B.; Golle, P. Private social network analysis: How to assemble pieces of a graph privately. In Proceedings of the 5th ACM Workshop on Privacy in Electronic Society, Alexandria, VA, USA,, 30 October 2006; pp. 89–98. [Google Scholar]
- Zhou, F.; Xu, Z.; Li, Y.; Xu, J.; Peng, S. Private graph intersection protocol. In Proceedings of the Australasian Conference on Information Security and Privacy, Auckland, New Zealand, 3–5 July 2017; pp. 235–248. [Google Scholar]
- Wei, Q.; Li, S.D.; Wang, W.L.; Du, R.M. Secure multi-party computation of graph intersection and union. J. Cryptologic Res. 2020, 7, 774–788. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volumn 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Li, S.D.; Xu, W.T.; Wang, W.L.; Zhang, M.Y. Secure maximum (minimum) computation in malicious mode. Chin. J. Comput. 2021, 44, 14. [Google Scholar]
- Freedman, M.J.; Hazay, C.; Nissim, K.; Pinkas, B. Efficient set intersection with simulation-based security. J. Cryptol. 2016, 29, 115–155. [Google Scholar] [CrossRef]
- El Gamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Desmedt, Y.; Frankel, Y. Threshold cryptosystems. In Proceedings of the Conference on the Theory and Application of Cryptology, Houthalen, Belgium, 10–13 April 1989; pp. 307–315. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Fouque, P.-A.; Poupard, G.; Stern, J. Sharing decryption in the context of voting or lotteries. In Proceedings of the International Conference on Financial Cryptography, Anguilla, British West Indies, 20–24 February 2000; pp. 90–104. [Google Scholar]
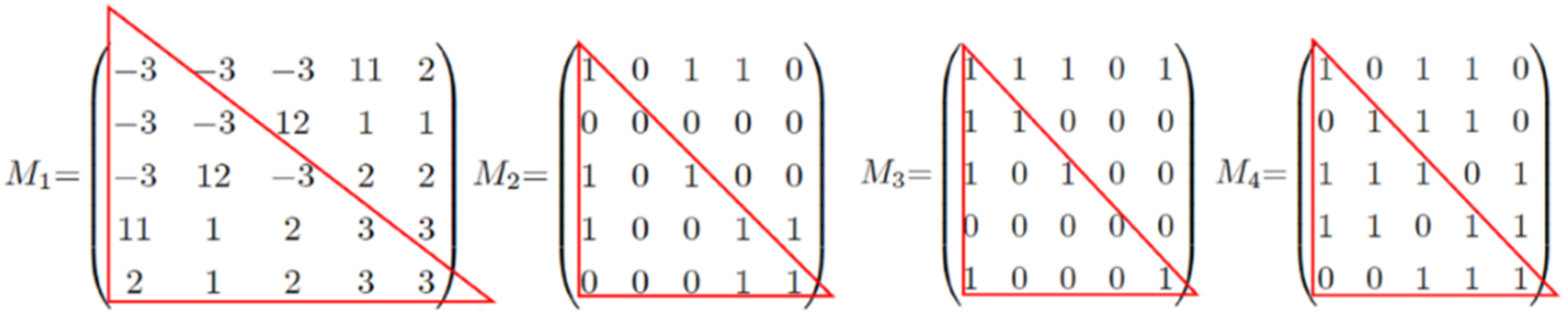

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Tu, X.-F.; Luo, D.; Xu, G.; Xiong, N.N.; Chen, X.-B. Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model. Electronics 2023, 12, 258. https://doi.org/10.3390/electronics12020258
Liu X, Tu X-F, Luo D, Xu G, Xiong NN, Chen X-B. Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model. Electronics. 2023; 12(2):258. https://doi.org/10.3390/electronics12020258
Chicago/Turabian StyleLiu, Xin, Xiao-Fen Tu, Dan Luo, Gang Xu, Neal N. Xiong, and Xiu-Bo Chen. 2023. "Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model" Electronics 12, no. 2: 258. https://doi.org/10.3390/electronics12020258
APA StyleLiu, X., Tu, X.-F., Luo, D., Xu, G., Xiong, N. N., & Chen, X.-B. (2023). Secure Multi-Party Computation of Graphs’ Intersection and Union under the Malicious Model. Electronics, 12(2), 258. https://doi.org/10.3390/electronics12020258







