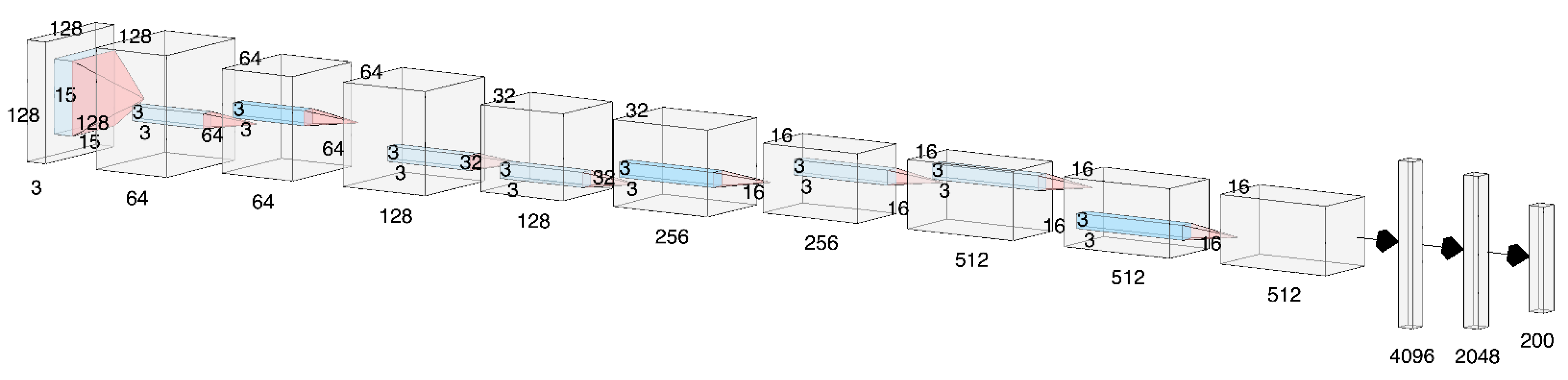
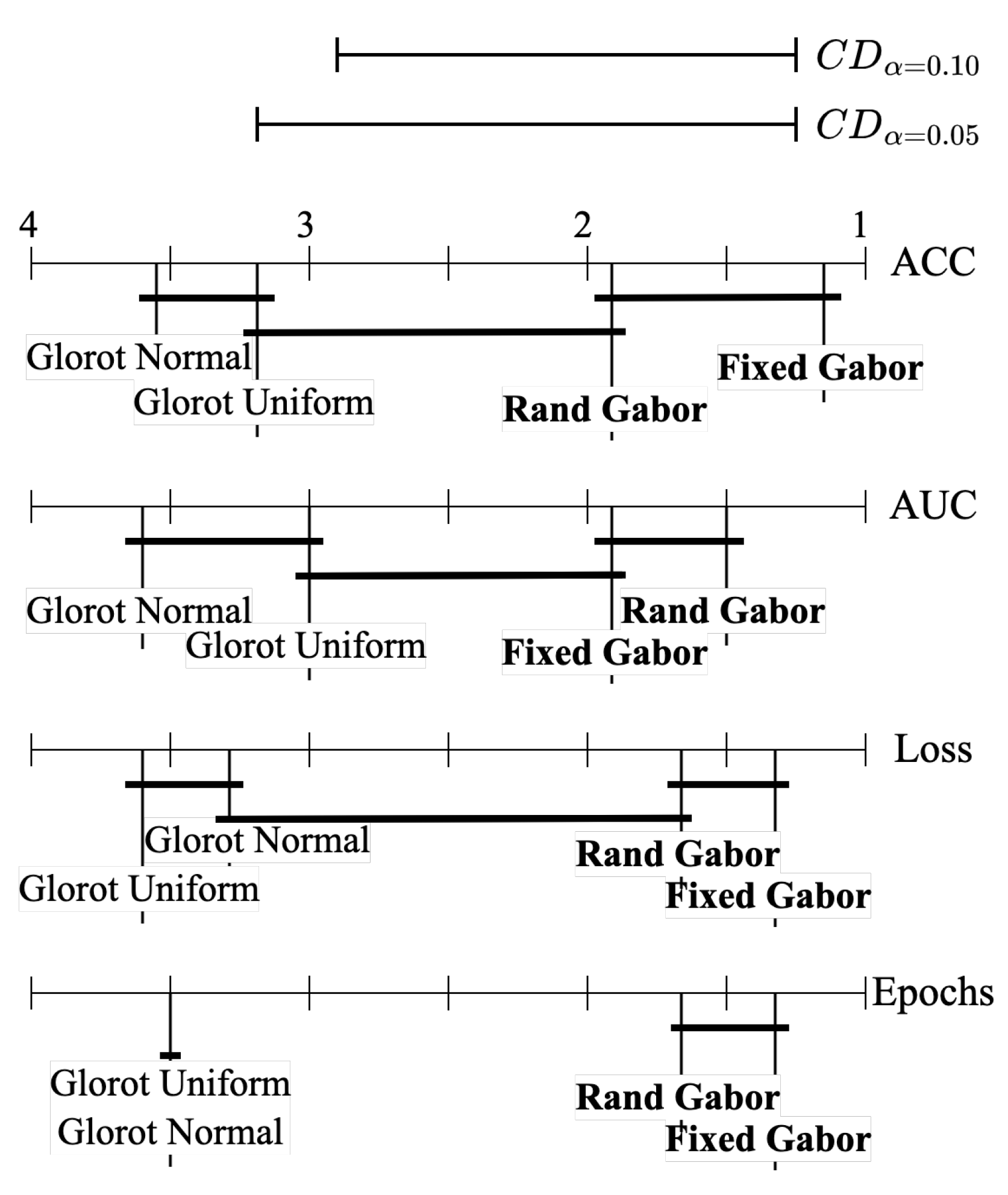
Appendix B. Statistical Analysis
For the statistical analysis that supports
Table 4, we performed the following:
The critical value at
is 5.417. We reject
with 99% confidence. The critical differences are:
Since the difference in rank between the randomized Gabor filter and the baseline Glorot normal filter is 1.83 and is less than the , we conclude that the Gabor filter is better. Similarly, since the difference in rank between the fixed Gabor filter and the baseline Glorot uniform filter is 2.17 and is less than the , we conclude that the Gabor filter is better.
For the statistical analysis that supports
Table 4, we performed the following:
The critical value at is 5.417. We reject with 99% confidence.
Since the difference in rank between the fixed Gabor filter and the baseline Glorot normal filter is 1.83 and is less than the , we conclude that the Gabor filter is better. Similarly, since the difference in rank between the random Gabor filter and the baseline Glorot uniform filter is 1.5 and is less than the , we conclude that the Gabor filter is better.
For the statistical analysis that supports
Table 5, we performed the following:
The critical value at is 5.417. We reject with 99% confidence.
Since the difference in rank between the fixed Gabor filter and the baseline Glorot normal filter is 2 and is less than the , we conclude that the Gabor filter is better. Similarly, since the difference in rank between the random Gabor filter and the baseline Glorot uniform filter is 2 and is less than the , we conclude that the Gabor filter is better.
For the statistical analysis that supports
Table 6, we performed the following:
The critical value at is 5.417. We reject with 99% confidence.
Since the difference in rank between the random Gabor filter and the baseline Glorot normal filter is 1.84 and is less than the , we conclude that the Gabor filter is better. Similarly, since the difference in rank between the fixed Gabor filter and the baseline Glorot uniform filter is 2.17 and is less than the , we conclude that the Gabor filter is better.
Appendix C. Additional Experiments
Table A1 and
Table A2 provide a comprehensive overview of the improvement in terms of the maximum accuracy and the AUC at the maximum accuracy for the Gabor-initialized CNN in comparison to traditional CNNs. This comparison is made under the constraint that the Gabor-initialized CNN is trained only up to the number of epochs where the traditional CNN reaches its maximum accuracy.
Table A3 and
Table A4 present a comparison of the minimum loss and number of epochs required to reach its minimum loss for the Gabor-initialized CNN in relation to the traditional CNN, with the constraint that the Gabor-initialized CNN is trained only up to the number of epochs where the traditional CNN reaches its maximum accuracy.
Table A5,
Table A6 and
Table A7 summarize the improvement in maximum accuracy, AUC at maximum accuracy, and minimum loss of the Gabor-initialized CNN in comparison to traditional CNNs under the constraint that the receptive filters of the Gabor-initialized CNN are frozen, while the filters in other layers are allowed to change.
Finally, the results of experiments conducted with different kernel sizes of the receptive layer of the CNN and image sizes of the datasets can be found in
Table A8,
Table A9,
Table A10,
Table A11,
Table A12,
Table A13,
Table A14,
Table A15,
Table A16,
Table A17,
Table A18,
Table A19,
Table A20,
Table A21,
Table A22,
Table A23,
Table A24 and
Table A25.
Table A1.
Improvement in maximum accuracy of epoch-constrained Gabor-initialized CNN with respect to traditional CNN when training period was constrained to maximum accuracy epoch of traditional CNN. Bold numbers indicate top results.
Table A1.
Improvement in maximum accuracy of epoch-constrained Gabor-initialized CNN with respect to traditional CNN when training period was constrained to maximum accuracy epoch of traditional CNN. Bold numbers indicate top results.
| Dataset | Base Maximum Accuracy | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.8839 | 0.004 | +0.0212 | 0.007 | +0.0253 | 0.006 |
| CIFAR-10 | 0.8024 | 0.004 | +0.0197 | 0.003 | +0.0212 | 0.005 |
| CIFAR-100 | 0.7132 | 0.003 | +0.0054 | 0.005 | +0.0053 | 0.005 |
| Caltech 256 | 0.5085 | 0.007 | +0.0131 | 0.008 | +0.0163 | 0.010 |
| Stanford Cars | 0.2326 | 0.070 | +0.1200 | 0.065 | +0.1576 | 0.068 |
| Tiny Imagenet | 0.5175 | 0.004 | +0.0128 | 0.003 | −0.0008 | 0.007 |
| Average | 0.6097 | 0.015 | +0.0320 | 0.015 | +0.0375 | 0.017 |
Table A2.
Improvement in AUC at maximum accuracy of epoch-constrained Gabor-initialized CNN with respect to traditional CNN when training period was constrained to maximum accuracy epoch of traditional CNN. Bold numbers indicate top results.
Table A2.
Improvement in AUC at maximum accuracy of epoch-constrained Gabor-initialized CNN with respect to traditional CNN when training period was constrained to maximum accuracy epoch of traditional CNN. Bold numbers indicate top results.
| Dataset | Base AUC | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.9515 | 0.003 | +0.0129 | 0.004 | +0.0164 | 0.004 |
| CIFAR-10 | 0.9719 | 0.001 | +0.0033 | 0.001 | +0.0026 | 0.001 |
| CIFAR-100 | 0.9621 | 0.002 | +0.0013 | 0.002 | +0.0022 | 0.002 |
| Caltech 256 | 0.8885 | 0.004 | +0.0086 | 0.004 | +0.0062 | 0.005 |
| Stanford Cars | 0.8077 | 0.026 | +0.0552 | 0.022 | +0.0645 | 0.026 |
| Tiny Imagenet | 0.9370 | 0.003 | +0.0023 | 0.004 | −0.0010 | 0.003 |
| Average | 0.9198 | 0.006 | +0.0134 | 0.006 | +0.0151 | 0.007 |
Table A3.
Improvement in minimum loss of Gabor-initialized CNN with respect to traditional CNN when training period was constrained to minimum loss epoch of traditional CNN. Bold numbers indicate top results.
Table A3.
Improvement in minimum loss of Gabor-initialized CNN with respect to traditional CNN when training period was constrained to minimum loss epoch of traditional CNN. Bold numbers indicate top results.
| Dataset | Base Minimum Loss | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.2960 | 0.012 | −0.0406 | 0.015 | −0.0553 | 0.013 |
| CIFAR-10 | 0.6555 | 0.013 | −0.0517 | 0.015 | −0.0567 | 0.013 |
| CIFAR-100 | 1.1823 | 0.020 | −0.0150 | 0.038 | −0.0192 | 0.029 |
| Caltech 256 | 2.6428 | 0.067 | −0.0908 | 0.038 | −0.0192 | 0.029 |
| Stanford Cars | 4.1857 | 0.356 | −0.6513 | 0.231 | −0.8913 | 0.264 |
| Tiny Imagenet | 2.7390 | 0.014 | −0.0522 | 0.024 | −0.0027 | 0.028 |
Table A4.
Improvement in minimum loss epoch of Gabor-initialized CNN with respect to traditional CNN when training period constrained to minimum loss epoch of traditional CNN. Bold numbers indicate top results.
Table A4.
Improvement in minimum loss epoch of Gabor-initialized CNN with respect to traditional CNN when training period constrained to minimum loss epoch of traditional CNN. Bold numbers indicate top results.
| Dataset | Base Epoch | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 70.6 | 13.5 | −7 | 5.4 | −14 | 9.8 |
| CIFAR-10 | 40.1 | 5.5 | −8.6 | 8.1 | −10 | 7.4 |
| CIFAR-100 | 70.2 | 6.5 | −6.2 | 3.3 | −8.8 | 7.7 |
| Caltech 256 | 42.1 | 5.1 | −3.5 | 2.7 | −5.2 | 3.5 |
| Stanford Cars | 74.0 | 14.9 | −5.1 | 4.4 | −6.4 | 3.9 |
| Tiny Imagenet | 32.2 | 4.6 | −5.2 | 5.6 | −5.9 | 6.1 |
Table A5.
Improvement in maximum accuracy of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
Table A5.
Improvement in maximum accuracy of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
| Dataset | Base Maximum Accuracy | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.8839 | 0.004 | +0.0029 | 0.009 | +0.0183 | 0.005 |
| CIFAR-10 | 0.8024 | 0.004 | +0.0086 | 0.005 | −0.0075 | 0.007 |
| CIFAR-100 | 0.7132 | 0.003 | +0.0022 | 0.004 | −0.0559 | 0.007 |
| Caltech 256 | 0.5085 | 0.007 | +0.0079 | 0.011 | +0.0012 | 0.012 |
| Stanford Cars | 0.2326 | 0.070 | +0.0924 | 0.096 | +0.1662 | 0.086 |
| Tiny Imagenet | 0.5175 | 0.004 | +0.0045 | 0.009 | −0.0391 | 0.004 |
| Average | 0.6097 | 0.015 | +0.0197 | 0.022 | +0.0139 | 0.020 |
Table A6.
Improvement in AUC of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
Table A6.
Improvement in AUC of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
| Dataset | Base AUC | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.9515 | 0.003 | +0.0020 | 0.006 | +0.0133 | 0.002 |
| CIFAR-10 | 0.9719 | 0.001 | +0.0012 | 0.001 | −0.0017 | 0.002 |
| CIFAR-100 | 0.9621 | 0.002 | −0.0003 | 0.003 | −0.0095 | 0.002 |
| Caltech 256 | 0.8885 | 0.004 | +0.0052 | 0.007 | +0.0048 | 0.006 |
| Stanford Cars | 0.8077 | 0.026 | +0.0408 | 0.035 | +0.0684 | 0.032 |
| Tiny Imagenet | 0.9370 | 0.003 | +0.0012 | 0.004 | −0.0081 | 0.003 |
| Average | 0.9198 | 0.006 | +0.0083 | 0.009 | +0.0112 | 0.008 |
Table A7.
Improvement in minimum loss of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
Table A7.
Improvement in minimum loss of Gabor-initialized CNN (frozen receptive convolutional layer variant) with respect to traditional CNN. Bold numbers indicate top results.
| Dataset | Base Minimum Loss | Random Gabor Filter | Repeated Gabor Filter |
|---|
| Mean | Stdev | Mean | Stdev | Mean | Stdev |
|---|
| Cats vs. Dogs | 0.2960 | 0.012 | −0.0100 | 0.018 | −0.0475 | 0.010 |
| CIFAR-10 | 0.6555 | 0.013 | −0.0352 | 0.019 | +0.0086 | 0.022 |
| CIFAR-100 | 1.1823 | 0.020 | −0.0099 | 0.035 | +0.2437 | 0.037 |
| Caltech 256 | 2.6428 | 0.067 | −0.0794 | 0.091 | −0.0466 | 0.068 |
| Stanford Cars | 4.1857 | 0.356 | −0.6217 | 0.502 | −1.0837 | 0.487 |
| Tiny Imagenet | 2.7390 | 0.014 | −0.240 | 0.027 | +0.1628 | 0.019 |
Table A8.
Improvement in maximum accuracy on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A8.
Improvement in maximum accuracy on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.8261 | 0.8303 | 0.8165 | 0.8143 | 0.8035 | 0.8037 | 0.7869 |
| Random Gabor () | −0.0202 | −0.0389 | −0.0114 | +0.0036 | +0.0120 | +0.0044 | +0.0094 |
| Repeated Gabor () | −0.0258 | −0.0174 | −0.0170 | −0.0120 | −0.0174 | −0.0020 | +0.0090 |
| 64 × 64 | Traditional CNN (Base) | 0.8015 | 0.8403 | 0.8381 | 0.8297 | 0.8425 | 0.8315 | 0.8279 |
| Random Gabor () | −0.0168 | +0.0038 | +0.0100 | +0.0132 | +0.0022 | +0.0128 | +0.0058 |
| Repeated Gabor () | +0.0126 | −0.0070 | +0.0204 | +0.0162 | +0.0044 | +0.0116 | +0.0180 |
| 128 × 128 | Traditional CNN (Base) | 0.8672 | 0.9026 | 0.8948 | 0.9022 | 0.8992 | 0.8804 | 0.8952 |
| Random Gabor () | +0.0062 | −0.0138 | −0.0022 | +0.0114 | +0.0150 | +0.0242 | +0.0150 |
| Repeated Gabor () | +0.0134 | +0.0120 | +0.0228 | +0.0144 | +0.0160 | +0.0341 | +0.0216 |
| 256 × 256 | Traditional CNN (Base) | 0.8932 | 0.8892 | 0.8926 | 0.8862 | 0.8924 | 0.8916 | 0.8870 |
| Random Gabor () | −0.0170 | −0.0058 | −0.0078 | +0.0076 | +0.0156 | +0.0214 | +0.0142 |
| Repeated Gabor () | −0.0214 | +0.0120 | +0.0142 | +0.0264 | +0.0136 | +0.0170 | +0.0240 |
Table A9.
Improvement in AUC at maximum accuracy on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A9.
Improvement in AUC at maximum accuracy on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.9028 | 0.9092 | 0.8947 | 0.8946 | 0.8789 | 0.8809 | 0.8650 |
| Random Gabor () | −0.0161 | −0.0391 | −0.0076 | −0.0012 | +0.0137 | +0.0024 | +0.0107 |
| Repeated Gabor () | −0.0208 | −0.0149 | −0.0110 | −0.0081 | −0.0110 | +0.0008 | +0.0095 |
| 64 × 64 | Traditional CNN (Base) | 0.8900 | 0.9232 | 0.9213 | 0.9077 | 0.9214 | 0.9127 | 0.9097 |
| Random Gabor () | −0.0179 | +0.0027 | +0.0053 | +0.0103 | +0.0022 | +0.0113 | +0.0081 |
| Repeated Gabor () | +0.0090 | −0.0066 | +0.0127 | +0.0146 | +0.0037 | +0.0116 | +0.0139 |
| 128 × 128 | Traditional CNN (Base) | 0.9461 | 0.9690 | 0.9641 | 0.9670 | 0.9651 | 0.9557 | 0.9638 |
| Random Gabor () | +0.0032 | −0.0094 | −0.0028 | +0.0071 | +0.0093 | +0.0148 | +0.0094 |
| Repeated Gabor () | +0.0068 | +0.0044 | +0.0118 | +0.0089 | +0.0097 | +0.0188 | +0.0103 |
| 256 × 256 | Traditional CNN (Base) | 0.9586 | 0.9565 | 0.9602 | 0.9531 | 0.9570 | 0.9565 | 0.9541 |
| Random Gabor () | −0.0099 | −0.0016 | −0.0056 | +0.0072 | +0.0086 | +0.0139 | +0.0087 |
| Repeated Gabor () | −0.0129 | +0.0054 | +0.0086 | +0.0178 | +0.0085 | +0.0121 | +0.0141 |
Table A10.
Improvement in minimum loss on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A10.
Improvement in minimum loss on Cats vs. Dogs dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.7039 | 1.0208 | 1.3793 | 0.8991 | 0.8574 | 0.9765 | 1.0263 |
| Random Gabor () | −0.0630 | −0.3510 | −0.7026 | −0.2184 | −0.1522 | −0.1801 | +0.1596 |
| Repeated Gabor () | −0.0696 | −0.3772 | −0.6521 | −0.2515 | −0.1687 | −0.1927 | −0.1891 |
| 64 × 64 | Traditional CNN (Base) | 0.8884 | 0.9717 | 0.8448 | 0.9905 | 1.2597 | 1.3066 | 1.4466 |
| Random Gabor () | −0.1744 | −0.2768 | −0.1251 | −0.3048 | −0.5674 | −0.4398 | −0.6611 |
| Repeated Gabor () | −0.2145 | −0.2895 | −0.1689 | −0.3397 | −0.5842 | −0.6421 | −0.6685 |
| 128 × 128 | Traditional CNN (Base) | 1.0480 | 0.8813 | 1.1060 | 0.7639 | 0.8840 | 1.0305 | 1.3318 |
| Random Gabor () | −0.3270 | −0.0753 | −0.3405 | −0.0858 | −0.1525 | −0.3765 | −0.5583 |
| Repeated Gabor () | −0.4209 | −0.2144 | −0.4912 | −0.2167 | −0.2957 | −0.3765 | −0.7697 |
| 256 × 256 | Traditional CNN (Base) | 1.1261 | 0.6374 | 0.7055 | 0.7233 | 1.1426 | 0.8459 | 0.8025 |
| Random Gabor () | −0.4575 | −0.0646 | −0.0882 | −0.0916 | −0.5824 | −0.2015 | −0.2225 |
| Repeated Gabor () | −0.4516 | −0.0561 | +0.0252 | −0.0221 | −0.5944 | −0.0720 | −0.1276 |
Table A11.
Improvement in maximum accuracy on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A11.
Improvement in maximum accuracy on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.7818 | 0.7896 | 0.7929 | 0.7712 | 0.7713 | 0.7744 | 0.7654 |
| Random Gabor () | −0.0049 | −0.0090 | −0.0122 | +0.0143 | +0.0124 | +0.0089 | +0.0101 |
| Repeated Gabor () | −0.0037 | −0.0028 | −0.0087 | +0.0283 | +0.0164 | +0.0234 | +0.0155 |
| 64 × 64 | Traditional CNN (Base) | 0.7086 | 0.7257 | 0.7199 | 0.7207 | 0.7115 | 0.7203 | 0.7219 |
| Random Gabor () | −0.0076 | −0.0129 | +0.0077 | +0.0143 | +0.0279 | +0.0393 | +0.0403 |
| Repeated Gabor () | −0.0098 | −0.0107 | +0.0206 | +0.0348 | +0.0466 | +0.0416 | +0.0394 |
| 128 × 128 | Traditional CNN (Base) | 0.7936 | 0.7988 | 0.8007 | 0.7930 | 0.7989 | 0.8004 | 0.8067 |
| Random Gabor () | +0.0086 | +0.0073 | +0.0146 | +0.0258 | +0.0228 | +0.0271 | +0.0177 |
| Repeated Gabor () | +0.0093 | +0.0113 | +0.0134 | +0.0273 | +0.0281 | +0.0199 | +0.0142 |
Table A12.
Improvement in AUC at maximum accuracy on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A12.
Improvement in AUC at maximum accuracy on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.9759 | 0.9773 | 0.9777 | 0.9744 | 0.9734 | 0.9737 | 0.9722 |
| Random Gabor () | −0.0011 | −0.0011 | −0.0027 | +0.0018 | +0.0023 | +0.0019 | +0.0018 |
| Repeated Gabor () | −0.0010 | −0.0006 | −0.0019 | +0.0036 | +0.0037 | +0.0034 | +0.0021 |
| 64 × 64 | Traditional CNN (Base) | 0.9575 | 0.9615 | 0.9606 | 0.9614 | 0.9598 | 0.9621 | 0.9623 |
| Random Gabor () | −0.0026 | −0.0019 | +0.0020 | +0.0032 | +0.0069 | +0.0073 | +0.0081 |
| Repeated Gabor () | −0.0018 | −0.0006 | +0.0050 | +0.0080 | +0.0104 | +0.0086 | +0.0076 |
| 128 × 128 | Traditional CNN (Base) | 0.9730 | 0.9724 | 0.9734 | 0.9725 | 0.9737 | 0.9733 | 0.9746 |
| Random Gabor () | +0.0008 | +0.0017 | +0.0011 | +0.0023 | +0.0023 | +0.0047 | +0.0033 |
| Repeated Gabor () | +0.0005 | +0.0029 | +0.0021 | +0.0044 | +0.0031 | +0.0023 | +0.0015 |
Table A13.
Improvement in minimum loss on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A13.
Improvement in minimum loss on CIFAR-10 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 1.4764 | 1.5682 | 1.9694 | 1.9144 | 1.6672 | 1.5935 | 2.1591 |
| Random Gabor () | −0.1391 | −0.2193 | −0.5082 | −0.5611 | −0.1535 | −0.1015 | −0.6806 |
| Repeated Gabor () | −0.0672 | −0.1756 | −0.6604 | −0.6354 | −0.0718 | −0.1837 | −0.8144 |
| 64 × 64 | Traditional CNN (Base) | 1.6460 | 1.9160 | 2.3001 | 1.6342 | 1.6378 | 1.8921 | 2.0575 |
| Random Gabor () | −0.0266 | −0.3585 | −0.6622 | −0.0978 | −0.1412 | −0.2156 | −0.4911 |
| Repeated Gabor () | +0.0670 | −0.3258 | −0.7804 | −0.0624 | −0.1956 | +0.3132 | −0.3499 |
| 128 × 128 | Traditional CNN (Base) | 1.4920 | 2.2684 | 1.2744 | 1.3457 | 1.3687 | 1.7287 | 1.4233 |
| Random Gabor () | −0.2609 | −1.1010 | −0.0477 | −0.1184 | −0.1824 | −0.3236 | −0.0045 |
| Repeated Gabor () | −0.2781 | −1.0944 | +0.2863 | −0.1774 | −0.2432 | −0.1496 | −0.0947 |
Table A14.
Improvement in maximum accuracy on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A14.
Improvement in maximum accuracy on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.5842 | 0.5740 | 0.5854 | 0.5488 | 0.5605 | 0.5678 | 0.5590 |
| Random Gabor () | −0.0237 | +0.0114 | −0.0281 | +0.0192 | +0.0201 | −0.0139 | +0.0081 |
| Repeated Gabor () | −0.0189 | +0.0003 | −0.0021 | +0.0023 | +0.0004 | −0.0086 | −0.0029 |
| 64 × 64 | Traditional CNN (Base) | 0.6803 | 0.6869 | 0.6807 | 0.6866 | 0.6898 | 0.6886 | 0.6867 |
| Random Gabor () | +0.0007 | +0.0025 | −0.0007 | −0.0015 | −0.0087 | −0.0094 | −0.0015 |
| Repeated Gabor () | +0.0039 | +0.0018 | +0.0027 | −0.0028 | −0.0080 | −0.0010 | −0.0006 |
| 128 × 128 | Traditional CNN (Base) | 0.7144 | 0.7065 | 0.7162 | 0.7164 | 0.7138 | 0.7123 | 0.7112 |
| Random Gabor () | −0.0060 | +0.0037 | +0.0018 | +0.0002 | +0.0012 | +0.0073 | 0.0059 |
| Repeated Gabor () | +0.0017 | +0.0106 | −0.0070 | −0.0041 | +0.0040 | +0.0086 | +0.0145 |
Table A15.
Improvement in AUC at maximum accuracy on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A15.
Improvement in AUC at maximum accuracy on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.9550 | 0.9503 | 0.9530 | 0.9525 | 0.9511 | 0.9514 | 0.9512 |
| Random Gabor () | −0.0025 | +0.0035 | +0.0003 | −0.0028 | +0.0023 | −0.0007 | −0.0004 |
| Repeated Gabor () | −0.0036 | +0.0018 | −0.0006 | +0.0025 | −0.0019 | +0.0020 | −0.0006 |
| 64 × 64 | Traditional CNN (Base) | 0.9636 | 0.9652 | 0.9659 | 0.9628 | 0.9655 | 0.9643 | 0.9652 |
| Random Gabor () | +0.0008 | +0.0002 | −0.0009 | +0.0030 | −0.0006 | +0.0025 | +0.0007 |
| Repeated Gabor () | −0.0004 | −0.0004 | −0.0007 | +0.0027 | −0.0012 | +0.0021 | +0.0006 |
| 128 × 128 | Traditional CNN (Base) | 0.9694 | 0.9686 | 0.9684 | 0.9690 | 0.9682 | 0.9691 | 0.9682 |
| Random Gabor () | +0.0008 | +0.0002 | +0.0010 | +0.0021 | +0.0028 | +0.0000 | +0.0016 |
| Repeated Gabor () | +0.0002 | +0.0011 | +0.0030 | +0.0013 | +0.0010 | +0.0007 | +0.0029 |
Table A16.
Improvement in minimum loss on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A16.
Improvement in minimum loss on CIFAR-100 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 4.3399 | 4.5608 | 4.0880 | 5.9439 | 4.1416 | 4.2599 | 5.1038 |
| Random Gabor () | +0.1598 | −0.6657 | −0.0989 | −1.7213 | +0.1809 | −0.2785 | +2.1429 |
| Repeated Gabor () | +0.4380 | −0.4634 | +0.7734 | −1.5532 | +0.5421 | +0.2966 | −1.1574 |
| 64 × 64 | Traditional CNN (Base) | 3.6348 | 3.7467 | 3.5715 | 3.8046 | 3.8158 | 4.0575 | 4.0832 |
| Random Gabor () | +0.1774 | −0.0744 | +0.0242 | −0.3521 | +0.2289 | +0.1263 | +0.2179 |
| Repeated Gabor () | +0.5789 | +0.3015 | +1.7995 | −0.0274 | +0.1685 | +0.8609 | +0.1275 |
| 128 × 128 | Traditional CNN (Base) | 3.4936 | 4.1385 | 4.1666 | 5.1151 | 3.7694 | 3.5885 | 4.0887 |
| Random Gabor () | +0.2320 | −0.2233 | −0.6036 | −1.3428 | +0.9635 | +0.0513 | −0.0090 |
| Repeated Gabor () | +0.4857 | −0.2240 | −0.1239 | −0.6645 | +0.0184 | −0.0016 | +0.1811 |
Table A17.
Improvement in maximum accuracy on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A17.
Improvement in maximum accuracy on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.3086 | 0.3084 | 0.3022 | 0.3096 | 0.3061 | 0.3099 | 0.2978 |
| Random Gabor () | −0.0007 | +0.0002 | +0.0195 | +0.0106 | +0.0064 | +0.0010 | +0.0008 |
| Repeated Gabor () | +0.0123 | +0.0020 | +0.0146 | +0.0115 | +0.0056 | +0.0008 | −0.0005 |
| 64 × 64 | Traditional CNN (Base) | 0.4296 | 0.4388 | 0.4375 | 0.4404 | 0.4403 | 0.4380 | 0.4313 |
| Random Gabor () | −0.0090 | −0.0028 | +0.0113 | +0.0025 | −0.0116 | +0.0119 | +0.0214 |
| Repeated Gabor () | +0.0039 | −0.0054 | +0.0082 | +0.0072 | +0.0113 | +0.0059 | +0.0059 |
| 128 × 128 | Traditional CNN (Base) | 0.5028 | 0.5025 | 0.5350 | 0.5200 | 0.5113 | 0.5195 | 0.5092 |
| Random Gabor () | +0.0151 | +0.0208 | +0.0008 | +0.0026 | +0.0211 | +0.0061 | +0.0041 |
| Repeated Gabor () | +0.0195 | +0.0128 | −0.0043 | +0.0036 | +0.0188 | +0.0051 | +0.0198 |
Table A18.
Improvement in AUC at maximum accuracy on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A18.
Improvement in AUC at maximum accuracy on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.8481 | 0.8419 | 0.8513 | 0.8574 | 0.8454 | 0.8474 | 0.8392 |
| Random Gabor () | −0.0021 | +0.0162 | +0.0019 | −0.0027 | +0.0050 | +0.0003 | +0.0057 |
| Repeated Gabor () | +0.0055 | +0.0095 | −0.0030 | +0.0005 | +0.0131 | +0.0037 | +0.0069 |
| 64 × 64 | Traditional CNN (Base) | 0.8741 | 0.8853 | 0.8846 | 0.8853 | 0.8837 | 0.8848 | 0.8840 |
| Random Gabor () | +0.0026 | −0.0037 | +0.0036 | +0.0033 | −0.0010 | +0.0060 | −0.0001 |
| Repeated Gabor () | +0.0037 | −0.0028 | −0.0007 | +0.0050 | +0.0114 | +0.0034 | +0.0041 |
| 128 × 128 | Traditional CNN (Base) | 0.9034 | 0.9097 | 0.9062 | 0.9036 | 0.9046 | 0.9049 | 0.9021 |
| Random Gabor () | +0.0053 | −0.0004 | +0.0072 | +0.0020 | +0.0006 | −0.0059 | +0.0036 |
| Repeated Gabor () | +0.0050 | +0.0002 | +0.0010 | +0.0028 | +0.0045 | +0.0044 | +0.0054 |
Table A19.
Improvement in minimum loss on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A19.
Improvement in minimum loss on Caltech 256 dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 8.1892 | 6.2550 | 7.0410 | 7.8705 | 8.5046 | 11.1519 | 5.8391 |
| Random Gabor () | −2.5809 | +0.6026 | −1.6581 | −2.3008 | +0.8493 | −0.4026 | −0.3982 |
| Repeated Gabor () | −1.6821 | +1.8756 | −1.0074 | −1.6438 | −0.5016 | −5.2436 | +2.1425 |
| 64 × 64 | Traditional CNN (Base) | 6.3774 | 8.1425 | 6.8721 | 6.7314 | 7.0304 | 8.6386 | 5.2090 |
| Random Gabor () | −0.8742 | −3.0356 | −1.2754 | −1.3800 | −1.0103 | −2.7627 | +0.8800 |
| Repeated Gabor () | −1.1548 | −2.6945 | +3.0506 | −0.1708 | +5.0498 | −2.1193 | +0.7651 |
| 128 × 128 | Traditional CNN (Base) | 4.9090 | 5.1978 | 13.0624 | 6.8160 | 6.3426 | 7.1236 | 7.1915 |
| Random Gabor () | +0.3547 | +0.1951 | −8.0269 | −1.6014 | −1.3128 | −1.7678 | −1.8235 |
| Repeated Gabor () | +0.7467 | +0.3598 | −7.7013 | −0.7981 | −0.6349 | +1.1454 | −1.4903 |
Table A20.
Improvement in maximum accuracy on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A20.
Improvement in maximum accuracy on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.0493 | 0.0426 | 0.0442 | 0.0425 | 0.0304 | 0.0334 | 0.0300 |
| Random Gabor () | −0.0088 | +0.0090 | −0.0002 | +0.0060 | +0.0133 | +0.0076 | +0.0009 |
| Repeated Gabor () | +0.0051 | +0.0024 | +0.0004 | +0.0059 | +0.0152 | +0.0115 | +0.0139 |
| 64 × 64 | Traditional CNN (Base) | 0.1774 | 0.1602 | 0.1498 | 0.1350 | 0.1386 | 0.0818 | 0.1143 |
| Random Gabor () | −0.0330 | +0.0081 | +0.0015 | +0.0019 | −0.0162 | +0.0436 | −0.0009 |
| Repeated Gabor () | −0.0339 | +0.0117 | +0.0326 | +0.0281 | −0.0092 | +0.0524 | +0.0410 |
| 128 × 128 | Traditional CNN (Base) | 0.4103 | 0.3879 | 0.4180 | 0.3598 | 0.3010 | 0.3102 | 0.3517 |
| Random Gabor () | −0.0151 | +0.0396 | +0.0157 | +0.0802 | +0.1398 | +0.1930 | +0.0600 |
| Repeated Gabor () | −0.0818 | +0.0274 | +0.0005 | +0.0029 | +0.1313 | +0.0788 | +0.0648 |
Table A21.
Improvement in AUC at maximum accuracy on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A21.
Improvement in AUC at maximum accuracy on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.7107 | 0.6970 | 0.7114 | 0.6907 | 0.6290 | 0.6427 | 0.6325 |
| Random Gabor () | −0.0198 | +0.0019 | −0.0198 | +0.0009 | +0.0526 | +0.0292 | +0.0041 |
| Repeated Gabor () | +0.0111 | −0.0038 | −0.0106 | +0.0173 | +0.0705 | +0.0448 | +0.0568 |
| 64 × 64 | Traditional CNN (Base) | 0.8211 | 0.8046 | 0.7911 | 0.7815 | 0.7713 | 0.7255 | 0.7472 |
| Random Gabor () | −0.0173 | −0.0063 | +0.0018 | +0.0030 | −0.0056 | +0.0358 | +0.0146 |
| Repeated Gabor () | −0.0150 | −0.0046 | +0.0154 | +0.0165 | +0.0045 | +0.0528 | +0.0388 |
| 128 × 128 | Traditional CNN (Base) | 0.8736 | 0.8831 | 0.8723 | 0.8808 | 0.8369 | 0.8344 | 0.8811 |
| Random Gabor () | +0.0020 | +0.0020 | +0.0180 | +0.0033 | +0.0455 | +0.0458 | +0.0032 |
| Repeated Gabor () | +0.0063 | +0.0017 | +0.0028 | +0.0030 | +0.0515 | +0.0278 | +0.0035 |
Table A22.
Improvement in minimum loss on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A22.
Improvement in minimum loss on Stanford Cars dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 7.3203 | 47.5599 | 8.8750 | 9.2702 | 22.8231 | 7.1648 | 9.1182 |
| Random Gabor () | +12.3424 | −37.8715 | +3.6937 | +3.4808 | −15.7108 | +0.3171 | +0.4810 |
| Repeated Gabor () | +7.1468 | −37.3148 | −2.6179 | +6.2107 | −4.7338 | +5.3186 | +7.1548 |
| 64 × 64 | Traditional CNN (Base) | 24.1874 | 7.3460 | 14.2081 | 10.4780 | 16.0974 | 17.0614 | 20.6991 |
| Random Gabor () | −13.0682 | +1.0896 | −6.3144 | +1.3075 | −3.0181 | −4.1803 | −0.5565 |
| Repeated Gabor () | −16.0293 | +13.3526 | +13.5375 | +2.7611 | −1.1857 | −0.2307 | −3.6890 |
| 128 × 128 | Traditional CNN (Base) | 18.8136 | 36.2230 | 18.1727 | 6.6971 | 6.5915 | 73.8066 | 6.7081 |
| Random Gabor () | −1.3699 | −26.1808 | −9.9487 | +9.0980 | +4.3474 | −66.8044 | +7.0920 |
| Repeated Gabor () | −4.3315 | −23.0504 | −9.2398 | +4.6752 | +34.7256 | −62.0934 | +4.2712 |
Table A23.
Improvement in maximum accuracy on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A23.
Improvement in maximum accuracy on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.3921 | 0.3950 | 0.3832 | 0.3712 | 0.3671 | 0.3649 | 0.3543 |
| Random Gabor () | −0.0077 | −0.0029 | −0.0419 | −0.0223 | −0.0294 | −0.0340 | −0.0083 |
| Repeated Gabor () | −0.0050 | −0.0465 | −0.0462 | −0.0453 | −0.0401 | −0.0612 | −0.0410 |
| 64 × 64 | Traditional CNN (Base) | 0.4806 | 0.4824 | 0.4739 | 0.4699 | 0.4659 | 0.4662 | 0.4562 |
| Random Gabor () | +0.0102 | −0.0021 | −0.0041 | −0.0072 | −0.0102 | +0.0002 | +0.0152 |
| Repeated Gabor () | −0.0037 | −0.0390 | −0.0186 | +0.0004 | −0.0244 | −0.0229 | −0.0021 |
| 128 × 128 | Traditional CNN (Base) | 0.5199 | 0.5233 | 0.5241 | 0.5216 | 0.5229 | 0.5218 | 0.5104 |
| Random Gabor () | +0.0113 | +0.0056 | +0.0081 | −0.0031 | −0.0018 | +0.0056 | +0.0170 |
| Repeated Gabor () | −0.0066 | −0.0153 | −0.0411 | −0.0126 | −0.0142 | −0.0099 | +0.0060 |
Table A24.
Improvement in AUC at maximum accuracy on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A24.
Improvement in AUC at maximum accuracy on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 0.9109 | 0.9113 | 0.9062 | 0.9056 | 0.9011 | 0.8991 | 0.8979 |
| Random Gabor () | −0.0002 | −0.0054 | −0.0118 | −0.0109 | −0.0079 | −0.0098 | −0.0006 |
| Repeated Gabor () | −0.0038 | −0.0181 | −0.0082 | −0.0163 | −0.0103 | −0.0172 | −0.0175 |
| 64 × 64 | Traditional CNN (Base) | 0.9361 | 0.9319 | 0.9333 | 0.9312 | 0.9308 | 0.9294 | 0.9262 |
| Random Gabor () | −0.0031 | +0.0008 | −0.0026 | +0.0002 | −0.0033 | −0.0006 | +0.0037 |
| Repeated Gabor () | −0.0093 | −0.0050 | −0.0094 | −0.0021 | −0.0039 | −0.0078 | −0.0018 |
| 128 × 128 | Traditional CNN (Base) | 0.9435 | 0.9418 | 0.9438 | 0.9432 | 0.9439 | 0.9428 | 0.9427 |
| Random Gabor () | −0.0006 | +0.0011 | −0.0013 | −0.0017 | −0.0014 | −0.0009 | +0.0013 |
| Repeated Gabor () | −0.0065 | −0.0068 | −0.0091 | −0.0089 | −0.0061 | −0.0056 | −0.0023 |
Table A25.
Improvement in minimum loss on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
Table A25.
Improvement in minimum loss on Tiny Imagenet dataset with different kernel sizes and image sizes. Bold numbers indicate top results.
| Image Size | Gabor Configuration | Kernel Size |
|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | 13 × 13 | 15 × 15 |
|---|
| 32 × 32 | Traditional CNN (Base) | 5.2912 | 5.2273 | 5.2322 | 5.1488 | 5.1689 | 5.2050 | 5.1729 |
| Random Gabor () | −0.2901 | −0.2618 | −0.2595 | −0.2248 | −0.1753 | −0.1808 | −0.1660 |
| Repeated Gabor () | −0.0636 | −0.0202 | −0.0505 | −0.0025 | −0.0429 | −0.0107 | −0.0384 |
| 64 × 64 | Traditional CNN (Base) | 5.1014 | 5.1428 | 5.1198 | 5.1246 | 5.0847 | 5.1234 | 5.0616 |
| Random Gabor () | −0.2692 | −0.2719 | −0.2538 | −0.2102 | −0.2546 | −0.1730 | −0.1027 |
| Repeated Gabor () | +0.1317 | +0.0625 | −0.0146 | −0.0464 | +0.0509 | −0.0955 | −0.0103 |
| 128 × 128 | Traditional CNN (Base) | 5.0659 | 5.0616 | 5.0584 | 5.0257 | 5.0092 | 5.0673 | 5.2985 |
| Random Gabor () | −0.2046 | −0.2492 | −0.3288 | −0.1116 | +0.0950 | −0.0409 | −0.5205 |
| Repeated Gabor () | +0.1017 | +0.0927 | +0.0865 | +0.0545 | +0.0739 | −0.0492 | −0.3941 |