Enhanced Grey Wolf Optimization Algorithm for Mobile Robot Path Planning
Abstract
:1. Introduction
2. Methods
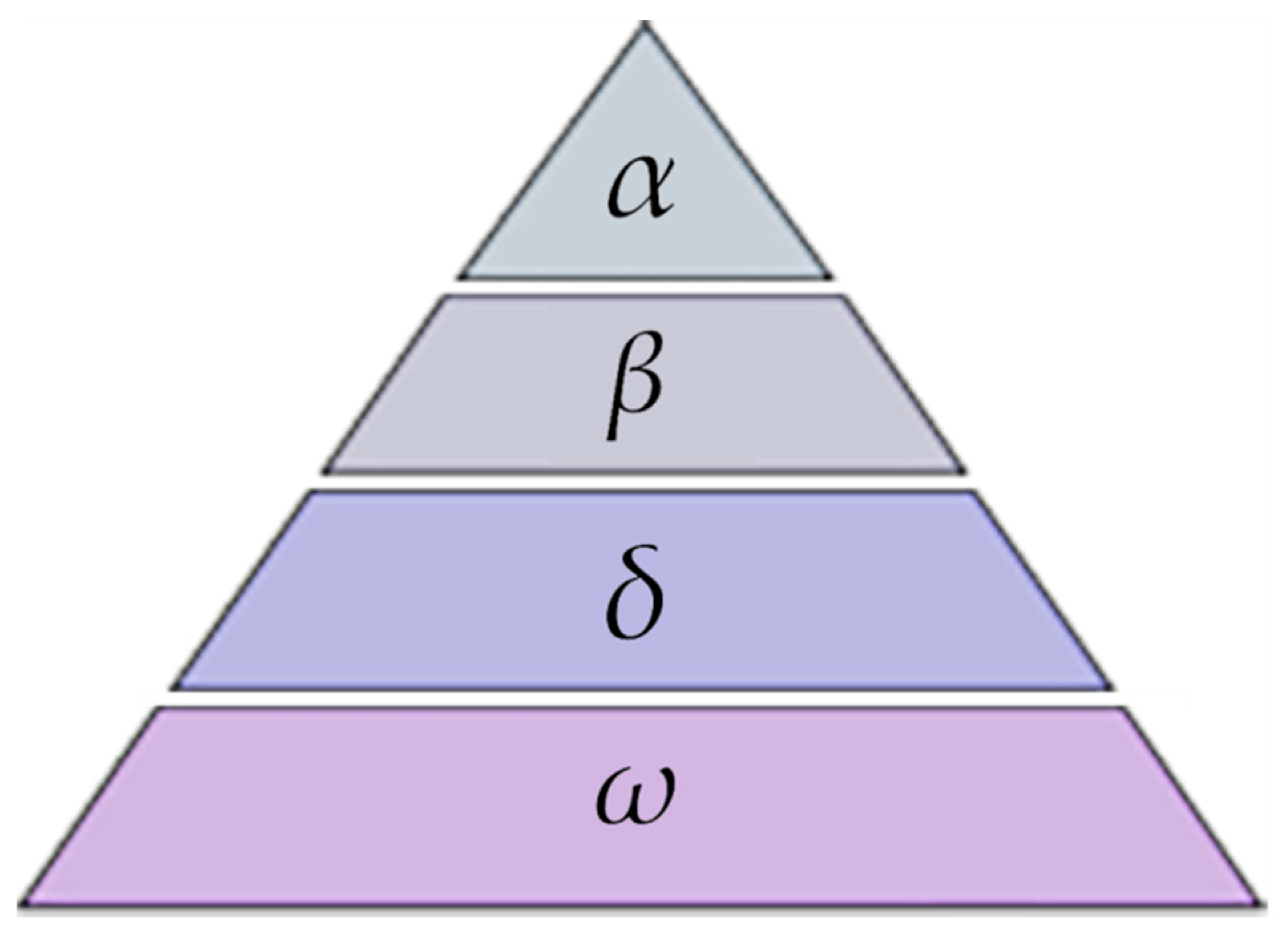
2.1. Grey Wolf Optimization (GWO) Algorithm
2.2. Hybrid Improved Grey Wolf Optimization (HI-GWO) Algorithm
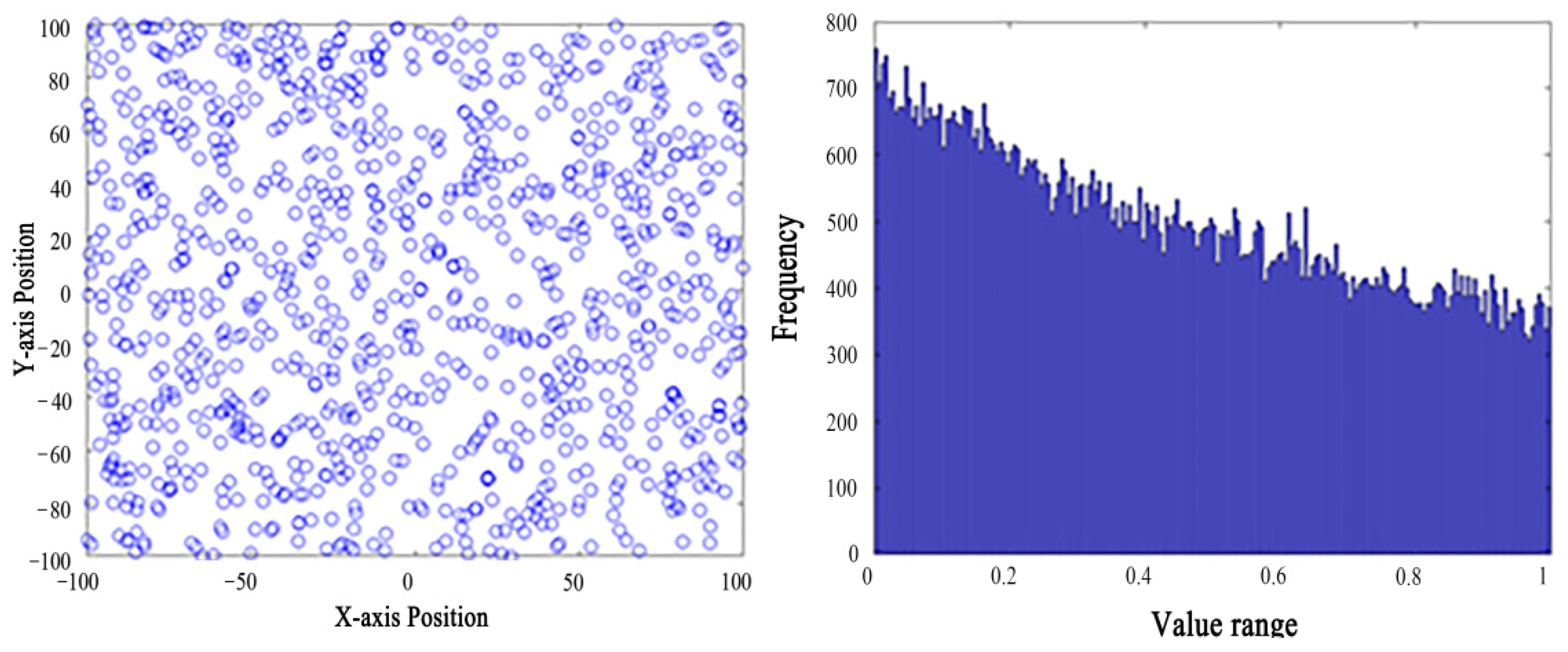
2.2.1. Population Initialization Based on Gauss Mapping
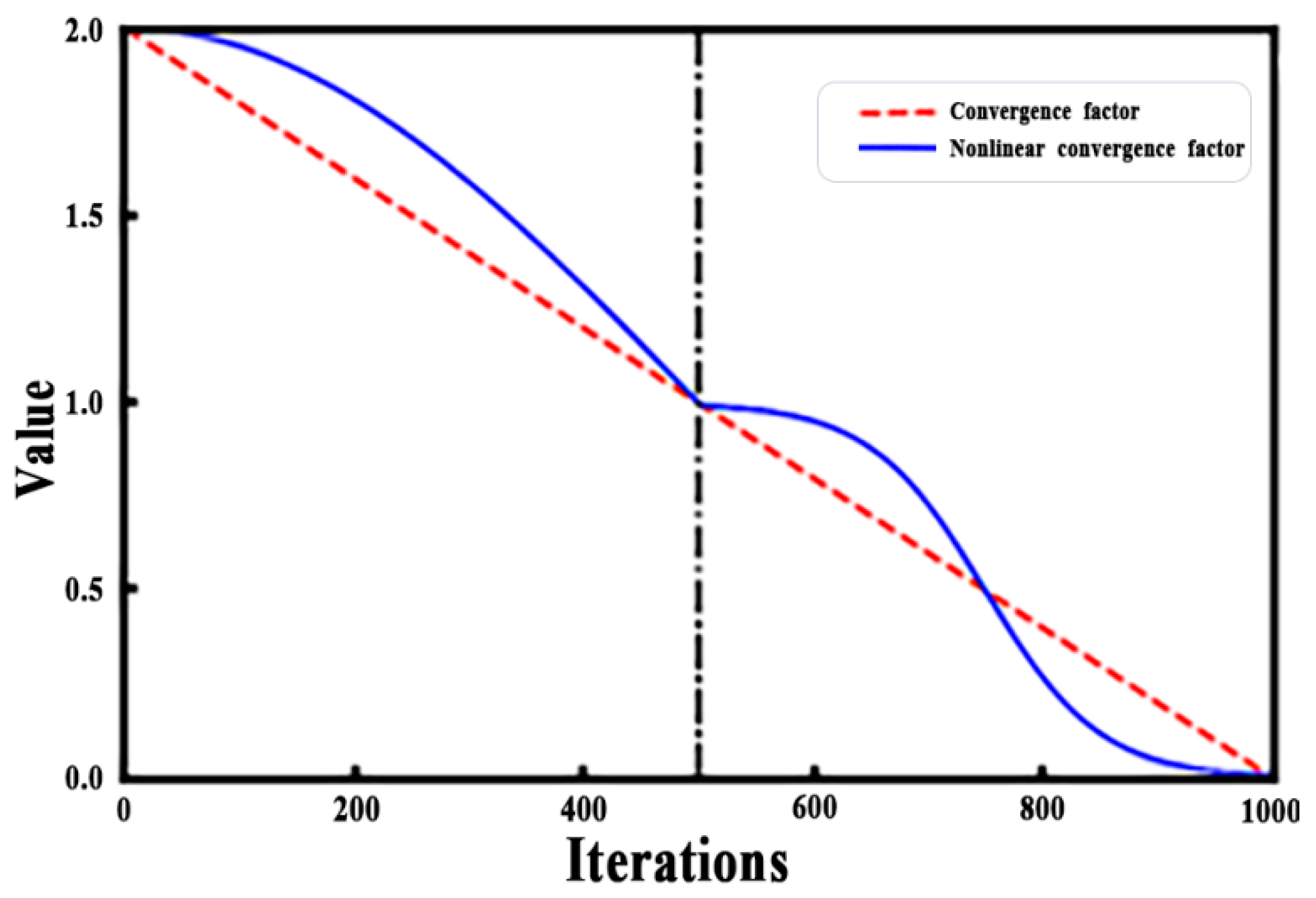
2.2.2. Nonlinear Convergence Factor
2.2.3. Improve the Levy Flight Strategy
2.2.4. Golden Sine Algorithm
2.2.5. Dynamic Position Update
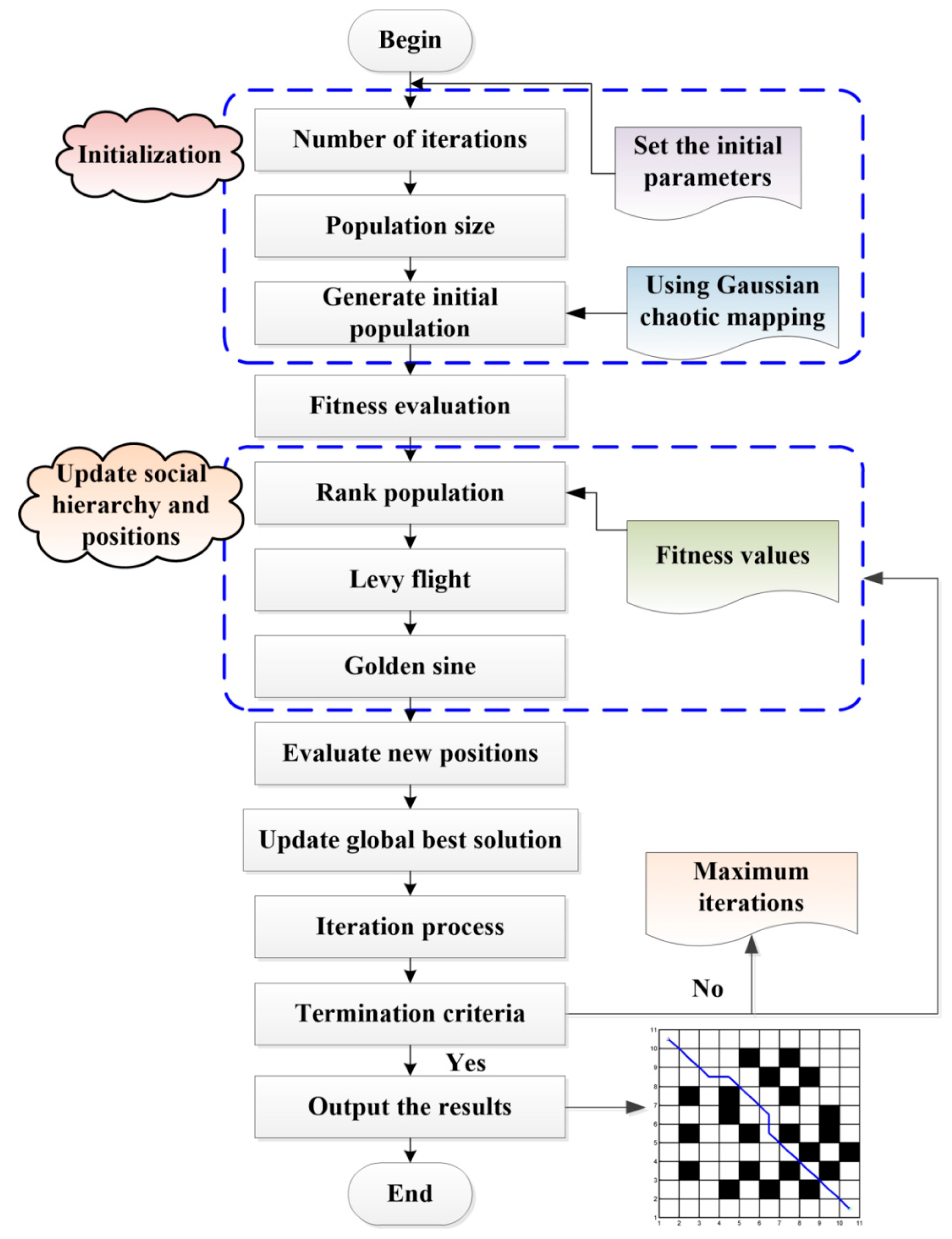
2.3. Implementation Steps of the Proposed Algorithm
- Step 1:
- Initialization. Set the number of iterations, population size, and other relevant parameters. Generate the initial population using Gaussian chaotic mapping to enhance population diversity.
- Step 2:
- Fitness evaluation. Calculate the fitness value for each individual as a measure of the solution quality.
- Step 3:
- Update social hierarchy and positions. Rank the population based on fitness values to establish the social hierarchy within the grey wolf pack. Higher-ranked wolves are more likely to become leaders, while lower-ranked ones play subordinate roles. Introduce Levy flight and sine algorithm to update the positions of each individual. Levy flight allows for longer jumps, exploring distant areas to enhance global search capability. The sine algorithm guides the search towards the most promising regions, improving solution accuracy and search speed.
- Step 4:
- Evaluate new positions. Compute the fitness value for each individual at their updated positions.
- Step 5:
- Update the global best solution. Update the global best solution based on the current best solution and its fitness value.
- Step 6:
- Termination criteria. Check if the termination criteria, such as maximum iterations or fitness threshold, are met.
- Step 7:
- Iteration process. If the termination criteria are not met, repeat steps 3 to 6. Continuously update individuals’ positions using the Levy flight and sine algorithm and calculate their fitness values.
- Step 8:
- Output the result. Output the obtained final optimal solution as the solution for mobile robot path planning.
3. Results and Discussion
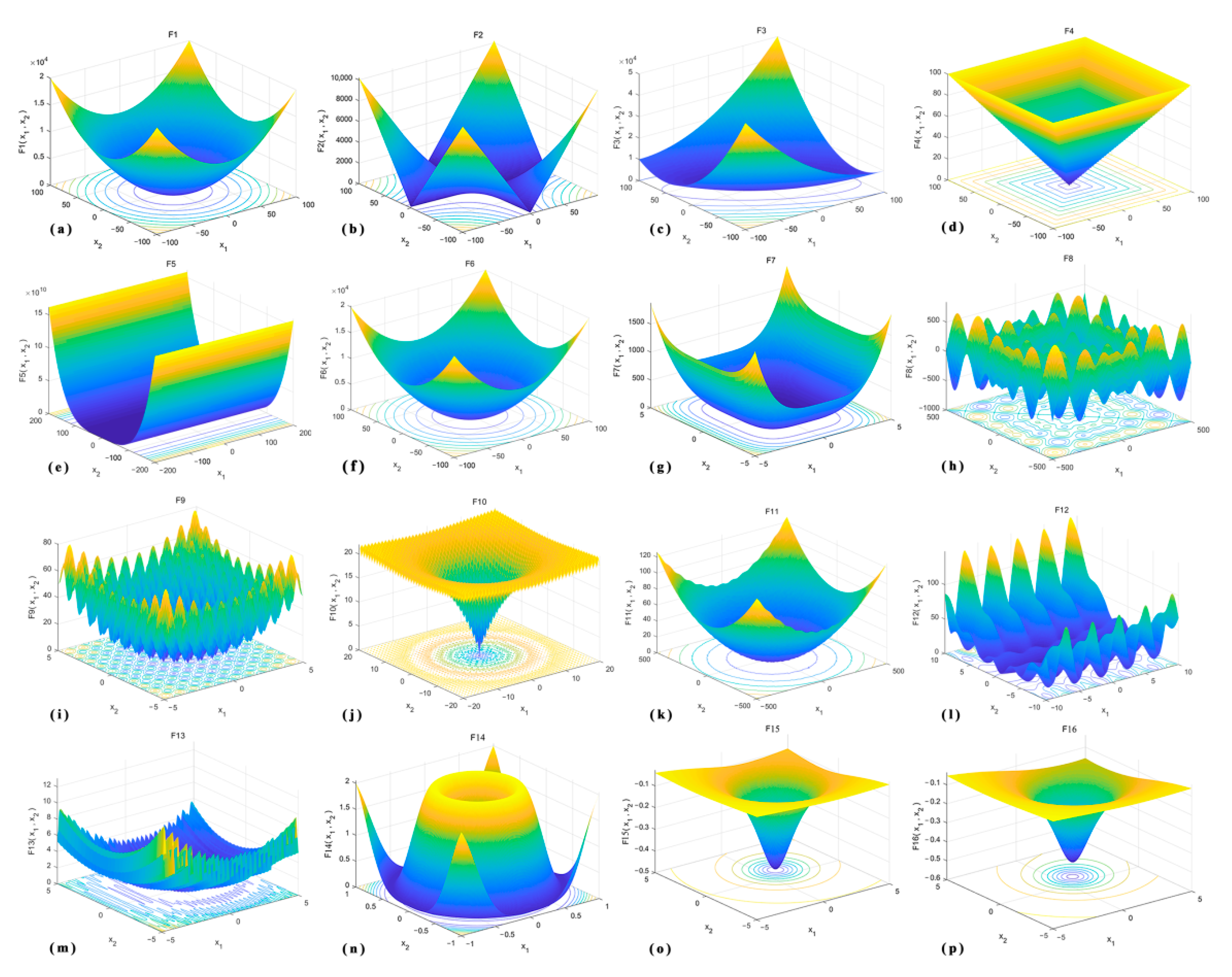
3.1. Standard Test Functions
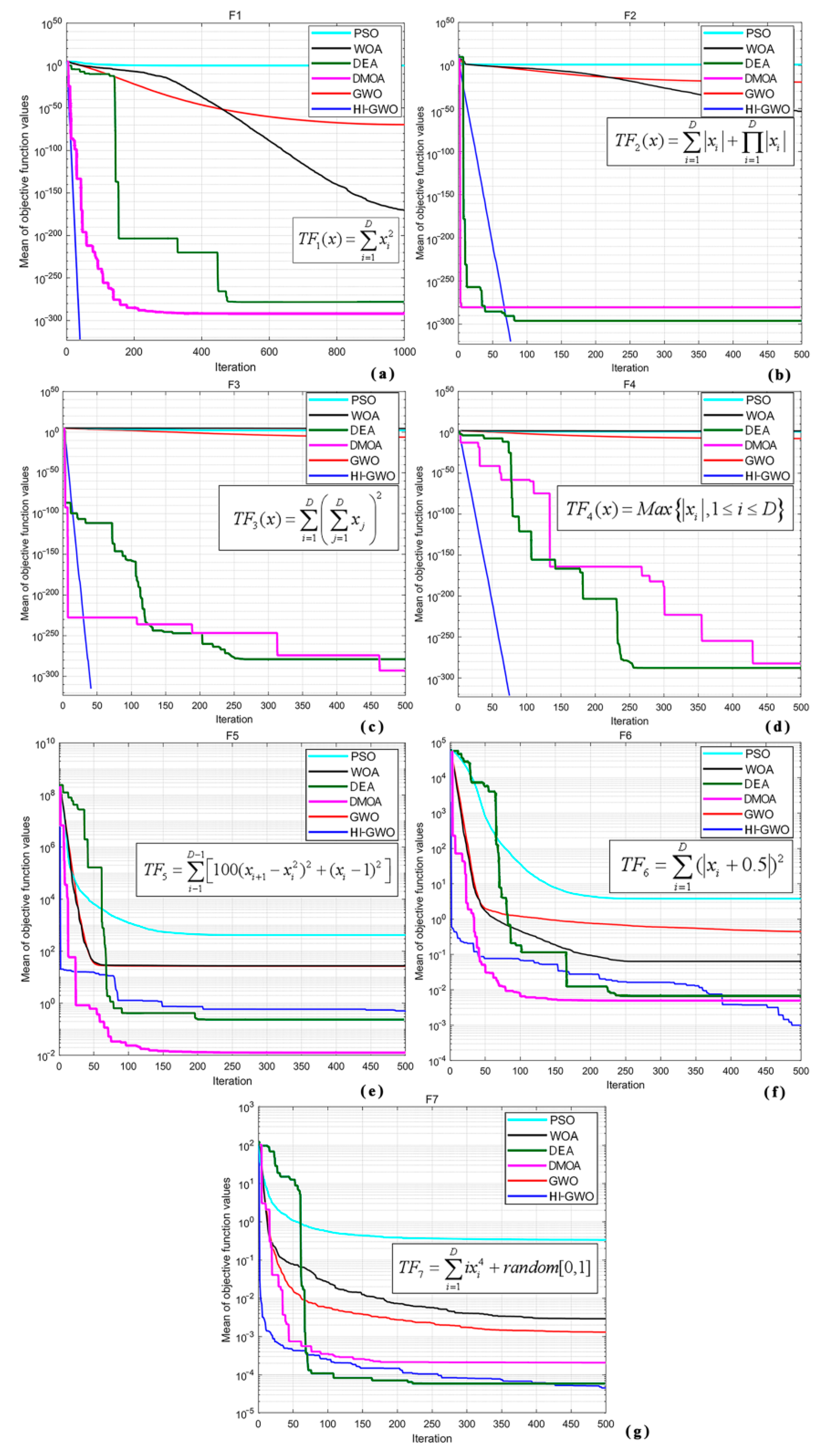
3.2. Analysis of Unimodal Test Function Experiments
3.3. Analysis of Multimodal Test Function Experiments
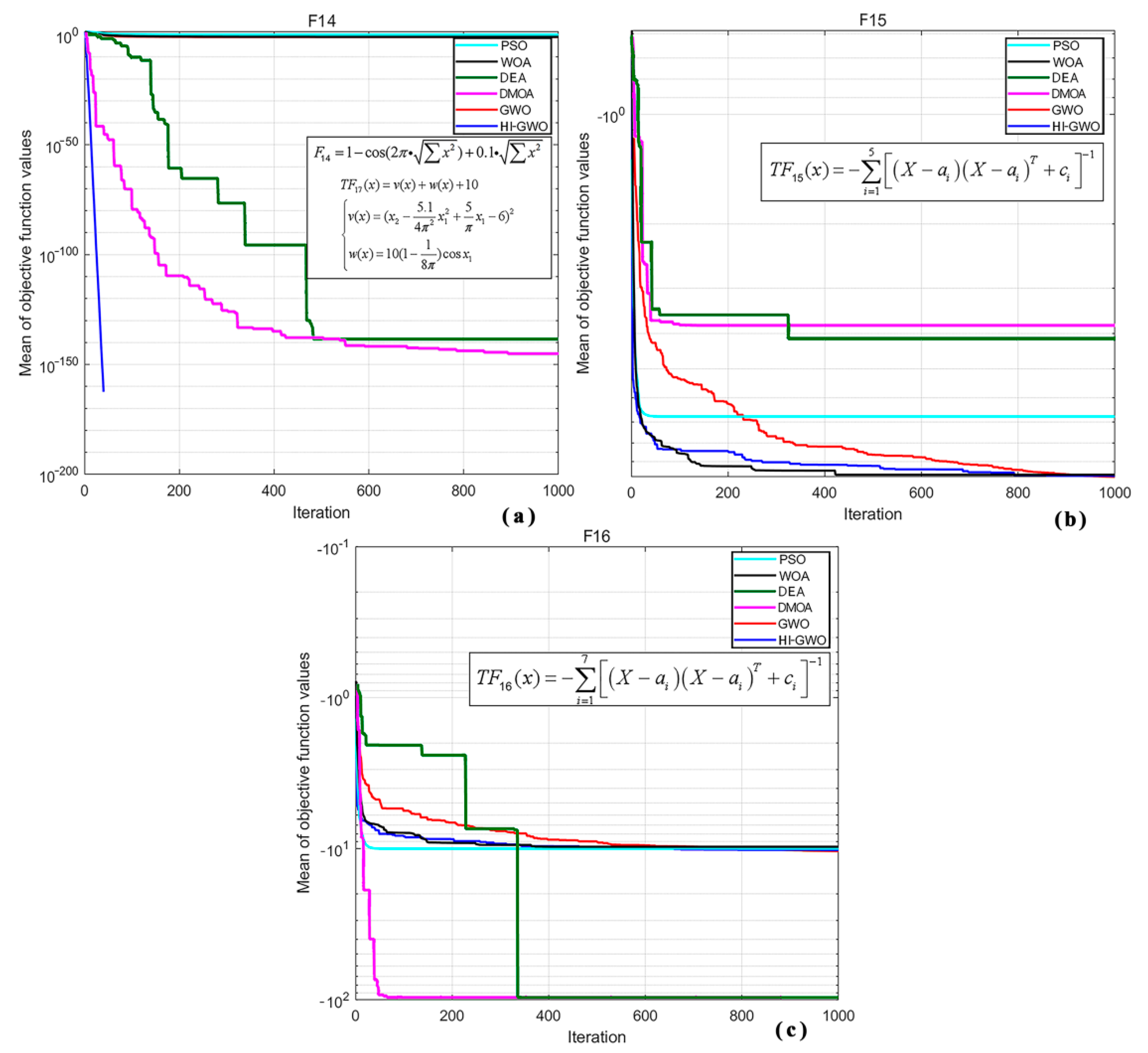
3.4. Analysis of Fixed-Dimensional Multimodal Test Function Experiments
3.5. Experimental Analysis
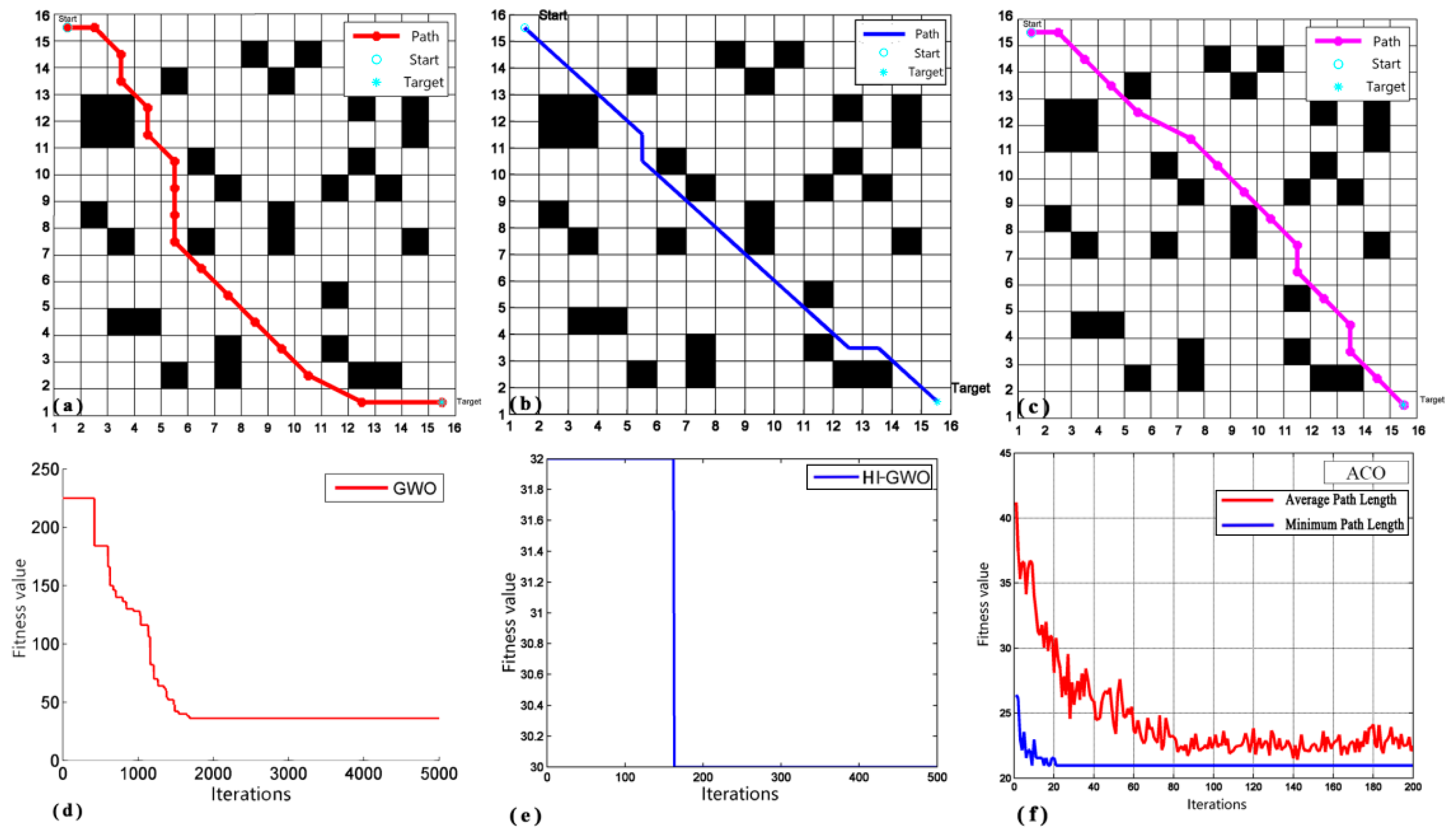
3.6. Mobile Robot Path Planning Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Function Name | Function Expression | Domain | Dimension | Optimal Solution |
|---|---|---|---|---|
| f1 | [−100, 100] | 30 | 0 | |
| f2 | [−10, 10] | 30 | 0 | |
| f3 | [−100, 100] | 30 | 0 | |
| f4 | [−100, 100] | 30 | 0 | |
| f5 | [−30, 30] | 30 | 0 | |
| f6 | [−100, 100] | 30 | 0 | |
| f7 | [−128, 128] | 30 | 0 |
| Function Name | Function Expression | Domain | Dimension | Optimal Solution |
|---|---|---|---|---|
| f8 | [−500, 500] | 30 | −419.98 × Dim | |
| f9 | [−5.12, 5.12] | 30 | 0 | |
| f10 | [−32, 32] | 30 | 0 | |
| f11 | [−600, 600] | 30 | 0 | |
| f12 | [−50, 50] | 30 | 0 | |
| f13 | [−50, 50] | 30 | 0 |
| Function Name | Function Expression | Domain | Dimension | Optimal Solution |
|---|---|---|---|---|
| f14 | [100, 100] | 30 | 0 | |
| f15 | [0, 10] | 30 | 10.1532 | |
| f16 | [0, 10] | 30 | 10.4028 |


References
- Yahia, H.S.; Mohammed, A.S. Path planning in Unmanned Aerial Vehicles (UAVs): Overview, Challenges, and Solutions. Util. Math. 2023, 120, 455–471. [Google Scholar]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Sabitri, P.; Muhammad, Y.; Sangman, M. Bio-Inspired Optimization-Based Path Planning Algorithms in Unmanned Aerial Vehicles: A Survey. Sensors 2023, 23, 3051. [Google Scholar]
- Faten, A.; Heba, K.; Kamal, Y. Bio-Inspired Multi-UAV Path Planning Heuristics: A Review. Mathematics 2023, 11, 2356. [Google Scholar]
- Jaafar, A.; Dheyaa, J. Lassical and Heuristic Approaches for Mobile Robot Path Planning: A Survey. Robotics 2023, 12, 93. [Google Scholar]
- Hazha, S.; Amin, S. Path planning optimization in unmanned aerial vehicles using meta-heuristic algorithms: A systematic review. Environ. Monit. Assess. 2023, 195, 30. [Google Scholar]
- Selcuk, A.; Tevfik, E. An immune plasma algorithm based approach for UCAV path planning. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 56–69. [Google Scholar]
- Ma, Z.; Chen, J. Adaptive path planning method for UAVs in complex environments. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103133. [Google Scholar] [CrossRef]
- Vincent, R.; Tarbouchi, M. Hybrid deterministic non-deterministic data-parallel algorithm for real-time unmanned aerial vehicle trajectory planning in CUDA. e-Prime-Adv. Electr. Eng. Electron. Energy 2022, 2, 100085. [Google Scholar]
- Wei, Y.; Feng, J.; Huang, Y.; Liu, K.; Ren, B. Path Planning of Mobile Robot Based on Improved Genetic Algorithm. J. Supercomput. 2022, 2365, 012053. [Google Scholar] [CrossRef]
- Yao, P.; Zhao, S. Three-Dimensional Path Planning for AUV Based on Interfered Fluid Dynamical System Under Ocean Current (June 2018). Inst. Electr. Electron. Eng. 2018, 6, 42904–42916. [Google Scholar] [CrossRef]
- Chen, Q.; He, Q.; Zhang, D. UAV Path Planning Based on an Improved Chimp Optimization Algorithm. Axioms 2023, 12, 702. [Google Scholar] [CrossRef]
- Wang, X.; Pan, J.; Yang, Q.; Kong, L.; Snášel, V.; Chu, S. Modified Mayfly Algorithm for UAV Path Planning. Drones 2022, 6, 134. [Google Scholar] [CrossRef]
- Manikandan, K.; Sriramulu, R. Optimized Path Planning Strategy to Enhance Security under Swarm of Unmanned Aerial Vehicles. Drones 2022, 6, 336. [Google Scholar] [CrossRef]
- Jarray, R.; Bouallègue, S.; Rezk, H.; Al-Dhaifallah, M. Parallel Multiobjective Multiverse Optimizer for Path Planning of Unmanned Aerial Vehicles in a Dynamic Environment with Moving Obstacles. Drones 2022, 6, 385. [Google Scholar] [CrossRef]
- Zheng, L.; Tian, Y.; Wang, H.; Hong, C.; Li, B. Path Planning of Autonomous Mobile Robots Based on an Improved Slime Mould Algorithm. Drones 2023, 7, 257. [Google Scholar] [CrossRef]
- Panwar, K.; Dee, K. Discrete Grey Wolf Optimizer for symmetric travelling salesman Problemp. Appl. Soft Comput. 2021, 105, 107298. [Google Scholar] [CrossRef]
- Muni, M.; Parhi, D.; Priyadarshi, K. Implementation of grey wolf optimization controller for multiple humanoid navigation. Comput. Animat. Virtual Worlds 2020, 31, e1919. [Google Scholar] [CrossRef]
- Sun, L.; Feng, B.; Chen, T.; Zhao, D.; Xin, Y. Equalized GreyWolfOptimizer with Refraction Opposite Learning. Comput. Intell. Neurosci. 2022, 2022, 2721490. [Google Scholar] [CrossRef]
- Li, J.; Yang, F. Task assignment strategy for multi-robot based on improved Grey Wolf Optimizer. J. Ambient Intell. Humaniz. Comput. 2020, 12, 6319–6335. [Google Scholar] [CrossRef]
- Xu, C.; Xu, M.; Yin, C. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Comput. Commun. 2020, 162, 196–203. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhang, J.; Zhong, M. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl. Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
- Liu, J.; Wei, X.; Huang, H. An Improved Grey Wolf Optimization Algorithm and Its Applicationin Path Planning. Inst. Electr. Electron. Eng. 2021, 9, 121944–121956. [Google Scholar]
- Mesa, A.; Castromayor, K.; Garillos-Manliguez, C.; Calag, V. Cuckoo search via Levy flights applied to uncapacitated facility location problem. J. Ind. Eng. Int. 2017, 14, 585–592. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Yang, L.; Li, J.; Zhang, J.; Liu, Y.; Sun, Y.; Yan, F. Research on Load Optimal Dispatch for High-Temperature CHP Plants through Grey Wolf Optimization Algorithm with the Levy Flight. Processes 2022, 10, 1546. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, Y.; Wang, Y. Parameter Identification of Jiles-Atherton Model Based on Levy Whale Optimization Algorithm. IEEE Access 2022, 10, 66711–66721. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. Enhanced leadership-inspired grey wolf optimizer for global optimization problems. Eng. Comput. 2019, 36, 1777–1800. [Google Scholar] [CrossRef]
- Karakoyun, M.; Ozkis, A.; Kodaz, H. A new algorithm based on gray wolf optimizer and shuffled frog leaping algorithm to solve the multi-objective optimization problems. Appl. Soft Comput. J. 2020, 96, 106560. [Google Scholar] [CrossRef]
- Li, Z. A local opposition-learning golden-sine grey wolf optimization algorithm for feature selection in data classification. Appl. Soft Comput. 2023, 142, 110319. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden Sine Algorithm: A Novel Math-Inspired Algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Tanyildizi, E. A novel optimization method for solving constrained and unconstrained problems: Modified Golden Sine Algorithm. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 3287–3304. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, L. Hyper-spectral Image Pixel Classification based on Golden Sine and Chaotic Spotted Hyena Optimization Algorithm. IEEE Access 2023, 11, 89757–89768. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Lin, W.; Lin, J. Continuous-domain ant colony optimization algorithm based on reinforcement learning. Int. J. Wavelets Multiresolution Inf. Process. 2021, 19, 2050084. [Google Scholar] [CrossRef]
- Papenhausen, E.; Mueller, K. Coding Ants: Optimization of GPU code using ant colony optimization. Comput. Lang. Syst. Struct. 2018, 54, 119–138. [Google Scholar] [CrossRef]



| Algorithms | PSO | WOA | DEA | DMOA | GWO | HI-GWO |
|---|---|---|---|---|---|---|
| Parameter configuration | c1 = 2; c2 = 2; Vmax = 2; Vmin = −2; ub = 100; lb = −100; Wmax = 0.8; Wmin = 0.2; | Pop = 50; Max_iter = 500 | Pop = 50; Max_iter = 500; Crossover Rate = 0.8; Scaling Factor = 1.3 | Pop = 50; Max_iter = 500; Mutation Rate = 0.2; Crossover Rate = 0.8 | Pop = 50; Max_iter = 500 | Pop = 50; Max_iter = 500 |
| Function Name | Metric | GWO | HI-GWO |
|---|---|---|---|
| f1 | Worst value | 1.44614 × 10−32 | 0 |
| Best value | 0.000126387 | 0 | |
| Mean value | 2.28638 × 10−33 | 0 | |
| Standard deviation | 3.74166 × 10−33 | 0 | |
| f2 | Worst value | 2.21951 × 10−19 | 0 |
| Best value | 1.46309 × 10−20 | 0 | |
| Mean value | 6.88322 × 10−20 | 0 | |
| Standard deviation | 5.2166 × 10−20 | 0 | |
| f3 | Worst value | 1.05028 × 10−6 | 0 |
| Best value | 7.88338 × 10−11 | 0 | |
| Mean value | 7.88338 × 10−11 | 0 | |
| Standard deviation | 2.44756 × 10−7 | 0 | |
| f4 | Worst value | 7.95624 × 10−8 | 0 |
| Best value | 2.80902 × 10−9 | 0 | |
| Mean value | 2.17452 × 10−8 | 0 | |
| Standard deviation | 2.07358 × 10−8 | 0 | |
| f5 | Worst value | 28.06617 | 1.1698 |
| Best value | 25.65672333 | 0.000726383 | |
| Mean value | 26.726 | 0.1436413 | |
| Standard deviation | 0.682807333 | 0.316787233 | |
| f6 | Worst value | 0.316787233 | 0.012863687 |
| Best value | 0.013620723 | 8.32301 × 10−6 | |
| Mean value | 0.447224667 | 0.001660262 | |
| Standard deviation | 0.302151333 | 0.003196104 | |
| f7 | Worst value | 0.00274467 | 0.00014252 |
| Best value | 0.000345297 | 1.48734 × 10−6 | |
| Mean value | 0.001173079 | 4.05533 × 10−5 | |
| Standard deviation | 0.0006349 | 3.94767 × 10−5 | |
| f8 | Worst value | −4153.945127 | −12064.97969 |
| Best value | −7449.276533 | −12569.34411 | |
| Mean value | −6159.986437 | −12472.28388 | |
| Standard deviation | 811.95658 | 139.31235 | |
| f9 | Worst value | 11.63951 | 0 |
| Best value | 9.46667 × 10−15 | 0 | |
| Mean value | 1.967464 | 0 | |
| Standard deviation | 3.447013333 | 0 | |
| f10 | Worst value | 5.439 × 10−14 | 8.88 × 10−16 |
| Best value | 3.62 × 10−14 | 8.88 × 10−16 | |
| Mean value | 4.321 × 10−14 | 8.88 × 10−16 | |
| Standard deviation | 4.62667 × 10−15 | 0 | |
| f11 | Worst value | 0.021814467 | 0 |
| Best value | 0 | 0 | |
| Mean value | 0.00306005 | 0 | |
| Standard deviation | 0.0065315 | 0 | |
| f12 | Worst value | 0.079921333 | 0.001794702 |
| Best value | 0.006867188 | 1.01184 × 10−6 | |
| Mean value | 0.028779633 | 0.000259836 | |
| Standard deviation | 0.017810267 | 0.00045103 | |
| f13 | Worst value | 0.835891667 | 0.00868251 |
| Best value | 0.092272739 | 2.77073 × 10−6 | |
| Mean value | 0.403428667 | 0.001255902 | |
| Standard deviation | 0.192737333 | 0.00224423 | |
| f14 | Worst value | 0.21987 | 0 |
| Best value | 0.099873 | 0 | |
| Mean value | 0.179786667 | 0 | |
| Standard deviation | 0.0411846 | 0 | |
| f15 | Worst value | −4.223663333 | −6.720826667 |
| Best value | −10.15290667 | −10.15201333 | |
| Mean value | −9.332596667 | −9.44987 | |
| Standard deviation | 1.880446667 | 0.916336 | |
| f16 | Worst value | −8.284113333 | −7.15689 |
| Best value | −10.40266333 | −10.40088667 | |
| Mean value | −10.27821333 | −9.079075862 | |
| Standard deviation | 0.503301063 | 0.912366 |
| Function Name | Metric | GWO | HI-GWO |
|---|---|---|---|
| f1 | Worst value | 1.82884 × 10−32 | 0 |
| Best value | 2.34449 × 10−33 | 0 | |
| Mean value | 2.48493 × 10−33 | 0 | |
| Standard deviation | 4.68714 × 10−33 | 0 | |
| f2 | Worst value | 2.2836 × 10−19 | 0 |
| Best value | 1.52938 × 10−20 | 0 | |
| Mean value | 6.9246 × 10−20 | 0 | |
| Standard deviation | 5.4266 × 10−20 | 0 | |
| f3 | Worst value | 1.5357 × 10−06 | 0 |
| Best value | 1.077 × 10−10 | 0 | |
| Mean value | 1.14783 × 10−7 | 0 | |
| Standard deviation | 3.65209 × 10−7 | 0 | |
| f4 | Worst value | 8.21204 × 10−8 | 0 |
| Best value | 2.88489 × 10−9 | 0 | |
| Mean value | 2.2739 × 10−8 | 0 | |
| Standard deviation | 2.13291 × 10−8 | 0 | |
| f5 | Worst value | 28.097954 | 1.2969124 |
| Best value | 25.682092 | 0.000989726 | |
| Mean value | 26.733 | 0.14540434 | |
| Standard deviation | 0.6933128 | 0.33781164 | |
| f6 | Worst value | 1.1371116 | 0.01281442 |
| Best value | 0.011864142 | 6.70086 × 10−6 | |
| Mean value | 0.4634684 | 0.001667801 | |
| Standard deviation | 0.3121814 | 0.003185422 | |
| f7 | Worst value | 0.002753862 | 0.000140153 |
| Best value | 0.000342429 | 1.67117 × 10−6 | |
| Mean value | 0.001173874 | 0.000039824 | |
| Standard deviation | 0.000628745 | 3.8028 × 10−5 | |
| f8 | Worst value | −4170.778866 | −12054.79357 |
| Best value | −7448.306932 | −12569.30542 | |
| Mean value | −6156.813568 | −12469.8668 | |
| Standard deviation | 808.394766 | 142.61796 | |
| f9 | Worst value | 10.857832 | 0 |
| Best value | 6.816 × 10−15 | 0 | |
| Mean value | 1.7461292 | 0 | |
| Standard deviation | 3.1409356 | 0 | |
| f10 | Worst value | 5.401 × 10−14 | 8.88 × 10−16 |
| Best value | 3.6294 × 10−14 | 8.88 × 10−16 | |
| Mean value | 4.3272 × 10−14 | 8.88 × 10−16 | |
| Standard deviation | 4.5862 × 10−15 | 0 | |
| f11 | Worst value | 0.022508466 | 0 |
| Best value | 0 | 0 | |
| Mean value | 0.003030603 | 0 | |
| Standard deviation | 0.006597526 | 0 | |
| f12 | Worst value | 0.07430358 | 0.002090372 |
| Best value | 0.006625902 | 1.08516 × 10−6 | |
| Mean value | 0.02885658 | 0.000277462 | |
| Standard deviation | 0.01676395 | 0.00051898 | |
| f13 | Worst value | 0.8048338 | 0.008343696 |
| Best value | 0.082709289 | 2.27115 × 10−6 | |
| Mean value | 0.39817 | 0.001226874 | |
| Standard deviation | 0.1909844 | 0.002160486 | |
| f14 | Worst value | 0.21987 | 0 |
| Best value | 0.099873 | 0 | |
| Mean value | 0.179945 | 0 | |
| Standard deviation | 0.04174324 | 0 | |
| f15 | Worst value | −4.473606 | −6.895714 |
| Best value | −10.15292 | −10.150726 | |
| Mean value | −9.392338 | −9.459046939 | |
| Standard deviation | 1.809041703 | 0.8691754 | |
| f16 | Worst value | −8.40935 | −7.07988 |
| Best value | −9.986564 | −10.400962 | |
| Mean value | −10.280934 | −9.362908163 | |
| Standard deviation | 0.478773796 | 0.9260868 |
| Function Name | Metric | GWO | HI-GWO |
|---|---|---|---|
| f1 | Worst value | 1.64031 × 10−32 | 0 |
| Best value | 0.000037916 | 0 | |
| Mean value | 2.45833 × 10−33 | 0 | |
| Standard deviation | 4.18634 × 10−33 | 0 | |
| f2 | Worst value | 2.19035 × 10−19 | 0 |
| Best value | 1.45757 × 10−20 | 0 | |
| Mean value | 6.7938 × 10−20 | 0 | |
| Standard deviation | 5.2027 × 10−20 | 0 | |
| f3 | Worst value | 0.028464289 | 0 |
| Best value | 9.44162 × 10−11 | 0 | |
| Mean value | 5.74319 × 10−8 | 0 | |
| Standard deviation | 3.13539 × 10−7 | 0 | |
| f4 | Worst value | 9.04465 × 10−8 | 0 |
| Best value | 2.8561 × 10−9 | 0 | |
| Mean value | 2.32812 × 10−8 | 0 | |
| Standard deviation | 2.28187 × 10−8 | 0 | |
| f5 | Worst value | 28.088809 | 1.1037777 |
| Best value | 25.658486 | 0.000832102 | |
| Mean value | 26.733967 | 0.13026576 | |
| Standard deviation | 0.6925951 | 0.29332583 | |
| f6 | Worst value | 1.1169545 | 0.01252402 |
| Best value | 0.006161516 | 5.10054 × 10−6 | |
| Mean value | 0.4524061 | 0.001622307 | |
| Standard deviation | 0.3092555 | 0.003107579 | |
| f7 | Worst value | 0.002753862 | 0.000140153 |
| Best value | 0.000342429 | 1.67117 × 10−6 | |
| Mean value | 0.001173874 | 3.9824 × 10−5 | |
| Standard deviation | 0.000628745 | 3.8028 × 10−5 | |
| f8 | Worst value | −4170.778866 | −12054.79357 |
| Best value | −7448.306932 | −12569.30542 | |
| Mean value | −6156.813568 | −12469.8668 | |
| Standard deviation | 808.394766 | 142.61796 | |
| f9 | Worst value | 10.857832 | 0 |
| Best value | 7.384 × 10−15 | 0 | |
| Mean value | 1.7461292 | 0 | |
| Standard deviation | 3.1409356 | 0 | |
| f10 | Worst value | 5.40 × 10−14 | 8.88 × 10−16 |
| Best value | 3.63 × 10−14 | 8.88 × 10−16 | |
| Mean value | 4.33 × 10−14 | 8.88 × 10−16 | |
| Standard deviation | 4.59 × 10−15 | 0.00 | |
| f11 | Worst value | 0.022508466 | 0 |
| Best value | 0 | 0 | |
| Mean value | 0.003030603 | 0 | |
| Standard deviation | 0.006597526 | 0 | |
| f12 | Worst value | 0.07755977 | 0.00198497 |
| Best value | 0.005989025 | 1.13393 × 10−6 | |
| Mean value | 0.02923882 | 0.000275676 | |
| Standard deviation | 0.017689595 | 0.000499535 | |
| f13 | Worst value | 0.7976553 | 0.011111255 |
| Best value | 0.078658297 | 2.36804 × 10−6 | |
| Mean value | 0.3943197 | 0.001398812 | |
| Standard deviation | 0.1907708 | 0.002771557 | |
| f14 | Worst value | 0.21687 | 0 |
| Best value | 0.099873 | 0 | |
| Mean value | 0.1790326 | 0 | |
| Standard deviation | 0.04212264 | 0 | |
| f15 | Worst value | −4.564768 | −6.920599 |
| Best value | −10.152923 | −10.15062 | |
| Mean value | −9.384764 | −9.507023232 | |
| Standard deviation | 1.815354269 | 0.8893289 | |
| f16 | Worst value | −8.5032 | −6.816907 |
| Best value | −10.194624 | −10.399588 | |
| Mean value | −10.290876 | −9.529245455 | |
| Standard deviation | 0.450210221 | 0.9985754 |
| Algorithms | 10 × 10 | 15 × 15 | ||||
|---|---|---|---|---|---|---|
| Optimal Solution | Average Solution | Path Nodes | Optimal Solution | Average Solution | Path Nodes | |
| ACO | 20 | 31 | [1,2,3,3,3,4,5,6,7,8] | 28 | 32 | [2,3,4,5,7,8,9,10,11,11,12,13,13,14] |
| GWO | 22 | 34 | [1,1,1,1,2,4,5,6,7,8] | 32 | 36 | [2,3,3,4,4,5,5,5,5,6,7,8,9,10,12] |
| HI-GWO | 13 | 21.5 | [1,2,3,4,5,6,6,7,8,9] | 20 | 27 | [1,2,3,4,5,5,6,7,8,9,10,11,12,13,14] |
| Algorithm | Map Dimension | Obstacle Rate | Path Length | Iteration | Number of Turns |
|---|---|---|---|---|---|
| ACO | 40 × 40 | 10% | 69.1543 | 200 | 35 |
| GWO | 67.3917 | 170 | 25 | ||
| HI-GWO | 57.4222 | 160 | 17 | ||
| ACO | 15% | 75.3969 | 220 | 35 | |
| GWO | 70.0652 | 180 | 23 | ||
| HI-GWO | 57.8782 | 160 | 11 | ||
| ACO | 20% | 70.0833 | 300 | 46 | |
| GWO | 101.4727 | 290 | 25 | ||
| HI-GWO | 60.1767 | 210 | 19 | ||
| ACO | 50 × 50 | 10% | 124.0243 | 400 | 80 |
| GWO | 96.3207 | 350 | 29 | ||
| HI-GWO | 71.5382 | 300 | 11 | ||
| ACO | 15% | 95.0538 | 410 | 77 | |
| GWO | 92.9756 | 370 | 34 | ||
| HI-GWO | 77.0133 | 320 | 15 | ||
| ACO | 20% | 102.468 | 490 | 101 | |
| GWO | 86.6332 | 450 | 34 | ||
| HI-GWO | 77.7915 | 380 | 24 |
| Algorithm | Map Dimension | Obstacle Rate | Path Length Ratio | Number of Iteration Ratio | Number of Turns Ratio |
|---|---|---|---|---|---|
| ACO | 40 × 40 | 10% | 16.97% | 20.00% | 51.43% |
| GWO | 14.17% | 5.88% | 32.00% | ||
| ACO | 15% | 23.24% | 18.18% | 68.57% | |
| GWO | 17.39% | 11.11% | 52.17% | ||
| ACO | 20% | 14.14% | 30.00% | 58.69% | |
| GWO | 40.69% | 27.58% | 24.00% | ||
| ACO | 50 × 50 | 10% | 42.32% | 25.00% | 86.24% |
| GWO | 25.735 | 14.29% | 62.06% | ||
| ACO | 15% | 18.89% | 21.95% | 80.52% | |
| GWO | 17.17% | 13.51% | 55.88% | ||
| ACO | 20% | 24.08% | 22.44% | 76.23% | |
| GWO | 10.20% | 15.56% | 29.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, L.; Nian, H.; Lu, Y.; Zhao, H.; Chen, Y. Enhanced Grey Wolf Optimization Algorithm for Mobile Robot Path Planning. Electronics 2023, 12, 4026. https://doi.org/10.3390/electronics12194026
Liu L, Li L, Nian H, Lu Y, Zhao H, Chen Y. Enhanced Grey Wolf Optimization Algorithm for Mobile Robot Path Planning. Electronics. 2023; 12(19):4026. https://doi.org/10.3390/electronics12194026
Chicago/Turabian StyleLiu, Lili, Longhai Li, Heng Nian, Yixin Lu, Hao Zhao, and Yue Chen. 2023. "Enhanced Grey Wolf Optimization Algorithm for Mobile Robot Path Planning" Electronics 12, no. 19: 4026. https://doi.org/10.3390/electronics12194026
APA StyleLiu, L., Li, L., Nian, H., Lu, Y., Zhao, H., & Chen, Y. (2023). Enhanced Grey Wolf Optimization Algorithm for Mobile Robot Path Planning. Electronics, 12(19), 4026. https://doi.org/10.3390/electronics12194026






