Information Technology for Maximizing Energy Consumption for Useful Information Traffic in a Dense Wi-Fi 6/6E Ecosystem
Abstract
:1. Introduction
- -
- analytically formalize the Wi-Fi 6/6E ecosystem’s energy consumption model, which takes into account the specifics of OFDMA and MU-MIMO, the influence of the communication channel characteristics on the speed of target information transfer, and details of energy consumption for the operation of the network infrastructure,
- -
- present the goal of the research based on the created model in the form of a statement of the optimization problem with restrictions,
- -
- present the process of solving the stated optimization problem in the form of information technology with a branch-and-bound hierarchy,
- -
- justify the adequacy of the proposed mathematical apparatus and demonstrate its functionality in the context of the research goal.
- -
- information technology for maximizing energy consumption for useful information traffic in a dense Wi-Fi 6/6E ecosystem,
- -
- a simulation model of energy consumption by the Wi-Fi 6/6E ecosystem, which takes into account the specifics of OFDMA and MU-MIMO.
2. Materials and Methods
2.1. Statement of the Research
2.2. The Markov Concept of the Energy Efficiency Assessment of the Edge Computing Infrastructure Peripheral Server Functioning over Time
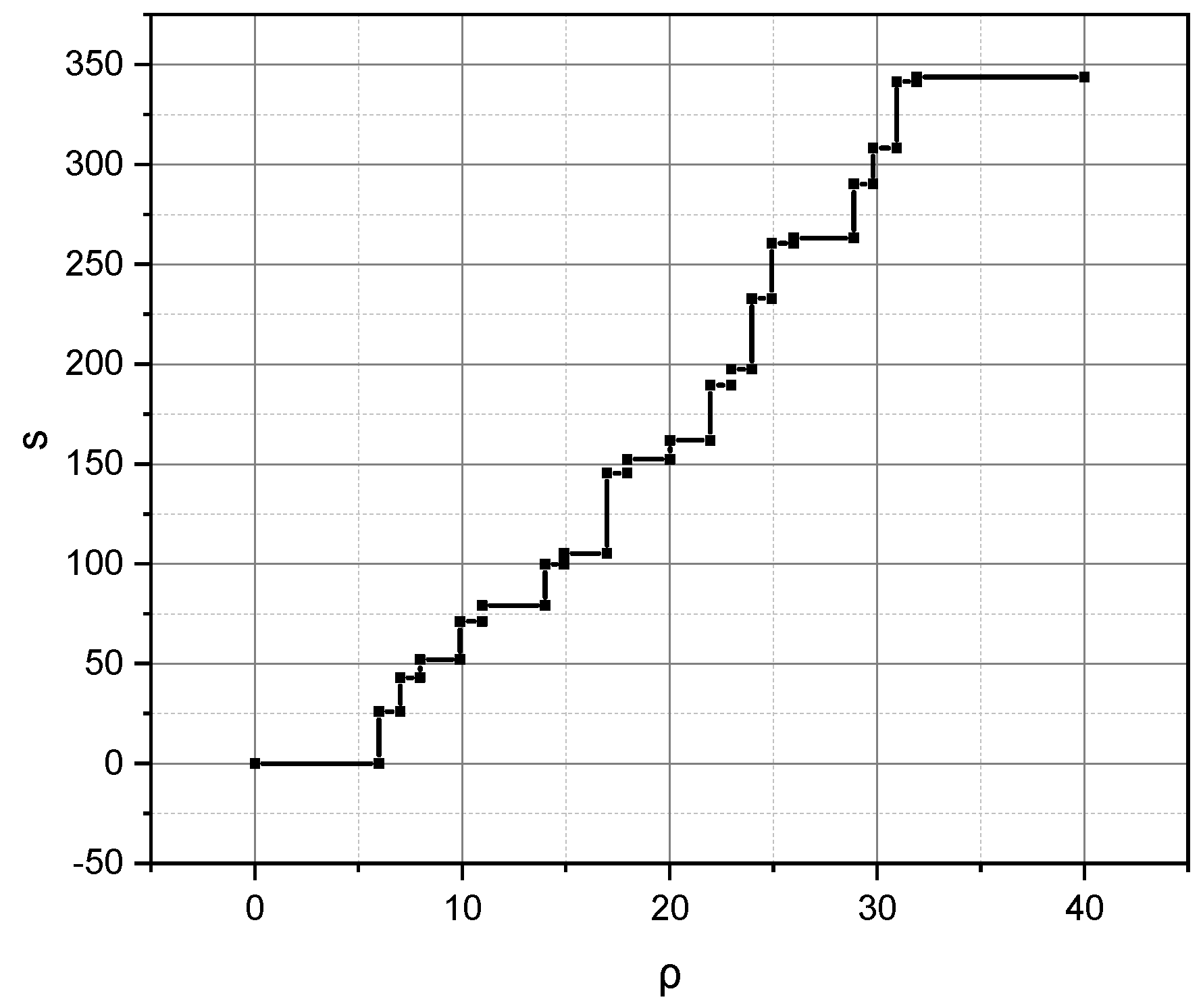
3. Results
- -
- the height at which the router is mounted: m;
- -
- the height of placement of the subscriber’s terminal: m;
- -
- mW;
- -
- noise spectral power density , : −175 dBpHz;
- -
- amplifier noise spectral power density , : 8 dB;
- -
- , ;
- -
- channel width: MHz;
- -
- subscriber’s adapter sensitivity: dBm;
- -
- router’s power consumption in standby mode : 850 mW.
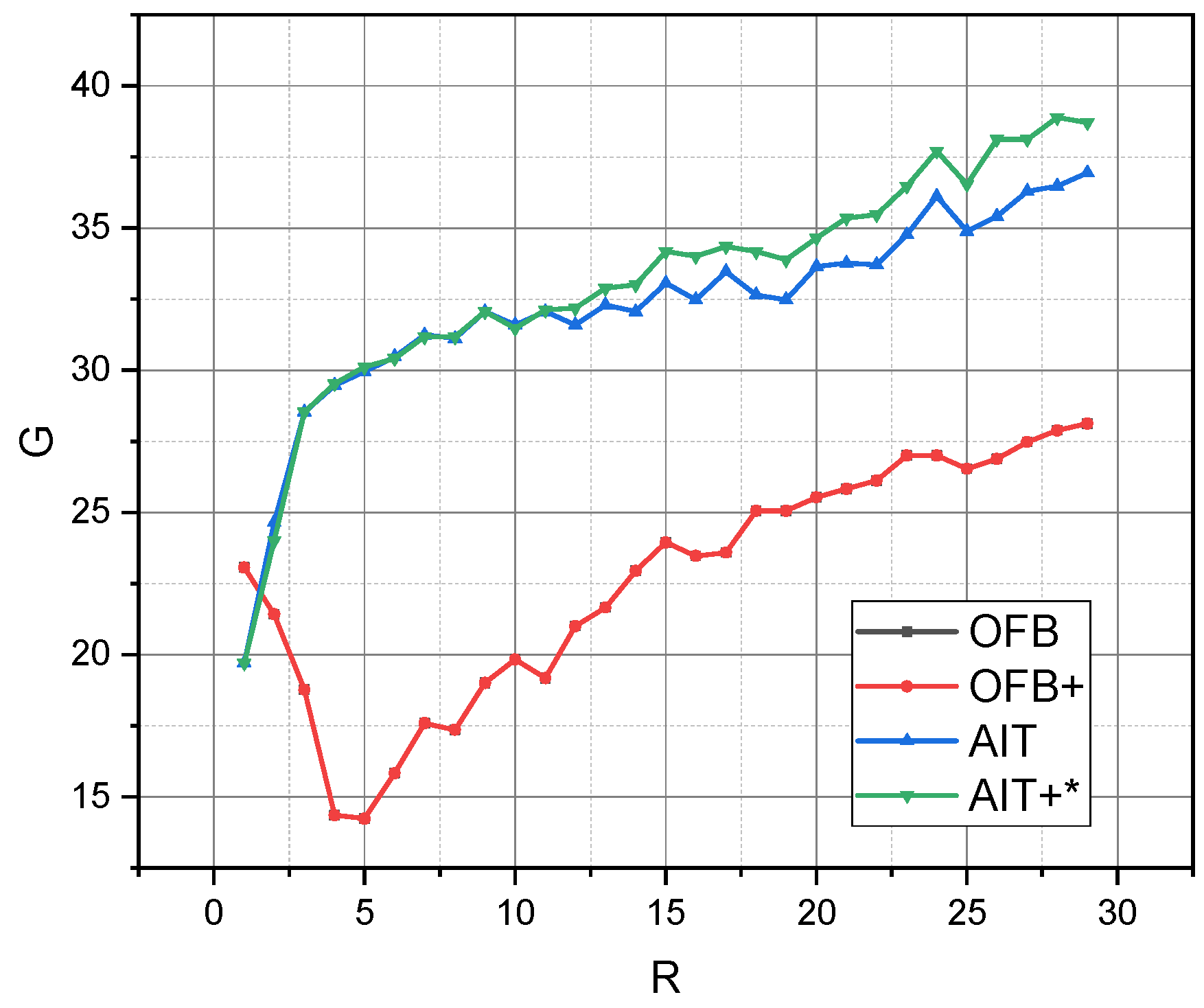
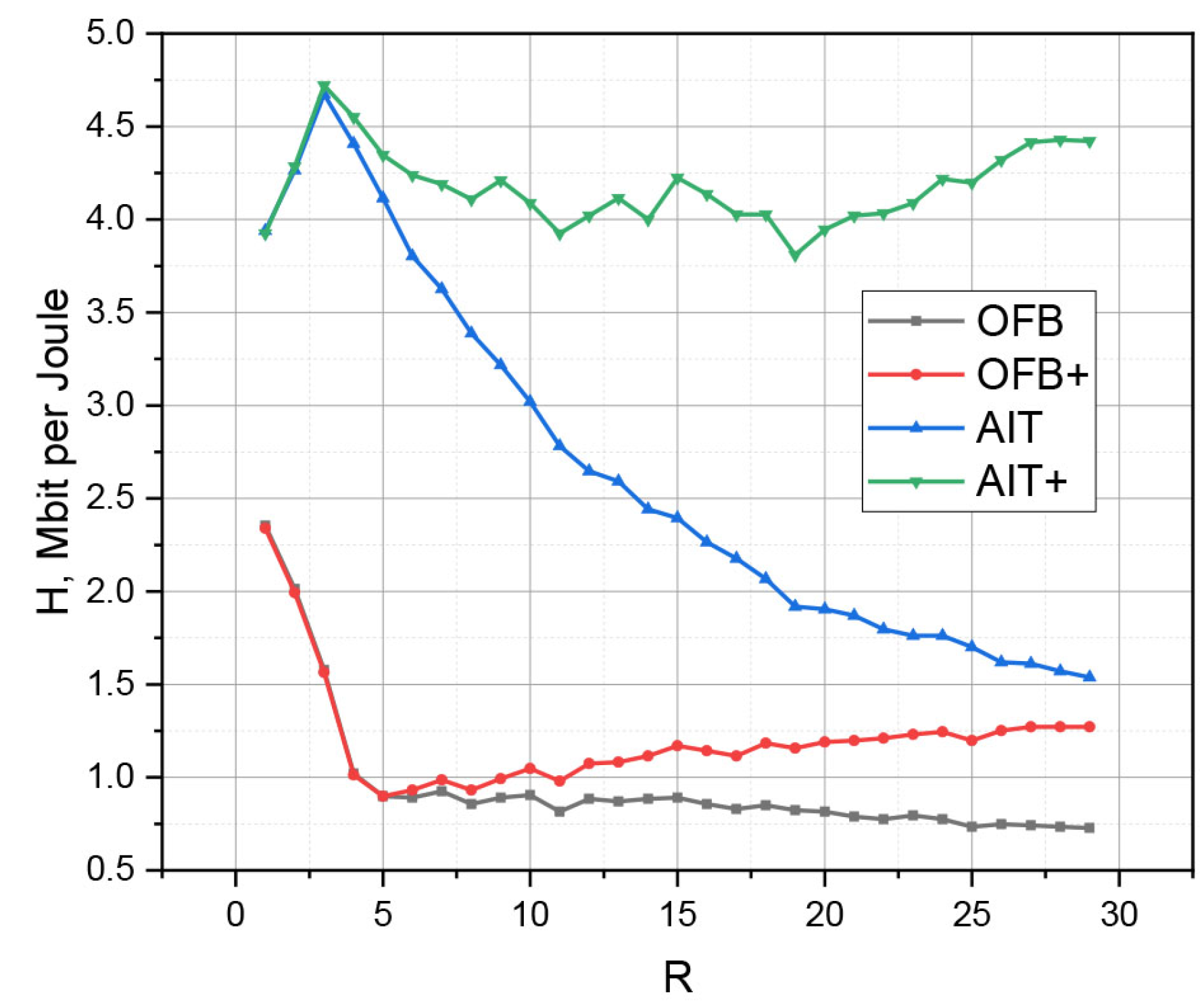
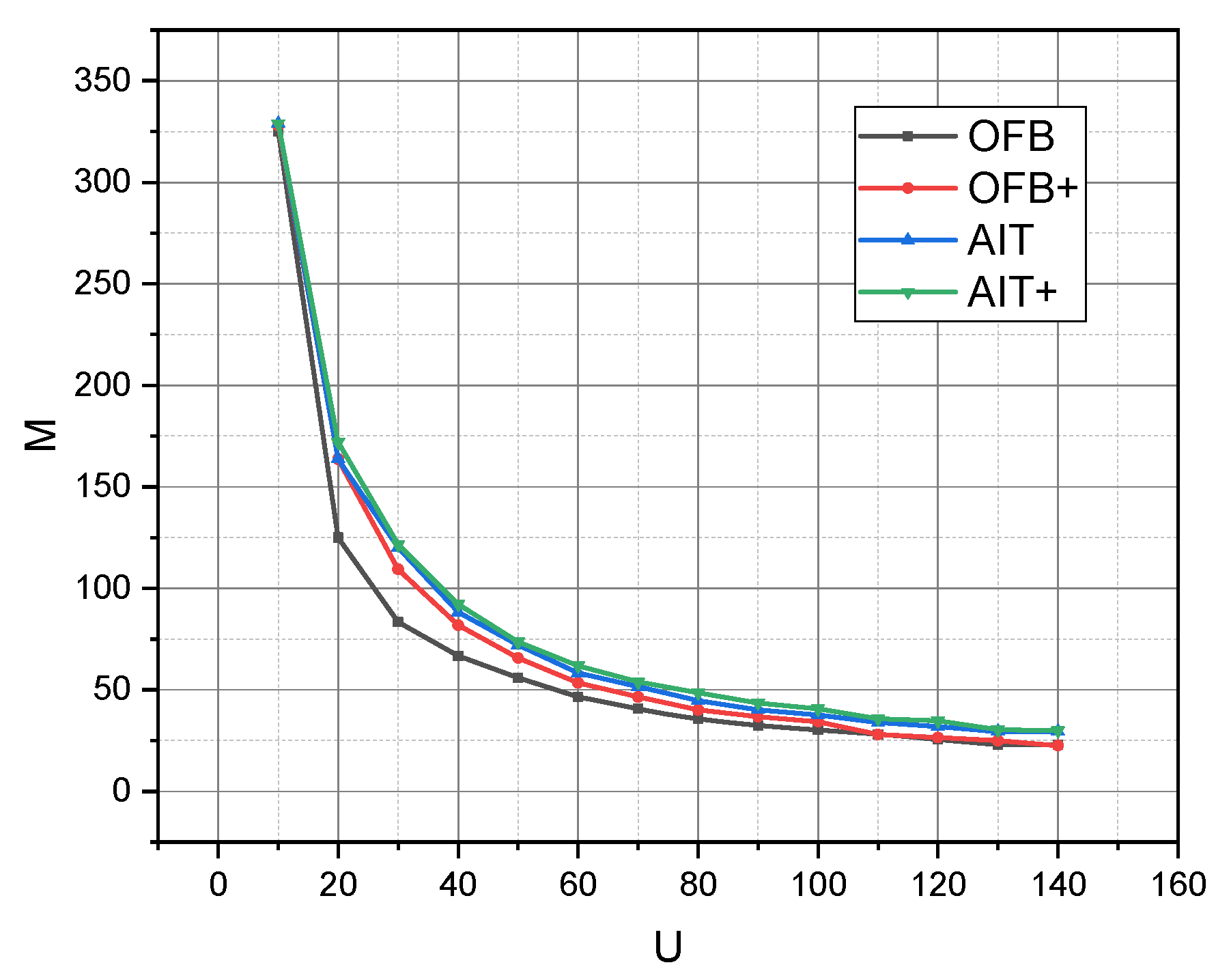
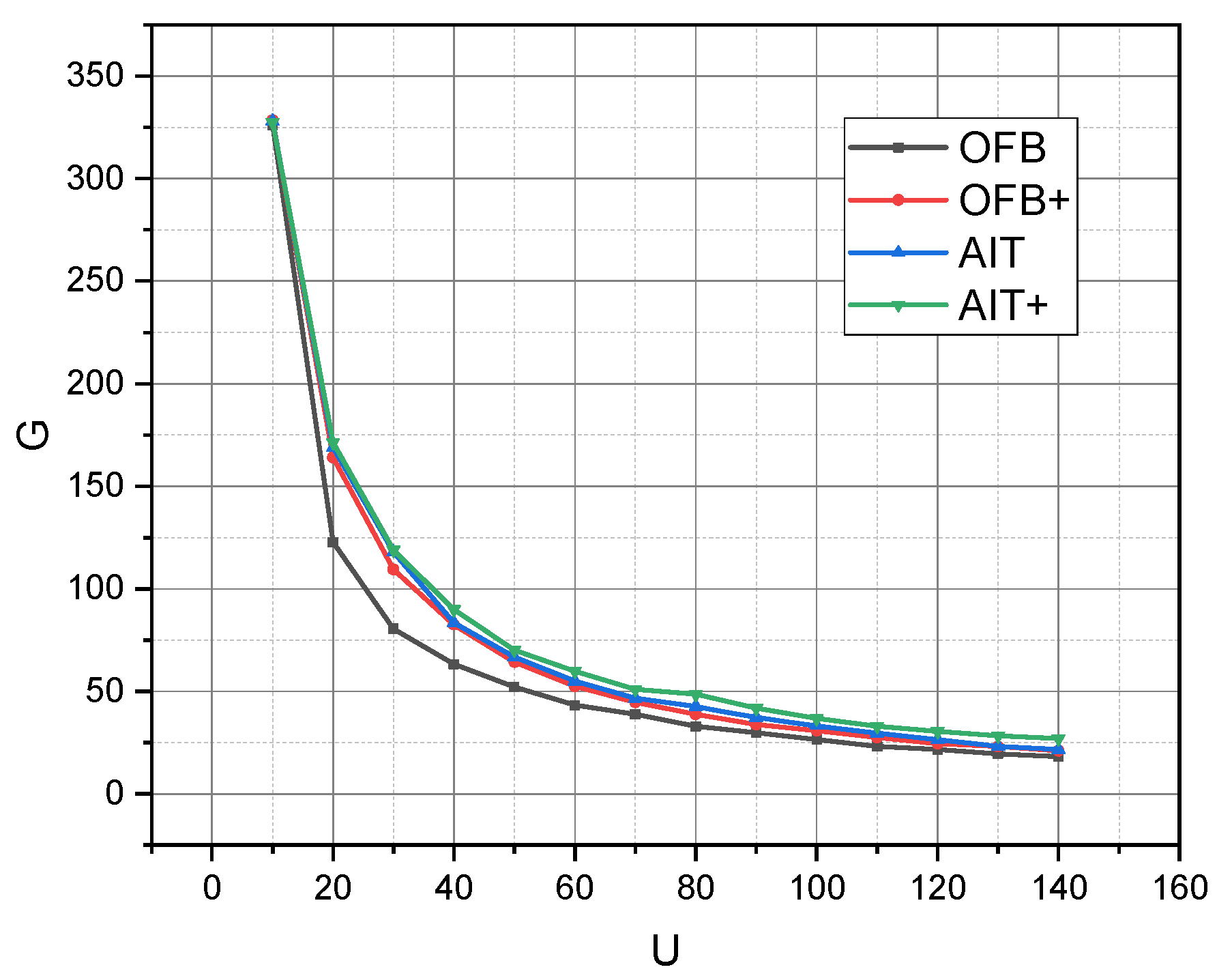
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mozaffariahrar, E.; Theoleyre, F.; Menth, M. A Survey of Wi-Fi 6: Technologies, Advances, and Challenges. Futur. Internet 2022, 14, 293. [Google Scholar] [CrossRef]
- Kovtun, V.; Izonin, I.; Gregus, M. Modeling a session of subject-system interaction in a wireless communication infrastructure with a mixed resource. PLoS ONE 2022, 17, e0271536. [Google Scholar] [CrossRef] [PubMed]
- Kovtun, V.; Grochla, K. Investigation of the competitive nature of eMBB and mMTC 5G services in conditions of limited communication resource. Sci. Rep. 2022, 12, 16050. [Google Scholar] [CrossRef] [PubMed]
- Bisikalo, O.V.; Kovtun, V.V.; Kovtun, O.V.; Danylchuk, O.M. Mathematical Modeling of the Availability of the Information System for Critical Use to Optimize Control of its Communication Capabilities. Int. J. Sens. Wirel. Commun. Control 2021, 11, 505–517. [Google Scholar] [CrossRef]
- Islam, G.Z.; Kashem, M.A. Efficient resource allocation in the IEEE 802.11ax network leveraging OFDMA technology. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 2488–2496. [Google Scholar] [CrossRef]
- Daldoul, Y.; Meddour, D.-E.; Ksentini, A. Performance evaluation of OFDMA and MU-MIMO in 802.11ax networks. Comput. Netw. 2020, 182, 107477. [Google Scholar] [CrossRef]
- Joo, S.; Kim, T.; Song, T.; Pack, S. MU-MIMO enabled uplink OFDMA MAC protocol in dense IEEE 802.11ax WLANs. ICT Express 2020, 6, 287–290. [Google Scholar] [CrossRef]
- Krishnamoorthy, V.K.; Izonin, I.; Subramanian, S.; Shandilya, S.K.; Velayutham, S.; Munichamy, T.R.; Havryliuk, M. Energy Saving Optimization Technique-Based Routing Protocol in Mobile Ad-Hoc Network with IoT Environment. Energies 2023, 16, 1385. [Google Scholar] [CrossRef]
- Dutta, P.; Ramyasree, J.; Sridhar, V.; Minchula, V.K.; Mohanta, H.C.; Mahfoudh, S.; Shah, S.B.H.; Singh, S.P. Evaluating the Efficiency of Non-Orthogonal MU-MIMO Methods in Smart Cities Technologies & 5G Communication. Sustainability 2022, 15, 236. [Google Scholar] [CrossRef]
- Lee, K.-H.; Kim, D. Cross-Layer Optimization for Heterogeneous MU-MIMO/OFDMA Networks. Sensors 2021, 21, 2744. [Google Scholar] [CrossRef]
- Kassa, L.; Deng, J.; Davis, M.; Cai, J. Performance of WLAN in Downlink MU-MIMO Channel with the Least Cost in Terms of Increased Delay. Electronics 2022, 11, 2851. [Google Scholar] [CrossRef]
- Belmonte-Fernández, Y. Modeling the received signal strength intensity of Wi-Fi signal using Hidden Markov Models. Expert Syst. Appl. 2021, 174, 114726. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, G.; Wang, H.; Zhang, C.; Yu, X. Channel Model and Performance Analysis for MIMO Systems with Single Leaky Coaxial Cable in Tunnel Scenarios. Sensors 2022, 22, 5776. [Google Scholar] [CrossRef] [PubMed]
- Riviello, D.G.; Di Stasio, F.; Tuninato, R. Performance Analysis of Multi-User MIMO Schemes under Realistic 3GPP 3-D Channel Model for 5G mmWave Cellular Networks. Electronics 2022, 11, 330. [Google Scholar] [CrossRef]
- Gkonis, P.K.; Trakadas, P.T.; Sarakis, L.E. Non-Orthogonal Multiple Access in Multiuser MIMO Configurations via Code Reuse and Principal Component Analysis. Electronics 2020, 9, 1330. [Google Scholar] [CrossRef]
- Ha, J.-G.; Ro, J.-H.; Song, H.-K. Throughput Enhancement in Downlink MU-MIMO Using Multiple Dimensions. Electronics 2019, 8, 758. [Google Scholar] [CrossRef]
- Hajj, M.; Wang, S.; Tu, L.; Azzi, S.; Wiart, J. A Statistical Estimation of 5G Massive MIMO Networks’ Exposure Using Stochastic Geometry in mmWave Bands. Appl. Sci. 2020, 10, 8753. [Google Scholar] [CrossRef]
- Bilyk, O.; Obelovska, K. Power Consumption Analysis at MAC-Sublayer of Wireless Sensor Networks. In Advances in Artificial Systems for Logistics Engineering; Springer: Cham, Switzerland, 2022; pp. 27–36. [Google Scholar] [CrossRef]
- Chen, M.; Gao, X.; Chen, C.; Guo, T.; Xu, W. A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models. Appl. Sci. 2022, 12, 11553. [Google Scholar] [CrossRef]
- Guérin, E.; Begin, T.; Lassous, I.G. An overview of MAC energy-saving mechanisms in Wi-Fi. Comput. Commun. 2023, 203, 129–145. [Google Scholar] [CrossRef]
- Wu, W.-C. Toward the energy efficiency of resource allocation algorithms for OFDMA downlink MIMO systems. J. Electron. Sci. Technol. 2019, 17, 100007. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Li, Y.; Zhu, Z.; Liu, G.; Liu, H. Energy Efficiency Optimization of Massive MIMO System with Uplink Multi-Cell Based on Imperfect CSI with Power Control. Symmetry 2022, 14, 780. [Google Scholar] [CrossRef]
- Imoize, A.L.; Obakhena, H.I.; Anyasi, F.I.; Sur, S.N. A Review of Energy Efficiency and Power Control Schemes in Ultra-Dense Cell-Free Massive MIMO Systems for Sustainable 6G Wireless Communication. Sustainability 2022, 14, 11100. [Google Scholar] [CrossRef]
- Alamu, O.; Olwal, T.O.; Djouani, K. An overview of simultaneous wireless information and power transfer in massive MIMO networks: A resource allocation perspective. Phys. Commun. 2023, 57, 101983. [Google Scholar] [CrossRef]
- Wiley, R. Signal Transmission in Natural Environments. In Encyclopedia of Neuroscience; Academic Press: Cambridge, MA, USA, 2009; pp. 817–822. [Google Scholar] [CrossRef]
- Dwivedi, R.; Srivastava, V.K. Fundamental optimization methods for machine learning. In Statistical Modeling in Machine Learning; Academic Press: Cambridge, MA, USA, 2023; pp. 227–247. [Google Scholar] [CrossRef]
- Koreshi, Z.U. Optimization and variational methods. In Nuclear Engineering Mathematical Modeling and Simulation; Academic Press: Cambridge, MA, USA, 2022; pp. 349–377. [Google Scholar] [CrossRef]
- IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks—Specific Requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 1: Enhancements for High-Efficiency WLAN. Available online: https://ieeexplore.ieee.org/document/9442429 (accessed on 27 July 2023).
- Fesenko, H.; Illiashenko, O.; Kharchenko, V.; Kliushnikov, I.; Morozova, O.; Sachenko, A.; Skorobohatko, S. Flying Sensor and Edge Network-Based Advanced Air Mobility Systems: Reliability Analysis and Applications for Urban Monitoring. Drones 2023, 7, 409. [Google Scholar] [CrossRef]
- Zaitseva, E.; Hovorushchenko, T.; Pavlova, O.; Voichur, Y. Identifying the Mutual Correlations and Evaluating the Weights of Factors and Consequences of Mobile Application Insecurity. Systems 2023, 11, 242. [Google Scholar] [CrossRef]
- Zaitseva, E.; Levashenko, V.; Rabcan, J. A new method for analysis of Multi-State systems based on Multi-valued decision diagram under epistemic uncertainty. Reliab. Eng. Syst. Saf. 2023, 229, 108868. [Google Scholar] [CrossRef]
- Marjasz, R.; Połys, K.; Strzoda, A.; Grochla, K. Improving Delivery Ratio in LoRa Network. In Proceedings of the 19th ACM International Symposium on Mobility Management and Wireless Access, Alicante, Spain, 22–26 November 2021. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtun, V.; Altameem, T.; Al-Maitah, M.; Kempa, W. Information Technology for Maximizing Energy Consumption for Useful Information Traffic in a Dense Wi-Fi 6/6E Ecosystem. Electronics 2023, 12, 3847. https://doi.org/10.3390/electronics12183847
Kovtun V, Altameem T, Al-Maitah M, Kempa W. Information Technology for Maximizing Energy Consumption for Useful Information Traffic in a Dense Wi-Fi 6/6E Ecosystem. Electronics. 2023; 12(18):3847. https://doi.org/10.3390/electronics12183847
Chicago/Turabian StyleKovtun, Viacheslav, Torki Altameem, Mohammed Al-Maitah, and Wojciech Kempa. 2023. "Information Technology for Maximizing Energy Consumption for Useful Information Traffic in a Dense Wi-Fi 6/6E Ecosystem" Electronics 12, no. 18: 3847. https://doi.org/10.3390/electronics12183847
APA StyleKovtun, V., Altameem, T., Al-Maitah, M., & Kempa, W. (2023). Information Technology for Maximizing Energy Consumption for Useful Information Traffic in a Dense Wi-Fi 6/6E Ecosystem. Electronics, 12(18), 3847. https://doi.org/10.3390/electronics12183847






