Abstract
This study addresses the poor robustness of the current beamforming algorithm for covariance matrix reconstruction and the high computational complexity in the covariance matrix reconstruction process. A robust beamforming algorithm based on the Complex Gauss–Legendre integral is proposed. The method firstly partitions the neighborhood of the interference signal and constructs the interference signal space using the complex Gauss-Legendre integral, then projects the received signal into the interference signal space to filter out the desired signal and complete the reconstruction of the interference noise covariance matrix, before finally correcting the steering vector mismatch using the improved optimal steering vector estimation method. The simulation results show that the method has good robustness and a low sidelobe in the presence of the steering vector mismatch and the presence of array perturbation. Compared with the previous works, the proposed CGL-ISV method provides a better beamforming performance.
1. Introduction
Beamforming is an important part of array signal processing and is widely used in wireless communications, microphone array signal processing, and radar [,,,]. However, in the case of array model mismatch, the algorithm performance can be greatly affected, especially when the training data contain the desired signal components, and small systematic errors can lead to severe degradation in the algorithm performance. In addition, the non-smooth variation in data due to vibration and motion of the antenna platform is also a significant cause of degradation in algorithm performance. In the presence of strong interference and platform disturbances, the beamformers’ weighting vector is insufficient to handle the non-stationary signal, resulting in a degraded algorithm performance. How to suppress strong disturbances and improve the robustness of beamforming algorithms to system errors has been a hot research topic.
Current research on algorithms to enhance the error of beamformers in the face of complex environments focused on two areas: the reconstruction of the covariance matrix and the correction of the steering vector (SV).
Techniques based on covariance matrix reconstruction fall into the following categories [,,,,]. The diagonal loading (DL)-based technique is one of the most widely used algorithms to achieve robustness by adding a scaled unit matrix to the covariance matrix. Although it is known to be effective in mitigating the effects of sample size and SV mismatch, the main drawback is the difficulty in choosing the optimal DL factor []. In order to remove the desired signal from the sample covariance matrix, a new technique based on the interference plus noise covariance matrix reconstruction method has recently been proposed []. In [], the interference plus noise covariance matrix was reconstructed using the Capon spectrum integrated with a corner sector separated from the signal of interest (SOI) direction. This beamformer achieves a good performance even in the presence of signal direction errors. This means that accurate array structure information is essential. However, they are ineffective in the presence of array calibration errors such as channel errors, antenna positioning errors and mutual coupling errors. The fundamental reason for this is that spectrum integration only takes into account directional estimation errors and ignores other potential errors.
Techniques for coping with SV mismatch fall into the following main categories. The main idea of eigenspace-based (ESB) beamforming algorithms is to estimate the signal plus interference subspace and modify the steering vector through its projection onto the subspace [,,]. The performance of ESB beamformers is limited under low signal-to-noise ratio (SNR) conditions where the signal subspace may be contaminated by the noise subspace [,]. Uncertainty-set-based techniques use the assumed spherical or ellipsoidal uncertainty set to constrain the SV and estimate the SV problem by solving for optimization []. However, when the SV mismatch is large, the range of the uncertainty set must be increased at the cost of a reduced output SNR. Khabbazibasmenj et al. proposed a robust beamforming method based on the estimation of the steering vector [], introducing the constraint of restricting the steering vector to a predefined observation sector, so that the method requires no a priori information other than the predefined observation sector. Both methods are only suitable for scenarios where only the steering vector error due to steering bias is present. When both steering bias and random error are present, the constraint does not take into account the random error in the SV, so the estimated SV deviates from the true SV and the orientation of the peak beam response deviates from the true orientation of the target.
To address the above problems, a robust beamforming algorithm based on the complex Gauss–Legendre integral is proposed in this paper. The complex Gauss–Legendre integral is introduced into the interference noise covariance matrix reconstruction. The low complexity and the high accuracy of the Gauss–Legendre integral are utilized to achieve an accurate calculation of the integral. Firstly, the neighborhood of the interference signal is partitioned, and the fifth-order Gauss–Legendre integral and the second-order Gauss–Legendre integral are selected for the neighborhoods near and far from the interference position, respectively, to obtain the interference signal subspace, which reduces part of the computation while ensuring excellent performance. The interference noise covariance matrix without the desired signal component is obtained after reconstruction by the projection of the sample covariance matrix into the interference signal space. To address performance degradation due to the mismatch problem, the steering vector is corrected using the reconstructed interference noise covariance matrix and an improved steering vector estimation method. The robustness of the algorithm to the mismatch problem is improved.
2. Data Model
Assuming a uniform line array of M elements with an array spacing of d, the data model for the received signal is as follows:
where denotes the noise signal; denotes the number of interfering signals; is the direction of arrival of the desired signal; is the direction of arrival of the interfering signal; its corresponding steering vectors are ; are the desired and interfering signals, respectively; , where represents the additive Gaussian white noise of the -th sensor.
is , the theoretical covariance matrix of the array, assuming that is a positive definite matrix, which can be expressed as follows
where is the power of the uncorrelated desired signal, interference signal and noise; denotes the conjugate transpose; is the M-dimensional unit matrix.
Linearly constrained minimum variance (LCMV) beamformers is a very classic algorithm in the field of beamforming. Its constraint condition is that there is no distortion response in the target direction and zero trap in other interference directions.
The LCMV beamformer is described as follows:
where , are the weight vectors of the array and its solution can be expressed as
In practice, the exact covariance matrix is not available, so the sampling covariance matrix is often used instead, i.e.,
where is the number of snapshots.
3. Algorithms
3.1. Interference Noise Covariance Matrix Reconstruction
Assume that the interfering signals are distributed in the neighborhood of the interference , and since the steering vectors of the signals at different angles satisfy approximate orthogonality with each other, i.e.,
the interference signal subspace can be constructed by integrating over the domain of the interference angle. The expression is
where contains all the spatial information in the interference signal region . In general, Equation (7) is calculated by means of discrete sampling.
where is the number of sampling points. As can be seen from Equation (8), the larger the number of samples, the higher the accuracy of the calculation, but the complexity of the calculation also increases.
To address the complexity problem, this paper will introduce a composite Gauss–Legendre integral to improve the efficiency of the calculation of the interference signal subspace while ensuring the accuracy of the calculation of the signal subspace. The Gauss–Legendre integral can be calculated by integrating the function in the interval [−1, 1] and using an interpolation of order for the product, as follows.
where is the weight function, generally taken as 1; is the product factor; is the product node. The product node is the zero of the Legendre polynomials; the expression is as follows:
From Equation (10), it can be seen that the accuracy of the calculation of the Gauss–Legendre integral is directly proportional to the order, but too high an order leads to an exponential increase in the amount of computation.
The interference neighborhood is divided into three regions: the region closest to the interference in the middle accounts for 20%, and the other two regions account for 40% each. The region closest to the interference take a higher-order Legendre polynomial and the two regions far from the interference take a lower-order Legendre polynomial. Because the region close to the interference contains most of the interference energy, the accuracy of the integration in this region directly affects the accuracy when solving the subspace of the interference noise signal. The neighborhood away from the interference also contains part of the energy of the interference signal. Therefore, this method can ensure the accuracy of the calculation of the interference noise signal subspace, while reducing the computational effort, which is convenient for engineering applications.
As an example of calculating an integral with a fifth-order Legendre polynomial, let in Equation (10) be solved for as 0 and . Bring into Equation (9) to obtain the following:
According to Gauss–Legendre’s principle of integration, choosing the fifth-order integral means that Equation (11) holds when takes . According to the Lagrange solution, the solution leads to .
The integration in the angular neighborhood of the interfering signal is transformed to prove that the integration can be solved for any interval with the following expression:
where . As an example, the reconstruction of the subspace of the interference signal given by Equation (13) can be realized by the Gauss–Legendre integral:
where .
For each of the interfering signals, Equation (13) is used to obtain the full interfering signal subspace. Compared with Equation (8), the construction of the interference signal subspace using the complex Gauss–Legendre integral only requires the calculation of the function values at the five product nodes, which avoids the tedious summation of discrete points and reduces the computational effort of the integral, which is beneficial to the engineering implementation. The sum of Q interference subspaces is obtained.
The eigenvalues are arranged in reverse order, i.e., . In the subspace of the preliminarily obtained interference, only the eigenvector corresponding to the large eigenvalue contains most of the interference energy. The eigenvectors corresponding to the first large eigenvalues in the subspace of the interference signal are taken to form a matrix , where the value of can be determined by the number of sources in the estimation algorithm or simulation. The value of should be chosen so that the projection matrix can best suppress the desired signal and ensure that the interference signal is not distorted.
To ensure that the matrix is a square matrix for projection calculation Let matrix , since the desired signal steering vector is orthogonal to the interference steering vector,
the data received from the array at can be projected into the interference signal subspace, filtering out most of the desired signal components.
The analysis shows that the projected data filter out most of the expected signal components and used to effectively estimate the interference covariance matrix:
A correction to Equation (18) gives the reconstructed interference noise covariance matrix as
where is the mean of the last small eigenvalues. The expression is as follows:
3.2. Steering Vector Correction
The adaptive beamformer is sensitive to model mismatch, and when there is a mismatch in the steering vector due to beam pointing bias, the adaptive beamformer may suppress the desired signal as interference, resulting in signal pair cancellation. To improve the robustness of the algorithm against steering vector mismatch errors, the optimal steering vector estimation method is used to reconstruct the expectation. An iterative search for the optimal steering vector estimation method is proposed in the literature [].
where is the error between the true and mismatched steering vectors. is a constant greater than 0 and close to 0. is added for matrix full rank, is the constraint matrix, is the constraint factor, and indicates take the norm. The constraint sets the search interval of the steering vector to the domain of , and the shape of the domain is determined by and . The method requires an accurate covariance matrix of the desired signal, and the interference components in the covariance matrix of the desired signal have a significant impact on the performance of the algorithm. Secondly, the algorithm does not impose a constraint on the error in the mismatch of the steering vector. To address the above problems, the above algorithm is improved in this paper. The original estimation of the steering vector using the expected signal covariance matrix is improved by replacing it with a reconstructed interference noise covariance matrix to avoid the interference component of the expected signal covariance matrix, affecting the performance of the algorithm. An upper bound on the error norm between the true and mismatched steering vectors is also added as a constraint, with the aim of limiting the algorithm to more accurately search for the optimum in this area.
where is the upper bound of . Equation (22) is a quadratic optimization problem and can be solved using the convex optimization toolbox.
The corrected steering vector can be obtained as
Substituting and the reconstructed into Equation (4) yields the array weight vector with the expression:
For this reason, the proposed method can be summarized as follows (Algorithm 1):
| Algorithm 1 The proposed covariance matrix reconstruction and steering vector estimation |
|
4. Simulation
In order to evaluate the performance of the proposed CGL-ISV algorithm for applications in the field of beamforming technology, several simulations have been carried out in the absence of a directional vector mismatch, as well as in the practical case with directional vector mismatch. Several evaluation indexes are defined as follows:
- Beampattern: For the far-field signal with THE Direction Of Arrival (DOA) and steering vector , the array outputs ARE . The array output is given by . According to the definition of the beampattern function, the expression of beampattern function is shown as follows:
- Output SINR: For an adaptive antenna array system, the output SINR is defined as the output signal power divided by the output interference-and-noise power. Normally, the dB is employed as the unit of the output SINR and is given bywhere is the covariance matrix of the desired signal, and is the covariance matrix of the interference-and-noise.
The experiments in this paper were performed on a Windows 64-bit operating system and the simulations were carried out via the MATLAB 2016a software. A uniform linear array with M = 16 sensors and isotropic sensors is assumed to be arranged at half wavelength, i.e., = 0.5, where the wavelength is denoted by the symbol . All signals are independent, and the noise is Gaussian white noise. In this section, SNR is set to 5 dB and the Interference and Noise Ratio (INR) is set to 30 dB. The actual signal DOA is 90° and the interference DOA is 70°, 110°. The snapshot is set to 1024, the steering vector mismatch is set to 2° and the observation angle range [0°, 180°] is sampled uniformly at different intervals. The sensor is placed on the Z-axis and the sensor position has random position perturbations in the Y and Z directions, with the perturbations being independent zero-mean Gaussian random variables. Parameters and are set to 0.1 and 0.3, respectively. For convenience, the algorithms based on the Gauss–Legendre integral and the complex Gauss–Legendre integral are denoted as GL and CGL, the algorithm based on the iterative search optimal vector estimation method is denoted as SVOA, and the algorithm based on the improved iterative search optimal vector estimation method is denoted as ISV.
4.1. The Beam Patterns
In Experiment 1, we simulated beam patterns without steering vector mismatch and the actual case with steering vector mismatch, respectively. Subsequently, the performance of the LCMV algorithm, the GL algorithm and the CGL algorithm in the beamforming domain is compared in Figure 1, where Figure 1a shows the beam pattern without steering vector mismatch and Figure 1b shows the presence of a 2° steering vector mismatch. Figure 1c shows the beam pattern for an array element position perturbation deviation of 0.02 mismatch, and Figure 1d shows the beam pattern for a position perturbation standard deviation of 0.20 mismatch.
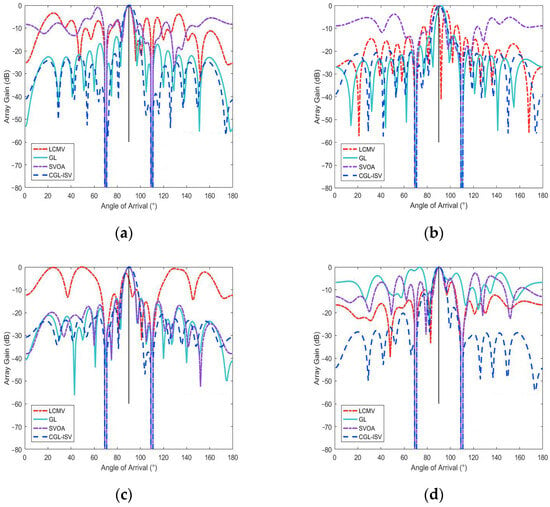
Figure 1.
Beampatterns. (a) Beampattern under non-mismatch scenario. (b) Beampattern under 5° mismatch scenario. (c) Beampattern under 0.02 position perturbation. (d) Beampattern under 0.20 position perturbation.
As shown in Figure 1, in the absence of steering vector mismatch, the four algorithms can effectively suppress the interference and maintain the distortion-free response of the desired signal. However, the LCMV method and the SVOA method have a relatively high level of sidelobe compared to the other two proposed methods. This is because both the GL and CGL-ISV exclude the influence of the desired signal component on the beamforming performance. In terms of interference rejection, CGL-ISV has the best performance. The subplots in Figure 1 show that the CGL-ISV has good interference suppression. All four algorithms can suppress interference in the steering vector mismatch. The GL has a relatively low sidelobe, but is not as good at handling the steering vector mismatch as the CGL-ISV. In the case of array perturbation, as the deviation in the position disturbance increases, the sidelobe of the beam will be distorted to varying degrees and the ability of to suppress the disturbance will also be reduced. Nevertheless, CGL-ISV still has the lowest sidelobes, accurate interference suppression and the deepest zero trap.
4.2. The Patterns of SINR with SNR
The simulation scenario of Experiment 2 is the same as that of Experiment 1, which represents the relationship between the output Signal to Interference and Noise Ratio (SINR) and the input signal-to-noise ratio. The SNR was taken to vary from −10 dB to 30 dB in 5 dB intervals and 200 Monte Carlo experiments were performed at each SINR to count the output SINR of the array, as shown in Figure 2. Observing and comparing the plots in Figure 2, we can conclude that the GL algorithm, SVOA algorithm and CGL-ISV algorithm outperform the LCMV algorithm, especially the CGL-ISV method, at higher signal-to-noise ratios. Through careful analysis, we can observe that the GL algorithm, SVOA algorithm and CGL algorithm perform quite consistently in ideal scenarios without mismatches. All three algorithms, on the other hand, remain stable in the mismatch condition because of the correction made to the steering vector. However, the GL algorithm has an advantage over the CGL-ISV algorithm in that the output SNR increases gradually, with an increasing SNR at higher-input SNRs in both the ideal case of no mismatch and the actual case of mismatch. Compared to the other algorithms, the CGL-ISV algorithm has a better performance with the highest output SINR.
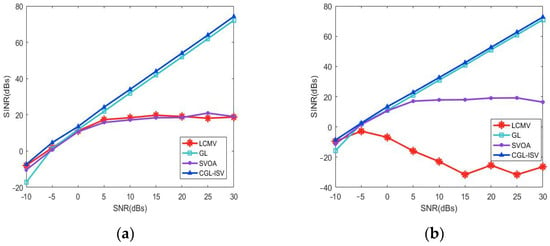
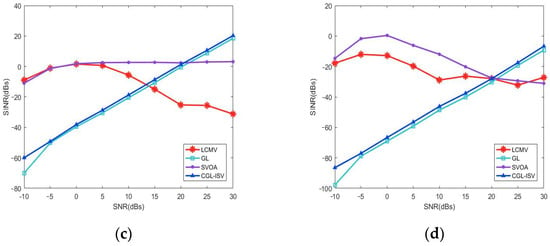
Figure 2.
Output SINR versus input SNR. (a) Output SINR versus input SNR under non-mismatch scenario. (b) Output SINR versus input SNR under 5° mismatch scenario. (c) Output SINR versus input SNR under 0.02 position perturbation. (d) Output SINR versus input SNR under 0.20 position perturbation.
4.3. The Patterns of SINR with Snapshots
The array SNIR curves in the above beamformer are given in Figure 2 for different snap counts, ranging from 24 to 1024 with an interval of 100. A total of 200 Monte Carlo experiments were performed at each snap count. The input SNR was 20 dB.
In Figure 3, when there is no array perturbation or steering vector mismatch, the output SINR of the LCMV tends to increase with the number of snapshots and the beamformer performs well. Once a mismatch occurs, the output SINR drops sharply as the number of snapshots increases, resulting in a degradation in beamformer performance. This is because when a mismatch occurs, the LCMV method treats the desired signal as an interfering signal, which is particularly noticeable at a high SNR. Even if the number of snapshots increases, the SINR does not increase. On the other hand, the CGL-ISV method has a better SINR performance than LCMV. This is because even if there is an error in the system due to the steering vector mismatch, the error can be moderated by the correction of the CGL-ISV algorithm. Thus, the CGL-ISV algorithm can improve SINR performance when there is a steering vector estimation error. However, the output SINR of the CGL-ISV-based beamforming algorithm does not change significantly with an increasing number of snapshots, both in the ideal case without mismatch and in the presence of mismatch, thus demonstrating an extremely stable performance.
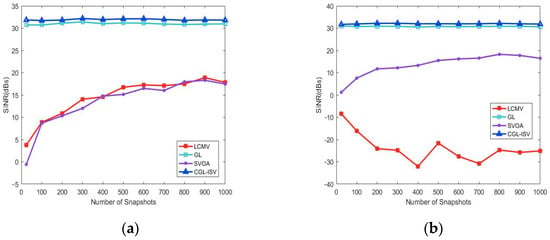
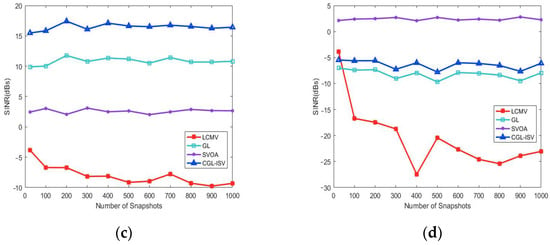
Figure 3.
Output SINR versus snapshots. (a) Output SINR versus snapshots under non-mismatch scenario. (b) Output SINR versus snapshots under 5° mismatch scenario. (c) Output SINR versus snapshots under 0.02 position perturbation. (d) Output SINR versus snapshots under 0.20 position perturbation.
4.4. The Patterns of SINR with Interferences
The purpose of the third experiment was to verify the output signal-to-noise ratio as a function of the number of interferences. The simulated scenario is the same as in experiment 3.
As can be seen in Figure 4, the performance of the LCMV and the SVOA is quite stable in the absence of mismatch, independent of the number of disturbances. In the presence of a 2° mismatch in the steering vector, the LCMV remains stable, but the output SINR is not as superior. The GL and CGL-ISV algorithms, on the other hand, perform reasonably well at low disturbance counts, with CGL-ISSV maintaining a particularly good performance at higher disturbance counts. In the presence of a 2% wavelength array perturbation, the LCMV, SVOA, and CGL-ISV maintain good performance overall, with the CGL-ISV algorithm maintaining a particularly superior performance at low interference counts. In the presence of a 0.20 perturbation, the output SINR of LCMV and SVOA algorithms increases with the increase in interference number, because the two algorithms can still maintain effective zero-trapping for interference in the presence of 0.20λ perturbation. With the increase in interference number, more interference is suppressed, increasing the strength of the received effective signal. However, GL and CGL-ISV algorithms still maintain their superior performance under low interference.
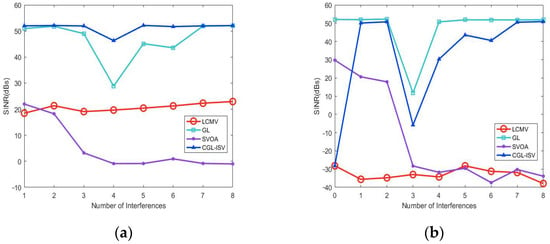
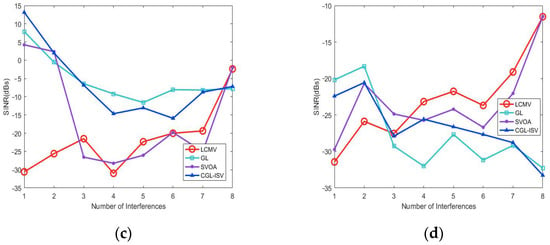
Figure 4.
Output SINR versus interference. (a) Output SINR versus interference under non-mismatch scenario. (b) Output SINR versus interference under 5° mismatch scenario. (c) Output SINR versus interference under 0.02 position perturbation. (d) Output SINR versus interference under 0.20 position perturbation.
5. Conclusions
In this paper, a beamforming algorithm based on a complex Gauss–Legendre integral is proposed. Compared with the previous results, this paper improved the robustness of the beamformers under non-ideal conditions and the maximum sidelobe level of the beams was suppressed. The simulation results show that the robust beamforming algorithm using CGL-ISV algorithm has better robustness and a lower sidelobe level than the original algorithm under the conditions of a high SNR and different snapshots.
Author Contributions
All authors have significantly contributed to the research presented in this manuscript; K.X. presented the main idea and wrote the manuscript; L.C. edited the manuscript; B.W. and Y.Z. reviewed and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Basic Research Program of Shaanxi, Program No. 2021JM-452.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saeed, M.; Osman, K. Robust adaptive beamforming for fast moving interference based on the covariance matrix reconstruction. IET Signal Process. 2019, 13, 486–493. [Google Scholar]
- Alon, A.; Miriam, D. A linearly constrained minimum variance beamformer with a pre-specified suppression level over a pre-defined broad null sector. Signal Process. 2015, 109, 165–171. [Google Scholar]
- Zhao, Y.; Li, W.X.; Mao, X.J.; Zhang, N. A beamforming null broadening method to resist array flow pattern error. J. Harbin Eng. Univ. 2018, 39, 163–168. [Google Scholar]
- Dang, J.; Zhang, Z.C.; Wu, L. Joint Beamforming for Intelligent Reflecting Surface Aided Wireless Communication Using Statistical CSI. China Commun. 2020, 17, 147–157. [Google Scholar] [CrossRef]
- Carlson, B.D. Covariance matrix estimation errors and diagonal loading in adaptive arrays. China Commun. 1988, 21, 397–401. [Google Scholar] [CrossRef]
- Elnashar, A.; Elnoubi, S.M.; El-Mikati, H.A. Further study on robust adaptive beamforming with optimum diagonal loading. IEEE Trans. Antennas Propag. 2006, 54, 3647–3658. [Google Scholar] [CrossRef]
- Du, L.; Li, J.; Stoica, P. Fully automatic computation of diagonal loading levels for robust adaptive beamforming. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 449–458. [Google Scholar] [CrossRef]
- Gu, Y.; Leshem, A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Duan, Y.; Gong, Y.; Yang, X.; Gao, W. Oblique Projection-Based Covariance Matrix Reconstruction and Steering Vector Estimation for Robust Adaptive Beamforming. Electronics 2022, 11, 3478. [Google Scholar] [CrossRef]
- Feldman, D.D. An analysis of the projection method for robust adaptive beamforming. IEEE Trans. Antennas Propag. 1996, 44, 1023–1030. [Google Scholar] [CrossRef]
- Huang, F.; Sheng, W.; Ma, X. Modified projection approach for robust adaptive array beamforming. Signal Process. 2012, 92, 1758–1763. [Google Scholar] [CrossRef]
- Jia, W.; Jin, W.; Zhou, S.; Yao, M. Robust adaptive beamforming based on a new steering vector estimation algorithm. Signal Process. 2013, 93, 2539–2542. [Google Scholar] [CrossRef]
- Li, J.; Stoicaand, P.; Wang, Z. on robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar] [CrossRef]
- Khabbazibasmenj, A.; Vorobyov, S.A.; Hassanien, A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information. IEEE Trans. Signal Process. 2012, 60, 2974–2987. [Google Scholar] [CrossRef]
- Fan, Z.; Liang, G.L.; Wang, Y.L. A zero-trap broadening robust adaptive beamforming algorithm. J. Electron. Inf. Technol. 2013, 35, 2764–2770. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).